3.A Brief Account on the Implications of Quantum Gravity
The existence of a maximal acceleration in quantum gravity has great implications for physicists venturing into the field of quantum gravity. Although it has been studied in the previous chapters we again bring it here using different methods for purposes of imposing general bounds on the acceleration, length, mass, energy and temperature. The study of maximal acceleration is wide and that is why we are going to spend a great deal of time here in analyzing the consequences of its existence. The problem is important in calculating various limiting cases for both the theory of quantum gravity (at the Planck epoch) and the theory of quantum electrodynamics. As we shall see, all the calculations undertaken in the process lead us to one thing, a consistent quantum theory of gravity.
To differ from Newton’s laws of motion and Einstein’s theory of general relativity, our acceleration will depend on the dimensionless coupling constant which determines the strength of the force in any given interaction as was described earlier
Where, c is the constant speed of light, e is the charge on an electron, α is the dimensionless coupling constant, ε is the permittivity of free space and G is the universal gravitational constant.
Various examples have been given below in which the theories of quantum gravity and quantum electrodynamics will act as limiting cases,
Maximal acceleration
For example, where the quanta exchanged between two electrons is a photon in the case of the electromagnetic force we have the electromagnetic coupling constant or the fine structure constant as,
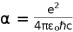
which deduces the acceleration to,

. This is the allowed maximum acceleration for quantum gravitational effects at the Planck epoch. But for the case where the quanta exchanged between two electrons is a graviton for a gravitational force, we have the gravitational coupling constant as,

which gives the acceleration on a quantum electrodynamics scale as,
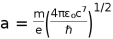
.
Minimal length
Then the minimal radius to which a gravitating body or an electron can collapse in a commoving frame can also be deduced as, If we equate Newton’s law of universal gravitation to our newly developed force as,

We obtain the area as,
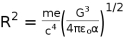
then for

, as in the first example, we obtain the minimum radius for a charged particle for quantum gravitational effects as,
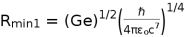
=

, or

, where

is the Planck length. Then the fine structure constant will be calculated as,

Hence solving one of the unsolved problems in physics. But for
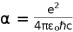
, we obtain the minimal radius due to torsion in the gravitational field as,

Minimal mass
On another note, we could derive the mass formula only if we equate the force

to our force formula

, then the mass expression is deduced as

This gives the Planck mass at
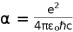
, Also the mass that incorporates all the constants of nature when

is deduced as,

=
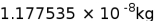
. This could be the mass of the graviton.
Energy
Then from Einstein’s proposal for the radiation of the gravitational energy, we have an expression for energy as,

, Where R is the radius of orbit of an electron around the nucleus of an atom, for

, and
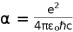
we obtain the maximum energy as,

. This is the Planck energy at the Planck epoch.
But for

and

we obtain the energy possessed by an electron of mass m in the electromagnetic field as,
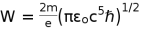
, Then at the Planck epoch when
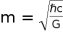
(the Planck mass), the energy required to accelerate an electron in the gravitational field will be given by,

.In the case where the energy of the quantized states of the hydrogen atom

, is equated to the energy of

, we obtain a crucial relationship between the fine structure constant and the principal quantum number n, as

. Then the smallest quantum number that will give the value of the fine structure constant will be given by, n=

. This is the lower limit for the quantum theory.
Then on the quantum gravitational scale, in which the Bohr’s quantized energy is equated to our energy

, we obtain the relationship between the principal quantum number n, the gravitational coupling constant

and the fine structure or the electromagnetic constant

as,

or

. This value implies an upper bound on the energy states for a combined theory of gravity and quantum mechanics between two protons.
Temperature
Last but not least, we could write a modified Unruh- Davis effect as,

, when it is equated to the Hawking temperature effect

, where

is the curvature of space, we obtain the curvature as,

, then for
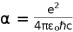
, we obtain the maximum curvature for quantum gravitational effects as,

. But when

, we obtain the curvature for quantum electrodynamics effects as,
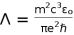
.


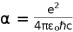 which deduces the acceleration to,
which deduces the acceleration to,  . This is the allowed maximum acceleration for quantum gravitational effects at the Planck epoch. But for the case where the quanta exchanged between two electrons is a graviton for a gravitational force, we have the gravitational coupling constant as,
. This is the allowed maximum acceleration for quantum gravitational effects at the Planck epoch. But for the case where the quanta exchanged between two electrons is a graviton for a gravitational force, we have the gravitational coupling constant as,  which gives the acceleration on a quantum electrodynamics scale as,
which gives the acceleration on a quantum electrodynamics scale as,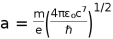 .
. We obtain the area as,
We obtain the area as,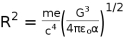 then for
then for  , as in the first example, we obtain the minimum radius for a charged particle for quantum gravitational effects as,
, as in the first example, we obtain the minimum radius for a charged particle for quantum gravitational effects as, 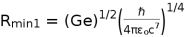 =
= , or
, or , where
, where  is the Planck length. Then the fine structure constant will be calculated as,
is the Planck length. Then the fine structure constant will be calculated as,  Hence solving one of the unsolved problems in physics. But for
Hence solving one of the unsolved problems in physics. But for 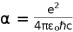 , we obtain the minimal radius due to torsion in the gravitational field as,
, we obtain the minimal radius due to torsion in the gravitational field as, 
 to our force formula
to our force formula  , then the mass expression is deduced as
, then the mass expression is deduced as  This gives the Planck mass at
This gives the Planck mass at 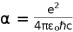 , Also the mass that incorporates all the constants of nature when
, Also the mass that incorporates all the constants of nature when is deduced as,
is deduced as,  =
=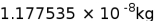 . This could be the mass of the graviton.
. This could be the mass of the graviton. , Where R is the radius of orbit of an electron around the nucleus of an atom, for
, Where R is the radius of orbit of an electron around the nucleus of an atom, for  , and
, and 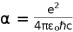 we obtain the maximum energy as,
we obtain the maximum energy as, . This is the Planck energy at the Planck epoch.
. This is the Planck energy at the Planck epoch. and
and  we obtain the energy possessed by an electron of mass m in the electromagnetic field as,
we obtain the energy possessed by an electron of mass m in the electromagnetic field as, , Then at the Planck epoch when
, Then at the Planck epoch when  (the Planck mass), the energy required to accelerate an electron in the gravitational field will be given by,
(the Planck mass), the energy required to accelerate an electron in the gravitational field will be given by, .In the case where the energy of the quantized states of the hydrogen atom
.In the case where the energy of the quantized states of the hydrogen atom  , is equated to the energy of
, is equated to the energy of  , we obtain a crucial relationship between the fine structure constant and the principal quantum number n, as
, we obtain a crucial relationship between the fine structure constant and the principal quantum number n, as . Then the smallest quantum number that will give the value of the fine structure constant will be given by, n=
. Then the smallest quantum number that will give the value of the fine structure constant will be given by, n= . This is the lower limit for the quantum theory.
. This is the lower limit for the quantum theory. , we obtain the relationship between the principal quantum number n, the gravitational coupling constant
, we obtain the relationship between the principal quantum number n, the gravitational coupling constant  and the fine structure or the electromagnetic constant
and the fine structure or the electromagnetic constant  as,
as,  or
or  . This value implies an upper bound on the energy states for a combined theory of gravity and quantum mechanics between two protons.
. This value implies an upper bound on the energy states for a combined theory of gravity and quantum mechanics between two protons. , when it is equated to the Hawking temperature effect
, when it is equated to the Hawking temperature effect  , where
, where is the curvature of space, we obtain the curvature as,
is the curvature of space, we obtain the curvature as,  , then for
, then for  , we obtain the maximum curvature for quantum gravitational effects as,
, we obtain the maximum curvature for quantum gravitational effects as,  . But when
. But when , we obtain the curvature for quantum electrodynamics effects as,
, we obtain the curvature for quantum electrodynamics effects as,  .
.