6.Hidden in plain sight2: From white dwarfs to Black Holes
A precise and consistent quantum theory of gravity has not yet been proved, not even by the self proclaimed geniuses of this time. We are aware and satisfied that classical General Relativity is the most precise description of gravity due to its predictable nature. The left hand side of Einstein field equation represents the metric of space time curvature while the right hand side represents the matter - energy content of the classical matter fields of pressure and energy density. It is known that quantum mechanics plays an important role in the behaviour of the matter fields but has no place in the Einsteins field equations.According to S.W.Hawking (1975), one therefore has a problem of defining a consistent scheme in which the space time metric is treated classically but is coupled to the matter fields which are treated quantum mechanically.
In this book we propose that, in order to estimate stellar parameters to a high degree of accuracy for both microscopic and macroscopic descriptions of white dwarfs and black holes one has to treat the right hand side of Einstein field equation quantum mechanically as,

, where
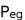
is the total pressure,
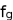
is the gravitational force,

is the electric force , G is the gravitational constant, c is the constant speed of light,
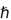
is the reduced planck constant and

is the mass of an Hydrogen atom.
Proof of the Chandrasker Mass Limit and the Lowest Principal Quantum Number from a New Approach to
Quantum Gravity
Although in the Bohr theory of an hydogen atom orbit quantization doesnot permit a lower orbit than the bohr radius of

, this section sets out to show that this is not the case with white dwarfs due to the state of a hydrogen atom under high pressure.
We know from the Chandrasker derivations that, the equation governing the hydrostatic equilbrium of a star is given by

o r
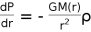
Where P denotes the total pressure,
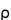
is density, and M(r) is the mass interior to a sphere of radius r.
We could however write the same equation in a different form given by

, where

(24)
The total Gravitational Binding Energy of a Star
The electric potential energy
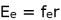
as we know it can be can be deduced from (24) and is given by,
where

is the gravitational potential binding energy given by

Using the principle of energy equipartition, we assume that the electric binding energy is of order the discrete energy of an hydrogen atom from Bohrs theory as,
where,

is the Coulomb constant, e is the charge on an electron and n is the principal quantum number.
From the above assumptions the gravitational binding energy is given as,

(25)
where

is the fine structure constant
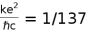
In Table 1 we list the values of

for several values of n-the principal quantum number. From this table it follows in particular, that the higher the principal quantum number, the higher the gravitational binding energy of a star.
The total gravitational binding energy of a star
|
n(Principal quantum number)
|
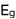 (Joules)
(Joules)
|
Remarks
|
|
0.003212
|
|
|
|
0.0345
|
|
White Dwarf
|
|
1
|
|
|
What do we conclude from the foregoing calculation? We conclude that equation (25) is at the base of the equilbrium of actual stars in relation to the energy state and binding energy of the Hydrogen atom. It differs from the Chandrasker calculation by the
introduction of a natural fine structure constant, providing the energy of proper magnitude for the measurement of stellar energies and therefore proving to be a better theory for stellar structure.This could be elaborated in detail by flowers original words,
"The Black-dwarf material is best likened to a single gigantic molecule in its lowest quantum state. On the Fermi-Dirac statistics, its high density can be achieved in one and only one way, in virtue of a correspondingly great energy content. But this energy can no more be expended in radiation than the energy of a normal atom or molecule. The only difference between Black-dwarf matter and a normal molecule is that the molecule can exist in afree state while the black dwarf matter can only so exist under high external pressure.
The Theory of White -Dwarf Stars and Black Holes; The Limiting Mass at the Lowest Principal Quantum Number
The gravitational energy is known to be of order
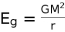
, M being the mass of a star. Then equating this to equation (25) we obtain the radius of a star as,

(26)
while the above equation states that the radius is proportional to the square of it's mass, the Chandrasker analysis is in disagreement, stating that r is inversely proportional to the cube root of the mass.
But at a point where r equation (26) approaches the schwarzichilds radius

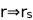 ,
,

We obtain an upper limit to the mass of,

(27)
Now consider equating the original solution of Chandrasker mass limit to our newly developed formula (27) , we have

, is a constant connected with the solution to the lane-Emden equation, and

, average molecular weight per electron,then
In the table below we list the values of M and r for several values of n-the principal quantum number, including the one calculated above.
The Mass limit and radius limit of a star
|
n(Principal quantum number)
|
M (Kilograms)
|
r (meters)
|
Remarks
|
|
|
|
34.153
|
|
|
0.0345
|
|
3944.601
|
Chandrasekar mass limit
|
|
1
|
|
|
Maximum mass of a white dwarf
|
What do we conclude from the foregoing calculation? We conclude that the formation of a white dwarf star or any other stellar structure will never exceed the Schwarzichild's radius of 34.153m, this will only happen at the most lowest quantum principal number of
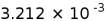
. For example, at the principal quantum number the size of the fine structure constant

, the mass obtained will be of

and r=176.443m. Therefore under high external pressure the minimum mass of a last star that is formed is of order

and this only occurs at r=34.153m under the lowest energy state below the known Bohrs radius of

.
What is Wrong With Hawking Temperature
In his paper "Particle creation by Black holes" Hawking pointed out that "In the classical theory black holes can only absorb and not emit particles. However it is shown that quantum mechanical effects cause black holes to create and emit particles as if they were hot bodies with temperature

". However this is not the case when the assumptions given in the first sections of this book are taken into account. For example, we know that, the electric potential energy is given by,
But treating the particles in the process General relativisticaly (at the Schwarzichild radius), the gravitational potential energy will be of order

, giving the electric energy as,
Now the thermal energy is given by

, where k is the Boltzmann constant.
By the principal of Equipartition

(28)
Note: in a limit where

is the planck mass
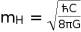
, equation 28 above for the temperature of a black hole reduces to the hawking temperature formula

For conditions at the centre of the Sun,

which is in disagreement with the Hawking temperature of

. This is left for the reader to analyse.
Entropy of a Black Hole
For derivations which i will not show here, I am led to the total
energy of a Black Hole given by,
where, A is the surface area of the event horizon
But since the entropy is energy per unit temperature,
Remember that temperature is given by equation(28),
Then the entropy will be given by,
This is in agreement with the Bekenstein-Hawking area entopy law
On the Development of a Quantum Gravity-Hydrostatic Equation and its Implication to Physics-Minimum Black hole mass
It is known that the equation governing the hydrostatic equilibrium of a star is given by,
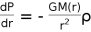
(29)
Where P denotes the total pressure,
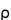
is density, and M(r) is the mass interior to a sphere of radius r.
what if we rewrite the above formula in a form given by,
 (30)
(30)
Where

is the gravitational force,
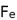
is the electric force, c is the speed of light,

is the reduced Planck constant and G is the gravitational constant. Let the pressure be,
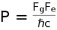
, this means that pressure is dependent on the product of the gravitational and electric forces in a quantum-relativistic realm. Therefore in simple terms, we can write (30) in its simplest form as,

and to include the density, we have
where

is schwarzichild's radius. thus at

, the star will form a black hole.
To differ from (29) we have formulated one of the first quantum gravity -hydrostatic equation. From (30) we can write the electric potential energy as,
where,
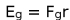
is the gravitational potential energy
at a point where the potential gravitational energy is in equilibrium with the potential electric energy the total energy is that of the Planck energy by,
since the Bohr energy of an hydrogen atom is given by,
then, using the principle of equipartition of energy
we deduce ,the gravitational potential energy as
this can be written in a simplest form as,
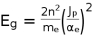
(31)
where,
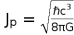
is the planck momentum 1.3035N.s

is the fine structure constant


is the mass of an electron

Then the total gravitational energy is calculated to be,
For a thermal energy kT, we estimate a temperature of
We know that, the gravitational potential energy is given by,
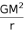
, and for
The radius mass relation can be written as,
For the solar mass

,

and if r is equal to the schwarzichilds radius

, then
The solar mass limit is given by
But for

compton wavelength then
From which mass reduces to,
This is the minimum mass of a Black hole
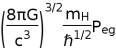
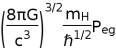
 , where
, where 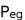 is the total pressure,
is the total pressure, 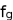 is the gravitational force,
is the gravitational force, is the electric force , G is the gravitational constant, c is the constant speed of light,
is the electric force , G is the gravitational constant, c is the constant speed of light, 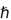 is the reduced planck constant and
is the reduced planck constant and  is the mass of an Hydrogen atom.
is the mass of an Hydrogen atom. , this section sets out to show that this is not the case with white dwarfs due to the state of a hydrogen atom under high pressure.
, this section sets out to show that this is not the case with white dwarfs due to the state of a hydrogen atom under high pressure. o r
o r 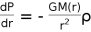
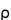 is density, and M(r) is the mass interior to a sphere of radius r.
is density, and M(r) is the mass interior to a sphere of radius r. , where
, where  (24)
(24)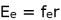 as we know it can be can be deduced from (24) and is given by,
as we know it can be can be deduced from (24) and is given by,
 is the gravitational potential binding energy given by
is the gravitational potential binding energy given by 

 is the Coulomb constant, e is the charge on an electron and n is the principal quantum number.
is the Coulomb constant, e is the charge on an electron and n is the principal quantum number. (25)
(25) is the fine structure constant
is the fine structure constant 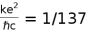
 for several values of n-the principal quantum number. From this table it follows in particular, that the higher the principal quantum number, the higher the gravitational binding energy of a star.
for several values of n-the principal quantum number. From this table it follows in particular, that the higher the principal quantum number, the higher the gravitational binding energy of a star.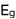 (Joules)
(Joules)



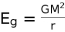 , M being the mass of a star. Then equating this to equation (25) we obtain the radius of a star as,
, M being the mass of a star. Then equating this to equation (25) we obtain the radius of a star as, (26)
(26)
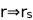 ,
,

 (27)
(27)

 , is a constant connected with the solution to the lane-Emden equation, and
, is a constant connected with the solution to the lane-Emden equation, and  , average molecular weight per electron,then
, average molecular weight per electron,then







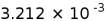 . For example, at the principal quantum number the size of the fine structure constant
. For example, at the principal quantum number the size of the fine structure constant  , the mass obtained will be of
, the mass obtained will be of  and r=176.443m. Therefore under high external pressure the minimum mass of a last star that is formed is of order
and r=176.443m. Therefore under high external pressure the minimum mass of a last star that is formed is of order  and this only occurs at r=34.153m under the lowest energy state below the known Bohrs radius of
and this only occurs at r=34.153m under the lowest energy state below the known Bohrs radius of  .
. ". However this is not the case when the assumptions given in the first sections of this book are taken into account. For example, we know that, the electric potential energy is given by,
". However this is not the case when the assumptions given in the first sections of this book are taken into account. For example, we know that, the electric potential energy is given by,
 , giving the electric energy as,
, giving the electric energy as,
 , where k is the Boltzmann constant.
, where k is the Boltzmann constant. (28)
(28)
 is the planck mass
is the planck mass 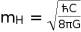 , equation 28 above for the temperature of a black hole reduces to the hawking temperature formula
, equation 28 above for the temperature of a black hole reduces to the hawking temperature formula 
 which is in disagreement with the Hawking temperature of
which is in disagreement with the Hawking temperature of  . This is left for the reader to analyse.
. This is left for the reader to analyse.


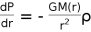 (29)
(29)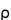 is density, and M(r) is the mass interior to a sphere of radius r.
is density, and M(r) is the mass interior to a sphere of radius r. (30)
(30)
 is the gravitational force,
is the gravitational force, 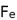 is the electric force, c is the speed of light,
is the electric force, c is the speed of light, is the reduced Planck constant and G is the gravitational constant. Let the pressure be,
is the reduced Planck constant and G is the gravitational constant. Let the pressure be, 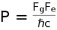 , this means that pressure is dependent on the product of the gravitational and electric forces in a quantum-relativistic realm. Therefore in simple terms, we can write (30) in its simplest form as,
, this means that pressure is dependent on the product of the gravitational and electric forces in a quantum-relativistic realm. Therefore in simple terms, we can write (30) in its simplest form as, and to include the density, we have
and to include the density, we have
 is schwarzichild's radius. thus at
is schwarzichild's radius. thus at  , the star will form a black hole.
, the star will form a black hole.
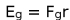 is the gravitational potential energy
is the gravitational potential energy



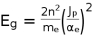 (31)
(31)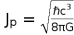 is the planck momentum 1.3035N.s
is the planck momentum 1.3035N.s is the fine structure constant
is the fine structure constant 
 is the mass of an electron
is the mass of an electron 


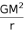 , and for
, and for 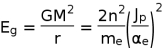


 ,
,  and if r is equal to the schwarzichilds radius
and if r is equal to the schwarzichilds radius  , then
, then

 compton wavelength then
compton wavelength then
