20.The Bekenstein Hawking Area-Entropy Law
The Unification of Quantum Mechanics and General Relativity into a Quantum theory of Gravity is one of the great scientific challenges of this generation. A definitive resolution will require solving one of the major problems of Quantum Gravity and that is, the Bekenstein-Hawking area-entropy law,

, where A is the surface area of the Schwarzschild black hole, a is the constant of the order of unity, c is a constant speed of light, k the Boltzmann constant,
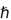
the reduced Planck constant and G is the Newton's gravitational constant.
Attempts towards this were done in the early 70s by Hawking who proved that a black hole emits thermal radiation with a temperature
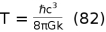
. According to Carlo Rovelli (Dec, 2003), Hawking beautiful result raises a number of questions. First, in Hawking's derivation the quantum properties of gravity are neglected. Are these going to affect the result? Second, we understand macroscopical entropy in statistical mechanical terms as an effect of the microscopical degrees of freedom. What are the microscopical degrees of freedom responsible for the entropy? Can we derive (81) from first principles? Because of the appearence of
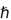
in (81), it is clear that the answer to these questions has since become standard benchmark against which a quantum theory of gravity can be tested.
This book presents a simple universal explanation of Black hole thermodynamics in a somewhat different form than that given by Loop Quantum Gravity (LQG), String theory and Hawking radiation theory. The major result of the book is the derivation of (81) from first principles using different methods for Schwarzschild and for other black holes, with a well defined calculation where no infinities
appear. As far as this book is concerned there is no other theory from which such a calculation can proceed. Hence the book is the only one from which a detailed quantum theory of gravity precedes and where the result of the Bekenstein-Hawking area entropy law can be achieved.
First Method
In this method we reduce the famous Einstein field equation (

where,the expression on the left represents the curvature of space time while the expression on the right represents the matter-energy content of the universe) to,

(83)
Where, R is the radius of a body of mass M,
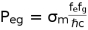
is the Pressure-Energy density relationship with the coupling of mass ( the ratio of the atomic mass, m to the Planck mass
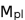
) and the electric

and gravitational force
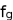
.
The ratio,

is introduced to correct for particles approaching the Planck length scale
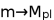
What is the total electric potential energy of a black hole? From (83), we could let the potential electric energy be,
We know that at the Schwarzichild radius
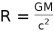
, the gravitational potential energy will be of order

, giving the electric energy from (81) as,
What is the temperature of a Black hole? Since the thermal energy is given by

, where k is the Boltzmann constant
By the principal of Equipartition
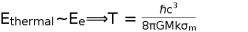
(84)
For

, we get the usual Hawking temperature of

(85)
We know that, entropy is energy divided by temperature. Having derived the temperature, What is the total energy of a Black hole?
Assuming a law which states that the intensity of the emitted radiation increases as the square of the electric force
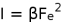
, where the constant

,
But we can also write the intensity in terms of energy as,
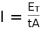
,
where t is time and A is the surface area of Schwarzschild black hole. The total energy of a Black hole will then be given as,
Let the time taken by a Black hole to evaporate be,

,
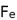
is known from (83), since from the Newtonian law of gravity
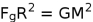
we then have the total energy of a black hole as,
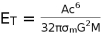
(86)
And Power is given by
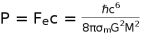
Then the entropy of a Black hole is given by
Substituting in (86) and (84) we obtain the Bekenstein-Hawking area entropy law,

(87)
Where the constant a=1/4
 , where A is the surface area of the Schwarzschild black hole, a is the constant of the order of unity, c is a constant speed of light, k the Boltzmann constant,
, where A is the surface area of the Schwarzschild black hole, a is the constant of the order of unity, c is a constant speed of light, k the Boltzmann constant, 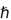 the reduced Planck constant and G is the Newton's gravitational constant.
the reduced Planck constant and G is the Newton's gravitational constant. , where A is the surface area of the Schwarzschild black hole, a is the constant of the order of unity, c is a constant speed of light, k the Boltzmann constant,
, where A is the surface area of the Schwarzschild black hole, a is the constant of the order of unity, c is a constant speed of light, k the Boltzmann constant, 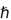 the reduced Planck constant and G is the Newton's gravitational constant.
the reduced Planck constant and G is the Newton's gravitational constant.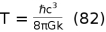 . According to Carlo Rovelli (Dec, 2003), Hawking beautiful result raises a number of questions. First, in Hawking's derivation the quantum properties of gravity are neglected. Are these going to affect the result? Second, we understand macroscopical entropy in statistical mechanical terms as an effect of the microscopical degrees of freedom. What are the microscopical degrees of freedom responsible for the entropy? Can we derive (81) from first principles? Because of the appearence of
. According to Carlo Rovelli (Dec, 2003), Hawking beautiful result raises a number of questions. First, in Hawking's derivation the quantum properties of gravity are neglected. Are these going to affect the result? Second, we understand macroscopical entropy in statistical mechanical terms as an effect of the microscopical degrees of freedom. What are the microscopical degrees of freedom responsible for the entropy? Can we derive (81) from first principles? Because of the appearence of 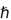 in (81), it is clear that the answer to these questions has since become standard benchmark against which a quantum theory of gravity can be tested.
in (81), it is clear that the answer to these questions has since become standard benchmark against which a quantum theory of gravity can be tested. where,the expression on the left represents the curvature of space time while the expression on the right represents the matter-energy content of the universe) to,
where,the expression on the left represents the curvature of space time while the expression on the right represents the matter-energy content of the universe) to, (83)
(83)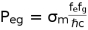 is the Pressure-Energy density relationship with the coupling of mass ( the ratio of the atomic mass, m to the Planck mass
is the Pressure-Energy density relationship with the coupling of mass ( the ratio of the atomic mass, m to the Planck mass 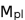 ) and the electric
) and the electric  and gravitational force
and gravitational force 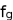 .
. is introduced to correct for particles approaching the Planck length scale
is introduced to correct for particles approaching the Planck length scale 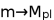
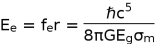
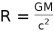 , the gravitational potential energy will be of order
, the gravitational potential energy will be of order  , giving the electric energy from (81) as,
, giving the electric energy from (81) as,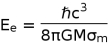
 , where k is the Boltzmann constant
, where k is the Boltzmann constant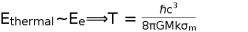 (84)
(84) , we get the usual Hawking temperature of
, we get the usual Hawking temperature of (85)
(85)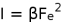 , where the constant
, where the constant  ,
,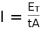 ,
where t is time and A is the surface area of Schwarzschild black hole. The total energy of a Black hole will then be given as,
,
where t is time and A is the surface area of Schwarzschild black hole. The total energy of a Black hole will then be given as,
 ,
, 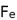 is known from (83), since from the Newtonian law of gravity
is known from (83), since from the Newtonian law of gravity 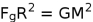 we then have the total energy of a black hole as,
we then have the total energy of a black hole as,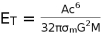 (86)
(86)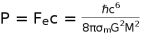
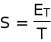
 (87)
(87)