28.Construction of a Consistent Physical Theory of Nature
A consistent theory of nature, simply the “theory of everything” is constructed using one of the profound ideas of “axioms”, that, when the Stoney units of measure are multiplied by the coupling constant (a dimensionless number) of a form
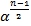
, one can easily calculate the mass of all particles in the universe and their length of time scales with accuracy provided the value of n is known. The mass of the electron is calculated at α=1/137.036 and n=21.32 while the mass of the earth is calculated at n= -29.99, hence solving one of the major unsolved problems in physics. The Planck mass is calculated and determined in principle to be 5.4556

Kg, a different value from the given value would lead to variations in our fundamental physical constants of electricity and gravity. The energy scales at given length scales in literature are also deduced in which a requirement to revisit our profound known physical theories is proposed.
One of the major unsolved problems in physics is developing a final theory, ultimate theory or theory of everything. In this paper we present a series of hypotheses and speculations leading inescapably to a conclusion that when the Stoney fundamental units of measure are multiplied by the electromagnetic coupling constant (fine structure constant) powered by any integer,

from 0,1,2,.....................,n, one gets to calculate the mass of all particles in the universe, the lengths between them and the time expressible at a scale of the known fundamental physical constants of nature. Our hypotheses may be wrong and our speculations idle, but the uniqueness and simplicity of our scheme are reasons enough that it be taken seriously.
Our starting point is the assumption that all of the fundamental
physical units of measure can be calculated and organized to demonstrate different branches and scales of physics whatsoever using the following formulas,
Length

(140)
Time

(141)
Mass

(142)
Where
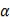
is the coupling constant for either electromagnetic or gravitational interactions, G is the universal gravitational constant, e is the elementary charge on an electron, c is the speed of light and
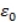
is the permittivity of free space, the meaning of n is left to be investigated as per the meaning of the theory.
case1:
We derive the fundamental units of measure at values of n=0, 1,2,3,4 and 5 only for the fine structure constant

where is the reduced Planck constant

.
At n=0
At n=1
At n=2
At n=3
At n=4
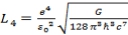
,
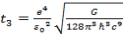
,
––––––––
At n=5

,

,
At n=0, we obtain the Planck natural units while at n=1, we obtain the Stoney units of measure
––––––––
case2:
We further derive the fundamental units of measure at values of n=0, 1, 2, only for the gravitational coupling

At n=0
At n=1
At n=2
It proves difficult to deduce the Planck units here, simply because the charge and mass do not cancel out. But if you set the ratio of charge to mass at n=0 in the above formulas as

, one obtains the Planck units. Also, one obtains the values of n=2 in Case1 when we substitute for

, in Case2, for n=2. This means that, the formulas which do not exist in case2 but are present in case1 can be calculated by applying a simple formula,
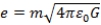
and vise versa is true.
When we substitute for

, at n=1, we obtain,
This represents formulae at a scale of general relativity, in which it is deduced here that, the mass of a particle in both the special and general relativity theory makes sense when multiplied by a constant

.
When

at n=2 above, we obtain
Where
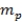
is the Planck mass

It should however be taken seriously from the above investigation that changing the number 2π in the formulas (case1, at n=0, the planck units/scales), will change the statement of the formula
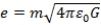
, which will mean that the values of the fundamental physical constants

,G are varying, therefore in order to maintain the constants unchanged we have to maintain the Planck units unchanged in formula as they are derived here. Thus the Planck mass will have a mass given by, 2.2176470119
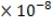

=5.4556
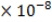
Kg.
At present there is no candidate theory of everything that includes the standard model of particle physics and general relativity. For example, no candidate theory is able to calculate the mass of an electron. However in this paper the mass of an electron is deduced when n=21.32 and α=1/137.036 as,

=

Also the proton mass is deduced at n= 18.26, and α=1/137.036 as,
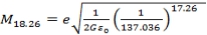
=

Other masses including the mass of the earth (n= -29.99) can be deduced in the same way. It is important to note that, the value of n is negative for massive particles (e.g mass of the Sun and earth) but positive for microscopic particles like electrons and protons.
It is hereby noted that the values of the energy scales corresponding to the given length scale are off the scale and do not necessarily represent phenomenon at each given length scale. The values of these energy scales for each interaction as quoted in scientific literature will prove to be different from the ones represented here.For example;
For atomic length scale with
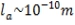
, the value of n to be used in calculating other scales will be given by n= -22.83, from which the energy scale can be calculated as,
For strong interaction length scale with

, the value of n to be used in calculating other scales will be given by n= -18.151, from which the energy scale can be calculated as,
For electroweak interaction length scale with

, the value of n to be used in calculating other scales will be given by n= -15.343, from which the energy scale can be calculated as,
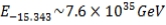
It is possible that the correct theory of everything has been found in the formulas given above. It therefore seems appropriate for the
reader or researchers to consider the calculation and determination of the values of the masses of all particles at given length/time scales in the universe with explicit accuracy, even if some people may consider such an enterprise premature or foolhardy. It is worth noting that the length and time scale through which one can probe the whole mass of the earth is

and

respectively. It is therefore important to know how one can calculate the mass of any particle with accuracy and then inquire with simplicity into the length and time scale at which such a particle can be studied. This then means that any consistent theory of nature like the one constructed would be able to deduce the required derived quantities (i.e. voltage, current, magnetic field etc) from the given formulas for fundamental physical units of measure of mass, length and time without a need to inquire into other theories like the standard model, string theory or quantum gravity.
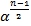 , one can easily calculate the mass of all particles in the universe and their length of time scales with accuracy provided the value of n is known. The mass of the electron is calculated at α=1/137.036 and n=21.32 while the mass of the earth is calculated at n= -29.99, hence solving one of the major unsolved problems in physics. The Planck mass is calculated and determined in principle to be 5.4556
, one can easily calculate the mass of all particles in the universe and their length of time scales with accuracy provided the value of n is known. The mass of the electron is calculated at α=1/137.036 and n=21.32 while the mass of the earth is calculated at n= -29.99, hence solving one of the major unsolved problems in physics. The Planck mass is calculated and determined in principle to be 5.4556  Kg, a different value from the given value would lead to variations in our fundamental physical constants of electricity and gravity. The energy scales at given length scales in literature are also deduced in which a requirement to revisit our profound known physical theories is proposed.
Kg, a different value from the given value would lead to variations in our fundamental physical constants of electricity and gravity. The energy scales at given length scales in literature are also deduced in which a requirement to revisit our profound known physical theories is proposed. from 0,1,2,.....................,n, one gets to calculate the mass of all particles in the universe, the lengths between them and the time expressible at a scale of the known fundamental physical constants of nature. Our hypotheses may be wrong and our speculations idle, but the uniqueness and simplicity of our scheme are reasons enough that it be taken seriously.
from 0,1,2,.....................,n, one gets to calculate the mass of all particles in the universe, the lengths between them and the time expressible at a scale of the known fundamental physical constants of nature. Our hypotheses may be wrong and our speculations idle, but the uniqueness and simplicity of our scheme are reasons enough that it be taken seriously. (140)
(140) (141)
(141) (142)
(142)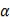 is the coupling constant for either electromagnetic or gravitational interactions, G is the universal gravitational constant, e is the elementary charge on an electron, c is the speed of light and
is the coupling constant for either electromagnetic or gravitational interactions, G is the universal gravitational constant, e is the elementary charge on an electron, c is the speed of light and 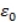 is the permittivity of free space, the meaning of n is left to be investigated as per the meaning of the theory.
is the permittivity of free space, the meaning of n is left to be investigated as per the meaning of the theory. where is the reduced Planck constant
where is the reduced Planck constant .
. ,
, 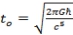 ,
, 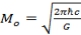
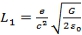 ,
, 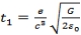 ,
, 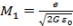
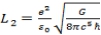 ,
,  ,
, 
 ,
,  ,
, 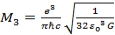
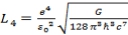 ,
, 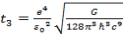 ,
,
 ,
,  ,
,

 ,
, 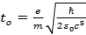 ,
, 
 ,
, 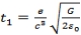 ,
, 
 ,
,  ,
, 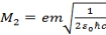
 , one obtains the Planck units. Also, one obtains the values of n=2 in Case1 when we substitute for
, one obtains the Planck units. Also, one obtains the values of n=2 in Case1 when we substitute for  , in Case2, for n=2. This means that, the formulas which do not exist in case2 but are present in case1 can be calculated by applying a simple formula,
, in Case2, for n=2. This means that, the formulas which do not exist in case2 but are present in case1 can be calculated by applying a simple formula, 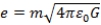 and vise versa is true.
and vise versa is true. , at n=1, we obtain,
, at n=1, we obtain,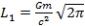 ,
, ,
, 
 .
. at n=2 above, we obtain
at n=2 above, we obtain ,
, ,
, 
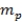 is the Planck mass
is the Planck mass 
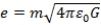 , which will mean that the values of the fundamental physical constants
, which will mean that the values of the fundamental physical constants  ,G are varying, therefore in order to maintain the constants unchanged we have to maintain the Planck units unchanged in formula as they are derived here. Thus the Planck mass will have a mass given by, 2.2176470119
,G are varying, therefore in order to maintain the constants unchanged we have to maintain the Planck units unchanged in formula as they are derived here. Thus the Planck mass will have a mass given by, 2.2176470119 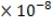
 =5.4556
=5.4556 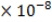 Kg.
Kg. =
=

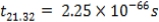
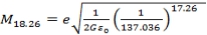 =
=
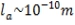 , the value of n to be used in calculating other scales will be given by n= -22.83, from which the energy scale can be calculated as,
, the value of n to be used in calculating other scales will be given by n= -22.83, from which the energy scale can be calculated as,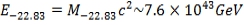
 , the value of n to be used in calculating other scales will be given by n= -18.151, from which the energy scale can be calculated as,
, the value of n to be used in calculating other scales will be given by n= -18.151, from which the energy scale can be calculated as,
 , the value of n to be used in calculating other scales will be given by n= -15.343, from which the energy scale can be calculated as,
, the value of n to be used in calculating other scales will be given by n= -15.343, from which the energy scale can be calculated as,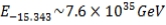
 and
and  respectively. It is therefore important to know how one can calculate the mass of any particle with accuracy and then inquire with simplicity into the length and time scale at which such a particle can be studied. This then means that any consistent theory of nature like the one constructed would be able to deduce the required derived quantities (i.e. voltage, current, magnetic field etc) from the given formulas for fundamental physical units of measure of mass, length and time without a need to inquire into other theories like the standard model, string theory or quantum gravity.
respectively. It is therefore important to know how one can calculate the mass of any particle with accuracy and then inquire with simplicity into the length and time scale at which such a particle can be studied. This then means that any consistent theory of nature like the one constructed would be able to deduce the required derived quantities (i.e. voltage, current, magnetic field etc) from the given formulas for fundamental physical units of measure of mass, length and time without a need to inquire into other theories like the standard model, string theory or quantum gravity.