CHAPTER I

FULL CIRCLE

IN THE YEAR 1604, Galileo Galilei formulated a law of falling bodies in a letter to his friend, Paolo Sarpi. “I have arrived at a proposition,” he wrote, “which is most natural and evident, and assuming it, I can demonstrate the rest; namely, that spaces traversed in natural motion are in the squared proportion of the times, and consequently the spaces traversed in equal times are as the odd numbers beginning with unity. And the principle is this, that the naturally moving body increases its velocity in the proportion that it is distant from the origin of motion.” This is a curious statement. For the first part is right, but one cannot explain how Galileo knew it, since it does not in fact follow from the principle, which is wrong. Under uniform acceleration, velocity varies directly as time, not distance, and any schoolboy learns the correct law by rote as either or both of two equations,

s = ½ gt² and s = ½ vt.

Even when he finally did get it right, Galileo could not so express it. Algebra had yet to be adapted to description of continuously developing quantities. He disposed only of the resources of ordinary language and of the geometry of Euclid and Archimedes. In 1632, after years of reflection and not a little frustration, he explained the law in Dialogue on the Two Chief Systems of the World, the great Copernican argument over which the Roman Catholic Church humiliated him; and there he repeated, “that the distances passed by the body departing from its rest are to each other in double proportion of the times in which those distances are measured.”

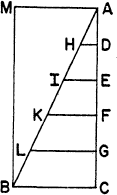
To that, Sagredo, the receptive interlocutor, now responds, “This is truly admirable; and do you say there is a mathematical demonstration for it?” And Galileo gratifies the request he has invited by expressing the relation between velocity, distance, and time as a triangle. Falling from rest at A, the body picks up speed through “infinite degrees of velocity.” The time of fall is laid off on the vertical AC. E Perpendiculars (DH, EI, etc.) represent the velocity after time AD, DE, etc., and the whole triangle is “the mass and sum of the whole velocity, with which in the time AC it passed such a certain space.” Or, to put it otherwise, the area of the triangle (½ vt) measures the distance traversed. And to find the distances travelled by a body moving at uniform velocity (BC), the triangle may be doubled into a rectangle (ACBM).

But though perfectly correct, this must still seem painful and clumsy to the modern reader. Velocity appears as one variable and time as the other, whereas it has become customary to think of velocity rather as a ratio of distance to time. Moreover, it measures the linear distance s by an area. Nor does the geometry yet derive the law in the form which relates distance to acceleration (s = ½ gt²). In 1638, Galileo published his final and scientifically his finest work, Discourses on Two New Sciences. There at last he achieved an explicit statement of both common forms of the law. The discussions of the “Third Day” work towards a renewed demonstration of the velocity-time relationship, in more elegant geometrical form than in the Dialogue, and in less elegant language. Next, Galileo proved what until now he had only asserted: the distances are as the squares of the times. This was far more difficult. He had to formulate graphically what he called “uniformly difform motion,” that is to say, a dynamical proposition involving acceleration in the essentially static forms of plane geometry.

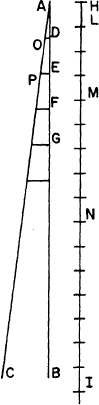
He represented the “flow of time” by simple extension, the line AB, on which AD and AE measure any two intervals. To the right, the line HI stands for the path of descent at uniform acceleration, so that HL is the distance traversed in time AD, HM in AE, etc. These things being so, then “I say that the space MH to the space HL is in the duplicate ratio that time AE has to time AD.” For, construct AC at any angle to AB. Then DO, EP, etc. will again represent maximum velocity at corresponding time. It followed from the previous (mean-speed) theorem that the spaces are equal which are traversed by one body at uniform acceleration from rest, and a second moving at a constant velocity which is one-half the maximum attained by the first. Thus, the distances of fall HL and HM would be equal to those traversed in times AD and AE at constant velocities one-half of DO and EP respectivity. But it had already been shown that the distances passed by two bodies in uniform motion are to each other as the product of the ratio of the velocities into the ratio of the times. Now, since EP is to OD as AE is to AD, then the ratio of velocities is in this case the same as the ratio of the times. “Therefore, the ratio of the spaces traversed is as the square of the ratio of the times. Q. E. D.”

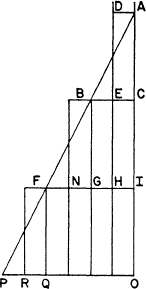
At this point, Salviati, who speaks for Galileo, stops the dialogue as if a light had dawned: “Please suspend your lecture for a moment while I speculate on a certain idea that has just now occurred to me.” And he puts the two forms of the law together. AI represents time again, AF is at any angle, and C is the mid-point of AI. Then (to condense the argument a bit), if the body falls freely to C, BC will be the maximum velocity, and the distance will be measured by the rectangle of uniform velocity erected on the base EC equal to ½ CB.

Moreover, if the body continued its descent at constant velocity BC, then in the interval CI it would cover twice the distance that it had described in time AC, starting from rest. But since the body is under uniform acceleration, its velocity during the time CI will increase by an amount FG equal to the parallel of the triangle BFG, which is equal to ABC. Then, adding to velocity GI (equal to BC) half of FG, which is the maximum velocity attained through acceleration, one gets the uniform velocity with which the same space would have been described in the time CI. And perhaps the drift is apparent without further paraphrasing. The rectangular areas which represent the space described increase in successive time intervals, “as the odd numbers beginning with unity, 1, 3, 5; … and in general, the spaces traversed are in the duplicate ratio of the times, i.e., as the squares of these times.”

These figures represent the earliest integrations applied to developing physical quantities and may be taken, therefore, to symbolize the germ from which has grown a mathematical science, not alone of proportions, but of nature. For there was nothing novel about expressing uniform motion in the abstract as a ratio of change in geometrical quantities. Galileo’s first triangle of motion was a mathematical commonplace, generally called the Merton Rule after the school of kinematic philosophy which flourished in that ancient Oxford College during the fourteenth century. Moreover, the mean speed theorem reduces to the law of acceleration, and needed rather to be stated helpfully than to be discovered. Everything, indeed, or nearly everything, that Galileo put together may be found in the writings of one or another of the late scholastics, in the aphorisms of Leonardo da Vinci, or in the works of some predecessor among the Renaissance mathematicians. But only Galileo, and he only after many a false start, developed the judgment and intuition and feel for the physical to select the elements of a physics from this olla podrida of mathematical techniques and philosophical assertions. His was the transforming touch of the mathematical physicist, the first of his kind, who would really change a situation instead of simply entering a discussion. That touch reveals itself thrice over in these passages. First, he derived the rule of uniform acceleration in a form applicable to freely-falling bodies. Then he included it in a general statement containing both the velocity-time and the acceleration-time-squared measures of path. Finally he applied it to the real case in nature and therein lay his genius.

For only Galileo would have given the discussion the turn it takes immediately after the last of these, his mathematical demonstrations. Simplicio, who upholds the Aristotelian case, bows before the force of geometry, “so that I am convinced that matters are as described, once having accepted the definition of uniformly accelerated motion. But as to whether this acceleration is that which one meets in nature in the case of falling bodies, I am still doubtful; and it seems to me, not only for my own sake, but also for all those who think as I do, that this would be the proper moment to introduce one of those experiments—and there are many of them, I understand—which illustrate in several ways the conclusions reached.” And Galileo reports on the famous experiments on inclined planes which he had imagined, and some of which he may quite probably have actually performed.

THESE WERE PORTENTOUS TRIANGLES. To the historian thinking broadly about the recent destiny and future prospects of western civilization, it may well appear that our own culture, in which whatever our temperament we are bound to live, is set off from those of Asia, Africa, and the world of antiquity by two fundamental factors. From one of these it emerged: its religious chrysalis was Christianity, investing history with the promise of fulfillment of a sort. The other it produced: the most dynamic, distinctive, and influential creation of the western mind is a progressive science of nature. Only there in the technical realm, indeed, does the favorite western idea of progress hold any demonstrable meaning. No one understands political power better than Machiavelli did. Picasso cannot conclusively be held a better or worse artist than Leonardo was. But every college freshman knows more physics than Galileo knew, whose claim is higher than any other’s to the honor of having founded modern science, and more too than Newton did, whose mind was the most powerful ever to have addressed itself to nature.

In its early days, science was distinct from technology, springing rather from thought and philosophy than from craftsmanship. Nowadays, however, and indeed for the last century and more, science has merged ever more intimately with technology, so arming it with power, so enhancing its capacities, that no words, nor any fears or dreams, may exaggerate what depends upon the employment. Nor is the future of our own world of the West alone in play through this, its great invention. Perhaps the historian may be pardoned a single prophecy, if it comes at the beginning of a book before his tale has made him pompous. Anxious though our moments are, today is not the final test of wisdom among statesmen or virtue among peoples. The hard trial will begin when the instruments of power created by the West come fully into the hands of men not of the West, formed in cultures and religions which leave them quite devoid of the western sense of some ultimate responsibility to man in history. That secular legacy of Christianity still restrains our world in some slight measure, however self-righteous it may have become on the one side, and however vestigial on the other. Men of other traditions can and do appropriate our science and technology, but not our history or values. And what will the day hold when China wields the bomb? And Egypt? Will Aurora light a rosy-fingered dawn out of the East? Or will Nemesis?

Albert Einstein once remarked that there is no difficulty in understanding why China or India did not create science. The problem is rather why Europe did, for science is a most arduous and unlikely undertaking. The answer lies in Greece. Ultimately science derives from the legacy of Greek philosophy. The Egyptians, it is true, developed surveying techniques and conducted certain surgical operations with notable finesse. The Babylonians disposed of numerical devices of great ingenuity for predicting the patterns of the planets. But no Oriental civilization graduated beyond technique or thaumaturgy to curiosity about things in general. Of all the triumphs of the speculative genius of Greece, the most unexpected, the most truly novel, was precisely its rational conception of the cosmos as an orderly whole working by laws discoverable in thought. The Greek transition from myth to knowledge was the origin of science as of philosophy. Indeed, knowledge of nature formed part of philosophy until they parted company in the scientific revolution of the seventeenth century.

In our own world, science continues to be what it was in Greece, conceptual thought mediating between consciousness and nature. But it is also something more. It has become determinate instead of simply speculative. For the scientific revolution reversed the direction in which information flows, and added body to the structure of communication. Greek science was subjective, rational, and purely intellectual. It started inside the mind whence concepts like purpose, soul, life, and organism were projected outward to explain phenomena in the familiar terms of self-knowledge. In those terms the success of an explanation depended only on its universality and capacity to satisfy the reason. Greek science scarcely knew experiment and never thought to move beyond curiosity to power. Modern science, on the other hand, is impersonal and objective. It takes its starting points outside the mind in nature and winnows observations of events which it gathers under concepts, to be expressed mathematically if possible and tested experimentally by their success in predicting new events and suggesting new concepts. Modern science has not abandoned rationality, but it is first of all metrical and experiential. Related to this is its association with technology as a continuation of that generalized thrust toward mastery of the world which began in the West with the Renaissance. Modern science, finally, seeks both to comprehend and control nature—though according to the positivist school of philosophers, whose persuasion dominates at the moment, comprehension is an illusory goal. For them prediction and control are everything.

A true revolution brings fundamental change through rebellion against constituted authority, but it is clear from the history of revolutions that to repudiate a debt is not to escape it. So it was that the creation of modern science in the Renaissance was at once a rebirth of Greek science and a bursting of its confines. To separate the new from the old in the Renaissance is always difficult, for humanists steeped in classical learning found antique words for new ideas. It is, however, no falsification of a complex situation—it is rather a first approximation toward resolving it—to say that science stirred into new life under the inspiration of Plato working against the cramping of learning within a fossilized Aristotelianism.

By Galileo’s time, the science and authority of Aristotle had led the western mind a long way to a dead end. Aristotle’s was the most capacious of philosophies. In principle it explained everything, dealing rather in reasons than structures, and preferring categories over abstractions. For example, Galileo could describe mathematically how a stone would fall under ideal conditions. He could not say why it fell. Aristotle’s physics, on the contrary, could not measure its motion. But this was not to be expected in a real world of friction and complexity where ideal conditions never occur. Aristotle could do more important things. He could explain why a stone fell, why sparks flew upward, and why the stars ran round in their courses.

Beneath its physical manifestation as translation, Aristotelian motion is metaphysical, an instance of change, an evidence of imperfection. Change is the act of things realizing their potentialities in a world striving ever to fulfill its creator’s will toward order, which is toward the good, so far as its corruption permits. In an orderly cosmos there is by definition a place for everything. Heavy things belong at the bottom. To say that the stone falls because it is of the class of things which are heavy constitutes, therefore, a full explanation. So, too, fire rises because it is light. The locus of that element is in the ethereal region, with air below it, water below that, and crude earth massed round the center. But what of an arrow? Here a distinction of motions must be introduced. Its motion is not natural but forced, not orderly but disorderly and violent. It must have a cause. Logic requires effects not to outlast their causes. Therefore, every motion against nature presupposes a moving agent, and demands explanation.

What, then, moves the arrow after it has parted from the bow-string? In a philosophy which is nothing if not universal, to have no answer would be to have no science, and after some hesitation, Aristotle meets the dynamical difficulty with the air. It is the surrounding medium closing in behind the projectile which urges it along its way. There can, therefore, be no motion in a void. There cannot even be natural motion, for in this case the medium serves to retard the body. In a vacuum a stone would fall instantaneously. Since that is absurd, nature knows no void, and the world must be a plenum, finite and by later standards rather small. But the inadmissibility of the void goes deeper than abhorrence of the vacuum. It goes all the way to the foundations. There is no such thing as place in a void, and the goal of this philosophy was to define the right and necessary place for every species of being according to the purpose that it served. Nor can there be existence in the nothing. In a void no stone could tell where to go, no flame find the way to leap. The very notion of direction or order would become meaningless. To admit the void is to accept the reign of chaos, wherein whirl is king, in lieu of our own world full of meaning.

So it is throughout Aristotle’s physics. It was a serious physics, a consistent and highly elaborated ideation of natural phenomena. It started from experience apprehended by common sense, and moved through definition, classification, and deduction to logical demonstration. Its instrument was the syllogism rather than the experiment or the equation. Its goal was to achieve a rational explanation of the world by showing how the myriad subordinate means are adapted to the larger end of order. Its operations were suited to these interests. Direct and minute observation, classification of forms by species, analysis of how the part serves the whole—these are useful acts up to a point in natural history, as the description of life and its environment was called until the nineteenth century. Not till then was biology ready to transcend the Aristotelian sense of purpose in nature and follow physics into objectivity. Aristotelian physics, too, had immense humane advantages denied to that which has supervened since Galileo. It easily fell in with a sense of Providence in nature. As the physical system sheltering the world view of Islam, Judaism, and Christianity, it became the scientific orthodoxy of all three religions which shaped the West in its emergence from the dark centuries after Rome. For Aristotelian physics made sense of the world and strengthened the hands of men of God and all those striving to redeem civilization, culture, and truth from barbarism.

There was only one trouble. It was wrong. For however congenial Aristotelian physics was to the self-knowledge of the minds that elaborated it, nature is not like that, not an enlargement of common sense arrangements, not an extension of consciousness and human purposes. She is more elusive, more coquettish perhaps and infinitely more subtle, hiding her ways from the merely dogged or the worthy, and only occasionally yielding to the truly curious those glimpses of great order and altogether inhuman beauty which are the reward of him who strikes the right note, and all the reward he seeks—that and fame. But who, asked James Clerk Maxwell two millennia later, “who will lead me into that still more hidden and dimmer region where Thought weds Fact, where the mental operation of the mathematician and the physical action of the molecules are seen in their true relation?” For the order is mathematical and the notes harmonious, Platonic rather than Aristotelian.

Not that Plato and Aristotle differed on all fundamentals. They were teacher and pupil. To both, nature appeared as the creation of artful mind, and order as the expression of rationality. Both took a humanistic rather than a naturalistic view of science. By explanation, both meant identification of what lofty purpose would reveal divine intelligence. But Aristotle addressed himself to physical and biological contrivance, and Plato to ideal being. Unlike Aristotle, Plato did not make a science. He inspired one—in Archimedes perhaps, and much later in Galileo certainly. His influence was less and more, the spell he cast over posterity at once sterilizing and stimulating: sterilizing in that he takes truth out of the world of things, stimulating in that he identifies ideal simplicity with mathematical reality. He speaks poetically to an aesthetic vision of nature, but never to common sense, which in puzzling he offends. What is truth, then, and what the good? They are the eternal and the perfect, being not becoming. The real is the ideal, and change the mirror of corruption. For Aristotle had simply transposed Plato’s metaphysics into physical terms so as to make a distinction between cosmology and physics, the one concerned with the heavenly regions beyond the moon, the other with our sublunary sphere where different laws obtain, where everything is mortal and contingent. Thus was the uniform cosmos of the earliest Greek philosophers dichotomized, and the chance missed of laying down a single science of heaven and earth. In science, Aristotelian kinematics was the most influential consequence of this distrust of change as prima facie evidence of imperfection. Only one motion is perfect in Plato, in Aristotle, and after them down to Kepler and the seventeenth century, namely circular motion, that by which the heavens go, for only in circles can motion occur as changelessness.

“God is always geometrizing,” Plato is supposed to have said. This, along with admiration for circles, Plato drew from the school of Pythagoras, in whose semi-legendary figure science retreats into a prehistoric mélange of myth, mysticism, and mathematics. In the search conducted by the pre-Socratic philosophers for the principle of unity in nature, the Pythagoreans hit upon the assertion that nature is made of number and that numbers have shape. In their eyes, the world is actually made of lines, triangles, squares, cubes, and circles, even as the nineteenth-century physicist might think it made of ninety-two varieties of material atoms. Numbers contain the form of things, at once real and ideal. In numbers lie the clean, eternal structures beneath the welter of appearance. Discovery of the irrationality of the square root of two, and of incommensurable quantities in general, is always described as having shocked this faith. But the shock helped, for it led to appreciation of geometric ratios like the Merton rule of motion, which would give Galileo his mathematical description of falling bodies. Indeed, the Pythagoreans may themselves have been the ones to make the first statement of physics as we know it. They studied stringed instruments and found the relationship between the length of a vibrating string and the pitch it emits, and thus they expressed the experience of harmony as a geometrical quantity. Nevertheless, like the influence of Plato after them, and in fact through Plato, their legacy moved down into the underworld of science, as well as out into its sane and wholesome reaches. As the misbegotten twin of a mathematical physics, they spawned the secret mania of numerology. Nostradamus was their heir as well as Galileo. Rosicrucianism is their progeny as well as relativity.

The two greatest of the Greek philosophical traditions laid ancient science under one final limitation. It was impossible in principle for either Plato or Aristotle to have made a mathematical physics because they agreed that mathematics and physics do not fit, and differed only over which was at fault. For Plato, mathematical relationships are eternal, ideal, and therefore real and true. But there is no such certainty, indeed no certainty at all, in the world of things, and physics is at best a “likely story.” For Aristotle, on the contrary, it is physics which deals with the real. Mathematics is true, to be sure, but only in the abstract. The world itself is made of qualities and forms and fine distinctions which may not be expressed in the precise, quantitative, absolutely unreal terms of mathematics. Ontologically speaking, ancient science fell between these stools. Archimedes might have retrieved it. His was a scientific intellect of the very highest order. In discernment and power, he was the peer of an Einstein. Everyone will recognize that the law of the lever, and more generally the principles of simple machines, represent just that marriage of geometry to physical objects which both Plato and Aristotle held to be impossible. Archimedes arrived at the concept of statical moment by abstracting from physical weight and combining its quantity with geometrical length in Euclidean ratios. Reciprocally, the Archimedean determination of the center of gravity of geometric figures introduced physical intuition into a mathematical problem. But Archimedes came late, the lamp was burning low, and his best pupil was Galileo, seventeen hundred years later, who set statics into motion to found our science of mechanics.

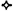
SO FAR AS PHYSICS WAS CONCERNED, the scientific revolution occurred on two levels, cosmology and dynamics. It would be complete only when Newton’s law of gravity united knowledge of heaven and earth, separate since Aristotle, into a single theoretical science of matter in motion. On both levels, the revolutionary inspiration came from Platonic criticism playing a ray of mathematical realism upon the vast mass of verbal distinctions into which Aristotelian natural philosophy had proliferated in the late Middle Ages, and from which it endlessly drew theological tidbits out of nature. Ultimately, dynamics proved the deeper level of scientific thought. But cosmology was the more dramatic.

The Renaissance inherited a complex situation in cosmology. The Aristotelian model of the universe was the well-known Chinese nest of crystalline spheres concentric about a logy, corrupt, and stationary earth. Each carried like luminous studs the moon, the sun, a planet, or the pattern of the fixed stars. Spin was communicated to the whole complex by an outermost shell. Beyond lay bliss. Borne in on every hand, by theology, poetry, literature, and philosophy, this gave the educated man his gross picture of the cosmos. It made sense of the diurnal motion of the heavens, but was no use to astronomers who had to follow and predict the visible motions of the planets along the zodiac. They advance at varying velocities, slowing at times to a pause and retreating a little before going forward once again. These inequalities are the projection onto each planet of the orbital motion of the earth. Appearances were further complicated by slight variations in latitude and by the uncertainty of all data. It is a myth that the ancients were accurate observers. Least important as a source of error was the actual ellipticity of orbits, for the amount by which they do depart from the circular was within the margin of error that this astronomy had to tolerate. The gravest irregularities, the retrograde motions of the planets, might have been saved by a heliocentric model of the solar system. The Pythagoreans are said to have believed in a central sun, and Aristarchos of Samos certainly proposed such a theory in the third century before Christ. But it was stillborn, and instead, astronomers saved the immobile earth for common sense by using in practice the purely geometric astronomy of Claudius Ptolemy.

Ptolemy compounded the apparent movements of each heavenly body from combinations of circular figures. He employed three devices, epicycle, eccentric, and equant. The epicycle places the planet on a small circle, the center of which describes a large circle called the deferent about the ultimate center of motion. The eccentric makes that center of motion in a particular case some point apart from the center of the earth. The equant is a point other than the center so taken that there is a uniform rate of increase in the angle formed by the diameter through the equant and a line joining it to a point on the circumference. Combinations of epicycles on epicycles, epicycles on eccentrics or equants, and whatnot, to the number of seventy-odd distinct constructions, gave an account of the anomalies. The geometrical virtuosity was admirable. It saved the phenomena, and the proto-positivist physics of the likely story asked nothing more. Moreover, it worked well enough to sustain the calculation of the calendar from Roman antiquity to the sixteenth century, when at last the accumulation of error exceeded the tolerable. Indeed, navigation is still practised as if the earth were at the center of the great display of celestial bearings.

Any revolution has deep roots in culture but begins with some definite act, often meant to purify corrupt practices and restore what some conservative radical imagines as a pristine state of things. In 1543 Nicolas Koppernigk, Copernicus as he latinized himself, published De revolutionibus orbium coelestium libri sex. It is an extremely difficult book. Nor have many or perhaps any modern writers, and certainly not the present one, combined in their own understandings the sympathy, the scholasticism, the latinity, the astronomy, the trigonometry, and the gothicism which would permit them to penetrate the true spirit of Copernicus’s life-work. But it does seem tolerably clear that astronomically he was just such a puritanical reactionary, at whose hand the old forms lost not only accretions but their rationale, and began giving way to new.

No scientist, in any case, has ever addressed himself to problems of greater magnitude relative to the state of knowledge. His theory rearranged the solar system and set the immobile earth to spinning daily on its axis while revolving annually about the sun, which replaced it at the center. That is a great and gross difference, and no denigrations must be allowed to obscure it, whether they refer to the conservatism of his mathematics, the obsessive circularity of his kinematics, or the monkish timidity of his life. Stock objections blocked assent for about a century, and to rehearse them will suggest how strongly his ideas had to swim upstream against the tide of common sense. Nor, in the absence of the principle of inertia and the composition of motions, is it any wonder that he tended to falter and keep his notions to himself. For on a moving earth we ought to feel ourselves rushing through the air. A stone dropped from a tower should land to the west of it. Cannonballs fired west should travel farther under the same charge than those fired east. The earth should whirl itself to pieces. We should all fly off like pebbles from a sling. “Those experiences,” wrote Galileo just ninety years later, “which overtly contradict the annual motion of the Earth, have so much more of the appearance of convincingness, that I cannot find any bounds for my admiration how reason was able in Aristarchos and Copernicus to commit such a rape upon their senses as, in despite thereof, to make herself mistress of their belief.” Even deeper, though less seriously intuitive than our feeling of immobility, was the prejudice against the unworthiness of the earth to be moving in circles through the heavens, that being a motion suited only to aethereal and immaterial bodies.

A Polish scholar, Copernicus was educated in Cracow, Bologna, and Padua. His father had died when he was a boy in Thorn, and he became the charge and protégé of an uncle, Lucas Watzelrode, an ecclesiastical statesman and a considerable figure in the Baltic world where the jurisdictions of Poland, the Church, and the military order of the Teutonic Knights mingled in late medieval confusion. Watzenrode became sovereign bishop of Ermland, an ecclesiastical principality with a narrow outlet to the Baltic at the cathedral town of Frauenburg. There Watzenrode arranged a canonry or prebend in the chapter for his nephew. For years Copernicus held his prebend as an absentee, loath like many a Pole and German before and since to return from Italy, where he went in 1496 immediately after his election. At Bologna and at Padua Copernicus was educated as a humanist in classics, medicine, geometry, and astronomy, and his intellectual world, perhaps even his spiritual world, was that of Greek and Latin antiquity. Later, he did into Latin a book of epistles on moral, pastoral, and mildly amorous subjects by one Theophylactus, an obscure Byzantine writer of the seventh century. But only in astronomy did Copernicus display the taste to select from antique learning that which would truly enter into the Renaissance movement to renew the world. And if like a good humanist he invoked in Aristarchos the license of antiquity, his originality is no more ambiguous than that of the whole culture of the Renaissance in its Janus posture. For Copernicus made heliocentricity part of science and not just speculation. With him it enters into the structure of the progressive knowledge of nature. His work added a determinate element. The whole history of science is his vindication, and criticism, therefore, must try to say what that element was.

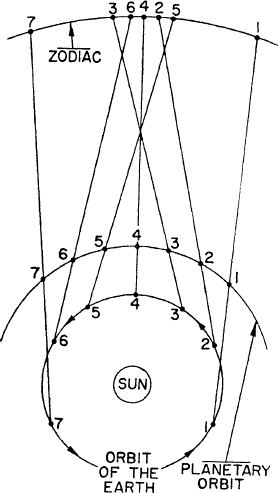
It may be illustrated in principle by an idealized diagram showing how the motion of the earth would “save” seven successive observations of one of the outer planets.

There is evidence that he experienced the simplicity and elegance of the Aristarchan idea as early as 1505 or 1506. The preface to his Revolutions says that he had kept the idea by him, not just for nine years as the Pythagoreans had enjoined, but for four times nine. It may have come to him like some conversion, just as he was about to depart for home. He had then spent his ten years in the sun, and in the open intellectual climate of Italy. If the great idea did occur in such fashion, it makes an affecting picture. He never left Poland again. There he spent the rest of his life, on that Baltic shore, living at his uncle’s residence in crabbed little Heilsburg until Watzenrode’s death in 1512, thereafter inhabiting a tower room in the crenellated wall of crabbed little Frauenburg. He would take an occasional hand in the Graustarkian governance and diplomacy of Ermland. He would peer through the mists and pore over Ptolemy and the tables of astronomy in a mood of gathering distaste. For Copernicus studied the figures, not the stars. And he worked at his system, which he intended to be more than an alternative set of geometrical hypotheses. He meant it as a real system of astronomy, to supplant the Ptolemaic devices used by astronomers, navigators, and calendars and to be, moreover, a true representation of the physical relations of sun, earth, moon, and planets.

Inevitably, the facts and figures were recalcitrant. Many were quite wrong. The execution of the work could not bear out the grand simplicity of its leading idea. That he stuck to that idea in the teeth of all the difficulties, daunted but not defeated by discrepancies, might be taken, perhaps, as a testimonial to the rationalizing role of theory in science, and to the virtue of a faith in some ultimate reason in things. It is no wonder that on completion of the work in 1532 or thereabouts, he hesitated to publish, and alluded now and again to legendary Pythagorean injunctions to secrecy. But he had not refrained from all communication. Quite early, probably in 1512, he circulated a sketch of his theory in manuscript. The Commentariolus it is called. News of his ideas spread in the gossipy world of Renaissance scholarship, widely enough for Luther to pass his famous remark about some fool who “went against Holy Writ.” Then in 1539 there arrived in Frauenburg one Georg Joachim Rheticus (as he called himself after his birthplace, though his real name was von Lauchen), a young professor of mathematics from Wittenberg, powerfully attracted to the rumors of heliocentricity, and all eagerness to learn what substance they might hold. Copernicus admitted him to scientific intimacy. Together they reviewed the data. Rheticus published the first authorized account, the Narratio Prima, at Dantzig in 1540.

Its success, or perhaps the urgings of Rheticus and other friends, persuaded Copernicus to commit his full treatise to the press. It is divided into six books. Book I contains a general description of the system of the world: the sun and not the earth is the center; what appears as the daily rotation of all the heavens is the effect of the earth’s spinning on its axis; the annual motion of the sun is the appearance of the actual revolution of the earth annually; the advances and retrogressions of the planets are projections of the same cause combined with their own motions; the distance from the sun to the earth or planets is very small compared to the remoteness of the fixed stars. Book II contains a star catalogue compiled from ancient and more recent astronomy, from which Copernicus computed the elements of the year. The remaining four books contain detailed mathematical theories, which is to say geometric devices and trigonometrical methods, for predicting the motions of the planets referred to the earth and to the sun, together with the real motions of the earth and moon. Printing was completed in Nuremberg in 1543, under the supervision of Andreas Osiander, a friend of Rheticus and a Lutheran theologian. He took the precaution, or the liberty, of adding a disarming preface to the effect that the author claimed for his system only mathematical convenience, not truth. This was incorrect. Copernicus was a mathematical realist in the Pythagorean tradition according to which figure and number contain the structure of things. But he never read the preface which said that his book was not true, nor the book itself, for he had been stricken by cerebral haemorrhage and lay on his deathbed when the first printed copy reached Frauenburg.

The Copernican Revolutions is a great work of science. Like all great works, it has had to survive a certain tradition of belittling scholarship, which in this case seems to imply that there was no real reason to prefer the heliocentric to the geocentric model, the two being geometrically interchangeable. Nor is the merit of Copernicus very evident when it is made to rest on simplicity in computation and economy in celestial motions. What with his reliance upon Ptolemaic data, his humanist’s deference for antique learning, and his own belief in circularity as the heavenly pattern, Copernicus saved nothing significant in motions out of the long years during which he struggled through thickets of computation. He had the misfortune, indeed, to complicate his problem unnecessarily by adding to the rotation and revolution of the earth a third motion, a top-like wobble, whereby the equinoxes precess (which did require some account) and the north pole points to Polaris on both sides of the orbit (which did not). Nor will the superiority of Copernicus appear in a game of counting epicycles between Ptolemy’s astronomy and his, the low score winning.

Copernicus, indeed, cannot satisfy such critics, for his criterion of elegance was different. It was not by eliminating epicycles that he thought to simplify and rationalize the procedures of astronomy: rather, it was by discerning the structure in things which befits the foundation of order. That foundation was the circle, the perfect figure. And it is the principle of circularity rather than of economy which conveys the inwardness of his vision of the world. Facts are pesky. Copernicus would subdue them by the epicycle. He would arrange them by the eccentric. And he did have to place the center of the orbit of the earth at a geometric point outside the sun in open space. But what had mortally insulted him in Ptolemaic astronomy was the equant. This saves the appearance of variable velocity by differentiating between uniform and circular motion. Copernicus thought it a cheat. In order to eliminate the equant, he added eccentrics and epicycles, and thus he lost to circularity motions that he had gained by sending the earth around the sun.

The superiority of the Copernican system, therefore, was conceptual rather than actual. Its vindication lay in the future when the data would be perfected, not in the past whence came its inspiration. Kepler might conceivably have proved that the sun goes around the earth in an ellipse. In a sense it does. But he could not have proved that Mars goes around the earth in an ellipse, because it does not. Moreover, there were important empirical respects in which the Copernican system actually was the simpler. With all the complications in detail, it exhibited one grand regularity which the Ptolemaic did not. The periods of revolution of the planets followed the same order as their distance from the center—the greater the radius, the longer the year. Given the complications of both systems, the effective radius was no simple line, of course, and the comparison might be made somewhat differently. In the Copernican system the angles subtended at the outer planets by the orbit of the earth exactly equalled the Ptolemaic angle subtended at the earth by the respective epicycles. Thus, in the Copernican system the relative contribution of the epicycle to the theory of each planet diminishes with the distance from the sun, while that of the deferent increases. As for the inner planets, it was a suspicious feature of the Ptolemaic construction that their deferents both equal that of the sun. Further, the Copernican order explained much more naturally why the sun and moon never appear to reverse their direction along the zodiac. And finally, it was far more reasonable—as Copernicus insisted—to think of the earth spinning daily, than to imagine what velocity such a rotation would impose upon the fixed stars.

These solid reasons will seem more persuasive in retrospect than will the Copernican aesthetic. Copernicus had steeped himself in the Pythagorean cult, Christianized in neo-Platonism. The sun itself had been the object of Pythagorean worship. In the tradition of Christian mysticism, illumination became the light of truth permeating the soul. And for Copernicus no arrangement was thinkable but that the sun, the lamp of the world, should occupy its center:

In the middle of all sits the Sun on his throne. In this loveliest of temples, could we place the luminary in any more appropriate place so that he may light the whole simultaneously. Rightly is he called the Lamp, the Mind, the Ruler of the Universe: Hermes Trismegistus entitles him the God Visible. Sophocles’ Electra names him the All-seeing. Thus does the Sun sit as upon a royal dais ruling his children the planets which circle about him.

But there is something meretricious about all this by the sixteenth century, or so it seems, and it is fortunate for the reputation of Copernicus that it does not have to rest upon his attainments in literature or philosophy.

Thus far our concern is with geometric conservatism tempered by a touch of sun-worshipping superstition. What, then, was determinate? What was there in the celestial gyroscopics of Copernicus to speak with such authority to the physical intuition of a Kepler or a Galileo? And ultimately it was just that, the physical element in his imagination, all wrong though it was, which seems to mark Copernicus out from the antique, whence he took data and techniques, and to lead forward into science. For his theory associated real physical events with a mathematical formalism. He needed something to make the earth turn, the earth and the celestial orbs, which he thought to be actual structures. He never looked beyond geometry, and based his kinematics as well as his computations upon circles. “Rotation is natural to a sphere,” he boldly wrote, “and by that very act is its shape expressed.” Put a globe in space, it will spin. This may not help much in the interpretation of nature, but it is the key to the interpretation of Copernicus. There was, moreover, one very important respect in which Copernican astronomy did enter into the development of physics, even if only critically. It was subversive of Aristotelian order. In a Copernican universe no physics could survive which depended on a central earth as the locus of the heavy. Not that many persons saw the point, or could yet relate celestial motions to terrestrial physics. But for cosmology too, the implications went beyond the choice of geometrical systems. Where does the world begin or end, if the earth is not the center? How deep are the stars set into space, if they are not pinpricks on the dome of the cosmos? Copernicus never said. One objection to his theory was that the stars show no annual parallax to the unaided eye. He met it by moving them out in hypothesis to where a parallax would be unobservable. And though the imagination could scarcely fail to travel on to an infinity of space and worlds (and created beings?), he wisely left that alarming prospect for more adventurous philosophers to discuss, one of whom, Giordano Bruno, burned for his temerity in the first year of the new century.

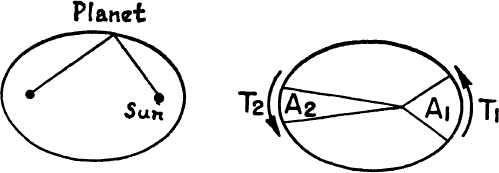
COPERNICUS FOUND his worthiest readers in Johannes Kepler and in Galileo. “I have confessed to the truth of the Copernican view,” wrote Kepler, “and contemplate its harmonies with incredible ravishment.” In Kepler science wore for a time the guise of music. His quality has been compared to Mozart’s. There is that same sweet sense of proportion, that same ear for the felicity of exact quantity. The laws which bear his name were only the three most enduring chords in the mathematical rhapsody over nature that occupied all his life. By the first, the planets revolve in ellipses about the sun at one focus. The second defines the quantity which does grow uniformly while velocity varies: the radial vector between sun and planet sweeps out equal areas in equal times. Kepler had these to publish in Astronomia Nova in 1609. The third he found only in time for his last book, De harmonice mundi—Harmony of the World—in 1619: the squares of the periods of the planets are proportional to the cubes of their mean distances from the sun.

Until Kepler, circularity had been the basis of cosmic order, things eternally rounding back on themselves. What, then, must have been the combination of imagination, devotion to fact, and faith in a deeper order, which nerved him to break the habit that had governed astronomy since its creation, to stretch the solar system into its true shape, and to put it on a mathematical footing more abstract than the perfection of the circle. His was one of the great elastic feats of the human mind, comparable in its novelty only to the enunciation of relativity, which also altered the fundamental shape science finds in nature. No scientist has ever taken his reader so utterly into his confidence as Kepler did. Were it not for his rare innocence, it would be embarrassing. He tells everything—his personal feelings, the humiliations of a horrible childhood, the indignities of his health, the defects of his wife, the follies of his own aggressions. If anyone has ever been objective about himself, Kepler was that man. Too myopic to observe the stars, he had to calculate upon them. Nor does he conceal anything of his science, his inspirations and his guesses, his false starts and disappointments, his stupidities and mistakes, his final and beautiful triumphs. He poured himself onto the page in a torrent of scientific consciousness, in a wealth of imagery and symbolic possibility flashing along on a great dark tide of trigonometric drudgery. He was a quite extraordinary person, and if (as has been said) he lifted the spell of circles, he casts his own spell over all who study him. “There is hardly a page in Kepler’s writings—some twenty solid volumes in folio—that is not alive and kicking,” observes Arthur Koestler, who has experienced that enchantment, and whose interesting book, The Sleepwalkers (of which the same is true), is its expression.

Kepler combined extravagance in emotion with meticulous devotion to fact, and unlike Copernicus, he had the facts. Or rather he obtained them, after the failure of a first book. He had studied theology and amused himself with cosmology at Tübingen, a Lutheran University. His own leanings were Calvinist, toward a God of predictable quantity, perhaps. He took a post as Provincial Mathematicus and teacher of astronomy at the Catholic University of Gratz in Styria. There he began teaching in 1594, at the age of twenty-three. Two years later he published an idea about the organization of the universe which came to him at the blackboard. The notion was that the five perfectly symmetrical solids of geometry concentric with the sun form the mathematical skeleton of the solar system. The orbit of Mercury is inscribed in an octahedron, which is circumscribed by the orbit of Venus, which is inscribed in an icosahedron, which is circumscribed by the orbit of Earth, and so on through the dodecahedron, tetrahedron, and cube, in and around which fit the remaining orbits. Kepler’s World Mystery is a vision of the organization of a Copernican cosmos in depth, and a further syncretism of Christianity and Pythagorean religiosity. It is also wrong. It does not fit. But though he soon recognized its failure in detail, Kepler never doubted that thus to seek the harmonic and geometric proportions of reality was to know God, “whom in the contemplation of the universe, I can grasp, as it were with my very hands.” And in 1600 he met the man who had the figures which he thought would fit his model to the facts. This was Tycho Brahe, just then taking up residence as Imperial Mathematicus to the half-mad Rudolf II in the Hapsburg capital at Prague.

Tycho was one of those admirable and indispensable laborers in the vineyard whose mission it is to observe or experiment upon nature with all the accuracy that ingenuity can command, but to whom the higher quality of theoretical insight is denied. In 1572 a magnificent nova startled all Europe and demonstrated change in heaven. But Tycho would not be persuaded of the Copernican system. At most he would concede a compromise, by which moon, sun, and sphere of fixed stars go around the earth, while the five planets go around the sun. This saved both the immobility of the earth and the most serious astronomical evidence for Copernicanism—the relationship of the period and radius of deferent to distance from the sun. Tycho was a Danish aristocrat, a rogue nobleman who had abandoned the violent preoccupations of his class for astronomy, though without attaining serenity. His King granted him the island of Hveen. There he constructed a fine observatory, Uraniborg, over which he ruled in feudal splendor for twenty years. Along the walls he had great quadrants constructed, one on a radius of fourteen feet. They brought the art of celestial observation to the highest accuracy of which the human eye was capable unaided by the telescope. The best of Tycho’s data were reliable down to one minute of arc, a tenfold improvement over what had gone before. Moreover, the usual practice of astronomy discontented Tycho. Astronomers would take observations at the nodes and syzygies, and interpolate the orbits between these points. He or his assistants, on the contrary, followed the planets nightly for over two decades, and pricked their observations on a great brass-sheathed globe which became their record.

He took his records with him when he quarreled with the King of Denmark and transferred his allegiance to the Emperor in Prague. There Kepler joined him, in retreat before a wave of Catholic suspicion of Protestants in Styria. Their relations of patron and supplicant were compounded in difficulty by those of waning monarch and heir apparent. For Tycho knew that there was in Kepler a theoretical power of the highest order, and sought to bind him to use the treasury of observations to establish the Tychonic theory. But he died in 1601, leaving Kepler to appropriate the data from his legal heirs and to succeed him as Imperial Mathematicus, a post which often went unpaid what with the habitual arrears in which the Hapsburg chancellery conducted its affairs.

Even before Tycho’s death, Kepler had been at work upon the theory of Mars, the most intractable of the planets because of its greater eccentricity, and also (fortunately) that for which the information was the fullest, since it is the nearest beyond the earth and is not lost in the sun like Venus and Mercury as a morning or an evening star. Kepler assumed two conditions, by virtue of which he started his thinking at one remove beyond the Copernican and toward the Newtonian. The first was geometrical—that the planes of the earth’s orbit and of Mars’ intersect in the center of the sun. The second was a related assumption, but physical and therefore more significant, since otherwise this could have been only a reversion to motion by the equant. When the Astronomia Nova finally appeared, its subtitle would be Physica Coelestis—Physics of the Heavens. From the beginning, Kepler’s embryonic feel for the mechanical led him to invest the sun with the power that causes motion in the planets. His object was celestial dynamics and not just a kinematics, his goal a force law and not just a law of motion. To the power in the sun he opposed in equilibrium another in each planet, the equal and unending contest between the two determining its orbit. (Kepler was a combative thinker, and saw his long pursuit of the true law as a personal contest between himself and Mars; or perhaps one should say a sportsmanlike thinker, since the game was conducted like chess, at a high pitch of tension but without acrimony.) It was reasonable to suppose that the power in the sun diminished with distance, and that an inverse proportion would govern the relation of the planet’s velocity to its distance from the source of power.

And now emerges one of the tantalizing coincidences with which Kepler’s intellectual career abounds. Among his physical discoveries was the optical law that the intensity of illumination on a surface diminishes as the square of the distance from the source of light. (This, like the law of gravity itself, derives rather from solid geometry than from the nature of light, and may be taken as an indication of how fruitful was the supposition that the world is really made on geometrical forms.) And since Kepler’s sun radiates power as well as light, science seems to tremble here on the brink of the Newtonian cosmology. But then one realizes that it could not take the plunge. Kepler’s anima motrix in the sun weakens at a linear rate with distance. Moreover, it is not a radial force. It is a tangential drag, suggested to Kepler’s mind by the analogy with magnetism. Kepler had been profoundly impressed by De magnete which William Gilbert published in 1600. Gilbert treated of loadstones and compass needles and beyond them of the suggestion that the earth itself is a great magnet aligning all little magnets by affinities. So thought Kepler on his grander scale of the cosmos, where affinities run between bodies related by their intrinsic natures. Such are the sun and the planets, and such the moving spirit which emanates from the sun and sweeps the planets along their appointed rounds. And in the absence of the principle of inertia, therefore, the vis motrix will appear less as an anticipation of gravitational force, requiring chiefly to be redirected at right angles, than as an expression of the ancient Aristotelian instinct that motion presupposes a mover.

Nevertheless, this was a physics, and it gave body to Tycho’s numbers. For years Kepler wrestled with those figures, striving to surprise in them the secret of Mars. He had already tacitly decided that the geometric and physical description of the orbit must be one, and that he had to do with an actual curve through space and not (like Ptolemy or Copernicus) with epicyclic combinations by which he might calculate. The figures for Mars in opposition to the sun gave him his point of departure. Using them, he must find the direction relative to the fixed stars of the line of apsides, the eccentric location thereon of the sun, and the radius. No rigorous solution was possible. It was a geometer’s nightmare, to be dealt with by main force of approximation and trial—and error, too. Kepler spares his reader none of the hopes or disappointments. “If thou”—he tells whoever is still with him—“art wearied with this tiresome method of computation, have pity on me, who had to go through it seventy times at least, with an immense expenditure of time; nor will it astound thee that the fifth year has almost passed since I encountered Mars….” Then when at last he thought he had the values right, he verified the orbit—and found disagreements amounting to eight minutes of arc between certain observed positions and those predicted by his theory.

That was a very small amount. Before Tycho it would have been undetectable. And nothing so testifies to Kepler’s conscience as his sacrificing six years of work to eight minutes of arc. For this tiny failure was not to be taken as an instance of the tiresome intractability of nature, to be fudged over in order to finish the job, but as an opportunity to learn something new. “If God has sent us an observer like Tycho,” wrote Kepler, “it is in order that we should make use of him.” Those eight minutes turned out, indeed, to be the fault which broke the circle. And their relation to the discovery of Kepler’s laws illustrates that often it is not the big problems which refine the scientific understanding, but the minuscule discrepancies: not the logical structure of Aristotelian natural philosophy, but the deep, small problem of what makes the arrow fly; not some gross breach of Newtonian physics into which Einstein stepped, but the almost undetectable absence of the aether drag. And Kepler now began to think that perhaps the orbit might be some figure other than a circle.

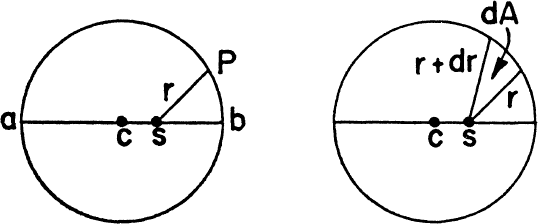
Pursuing that possibility, he found his so-called second law (of equal areas in equal times) before the first law (of elliptical orbits). He had, indeed, been using it as a calculating device before enouncing it as a governing principle, and the purported derivation is a comedy of errors with a happy ending rewarding virtue in the truth. He hesitated for a time, thinking that his difficulty might lie in this method of computing. He had in fact reason to doubt it, for the assumption that the velocity varies inversely as distance from the eccentric sun holds true only for the ends of the apsidal diameter, where the sun-planet vector and the tangent are perpendicular. Moreover, when he did decide to commit his fortunes to the equal area theorem, he committed a yet more fearful solecism in demonstrating it. The time, he said, to traverse an infinitesimal arc will be proportional to the distance from the sun. The sum of these distances, therefore, measures the area swept out in the orbit, and any particular segment of the area will be measured by the time the sun-planet vector requires to traverse it—hence, equal areas in equal times. And this reasoning is absolutely false, of course. It is if he were to have said, dr ~ dA, and therefore Σ r = A. Kepler must certainly have known better. But he also knew that the result was right, and that the two errors cancel; and he pressed on, having left Mars to itself for a bit while investigating more closely the motion of the earth. For it was in relation to the latter, considered from a fixed point in the orbit of Mars, that Kepler stated the law of equal areas.

The data encouraged him in his abandonment of tradition, for they seemed to give an oviform curve falling symmetrically inside the circle along two sides. But what curve? At first he supposed it to be the profile of an egg, with the sun nearer the pointed end. He had yet to think of a figure around two geometrical foci and one center of force. Nor will it do to follow step by step as he tacked and turned, using the right answer before he knew he had it. Investigating the geometrical properties of his ovoid was a lamentable task, to which conic sections gave no access, and he was driven to use the ellipse as a manageable approximation to the “true” curve. Thus, he came upon another of his coincidences. The maximum width of the crescent which would have filled the ovoid to a semicircle on one side was .00429 times the radius. Quite independently of this measurement, Kepler determined that the maximum angle formed at Mars between the sun and the center of the orbit is 5° 18’. He was living with all these numbers, and it struck him that the secant of that angle is 1.00429. This could not be chance. What he did not know—tantalizing is too feeble a word this time—is that this relation is one of the conditions defining an ellipse, and that he had made an arithmetical mistake in the testing. Thus, he was driven off onto a theory of librations—a kind of breathing of the orbit in and out—whereby the resultant motion is compounded of the orbital revolution and a radial oscillation by the diameter, only to find, after going back to the egg, then returning in desperation to the ellipse, which he now constructed geometrically with the sun in one focus, that this was the identical figure at which he had already arrived trigonometrically months and months before. For it must be remembered that all this was done without analytical geometry, and without regular tables of logarithms.

It is too much, one feels on reading Kepler; no one should have had to go through this. And it was worse than it seems. For Kepler’s laws could not be to him what they are to science, expressions reducible to a unified system of dynamics. Lacking analytical geometry, they did not follow one out of the other. For Kepler himself they were simply snatches of melody in search of a symphony. They held but little of the fulfillment which had deluded him for the moment in his youthful vision of the five perfect solids. He had still to perceive the geometric structure of the cosmos in depth. His ellipses were a sorry substitute for circles, after all—a “cartful of dung,” he called them, in a fit of disgust at their irrationality, before he had found anything to relate the two-dimensional shape of the orbits to the structure of the solar system in depth. Meanwhile, the news came of Galileo’s telescope and the moons of Jupiter. Rudolf was deposed, for whom Kepler had cast horoscopes—but only when they would do no harm. He believed that his own life had been affected by the configurations of the planets at his conception and at his birth, but hesitated to lend himself to a statesman’s retreat from reality into astrology. He obtained a post as provincial mathematician in Linz, the dullest of Austrian cities. And there he set himself to composition of De harmonice mundi, the last of his great books, of which the writing was interrupted by the necessity to defend his horrible old mother, who had been indicted as a witch, perhaps with some reason.

The harmonies of which he treated are ideal geometric proportions according to which God had created all the manifestations of being. Just so the octave, the fifth, and the fourth which we perceive as harmonies are given by invariable ratios between the lengths of instrumental strings. In geometry itself there are concords (the regular polygons and solids) and discords (irregular shapes which cannot be constructed by rule, like the seven-sided figure). Plane geometry deals with symbols of the two-dimensional material world. The sphere stands in its three-dimensional perfection for the Holy Trinity. The plane section of the sphere contains the dual aspect of man—body and spirit.

Thus, in cosmology Kepler was bound to search for a reason in things deeper (in every sense) than his ellipses. Where is the harmony in the world? He tried the parts in every way, like a blind man with a jigsaw puzzle. Do the planetary periods follow a harmonic series, investing the third dimension of time with meaning? But he could find no regularity in that progression. Perhaps the sizes or volumes of the planets hold the secret? There was no evidence. Perhaps some ratio hides in the variation of solar distance as between the successive planets? Nothing there. Perhaps in the relation between greatest and least speeds? Or between mean speeds? Now he felt a little closer. He moved in imagination to the sun, and examined the least and greatest values of the angular velocities of each of the planets. And now (he saw) his faith was founded. For Saturn the ratio is 4:5, the major third; for Jupiter it is the minor third; for Mars, the fifth: thus in the music of the spheres, played to the mind’s ear, Saturn and Jupiter take the bass part, Mars the tenor, Earth and Venus the alto, and Mercury the soprano.

Such was the route by which Kepler came upon his third law, which at last established the connection he had ever been seeking between a planet’s motion and its distance, between the operation and the structure of the solar system. It was a very unexpected correlation, that the squares of any two periods are to each other as the cubes of the mean distances. Nor could it have then been found but by repeated trials. Indeed, Kepler’s reader will himself experience a certain difficulty in finding it among the fantasies and ecstasies of this last book. But it is not, perhaps, quite true to say that Kepler himself saw no more in it than in his Pythagorean flights of musical geometry. The preface to the chapter which reveals this relationship contains his famous and often quoted Te Deum:

Eighteen months ago the first dawn rose for me, three months ago the bright day, and a few days ago the full sun of a most wonderful vision; now nothing can keep me back. I let myself go in divine rage. I defy the mortals with scorn in this, an open confession. I have stolen the golden vessels of the Egyptians to make out of them a holy tabernacle for my God, far from the frontiers of Egypt. If you pardon me, I will be delighted; if you are angry with me, I shall bear it. Behold the die is cast, I am writing a book for my contemporaries or—it does not matter—for posterity. It may be that my book will await its readers for a hundred years. Has not God Himself waited six thousand years for someone to contemplate His work with understanding?

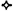
NEITHER COPERNICUS NOR KEPLER ever broke with the medieval or the baroque in their mathematicism. Their cosmos was built according to a geometrical structure, as a cathedral may be which is embellished with gargoyles and figures of saints. But the Platonic forms were hung about with these Gothic excrescences of the North, nor was it always easy to tell whether the rich animistic symbolism pertained to the decoration or the fabric.

In Galileo there is no such doubt. His Platonism was in the Archimedean rather than the Pythagorean tradition, and his thought and work brought to bear on nature the clean, clear light of Italian classicism. The Latin genius speaks out in Galileo. His is the passionate objectivity of Machiavelli, which says that wishes do not signify—this is how the world works. He stripped from the skeleton of the cosmos the obscuring layers of sentience and pious moral and edifying lesson, and left as object of the search the hard, straight bones of Euclidean dimension, Platonism bleached bare, sterilized of its mystical nonsense in the Tuscan sun. A loftier humanism replaces anthropomorphic sentimentality in Galileo’s natural philosophy. In the Dialogue Sagredo retorts on the common prejudice which attributes it “to natural bodies as a great honour and perfection that they are impassible, immutable, inalterable, etc: as, conversely, I hear it esteemed a great imperfection to be alterable, generable, mutable, etc:”

“The more I delve into the consideration of the vanity of popular discourses, the more empty and simple I find them. What greater folly can be imagined than to call gems, silver, and gold noble and earth and dirt base? For do not these persons consider that, if there were as great a scarcity of earth as there is of jewels and precious metals, there would be no king who would not gladly give a heap of diamonds and rubies and many ingots of gold to purchase only so much earth as would suffice to plant a jessamine in a little pot or to set a tangerine in it, that he might see it sprout, grow up, and bring forth goodly leaves, fragrant flowers, and delicate fruit? It is scarcity and plenty that make things esteemed and despised by the vulgar, who will say that here is a most beautiful diamond, for it resembles a clear water, and yet would not part with it for ten tons of water. These men who so extol incorruptibility, inalterability, etc., speak thus, I believe, out of the great desire they have to live long and for fear of death, not considering that, if men had been immortal, they would not have had to come into the world. These people deserve to meet with a Medusa’s head that would transform them into statues of diamond and jade, that so they might become more perfect than they are.”

And it epitomizes Galileo’s lifelong position that it should have been he who distinguished between primary and secondary qualities in bodies. The primary he defined as properties essential to metrical description—length, width, weight, figure. The secondary—color, taste, odor, texture—are those which are modes of perception in us, rather than real essences permeating matter. The difference is that between object and subject.

Galileo Galilei was born in Pisa in 1564, the son of a Florentine musician. He studied mathematics and natural philosophy and discovered, so it was said, the isochronism of the pendulum when he was nineteen by considering the swing of the great lamp in the nave of the cathedral. In 1592 he moved to Padua. His lectern may still be seen preserved in that university, where Vesalius and Galileo lectured, and Copernicus and Harvey studied, and which has a juster claim than any other to recognition as the nursery of modern science.

There was little novelty in addressing oneself to the failure of the Aristotelian theory of motion. Galileo’s kinematics derived from the Merton tradition and his dynamics from a related fourteenth century school, that of Jean Buridan and the University of Paris. They were dissatisfied with the absurdity of an explanation which would sustain the flight of heavy cannon balls by virtue of the air pressure in their wake. This made the air at once resistant and propellant. And instead they proposed as the cause of motion an impetus impressed upon the missile. The conception wears something of the aspect of momentum. Impetus varied proportionately to velocity and the amount of prime matter. Nevertheless, though a great step forward, the theory proved incapable of objectifying motion. Impetus remained an indwelling quality consumed in the process that it caused. Nor did it work a conceptual separation between motion and the missile.

What was original, therefore was Galileo’s ultimate conception of motion, not his criticism of Aristotle. Indeed, so original was it that it may be taken as one of those exceedingly rare events, a true mutation in ideas, a break with the past. It altered man’s consciousness of a real world outside himself in nature. This new world is to be grasped rather by measurement than by sympathy. In it an Archimedean science is possible, not just of statics contemplating things at rest, but of dynamics studying to know things in motion. One may say with some confidence what was revolutionary in Galileo’s law of falling bodies: It was that he treated time as an abstract parameter of a purely physical event. This enabled him to do what no Greek had done, to quantify motion in number. Galileo spent twenty years wrestling with the problem before he got free of man’s natural biological instinct for time as that in which he lives and grows old. Time eluded science until Galileo. The dimensionality of space is evident at a much lower level of abstraction. Again and again, Galileo himself tried to find a general expression for the velocity of a body in relation to the distance it had fallen. And always he failed.

Ultimately he expressed velocity in relation to the time of fall, and he succeeded. But how difficult this idea was! The magnitude of the conception is hidden from us by its very success. Thanks to Galileo, we are all bound to be physicists to some extent, in virtue of what seems like simple consciousness. It is ever the lot of scientific innovation thus to disappear into the drabness of common sense, and we need an effort of imagination to move back into the scholastic definition of motion. The necessity may itself be taken as a measure of Galileo’s achievement. History is easier than discovery, after all. To return to Aristotle is to move into a world of human association and (in scholasticism) of religious comforts. This demands only patience and tact, whereas to look forward out of the Renaissance into Galileo’s world was to stand alone peering into a nature deprived of sympathy and all humane association. That required both courage and power of abstract thought, which, one of the greatest of gifts, goes against the grain in all but the rarest temperaments. For sentiment rebels against the condition that nature sets the natural philosopher. This is that science communicate in the language of mathematics, the measure of quantity, in which no terms exist for good or bad, kind or cruel, and that she abandon our language of will and purpose and hope—abandon or denature or impoverish it, turning force, for example, from personal power into mass-times-acceleration.

It must prove very interesting to the historian of science that a leading man of letters of our own time should write upon his subject. Arthur Koestler’s The Sleepwalkers has already been mentioned. In no other book do Copernicus and Kepler come to life as there. Moreover, the author has given himself more trouble to master the texts than many professional scholars have done who have written of the scientific revolution. Nor is it meant as denigration of a distinguished piece of work if one historian of science alludes to the interpretation as an instance of the offense that science does give to the literary intelligence. It is an instance over which the scientist and the educator would do well to pause. They might ponder it amidst all the wishful slogans about some ultimate unity in science and the humanities. For Kepler is the hero of the story precisely in the degree that his was a “sleepwalking” genius—unconscious, irrational, and gestalt-like. His was a divine madness, his an expression of Pythagorean myth emergent from the collective subconscious of man the eternal artist, man one with nature: “One of the points that I have laboured in this book” writes Koestler, “is the unitary source of the mystical and scientific modes of experience; and the disastrous results of their separation.” Inside minds like Kepler’s, “We find no abrupt break with the past, but a gradual transformation of the symbols of their cosmic experience—from anima motrix into vis motrix, moving spirit into moving force, mythological imagery into mathematical hieroglyphica—a transformation which never was, and one hopes, never will be entirely completed.”

For Koestler, Galileo is the villain because he sought to force that transformation, and to make that break: “He was utterly devoid of any mystical, contemplative leanings, in which the bitter passions could from time to time be resolved; he was unable to transcend himself and find refuge, as Kepler did in his darkest hours, in the cosmic mystery. He did not stand astride the watershed; Galileo is wholly and frighteningly modern.” He would reduce all nature to his primary qualities of size, figure, number, and motion, and classify everything else as subjective and secondary. Thus began the “Fatal Estrangement” between science and ethics, which has left us in a world in which we have no place. There we drift toward a state of nihilism where ignorant technicians clash by night. For scientists have absolved themselves of moral responsibility and eschewed understanding in favor of measurement. It is in Galileo that we are for the first time asked to abstract our judgment of achievement from our judgment of character. Thus Koestler—nor does the point depend upon his hostile estimate of Galileo’s character.

Now then, one may react differently to Galileo, rather in admiration at his daring than in revulsion from the cruel edge of objectivity. One may feel that it is precisely the interest and the merit of Galileo that he does put it up to us to accommodate ourselves to reality, instead of indulging the primitive illusion that there is a refuge in nature or in myth or in collectivity. Nevertheless, the historian will feel confirmed by this response of a more sensitive temperament in his own instinct that the intellectual history of modern science does begin with Galileo, and with the transformation he wrought in the conception of motion. Things in motion, after all, are what science studies.

In any case, we are all brought up in that idea of motion as a relative and persistent state of bodies which is implicit in Galileo and explicit in Newton. Taking it for granted in our early education, we never learn to see how contrary it is to experience, wherein motion always does wear out, nor how very abstract the idea is. It is abstract. Galilean motion has no existence apart from bodies moving in relation to each other, but has no effect upon those bodies. It is no longer a process. It is a pure relation to be described by a mathematical expression. The world of experience never displays this ideal relationship. But though the actual event always falls short, nevertheless the ideal or the mathematical is the way to grasp it. We are to think about the perfect fit and not about the wrinkles in the garment. No longer is local motion a special, temporal case of the metaphysics of change. No longer is it one kind of development by which things realize the ends their natures prescribe, as the boy grows into the man and the man strives to lead the good life. No longer is it the manifold expression of a cosmic tension toward order and the good. There is no meaning henceforth in motion, but only quantity: the abstract quantity, velocity, which has one component in time and one in distance. Nor are these dimensions what we reach through and live through. They are lines in Euclid.

Had Galileo restricted himself to mechanics, he would never have given that offense which raised him up to become one of the great tragic figures in the history of human creativity. But he was no mere technician, no bloodless mathematician. He was a humanist, a man of charm and taste and literary grace. He had the full gift of civilization. Wine, he used to say in the nicest of definitions, was light held together by moisture—“Il Vino era Luce impastata con humore.” He was far more than a physicist. He was a natural philosopher who saw beyond the crucial little problem of falling bodies, about which it is difficult to feel strongly, to the great vision of a universe and a science in which the real is described by the ideal, the concrete by the abstract, matter by mind. “The book of nature is written in mathematical characters,” he declared in Il Saggiatore. And there lies the heart of the issue between natural philosophy as understood by Galileo, and scholastic philosophy as understood by educated Christendom in general, and by Robert Cardinal Bellarmine in particular, whose mind was behind the acts of the Roman Curia. Bellarmine was a Jesuit, a soldierly statesman of his Church. He produced the catechism it still enjoins. In its opinion he was a saint. He was, at all events, a tenacious statesman, bringing continuity to papal policy in successive reigns and accepting the responsibility for seeing the Church and civilization itself safely through the philosophical confusions and civil disorders created by the Reformation and its aftermath of conflict.

Copernicanism became involved in those confusions through no fault of Bellarmine’s. For him, the attitude to be adopted towards this new cosmology was a matter of policy, not truth. He already had the truth, which it was his mission to defend, and it did not lie in the mathematical description of nature. It lay in the whole structure of Catholic thought, to which geometry was quite irrelevant. Nor could the professors and the guardians of scholastic thinking allow it any relevance. Good Aristotelians, their real world was contingent, compounded of qualities and meanings and fine distinctions and physical objects not to be understood mathematically. In the heavens everything is perfect, and physics does not treat of perfection. Rome had felt no hostility towards the heliocentric hypothesis during Copernicus’s lifetime, nor in the decades since his death. On the contrary, in 1536 Cardinal Schoenberg, an intimate of the papal court, wrote Copernicus urging him to publish, for the honor of their compatriots and the benefit of the learned world.

Nor did Galileo anticipate theological opposition when he turned on his own account to Copernicus. It was the philosophers, the professors, and the pedants of Padua whom he was bound to provoke and among whom he must walk warily. From his earliest maturity, Galileo’s instinct for theoretical elegance told him that Copernicus was right. But he could scarcely think to establish a physical picture which could not be proved by a mathematical philosophy of nature which few believed. Then in 1610 there came to hand the telescope. This was something which anyone could understand grosso modo, and in which everyone would be interested. The big facts leaped to view. The moon was no celestial jewel, but a pitted mass of dead rocks. Out beyond, there circled around Jupiter its satellites, the “Medici planets” as Galileo cannily wished to call his finds, a miniature Copernican system for all to see.

It took Galileo time to learn that some would decline to look. “What shall we make of this,” he wrote to Kepler—il signor Gleppero as he appears in one document—when certain scholastic philosophers did refuse to peer through the telescope, “shall we laugh or shall we cry?” For worldly affairs are only to be mastered in their ordinariness and complexity, and Galileo had a quality of scornful innocence about them, a kind of self-righteousness, which is characteristic of minds capable of great sophistication when addressed to nature, where elegance and simplicity are goals of thought. His difficulties with the Church did not arise from any innate hostility of religion to science or any opposition between truth and knowledge. They were the consequence of that failure which in some degree is bound to afflict communication between the man of science and the man of the world. How could Galileo imagine that men would not wish to be told how the world is made, just because to learn might be disturbing? How could the ecclesiastics in Rome, responsible for faith, morals, and the order of civilization, understand Galileo’s passion for overturning the settled structure of natural philosophy against both common sense and orthodoxy? They were utterly ignorant of mathematical reasoning, the cardinals and monks, nor could they possibly appreciate the force it carries.

The drama between science and the church, therefore, unfolds with that inevitability which is tragic because it arises from the characters of men rather than the necessities in things. In 1610 Galileo returned from Padua to Florence at the invitation of the Grand Duke. There his views were soon denounced from the pulpit by two monks, self-appointed guardians of morality of the type which makes no distinction between originality and infidelity. Echoes came back from Rome. Galileo took alarm, not for himself, but lest the authorities, through inability to judge what science held for the future, should require Catholics to choose between faith and reason.

To Rome he went, therefore, to educate the authorities. Like many who need education, they did not know it and resented the implication. “He is passionately involved in this opinion,” wrote back the Florentine ambassador in anxiety to the Grand Duke, “as if it were his own business, and he does not see and sense what it might involve; here the monks are all powerful, and they do not like him; so that the climate of Rome is getting very dangerous for him, and especially in this century; for the present Pope, who abhors the liberal arts and his kind of mind, cannot stand all these novelties and subtleties,” And the only reward of Galileo’s effort was an injunction in 1616 from the Congregation of the Index declaring the Copernican doctrine erroneous. It was not to be “held or defended,” though it might still be used confidentially as a mathematical device.

Then in 1623 the old Pope died, to be succeeded by Maffeo Barberini as Urban VIII, and Galileo took heart. For the new Pope had the reputation of a humanist. And now Galileo proposed to write a book, “full of geometry, astronomy, and philosophy,” not ostensibly to prove the Copernican hypothesis, but in the Platonic form of Dialogue on the Two Chief Systems of the World. The discussion was to remain hypothetical. It is doubtful that he really meant to deceive the Pope. But his wit and knowledge were too much for his prudence. Simplicio, the Aristotelian, is overwhelmed and made to accept defeat after defeat protesting, with a kind of humiliated affability, that he remains convinced of his point of view, though he cannot make it prevail. The deportment of Salviati, the Platonist-Copernican, wears that air of divine malice which is what gives offense in a superior understanding where it is likely to appear as arrogance. There was simplicity in Galileo, as there is in science, but no humility. The attempts of Sagredo to hold the balance are as patently unconvincing as the disclaimer of the preface where Galileo says “I have personated the Copernican in this discourse, proceeding upon an hypothesis purely mathematical.”

Indeed, the reader is left to feel that only a fool could reject the Copernican universe or fail to perceive the elegance of the mathematical structure of being. This was certainly not what the Pope had authorized, since he did fail to perceive it, and it is not surprising that Galileo should have been summoned to Rome in 1633 and forced by all the fearful authority of the Inquisition to abjure in the name of Catholic truth his belief that the earth moves. There are those who would have had him choose the part of martyr. They forget that he was a Catholic, loyal to his church when its servants erred. And another element obscures the inevitability of a conflict between science and religion and removes this most embarrassing episode in the intellectual history of Rome from the realm of truth to that of politics. Galileo’s condemnation turned on his failure to obey an injunction not to discuss the Copernican system. Such a document was introduced into evidence, to which he was refused access. But he could not have disobeyed it. He had never seen it. For it seems to have been a forgery slipped into the file by certain priests among his enemies.

Galileo’s abjuration degraded all concerned, reducing scientist and churchman to the least common denominator of politician. But what was intellectually a larger retribution awaited Galileo’s Dialogue. For the triumph over Aristotelianism of that great book is literary rather than scientific. In his anxiety to establish a mathematical science uniting heaven and earth in a single physics, Galileo pressed eagerly forward over difficulties. Had he instead stopped to resolve them, he would not have had a unified cosmos with which to replace Aristotle’s. But he would have followed the logic of his own law of falling bodies, and classical physics might bear his name instead of Newton’s.

Motion is again the problem, the silver cord of all who could not make the break with Greece. Though Galileo took motion as natural and made it persist, thus opening the way to conservation and force laws, he failed, nevertheless, to formulate the principle of inertia, the first of Newton’s laws and the cornerstone of classical dynamics. This was because when forced to choose between cosmic order and the absolute mathematicization of nature, he too chose order. For the function of science in Greece was to explain the universe in a single rationale, and not simply to generalize some limited set of phenomena. A universe which can be explained, a cosmos which we can fit, must be finite, and even Galileo never quite confronted the prospect of infinity. Consequently natural motion for Galileo, inertial motion, is that motion which neither rises nor falls, which is equi-distant from the center of the earth. It is, therefore, circular motion. No longer the center of the cosmos, the earth remains the center of motion.

Galileo had what he needed to break the circle. His own law of falling bodies contained the parabolic trajectory of projectiles. But in the third day of the Dialogue he failed to draw the deduction and made a body falling from rest follow a semi-circle to the center of a rotating and hypothetically permeable earth. He had what he needed. Kepler sent him the Astronomia Nova containing the law of elliptical orbits. And the physical force holding a planet in an elliptical orbit is mathematically identical with the force that makes earthbound projectiles follow a parabola. Both curves are conic sections. But he paid no attention. He wished to make Copernicus, not chaos, prevail. With rectilinear inertia but without gravity, things will fly off in straight lines to infinity. Had Galileo abandoned circularity, had he thought on Kepler’s work which he admired but found no time for, he might have made inertia rectilinear. He might have united heaven and earth by the force of gravity. But he did not: for physical proof of the rotation of the earth, he adduces the tides, sliding around in the basins of the sea like broth in a wobbling cup.

Indeed, he knew he did not have motion right in the Dialogue. And a final achievement awaited this extraordinary man. Neither his humiliation by the Holy Office, nor his inner sense of having overreached himself in his magnum opus, led him to abandon science or accept senility. Confined by order of the Pope to his house above Florence in Arcetri, with failing eyesight and in faltering health, he wrote the truly scientific Discourses on Two New Sciences. One of these is what we call strength of materials. That he should present statics in such guise is an indication of how he had solidified Archimedean abstractions in physics proper. The other is “local motion.” And now he does treat it geometrically as if it persists along the tangent, without betraying undue guilt at the implication that its departure from the circumference is undetectable and insignificant at ordinary distances. (This is the same approximation which Archimedes makes in considering the radially directed force of a weight at the extremity of a lever as perpendicular to the beam.) No great cosmic or philosophical questions intrude into this unimpassioned treatise. The same names conduct the discussion. But it is about as controversial and stirring as some freshman lecture on mechanics, of which, indeed, it is the ultimate source.

The crowning irony of Galileo’s career is that the failure of the great Dialogue should be so much more interesting than the success of the unobjectionable Discourses. And even here he foreshadows the dilemma with which history confronts us when it considers science as a creation of the human spirit. For Koestler is right in a sense. The success of science does stand in an inverse relation to its appeal. And one must differ from his judgment, not in denying the inhumane character of science once created, but in rejecting the implication that the dilemma may be escaped by lamenting science, or softening it, or changing what it says about nature. That way lies the romantic sentimentality of Slavic and Teutonic culture. That way lies surrender of the measure of independence which science by its determinate toughness has won for scholarship and thought. That way lies, finally, the unforgivable vulgarity which resents what surpasses the common understanding, and which ends in the darkness at noon foretold by Galileo in an autograph note written in the margin of his own copy of the Dialogue:

In the matter of introducing novelties. And who can doubt that it will lead to the worst disorders when minds created free by God are compelled to submit slavishly to an outside will? When we are told to deny our senses and subject them to the whim of others? When people devoid of whatsoever competence are made judges over experts and are granted authority to treat them as they please? These are the novelties which are apt to bring about the ruin of commonwealths and the subversion of the state.