CHAPTER X

FIELD PHYSICS

YET, AFTER ALL, the history of physics holds less heat than light. Nor could a relation go unsuspected by anyone who had ever reflected on the implication of a burning lens for the interaction of radiation and matter. In 1800 the King’s Astronomer, Sir William Herschel, published in Philosophical Transactions a series of “Experiments on the solar, and on the terrestrial rays that occasion heat.” He showed (what was not entirely novel) that heat is radiant; that “the prismatic colours, if they are not themselves the heat-making rays, are at least accompanied by such as have a power of occasioning heat”; that these are subject to laws of reflection and refraction; that heat rays are of differing refrangibility, the strongest associated with the red; and finally, that rays of heat inhabit a portion of the unseen spectrum “beyond the confines of the red.” A few years later J. W. Ritter darkened silver chloride with ultraviolet light. Thus, the Newtonian spectrum found itself bracketed by invisible radiation.

The movement of criticism which now began to study light, not as a stream of luminous corpuscles but as the effect of vibration in a continuous medium, could hardly have failed to carry over into heat. That criticism directed attention rather to the properties of the medium than to the nature of light. And physics had dismissed the “emission” theory of light before the caloric theory of heat began to go the same way—toward its destiny in energetics. The analogy, indeed, seems to have been what suggested to Carnot those rising doubts about the substantiality of caloric which he confided to his notebook after publishing The Motive Power of Heat:

Light is nowadays regarded as the result of vibratory motion in an aethereal fluid. Light produces heat, or at least it accompanies radiant heat and travels at the same velocity. It would be ridiculous to suppose that it is an emission from bodies, while the light that attends it is only motion.

It is time, therefore, to turn back and take up the thread of optics.

The nineteenth-century wave theory of light is a classic case of independent discovery, and of the hurts which that recurrent coincidence inflicts on the discoverers. “When one thinks one has made a discovery,” wrote Augustin Fresnel in 1816 to Thomas Young, who had published the same interference phenomena in 1802 and 1804, “one does not learn without regret that one has been anticipated; and I shall admit to you frankly, Monsieur, that regret was my sentiment when M. Arago made me see that there were only a few really new observations in the Memoir which I had presented to the Institute. But if anything could console me for not having the advantage of priority, it would be to have encountered a scientist who has enriched physics with so great a number of important discoveries. At the same time, that experience has contributed not a little to increasing my confidence in the theory which I had adopted.” Perhaps, however, the relationship of Young and Fresnel should be described as one of independent rediscovery, and thereby as an illustration of the influence that style and cultural tradition do have in science. For Young regarded himself as one who was renewing the undulatory aspects of Newton’s own optical views. He sought to recommend his theory by associating it with Newton’s authority. At the same time, he would deliver the master from the hands of the epigones of analytical mechanics and restore the full Newtonian science of light with its original sophistication enhanced by new empirical detail. Fresnel, on the other hand, though his theory differed from Young’s only in superior mathematical expression, thought himself to be applying a principle from Huygens to “a system of undulations, where light is nothing but the vibrations of a universal fluid agitated by the rapid movements of the particles of luminous bodies”—applying it, that is to say, to a model of space-matter drawn from Cartesian physics.

In the realm of intellectual habit, national styles do certainly persist. It is hardly too much to say that at the outset of the nineteenth century, aether was an English medium, and caloric a French one; and it is a curious byplay of the history of ideas that Young began by assimilating caloric to aether, or heat to light, and Fresnel the contrary (curious but unimportant, since it came to the same thing, and in recounting his actual experiments, Fresnel tended toward employing aether, the traditional luminiferous medium). Young’s method in his first memoir consisted in reprinting long passages from Newton’s optical writings in order to bring out their consistency with undulatory views. His first and fundamental hypothesis: “A luminiferous ether pervades the Universe, rare and elastic in a high degree,” is elaborated from the query in which Newton asks: “Is not the heat conveyed through the vacuum by the vibration of a much subtiler medium than air? And is not this medium the same with that medium by which light is refracted and reflected, and by whose vibration light communicates heat to bodies, and is put into fits of easy reflection, and easy transmission?”

Fresnel for his part, true to the provincial universalism of French learning, never knew English and could never read Newton’s Optics except in the translation by Marat, who was hardly equipped to give entry into the fullness of Newton’s meaning. For Fresnel the Newtonian theory of light consisted only in the emission of particles, which were in light what atoms were in matter. He began his first memoir by saying that Newton had been obliged to imagine them streaming through space unobstructed by the caloric that fills it. Fresnel refutes this view (which Newton had never held, of course) in pointing out that black bodies under illumination would increase indefinitely in temperature since they absorb all the light that falls on them and convert it into caloric. Similarly, if refraction in (say) glass were explicable by the greater attraction exerted by molecules of glass over corpuscles of light, then a refracting surface should not only bend light but draw heat and thus be warmer than the adjacent air. Finally, Fresnel thought it implausible that particles responsible for the various colors should travel each species at its own velocity. “Periodic variations in the affections of light are much better conceived as produced by vibrations of caloric.” Heat itself, suggested Fresnel at the end of his earliest memoir, may more probably manifest vibration in caloric than the emission of a substance. That the latter view prevailed he attributed, acutely enough, to the importance of chemical interests in the study of heat. But in explosions heat and light appear at once; it is reasonable to think that both manifest vibration in caloric; and however that may be, “the continual vibration of caloric and of the particles of bodies cannot be doubted: the force and nature of these vibrations ought to have a great influence on all the phenomena embraced by physics and chemistry, and it seems to me that up till now the study of these two sciences has been overly abstracted one from the other.”

So different, then, were the standpoints—one ostensibly Newtonian, the other counter-Newtonian—from which Fresnel and Young reached the same conclusion. The arguments, too, display the strength and weaknesses of the French and English minds in science: the one systematic, rigorous, theoretical, and formal; the other ingenious, inventive, concrete, and physical; the one too elegant to dare the brusquer innovations, the other too deficient in taste to feel the force of elegance. For Young could never understand that Fresnel’s analytical elaboration of wave mechanics improved upon the ideas that he had struck out, nor that it was Fresnel’s mathematical demonstration and formalization which wrought the conversion to the wave theory of light.

“I am sincerely delighted,” he wrote to Arago,

with the success which has attended Mr. Fresnel’s efforts, as I beg you will tell him; and I think some of his proofs and illustrations very distinctly stated; but I cannot fully adopt your expression in the letter you wrote by Mr. Dupin, that his memoir may be “considéré comme la démonstration de la doctrine des interférences”; for neither I nor any of those few who were acquainted with what I had written can find a single new fact in it of the least importance….

An element of injustice, therefore, attends the equal eminence which history has accorded to their pedestals in refusing to distinguish between their claims. Certainly the priorities were Young’s. But it was the work of Fresnel which commanded assent, nor would he have missed any essential element if Young had never been there first.

BECAUSE YOUNG WAS THERE FIRST, the historian will begin with him. Nor must one seem to denigrate the brilliance and ingenuity of this, perhaps the most various scholar to emerge from the traditions enjoined by English Dissent, and from the disabilities which it enjoyed a little. Young came from a Quaker family of mercers and bankers in Somerset. As a young man he rebelled against the Friends to become outwardly an Anglican. The Quaker way never deserted him, however, plain but of the best sort. When on his deathbed, he continued working on a dictionary of Egyptian languages, using a pencil after he could no longer handle a pen. To a friend who remonstrated he answered that the work would be a satisfaction if he finished it, and if he did not, it would still be a satisfaction never to have spent an idle day in his life. Young intended himself for the profession of medicine and practiced for a time. But these qualities of rigidity and austerity, this high sense of self-reliance, made for prickly comfort. He failed on the personal and sympathetic side of medicine. His real interest was natural philosophy, and his patients felt it. In 1801 he succeeded Humphry Davy as Professor at Rumford’s Royal Institution. Afterwards he gathered his Lectures on Natural Philosophy into a vast compendium, which remains the most valuable single source for the whole state of physics in the first decade of the nineteenth century. But neither were his qualities suited to ingratiating the subject with fashionable ladies or unfashionable working men, and he did not teach for long.

Few could ever have met the standards he set himself. He was manually skilled and knew how to grind lenses and turn a lathe. He had a great bent for grammar, learned Greek, Latin, Hebrew, Chaldee, Syriac, and Samaritan, and read the classics of Italian and French literature together with English. Perhaps, however, languages confronted his intelligence mainly as another set of structures to be resolved into elements. Certainly his mastery lent Young no saving touch of literary grace. In the sciences he put himself through the entire works of Newton, Linnaeus, Lavoisier, Black, and Boerhaave. He studied in London, Edinburgh, Gottingen, and Cambridge. Discouraged at the incomprehension which greeted his wave theory of light, he turned away from physics and became interested in the Rosetta Stone, which in 1799 had been unearthed near the Nile by soldiers attached to Napoleon’s Egyptian expedition, appropriated on its surrender by the British, and puzzled over for fifteen years by archaeologists to whom the message remained inscrutable. Young brought to the inscription his linguistic virtuosity, and seized upon the principle of hieroglyphic writing. In this discovery, too, his priorities were dimmed in luster by a Frenchman, Champollion, who carried the work through to a systematic conclusion. Though Young refused a post as editor of the fourth edition of the Encyclopedia Britannica, he was its most prolific contributor. He became interested, finally, in problems of the early insurance industry and is counted a founder of actuarial science. Thomas Young, in short, was a prodigy, and if he had had a more systematic training, if there had been such a thing as a scientific profession in the England of self-help, private endeavor, and new wine in old bottles, there is no telling what his energies might have accomplished. He even proposed the word “energy” for vis viva fifty years before Helmholtz.

As Helmholtz too would do, Young came to physics from physiological studies. He measured the accommodation of the eye to varying distances, and identified astigmatism and color-blindness as specific conditions. His discussion of colors as modes of perception is in the most sophisticated Newtonian tradition. In 1801 he gave the annual Bakerian lecture before the Royal Society, and published it in Philosophical Transactions in 1802. An experimental paper followed in the same year, and a second Bakerian lecture in 1804. Young was too preoccupied with developing his views to distinguish quite as explicitly as we may do between the elements of his work: the general hypothesis that light manifests waves, the law of interference of light, the experimental demonstration of that law, and its success in predictions and computations. Nevertheless, thus to analyze his contribution will do no violence to the order of his thoughts, though it may somewhat subdue their press and hurry. He advanced the hypothesis in passages chosen from Newton: “That fundamental supposition is, that the parts of bodies, when briskly agitated, do excite vibrations in the ether, which are propagated every way from those bodies in straight lines, and cause a sensation of light by beating and dashing against the bottom of the eye, something after the manner that vibrations in the air cause a sensation of sound by beating against the organs of hearing.” Nor was the “prepossession” which Young felt for this notion a question of new evidence, but only of reflections neglected in the nearly universal assent commanded by optical atomism. And it is intriguing that this breach, which was to widen and bring the properties of aether into the arena of physical discussion, should have begun with the consideration which a century later would dissipate the aether in relativity: “How happens it,” inquired Young, “that, whether the projecting force is the slightest transmission of electricity, the friction of two pebbles, the lowest degree of ignition, the white heat of a wind furnace, or the intense heat of the sun itself, these wonderful corpuscles are always propelled with one uniform velocity?” Moreover, without admitting an element of periodicity (what Newton himself had called fits of easy transmission and easy reflection), it was quite impossible to explain why a refracting surface should always reflect some portion of an incident ray.

Moving beyond these generalities, Young made a close study of Newton’s experiments on the colors of “thin plates” which appear in oil films or soap bubbles. They converted him to the “truth and sufficiency” of the undulatory system. Newton had produced them (it may be remembered) by pressing a plane surface of optical glass to another, ground ever so slightly convex. The circular wedge of air then gave “Newton’s rings,” a concentric spectrum, and he measured how deep the “thin plate” was at the point corresponding to each refracted band. Young discussed these appearances only in a qualitative way in his first Bakerian lecture, rather to remove objections to the wave theory than to insist upon proofs. The edge of shadow was the gravest. Shadows had prevented Newton himself from making the wave theory more than an auxiliary notion brought in to help save the evidence for periodicity. For light does certainly appear to travel in straight lines. Apart from the difficulties of the case, important circumstances would incline Newton away from the wave theory. In his eyes, it was not that alone. It was also a pressure theory of light, which is to say a feature of Cartesian cosmology. Query twenty-eight in the Optics had in view less Huygens than Descartes: “Are not all hypotheses erroneous, in which light is supposed to consist in pression or motion propagated through a fluid medium?—If it consisted in pression or motion, propagated either in an instant, or in time, it would bend into the shadow.” But other reasons may have hidden the merit of Huygens, waves from Newton, factors deeper than his failure to abstract from Cartesian vortices. It was a defect of his great mathematical qualities that he adhered to the purest Euclidean formalism. Newton had been brought up, moreover, in the tradition by which light, even the light that he had fragmented, was taken to be luminous geometry. And the geometric constructions in which Huygens clothed his more physical notion of an undulating medium were more complicated than the linear tracing of rays obeying the equal law of reflection and the sine law of refraction.

Young, in his first memoir, developed Huygens’ demonstrations verbally, showing that the radial development of a wavefront does satisfy those laws of reflection and refraction. In a general way he suggested how the mutual interference of waves of differing frequency or phase might make Newton’s rings appear. To introduce this idea in so offhand a fashion was characteristic both of the resourcefulness of Young’s temper, and of its limitations. For in it he makes the very important distinction between the motion of a wave system and the motions of the particles it sets to oscillating. But Young leaves this all implicit: “It is well known that a similar cause produces in sound, that effect which is called a beat; two series of undulations of nearly equal magnitude cooperating and destroying each other alternately, as they coincide more or less perfectly in the times of performing their respective motions.” Young imagined an experiment for breaking light into colors in a way that supported the analogy. He scratched a polished surface to a depth of the order of magnitude of the wave lengths concerned, and represented the reflected hues as component vibrations of the original beam thus put out of phase.

Thereafter, Young worked systematically to develop and demonstrate this principle of interference, which he now began to distinguish from the more hypothetical question of the undulatory system. Interference at least admitted of demonstration in the laboratory, as a “simple and general law, capable of explaining a number of the phenomena of coloured light, which, without this law, would remain insulated and unintelligible.” And Young’s experimental papers set this more positive tone. The first of them, presented to the Royal Society later in 1802, opens with an explicit statement of his law of interference:

Wherever two portions of the same light arrive at the eye by different routes, either exactly or very nearly in the same direction, the light becomes most intense when the difference of the routes is any multiple of a certain length, and least intense in the intermediate state of the interfering portions; and this length is different for light of different colours.

And this Young demonstrated with a series of simple and forceful experiments which opened to observation two new classes of phenomena. First, he examined the fringes of darkness to bring out the facts of “inflection” into the geometric shadow and diffraction by tiny orifices. This led him secondly, to “mixed plate” effects, which he created by varying the sequence between media of different optical properties and refractive indices.

Young began at the edges of shadows, particularly those cast by objects so narrow that their shadows were, in fact, mostly edge. He tried splitting the sight of a candle by threads stretched close across his eye. First he used a horse hair. It was too coarse. A single strand of woollen fiber did better, and a span of silken floss best of all. Fringes of color bisected the flame. They appeared capable of measurement.

I therefore made a rectangular hole in a card, and bent its ends so as to support a hair parallel to the sides of the hole: then, upon applying the eye near the hole, the hair of course appeared dilated by indistinct vision into a surface, of which the breadth was determined by the distance of the hair and the magnitude of the hole, independently of the temporary aperture of the pupil. When the hair approached so near to the direction of the margin of a candle that the inflected light was sufficiently copious to produce a sensible effect, the fringes began to appear; and it was easy to estimate the proportion of their breadth to the apparent breadth of the hair, across the image of which they extended. I found that six of the brightest red fringes, nearly at equal distances, occupied the whole of that image. The breadth of the aperture was 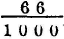, and its distance from the hair 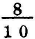of an inch: the diameter of the hair was less than 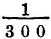of an inch; as nearly as I could ascertain, it was 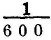. Hence, we have 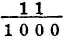for the deviation of the first red fringe at the distance 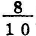; and, as 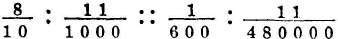, or 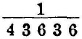for the difference of the routes of red light where it was most intense. The measure deduced from Newton’s experiments is 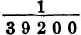. I thought this coincidence, with only an error of one-ninth of so minute a quantity, sufficiently perfect to warrant completely the explanation of the phenomenon….

A later experiment reduced the light source to a pin-prick admitting a sunbeam through a screen. In place of the hair, Young held a slip of a card edge-on in the ray. He blocked one side. The “internal” fringes disappeared on both sides of the shadow; thus, he could conclude that fine objects produce internal fringes by interference between rays inflected round either side, and external fringes (which had remained unaffected on the open side), by interference between direct rays and those reflected (or deflected) by the edge. (Unfortunately this was not correct, since Young was still thinking about longitudinal waves.)

Next, he substituted a lock of woollen hairs for the single strand between his eye and the candle, and he saw a halo around the flame, not unlike Newton’s rings. He tried the comparison with “mixed plates,” in which substances of different refractive indices were substituted for the “plate” of air between the glass surfaces. He moistened and pressed together two pieces of plate glass so that droplets of water mixed with air would perform the office of the hairs. The effect led him to consider the old question: whether the velocity of light is greater in a rare or a dense medium. Wave theory required that it be the rarer substance, but direct measurements of so small a difference still eluded technique. Fortunately for the theory, however, Newton’s rings become smaller as the density of the medium increases, which fact would imply that the wave length is shorter and the velocity less.

Moreover, the wave theory saved an otherwise very puzzling phenomenon of “mixed plates.” In Newton’s rings the central spot corresponds to the zone where the glass surfaces touch. That spot is black. One sees it under other circumstances, notably on the breaking of a soap bubble. It appears at the moment of vanishing, just as the liquid thins until the tension is unbearable. Young thought it odd that the least possible depth of the medium should black out light: “The actual lengths of the paths very nearly coincide, but the effect is the same as if one of the portions had been so retarded as to destroy the other.” Since the difference in trajectories was infinitesimal, it must (Young supposed) be reflection at the surface of an optically rarer substance which retards the wave by half an interval. But this led to verifiable consequences. Suppose a beam be passed through two progressively rarer refracting substances. “The effect would be reversed, and the central spot, instead of black, would become white; and I have now the pleasure of stating, that I have fully verified this prediction, by interposing a drop of oil of sassafras between a prism of flint-glass and a lens of crown glass: the central spot seen by reflected light was white, and surrounded by a dark ring.”

It was one of those satisfactions given only by science and the more precise kinds of scholarship, in which a prediction deduced from pure principle is realized in hard fact—a small triumph, but within its compass absolute, thus ministering innocently enough to the expert’s self-esteem. By the time Young gave his lectures at the Royal Institution, he had devised a fine demonstration of interference effects or “beats” in light. He made a grating consisting of two minute apertures which diffracted elements of a monochromatic wave front. Bands of light and dark alternated on the screen, and from their dimensions Young recalculated, more closely now, the wave lengths of the different colors that he tried:

The middle of the two portions is always light, and the bright stripes on each side are at such distances, that the light coming to them from one of the apertures must have passed through a longer space than that which comes from the other, by an interval which is equal to the breadth of one, two, three or more, of the supposed undulations, while the intervening dark spaces correspond to a difference of half a supposed undulation, of one and a half, of two and a half, or more.

From a comparison of various experiments, it appears that the breadth of the undulations constituting the extreme red light must be supposed to be, in air, about one 36-thousandth of an inch, and those of the extreme violet about one 60-thousandth: the mean of the whole spectrum, with respect to the intensity of light, being about one 45-thousandth.

All this seems persuasive in retrospect. Later in the nineteenth century, it seemed more than that: it seemed conclusive, for the community of physics experienced a conversion and swung from one pole to the other—from particles to waves. Young himself made few converts, however, and the reserve which his work evoked has a bearing on the grammar of dissent in science. Personal factors no doubt weakened his effect. There hung about him, even in his Anglicanism, an invidious air of Quaker self-righteousness in argument. He would return a sharp answer and draw wrath. Moreover, he wrote badly. His papers are short but wordy, achieving cogency mainly in the quotations and in occasional flashes of scorn. Consider, for example, the unlucky clarity of this statement, made when he was still a young man, in which he dismissed a treatise on harmonics by an aged, much respected mathematician: “Dr. Smith has written a large and obscure volume, which, for every purpose but for the use of an impracticable instrument, leaves the whole subject precisely where it found it.” The republic of letters was not sorry, therefore, when Young’s own papers on light were pilloried in the Edinburgh Review by another whom Young had insulted, Henry Brougham, a shallow Scotch rhetorician and pseudo-Bacon, whose later political career is the most difficult to admire in the annals of Victorian opportunism.

But an important vein of resistance went deep into the very structure of classical physics. It is comparable to Newton’s own inability to feel the full force of wave theory, and has to do with the influence on science of canons of style and language, which is to say of mathematical taste and technique. Mathematicians are bound to hold an influential voice in any scientific situation, and they can be reasoned with only in their own tongue. Moreover, neither simple conservatism nor Newtonian idolatry was what kept Laplace and Poisson and the French analytical school faithful to a corpuscular model of light. For they were accustomed to think no longer in Euclidean geometry, to be sure, but in the formalism which they had developed for the abstract dynamics of point masses, and into which they and their predecessors of the Enlightenment had cast the whole science of mechanics. It remains the great, the peculiar merit of Young’s law of interference that it distinguishes between the motion of the waves (which are continuous) and of the particles (which are not), and the actual displacements of which compound the influence of the several systems of waves traversing the medium. The distinction invited creation of a dynamics of waves, instead of a dynamics in which the elements are point-masses, now idealized and again concretized. This was all unwitting in Young. He did suggest that aether waves might convey electricity along with heat and light—three manifestations, it may be, of one physical reality. But Young was not the man to develop wave dynamics theoretically. He only exhibited the physical evidence, experiments to exemplify and extend the unreasonable proposition that light on light gives bands of darkness. And he illuminated those bands with insights only, and not with theory.

FRESNEL’S ADVANTAGE lay in his education at Polytechnique, where students began with theory. An early discovery, one of his happiest, determined that external fringes of shadow develop along a hyperbolic trajectory as the screen is moved away from the object. Arago had just informed him of Young’s work, and Fresnel was writing to inquire precisely how Young had forestalled him. If Young had really done so, then he should have reached the same formulations, and particularly this of the hyperbolic path: “For I must say that it was in no sense observation, but rather theory, that led me to this result, which experiment subsequently confirmed.” The ultimate problem of that theory was very serious, and Fresnel soon saw its scope. It was to reconcile the specificity of color, and indeed the whole ontology of matter, with the permeation of space by light and heat. Atomism served the former purpose. But for the latter, vibrations in an elastic medium afforded the simpler hypothesis. And Fresnel’s rebuke to the classical mechanists may be read as a prophecy of the course which physics would be bound to traverse across the nineteenth century:

The first [corpuscular] hypothesis has the advantage of leading to more obvious consequences, because analytical mechanics applies to it more easily. The second [undulatory] hypothesis presents, on the contrary, great difficulty on this score. But in choosing a theory, one should pay attention to simplicity in the hypothesis only. Simplicity in computation can be of no weight in the balance of probabilities. Nature is not embarrassed by difficulties with the calculus. She avoids complication only in means.

Fresnel was of that generation of Frenchmen which Stendhal understood, soaring into youth amid the expanding Napoleonic universe, only to confront maturity in the closed world of bourgeois France. Fresnel himself, the founder of wave mechanics; Sadi Carnot, the formulator of thermodynamics; Evariste Galois, an Einstein avant la lettre—they were like Julien Sorel, eaglets who did not long survive the eagle. Galois died at twenty-one, Carnot at thirty-five, Fresnel at thirty-nine. By profession Fresnel was a civil engineer serving in the Corps des Ponts et Chaussées, responsible since the mid-eighteenth century for the finest highway system in the world. Nor did the tradition of French engineering science imply any scorn of innovation or application. Fresnel carried his studies of light into the design of the lenticular light-house beacon. Its echelon lens replaced the feeble torches and lanterns for which ship captains had anxiously had to peer. Those studies began, indeed, as the distractions of isolation, when Fresnel was at work upon the Napoleonic roads in remote corners of France.

The materiality of light and heat had been presented to students at Polytechnique as an example of a subject in an unsatisfactory condition. Political mistakes during the hundred days gave Fresnel an involuntary leave at his family’s house at Mathieu in Normandy, quite near to Caen. There with homemade apparatus he found the same phenomena which Young had made appear. He put himself into touch with Arago and the Institute, into which the Academy of Sciences had been incorporated. Some members encouraged him. Others criticized. He got occasional leave for visits to Paris and to proper laboratories. Though Laplace and his circle never adopted his views, they did support his election to the Institute in 1823. That recognition was unanimous. His health was already ruined, and he died in four years of tuberculosis, the disease of nineteenth-century genius, after only six or seven years spent in creative work. But it must not be supposed that Fresnel’s contribution consists only of deep intuitions embodied in a few equations. His memoirs on optics, together with discussion of them by the referees of the Institute, occupy two immense volumes of his Oeuvres, and his engineering writings fill a third. If, therefore, we adopt Young’s distinction between the wave hypothesis of light and the (phenomenalistic) law of interference, and assign the latter to Young, it was Fresnel who created the truly mathematical theory of light as waves, and who thereby converted the scientific community to his model of things.

Rather than follow Fresnel across the ground already traversed by Young, it will advance the subject faster to specify the breaches he exploited in the theoretical attack. What was decisive in Fresnel’s tactics was the device of considering each point in an oscillating medium as a center of propagation of spherical wavelets. The idea was in Huygens, who for lack of the calculus could not develop it. Fresnel did dispose of the infinitesimal analysis, and improved his opportunity by combining it with the principle of interference. By his argument, the only detectable result of the composition of motions within the medium is the advancing wave front. All but the radially directed elementary oscillations destroy each other, and the resultant motion of the wave, an envelope of elementary wavelets, contains, therefore, rectilinear propagation of its effects as a special case. From this it was predictable (and Fresnel did predict) that diffracted waves would appear on a screen as alternating bands of light and dark, according as the coincident rays differed by an even or odd number of half wave-lengths. And this, of course, simply embedded Young’s law of interference more intimately into the wave theory than had his own unadorned statement of the facts.

Fresnel’s further prediction of the hyperbolic trajectory of external fringes illustrated the power of his method in more arresting fashion. And though Young had seen this evidence experimentally (as Newton had, indeed, and before him, Grimaldi), he had not appreciated what a very interesting result it was, nor made more of it than other more trifling appearances. Fresnel illustrated the phenomenon with a diagram. S is a light source, and AB a narrow object in the shadow of which fringe patterns are to form. Fresnel treats the ends A and B as centers of diffraction. The solid lines represent the enveloping wave fronts of the three systems emanating from S, A, and B and taken at the nodes of compression. (For Fresnel is still supposing longitudinal percussion waves on the model of those which stand in an organ pipe.) The dotted lines, on the other hand, represent the foci of the dilated phase. Then the trajectories of the dark bands are F₁, F₂ externally, and f₁, f₂ internally. Geometric analysis shows that F₁, F₂, etc. are neither circular nor rectilinear but hyperbolic. And experiment answers perfectly to this prediction. Moreover, the theory explained how it is that the number of internal fringes is greater nearer the object.

Impressed by the importance of these optical questions, the Academy proposed as its annual competition in 1818:

1° To determine by exact experiments all the effects of diffraction of luminous rays, direct and reflected, when they pass either separately or simultaneously close to the extremities of one body or of several bodies of limited or indefinite extension, with special attention to the intervals between these bodies, as well as to the distance from the source of light rays.
2° To conclude by means of mathematical inductions from these experiments what the motion of rays is in their passage close to bodies.

Fresnel assembled his theories and experiments into the winning memoir. Laplace, Poisson, and Biot sat on the Commission, all three skeptical if not downright hostile, along with Arago, who was enthusiastic, and Gay-Lussac, who was impartial. Speaking as a mathematician, Poisson observed that Fresnel’s integrals entrained a paradox. At certain distances the intensity of diffracted light at the center of the geometric shadow of a tiny disc should be identical with the illumination at the apex of the conical projection of an aperture of the same diameter. An obstacle and a hole would thus be indistinguishable by diffracted light. They challenged Fresnel to test this alarmingly implausible consequence. He performed the experiment—with perfect success. And he later read a little lesson to the mathematicians who had preferred to tighten the grasp which their accustomed equations had given them on corpuscles. Already the wave hypothesis “furnishes much more extensive methods of computation. That is one of the least equivocal characteristics of the reality of a theory. When a hypothesis is true, it ought to lead to the discovery of numerical relations….”

Nor was Fresnel indifferent to ampler implications. His equations are of the same type as those which Maxwell would later throw over the electromagnetic field of force. They are second-order partial differential equations which contain both the propagation and refraction of light. Was anything implied, then, about the interaction between aether and the ordinary stuff of physics, ponderable matter in motion? On the one hand, the fact of aberration relates the motion of the earth to the light from the stars. On the other hand, Arago had just shown in a very celebrated experiment that the motion of the earth has no influence on prismatic refraction of rays from the fixed stars. Does an atmosphere of aether move with bodies, therefore? Or do they sail through it? Fresnel never solved that problem. But to raise it was a great and a portentous thing, and raise it he did in a most intriguing speculation. Ponderable bodies, he suggested, convey in their interstices only a portion of the aether with which they coincide in space. That amount, a kind of specific aethericity (the phrase is not his), represents the excess over some hypothetical minimum which any body of equal volume will contain. Now, considering the luminiferous function of aether, Fresnel assumed that the total aether in a transparent body is proportional to the square of its refractive index. That, in turn, is the ratio between the velocity of light in vacuo and in the body. Finally, the velocities of the body and of light add vectorially, so that the absolute velocity of light within the body becomes a measure of the quantities of aether which pertain to space and to the body. Thus, thought Fresnel, the theory of propagation of light will contain whatever results would flow from the motion of the aether.

Years later, Hippolyte Fizeau tested this hypothesis in a fine experiment which he published in 1859 in Annales de chimie et de physique. It is less famous, for some reason, than the failure of Michelson and Morley to detect the aether drag, but no less significant. For it showed that the velocity of light increases in a medium according to the formula, v 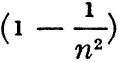, where v is the velocity of the medium, and n its refractive index. His apparatus consisted of parallel tubes through which he sent water at high speeds in opposite directions. He split a single beam of light into two fractions, and with a mirror he made each traverse the tubes in opposite directions. He then compared the interference fringes produced by light moving with and against the current and found them displaced in opposite senses by measurable and reproducible amounts. If, therefore, the aether functions as a medium, its state of motion should also have a detectable influence on the velocity of light. But the existence of the aether was not then, of course, the point at issue. Fizeau designed his experiment to choose between three alternatives: first, that aether accompanies bodies in their motion; second, that bodies move through aether; or third, that the truth lies in between, so that the velocity of light should be increased by some specific amount less than the velocity of the medium. This last was the finding which Fizeau thought he had established, all alien though it was to the either-or outlook of nineteenth-century physics.

Some years earlier, indeed, a different experiment by Fizeau had sealed the victory of the wave theory. This one he performed in 1849 with Foucault, who also mounted the great pendulum in the dome of the Pantheon and for the first time demonstrated the rotation of the earth. The wave theory of light was a belief less well established, perhaps. But in this case, too, the experiment preached to the converted. Most physicists had already adopted the wave picture by mid-century. The old emission theory explained refraction by the superior attraction of the denser medium for the corpuscles of light. Its velocity should therefore be greater in water than in air. Only instruments more precise than any of Fresnel’s generation could detect the difference. Fizeau and Foucault disposed of such instruments and showed the contrary to be true. It seemed a coup de grâce to particles of light.

This is to anticipate, however, for Fresnel’s work on diffraction did not necessarily transcend the formal. For the study of interference, analogy with sound waves sufficed, wherein vibrations pulse back and forth in the direction of propagation of the wave. Hereafter, however, in the final stages of his work, Fresnel moved beyond Young in conceptualization as well as in formalization, and introduced the notion of transverse light waves. This, if we may not quite call it the optical revolution against mechanics, was certainly an optical rebellion against classical dynamics. Polarization led him on—polarization and the special case of it in double refraction. Iceland spar had aroused optical curiosity ever since Newton’s generation. A crystal of that mineral will split a ray into two refracted beams, one obeying the ordinary sine law, and the other straying off at an idiosyncratic angle. Huygens made room for double refraction by supposing that the crystal put the aether into two wave systems: one expanding spherically to convey the ordinary ray, the other ellipsoidally for the extraordinary.

The gem tourmaline complicated the explanation, and indeed escaped it. It, too, shows double refraction. If a crystal be split and one slice rotated at right angles, the pair becomes opaque. Tried with Iceland spar, moreover, tourmaline will transmit the ordinary ray alone in one position, and the extraordinary ray when turned through ninety degrees. That light has “sides” was a proposition to be explained in the corpuscular theory only by supposing its particles to be either unsymmetrical or possessed of a qualitative polarity akin to magnetism. Neither prospect pleased. The wave theory did not help, on the other hand, so long as it imagined vibrations normal to the front. Young (once again) saw the problem and set a friend to working on polarization. He even suggested that waves oscillating transversely would yield such asymmetries. But this was a passing fancy, to which Young recurred as a fiction on occasion; he thus left this notion, too, to Fresnel to incorporate integrally into theory.

He came to it gradually. In 1809 Malus found that light which is reflected at angles within a range characteristic for certain surfaces—glass, water, polished metals—will traverse a crystal of Iceland spar as if it were one of the two fractions produced by a preliminary refraction through another crystal. That reflection also polarizes light greatly widened the interest of the phenomenon. From the beginning Fresnel had hoped that his own researches might bear on polarization. He discussed with Ampère how it might happen that rays polarized in different senses will never interfere. And Ampère, always ingenious and imaginative, threw out the notion that two wave systems might be compounded of transverse oscillations perpendicular to each other and of equivalent frequency and amplitude. Then if they were out of phase and destroyed one another, the forward motions alone might appear—hence the apparent independence of polarized rays. Fresnel took this idea and gradually qualified the notion of a forward component until ultimately he dropped it altogether and made the discreteness consist in the inclination of the planes of vibration.

It took determination, for the mechanical objections seemed insuperable to his colleagues. The elasticity of a solid might support such shear waves. The force in which rigidity consists would serve to bring each particle back across the point of equilibrium as gravity returns the pendulum after every upswing. In a fluid, on the other hand, only a harmonic sequence of impacts would send each oscillating particle back from the extreme amplitude of the wave across the mean. But what in a fluid would perform this office if it were oscillating at right angles to the direction of impact? Even Arago refused to follow Fresnel in these final “acrobatics.” For it required little less to compose the wave motion of a beam in the round from an infinity of coaxial plane vibrations, each oscillating independently of the others in the same tube of space and in the same fluid medium, the nature of which did not admit of such motion. In deference to Arago, Fresnel withheld this feature of his theory until 1821.

He also deferred to his own conscience. He had thought of transverse vibrations before Young, always “more daring in his conjectures,” but he would not rush the idea into print before satisfying himself that it could march with the principles of mechanics. And he had to satisfy himself, for as his thoughts progressed, he came to see transverse vibration as a necessary part of his theory. Otherwise, the undulatory system would fail in its claim to conceptual simplicity and coherence. There was one special case of double refraction which it could contain on no other terms. This was the action of biaxial crystals. It might seem a detail, even a trivial detail. But given Fresnel’s temperament, progressive resolution of new and more difficult problems replenished his courage. It will be best to abstract an account of his views from the two lengthy memoirs on double refraction in which he developed and perfected them. In the second of these Fresnel squarely faced Laplace and the corpuscular school:

The theory which we combat, and against which other objections may be raised, has led to no discovery. The learned computations of M. de Laplace, remarkable though they may be as elegant applications of mechanics, have taught us nothing new on the laws of double refraction. We do not think, however, that the advantage to be drawn from good theory ought to be confined to computing forces, when the laws of the phenomena are already known. That would contribute too little to the advancement of science. Certain laws there are, so complicated or so singular, that observation assisted only by analogy could never discover them. In order to divine these enigmas, it is necessary to be guided by a theory resting on a true hypothesis. The theory of luminous vibrations has that character and affords these precious advantages. We owe to it the discovery of the most complicated laws of optics, and the most difficult to divine; whereas all the other discoveries, numerous and important though they are, which have been made in that science by physicists partial to the emission system, beginning with those of Newton, are rather the fruit of their observations or their sagacity than they are mathematical consequences deduced from the Newtonian system.

What gave Fresnel such confidence was the success of his prediction of the refractive effects in biaxial crystals. In crystals symmetrical around a single axis, one would still expect the ordinary ray to follow the usual laws of refraction. But in biaxial crystals this should no longer be the case. The molecules should be subject to asymmetrical tensions in all directions, and the elastic effects should, therefore, be different from those of mediums isotropic even in one plane. “This is precisely what I verified by experiment, a month after having communicated it to M. Arago: it is true that I did not present him this result as a certain fact, but as so necessary a consequence of my theoretical ideas that I should be obliged to abandon them if experiment had failed to confirm this singular character of double refraction in biaxial crystals.” For in Fresnel, theory itself takes on an almost crystalline structure, so that the pattern of ideas must touch the facts not just here and here and there, but at every point, while the failure of new facts to appear where called for would not just mar one facet but would demolish the whole shape of thought.

An earlier note argues in qualitative terms the mechanizability of a transverse wave picture. Analytical mechanics, Fresnel points out, has admitted as the force of propagation only the differential state of dilation or condensation between successive phases. Their equations compose elastic fluids of points which may be crowded together or separated according as impacts are more or less frequent. But these equations can scarcely be supposed to express the true state of things. In reality the particles of a fluid are separated by distances that are very great compared to their diameters. In reality (it may be) they never touch, and true equations of fluid dynamics must, therefore, be concerned with such spatial relations, rather than with Newton’s laws. No terms in the classical equations of the “geometers” allow for the motions that will be set up, should one layer of a fluid be supposed to slip between others. And Fresnel asks us to imagine three parallel rows of particles in a state of equilibrium between their mutually repulsive forces. If the molecules of the outside rows are opposite one another, those of the middle row will be staggered at the intervals. Suppose the molecules of this row to be displaced longitudinally. Since equilibrium obtained, the repulsive forces will tend to restore each to its initial spot. Vibration will be set up, therefore, compensated according to the law of action and reaction by vibrations in the outside rows. And these last displacements will have both a longitudinal and a lateral component. This is a development, evidently, of Ampère’s idea. And it is not, perhaps, worth repeating the turn Fresnel gives to the argument to show that under aethereal conditions only the lateral component will be sensible. The point is only to picture the possibility of transverse waves in a fluid as a mechanism in which polarization could, and indeed must, consist.

Thus, direct light may be considered as the reunion, or more exactly as the rapid succession of systems of waves polarized in every direction. In this way of looking at things, the act of polarization no longer consists in creating transverse motions, but in decomposing them along two invariant directions at right angles, and in separating the two components one from the other. For then the oscillations in each will always occur in the same plane.

The memoirs on double refraction develop this picture mathematically. Fresnel would analyze a three-dimensional bundle of radiation by resolving the actual oscillations in a ray into components projected upon two planes at right angles through the axis. This was simply an application of geometric composition and decomposition of motions to his model, followed by a derivation of the laws of optics expressed so as to include (for the first time) the phenomena of polarization. For his analysis of double refraction, Fresnel went back to the geometric constructions of Huygens, who had made the ordinary ray develop as a spherical wave surface, and the extraordinary ray as elliptical. This fitted the shape of things but had found no basis in the corpuscular constitution of light. And by a most elegant transformation into analytical terms, which he himself regarded as his most signal achievement, Fresnel made that missing connection between the evidence from interference for the constitution of light as vibrations in aether, the inference from polarization that those vibrations are transverse, and the prediction therefrom of idiosyncratic refractions in particular species of crystal. His equations related the two refractive indices of biaxial crystals to the proportions of their major and minor axes. Thus, he contained all the phenomena of optics in laws of the propagation of waves.

By those laws every point in a medium traversed by a vibration becomes itself a center of infinitesimal waves. The wave front is an envelope. In an isotropic medium the waves are spherical, and in an anisotropic medium they have the form of a more complicated surface of the fourth degree, depending on what axes of symmetry the medium may display.

The full generality of this synthesis lay beyond the power of Fresnel’s own generation to appreciate. Nor, indeed, will his mechanical models of shear waves, his details of crystalline molecules tensed into unsymmetric patterns and setting up corresponding off-beats in the aether, quite bear the theoretical weight he put on them. Nevertheless, the generality and power of his own discussion forced the reorientation of physics toward the periodic aspects of radiation. He recaptured optics from the mechanists, turned light from corpuscles back to waves, and made this study an arena for the physics of the continuum instead of the physics of particles. And if this last, of the transversity of vibrations, was less crucial to his system than he fondly believed, at least it did set physicists upon what must seem in retrospect the most portentous train of thought in nineteenth-century physics: the mechanical properties of the aether—the medium for action at a distance—for the propagation of phenomena through space. So disconcerting were the requirements of transverse vibrations that Fresnel forebore to dwell upon anything beyond the evidence. Not so Young, who had no such stake in theory to lose, and who, since he had had the first word, may also be allowed the last:

This hypothesis of Mr. Fresnel is at least very ingenious, and may lead us to some satisfactory computations: but it is attended by one circumstance which is perfectly appalling in its consequences.… It is only to solids that such a lateral resistance has ever been attributed: so that if we adopted the distinctions laid down by the reviver of the undulatory system himself [i.e. Young] in his Lectures, it might be inferred that the luminiferous ether, pervading all space, and penetrating almost all substances, is not only elastic, but absolutely solid!!!

SCIENCE HAS KNOWN no tidier investigator than Michael Faraday. The papers collected in Experimental Researches in Electricity report researches extending over a quarter of a century, from 1831 until 1855. He numbered the paragraphs consecutively throughout the sequence. On November 20, 1845, he read before the Royal Society the nineteenth series. It announces magnetic rotation of the plane of polarized light, and paragraph two thousand, two hundred and twenty-two reads:

The relation existing between polarized light and magnetism and electricity is even more interesting than if it had been shown to exist with common light only. It cannot but extend to common light; and, as it belongs to light made, in a certain respect, more precise in its character and properties by polarization, it collates and connects it with these powers, in that duality of character which they possess, and yields an opening, which before was wanting to us, for the appliance of these powers to the investigation of the nature of this and other radiant agencies.

And he goes on to say in the next paragraph but one:

The magnetic forces do not act on the ray of light directly and without the intervention of matter, but through the mediation of the substance in which they and the ray have a simultaneous existence; the substances and the forces giving to and receiving from each other the power of acting on the light.

Writers of science fiction, and of science for young people, might reflect on their responsibility, and their opportunity. It was one of their predecessors who drew Faraday toward science, a Mrs. Marcet, author of Conversations on Chemistry. “Do not suppose,” wrote Faraday of his childhood, spent in poverty, “that I was a very deep thinker, or was marked as a precocious person. I was a very lively imaginative person, and could believe in the Arabian Nights as easily as in the Encyclopaedia. But facts were important to me, and saved me. I could trust a fact, and always cross-examined an assertion. So when I questioned Mrs. Marcet’s book by such little experiments as I could find means to perform, and found it true to the facts as I could understand them, I felt that I had got hold of an anchor in chemical knowledge, and clung fast to it. Thence my deep veneration for Mrs. Marcet—first as one who had conferred great personal good and pleasure on me; and then as one able to convey the truth and principle of those boundless fields of knowledge which concern natural things, to the young, untaught, and inquiring mind.” Faraday’s father was a blacksmith who could not provide the boy with education or surround him with external graces. All his grace, and it was lovely, was native to his mind and to his hands. The history of science has known no sweeter disposition, nor any gentler spirit, qualities not often associated with the urge toward discovery, or the ambition to be recognized. His ambition, or rather passion, was different. It was to lead the life of a philosopher. For he preferred the term “philosophy” to science.

For a man of no education, no other route than the experimental was open. At the age of thirteen Faraday was apprenticed to a bookseller. The business then included the binding of sheets received from the printer. For the statutory seven years Faraday bent to the task, hating trade all the while and losing himself in chemistry and physics in the hours after work. In 1812 he managed to attend lectures by Humphry Davy at the Royal Institution. He wrote out a fair and formal copy of his notes, bound them in the shop, and sent them to Davy, with a letter asking for a job in any scientific capacity. Davy was a skillful scientist, who had brought the first measure of order into electrochemistry and made it the most active sector of physical research in the previous decade. He advised Faraday against abandoning the security of his craft for the chances and limited opportunities of science, and then when he persisted, gave him a post as laboratory assistant. There is a charming memoir, Faraday as a Discoverer, by his younger colleague (disciple is perhaps the word) John Tyndall, who writes, “Davy was helpful to the young man, and this should never be forgotten.” Neither, unfortunately, can a disfiguring careerism in Davy’s conduct be forgotten, nor the unhappy jealousy of a more brilliant junior which in 1823 led him to oppose (unsuccessfully) his own protégé’s election to the Royal Society. But Faraday never allowed this episode to spoil the regard he felt for his patron.

Faraday’s researches of the 1820’s were mostly chemical, worthy enough but not yet seminal. He had still to develop, in Tyndall’s words, “the power which Faraday possessed in an extraordinary degree. He united vast strength with perfect flexibility. His momentum was that of a river, which combines weight and directness with the ability to yield to the flexures of its bed. The intentness of his vision in any direction did not apparently diminish his power of perception in other directions; and when he attacked a subject, expecting results, he had the faculty of keeping his mind alert, so that results different from these which he expected should not escape him through preoccupation.” Alone among the great scientists, Faraday might be taken in his success as justifying the suspicion which Diderot had once expressed for mathematics with its haughty spirit, and the democratic preference for the common touch of craftsmanship as conferring on the humble soul a power of divination, the ability to sense by manual inspiration how it must be with nature. Indeed, a German colleague once hit on the same figure as Diderot in evoking this artisan-like ability to “subodorer” the truth. “Er riecht die Wahrheit—he smells the truth,” said Kuhlrausch of Faraday.

A philosopher of science who should study Faraday might well be led to write of prophetic rather than simply predictive validation of theories. For the sobriety with which he curbed his imagination in the laboratory never stultified him. Tyndall writes, too, of his ability to exalt a subject out of the microcosm of the laboratory into the macrocosm of nature; of how he would move out in his mind’s eye from the little magnet in the Royal Institution attended by its curvilinear pattern of iron filings to the earth as a great magnet, with lines of force running through the atmosphere and through the seas, continually cut (it might be) by the flowing and ebbing of the tides, and inducing (if so) electrical currents in the oceans and the air; and too, of how difficult he was to follow for those who had been trained to express theoretical ideas in the mathematical formalism of conventional science.

He does not know the reader’s needs, and he therefore does not meet them. For instance, he speaks over and over again of the impossibility of charging a body with one electricity, though the impossibility is by no means evident. The key to the difficulty is this. He looks upon every insulated conductor as the inner coating of a Leyden jar. An insulated sphere in the middle of a room is to his mind such a coating; the walls are the outer coating, while the air between both is the insulator, across which the charge acts by induction. Without this reaction of the walls upon the sphere you could no more, according to Faraday, charge it with electricity than you could charge a Leyden jar, if its outer coating were removed. Distance with him is immaterial. His strength as a generalizer enables him to dissolve the idea of magnitude; and if you abolished the walls of the room—even the earth itself—he would make the sun and planets the outer coating of his jar.

Criticism can only speculate about the influence on his work of his entire ignorance of mathematics. Certainly he was the last physicist who could have borne up under such a handicap, and those not gifted mathematically would, no doubt, like to argue that it was a positive advantage to him, that it threw him back upon the experimental way he trod with a success unmatched before or since. Faraday himself liked to tick off the mathematicians on occasion, though always very gently. As against Arago, Babbage, and Herschel, his first paper on electromagnetic induction demonstrated (among other things) that the force whirling the copper plate was tangential. “It is quite comfortable to me,” he wrote in a private letter, “to find that experiment need not quail before mathematics, but is quite competent to rival it in discovery.” Nevertheless, it is difficult to think that a command of mathematics would not have advanced him further. As it was, he had to rely upon analogy rather than abstraction as an instrument of ordering and a guide to fruitful experiment. He wielded it with all possible finesse and achieved real elegance, the first physicist since Newton to do so in the British experimental tradition, but at a fearful cost in efficiency. Analogy, after all, depends upon a kind of linear transfer of ideas from one area to another, while abstraction frees ideas from the physical and poises the mind for the thought experiment. Only a mind as distinguished as Faraday’s could have kept its bearings amid the mass of his experiments. “Faraday’s resources as an experimentalist were so wonderful,” admitted Tyndall, “and his delight in experiment was so great, that he sometimes almost ran into excess in this direction. I have heard him say that his paper on vibrating surfaces was too heavily laden with experiments.” No scientist except Kepler has left a fuller record of his thoughts and trials. His Diary, published recently in some seven volumes, records his private thinking. But the papers he printed are themselves almost transcriptions of a laboratory notebook, full of weights, lengths, circumstances, results, discrepancies, false trails, failure, and success. They are not good reading. Already the literature of science wilts under the blight of the passive voice. Only occasionally did he loose his pen publicly to write down the speculations about how the world is made that filled his mind and guided his hand through all this mass of fact.

It is, moreover, very curious, and very wonderful, that he could distinguish by a kind of instinct those of his ideas which were subsidiary, from those which were fundamental and which guided the whole course of experiment through the forty years or more of his career. The former he would abandon without a sign of regretting the fate that his brainchildren suffered at his own hands. The latter illustrate rather the special faith that does animate science:

I have long held an opinion, almost amounting to conviction, in common I believe with many other lovers of natural knowledge, that the various forms under which the forces of matter are made manifest have one common origin; or, in other words, are so directly related and mutually dependent, that they are convertible, as it were, one into another, and possess equivalents of power in their action.

Instead of leading Faraday toward heat, however, and thence into thermodynamics, this conviction drew him to the deeper relations, as he believed the ultimate unity, of electricity, magnetism, and gravity. For there was given to him as to few scientists a sense of the spatial. He would almost see the moving wire slice through the lines of force and the current stir within. Perhaps, after all, it was the reward of his incapacity for abstraction, this vision of nature in the round, and in depth—deeper even than Tyndall said. He was a Victorian Kepler following on no Pythagoras and knowing no geometry—a laboratory Leonardo who could see but could not draw. His passion for knowing nature transcended the modes of expression open to a man of the nineteenth century. And always there was innocence, and that saving modesty. In the world he deported himself like the elder that he was of his strict, Nonconformist congregation. To the historian reading through his papers the speculative passages come as welcome respites from the interminable experimental detail to which Faraday’s conscience condemns him. But the reprieves are brief: “I shall do better to refrain from giving expression to these vague thoughts (though they will press in upon the mind), and first submitting them to rigid investigation by experiment, if they prove worthy, then present them hereafter to the Royal Society.”

The fact of electromagnetic interaction was already ten years old in August 1831, when Faraday wound two coils of copper wire onto opposite sides of an iron ring, completed one circuit by a wire passing by a magnetic needle and the other through a battery of wet cells, and found that the pointer would kick one way at make and the other at break. It was the first transformer. The obvious similarities, formal and physical, between magnetism and static electricity fed the general suspicion of some connection between these manifestations. In 1820 Hans Christian Oersted succeeded in the search. His is perhaps the only major discovery ever to come out of one of those lecture demonstrations in which professors carefully contrive the surprises they practice on nature and their students. Nothing happened when he tried the compass needle at right angles to a wire bearing a current. Then he turned it parallel and found that the wire, when placed below the magnetic pole, would “drive it toward the east, and when placed above it, toward the west.” Thus, in this situation the current acts in its conductor like a magnet.

Word of his effect reached Paris, where its interest was immediately apparent. Ampère took up the investigation and immediately established the mutual influences of currents over each other, the conductors attracting each other if the currents are in the same direction and repelling in the contrary case. But Ampère was a polytechnician, and true to his education he named the new subject electrodynamics and concentrated on embracing induction in the formalism of analytical mechanics. That he seemed to do so was a triumph of mathematical virtuosity. For he had to treat the elements of each current infinitesimally and assume that the force joining any two is radial. He announced himself at the outset as one for whom scientific explanation consisted in reducing phenomena to the description of equal and opposite forces between pairs of particles. He brought great clarification and abolished the distinction between frictional electricity and galvanic. By analogy with the history of mechanics, the term statical applied to the former, once it was seen to be a special case, a kind of arrested dynamics. That appeared as “tension” (or potential) in the one case which causes continuous flow in the other. Only electricity in motion, Ampère pointed out, wraps a magnetic influence around itself, or affects another current across the space between conductors. And it was left to Faraday to find the missing piece in the puzzle of induction, the inverse creation by magnetism of an electrical current, and to meditate about the space where these effects transpire, in configurations quite inescapably curvilinear, and by forces which took their purchase on bodies tangentially and not centrally. There lay the difficulty. Since Kepler there had been no tangential drag in physics.

Reciprocity required that if electricity is convertible into magnetism, magnetism ought to be convertible into electricity. Faraday began systematic experiments on his return to the Royal Institution from a summer vacation in 1831. Nor did he come to the problem as an electrical novice. Though he had until then worked primarily on chemistry, he had given thought to the new science of induction. As early as 1821, he had made a bar magnet revolve around a wire by weighting one end with platinum and floating it upright in a mercury bath into which the wire dipped, thus completing a voltaic circuit. Reciprocally, he made a wire revolve around a fixed magnet. Logically enough, he next tried to make the wire or magnet rotate in place in the center of the cup of mercury. He failed and—this was how his mind always worked—suspected that perhaps the current turns within the conductor. So he bent it into a crank shape. He was right. Now it did turn. And he devised an arrangement delicate enough to show the rotation of a conductor in the magnetic field of the earth.

His first attempts to induce the electrical current held similar disappointment, which he exploited with the same importunate instinct. He had expected to generate a continuous flow of galvanic electricity in his second circuit, comparable to the continuing magnetism set up by electricity in motion. Instead, he got only that quick flick of the needle, at the moment of connecting the battery, and then inert quiescence until he broke the circuit, which expired with an equally feeble twitch the other way. Einstein once said that experiments are dull to read about and exciting only to do. Certainly no summary can do justice to the patience and ingenuity with which Faraday substituted helices for simple coils, with and without iron cores, altered his connection, tried its parts in every possible plane vis-à-vis the others, and then bethought himself of an experiment by Arago, in which a permanent magnet hanging over a copper disc has no effect until it begins to rotate, when the disc is constrained to follow, and vice versa. May not induced currents be the agent? And if so, it is the motion of magnetized metal relative to the copper which creates them. Faraday had, in any case, hoped to create electricity from magnetism, rather than simply to provoke one current by another. And now he dispensed with the battery, connected a galvanometer between the ends of a wire wound into a tight coil or helix around an open iron cylinder, and tried thrusting a bar-magnet into the hole. Everyone knows of his success: “A powerful pull whirling the galvanometer needle round many times was given,” says the Diary. Still it was only on inserting or withdrawing the magnet that the current stirred. But now Faraday saw that he must exploit the fact rather than overcome or evade its limitations, and thus find a way to enlarge and continue it. This simply required ingenuity. He mounted a copper plate to rotate between the poles of a great magnet belonging to the Royal Society, and drew from this the first electrical current to be sustained otherwise than chemically. It needed only the substitution for the disc of a coil wound round an armature to become the magneto; and what followed was in all the long history of science the first truly portentous application of a major piece of basic research (as opposed to rational method) to the occasions of industry.

Faraday’s own imagination moved in another direction, outward as was his wont toward the great magnet of the earth, and then inward toward the simplest and most elegant representation of the contrivances of nature. First he devised various arrangements for inducing a current by the action of the magnetic field of the earth alone. The most economical consisted only of a copper plate rotated at right angles to the line of a dipping needle: “The effect at the needle was slight but very distinct and could be accumulated upon the needle by reversion and reiteration of motion.” It was always Faraday’s hope to detect the grand analogue of such artificial local currents, and to observe electrical currents induced between Dover and Calais in the tides of the Channel. In that he was disappointed. But he did use the magnetism of the earth in the Second Series of his Experimental Researches. He formed a single strand of copper wire into a rectangle, with a galvanometer included in one of the long sides. Then when the wire was rotated around the galvanometer, the needle would swing in angles up to 90°. This with a single wire, he noted in his Diary, was a “truly elementary experiment,” the results “beautiful,” and (as he remarked in the published paper), “The exclusion of all extraneous circumstances and complexity of arrangement, and the distinct character of the indications afforded, render this single experiment an epitome of nearly all the facts of magneto-electric induction.” An entry in his Diary of March 26th contains a most characteristic instance of the working of his mind, and of the solid sense of the spatial in which his thinking would issue. In one short statement, and a notebook sketch, he relates the new, electro-magnetic dimension of physics to motion, the classic preoccupation of science:

The mutual relation of electricity, magnetism, and motion may be represented by three lines at right angles to each other, any one of which may represent any one of these points and the other two lines the other points. Then if electricity be determined in one line and motion in another, magnetism will be developed in the third; or if electricity be determined in one line and magnetism in another, motion will occur in a third. Or if magnetism be determined first then motion will produce electricity or electricity motion. Or if motion be the first point determined, magnetism will evolve electricity or electricity magnetism.

From these, his truly seminal discoveries, Faraday turned to an exploitation of the vast terrain of electromagnetic happenings, and first of all to establishing the identity of what some still took to be different kinds of electricity, “common, animal, and voltaic,” for otherwise there could be no confidence in the uniformity of his results. And he imagined a series of experiments to exhibit identical effects physically, thermally, physiologically, and chemically, whether his electricity was produced by friction, a battery, or a fish. This held neither surprise nor disappointment, but in the course of these rather routine demonstrations, Faraday did think to notice what was not entirely novel: that when water turns to ice, it ceases to conduct. Immediately he turned his interests towards the physical state of conductors, and found it to be a general law that solutions cease to pass the electrical current when they congeal. The contrary is true of heat, he remarked, which is conducted more readily across ice and other solids than through liquids. The difference might open some insight into the “corpuscular condition” of the substances concerned, but Faraday left the structure of matter in abeyance for the nonce to concentrate on the mechanism of electrolysis, as he was the first to call it. For it seemed that substances convey currents chemically, and batteries produce them, at the price of their own decomposition.

The researches on electrolysis were a brilliant and characteristic digression, displaying Faraday’s imagination to the very best advantage—and his clarity of mind. A curious feature of his scientific personality here emerged into peculiar prominence. Though he had no mathematics, he chafed, nevertheless, in the prison house of vulgar symbols and naïve models. And perhaps it was the combination of these qualities and disqualities, so to say, which led him beyond the abstractions he could not express into a kind of intimacy with nature to which no mathematician might attain. Neither, unhappily, might Faraday share it. The hydraulic image suggested by the phrase “electric current” aroused his special impatience, and he proposed to liberate physics from bondage to all terms which pre-judged an investigation. Poles imply attraction. He coined in their place the word “electrode,” paired off as anode and cathode. A material which conducts in decomposing is an electrolyte, and its constituent “ions” are cations and anions. Poles imply attraction or repulsion. But “according to my view the determining force is not at the poles, but within the body under decomposition; and the oxygen and acids are rendered at the negative extremity of that body, whilst hydrogen, metals, etc., are evolved at the positive extremity…. The poles, as they are usually called, are only the doors or ways by which the electric current passes into and out of the decomposing body; and they of course, when in contact with that body, are the limits of its extent in the direction of the current.” In place of poles, therefore, he coined “electrode” as a word implying nothing inconsistent with this or any picture.

How many physicists, one wonders, know why anode stands for positive and cathode for negative? “Wishing for a natural standard of electric direction to which I might refer these, expressive of their difference and at the same time free from all theory, I have thought it might be found in the earth. If the magnetism of the earth be due to electric currents passing round it, the latter must be in a constant direction, which, according to present usage of speech would be from east to west, or, which will strengthen this help to the memory, that in which the sun appears to move.” In any electrolysis, therefore, Faraday imagines the solution placed so that the current through it will be parallel to that around the earth and in the same direction; then the electrodes will have an invariant reference, and that towards the east will be called the anode (“ana,” upward, toward the rising sun; and “hodos,” way) and its opposite the cathode (“kata,” downward, toward the setting sun). Analogously, a material which does conduct in decomposing is an electrolyte, and its constituent “ions” are anions or cations. “These terms being once well-defined, will, I hope, in their use enable me to avoid much periphrasis and ambiguity of expression. I do not mean to press them into service more frequently than will be required, for I am fully aware that names are one thing and science another.”

So far are we from Condillac, and Faraday went on immediately to substantive matters, determining by electrochemistry the equivalent weights of electrolytic substances. The evidence was, of course, a powerful confirmation of Dalton’s law of definite proportions, and therefore of the atomic theory of matter. And there is a certain irony in this. For in Faraday’s determination to transcend a fluid conception of electricity, he imagined his ions ferrying that charge in motion which was the current across the decomposing mass. In disembodying the current, therefore, he added body to the corpuscular image of matter, and so successfully that a century later his model of electrolysis still served the needs of textbooks. But he himself, the more he thought on the structure of matter and its relation to electromagnetism, the more he despaired of the corpuscular account as a sufficient representation of the texture of reality. Once again his inquiry turned out of the common path he had just widened toward the mechanism of induction and conduction, which was to say the relationship of force to matter. This was the preoccupation which would engulf his later years. For him, all untrained in academic philosophy, it could be no metaphysical problem, as it was for Mayer and for Helmholtz. It was altogether physical. No more than Newton could he accept the notion of action at a distance. But neither could he bring to a happy issue the attempt which he began in 1837, and continued for several series of experiments, to see induction and conduction as the action of “contiguous particles,” passing on or delaying the electrical impulse according to their specific properties, or perhaps their freedom to move. The analogy contrasted the behavior of an electrolyte in the liquid and in the solid state, and it failed. He could never escape consideration of the distances between bodies. If action or induction at a distance does occur, it must be in straight lines between centers of force, like gravity. But magnetic and electrical forces are not radial; they seem to curve through space; and it was now that Faraday began to write of lines of force, generalizing the possibilities apparent in the patterns assumed by iron filings round a magnet. But then it must be the medium, somehow, and not the mechanistic jostlings of the particles which will lift the curse of unintelligibility from action at an apparent distance. Tyndall tells of the difficulty of following Faraday’s thinking through the experiments which lodged these musings in the laboratory.

It would, however, be easy to criticize these researches, easy to show the looseness, and sometimes the inaccuracy, of the phraseology employed; but this critical spirit will get little good out of Faraday. Rather let those who ponder his works seek to realize the object he set before him, not permitting his occasional vagueness to interfere with their appreciation of his speculations. We may see the ripples, and eddies, and vortices of a flowing stream, without being able to resolve all these motions into their constituent elements; and so it sometimes strikes me that Faraday clearly saw the play of fluids and ethers and atoms, though his previous training did not enable him to resolve what he saw into its constituents, or describe it in a manner satisfactory to a mind versed in mechanics. And then again occur, I confess, dark sayings, difficult to be understood, which disturb my confidence in this conclusion. It must, however, always be remembered that he works at the very boundaries of our knowledge, and that his mind dwells in the “boundless contiguity of shade” by which that knowledge is surrounded.

Such, in any case, were his dilemmas and preoccupations, and in 1841 Faraday collapsed under their weight. He was just fifty years of age. His prostration is always attributed to overwork, and indeed no scientist in all history comes to mind who ever spent such long and faithful hours in the laboratory. Nor is historical understanding much enriched by retrospective and amateur psychoanalysis. Nevertheless, it is moving to think for a moment of the tensions under which Faraday lived: a great physicist, ignorant of the language of his science; a daringly speculative thinker, constrained, both by his own deficiencies and the intellectual fashion of the time, into the paths of the most dutiful, painstaking, and arduous experimentalism; a proud and passionate nature, under the dual code of the Nonconformist conscience and the Victorian way of life. Generosity came naturally to him. But it may be that moderation did not. They were terrible problems on which he brooded, and if one turns from these to one of the many likenesses that survive, they make a painful contrast with an element of childlike simplicity, almost of beauty, in his face. Could it have hurt him that he was of such very short stature, not much over five feet tall? In any case, his collapse was one of those nervous catastrophes to which the Victorians were prone. Similar crises, to recall two examples, beset John Stuart Mill and Florence Nightingale. All his life Darwin suffered from prostration. For two years Faraday could do no science and see no company. Ultimately the classic nineteenth-century remedies worked their slow magic—the loving care of a devoted helpmate, the soothing influence of Alpine scenery. And Faraday resumed his studies.

But with a difference. Speculation and theory about the structure of things occupied an increasing sector of his attention. They became, one begins to feel, the object of his search instead of the recreations of his imagination. Not that he gave over spending his days in the laboratory, or ceased to make discoveries great and small. In the hope of getting closer in to the actual contiguity of particles, he tried examining with polarized light—and discovered its rotation under magnetism. He entitled the paper reporting these researches “The Magnetization of Light, and the Illumination of the Lines of Magnetic Force.” “A few years ago,” runs paragraph 2,614, “magnetism was to us an occult power, affecting only a few bodies; now it is found to influence all bodies, and to possess the most intimate relations with electricity, heat, chemical action, light, crystallization, and through it, with the forces concerned in cohesion; and we may, in the present state of things, well feel urged to continue in our labours, encouraged by the hope of bringing it into a bond of union with gravity itself.” And a little later, in words which might have been written very much later and by a greater thinker, “Here end my trials for the present. The results are negative. They do not shake my strong feeling of the existence of a relation between gravity and electricity, though they give no proof that such a relation exists.”

The inclusion of crystallization refers to Faraday’s investigation of the magnetic properties of crystals, no doubt on the analogy which had led from double refraction to an understanding of polarized light. He, too, found strange effects, having to do with directions of force. Certain crystals—metallic bismuth, for example—experienced neither attraction nor repulsion in the grip of magnetic forces, but simply aligned themselves with their magnetic axes tangent to lines of force, so that they might offer the least resistance. “I do not remember,” he wrote, “heretofore such a case of force as the present one, where a body is brought into position only, without attraction or repulsion.” And it is time to introduce the meditations of his later years, which consisted in the gradual possession of his mind by belief in the physical existence of lines of force.

In earlier years, in the 1830’s and 1840’s, Faraday treated lines of force only as representations of direction. It is not clear at what point he began to think of them as really existent in the physical condition of space. Indeed, the germ of belief must have been in his first observation of the pattern assumed by iron filings around a magnet. What is clear is that the wish to believe grew upon him in the 1840’s. Experiments multiplied in which he investigated magnetic and “diamagnetic,” conducting and insulating properties of bodies. He would represent his findings in ever more explicit drawings of lines of force streaming concavely together through those bodies which support magnetism or electricity, or bending convexly outward to strain away from bodies repellant to those forces.

The graphic advantage was great—so great that for a century teachers taught that the quantity of induced electricity is proportional to the number of lines of force cut by the armature. Surely the majority of persons who remember anything about induction still remember this. Certainly Faraday himself saw his magnets as loci of a host of lines of force, pinching and clustering together as they streamed in from magnetically neutral space to pass through the magnet, spreading and streaming away, on the other hand, to avoid as far as possible inhospitable “diamagnetic” bodies. And whatever the psychological explanation of Faraday’s gradual surrender to the wish to believe, it is clear what the physical phenomena were that fed it. To begin with, the curvilinear form of electromagnetic lines of force argued their physical existence. Sometimes Faraday seems to betray an instinct that only the mathematical may follow the straight Euclidean line, and that his lines of force are what constrain the physical away from the abstract. It is true that his hope of penetrating beneath the abstractions of classical dynamics into a real physics of unified force was frustrated by the radial direction of gravity, and the radical incompatibility of tangential and central forces. But neither could Ampère’s equations from classical dynamics adequately describe the condition of the electromagnetic medium. To Faraday, therefore, belongs the honor of identifying that incompatibility which he could not resolve. Ampère and the analytical school, for their part, sought rather to preserve appearances in mathematics. Moreover, in thinking on the physical foundations of force, Faraday felt gathering dismay at action-at-a-distance, across a space which entered science only as a permission to ignore fundamental difficulties. All the physics which had supervened since Newton did not armor over that Achilles’ heel.

In 1844 the Philosophical Magazine published an essay in the form of a letter to Richard Taylor in which Faraday freely and explicitly discussed the perplexities that afflicted him at the very foundations of physics. These, it must be remembered, were the decades of mounting triumph for the atomic theory in chemistry, and also in crystallography. And yet, Faraday points out, the implications of atomism as a hypothesis of the constitution of matter go beyond the facts of definite proportions, equivalents, and constant composition. In the minds of those whom the atomic theory pleased there was surely something more than the sum of those phenomena. Faraday himself had often sought to imagine how the corpuscles of bodies convey or repel charge and current. But ultimately, atomism could not please him as a representation of reality: “Light and electricity are two great and searching investigators of the molecular structure of bodies, and it was whilst considering the probable nature of conduction and insulation in bodies not decomposable by the electricity to which they were subject, and the relation of electricity to space contemplated as void of that which the atomists called matter, that considerations something like those which follow were presented to my mind.”

If the common atomic view of the constitution of matter were correct, the particles of matter are one kind of thing, and space quite another. They are raisins and the cake, such that “space must be taken as the only continuous part, for the particles are considered as separated by space from each other. Space will permeate all masses of matter in every direction like a net, except that in place of meshes it will form cells, isolating each atom from its neighbours, and itself only being continuous.” What, then, of a piece of shellac, a non-conductor? It must follow from the atomic theory that space is an insulator, for if it were atoms rather than space which insulates, the space in the most resistant of bodies would still conduct around the atoms. But what of metals? What of platinum or copper? For by the atomic theory again, space alone is the continuous aspect of matter, and therefore, space is a conductor. Thus, “the reasoning ends in this, a subversion of that theory altogether; for if space be an insulator it cannot exist in conducting bodies, and if it be a conductor it cannot exist in insulating bodies. Any ground of reasoning which tends to such conclusions as these must in itself be false.”

Such were the contradictions which led Faraday to repudiate atoms-and-the-void as a model of reality. He did recognize how naturally the phenomena of crystallization, and of chemistry and physics generally, grouped themselves around the acknowledgment of centers of force. “I feel myself constrained, for the present hypothetically, to admit them.” But he would admit as little as possible. In place of the conventional picture he preferred the atoms of Boscovich, an eighteenth-century Jesuit philosopher somewhat out of the main stream of science, who had defined atoms only as centers of force, and not as particles of matter in which powers somehow inhere. To blur the ultimate massy atom of chemistry into a vaguer focus of such manifestations as we can observe would in no way injure its capacity to order that science. But it would immensely ease the task of imagining what happens in the case of electrical conduction, chemical reaction, and the interactions of heat, electricity, and magnetism with matter. What Faraday pleads for, indeed, is nothing less than abolition of the boundary between matter and space in order to assimilate both to the manifestations of energy in extension. If we consider a conductor, say potassium, we can scarcely imagine that its conducting power belongs to it “any otherwise than as a consequence of the properties of space.” So, too, its properties in relation to light, or magnetism, or even solidity, specific gravity, and hardness: “For where is the least ground (except in a gratuitous assumption) for imagining a difference in kind between the centres of two contiguous atoms and any other spot between those centres? A difference in degree, or even in the nature of the power consistent with the law of continuity, I can admit, but the difference between a supposed little hard particle and the powers around it, I cannot imagine.”

And it is indeed interesting, and to anyone with a sense of the drama of culture across the centuries, it is moving to read Faraday, whose own untutored, self-taught state surely left him the nearest thing to a child of nature, not to say a noble savage, that the history of science can show, coming, after a lifetime spent on doing science with his own hands, to that same dilemma between atoms and the continuum which has given structure to the history of science since its opening in Greece. By now, indeed, what with the success of analytical mechanics, it was a turn-about tale, with the mathematicians enlisted in the service of atoms. And it was rather Faraday who came down, the greatest of the empiricists and the first of them to do so, on the side of the continuum and the unity of nature. “Now the powers we know and recognize in every phenomenon of the creation, the abstract matter in none; why then assume the existence of that of which we are ignorant, which we cannot conceive, and for which there is no philosophical necessity?” For in Faraday it is not geometry, as it had been in Descartes and would be again in Einstein, which encompasses matter and energy in extension. It is imagination. “To my mind, therefore, the … nucleus vanishes, and the substance consists of the powers; … and indeed, what notion can we form of the nucleus independent of its powers?” In this view, atoms will be highly amorphous, instead of being hard little balls bounding and rebounding. They will no longer have to be assigned any determinate shape, nor any exclusive location. “If an atom be conceived to be a centre of power, that which is ordinarily referred to under the term shape would now be referred to the disposition and relative intensity of the forces.” And finally,

The view now stated of the constitution of matter would seem to involve necessarily the conclusion that matter fills all space, or, at least all space to which gravitation extends (including the sun and its system); for gravitation is a property of matter dependent on a certain force, and it is this force which constitutes the matter. In that view matter is not merely mutually penetrable, but each atom extends, so to say, throughout the whole of the solar system, yet always retaining its own center of force.

Thus would Faraday save the “old adage, ‘matter cannot act where it is not,’” and these were the dark views to which Tyndall alluded, these the “flashes of wondrous insight and utterances which seem less the product of reasoning than of revelation.” These, too, were the “theoretic views” of which Faraday persuaded very few. Nor was Tyndall, for all his sympathy and admiration, among them.

A final word of caution must be said against the allusion in many books of physics to Faraday as the founder of field physics. In the most important sense, no doubt, he was, in that he re-addressed the science to the properties of space, and required it to pay attention to the propagation of phenomena instead of simply to the dimensions of bodies, serving as parameters of ever more analytical and elegant equations. But he did not write of fields. His space is full of tubes of force. Nor was he the one to identify the structure of space with the mechanical properties being visited by wave theory upon the aether. About the aether, indeed, Faraday maintained that reserve which forsook him when it came to his own tubes of force. Even about space and matter he retreated in practice back into that necessity which he had admitted for centers of force in his own thinking, and for some distinction. He was not the man to plunge physics back into Cartesianism. In Series 25 of his Researches appears an experimental paper addressed to the Royal Society in 1850, and paragraph 2,777 contains these observations:

It seems manifest that the lines of magnetic force can traverse pure space, just as gravitating force does, and as static electrical forces do; and therefore space has a magnetic relation of its own, and one that we shall probably find hereafter to be of the utmost importance in natural phenomena. But this character of space is not of the same kind as that which, in relation to matter, we endeavour to express by the terms magnetic and dia-[non-]magnetic. To confuse them together would be to confound space with matter, and to trouble all the conceptions by which we endeavour to understand and work out a progressively clearer view of the mode of action and the laws of natural forces. It would be as if, in gravitation or electric forces, one were to confound the particles acting on each other with the space across which they are acting, and would, I think, shut the door to advancement. Mere space cannot act as matter acts, even though the utmost latitude be allowed to the hypothesis of an ether; and admitting that hypothesis, it would be a large additional assumption to suppose that the lines of magnetic force are vibrations carried on by it; whilst as yet, we have no proof or indication that time is required for their propagation, or in what respect they may in general character assimilate to, or differ from, the respective lines of gravitating, luminiferous, or electric forces.

For Faraday’s thinking about these problems contains no refuge for small minds.

TO MOVE without preliminaries from Faraday’s reflections about the electromagnetic relations of space into the field theory of James Clerk Maxwell will convey the intimacy in which the physical discoveries of the one merged into the theoretical formulations of the other, so that something like an intellectual continuum joined their thinking. Certainly Maxwell himself conceived the problem of electrodynamics from the very outset to be the mathematical, and not simply the intuitional description of the tensions and convolutions in continuous media.

Unrepentant over the ignominious decline of the corpuscular theory of light, the continental analysts had proceeded in the wake of Coulomb and Ampère to express electromagnetic forces in the differential formalism which had served classical mechanics, and just failed in optics. They resolved electrical and magnetic charges into infinitesimal elements of electricity and magnetism, and currents into point-masses in conservative motions serving Newton’s laws. They displayed the effects of attraction, repulsion, and induction as interaction of particles at a distance, taking their ultimate license to do so, of course, from the Newtonian law of gravity and the extension of the inverse-square relationship to electromagnetic forces. It was, as Maxwell admitted, a powerful method, “warranted by the universal consent of men of science.” Faraday’s lines of force had evoked no such consent. Indeed, few mathematical physicists paid them serious attention, and most regarded them with either indulgence or a touch of scorn as another instance of the mathematical incapacity and consequent theoretical immaturity or barbarism of the English experimental tradition.

Not so Maxwell, to whom it seemed that Faraday had stated the laws he discovered “in terms as unambiguous as those of pure mathematics,” and for whom the mathematician’s part was to receive physical truths, deduce other laws capable of being tested by experiment, and thus to assist the physicist in arranging his own ideas. Those truths were that currents are produced by changes in the magnetic or electrical state of the medium surrounding a conductor, and that no complete description could be yielded, therefore, by any action-at-a-distance analysis which ignored the reality and efficacy of the strains and stresses in the medium. He would be Faraday’s mathematicus.

In the following investigation, therefore, the laws established by Faraday will be assumed as true, and it will be shown that by following out his speculations other and more general laws can be deduced from them. If it should then appear that these laws, originally devised to include one set of phenomena, may be generalized so as to extend to phenomena of a different class, these mathematical connexions may suggest to physicists the means of establishing physical connexions; and thus mere speculation may be turned to account in physical science.

And this was the program of the charming and ingenious memoir, “On Faraday’s Lines of Force,” which Maxwell published in 1856 in the Transactions of the Cambridge Philosophical Society. Faraday himself was astonished and delighted. “I was at first almost frightened,” he wrote, “when I saw such mathematical force made to bear upon the subject, and then wondered to see that the subject stood it so well.”

But how might anything so nebulous in the minds of others as Faraday’s lines of force be quantified? And it was the peculiar turn, one almost wrote the Scotch turn, of his ingenuity, at once rational and handy, which made Maxwell precisely the right man in the right place to answer to that opportunity. Physics must steer, he said in effect at the outset of his paper, between the Scylla of the abstract and the Charybdis of the concrete.

We must therefore discover some method of investigation which allows the mind at every step to lay hold of a clear physical conception, without being committed to any theory founded on the physical science from which that conception is borrowed, so that it is neither drawn aside from the subject in pursuit of analytical subtleties, nor carried beyond the truth by a favourite hypothesis.

In order to obtain physical ideas without adopting a physical theory, we must make ourselves familiar with the existence of physical analogies. By a physical analogy I mean that partial similarity between the laws of one science and those of another which makes each of them illustrate the other. Thus all the mathematical sciences are founded on relations between physical laws and laws of numbers, so that the aim of exact science is to reduce the problems of nature to the determination of quantities by operations with numbers. Passing from the most universal of all analogies to a very partial one, we find the same resemblance in mathematical form between two different phenomena giving rise to a physical theory of light.

Thus, Maxwell specified, there had been two alternative models for light. That of particles in inertial motion did (and still does) account for the direction of light beams, and was long thought to be the true explanation of refraction. That of waves, on the other hand, though it carries science much farther, must not simply for that reason be confused with the truth of things. For it rests on a resemblance “in form only” (the italics are Maxwell’s) between the laws of light and those of vibrations. Maxwell introduced the warning preliminary to cautions he addressed to attraction-at-a-distance and gravity as a model for electro-magnetism. Nor can he then have foreseen to what lengths he would push comparisons. But a sound intuition had planted in this, his first important memoir, the seeds of a relation between the wave theory of light and the electro-magnetism which was his subject.

For the moment, however, his concern was the continuity of those lines of force in spaces and situations where electromagnetic effects obtained, and he turned, not yet to waves, but to a more primitive manifestation of the continuum—to the behavior of a fluid so defined as to be the physical expression of mathematical relations.

He reminds us what Faraday meant by a line of force: a line passing through any point of space so that it represents the direction of the force exerted by a surface electrified positively on a particle of like sign, or on an elementary north pole. We might fill all space with such lines and thus have a geometric model indicating the direction of some force at every point. But still we should need to know its intensity, and for this we body the image into three dimensions and consider these curving forms “as fine tubes of variable section carrying an incompressible fluid.” Now we can have an expression of intensity, since velocity will vary inversely as the cross-section of the tube. Moreover, electrical and magnetic forces have properties which allow us an immense simplification of the picture. We can so reduce the tubes in imaginary diameter as to leave no gaps. “The tubes will then be mere surfaces, directing the motion of a fluid filling up the whole space.” And what these images express, of course, is a return from the algebraic or analytical to the palpable and the geometric imagination.

By referring everything to the purely geometrical idea of the motion of an imaginary fluid, I hope to attain generality and precision, and to avoid the dangers arising from a premature theory professing to explain the cause of phenomena. If the results of mere speculation which I have collected are found to be of any use to experimental philosophers, in arranging and interpreting their results, they will have served their purpose, and a mature theory, in which physical facts will be physically explained, will be formed by those who by interrogating Nature herself, can obtain the only true solution of the questions which the mathematical theory suggests.

For Maxwell’s was an extraordinary fluid, not at all like Carnot’s caloric. “It is not even,” he immediately pointed out, “a hypothetical fluid which is introduced to explain actual phenomena. It is merely a collection of imaginary properties which may be employed for establishing certain theorems in pure mathematics in a way more intelligible to many minds and more applicable to physical problems than that in which algebraic symbols alone are used,” Thus, it was to resemble ordinary fluids only in its perfect flowiness and incompressibility. It was to have no mass and to be capable of inertial motion only in direction, so to say, but not in acquiring momentum. Those were its physical properties, or disproperties. Its advantages lay in its mathematical properties, for such a fluid became accessible to the mathematical operations developed for hydrodynamics. Electrical or magnetic intensity might be assimilated to the velocity of the fluid, and the lines of force to flow-lines. Any consistent system of units might apply, by so defining the tubes of flow (force) that a unit of volume passed any section in a unit of time. By assuming the unit as small as desired, one could reduce the tubes to infinitesimal proportions, fill the whole of the space under consideration with unit tubes, define thereby the motion of the whole quantity of fluid, and even ascertain the state of its motion at any given point of space. Nor need one confine one’s image to the description of closed circuits. The tube might end in the boundary to the space of the experiment, in which case what lies beyond is like Carnot’s inexhaustible reservoir or unfillable sink for caloric. But even this is not necessary. The fluid might be supplied or swallowed up within the space. We need suppose only a source or a sink capable of yielding or disposing of unit fluid in unit time: “There is nothing self-contradictory in the conception of these sources where the fluid is created, and sinks where it is annihilated. The properties of the fluid are at our disposal, we have made it incompressible, and now we suppose it produced from nothing at certain points and reduced to nothing at others.” Sources and sinks will be assigned a value equal to the number of units which they emit or absorb in unit time, and Maxwell will in fact use the two the same way, simply assigning to the one a positive value and to the other a negative.

His fluid defined with such sang froid, and in greater detail than this summary indicates, Maxwell put it before the reader as the object of a mathematical analysis. He derived the relations of velocity, pressure, and work which would obtain in its uniform motion through a resisting medium. And with these he had expressions of flux for Faraday’s lines of force, considered as the flow lines of his fluid. And he proceeded to apply them to major instances of electromagnetic action: static electricity, permanent magnets, induced magnetism, and electrical currents—leaving for future consideration the analysis of what he had not yet named the electromagnetic field.

Paradoxes keep rising out of Maxwell’s originality of mind as if to protect his privacy from the intrusion which interpretation is bound to perpetrate. On the one hand, he took as his mission the mathematicization of Faraday’s discoveries. But on the other hand, mathematicization was to him no end in itself, was not at all the desideratum of a science that it was to the continental school. “My aim,” he writes after having applied his mathematical fluid to these first manifestations of electromagnetism, “has been to present the mathematical ideas to the mind in an embodied form, as systems of lines or surfaces, and not as mere symbols, which neither convey the same ideas, nor readily adapt themselves to the phenomena to be explained.” For it is not to mathematics that he looks for clarity: it is to physics. He himself committed no impertinence of interpretation against Faraday, his master: “The conjecture of a philosopher so familiar with nature may sometimes be more pregnant with truth than the best established experimental law discovered by empirical inquirers, and though not bound to admit it as a physical truth, we may accept it as a new idea by which our mathematical conceptions may be rendered clearer.”

Maxwell was referring to Faraday’s temporary hypothesis of an “electrotonic state,” some special condition into which bodies are put by the mere presence of magnets or currents. It is undetectable so long as undisturbed, but it betrays any change by the appearance of a current or a magnetic impulse, and vice versa. Faraday himself had abandoned the notion as superfluous and given his spatial hostages to fortune rather in the form of lines of force. Maxwell recurred to it in the latter part of his paper—in a much more tentative way, however, than he had handled electrostatics, magnetism, interacting closed currents, and other specific effects. His fluid no longer served, and as always when this became true of one of his models, he dropped it: “The idea of the electrotonic state … has not yet presented itself to my mind in such a form that its nature and properties may be clearly explained without reference to mere symbols.” He did derive mathematical expressions to show that the phenomena of induction are not explained by an account of the currents alone, but that the effects presupposed a contribution from configurations in the medium.

The second of his mentors, William Thomson, had already investigated formal analogies between electrical phenomena and elasticity, and had compared the displacement from equilibrium in an incompressible solid under strain to the distribution of forces in an electrostatic system. Maxwell may have been guided, too, by the thought that the transversity of light waves required an aether mathematically identical with an elastic solid. In any case, he looked to a study of the laws of elastic solids and viscous fluids to furnish him with “a mechanical conception of this electrotonic state adapted to general reasoning.” And though he did not arrive at that conception in this first paper, he did state in verbal form a first approximation to what would become Maxwell’s laws of the field, once he had conceived the field more clearly in his mind and named it. One may, perhaps, quote the third of his laws as an illustration of the stage his thought had reached, “The entire magnetic intensity round the boundary of any surface measures the quantity of electric current which passes through that surface.” Already he was thinking of directions and intensities in space, of the “electro-tonic state at any point of space as a quantity determinate in magnitude and direction.” And it was not some lag in his mathematicization which left Maxwell dissatisfied with the state to which this paper brought his subject. He stood at the opposite pole from Lagrange, whose goal had been to free mechanics of all graphic elements, and held rather that

The discussion of these functions would involve us in mathematical formulae, of which this paper is already too full. It is only on account of their physical importance as the mathematical expression of one of Faraday’s conjectures that I have been induced to consider them at all in their present form. By a more patient consideration of their relations, and with the help of those who are engaged in physical inquiries both in this subject and in others not obviously connected with it, I hope to exhibit the theory of the electro-tonic state in a form in which all its relations may be distinctly conceived without reference to analytical calculations.

As the form did take shape in Maxwell’s mind, it became, in its detail and in its ingenuity, in its fertility and in a kind of mechanistic wit, the most engaging (in every sense) of all the imaginary constructs by which Maxwell vivified mathematical analysis in his peculiar pictorial physics. He published the second of his seminal memoirs, “On Physical Lines of Force,” in installments in the Philosophical Magazine in 1861 and 1862. There the word “field” entered into physics. Now he treated not just of the streaming of his lines, their number and direction, but of the whole state of the medium. He went beyond flux to the field and studied its electromagnetic effects considered mechanically. What are the tensions in a medium, and what the motions, which will connect magnetic attraction with electromagnetism and induction? If that can be answered, “We shall have found a theory which, if not true, can only be proved to be erroneous by experiments which will greatly enlarge our knowledge of this part of physics.”

Maxwell generously indicated the course his thinking had taken since his earlier memoir. He had been meditating upon the remarkable formal analogies between the mathematical laws of attraction, conduction, and elasticity in rigid bodies—phenomena which otherwise seem to have little relation one to the other. In 1847 William Thomson had shown that electromagnetic forces might be represented as displacements of particles of a rigid solid under strain. If the angular displacement at every point in the solid is made proportional to the electromagnetic force at a comparable point in the field, then the absolute displacement of the particle will correspond to that of the electrotonic state in the field, and the displacement relative to a neighboring particle to the quantity of the electrical current. The problem, therefore, was to find a physical picture which would make sense of this mathematical assimilation of effects in an electromagnetic field to stresses and strains in an elastic solid.

Magnetism, however, presents certain features that differentiate its effects from electricity, and Maxwell began with magnetic force. These phenomena appear to exhibit two fundamental characters: first, a stress along the line of force, which must by the mutual behavior of magnets be a tension along the line, like that in a rope, rather than a pressure, as in the case of gravitational force, which acts in the opposite direction when the configuration of lines is the same. (That is to say, if we calculate the lines between two north poles and two gravitating bodies, they avoid each other and spread out into space in both cases, but the magnetic effect is repulsion and the gravitational is attraction.) So magnetism argues a tensional strain along each line of force. But it displays a second, and perhaps more interesting configuration. Magnetic tubes of force tend to contract longitudinally under axial tension, but to spread out equatorially into space. And “the next question is, what mechanical explanation can we give of this inequality of pressures in a fluid or mobile medium? The explanation which most readily occurs to the mind is that the excess of pressure in the equatorial direction arises from the centrifugal force of vortices or eddies in the medium having their axes in directions parallel to the lines of force.” Moreover, when one compares magnetism to electricity, the connection “has the same mathematical form as that between certain pairs of phenomena, of which one has a linear and the other a rotatory character.” Faraday had already discovered the latter quality experimentally in the magnetic rotation of the plane of polarized light. But Maxwell deferred these last comparisons to the end of his memoir, since they might lead even deeper into nature than the model under construction.

With that model, Maxwell’s imagination was off into what may well be described as his neo-Cartesian fantasy—a new physics of the vortex. Now, Faraday’s tubes of force became not the stream lines of a mathematical fluid, but rather a system of roller bearings filling all space. Maxwell now made each magnetic tube of force rotate on its axis instead of flow along it. Investigating the mechanical conditions of equilibrium in such a state of affairs, Maxwell showed that at every point in the medium the pressures will be different, that the direction of least pressure will follow that of the lines of force, and that the ratio of greatest and least pressures will be the square of the intensity of the force at any point. This, in turn, will yield the ordinary laws by which magnets act on currents. But this is only the beginning. Our model does not yet tell us why the vortices producing magnetism should rotate at all, or why they should be arranged to exhibit the laws of force in a magnetic field. “We have, in fact”—and this is the second part of the memoir, which applies the theory of magnetic vortices to the electric current—“We have, in fact, now come to inquire into the physical connexion of these vortices with electric currents, while we are still in doubt as to the nature of electricity, whether it is one substance, two substances, or not a substance at all, or in what way it differs from matter, and how it is connected with it.” Truly, as Maxwell observed in passing, these problems are “of a higher order of difficulty.” For to know why a particular distribution of vortices indicates an electric current would lead a long way toward answering a very important question indeed, namely: “What is an electric current?”

A preliminary mechanical difficulty had to be resolved. The theory required that all the vortices revolve in the same direction. But how could this be, if they lay side by side? One gear-wheel engaging another turns it in the opposite direction. And Maxwell turned to the real engineers in his extremity, and imported into the aether the device of the “idle” wheel: “The hypothesis about the vortices which I have to suggest is that a layer of particles, acting as idle wheels, is interposed between each vortex and the next, so that each vortex has a tendency to make the neighbouring vortices revolve in the same direction with itself.” But Maxwell needed play in his medium and could not do with fixed axles for his aetherial idle wheels; he pursued the engineers into even more intimate detail and adopted specifically the analogy of Siemens’s governor on steam-engines, which employed idle wheels whereof the centers were capable of translation. In such a case the motion of the center is half the sum of the circumferential motion of the driving wheels on either side. “Let us examine,” writes Maxwell, “the relations between the motions of our vortices and those of the layer of particles interposed as idle wheels between them.”

That examination yielded other restrictions which must be imposed, chief among them that the idle tubes must be held to a thickness of one molecule, and that they must rotate between the vortical tubes of force without slippage. But perhaps this much will exemplify the capacity of Maxwell’s imagination for literal detail. It makes a truly startling combination with the grandiosity of the scheme as a whole, which—it must be remembered—was no less than a mechanical explanation, in principle though not in actual fact, of magnetism and electricity. Thus, magnetism becomes the kinetic energy of rotation of the vortices of a medium filling all space; the tangential pressures called into play by the transmission of rotation from one part of the field to another then constitute electromotive force; next, the electric current becomes the translation of the particles of the medium under the influence of that force directed along the idling layer, which is turning between the vortices without developing angular momentum since it is unimolecular in depth; finally, the resistance to this translation transforms energy into heat, and is the only occasion by which electromagnetic energy is degraded in the operations of the field.

All this can be calculated. And we are justified, therefore, in our initial assumption that, “Magneto-electric phenomena are due to the existence of matter under certain conditions of motion or of pressure in every part of the magnetic field, and not to direct action at a distance between the magnets or currents.” It remained to cover electrostatics with the model, which Maxwell accomplished by considering the statical electricity accumulated on condensing surfaces as the potential energy of strain stored up in physical displacements of the medium.

Thence flowed consequences far more interesting than any following out of magnetism as the kinetic energy of aethereal rotation. The first was specific and had to do with a new theory of the dielectric; the second, universal and assimilated electromagnetism to light. Throughout the entire analysis of the model, Maxwell had to assume that the substance of the medium possesses the perfect elasticity of rigid bodies. He saw conduction of the current as the flux of particles. Insulators would not, by definition, transmit that flux. But while barring the current, they did transmit electrical effects. And Maxwell hit on one of his nicest analogies in illustrating what the physicist means by a dielectric: “A conducting body may be compared to a porous membrane which opposes more or less resistance to the passage of a fluid, while a dielectric is like an elastic membrane which may be impervious to the fluid, but transmits the pressure of the fluid on one side to that on the other.”

Thus, there is no flow of particles in the walls of a Leyden jar. What induction, or charging, may be thought to do is to polarize each molecule in situ. “We may conceive that the electricity in each molecule is so displaced that one side is rendered positively, and the other negatively electrical, but that the electricity remains entirely connected with the molecule, and does not pass from one molecule to another.” Across the whole surface the effect will be, therefore, a linear displacement, which though it is not a current, and is indeed rather a sudden strain, may nevertheless be considered as the beginning of a current and be analyzed accordingly: “We cannot help regarding the phenomena as those of an elastic body, yielding to a pressure, and recovering its form when the pressure is removed.” And of all Maxwell’s figures, this displacement current in a dielectric was the most puzzling to his contemporaries. It was as if he had tried to blur the clear distinction which allowed them to say categorically when a current is not a current. It did not help towards clarity that in later discussion he abandoned the physical lurch of the electrified molecule into a position of polarized strain and substituted an abstract change in the structure of aether. It forced, or would have forced had it been accepted, a change in the conception of condensers. Instead of considering their coatings as termini where currents ended and charge accumulated, it would have closed all currents through the body of the dielectric. But important though that is for sophisticated thinking about the nature of electrical energy, it was the second consequence of his model as an electrostatic medium which (for a welcome once) combined drama with depth.

Maxwell had seen immediately that the wave theory of light required of a medium just the same sort of elasticity as did his field theory of electromagnetism. The equations took the same form. It was possible from his elastic-solid model of the medium to compute the velocity with which a shear wave would be propagated, which on the analogy is the same as an electromagnetic wave. In 1856 two German physicists, Weber and Kohlrausch, working on quite a different hypothesis, had determined the velocity with which an electrical impulse will be propagated along a wire. They were concerned with the proportionality of units between electrodynamics and electrostatics. That factor must have the dimensions length over time, which is to say of velocity, since electrostatic repulsion is the same type of quantity as electrodynamic repulsion between two lengths of wire carrying a certain charge in a certain time. They measured the velocity experimentally and found the value to be almost 3.1 × 10¹⁰ centimeters per second. But in 1849 Fizeau had already refined the determination of the speed of light by rotating a cut-out perforated wheel at such a speed that a ray of light passed through a gap between the teeth was reflected and arrested on the return by one of the teeth. The dimensions and angular velocity permitted calculation of the speed of light. His figure (an improvement on that known from eclipses of the moons of Jupiter) was 3.15 × 10¹⁰ centimeters per second.

“The velocity,” wrote Maxwell, “of transverse undulations in our hypothetical medium, calculated from the electromagnetic experiments of MM. Kohlrausch and Weber, agrees so exactly with the velocity of light calculated from the optical experiments of M. Fizeau, that we can scarcely avoid the inference that light consists in the transverse undulations of the same medium which is the cause of electric and magnetic phenomena.”

Now it is not only the form of equations which are the same. The italics are Maxwell’s—and well they might be!

Finally, in his third and definitive paper, “A Dynamical Theory of the Electromagnetic Field,” Maxwell sloughed off all this structure of imaginary mechanical detail. But out of sight was not out of mind, either for him or for his science, for the crucial terms and the ideas they express remain: the electromagnetic flux from his first paper, displacements and fields from the second, and from the third the very conception of a marriage of electricity and dynamics in the theory of the medium. Thus electrodynamics remains the science of the energy of the field: “The theory I propose may therefore be called a theory of the Electromagnetic Field, because it has to do with the space in the neighbourhood of the electric or magnetic bodies, and it may be called a Dynamical Theory, because it assumes that in that space there is matter in motion, by which the observed electromagnetic phenomena are produced.” And though he abandoned all specific models, he must not be supposed to have abandoned the principle of mechanism. That is to say, electromagnetic phenomena are clearly expressions of motions of some kind, causally interrelated and communicated by forces. They were subject, therefore, to the general laws of dynamics, and specifically served the conservation of energy. Only gravity escaped the unification which Maxwell’s Laws of the field imposed on magnetism, electricity, and light. It still seemed to act at a distance between like bodies. Nor was Maxwell optimistic: “As I am unable to understand in what way a medium can possess such properties, I cannot go any further in this direction in searching for the cause of gravitation.”

Whoever understands those laws will already know them as familiarly as the law of falling bodies. Whoever does not, will scarcely appreciate their symmetry. Still, there is an astringency about the mere appearance of the field equations which may be salutary as the distillation of an imagination so various as Maxwell’s

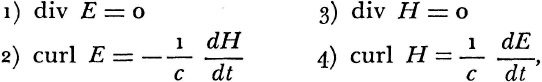
where E is the intensity of the electrical field; H, of the magnetic field; t is time; c, the velocity of light; and div and curl, certain mathematical operations in vectorial analysis, i.e. a way of specifying a directional aspect in the effective quantities.

Einstein once observed that the statement of those laws had been the most important event in physics since Newton. And from having followed the route of Maxwell’s mind we may, perhaps, appreciate what it is that these laws do. They connect in every respect the amount, the flux, and the interrelation of an electrical field with the magnetism it induces, and vice versa. The velocity of propagation appears as a constant, time as a parameter, and space by virtue of the definition of the field. These equations connect phenomena in a different way from Newton’s. Newton’s laws conserve energy in the motions of systems of bodies and take no account of the space in between; Maxwell’s laws conserve energy in its gradations in space and take no account of bodies as such.

Nevertheless, Maxwell had pressed himself more closely into the problem of describing electromagnetic effects than relativity theorists have supposed who would represent his attention spread out over all space, or his soul committed to the aether. His equations in the form just given are abstracted into free space, or free aether, where there are fields but no charges or currents. In fact, he was much concerned with both, and his own expression of his equations is correspondingly less laconic. A surprise may await the physicist who would pursue Maxwell’s laws to their first statement. The vectorial notation does not appear. In another memoir, however, Maxwell did coin the wonderfully graphic term “curl” for the operation that mathematicizes the behavior of lines of force wrapping around a wire. It is like Newton inventing “fluxions” out of the necessities of his physical ideas, and then not using the calculus to explain them. Instead, therefore, of the four equations now usually given as his laws, there are twenty. Figuring therein are as many variables which he called electromagnetic momentum, magnetic intensity, electromotive force, true current, displacement current, total current—each of which has three components along the x, y, and z axes—and finally two undirected (or scalar) quantities, free electricity and electric potential. For the relations among any of these quantities and those of the others which might concern a particular problem, were what interested Maxwell. He was concerned with conservation of energy, not with aether or the structure of space. He might, indeed he would, abstract with the greatest generality from particular mechanical images, and warn that he used terms like momentum and elasticity in an illustrative sense only.

In speaking of the Energy of the field, however, I wish to be understood literally. All energy is the same as mechanical energy, whether it exists in the form of motion or in that of elasticity, or in any other form. The energy in electromagnetic phenomena is mechanical energy. The only question is, Where does it reside? On the old theories, it resides in the electrified bodies, conducting circuits, and magnets, in the form of an unknown quality called potential energy, or the power of producing certain effects at a distance. On our theory it resides in the electromagnetic field, in the space surrounding the electrified and magnetic bodies, as well as in those bodies themselves, and is in two different forms, which may be described without hypothesis as magnetic polarization and electric polarization, or, according to a very probable hypothesis, as the motion and strain of one and the same medium.

For Maxwell was a nineteenth-century physicist, after all, and the prince of nineteenth-century physicists.

BUT FIELD PHYSICS tells only half the story, nor has physics yet decided which was the more important half. “Modern physics,” wrote Max Planck in the centennial symposium, Clerk Maxwell, 1831-1931, “recognized two main conceptual schemes, the physics of discrete particles and the physics of continuous media, and it is since Maxwell’s time that the distinction between them first became more apparent. These schemes correspond nearly but not quite to the physics of Matter and the physics of the Aether. In both regions Maxwell introduced new and fruitful ideas.” Planck did not specify the exceptions contained in that “not quite.” Perhaps he had in mind that Maxwell’s kinetics arrested the anti-mechanistic tenor of energetics, hitherto the physics rather of force than of matter, by reducing thermodynamics to the behavior of particles. Maxwell himself was a better historian of science than Planck—as a scientist, indeed, he took the subject very seriously. He knew how old the issue was, and how modern, and once lectured to the British Association on the subject of molecules:

The mind of man has perplexed itself with many hard questions. Is space infinite, and in what sense? Is the material world infinite in extent, and are all places within that extent equally full of matter? Do atoms exist, or is matter infinitely divisible?

The discussion of questions of this kind has been going on ever since men began to reason, and to each of us, as soon as we obtain the use of our faculties, the same old questions arise as fresh as ever. They form as essential a part of the science of the nineteenth century of our era, as of that of the fifth century before it.

In the nineteenth century the discussion carried reason into the laboratory to deal with atoms, leaving the geometers’ imagination outside to deal with continuity. For particle physics has been peculiarly associated with the laboratory tradition, to which Maxwell equally belongs by virtue of having planted his feet so firmly in both camps. This is a corporate tradition, a little sectarian perhaps, but not lonely like that of mathematical idealism, into which a Descartes or an Einstein withdraws to take thought. Maxwell, indeed, was the founder of that laboratory which was to the second scientific revolution in physics almost what Padua had been to the first—the Cavendish Laboratory in Cambridge. There he held the first chair of experimental physics in the university.

A Cambridge man himself, he had gone back to Scotland as professor of natural philosophy at Aberdeen, and thence to King’s College, London, in 1860. His own most creative work occupied the five years he spent in London. As a teacher of general physics he was not a success. Ideas would occur as he lectured to divert him from the path he had intended. Bending over their notebooks, his students could not follow. He retired to his family property in 1865. It is a pity that the Cambridge post was not established until 1871, nor the laboratory under way until 1874, because Maxwell died in 1879 at the age of forty-nine; and it was only as the director of a laboratory that he came into his own in the communication of his science. There he was at his best, in the inner circle atmosphere which a great laboratory creates. His charm and his wit, his quizzical turn of mind, needed intimacy to flourish. His verses still form part of the oral tradition of physics, the personal lore which physicists hand on from one generation to the next in a kind of pale Pythagoreanism—pale but a little heavy, for to the outsider the verses do not seem very good.

The quizzical quality emerges in his scientific work, in the fun he evidently had with the mechanistic detail of his electrodynamic aether models, in experiments to determine how a cat lands on its feet, and in turns of phrase: “The top which I have the honour to spin before the Society …”—so he introduces a paper on “the motions of a body of invariable form about a fixed point, with some suggestions as to the Earth’s motion.” His first paper on particle physics, the paper which won him reputation, was a dynamical study of the conditions of equilibrium in Saturn’s rings. From there to the kinetic theory of gases was a reduction in scale, but not in importance. For Maxwell imported into molecular science that technique of analysis upon which it has thriven ever since, statistical mechanics. He resigned himself to statements of probability, and made the most of this inevitable rape upon the reason.

The kinetic theory of gases started in the attempt to extend dynamical considerations over phenomena which normally preoccupied the chemists. What we mean by explanation, Maxwell pointed out in an address “On the Dynamical Evidence of the Molecular Constitution of Bodies,” is just that we should extend over some set of phenomena a principle applicable to others. No chemist would have presumed that the various geometrical constructions he imagined for his compound molecules were anything more than a symbolic shorthand for the physical relations of the constituents. Most physical theories had been constructed by just such methods of hypothesis—calculating what would happen if some hypothesis were true, and then comparing to actual events. The difficulty in chemistry, as in most branches of physics at similar stages, was that speculators lacked terms or methods of sufficient generality at the early stages of induction. But help was at hand: “In the meantime the mathematicians, guided by that instinct which teaches them to store up for others the irrepressible secretions of their own minds, had developed with the utmost generality the dynamical theory of a material system.” And surely the most unobjectionable hypothesis about the constitution of bodies is that which assumes no more than that they are material systems serving the laws of mechanics, the most general yet established. But only in the case of gases can we reasonably expect the particles of matter to enjoy sufficient freedom from undetectable and indistinguishable relations to reward dynamical analysis.

The first kinetic model of gases was imagined by Daniel Bernoulli in a treatise of Hydrodynamica in 1738. Applying the corpuscular philosophy literally enough to confined airs, he considered pressure as the effect of bombardment of the container by particles travelling in paths resolved normally to the sides. In the early nineteenth century one Le Sage, another Genevan, radically enlarged the model to cover the entire universe, and in Lucrèce newtonien he imagined gravity to be caused by the impact of atoms streaming at random through infinite space. If there were only one body in the universe, there would be no effect. But since there are more, each masks the others from a certain proportion of the corpuscular bombardment, and the effect is a diminution of pressure between bodies which gives the appearance of gravitational attraction. Maxwell devoted some pages to this fancy in his article “Atom” in the ninth edition of the Encyclopedia Britannica; nor though he saw the grave objections, chiefly that it fails to permit a steady state of temperature in bodies undergoing bombardment, did he read it right out of court.

A little-studied English physicist of the same generation, John Herapath, recurred during his lifetime to a favorite hypothesis which made Boyle’s law a consequence of molecular kinetics. He followed Bernoulli in making the pressure on any face of a cubical container equal to 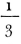MV². He also assumed, less fortunately, that temperature is measured by the momentum of the particles. This gave him pressure as proportional to the square of the absolute temperature, so that his computation of absolute zero, the rate of diffusion, the value of Avogadro’s number, and the relation of specific heat to atomic weight would have been wrong even if based on sufficient data. But it was a brave attempt, and permitted computation in cases where temperature was held constant. For example, Herapath gave the relation

where p is pressure and ρ density, from which Joule calculated in 1848 the average velocity of the hydrogen molecule as 6,055 feet per second at 32° F and atmospheric pressure.

Clausius took up the subject in 1857, and so deepened what had hitherto been vulnerable to criticism as the occasional resort of the mechanistic enthusiast or crank that kinetics carried off for a time the main stream of thermodynamic reasoning. His paper “On the Kind of Motion We Call Heat” inaugurated the dynamical study of gases as an actual program of analysis and not just an assertion of particulate policy. He grappled with the problem that others had evaded in their postulates of ideal gases, consisting of point-masses. Arguing that the total energy of a gas must be divided between the various modes of motion of its molecules, he developed a partition expression for that portion of the total kinetic energy due to the motion of molecules in translation and that due to their spin about their own axes. This explained why the specific heat of gases is greater than what had been predicted so long as all the heat, like all the pressure, was supposed to manifest translational momentum. The pressure, too, would be affected by whatever mutual attractions or repulsions molecules might exert over one another. And on purely analytical grounds Clausius developed approximations to diminish these discrepancies.

In a second paper of 1859 Clausius addressed himself to a further embarrassment with which experience confronted the kinetic theory of gases. Gases do not diffuse with nearly the velocity which the theory expected of the average molecules. The deficiency Clausius attributed to the short path each can follow before it hits another and is deflected in some new direction. Thus, as in a crowd dispersing, each individual bounces this way and that, making much less time than if he could step straight out, and the rate of progress is a function both of velocity and the mean free path.

With these refinements, theoretical predictions of the pressure, volume, density, and temperature relations of actual gases came closer to laboratory measurements than before, but agreement was still far from reliable; and it was at this point that Maxwell stepped into the kinetic scene with a new and a portentous analytical idea, which he had employed in the management of his computations of the motion of particles in the rings of Saturn. Clausius and the others had considered the molecules of a gas as if all moved at the same velocity. It was, of course, an unreal assumption, but Clausius seems to have seen no alternative except the desperate, indeed the impossible, expedient of following every molecule throughout its whole career in the experiment. Maxwell published his first paper on the subject, “Illustrations of the Dynamical Theory of Gases,” in 1860, the year before his second paper on lines of force. They both display the same imaginative use of models. Clausius had determined no parameters for his algebraic expression relating the mean free path to the distance between the centers of mass of particles at collision. It seemed to Maxwell that experimental data for the viscosity, heat conductivity, and diffusion of gases would permit such computations: “In order to lay the foundation of such investigations on strict mechanical principles, I shall demonstrate the laws of motion of an indefinite number of small, hard, and perfectly elastic spheres acting on one another only during impact.” And if the results turned out to be consistent with known gas laws, then they might lead in to more accurate knowledge of the constitution of matter: they might, in other words, bear upon the fundamental discussion of atomism.

But first he must grapple with the distribution of velocities, and to this end Maxwell introduced into a fundamental physical problem the calculus of probability, that mode of analysis which had hitherto seemed natural when applied to games or affairs, but an admission of our inability to know nature when things were the object of study. Not that Maxwell himself regarded its rigor as equal to that of strict dynamics, but no other method presented itself, either experimental or mathematical. Thus, Maxwell inaugurated in this memoir the science of statistical mechanics. Except under very rare conditions of impact, collisions would be bound to alter the velocity of particular molecules. But in a steady state, distribution of velocities from zero to infinity must follow some definite law. One might, therefore, describe the system by computing what portion of the molecules would be at each velocity.

Though he did not then draw the famous bell-shaped curve, and though the later refinements were serious by which Boltzmann would win the honor of co-namesake, nevertheless Maxwell did ascertain that distribution in principle. And the most interesting thing about the pattern is that it was not new. The velocities might be plotted on a diagram in which each is measured by a vector drawn from any fixed point. Then if a dot be recorded at the far end of each vector, the same diagram could represent bullet-holes spattered around the bull’s eye of a target, or an astronomer’s record of successive observations of the same fixed star. It was Gauss’s law of error, turning up thus unexpectedly in the hitherto deterministic physics of particles.

In retrospect, the method will seem the most significant contribution of this paper, but the immediate results were startling enough to speak for its value. With the results of experiments on air by Stokes, Maxwell’s first kinetic equations gave 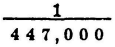of an inch as the mean free path, and an average of 8,077,200,000 impacts per particle per second at standard conditions. As a surprising consequence of one equation, viscosity turned out to be independent of density in a gas—a result which no experiment then confirmed, but which did establish itself as the theory took on sophistication and refinement. But for Maxwell perhaps the most encouraging success was his confirmation of Gay-Lussac’s law of combining volumes. Early in the nineteenth century Gay-Lussac had argued on strictly chemical grounds that different gases at the same temperature and pressure must contain the same number of molecules in unit volume. Now Maxwell found the identical result by a kinetic consideration of the simple diffusion of one gas into another. When diffusion is complete, the average kinetic energy is the same for a particular molecule in either gas. This will also be a state of equal temperature. It follows that the condition of equal temperature is that the average kinetic energy of a single molecule should be the same. It had been established that the pressure of a gas is given by two-thirds the kinetic energy in unit volume. Hence, if pressure and temperature are the same, then total kinetic energy as well as average kinetic energy of each molecule are equal, and hence unit volume must contain equal numbers of molecules. It made a precise example of what Maxwell meant by explanation, gathering chemical and dynamical considerations under the one principle of atomism, and thus strengthening the principle in these mutual supports.

The kinetic theory of gases remained far from perfect. Its great difficulty, which it did not overcome in Maxwell’s lifetime, was to divide the total energy of the molecules between translation, rotation, and the various modes of vibration of which the atoms might be capable. Pressure had to depend on the kinetic energy of translation alone. Specific heat would depend on the rate at which total energy would rise with temperature. Theoretically the ratio of specific heats at constant pressure and constant volume would yield the ratio of the increments of the whole energy to that of translation. But except for the infrequent monatomic gases, the ratio predicted by theory was always too high for the observed value. The more complicated and various the modes of vibration which do occur in the poly-atomic molecule, the worse the disagreement with gases, which obstinately refused to absorb as much heat as they seemed to need.

In his first paper Maxwell proved that the known relation between specific heats ruled out the assumption (with which he had himself begun) of hard, spherical particles. And in 1866 Maxwell published his greatest memoir on the subject, “On the Dynamical Theory of Gases.” Therein he abandoned his model to the facts as cheerfully as when he discarded the mathematical and dynamical fluids on which he had forged his field equations. In lieu of the description of the molecule as minuscule, impenetrable, elastic, round, and free flying, he substituted other mathematically more convenient characteristics. He had confirmed by experiments of his own the most surprising, if not the most seminal, consequence of his earlier formulations—that viscosity is independent of density. Now he invented a molecule that would yield that fact with a certain facility.

This idea too he may have owed to Faraday, for his second paper fuzzes the effective molecule from an impacting sphere into a body which exerts intermolecular forces to some certain distance beyond its physical surface. Since it is still a question of molecular motion, the force must be repulsive. And he makes the new molecule one that repels its kind with a force inversely as the fifth power of the distance between them. The advantage is mathematical. Maxwell needed to assume no particular conditions in molecular collisions beyond the conservation of energy and momentum. In particular, he need not concern himself with the distribution of velocities in a gas which, instead of being in a steady state, is streaming or diffusing. Assuming billiard-ball molecules, Boltzmann labored for years over that intractable problem, employing one horrible approximation after another. Maxwell simply abolished the difficulty by altering the nature of the encounter. With a repulsive force of high enough inverse power, molecules at any considerable distance from each other will move at almost constant velocity. Only when they come close do they change speed or direction. But if we are concerned with conservation and not with summing up impacts, we need not know how much of the total velocity pertained to each. With a fifth-power law, the closest approach in a head-on collision is inversely proportional to the fourth root of the relative velocity; and the relative velocity (which is what no man could determine or postulate in a streaming gas) disappeared from the final equation of viscosity. So Maxwell used a fifth-power law, and then compared the consequences to nature. Boltzmann was overwhelmed with magniloquent admiration, and Max Planck’s centennial essay quotes his Wagnerian account of the impression which the memoir made on him:

At first are developed majestically the Variations of the Velocities, then from one side enter the Equations of State, from the other the Equations of Motion in a Central Field; ever higher sweeps the chaos of Formulae; suddenly are heard the four words: “put n = 5.” The evil spirit V (the relative velocity of two molecules) vanishes and the dominating figure in the bass is suddenly silent; that which had seemed insuperable being overcome as if by a magic stroke. There is no time to say why this or why that substitution was made; who cannot sense this should lay the book aside, for Maxwell is no writer of programme music, who is obliged to set the explanation over the score. Result after result is given by the pliant formulae till, as unexpected climax, comes the Heat Equilibrium of a heavy gas; the curtain then drops.

In fact another curtain was going up on the physics of particles, but we cannot stay to watch that play, which is still in progress. It will be enough to identify the character with which Maxwell had at the end invested the protagonists in the drama of classical physics, thus drawing to its close. Maxwell’s influence throughout was nothing if not unexpected, and nowhere more than in the turn which he gave to the dialogue between atoms and the continuum. For he switched the roles. On the one hand, he took electromagnetism out of the domain of mechanistic formalism, and paired or even united it with the new optics in the physics of the continuum. On the other hand, he retrieved thermodynamics from the Schwärmerei of energetics, and turned the study of energy into a special case of the dynamics of particles of matter in motion.

In effect, therefore, Maxwell blocked the escape from mechanics into energetics. The astringency of his physical wit nowhere appears to more characteristic advantage than in his invention of a daemon to deflate the pretensions of the second law as a mystique of nature. In imagination he conjured up a box with two compartments, one containing a hot gas and the other a cold one. The partition contains a trap door, manned by a daemon whose senses and responses are of the same order of fineness and quickness as the darting molecules. Whenever a fast molecule approaches the door from the colder side, he might flip it open and let it through, and thus he would make heat pass from a cold body to a hot one. For it was clear to Maxwell that the second law had a status in science quite different from the first. The conservation of energy was his cornerstone, embedded in the nature of things. But the second law is statistical, expressing (as Maxwell thought) rather our incapacities to know or act than the nature of physical reality. Though he inaugurated statistical mechanics, he was still too close to the eighteenth century and the Enlightenment, still too far from the twentieth and positivism, to suppose that the order of things might itself be an order of chance, or that (like the second law) all science is about itself and its own operations. Maxwell could not foresee the predicament of the physicist as himself a daemon, intruding willy-nilly into nature, though without the compensating advantage of choice.

Well versed in the philosophical history of science, he knew the traditions which the two aspects of his physics carried on. “There are thus,” he wrote in his paper on “Atoms” for the Britannica,

two modes of thinking about the constitution of bodies, which have had their adherents both in ancient and in modern times. They correspond to the two methods of regarding quantity—the arithmetical and the geometrical. To the atomist the true method of estimating the quantity of matter in a body is to count the atoms in it. The void spaces between the atoms count for nothing. To those who identify matter with extension, the volume of space occupied by a body is the only measure of the quantity in it.

As for Maxwell, his atomism saved his own scientific soul alive from the Cartesian fallacy into which his mathematicization of Faraday’s electromagnetic medium might otherwise so easily have led him. The opening sentences of the great memoir, “On the Dynamical Theory of Gases,” clearly distinguish between the functions of geometry, concerned with extension, and the advantage of atomism, which allows science its grasp on the properties of bodies:

Theories of the constitution of bodies suppose them either to be continuous and homogeneous, or to be composed of a finite number of distinct particles or molecules.

In certain applications of mathematics to physical questions, it is convenient to suppose bodies homogeneous in order to make the quantity of matter in each differential element a function of the co-ordinates, but I am not aware that any theory of this kind has been proposed to account for the different properties of bodies. Indeed the properties of a body supposed to be a uniform plenum may be affirmed dogmatically, but cannot be explained mathematically.

Nevertheless, Maxwell was not without hope of resolving the difference and arriving at a unification of aether and atoms, field physics and molecular physics. In the article on atoms, wherein he allowed his fancy freer reign, he explored a speculation which Sir William Thomson (Lord Kelvin to be) had spun out of certain mathematical investigations by Helmholtz into the theory of rotational motion in fluids. The discussion presents itself as a kind of aethereal hydrodynamics. He invests his fluid with convenient physical properties. It is to be homogeneous, incompressible, and devoid of viscosity. Its motion is to be continuous in space and time. It is, in fact, to be very like Maxwell’s first mathematical fluid, except that it is a material substance. Nor need we worry whether such a fluid exists, so long as its properties are mutually consistent. Of these, the most significant is that such a fluid cannot be molecular. If it were, the volume would increase discontinuously with mass in any container being filled. And Helmholtz proved by mathematical analysis that when rotational motion is set up in such a fluid, the vortex lines are permanent and always contain the same points. Moreover, if a tube be formed bounded by a surface through which run vortex lines, such a tube must return into itself (unless it is infinite) and may be called a ring. These rings are invariant in volume, conservative in rotation, and discrete in identity within the fluid, though continuous in extension throughout it. They display, in other words, just those properties which are requisite in atoms: constant magnitude, capability of internal motion, and sufficient variety in characteristics of shape or size so that they might explain the properties of bodies. Such a medium would combine heterogeneity in its motion with homogeneity and continuity in its density and extensive properties. Might it not, fancied Maxwell, unify a physics still shifting between atoms and the void, now concerned with kinetics and again with fields?

The disciple of Lucretius may cut and carve his solid atoms in the hope of getting them to combine into worlds; the followers of Boscovich may imagine new laws of force to meet the requirements of each new phenomenon; but he who dares to plant his feet in the path opened up by Helmholtz and Thomson has no such resources. His primitive fluid has no other properties than inertia, invariable density, and perfect mobility, and the method by which the motion of this fluid is to be traced is pure mathematical analysis. The difficulties of this method are enormous, but the glory of surmounting them would be unique.

Maxwell never quite said whether this fluid in which the vortex rings are atoms is the aether; but it is certainly very like the aether, as indeed it is in its mathematical properties very like the field-fluids of his papers on the lines of force. We do not, in any case, go beyond the evidence in seeing how the latter evolved in his scientific consciousness into the aether which filled all space. And historically at least, it is important to press the point a certain way. For it permits us to distinguish between Newton’s aether and Maxwell’s both in form and function. Newton’s aether (to recall that argument) was hypothetical and ancillary to his physics, which would have suffered only in intelligibility but not in structure were it away. Not so Maxwell’s, whose unification of light and electro-magnetism in field theory worked the aether right into the bone and texture of classical physics. In Newton, space is the arena of physics, the housing of reality, and aether is only what he imagines to fill it. The distinction will impose itself when it is remembered that space in Newton is continuous Euclidean extension, but that aether is particulate.

Maxwell’s aether has changed its texture. It is not particulate, not corpuscular, not atomic. The findings of kinetics alone would rule that out. “A molecular aether would be neither more nor less than a gas,” he pointed out in a lecture on the “Molecular Constitution of Bodies.” It would be subject to the gas laws. “Its presence, therefore, could not fail to be detected in our experiments on specific heat, and we may therefore assert that the constitution of the aether is not molecular.” Its presence might, of course, be detected in another way, consistent with its function as the continuous medium filling all space and transmitting transverse vibrations of electromagnetic and luminous energy. And Maxwell evoked the image of the “great ocean of aether.” Do dense bodies drag some portion of it with them in their passage? Or does aether simply stream through them, “as the water of the sea passes through the meshes of a net when it is towed along by a boat”? If it were possible to compare the velocities of light in opposite directions between two points on earth, that question might be answered. Unfortunately the theory predicted a difference of only about one hundred millionth of the time of transmission—too small to be detected. Maxwell had himself designed and performed a spectroscopic experiment by which he hoped to find a difference in the deviation of a ray from a distant star according as it traversed a prism in the direction of the earth’s motion, and perpendicular thereto. The results were negative. But physics was only at the most preliminary state of its investigations of the theory of the aether, which would require unparalleled delicacy in conception as in execution. And near the time of his death Maxwell could say with confidence only this:

Whatever difficulties we may have in forming a consistent idea of the constitution of the aether, there can be no doubt that the interplanetary and interstellar spaces are not empty, but are occupied by a material substance or body, which is certainly the largest, and probably the most uniform body of which we have any knowledge.

And in practice Maxwell’s physics went further than he knew, all discernment though he was. For both in form and function—continuous in the one and energetic in the other—so full was Maxwell’s space of aether, that no physical distinction might be saved between them. Any question asked about the one would implicate the other. And it would take a more critical, a more abstract Cartesianism than that of Thomson’s vortex molecules to restore reason to this science, or vice versa. It is easy for us, wise after the event (and it will grow easier as elementary physics courses are revised and these ideas are taught to children) to see how the complications which all these different requirements were introducing into the aether were giving it the character of circles before Kepler, of light before Newton, of phlogiston before Lavoisier, and of adaptation before Darwin. It was time for a new look.

But that is to anticipate, and nothing is more unhistorical or unfair to those who went before. And it will be just, therefore, and in keeping with the duality of Maxwell’s own creation, to leave him as the ultimate impresario of classical physics, who brought the chief characters, the atom and the aether, to the center of the stage, and there left them all exposed to the winds of criticism blowing up out of positivism.