Footnotes
1 David Sklansky - The Theory of Poker, Chapter 23: “The Psychology of Poker” discusses multiple level poker thinking.
2 Colin F. Camerer - Behavioral Game Theory, pp.16-20 and pp.209-218.
3 Brit Grosskopf and Rosemarie Nagel - The Two-Person Beauty Contest.
http://erl.tamu.edu/bgrosskopf/sdarticle.pdf
4 This is a potential explanation for why so few people pick zero in the n-person game.
5 The term zero-sum means that the payoffs to each player sum to zero, or equivalently, to any constant number. Poker is zero-sum because the winnings of one player must necessarily be the losses of another. The case with more than 2 players (known as n-player game theory) is more complicated. This is because players can improve their payoffs by forming alliances amongst each other. Explicit collusion is of course forbidden in poker. However, two players can form an implicit “alliance” in limit poker by having one player bet and the second player raise, cutting down the odds received by the other players and forcing them to fold more hands. The trouble with n-player game theory is that there are many such alliances that can be formed and must be considered. For more on this issue, see Bill Chen and Jerrod Ankenman - The Mathematics of Poker, Chapter 29: “Three’s a Crowd: Multiplayer Games.”
6 The theory of two person zero-sum games began with John von Neumann and Oskar Morgenstern - The Theory of Games and Economic Behavior. They showed how to optimally play such games with their “minimax theorem,” — essentially the final word on how to optimally play a two-person zero-sum game. They were also some of the first people to attempt to apply these ideas to some simple versions of poker.
7 Bill Chen and Jerrod Ankenman christened this concept “alpha.” See The Mathematics of Poker, p.113. However, the relationship has been known for a long time. See, for example, David Sklansky - The Theory of Poker, Chapter 19: “Game Theory and Bluffing.” Also see “Appendix B: Game Theory” starting on page 383.
8 This is named after John Forbes Nash who showed that there is an optimal way to play any n-person, finite game. In the case of a two person zero-sum game, the Nash equilibrium is equivalent to the minimax theorem.
9 Polaris has been created by the Computer Poker Research Group at the University of Alberta.
http://poker.cs.ualberta.ca/
10 Darse Billings et al. - Approximating Game-Theoretic Optimal Strategies for Full-scale Poker.
http://webdocs.cs.ualberta.ca/~games/poker/publications/IJCAI03.pdf
11 The information in this paragraph is taken from an article by Bryce Paradis on poker robots in the Two Plus Two Online Magazine.
12 This model is known as the U[0,1] model and goes back as far as John von Neumann and Oskar Morgenstern - The Theory of Games and Economic Behavior.
13 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, Chapter 10: “Facing The Nemesis: Game Theory.”
14 Sonia’s homepage is on http://pokerparadime.com/.
15 Approximately 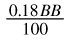 over 730,000 hands. It’s actually very impressive that Polaris manages to lose so little against Sonia; most humans lose much more. It shows that any mistakes Polaris is making are worth relatively little in terms of EV for Sonia’s potential exploitations. This provides strong evidence that Polaris’s strategy isvery good and worth studying further. http://pokerparadime.com/MessageBoard?messageid=158
over 730,000 hands. It’s actually very impressive that Polaris manages to lose so little against Sonia; most humans lose much more. It shows that any mistakes Polaris is making are worth relatively little in terms of EV for Sonia’s potential exploitations. This provides strong evidence that Polaris’s strategy isvery good and worth studying further. http://pokerparadime.com/MessageBoard?messageid=158
16 Mike Caro - Caro’s Book of Poker Tells.
17 Nesmith C. Ankeny - Poker Strategy, p.28, Table 2.3.
18 This is not as true in jacks-or-better to open draw poker played with a joker which would either count as an ace or could be used to complete a straight or a flush. This game was widely played in the cardrooms of California before the legalization of hold ’em in 1987. See Mason Malmuth - Winning Concepts in Draw and Lowball for more information.
19 David Sklansky - The Theory of Poker, “The Cost of Giving Your Hand Away,” p.63.
20 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, p.96.
21 Probabilities derived from Nesmith C. Ankeny - Poker Strategy, p.28, Table 2.3.
22 Chris Ferguson - No-Limit Hold ’Em: How to Bet, printed in Michael Craig (Editor) - The Full Tilt Poker Strategy Guide, p.18.
23 This is known as a belief in “the law of small numbers,” as humans overestimate the likelihood that even a small sample represents the process that it is drawn from. This is related to the well known “gambler’s fallacy” where roulette players wait for a long string of either red or black before placing a large bet on the other color, erroneously reasoning that the other color is “due.” Amos Tversky and Daniel Kahneman - Belief in the Law of Small Numbers, printed in Daniel Kahneman, Paul Slovic, and Amos Tversky (Editors) - Judgment Under Uncertainty: Heuristics and Biases, pp.23-31. Tversky and Kahneman’s work is based on finding common errors in decision making that violate the norms of statistical and economic theory, some of which will be
discussed in “Risk Preferences: From EV to EU” and “Psychological Biases” starting on pages 278 and 299 respectively.
24 The first time I read about this concept was in Bob Ciaffone - Improve Your Poker, pp.106-107, but the first time it appeared in print was in David Sklansky and Mason Malmuth - Hold ’em Poker for Advanced Players.
25 Chris Ferguson - No-Limit Hold ’Em: How to Bet, printed in Michael Craig (Editor) - The Full Tilt Poker Strategy Guide, p.20.
26 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, Chapter 21: “A Case Study: Using Game Theory.”
27 Nick Christenson and Russell Fox - Winning Strategies for No-Limit Hold’em. They devote Part 2 of their book (just under a hundred pages) to bet sizing.
28 Chris Ferguson advocates the same strategy, “After the flop, I ignore my actual holding and decide how much I’m going to bet if I bet.” Chris Ferguson - No-Limit Hold ’Em: How to Bet, printed in Michael Craig (Editor) - The Full Tilt Poker Strategy Guide, p.24.
29 Nick Grudzien and Geoff Herzog - Winning In Tough Hold ’em Games is a good starting point for figuring out individual hand thresholds in preflop limit hold ’em.
30 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, p.266; Chris Ferguson - No-Limit Hold ’Em: How to Bet, printed in MichaelCraig (Editor) - The Full Tilt Poker Strategy Guide, p.20. These authors are discussing the game of no-limit hold ’em. However, the arguments for never limping first-in for limit hold ’em are even stronger. In general, implied odds are a much greater consideration in no-limit than in limit (assuming large stack sizes) since in limit the size of future bets are restricted by the rules of the game. Therefore, it’s much more about winning the current pot than maximizing the chances of winning future bets. For this reason, raising first-in is imperative as it gives you a chance of winning the pot outright. The only exception is playing first-in as the small blind versus the big blind where there are some arguments for calling over raising (especially in games where the small blind is two-thirds the size of the big blind). This situation will be discussed later on.
31 There is a possible exception to the above. In games where a bet and four raises is allowed, as opposed to the more common bet and three, it can make sense to fold your weakest raising hands for two more bets after a first-in raise. The reason should be obvious.
32 However, perhaps the initial raiser should in some instances fold a few of his worst hands to a cap. Offsuit dominated hands, such as very low aces, seem like good candidates to fold.
33 There are exceptions in multiway pots. For example, if a player limps with hands that are pretty good, but probably should be folded, that will hurt you if you are on his immediate left.
34 Other than the fact that if you always raise, you never have to consider the strategy changes you would make postflop when the pot is smaller.
35 See for example Polaris’s capping strategy in “Appendix to Rules for Preflop Limit Hold ’em: Polaris’s Non-Standard Preflop Plays” starting on page 60.
36 A number of high stakes professionals also play this way. See KPR16's first video for cardrunners.com, dated 16/12/2007. http://www.cardrunners.com/poker-videos/kpr16-1-50100-lhe-kpr16/
37 Another reason to cap is the odds you will get from this play. However, another reason not to cap is that it increases the chance that you can raise on the flop to thin the field.
38 These two recommendations are close to the range of hands the heads-up robot Polaris folds, although you could certainly fold a few more hands without much effect on your strategy. The 2008 GTO version of Polaris raises approximately 82.2 percent of hands from the button. (See“Man Versus Machine” starting on page 221 for more on Polaris’s preflop strategy.)
39 Against players who limp frequently and only raise their better hands in the small blind, this 95 percent number to call raises is probably too high. However, this type of player is extremely rare today.
40 Sonia is an exploitive robot, so her decision to call on the button is largely driven by her perception of her opponent. It’s interesting that her exploitive style against many humans involves calling on the button as this is a play most associated with bad human players. Polaris calls on the button only extremely rarely.
Both bots also use capping (unlike me). But again, Sonia is an exploitive bot, so her choice of capping doesn’t tell us anything about her estimate of GTO play unless she is playing against herself. Polaris does sometimes cap, but not frequently, and since Polaris is a GTO robot this supports my idea that never capping heads-up is a good approximation of an unexploitable strategy. Interestingly, Polaris uses preflop capping in conjunction with an interesting postflop strategy: often capping preflop and then checking behind the flop. This isn’t a strategy most humans would have considered, and I feel strongly that never capping is a good way to play with our current knowledge of the game. See the appendix to this chapter starting on page 60 for more analysis of Polaris’s unusual preflop strategy.
41 The Computer Poker Research Group’s page for the match is at http://webdocs.cs.ualberta.ca/~games/poker/man-machine.
42 The hand histories for this match used to be on Stoxpoker.com, but I can no longer find them after the merger with Cardrunners.com. I will also analyze other parts of this match later on in this book.
43 See “Checking Back the Flop” starting on page 116 for more discussion.
44 Ray Zee - High-Low-Split Poker, Seven-Card Stud and Omaha Eight-or-Better, for Advanced Playerhas an in-depth discussion of opening hand values in Omaha eight-or-better.
45 See “Information Hiding” starting on page 21 for more discussion.
46 This analysis is more clear cut with one draw left.
47 Rare exceptions could occur in eight-or-better tournaments.
48 For a discussion of third street hand values in each stud variant, I recommend David Sklansky, Mason Malmuth, and Ray Zee - Seven-Card Stud for Advanced Players; Ray Zee - High-Low-Split Poker, Seven-Card Stud and Omaha Eight-or-Better, for Advanced Players; David Sklansky - Sklansky on Poker, (for Razz).
49 David Sklansky - Tournament Poker For Advanced Players, p.56.
50 David Sklansky - The Theory of Poker, Chapter 4: “The Ante Structure.”
51 See David Sklansky, Mason Malmuth, and Ray Zee - Seven-Card Stud for Advanced Players for more discussion.
52 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, Chapter 12: “Headsup With High Blinds: The Jam-or-Fold Game.” They suggest playing this way with stacks of 10 big blinds or under.
53 David Sklansky and Ed Miller - No Limit Hold ’Em: Theory and Practice, “Raising Before the Flop,” pp.98-110, “Concept no. 14,” p.255.
54 Dan Harrington and Bill Robertie - Harrington on Cash Games Volume 1, Part Three: Tight-Aggressive Preflop Play, pp.123-216.
55 Dan Harrington and Bill Robertie - Harrington on Cash Games Volume 1, “Adopting Complementary Strategies,” pp.136-139.
56 Dan Harrington and Bill Robertie - Harrington on Hold ’em: Volume 1: Strategic Play, “The Squeeze Play: Exploiting the Sandwich Effect, pp.206-208.
57 John Feeney - Inside the Poker Mind, “Multiple Changing Images,” pp.196-200.
58 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, Chapters 10-17 cover the 12 single street games, Chapters 19 and 20 cover multi-street games.
59 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, p.114.
60 Chris Ferguson, Tom Ferguson, and Cèphas Gawargy - Uniform[0,1] Two-Person Poker Models.
http://www.math.ucla.edu/~tom/papers/poker2.pdf
61 John von Neumann and Oskar Morgenstern - The Theory of Games and Economic Behavior.
62 Chris Ferguson, Tom Ferguson, and Cèphas Gawargy - Uniform[0,1]
Two-Person Poker Models, p.16.
http://www.math.ucla.edu/~tom/papers/poker2.pdf
63 Both are related to the constant christened “alpha” by Bill Chen and Jerrod Ankenman. See The Mathematics of Poker, pp.198-203. The size of our check-fold region will be alpha*(check-call); our bluff region is alpha*(value bet). As the pot grows, alpha = 1/(p+1) decreases, hence, the check-fold and bluff regions become smaller. Also see “Appendix B: Game Theory” starting on page 383.
64 William Jockusch - Pot-Limit Omaha, Understanding Winning Play,
“The Blush,” pp,159-160. Blockers are discussed more generally on pp.161-165.
65 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, pp.230-232.
66 This is because your opponent is calling to win just half the pot. As the pot size decreases, the bluffing ratio increases and the calling ratio decreases.
67 28th February 2008, http://hoss-tbf.livejournal.com.
68 This feature is present in some of the multi-street games in Bill Chen and Jerrod Ankenman - The Mathematics of Poker. “Example 20.5 - The One-and-a-Half-Street Clairvoyance Game,” pp.257-262.
69 David Sklansky and Ed Miller - No Limit Hold ’Em: Theory and Practice, “Concept No. 33: Be willing to risk free cards to manage the pot size and induce bluffs,” pp.270-272.
70 This was calculated with Cardrunners EV.
http://www.cardrunners-ev-calculator.com.
71 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, p.272.
72 There are exceptions in no-limit. Also, in limit, it’s possible that against certain opponents a bet is better than a check-raise.
73 Betting into the aggressor on the river is a play that is covered in the chapter “Head-Up on the End” starting on page 199 in The Theory of Poker by David Sklansky.
74 We don’t recommend this for human players against tough opponents.
75 David Sklansky - The Theory of Poker, Chapter 17: “Position.”
76 KPR16's first video for cardrunners.com covers this concept, dated 16/12/2007.
http://www.cardrunners.com/poker-videos/kpr16-1-50100-lhe-kpr16/
77 See David Sklansky - Sklansky on Poker 55-56 for more discussion of the protected pot.
78 David Sklansky and Mason Malmuth - Hold ’em Poker For Advanced Players: “When the Pots Get Big” pp.167-169.
79 10th March 2008, http://hoss-tbf.livejournal.com.
80, Danny Ashman - Secrets of Short-handed No Limit Hold ’em, pp.122-124. Ashman originally bet top pair, top kicker on a three-flush board on the river. His opponent then raised, and Ashman felt his hand was no good. But since he had the blocker to the nut flush, Ashman decided to make a large reraise all-in as a bluff, and his opponent folded the second nut flush. This hand would never happen in limit poker.
81 Hyperborean08-Equilibrium (8-0), 2008 Annual Computer Poker Competition.
http://webdocs.cs.ualberta.ca/~pokert/2008/results/index.html This is the same version of Polaris that lost only 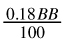 against Sonia.
against Sonia.
82 The statistics in this chapter are from http://forumserver.twoplustwo.com/18/high-stakes-limit/play-sonia-heads-up-paradime-408776/.
83 http://pokerai.org/pf3/viewtopic.php?f=3&t=1027
84Thanks To Emil Jonsson for this image on Polaris.
85 David Paul Schnizlein - State Translation in No-Limit Poker. http://webdocs.cs.ualberta.ca/~games/poker/publications/schnizlein.m sc.pdf
86 See notes 27 and 28 on both on page 30.
87 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, pp.151-153. It must be noted that there are only two individual hands that have any incentive to bet in this game: The nut hand wants to extract calls from the bluff-catcher hand, and the nut low wants to force the bluff-catcher to fold. The bluff-catcher hand never bets because the worse hand will fold and the nut hand will call, so betting never makes sense. Given that there are so few individual hands, it’s not surprising that the
two betting hands make exactly the same sized bet to hide information.
88 Bill Chen and Jerrod Ankenman - The Mathematics of Poker, pp.154-157.
89 Say the pot is $100 on the flop and your stack has $1,300 left. You should make a pot sized bet on each street because by betting $100 + $300 + $900 you end up all-in by the river and have bet a constant fraction of the current pot on each street. Chris Ferguson and Tom Ferguson - The Endgame in Poker, printed in Stewart N. Ethier and William R. Eadington (Editors) - Optimal Play, pp.79-106; Bill Chen and Jerrod Ankenman - The Mathematics of Poker,pp.237-243.
90 See David Sklansky and Ed Miller - No Limit Hold ’em: Theory and Practice, pp. 135 - 142.
91 For example, there was one famous multiway bluff in the fifth series of High Stakes Poker where he bluffed Barry Greenstein off of the A♥A♣ and Peter Eastgate off of the 4♥2♦, on a T♦2♣2♠7♦ board.
92 David Sklansky and Mason Malmuth — Gambling for a Living (1998) suggest a range of 200-300BB
93Win rate is otherwise known as expected value (EV), or expectation. Variance is a measure of how far your results will deviate from your expectation, on average. In order to prevent below average realizations cancelling out above expectation results, the deviations are squared before being averaged (since either a negative or positive number multiplied by itself will result in a positive number). This is why the square root of the variance, the standard deviation, is also often used as a measure of dispersion.
94 Mason Malmuth - Gambling Theory and Other Topics was the first to base bankroll requirements on the relationship of the win rate to the standard deviation. The first edition of this book appeared in 1987, eleven years before Gambling for a Living.
95 I thoroughly recommend William Poundstone - Fortune’s Formula to the interested reader for more on the subject.
96 The main reason they will be doing this will often be because bigger games are tougher to the point that their hourly rate is actually smaller.
97 Using a utility function, see “Risk Preferences: From EV to EU” starting on page 278, the Kelly criterion is equivalent to the function U(x) = ln(x). The Kelly-optimal bet can also be expressed as the bet size that maximizes the geometric growth rate of a portfolio.
98 William Chin and Marc Ingenoso - Risk Adjustment for Poker Players, printed in Stewart N. Ethier and William R. Eadington (Editors) - Optimal Play, pp.131-139.
99 This combination of win rate and standard deviation means that 95 percent of this player’s hourly results will fall in the interval [-19BB, +21BB]. This seems reasonable for live play.
100 This is a strong rule of thumb first shown by Mason Malmuth -Gambling Theory and Other Topics. However, it’s not a hard and fast law. For example, in poker, the ability to read hands well should increase your win rate and lower your variance at the same time. Thus counter examples to this rule do exist.
101 Ken Binmore - Rational Decisions does a good job of explaining expected utility theory. Expected utility theory has the same parents as game theory, both were conceived by John von Neumann and Oskar Morgenstern in The Theory of Games and Economic Behavior.
102 Using calculus, these conditions could be stated as: f'(x) > 0, f' (x) < 0.
103 The natural logarithm is the inverse function of y = ex, where e is mathematical shorthand for the infinite number 2.718281 …
104 Expected utility aficionados among you might point out that similar gambles to St. Petersburg can be constructed that result in the same anomalous behavior of making us want to bet our entire wealth — even for risk averse individuals. The problem here is not to do with risk aversion, but with the concept of unbounded utility — that utility willalways increase with more wealth. This is more of a philosophical issue than a real world issue, at least as far as poker is concerned. See Ken Binmore - Rational Decisions, “Unbounded Utility” pp.55-58.
105 Any positively sloped straight line is equivalent since it will satisfy the conditions for risk neutrality: f'(x ) > 0, f' (x) = 0.
106 Some of the larger tournaments today are now paying the top 25 percent of the finishers. Could it be that the tournament directors have learned that if too many people leave with nothing, there may not be as many entries in the future?
107 This is an element of Kahneman and Tversky’s prospect theory. There are a number of aspects to prospect theory, and this is among the least relevant to poker. Consider consulting Daniel Kahneman and Amos Tversky (Editors) -Choices, Values, and Frames.
108This is the issue of “framing,” another element of prospect theory. See “Psychological Biases” starting on page 299.
109 Baba Shiv et al. - Investment Behavior and the Negative Side of Emotion, printed in George Loewenstein (Editor) - Exotic Preferences, pp.613-624.
110 Don Ross, Carla Sharp, Rudy E. Vuchinich, and David Spurrett - Midbrain Mutiny, The Picoeconomics and Neuroeconomics of Disordered Gambling; Daniel Goleman Biology of Brain may Hold Key For Gamblers, The New York Times. http://www.nytimes.com/1989/10/03/science/biology-of-brain-may-hold-key-for-gamblers.html
111 The first empirical study to put the coefficient of loss aversion around the region of 2-2.5 is Daniel Kahneman, Jack Knetsch, and Richard Thaler - Experimental Tests of the Endowment Effect and the Coase Theorem, printed in Colin F. Camerer, George Loewenstein, and Matthew Rabin (Editors) - Advances in Behavioral Economics, pp.55-74.
112 Matthew Rabin - Diminishing Marginal Utility of Wealth Cannot Explain Risk Aversion, printed in Daniel Kahneman and Amos Tversky (Editors) - Choices, Values, and Frames, pp.202-208.
113 Laurie R. Santos and M. Keith Chen - The Evolution of Rational and Irrational Economic Behavior: Evidence and Insight from a Non-human Primate Species, printed in Paul W. Glimcher, Colin F. Camerer, Ernst Fehr, and Russell A. Poldrack (Editors) - Neuroeconomics: Decision Making and The Brain, pp.81-93. These monkeys systematically prefer identical risky gambles when they are framed as gains instead of as losses.
114 It could well be that loss aversion is an important evolutionary strategy. All animals need to compete for scarce resources in order to survive, e.g. birds spend a large amount of time building and maintaining nests, and spiders spend time spinning webs. Were it not for loss aversion, it would be a lot easier to steal these resources off other members of your species rather than to invest the time building them yourself. However, loss aversion causes incumbent animals to expend more energy fighting for a resource (trying to avoid a loss) than it is worth to an attacker to steal it, and hence make them not worth stealing. This avoids costly zero-sum battles among members of a species. Herbert Gintis - The Bounds of Reason, Chapter 11: “The Evolution of Property Rights.”
115A recent study shows that prospect theory does a better job of explaining contestants’ decisions in the popular television program Deal or No Deal. Thierry Post et al. - Deal or No Deal? Decision Making under Risk in a Large-Payoff Game Show. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=636508#
116 Rajnish Mehra and Edward C. Prescott - The Equity Premium: APuzzle. http://www.academicwebpages.com/preview/mehra/pdf/The%20Equit y%20Premium%20A%20Puzzle.pdf
117 Shlomo Benartzi and Richard H. Thaler - Myopic Loss Aversion and the Equity Premium Puzzle, printed in Richard H. Thaler (Editor) - Advances in Behavioral Finance Volume Two, pp.202-223.
118 Ola Svenson - Are We All Less Risky and More Skilful Than Our Fellow Drivers?
http://heatherlench.com/wp-content/uploads/2008/07/svenson.pdf
119 Gary Belsky and Thomas Gilovich - Why Smart People Make Big Money Mistakes and How to Correct Them, Chapter 6: “The Ego Trap.”
120 Brandon Adams - Broke, includes a fictional account of a poker player losing everything with some poor investing decisions.
121 Jason Zweig - Your Money and Your Brain, Chapter 5: “Confidence.”
122 Seth A. Klarman - The Margin of Safety, Chapter 6: “Value Investing: The Importance of a Margin of Safety”; Benjamin Graham - The Intelligent Investor.
123 Daniel Kahneman and Amos Tversky (Editors) - Choices, Values, and Frames, pp.4-7.
124 Hersh Shefrin and Meir Statman - The Disposition to Sell Winners Too Early and Ride Losers Too Long: Theory and Evidence, printed in Richard H. Thaler (Editor) - Advances in Behavioral Finance, pp.507-525.
125 William Poundstone - Priceless explores a number of consumer irrationalities that companies exploit to their advantage.
126 Antonio Damasio - Descartes’ Error: Emotion, Reason and the Human Brain. This book studies patients with damage to a specific part of the brain that regulates emotion. These patients are able to make good inferences when presented with abstract problems, but they are wholly unable to make fruitful choices in their own life. One example in the book is of a patient taking over half an hour dispassionately debating the merits of which day to schedule the next appointment on before Damasio gently suggested one. It turns out that we don’t make decisions by rationally considering all of the pros and cons, but by using emotions as a quick indicator of which way we should lean.
127 Thomas Gilovich - How We Know What Isn’t So, pp.54-56. Gilovich attributes the greater memorability of losses to the gambler’s need to rationalize and find reasons for their losses. At least in my case, I remember losses so vividly because of my instinctive emotional reaction.
128 Carol Tavris and Elliot Aronson - Mistakes Were Made, But Not by Me.
129 George Loewenstein, Ted O’Donoghue, and Matthew Rabin - Projection Bias in Predicting Future Utility, printed in George Loewenstein (Editor) - Exotic Preferences, pp.345-382.
130 Daniel Gilbert - Happiness.
131 S. J. Solnick and D. Hemenway - Is More Always Better? A Survey on Positional Concerns, printed in the Journal of Economic Behavior and Organization.
132 George F. Loewenstein and Drazen Prelec - Preferences for Sequences of Outcomes, printed in Daniel Kahneman and Amos Tversky (Editors) - Choices, Values, and Frames, pp.565-577; Robert H. Frank and Robert M. Hutchens - Wages, Seniority, and the Demand for Rising Consumption Profiles, printed in Colin F. Camerer, George Loewenstein, and Matthew Rabin (Editors) - Advances in Behavioral Economics, pp.548-571.
133 Robert H. Frank - Frames of Reference and the Intertemporal Wage Profile, printed in George Loewenstein and Jon Elster (Editors) - Choice Over Time, pp.371-382. Frank covers both the issue of interpersonal comparisons and the desire for increasing consumption over time. For the first issue, Frank remarks that he “felt” richer earning $480 a year in Nepal than when he earned $13,000 a year in the United States, since the $480 a year was more than enough to put him in the upper half of the income distribution in Nepal. For the second issue, Frank says that many professions, such as airline pilots, pay higher compensation for more years of experience even though productivity doesn’t increase. Both issues are particularly salient for poker players as you will naturally compare yourself to other players earning large sums of money, and higher stakes players will likely see their expected yearly winnings steadily decrease as the games become tougher.
134 Daniel Nettle - Personality: What Makes You the Way You Are discusses personality in terms of the five-factor model. Richard L. Peterson - Inside the Investor’s Brain, Chapter 12: “Personality Factors” examines the five-factor model in relation to investing.
A five-factor study has been performed on a sample of online players, see Paul Fayngersh and Mark Kizelshteyn - The Personality of Online Poker Players: An Initial Enquiry. They find that poker players tend to be low on extraversion, conscientiousness, and agreeableness. They also find that neuroticism and win rate are negatively correlated (players low on neuroticism win more).
http://fifthidea.com/personality/
135 Babiak and Robert D. Hare - Snakes in Suits: When Psychopaths Go to Work.
136 If you want to know more about discounted cash flow valuation (for stocks), I would suggest Tim Koller, Marc Goedhart, and David Wessels - Valuation: Measuring and Managing the Value of Companies.
137 Roger G. Ibbotson et al. - Lifetime Financial Advice: Human Capital, Asset Allocation, and Insurance.
http://www.cfapubs.org/doi/pdf/10.2470/rf.v2007.n1.4580
138 Elroy Dimson, Paul Marsh, and Mike Staunton - Triumph of the Optimists.
139 This is just using the formula for the infinite sum of a geometric progression:  a where a = Year 1 cash flow and 1− r discount rate in decimal form. Of course, our careers are not infinitely long, but with a high enough discount rate the sum is dominated by the first few terms.
a where a = Year 1 cash flow and 1− r discount rate in decimal form. Of course, our careers are not infinitely long, but with a high enough discount rate the sum is dominated by the first few terms.
140 Ian Ayres and Barry Nalebuff - Lifecycle Investing, pp.150-153; Moshe A. Milevsky - Your Money Milestones, p.6.
141 Aswath Damodaran - Strategic Risk Taking, Chapter 8: “Real Options.”
142 Alan N. Schoonmaker - The Psychology of Poker, “Don’t Quit Your Day Job,” pp.295-298.
143 Moshe A. Milevsky - Are You a Stock or a Bond?
144 Lawrence J. Kotlikoff and Scott Burns - Spend ‘til The End uses the consumption smoothing approach to personal financial advice. In economics, the life-cycle hypothesis states that we should consume, in each year, an amount equal to their lifetime expected annual earnings. For a high stakes player, his lifetime expected earnings will be lower than his current earnings, implying a high savings rate.
145 Richard H. Thaler - The Winner’s Curse, Chapter 8: “Intertemporal Choice.” The observation of preferences reversing based on time until delay is known as hyperbolic discounting. The correct way to treat rewards over time is known as exponential discounting where the choice between two rewards is independent of a constant delay.
146 Don Ross, Carla Sharp, Rudy E. Vuchinich, and David Spurrett - Midbrain Mutiny, The Picoeconomics and Neuroeconomics of Disordered Gambling, Section 3.2: “Intertemporal Choice and Impulsivity.”
147 Dan Ariely - Predictably Irrational, Chapter 6: “The Problem of Procrastination and Self-Control.”
148 Richard H. Thaler and Cass R. Sunstein - Nudge, Chapter 6: “Save More Tomorrow.”
149 Thomas C. Schelling - Self-Command: A New Discipline; George Ainslie and Nick Haslam - Self-Control, both printed in George Loewenstein and Jon Elster (Editors) - Choice Over Time, pp.167-209. People high in conscientiousness (see page 316) will find it easier to
control their behavior with the use of personal rules and other devices.
150 John Norstad - Investing in Total Markets.
http://homepage.mac.com/j.norstad/finance/total.html
151 James Surowiecki - The Wisdom of Crowds.
152 John C. Bogle - Common Sense on Mutual Funds, and Charles D. Ellis - Winning the Loser’s Game. Both (implicitly) advocate the CAPM view persuasively. Both books emphasize the concept that costs matter — paying 1 percent a year in fees may not seem a lot, but it will be a huge drag on compound returns over time. This is why it’s difficult to find financial advisors/planners who are able to add value after costs —the best course in investing is to do it yourself.
153 Through the Vanguard Total Stock Market ETF (VTI).
154 This is the two-fund/Tobin separation theorem. Peter L. Bernstein - Capital Ideas.
155 Moshe A. Milevsky - Are You a Stock or a Bond? This book is about mixing your career risk with your financial asset risk to arrive at your desired total risk level. For people with safe careers, Milevsky advocates some very high risk portfolios.
156 The efficiency of this insurance policy will depend on the sites you play on. Many poker sites are privately owned, in which case their securities don’t trade in the open market. The insurance would work best if the put option was on a site that you play on, and that the listed company is a relatively “pure” online gambling play — a company that has diversified into other sectors will have a lower correlation.
157 John Y. Campbell and Luis M. Viceira - Strategic Asset Allocation, Chapter 6: “Human Wealth and Financial
Wealth.”
158 Michael Craig - The Professor, the Banker, and the Suicide King.
159 Ian Ayres and Barry Nalebuff - Lifecycle Investing. Ayres and Nalebuff suggest that many young investors should start off at 2-to-1 leverage — i.e. $200 worth of stock for every $100 of assets.
160 Brownian motion is used in the random walk theory of stock prices.
161 Bruce Greenwald and Judd Kahn - Competition Demystified.
162 I’ve heard of players moving out to Eastern Europe to bankroll and teach locals how to profitably shortstack small stakes no-limit and keeping their rakeback in return.
163 Known as the Lotka-Volterra model.
164 Robert J. Shiller - Irrational Exuberance, Chapter 6: “New Era Economic Thinking.”
165 In my experience the Greeks are among the very worst at online poker. They may feel happy losing lots of money at gambling due to cultural issues, but that same attitude has led to the country being one of the hardest hit by the credit crunch, and is now nearly bankrupt. With such a severe recession in their country, it’s unlikely many of them will be able to continue with their online gambling habits. Michael Lewis -
Beware of Greeks Bearing Bonds, Vanity Fair.
http://www.vanityfair.com/business/features/2010/10/greeks-bearing-bonds-201010
166 I played 30,000 hands of $5-$10 this year to clear a promotion. I paid  in rake and almost exactly broke even. I also suffered a 500 big bet downswing in this stretch, and these downswings are much more likely when your win rate is around zero.
in rake and almost exactly broke even. I also suffered a 500 big bet downswing in this stretch, and these downswings are much more likely when your win rate is around zero.
167 The prisoners’ dilemma is sometimes written in the singular (i.e. the prisoner’s dilemma). I think this is wrong, as you will come to see, but if you only consider your own payoff, the game has a simple optimal strategy. However, the dilemma involved is very much a group one: How can the socially optimal payoff be enforced?
168 Robert Axelrod - The Evolution of Cooperation.
169 Robert H. Frank - Passions Within Reason explores ways of resolving various prisoners’ dilemmas in life.
170 You should be risk averse in regards to game selection — only selecting plus-EV tables. When you are playing in a game, you should be acting effectively risk neutral: the size of an individual pot relative to your bankroll is small, and if you systematically avoid zero-EV plays, this can have negative knock-on effects for the strength of your overall strategy.
171 Colin F. Camerer - Behavioral Game Theory, Section 5.5: “The ‘Groucho Marx’ Theorem in Zero-Sum Betting,” pp.239-242. Paul Milgrom and Nancy Stokey - Information, Trade and Common Knowledge.
http://www.stanford.edu/~milgrom/publishedarticles/Information%20 Trade%20and%20Common%20Knowledge.pdfJohn Geanakoplos - Common Knowledge. http://www.mbs.edu/home/jgans/agt/papers/Geankoplos.pdf
172 Unless you also have information you know he doesn’t have.
173 Fischer Black - Noise, printed in Richard H. Thaler (editor) - Advances in Behavioral Finance, p.6.
174 Bayes’ theorem shows us the optimal way to update prior beliefs on the basis of new information. Bill Chen and Jerrod Ankenman - The Mathematics of Poker, pp.35-44; Ken Binmore - Rational Decisions.
175 This is Phil Galfond’s view.
http://www.bluefirepoker.com/post-comment.aspx?postid=2052
176Jonathan Wilson - The Anatomy of England, p.151.
177 See also Leonard Mlodinow - The Drunkard’s Walk, particularly Chapter 10, for how the same idea is at work in other areas of life.
178 Thomas Schelling - Self-Command: A New Discipline, printed in George Loewenstein and Jon Elster (Editors) -Choice Over Time, pp.167-176.
179 A great example of this is when John Duthie won a tournament for £1,000,000 in 2000. He put some of the money into a joint bank account with his father-in-law — someone who would disapprove of him gambling the money away at a later date. Victoria Coren - For Richer, For Poorer, pp. 268-270.
180 The graduate student wasn’t a poker player, but it’s very much the sort of thing an irrationally exuberant young poker player could do. He is known as “Market Timer.” Ian Ayres and Barry Nalebuff - Lifecycle Investing.
181 We can see that the relationship between the bettor’s bluffing ratio and the caller’s folding ratio is preserved in this application with pot-sized bets. For every two value bets the bettor has one bluff, that is a bluffing ratio of one-half. Similarly, the caller folds exactly half his hands, that is a folding ratio of one-half. To get the caller’s calling ratio, you take one minus the bettor’s bluffing ratio (and in this case the calling ratio is one-half again).
182 Thanks to Emil Jonsson for this data on Polaris.
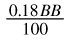 over 730,000 hands. It’s actually very impressive that Polaris manages to lose so little against Sonia; most humans lose much more. It shows that any mistakes Polaris is making are worth relatively little in terms of EV for Sonia’s potential exploitations. This provides strong evidence that Polaris’s strategy isvery good and worth studying further. http://pokerparadime.com/MessageBoard?messageid=158
over 730,000 hands. It’s actually very impressive that Polaris manages to lose so little against Sonia; most humans lose much more. It shows that any mistakes Polaris is making are worth relatively little in terms of EV for Sonia’s potential exploitations. This provides strong evidence that Polaris’s strategy isvery good and worth studying further. http://pokerparadime.com/MessageBoard?messageid=158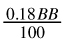 against Sonia.
against Sonia. a where a = Year 1 cash flow and 1− r
a where a = Year 1 cash flow and 1− r  in rake and almost exactly broke even. I also suffered a 500 big bet downswing in this stretch, and these downswings are much more likely when your win rate is around zero.
in rake and almost exactly broke even. I also suffered a 500 big bet downswing in this stretch, and these downswings are much more likely when your win rate is around zero.