
Your Student Tools contain tons of informational videos, practice tests, helpful articles, and more to help with your GRE preparation. Head over there and take advantage of this fantastic resource!
This chapter contains an overview of the content and structure you’ll see on the Math section of the GRE. It provides valuable information on pacing strategies and the various question formats you’ll encounter on the GRE. It also goes over how to use basic test-taking techniques such as Process of Elimination and Ballparking as they relate to math questions. After finishing this chapter, you’ll have a good idea of what the Math section of the GRE looks like and some basic approaches to help you navigate it.
The GRE Math section primarily tests math concepts you learned in seventh through tenth grades, including arithmetic, algebra, and geometry. ETS alleges that the Math section tests the reasoning skills that you’ll use in graduate school, but what the Math section primarily tests is your comfort level with some basic math topics and your ability to take a test with strange-looking questions under timed conditions.
The Math section of the exam consists of two 35-minute sections, each of which will consist of 20 questions. The first 7 or 8 questions of each section will be quantitative comparisons (quant comp, for short). The remainder will consist of multiple-choice or numeric-entry questions.
Junior High School?
The Math section of the GRE mostly tests how much you remember from the math courses you took in seventh, eighth, ninth, and tenth grades. But here’s some good news: GRE math is easier than SAT math. Why? Because many people study little or no math in college. If the GRE tested college-level math, everyone but math majors would bomb the test.
If you’re willing to do a little work, this is good news for you. By brushing up on the modest amount of math you need to know for the test, you can significantly increase your GRE Math score. All you have to do is shake off the dust.
The beauty of a standardized test is that it is, well, standardized. Standardized means predictable. We know exactly what ETS is going to test and how they’re going to test it. The math side of the test consists of a series of utterly predictable questions, to which we have designed a series of highly scripted responses. ETS wants you to see each problem as a new challenge to solve. What you will find, however, is that there are only about 20 math concepts that are being tested. All of the questions you will see are just different ways of asking about these different concepts. Most of these concepts you already know. Once you recognize what’s being tested, even the trickiest questions become familiar and easy to solve.
In constructing the Math section, ETS is limited to the math that nearly everyone has studied: arithmetic, basic algebra, basic geometry, and elementary statistics. There’s no calculus (or even precalculus), no trigonometry, and no major-league algebra or geometry. Because of these limitations, ETS has to resort to traps in order to create hard problems. Even the most commonly missed GRE math problems are typically based on relatively simple principles. What makes the problems difficult is that these simple principles are disguised.
Many test takers have no problem doing the actual calculations involved in the math questions on the GRE; in fact, you’ll even be allowed to use a calculator (more on that soon). However, on this test, your ability to carefully read the problems and figure out how to set them up is more important than your ability to make calculations.
As you work through this section, don’t worry about how quickly you’re doing the problems. Instead, take the time to really understand what the questions are asking; pay close attention to the wording of the problems. Most math errors are the result of careless mistakes caused by not reading the problem carefully enough!
You can do all the calculations right and still get a question wrong. How? What if you solve for x but the question asked for the value of x + 4? Ugh. Always reread the question before you choose an answer. Take your time and don’t be careless. The problem will stay on the screen as long as you want it to, so reread the question and double-check your work before answering it.
Or how about this? The radius of the circle is 5, but when you copied the picture onto your scratch paper, you accidentally made it 6. Ugh! If you make a mistake copying down information from the screen, you’ll get the question wrong no matter how perfect your calculations are. You have to be extra careful when copying down information.
As we mentioned before, on the GRE you’ll be given an on-screen calculator. The calculator program on the GRE is a rudimentary one that gives you the five basic operations: addition, subtraction, multiplication, division, and square root, plus a decimal function and a positive/negative feature. It follows the order of operations, or PEMDAS (more on this topic in Chapter 10). The calculator also has the ability to transfer the answer you’ve calculated directly into the answer box for certain questions. The on-screen calculator can be a huge advantage—if it’s used correctly!
As you might have realized by this point, ETS is not exactly looking out for your best interests. Giving you a calculator might seem like an altruistic act, but rest assured that ETS knows that there are certain ways in which calculator use can be exploited. Keep in mind the following:
Calculators Can’t Think. Calculators are good for one thing and one thing only: calculation. You still have to figure out how to set up the problem correctly. If you’re not sure what to calculate, then a calculator isn’t helpful. For example, if you do a percent calculation on your calculator and then hit “Transfer Display,” you will have to remember to move the decimal point accordingly, depending on whether the question asks for a percent or a decimal.
The Calculator Can Be a Liability. ETS will give you questions that you can solve with a calculator, but the calculator can actually be a liability. You will be tempted to use it. For example, students who are uncomfortable adding, subtracting, multiplying, or dividing fractions may be tempted to convert all fractions to decimals using the calculator. Don’t do it. You are better off mastering fractions than avoiding them. Working with exponents and square roots is another way in which the calculator will be tempting but may yield really big and awkward numbers or long decimals. You are much better off learning the rules of manipulating exponents and square roots. Most of these problems will be faster and cleaner to solve with rules than with a calculator. The questions may also use numbers that are too big for the calculator. Time spent trying to get an answer out of a calculator for problems involving really big numbers will be time wasted. Find another way around.
A Calculator Won’t Make You Faster. Having a calculator should make you more accurate, but not necessarily faster. You still need to take time to read each problem carefully and set it up. Don’t expect to blast through problems just because you have a calculator.
The Calculator Is No Excuse for Not Using Scratch Paper. Scratch paper is where good technique happens. Working problems by hand on scratch paper will help to avoid careless errors or skipped steps. Just because you can do multiple functions in a row on your calculator does not mean that you should be solving problems on your calculator. Use the calculator to do simple calculations that would otherwise take you time to solve. Make sure you are still writing steps out on your scratch paper, labeling results, and using setups. Accuracy is more important than speed!
Of course, you should not fear the calculator; by all means, use it and be grateful for it. Having a calculator should help you eliminate all those careless math mistakes.
Each of the two Math sections contains 20 questions. Test takers are allowed 35 minutes per section. The first 7 or 8 questions of each Math section are quantitative comparisons, while the remainder are a mixed bag of problem solving, all that apply, numeric entry, and charts and graphs. Each section covers a mixture of algebra, arithmetic, quantitative reasoning, geometry, and real-world math.
Much like the Verbal section, the Math portion of the GRE contains a variety of different question formats. Let’s go through each type of question and discuss how to crack it.
These questions are the basic five-answer multiple-choice questions. These are great candidates for POE (Process of Elimination) strategies we will discuss later in this chapter.
These questions appear similar to the standard multiple-choice questions; however, on these you will have the opportunity to pick more than one answer. There can be anywhere from three to eight answer choices. Here’s an example of what these will look like:
If 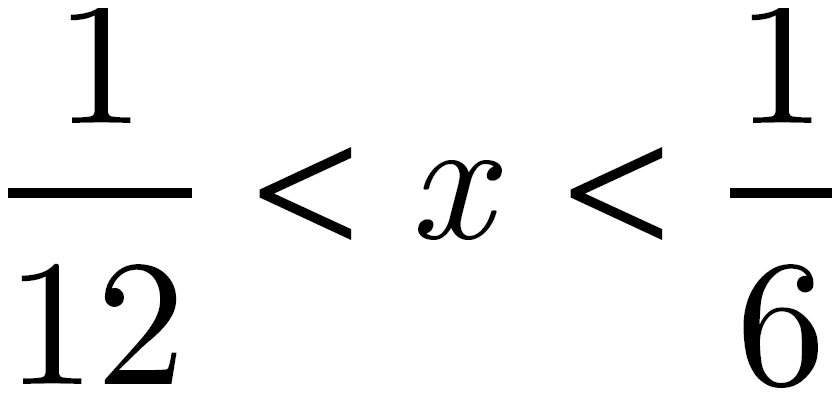 , then which of the following could be the value of x?
, then which of the following could be the value of x?
Indicate all such values.





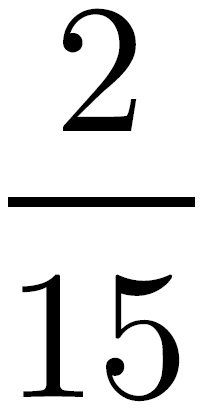



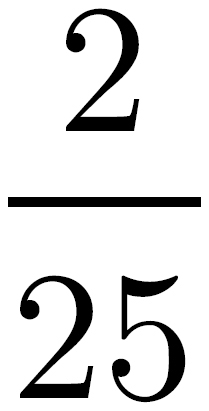
Your approach on these questions won’t be radically different from the approach you use on standard multiple-choice questions. But obviously, you’ll have to consider all of the answers—make sure you read each question carefully and remember that more than one answer can be correct. For example, for this question, you’d click on (C) and (D). You must select every correct choice to get credit for the problem.
Quantitative comparison questions, hereafter affectionately known as “quant comp” questions, ask you to compare Quantity A to Quantity B. These questions have four answer choices instead of five, and all quant comp answer choices are the same. Here they are:
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Your job is to compare the two quantities and choose one of these answers.
Quant comp problems test the same basic arithmetic, algebra, and geometry concepts as do the other GRE math problems. So, to solve these problems, you’ll apply the same techniques you use on the other GRE math questions. But quant comps also have a few special rules you need to remember.
Because there are only four choices on quant comp questions, after you use POE to eliminate all of the answer choices you can, your odds of guessing correctly are even better. Think about it this way: eliminating even one answer on a quant comp question will give you a one-in-three chance of guessing correctly.
Any quant comp problem that contains only numbers and no variables must have a single solution. Therefore, on these problems, you can eliminate (D) immediately because the larger quantity can be determined. For example, if you’re asked to compare  and
and  , you can determine which fraction is larger, so the answer cannot be (D).
, you can determine which fraction is larger, so the answer cannot be (D).
You don’t always have to calculate the exact value of each quantity before you compare them. After all, your mission is simply to compare the two quantities. It’s often helpful to treat the two quantities as though they were two sides of an equation. Anything you can do to both sides of an equation, you can also do to both quantities. You can add the same number to both sides, you can multiply both sides by the same positive number, and you can simplify a single side by multiplying it by one.
If you can simplify the terms of a quant comp, you should always do so.
Here’s a quick example:

|
Quantity A |
Quantity B |
|
|
|
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It
Don’t do any calculating! Remember: Do only as much work as you need to in order to answer the question! The first thing you should do is eliminate (D). After all, there are only numbers here. After that, get rid of numbers that are common to both columns (think of this as simplifying). Both columns contain a 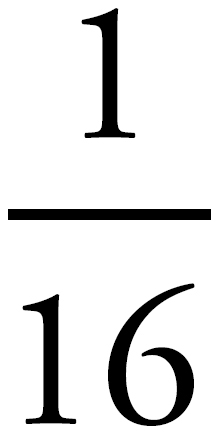 and a
and a  , so because we’re talking about addition, they can’t make a difference to the outcome. With them gone, you’re merely comparing the
, so because we’re talking about addition, they can’t make a difference to the outcome. With them gone, you’re merely comparing the  in column A to the
in column A to the  in column B. Now we can eliminate (C) as well—after all, there is no way that
in column B. Now we can eliminate (C) as well—after all, there is no way that  is equal to
is equal to  . So, we’re down to two choices, (A) and (B). If you don’t remember how to compare fractions, don’t worry—it’s covered in Chapter 10 (Math Fundamentals). The answer to this question is (B).
. So, we’re down to two choices, (A) and (B). If you don’t remember how to compare fractions, don’t worry—it’s covered in Chapter 10 (Math Fundamentals). The answer to this question is (B).

Okay, let’s talk about another wacky question type you’ll see in the Math section.
Some questions on the GRE won’t even have answer choices, and you’ll have to generate your own answer. Here’s an example:

Each month, Renaldo earns a commission of 10.5% of his total sales for the month, plus a salary of $2,500. If Renaldo earns $3,025 in a certain month, what were his total sales?
Here’s How to Crack It
On this type of question, POE is not going to help you! That means if you’re not sure how to do one of these questions, you should immediately move on. Leave it blank and come back to it in your second pass through the test.
If Renaldo earned $3,025, then his earnings from the commission on his sales are $3,025 – $2,500 = $525. So, $525 is 10.5% of his sales. Set up an equation to find the total sales:  where x is the amount of the sales. Solving this equation, x = 5,000. (We’ll review how to set up and solve equations like this in later chapters.)
where x is the amount of the sales. Solving this equation, x = 5,000. (We’ll review how to set up and solve equations like this in later chapters.)
To answer this question, you’d enter 5000 into the box. Alternately, you could transfer your work directly from the on-screen calculator to the text box.

The basic test-taking strategies covered in Chapter 2 are effective for the entire test. They can be critical to your level of success on the GRE. They are time-tested and proven to be effective. You should always be mindful of them and take a few minutes to review them before working through the Math section.
Here are some strategies that will help you on the Math section, specifically. We’ll show you how to use them as we go through specific question types in the chapters ahead, but for now, read through the strategies and get a sense of what they are before moving on.
It’s extremely important to be mindful that the strategies that follow are secondary to actually solving the problem. There is no ambiguity when it comes to the correct answer on a problem in the Math section, and actually solving the problem should be your primary goal. However, there are times when you may encounter a problem that seems overly difficult or complicated, or you are running out of time on a section. In those cases, these strategies may be helpful.
Use POE whenever you can on questions that are in standard multiple-choice format. It’s good practice to always read the answer choices before you start to solve a math problem because often they will help guide you—you might even be able to eliminate a couple of answer choices before you begin to calculate the answer.
Say you were asked to find 30 percent of 50. Wait—don’t do any math yet. Let’s say you glanced at the answer choices and you see these:
 5
5
 15
15
 30
30
 80
80
 150
150
Think about it. Whatever 30 percent of 50 is, it must be less than 50, right? So any answer choice that’s greater than 50 can’t be right. That means that you should eliminate both (D) and (E) before you do any calculations! Thirty percent is less than half, so you can eliminate anything greater than 25, which means that (C) is gone too. What is 10 percent of 50? Eliminate (A). You’re done. The only answer left is (B).

This process is known as Ballparking. Remember that the answers are part of the question, and there are four times as many wrong answers as there are right answers. In the example above, the correct answer is fairly easy to calculate. This question is not representative of the difficulty of a GRE problem. While Ballparking is not a substitute for actually solving the problem, and should only be used as a last resort, it can help you to eliminate wrong answer choices that are clearly “out of the ballpark” and increase your odds of zeroing in on the correct answer.
ETS likes to include “trap answers” in the answer choices to their math problems. Trap answers are answer choices that appear correct upon first glance. These answers often look so tempting that you’ll choose them without actually bothering to complete the necessary calculations. Watch out for this! If a problem seems way too easy, be careful and double-check your work.
Here’s a GRE example:

The price of a jacket is reduced by 10%. During a special sale, the price is discounted by another 10%. The special sale price is what percent less than the original price of the jacket?
 15%
15%
 19%
19%
 20%
20%
 21%
21%
 25%
25%
Here’s How to Crack It
The answer might seem like it should be 20 percent. But wait a minute! Is it likely that the GRE is going to give you a problem that you can solve just by adding 10 + 10? Probably not. Choice (C) is a trap answer.
To solve this problem, imagine that the original price of the jacket is $100. After a 10 percent discount, the new price is $90. But now when you take another 10 percent discount, we’re taking it from $90, not $100. Ten percent of 90 is 9, so the final price is $90 – $9 = $81. That represents a 19 percent total discount from the original price of $100. The correct answer is (B).

Suppose you’ve eliminated three of the five answers you know are wrong and you’re down to two. You marked it and have come back to it. At this point, you can just guess–not bad considering your chances of being right have gone from twenty percent to fifty percent. However, there is only one way to correctly answer every question on the GRE, so if you can’t see why one of the remaining answer choices is wrong, you are missing something. Take a fresh look at the question and remind yourself what the answer should look like. Find it! If you are still stuck, Mark and Move.
Here’s a GRE example:

At a certain factory, each employee either drives to work or takes the bus. The ratio of employees who take the bus to work to those who drive to work is 2 : 5. If 120 employees drive to work, how many employees work at the factory?
 240
240
 168
168
 110
110
 48
48
 24
24
Here’s How to Crack It
If 120 workers drive to work, there must be at least that many who work in the factory, so you can eliminate (C), (D), and (E) immediately. You marked it and now you’ve come back to the question to choose between (A) and (B). The ratio is 2 : 5, which means that for every 2 workers who take the bus to work, there are 5 workers who drive to work. So the total number of workers must be a multiple of 2 + 5 = 7. 168 is a multiple of 7, but 240 is not a multiple of 7, so the answer is (B).

There may be cases on the GRE when you are running out of time and you are going to have to guess on a question. POE can turn these questions into potential points. Before you just guess on a question, quickly consider if some of the answer choices are clearly wrong. If you can eliminate a couple of choices, you’ve increased your chances of getting a free point!
Consider this GRE example:

A 100-foot rope is cut so that the shorter piece is 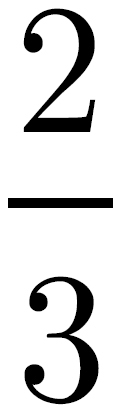 the length of the longer piece. What is the length of the shorter piece in feet?
the length of the longer piece. What is the length of the shorter piece in feet?
 75
75
 66
66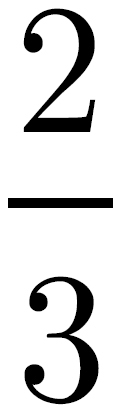
 50
50
 40
40
 33
33
Here’s How to Crack It
Before we dive into the calculations, let’s use a little common sense. The rope is 100 feet long. If we cut the rope in half, each part would be 50 feet. However, the rope was cut into two unequal pieces—a shorter piece and a longer piece. The shorter piece must be less than 50 feet, so you can eliminate (A), (B), and (C) immediately. By the way, the correct answer is (D), but solving this problem was not the point of the exercise. The point here to show you that we can quickly eliminate answer choices to improve the odds of guessing correctly, if guessing is necessary.

Make sure you learn the content of each of the following chapters before you go on to the next one. Don’t try to cram everything in all at once. It’s much better to do a small amount of studying each day over a longer period; you will master both the math concepts and the techniques if you focus on the material a little bit at a time. Just as we have been telling you in earlier chapters, let the content sink in by taking short study breaks between study sessions and giving yourself plenty of time to prepare for the GRE. Slow and steady wins the race!
Practice may not make perfect, but it sure will help. Use everyday math calculations as practice opportunities. Balance your checkbook without a calculator! Make sure your check has been added correctly at a restaurant, and figure out the exact percentage you want to leave for a tip. The more you practice simple adding, subtracting, multiplying, and dividing on a day-to-day basis, the more your arithmetic skills will improve for the GRE.
After you work through this book, be sure to practice doing questions on our online tests and on real GREs. There are always sample questions at www.ets.org/gre, and practice will rapidly sharpen your test-taking skills.
Finally, unless you trust our techniques, you may be reluctant to use them fully and automatically on the real GRE. The best way to develop that trust is to practice before you get to the real test.
The GRE contains two 35-minute Math sections. Each section has 20 questions.
The GRE tests math concepts up to about the tenth-grade level of difficulty.
You will be allowed to use a calculator on the GRE. The calculator is part of the on-screen display.
The Math section employs a number of different question formats, including multiple-choice, numeric entry, and quantitative comparison questions.
Use the Two-Pass system on the Math section. Find the easier questions and do them first. Use your remaining time to work some of the more difficult questions.
When you get stuck on a problem, walk away. Do a few other problems to distract your brain, and then return to the question that was giving you problems.
Ballpark or estimate the answers to math questions, eliminating answers that don’t make sense.
Watch out for trap answers. If an answer seems too easy or obvious, it’s probably a trap.
Always do your work on your scratch paper, not in your head. Even when you are Ballparking, make sure that you are eliminating answer choices on your scratch paper. If your hand isn’t moving, you’re stuck and you need to walk away, or you’re doing work in your head, which leads to errors.