Chances are you probably haven’t used the Pythagorean Theorem recently or had to find the area of a circle in quite a while. However, you’ll be expected to know geometry concepts such as these on the GRE. This chapter reviews all the important rules and formulas you’ll need to crack the geometry problems on the GRE.
On the math section of the GRE, about 25% of the questions you will encounter are geometry questions. Geometry questions come in all shapes and sizes–literally and figuratively. The GRE can ask you about a variety of geometric shapes of any possible size. GRE geometry questions are asked in all question types–Quant Comp, multiple choice, numeric entry, all that apply–and span all difficulties.
Luckily, the GRE typically only asks about a handful of shapes and concepts. If the GRE did not have any limitations on what concepts or figures could be tested, the scope of the geometry section would be enormous.
This chapter is going to re-introduce you to the basics of each shape and the types of information the GRE could ask about in general. The next chapter focuses on how the GRE takes this information and tests it.
It is worth repeating that this chapter does not contain GRE-specific questions. This chapter presents the foundational knowledge needed to tackle GRE geometry questions. In this chapter, you’ll learn about figure types, equations necessary to solve for certain aspects of figures, and basic relationships between figures. The next chapter presents questions that are specific to the GRE but does not cover any of these introductory concepts.
Unsure whether you should tackle this chapter or skip straight to the next chapter?
Take this short quiz to find out!
1. What is the formula for the volume of a rectangular solid?
2. If the radius of a circle is 4, what is its area?
3. What is the equation of a line?
4. How many degrees are there in a line?
5. What is the sum of the interior angle measurements of a figure with 6 sides?
6. What is the formula for the perimeter of a rectangle?
7. The side lengths of what kind of triangle can be found using the Pythagorean Theorem?
8. What is the equation for the slope of a line?
9. How many degrees are in a circle?
10. What is the formula for the area of a triangle?
The answers to these questions are at the back of this chapter.
So, how’d you do? If you got more than two questions wrong, you should start with this chapter. Lucky for you, we can dive in right now.
The following tables show a list of shape types, what can be asked about them, and geometry vocabulary the writers of the GRE can use. Once you’re confident in your ability to maneuver through all these topics, move onto the next chapter. That chapter contains more explicit information about geometry on the GRE, including questions that mimic the types of questions that you’ll see on test day. When scanning the table below, if you see only a couple of items that you are unsure of feel free to flip to those sections and ignore the rest. If nothing on this table looks familiar to you, then prepare to spend time in this chapter before moving on to the next.
|
Figure |
What to Know |
|
3D Figures |
|
|
Circles |
|
|
Coordinate Plane |
|
|
Degrees, Lines, and Angles |
|
|
Other Figures |
|
|
Rectangles |
|
|
Right Triangles |
|
|
Squares |
|
|
Triangles |
|
The chapter is organized by progressing complexity. We’ll start by looking at the most straightforward topics and gradually move into the more complex.
For the GRE, you will need to know that:
A line is a 180-degree angle. In other words, a line is a perfectly flat angle.
When two lines intersect, four angles are formed; the sum of these angles is 360 degrees.
When two lines are perpendicular to each other, their intersection forms four 90-degree angles. Here is the symbol ETS uses to indicate perpendicular lines: ⊥.
Ninety-degree angles are also called right angles. A right angle on the GRE is identified by a little box at the intersection of the angle’s arms.
There are two important concepts that you need to understand regarding degrees, lines, and angles. These are vertical angles and parallel lines.
Vertical angles are the angles that are across from each other when two lines intersect. Vertical angles are always equal. In the drawing below, angle x is equal to angle y (they are vertical angles) and angle a is equal to angle b (they are also vertical angles).
On the GRE, the measure of only one of the vertical angles is typically shown. But usually you’ll need to use the other angle to solve the problem.
Parallel lines are lines that never intersect (they have the same slope). When a pair of parallel lines is intersected by a third line, two types of angles are formed: big angles and small angles. Any big angle is equal to any big angle, and any small angle is equal to any small angle. The sum of any big angle and any small angle is 180°. When ETS says that two lines are parallel, this is what is being tested. The symbol for parallel lines (||) and the word parallel are both clues that tell you what to look for in the problem.
Look at the following exercise and answer the questions about degrees, lines, and angles. Answers can be found in Part V.
Circle Yes or No if the groups of angle measurements below could be the measurements of the figure above. The measurements in each group are listed in no particular order.
|
Yes |
No |
30°-30°-200°-100 ° |
|
|
Yes |
No |
90°-90°-90°-90° |
|
|
Yes |
No |
60°-40°-80°-80° |
|
|
Yes |
No |
80°-100°-80°-100° |
|
|
Yes |
No |
5°-5°-175°-175° |
6. Label the correct measure of each of the angles.
Each triangle contains three angles that add up to 180 degrees. The angles can be any positive number so long as they sum to 180 degrees. An equilateral triangle is a triangle in which all three sides are equal and each angle is 60 degrees. An isosceles triangle is a triangle in which two of the three sides are equal and two of the angles are also equal.
In any triangle, the longest side is opposite the largest interior angle; the shortest side is opposite the smallest interior angle. Furthermore, equal sides are opposite equal angles.
An equilateral triangle has to have angles that measure 60 degrees each. An isosceles triangle can have angles that have any measure so long as the two of the angles are equal and all three angles have a sum of 180 degrees.
The perimeter of a triangle is a measure of the distance around it. All you must do to find the perimeter of a triangle is add up the lengths of the sides.
Why is it impossible for the following triangle to exist?
This triangle could not exist because the length of any one side of a triangle is limited by the lengths of the other two sides. This can be summarized by the third side rule:
The length of any one side of a triangle must be less than the sum of the other two sides and greater than the difference between the other two sides.
This rule is not tested frequently on the GRE, but when it is, it’s usually the key to solving the problem. Here’s what the rule means in application: take the lengths of any two sides of a triangle. Add them together, then subtract one from the other. The length of the third side must lie between those two numbers.
Take the sides 3 and 5 from the triangle above. What’s the longest the third side could measure? Just add and subtract. The third side must be shorter than 5 + 3 = 8 but longer than 5 – 3 = 2.
Therefore, the third side must lie between 2 and 8. It’s important to remember that the third side cannot be equal to either 2 or 8. It must be greater than 2 and less than 8.
For the GRE, knowing two sides of a right triangle is enough to find the third side using the Pythagorean Theorem. If the problem doesn’t indicate that the triangle is a right triangle, it’s not possible to find the third side—only a range of possible values.
For geometry outside of the GRE, you could use trigonometry to find the length of the missing side of a non-right triangle. But, the GRE does not test this.
The area of any triangle is equal to its height (or altitude) multiplied by its base divided by 2.
The height of a triangle is defined as the length of a perpendicular line drawn from the point of the triangle to its base.
This area formula works on any triangle.
Consider the following statements about different triangles and fill in the blanks. Answers can be found in Part V.
1. A triangle with two equal sides also has two equal and is called an triangle.
2. The height of a triangle with a base of 3 and an area of 18 is .
3. A triangle with side lengths 2 and 6 has a third side length of between and .
4. A certain isoceles triangle has angle measurements of 20, 20, and .
5. The perimeter of a triangle with a single side length of 5 and two angles of 60 degrees is .
Right triangles are triangles in which one interior angle measures 90 degrees. Right triangles are easily identifiable due to the presence of the indicator for right angles.
Like all triangles, right triangles have interior angles that total 180 degrees. One of the angles is 90 degrees, so the other two angles have a sum of 90 degrees.
Calculating the area of a right triangle is no different from calculating the area of any other triangle. The equation is the same.
The base and the height of the triangle are the legs of the triangle. The legs are the two shortest sides. The longest side is called the hypotenuse. In order to calculate the area of a right triangle, it’s necessary to know how to calculate the lengths of the three sides of a right triangle.
The lengths of the three sides of a right triangle can be found using the Pythagorean Theorem, which is the equation:
a2 + b2 = c2
This theorem states that in a right triangle, the square of the length of the hypotenuse, which is the longest side, is equal to the sum of the squares of the lengths of the two other sides. In the equation above, c is the length of the hypotenuse and a and b are the lengths of the legs (short sides) of the triangle.
Try out calculating the area and the length of the missing side for the following right triangles. Answers can be found in Part V.
Certain right triangles have properties that make them “special.” These properties allow you to quickly identify any missing side or angle measurements of the right triangle. They are called Pythagorean Triples.
The two most common Pythagorean Triples are 3 : 4 : 5 and 5 : 12 : 13.
Note that a triangle could have sides with actual lengths of 3, 4, and 5, or 3 : 4 : 5 could just be the ratio of the sides. If you double the ratio, you get a triangle with sides equal to 6, 8, and 10. If you triple it, you get a triangle with sides equal to 9, 12, and 15.
These special right triangle side measurements allow you to easily determine the value of any missing side. If you know these ratios, you may be able to save yourself the time of working with the Pythagorean Theorem. But, don’t worry–if you are unsure whether the relationship of the side lengths is a special right triangle, you can always use the Pythagorean Theorem.
For every triangle, there is a relationship between the value of the angle measurement and the length of the side opposite that angle measurement. The greater the angle measurement, the greater the length of the side opposite it. This statement is true for all triangles, including right triangles.
But, for certain angle measurements in right triangles, there is a more concrete relationship between the angle measurements and the side lengths. This relationship exists for right triangles with angle measurements of 30 : 60 : 90 and 45 : 45 : 90.
If you take an equilateral triangle and draw in the height, you end up cutting it in half and creating a right triangle. The hypotenuse of the right triangle has not changed; it’s just one side of the equilateral triangle. One of the 60-degree angles stays the same as well. The angle where the height meets the base is 90 degrees and the length of the side that was the base of the equilateral triangle has been cut in half. The smallest angle, at the top, opposite the shortest side, is 30 degrees. The ratio of sides on a 30 : 60 : 90 triangle is x : x
: 2x. Here’s what it looks like:
This is significant for two reasons. The first is that if you see a problem with a right triangle and the hypotenuse is double one of the legs or there is a anywhere in the problem, you know what to look for. The second is that you always know the area of an equilateral triangle because you always know the height. The height is one half of one side of the equilateral triangle times the square root of 3.
If you take a square and cut it in half along its diagonal, you create an isosceles right triangle. The two sides of the square stay the same. The 90-degree angle stays the same, and the other two angles that were 90 degrees each get cut in half and are now 45 degrees. The ratio of sides in a right isosceles triangle is x : x : x
. Here’s what it looks like:
This is significant for two reasons. First, if you see a problem with a right triangle and there is a that are equal anywhere in the figure, you know what to look for. Second, you always know the length of the diagonal of a square because it is the length of one side times the square root of 2.
In the following exercise, match the figure with the value of x. Answers can be found in Part V.
2
45
4
15
60
24
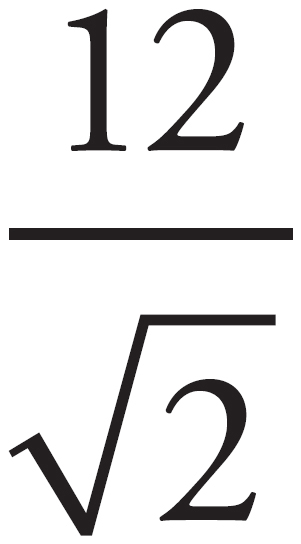
5
30
This chapter covers the perimeter and area of rectangles, as well as a rectangle’s relationship to a triangle. While it is true that parallelograms and squares are related to rectangles, these each have their contents in their own sections. This section deals specifically with rectangles.
The perimeter of a rectangle is the sum of the lengths of its four sides.
perimeter = 4 + 8 + 4 + 8 = 24
The area of a rectangle is equal to its length times its width. For example, the area of the rectangle above is 8 × 4 = 32.
Each corner of a rectangle is a 90-degree angle, which means that the total interior angles of a rectangle is 360 degrees.
Work through the following exercises on rectangles to determine the area and perimeter. Answers can be found in Part V.
1. How many possible integer perimeters are there for a rectangle with an area of 24?
2. What are the perimeter and area of the rectangle shown above?
3. What are the perimeter and area of the rectangle shown above?
4. What is the sum of the interior angles of a rectangle with an area of 108?
5. For each of the following base-height combinations, indicate whether the area or perimeter of the corresponding rectangle is greater.
Base = 6, Height = 6
Base = 12, Height = 2
Base = 3, Height = 4
Base = 1, Height = 1
A square is a rectangle with four equal sides. Like the interior angles of a rectangle, the interior angles of a square have a sum of 360 degrees. The three primary concepts tested about squares on the GRE are perimeter, area, and the relationship to triangles.
All squares are rectangles, but not all rectangles are squares.
Because the sides of a square are equal, the perimeter of a square can be found by either adding the sides together or multiplying one of the side lengths by 4. This creates the equation:
Perimeter = 4(side)
The area of a square is equal to the length of any side times itself. In other words, the area of a square can be represented by the equation:
Area = side2
A square has four 90-degree angles, as shown below:
Placing a diagonal line that extends from one corner to the other of a square bisects the corners and splits the 90-degree angle into two 45-degree angles.
The diagonal line splits the square into two 45:45:90-degree right triangles. The sides of a 45:45:90-degree right triangle are in a relationship of x : x : x. Therefore, if you know the side length of one of the sides of the square, you know the length of the diagonal. Similarly, if you know the length of the diagonal, you can determine the length of the sides.
This is true for squares only. The corners of rectangles that are not squares are not split evenly by the diagonal line extending from one corner to the other.
Determine whether the following statements regarding different squares are True or False. Answers can be found in Part V.
|
True |
False |
The perimeter of a square with side length 2 is 4. |
|
|
True |
False |
The area and perimeter of a square with side length 4 are equal. |
|
|
True |
False |
The diagonal of a square with side length 3 is 6. |
|
|
True |
False |
The side length of a square with a diagonal of 7 is |
|
|
True |
False |
The interior angles of a square have a sum of 180 degrees. |
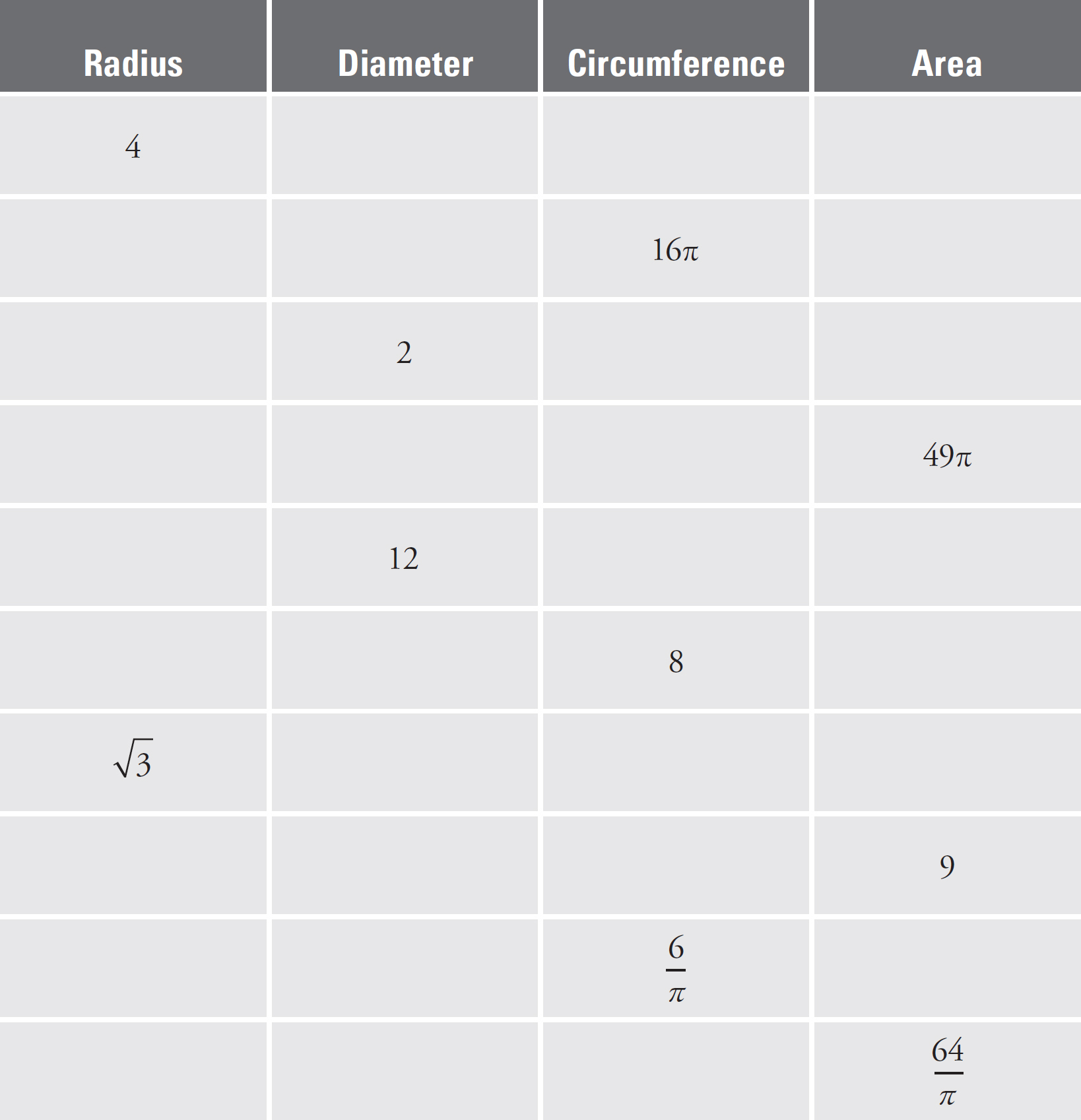
There are myriad topics about circles that are tested on the GRE, but some are more common than others. This section covers these topics–from the obscure to the typical–and groups them into three primary categories: Radius & Diameter, Circumference, and Area.
The radius of a circle is any line that extends from the center of the circle to a point on the circumference of the circle. The diameter of a circle is a line that connects two points on the circumference of the circle through the center of the circle. Therefore, the diameter of a circle is twice the length of the radius.
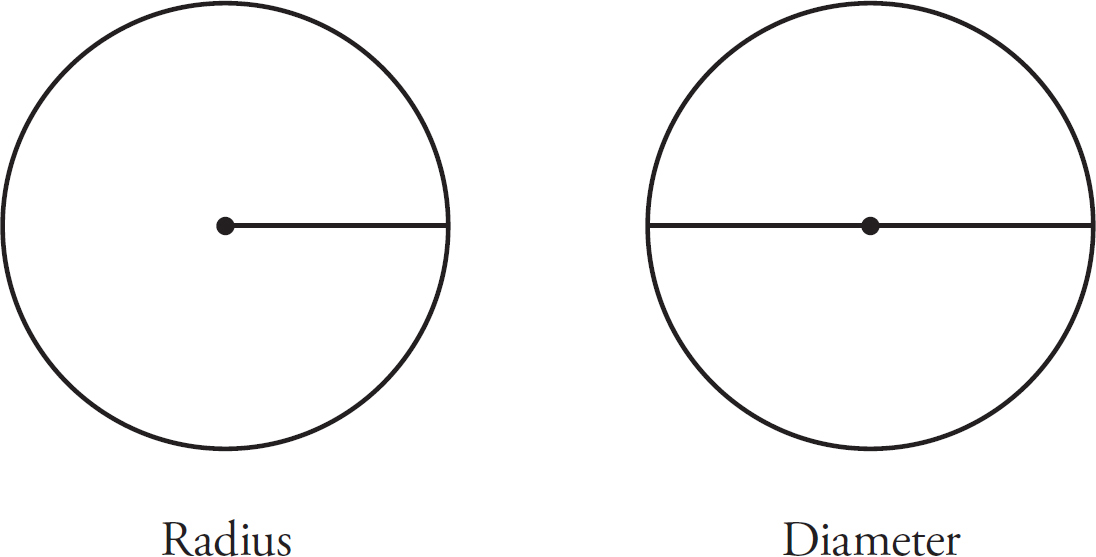
Solving geometry problems on the GRE typically involves finding the radius of the circle. The radius of the circle is central to finding the circumference and the area of a circle.
The circumference of a circle is the distance around the outside of the circle, as shown below.
The circumference of a circle is found by the equation:
circumference = 2πr or πd
The value of π can be approximated as a little over 3. If the diameter of a circle is 4, then its circumference is 4π, or a little over 12. If the diameter of a circle is 10 then its circumference is 10π, or a little more than 30.
When solving for the area or circumference of a circle, it’s typically best to leave π as a symbol, instead of converting it to a number. It is easier to recognize opportunities to cancel out π when it is in symbol form.
Understanding what the circumference of a circle is and how to derive it is essential to understanding several other elements of a circle, such as chords, arcs, and central angles. A chord is a line that connects two points on the circumference of a circle. The diameter of a circle is the longest chord in the circle. However, keep in mind that the radius is not a chord because it only touches one point on the circumference. An arc is a section of the outside, or circumference, of a circle. Any angle formed by two radii is called a central angle. There are 360 degrees in a circle, so if there is an arc formed by a 60-degree central angle, and 60 is 
of 360, then the arc formed by this 60-degree central angle is of the circumference of the circle. Chords, arcs, and central angles are typically represented as shown below:
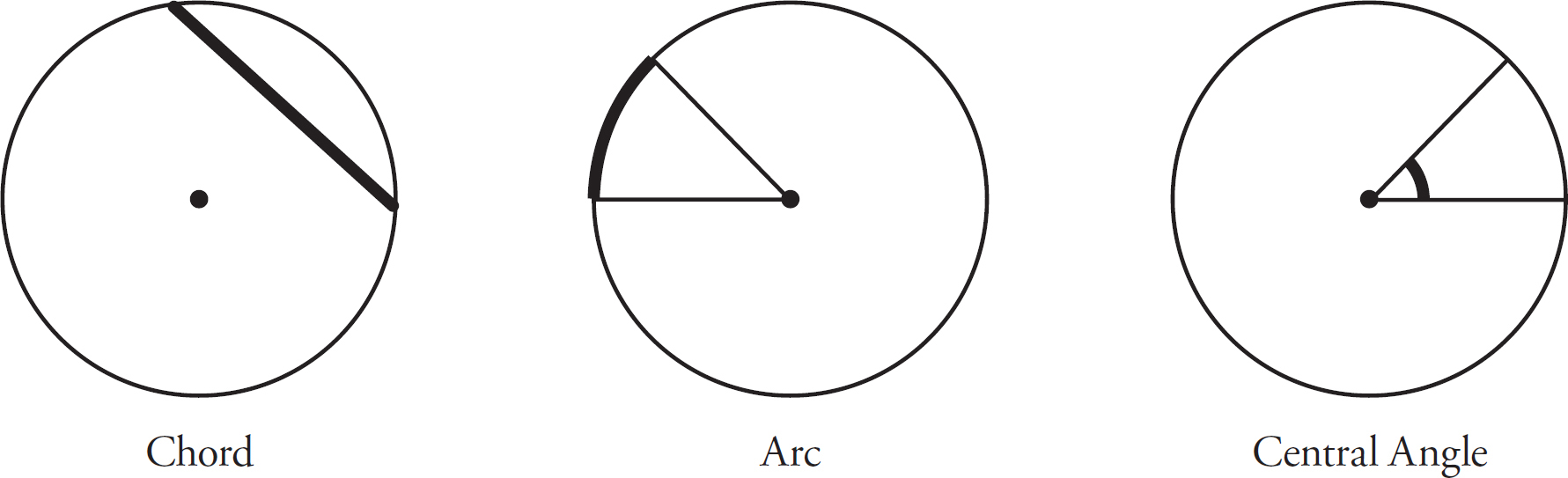
There are 360 degrees in every circle. This is important to know, as the GRE likes to carve up circles into smaller wedges and ask you questions about the size of those wedges. If you can determine the central angle of those wedges, you are usually on your way to the correct answer.
The area of a circle is the amount of space inside the circle. The equation for the area of the circle is:
area = πr2
The area of a circle is represented by the shaded area inside the circle below:
Now it’s time to practice. Use the information provided in the table below to determine the missing information. Answers can be found in Part V.
There are several figures tested on the GRE that are not easily categorized. This section covers some of those figures and how to work with them to solve for degrees, area, and perimeter. These other figures are separated into three groups–polygons, parallelograms, and trapezoids.
Polygons are figures like pentagons, hexagons, and octagons. A polygon is a figure with at least three straight sides and angles, and typically five or more. For the purposes of this discussion, we are going to focus on polygons with more than four sides. The GRE sometimes refers to these figures by name, such as labeling a figure a hexagon. Other times, the GRE mentions the number of sides of the figure, instead of the name of the figure. Typically, if the GRE references the name of the figure, the name is accompanied by a figure. However, if the GRE refers the figure by the number of sides, they do not always show a figure.
Sometimes the GRE refers to a polygon as a regular figure. For instance, they may reference a regular pentagon or a regular five-sided figure. The word regular means the figure has equal sides and angles. If the figure is not regular, than the lengths of the sides and the angles are not necessarily equal.
One kind of problem asked about polygons involves determining the degree measure of the angles inside the figure. The equation for determining the measure of the total angles in a polygon is:
180(n – 2)
This equation actually works for any polygon, including triangles, rectangles, and squares. However, it is best to commit to memory the total angle measure for triangles, rectangles, and squares.
where n is the number of sides in the figure. By extension, if you want to find out the measure of a single interior angle in a regular polygon, the equation is:
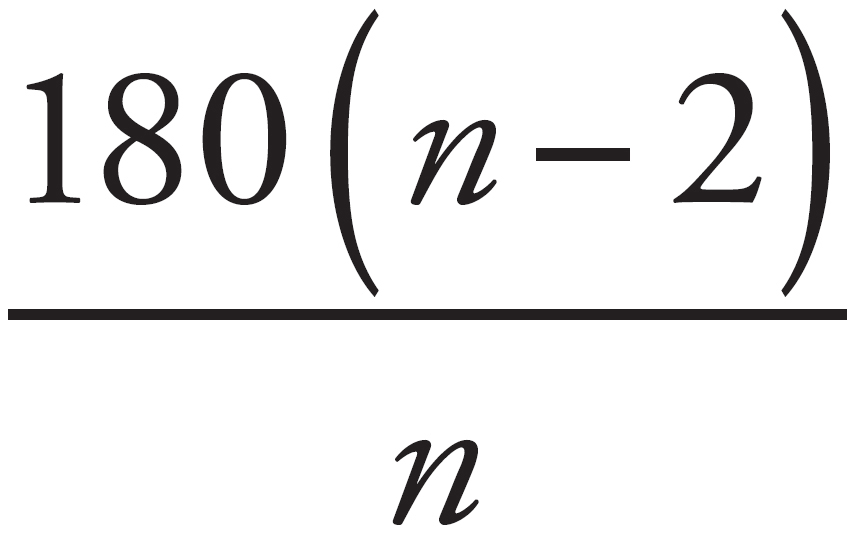
Once the measures of interior angles are found, it’s possible to determine several different measures of the figure such as the area of the whole figure or the area of a section.
Polygons that are not regular polygons cannot use this equation. A regular polygon has an even distribution of the total angle of the figure between all of its sides because all side lengths and angles are equal.
Solving for the area of a figure with more than four sides can be tricky. Take a look at the following regular six-sided figure:
How would you go about solving for the area of the entire figure?
This process begins by realizing that the straight-line distance between the center of the figure and each of the corners of the figure is the same. This is true of all regular polygons. A triangle with two equal sides can be created using this piece of knowledge.
Because the two lengths inside the figure are equal, the angles opposite both lengths are equal.
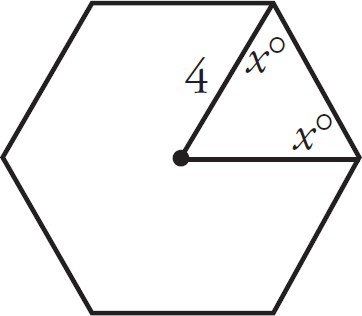
The central angle created by the intersection of the two lengths inside the figure is a portion of the entire area of the figure. There are 6 sides to the figure, so the entire area is 180(6 – 2) = 180(4) = 720. The degree measure of the interior angle is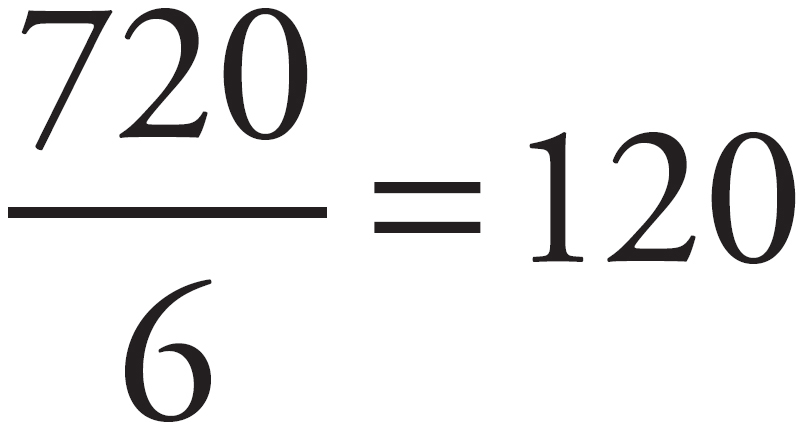 
. If the figure is split up into 6 equal triangles, a total of 12 angles are created. Each 120-degree angle is split in half. Therefore, each interior angle is 60 degrees, which means the third angle is also 60 degrees since a triangle has a total of 180 degrees. If the triangle has three equal angles, it is equilateral and also has three equal sides, so all sides are 4.
Draw in the height of the triangle that splits the base in half and this creates a 30:60:90-degree right triangle with side lengths 
. The area of this triangle is 
. Since there are six equal triangles in all, multiply the area of this triangle by 6. So, the area of the whole figure is 
.
Determine the total interior angles and a single interior angle for each of the following regular polygons. Answers can be found in Part V.
Parallelograms on the GRE often look like this:
The sides of a parallelogram that are opposite each other are parallel. Finding the perimeter and area of a parallelogram requires the height of the figure. The height of the figure is used to determine the area of the figure or the length of the slanted side of the figure.
To find the area of a parallelogram, it is necessary to determine the height by dropping a line from one of the corners straight down, as shown by the dotted line below:
The dotted line in the figure above is the height of the figure. Where the dotted line intersects with the base is a right angle. To find the area of the parallelogram, multiply the height by the length of one of the bases. The equation for the area of a parallelogram is:
Area = base × height
The base is the top or the bottom of the figure, as indicated by the thick lines below:
The height of a parallelogram creates a right triangle with one of the sides of the parallelogram. If the parallelogram provides the length of the slanted side of the figure and the length of the base of the right triangle, you can solve for the height of the parallelogram by using the Pythagorean Theorem. The figure below has sides labeled a, b, and c to represent the different variables of the Pythagorean Theorem.
Solving for the perimeter of a parallelogram follows a similar pattern. You can use the height of the figure and the base of the triangle created by the height to solve for the length of the slanted edge.
A trapezoid is a quadrilateral with only one set of parallel sides. A trapezoid could look like this:
Anytime there is an unfamiliar figure, look for ways to split that figure up into more familiar shapes.
In the case of the figure above, the parallel sides are the top and the bottom of the figure. The GRE tests the area and perimeter of trapezoids. The most effective way to solve for the area of the figure is to split the trapezoid into more familiar shapes and solve for the area of each of those shapes individually. For instance, the trapezoid above can be split into two right triangles and a rectangle:
You can then solve for the area of each of these familiar shapes individually and add them together to get the area of the trapezoid.
Finding the perimeter of a trapezoid follows a similar pattern to finding that of a parallelogram. Finding the lengths of the sides typically involves using the Pythagorean Theorem.
Now work on solving for the area of the parallelogram and trapezoid below. Answers can be found in Part V.
In a coordinate system, the horizontal line is called the x-axis and the vertical line is called the y-axis. The four sections of the coordinate plane formed by the intersection of these axes are called quadrants. While it is not strictly necessary to know the ordering of the quadrants for most coordinate plane problems, occasionally the quadrant numbers are asked about directly or mentioned as a compass on a question. So being familiar with them is a good idea. The point where the axes intersect is called the origin and its coordinates are (0, 0). This is what it looks like:
To express any point in the coordinate system, you first give the horizontal value, which is the value of the point associated with the x-axis. Next, you provide the vertical value, which is the value of the point associated with the y-axis. This creates the coordinates of the point, or (x, y). In the diagram above, point A can be described by the coordinates (2, 4). That is, the point is two spaces to the right of the origin and four spaces above the origin. Point B is described by the coordinates (–6, 1). That is, it is six spaces to the left and one space above the origin. What are the coordinates of point C?
The coordinate plane is often used to test shapes drawn onto the plane, such as circles, triangles, or rectangles. However, information about lines found on the plane, such as intercepts, the equation of a line, slope, points on a line, and perpendicular and parallel lines is also fair game for the GRE.
The x-intercept and y-intercept are the points at which a line on the coordinate plane crosses the x-axis or y-axis, respectively. The point at which a line crosses the x-axis happens when the coordinate of the point has a y-value of 0. The point at which a line crosses the y-axis happens when the coordinate of the point has an x-value of 0. Therefore, in order to determine the x-intercept or y-intercept, find the value of the x- or y-coordinate when the y or x coordinate is equal to 0.
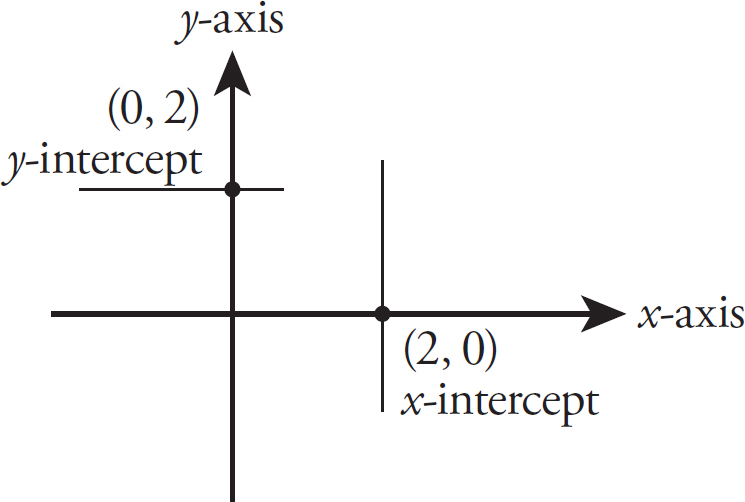
Trickier questions involving the coordinate system might give you the equation for a line on the coordinate plane. The equation of a line is:
y = mx + b
In this equation x and y are both points on the line, b stands for the y-intercept, and m is the slope of the line. Slope is defined as the vertical change divided by the horizontal change, often called “rise over the run” or “the change in y over the change in x.”
Sometimes on the GRE, m is written instead as a, as in y = ax + b. If you see this, don’t worry. Nothing has changed about the equation for the line or the slope if m is written as a.
Slope can be any number, positive or negative, and this designation dictates how a line appears on the coordinate plane. A line with a positive slope trends upward from Quadrant III to Quadrant I and a line with a negative slope trends downward from Quadrant II to Quadrant IV.
If the problem provides 2 points on a line, or one point on a line and the slope, it is possible to determine the location of other points on the line. The equation of a line can be used, in combination with the information provided, to determine missing points. Typically, the GRE provides one of the points on the line and then ask to determine either the x- or y-coordinate of a missing point.
For instance, if a question provided the information that a line passes through the origin and has a slope of 3, you could determine that the line also passes through the point (1, 3). You can do this by setting up a proportion. If the slope of the line is 3, the line passes through the origin, and the slope of the line is the change in y over the change in x, then the following equation can be written:
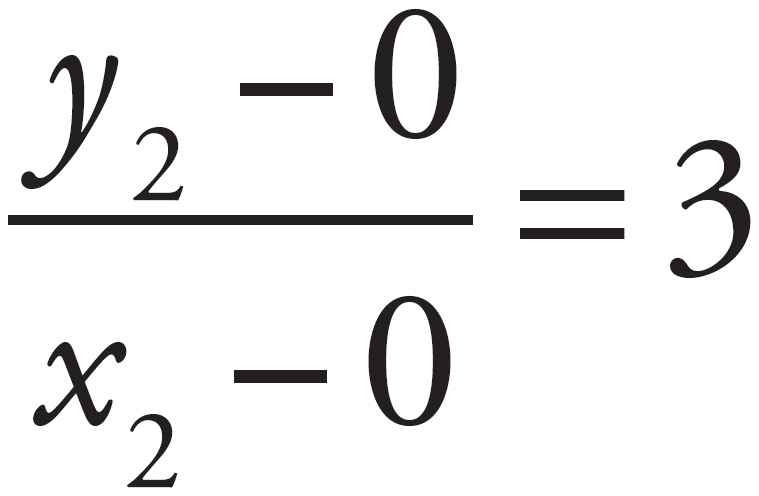
The slope can be rewritten as 
. If you solve for the slope, you determine that y2 = 3 and x2 = 1. The value of the missing point can be any (x, y) combination that results in a value of 3 for the expression 
. Alternatively, if a problem provides to you two points on a line, it is possible to find a third point. Use the two points to determine the slope and then use one of the points and the slope in the same manner shown above.
Perpendicular lines are lines with slopes that are negative reciprocals of each other. These lines intersect at a right angle. Parallel lines are lines with the same slope. Parallel lines will never intersect.
Work your way through the following exercise and determine whether the statements provided are True or False. Answers can be found in Part V.
|
True |
False |
A point with coordinates (10, 6) is in Quadrant II. |
|
|
|
|
|
|
|
True |
False |
The coordinates of point (A) could be (–2, –5). |
|
|
True |
False |
A line perpendicular to the line with equation y = 2x + 2 has a slope of |
|
|
True |
False |
A line that passes through the origin and point (–2, –1) also passes through the point (–1, 2). |
|
|
True |
False |
The slope of a line that passes through points (1, 2) and (–1, 6) is 2. |
|
|
True |
False |
A line with equation 3x + 2y = 6 has a positive slope. |
|
|
True |
False |
The equation of a line that passes through the origin and point (2, 6) is y = 3x. |
|
|
True |
False |
The x- and y-intercepts of a line that passes through points (3, 1) and (–1, 9) are |
3D figures on the GRE typically come in one of two forms: cylinders or rectangular solids. In order to answer most questions regarding 3D figures, you’ll need to know how to calculate the surface area and volume of each figure, and how to find the length of the diagonal of a rectangular solid or cube.
When represented visually, cylinders look like some variation of the following:
A cylinder may also be described as a right circular cylinder. No matter how a cylinder is represented, the most common concepts to test about this figure are surface area and volume.
Surface area is the area of the outer part of a figure. For example, the surface area of a can of soup is the area of the top and bottom of the can plus the area of the curved sides of the can.
Volume is the amount of space that a substance could occupy. The volume of a can of soup is the amount of soup that can fit inside the can.
The GRE can also use the concept of circular cylinder in word problems and refer to them as a word that describes a cylinder, such as “tanks,” “circular cylindrical tanks,” “tubes,” and “pipes.”
The surface area of a cylinder is calculated by the equation:
Surface Area = 2πr(height) + 2(πr2)
This equation looks like a lot. But, let’s break it down into its individual components.
The surface area of a cylinder is the sum of the area of the top of the cylinder, the area of the bottom of the cylinder, and the area of the curved side of the cylinder. The curved side of the cylinder is actually a rectangle that has been curved. Imagine taking a rectangular piece of paper and rolling it so two opposing edges now touch. Alternatively, imagine what would result if you removed the top and bottom from a can of soup, cut the resulting piece straight down just one side, and flattened it out. The height of the resulting rectangle is the same as the height of the can. However, the length of the rectangle is equal to the circumference of the top or bottom of the can. The circumference of a circle is found by the expression 2πr. Visually, the length and height of a cylinder can be represented by something like this:
On the GRE, the area of the top of the cylinder and the area of the bottom of the cylinder are equivalent circles.
The equation for surface area given above is just the sum of the areas of all these individual components. This can be represented graphically as:
In order to solve for the surface area of a circular cylinder, it is necessary to have, or be able to derive, a value for the radius of the top or bottom of the cylinder as well as the height of the cylinder.
The volume of a cylinder is calculated by the equation:
Volume = πr2(height)
The volume of a cylinder is the value of all the space inside the cylinder.
In the cylinder above, the volume is represented by the shaded area. Consider volume as the amount of water it would take to fill the cylinder. If water were to be poured into the cylinder, the water would first fill up the area of the bottom of the cylinder and then fill that area for the entirety of the height of the cylinder. This is the information that the equation for the volume of a cylinder is asking for–solve first for the area of the base of the cylinder and then multiply it by the height.
Now that you’re equipped with some knowledge about finding surface area and volume for a cylinder, fill in the blanks in the following exercises. Answers can be found in Part V.
Area of the curved side of the figure:
Area of the top of the figure:
Surface area:
2. A cylinder with a volume of 18π and a radius of 3 has a height of .
3. What is the volume of a cylinder with a height of 4 and the following measurements:
a radius of 3 ?
a base with an area of 4π ?
a diameter of 8 ?
4. Determine the surface area of cylinders with the following measurements:
Height 2; Radius 3
Height 3; Radius 2
Height 5; Radius 1
Height 1; Radius 3
When represented visually, rectangular solids or cubes look like this:
The most commonly tested concepts with rectangular solids are volume and surface area. However, occasionally the GRE tests the length of the diagonal of the rectangular solid or cube.
Surface area is the area of the outer part of the rectangular solid. This is represented by the area of the top and bottom, front and back, and both sides of the figure.
Volume is the amount of space inside the figure. This is the amount of space that could be occupied by a substance placed inside the rectangular solid.
It is easier to visualize the items required to calculate the surface area and volume by placing dotted lines in the figure to represent the missing edges. This makes it clear that there are 6 faces (flat sides) that create the outside of the figure. The sum of the areas of each of these six sides is the surface area.
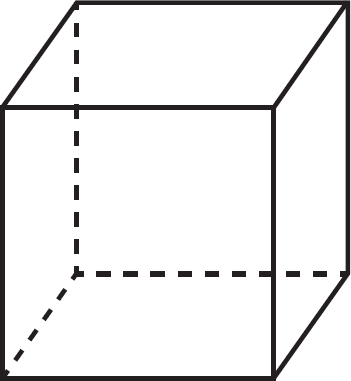
Don’t be afraid to draw in these dotted lines on your own figure during the test if it makes the figure easier to look at.
The diagonal of the rectangular solid or cube is the longest distance between two corners. This is represented by the xxx dotted line below.
The surface area of a rectangular solid is calculated via the equation:
Surface Area = 2(length × width) + 2(length × height) + 2(width × height)
For a regular rectangular solid, the side lengths are labeled as follows:
Let’s look at each of the components of the equation for surface area independently.
The expression length × width produces the area for the top or the bottom of the figure. The equation for surface area multiplies this by 2 to represent the area of both the top and bottom of the figure. The expression length × height represents the area of the front or back of the rectangular solid and this is also multiplied by 2 to represent the front and the back. Finally, the expression width × height represents the area of one of the sides of the rectangular solid. The product is multiplied by 2 to account for both faces on the sides.
Ultimately, the surface area of a rectangular solid or cube is the sum of the areas of the faces. For a cube, this equation is greatly simplified. A cube is a rectangular solid that has equal length, width, and height. To find the surface area of a cube, the expression is 6(s2), where s is the length of one of the edges of the cube.
The formula for the surface area of a cube is just the formula for the area of a square multiplied by 6.
The equation for the volume of a rectangular solid is simpler than that of the surface area of the rectangular solid. The equation for the volume of a rectangular solid is:
Volume = length × width × height
Therefore, calculating the volume of a rectangular solid only involves figuring out the values of the length, width, and height.
The volume of a cube is found by the expression s3, where s is the value for either the length, width, or height of the cube.
In the figure below, the diagonal of a rectangular solid is depicted by the dotted line. The diagonal of a rectangular solid is the straight-line distance between points A and B. This is the longest length inside of a rectangular solid.
Solving for the distance between A and B requires only one equation. The equation is:
a2 + b2 + c2 = d2
In the equation, d is the value of the diagonal distance while a, b, and c are the dimensions of the rectangular solid. If you’re familiar with right triangles, this equation will remind you a lot of the Pythagorean Theorem. In fact, this equation is called the Super Pythagorean Theorem.
Great work!
Now work with the following rectangular solids and determine their surface area, volume, and diagonal length. Answers can be found in Part V.
Surface Area:
Volume:
Diagonal Length:
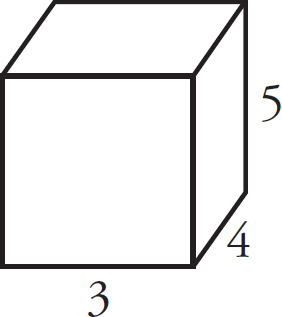
Surface Area:
Volume:
Diagonal Length:
Surface Area:
Volume:
Diagonal Length:
Surface Area:
Volume:
Diagonal Length:
Notice any similarities between the rectangular solids in questions 2 and 4? That’s right—their values are the same. When calculating the surface area, volume, and diagonal of a rectangular solid, it typically does not matter what edge receives what length or label. The only time it does matter is if another figure shares one of the edges.
1. V = Length × width × height
2. 16π
3. y = mx + b
4. 180
5. 720
6. P = 2(length) + 2(width)
7. Right triangle
8. 
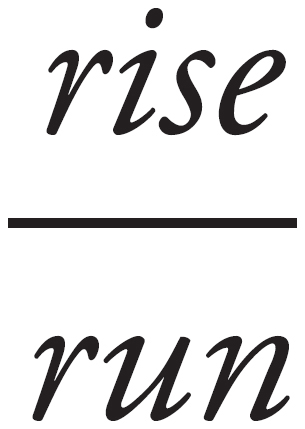or 
9. 360
Cylinders and rectangular solids are the most common types of 3D figures on the GRE. Know how to find the surface area and volume of each.
Using the radius of a circle, it is possible to determine the area and circumference of that circle.
Calculate the arc length or interior angle of a portion of a circle using the area or circumference and a proportion.
Use coordinate geometry to calculate the x- or y-intercept of a line, the equation of a line, slope, points on a line, or whether two lines are parallel or perpendicular.
There are 180 degrees in a line. Parallel lines intersected by the same line create big angles and small angles. Vertical angles are equal.
The area of polygons, such as hexagons and octagons, is determined by splitting the figure up into familiar shapes.
Right triangles are a special kind of triangle. The side lengths of right triangles are calculated using the Pythagorean Theorem.
Know how to calculate the perimeter and area of a square. Also know the relationship between squares and right triangles.
The Third Side Rule can be used to find a range of possible values for a missing side of a triangle. The equation for the area of a triangle is exactly half of the equation for the area of a rectangle.
