
Now that you know the basics of geometry on the GRE, it’s time to put those skills to the test. This chapter contains practice problems and solutions, actionable advice on how to crack certain problem types, and information about specific types of questions you may encounter on test day.
The previous chapter explored the basics of geometry on the GRE. It covered the types of figures you can expect to see, what you might be expected to calculate, and the calculations necessary to get to the correct answers. While the previous chapter focuses mostly on what geometry concepts the GRE tests, this chapter focuses on how those geometry concepts are tested on the GRE.
This chapter does not discuss, in any detail, what figures look like, their specific properties, or the equations needed to solve for specific measurements. This chapter assumes a basic working knowledge of geometry rules and formulas. We covered all the rules and formulas that you need to know in the previous chapter.
Unsure whether you should tackle this chapter or start with the previous chapter?
Take this short quiz to find out!
“Should I Do This Chapter?” Quiz
1. What is the formula for the volume of a rectangular solid?
2. If the radius of a circle is 4, what is its area?
3. What is the equation of a line?
4. How many degrees are there in a line?
5. What is the sum of the interior angle measurements of a figure with 6 sides?
6. What is the formula for the perimeter of a rectangle?
7. The side lengths of what kind of triangle can be found using the Pythagorean Theorem?
8. What is the equation for the slope of a line?
9. How many degrees are in a circle?
10. What is the formula for the area of a triangle?
The answers to these questions are at the back of this chapter.
So, how’d you do? If you got more than two questions wrong, you might want to consider starting with the previous chapter.
For those of you who are continuing forward with this chapter (or for those of you who rejoined us after a sojourn with the previous chapter), welcome! This chapter shows you how the GRE typically tests geometry concepts. It is filled with sample GRE problems to test your skills. We will be with you the whole time to walk you through how to answer these sample problems. Along the way, we’ll reveal to you some important tips and tricks for how to increase your odds of getting the question correct, and trends for how the GRE likes to test geometry concepts.
There is also a 15-question drill at the end of this chapter. Answer the questions in that drill when you feel confident in the material contained within the chapter. This is the most obvious place to test yourself in this chapter. Meanwhile, the questions contained in the body of the chapter are explained immediately following each question. When possible, we’d recommend that you try to answer each question before reading the explanation. Don’t be bothered if you get the question wrong–that’s how you learn!
We’ll start by looking at the most straightforward topics and gradually move into the more complex. The questions each try to outline a common way the GRE tests a specific topic.
Without any further preamble, let’s get started.
While every geometry question on the GRE is unique and requires a unique combination of equations, there are a couple of universal tips that can be applied across all problems.
Draw the figure and label any information from the problem on the figure.
Oftentimes, GRE geometry problems provide or describe a figure. Occasionally, problems describe a relationship among data points that create a common figure when drawn. Even if a figure is provided for a given question, that figure appears on a computer screen. Avoid trying to do calculations in your head by first drawing or redrawing the figure from the problem on your scratch paper and labeling any information from the problem on the figure.
Figures are not necessarily drawn to scale.
Figures provided to you on the GRE may not be drawn to scale, so be skeptical of them. Always make sure to draw and label figures based on the information provided in the problem.
Consider the following question, which asks about angles and lines:


|
Quantity A |
Quantity B |
|
a + b |
180 |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Degrees, lines, and angles are asked about in conjunction with other basic shapes to make these questions more difficult.
Here’s How to Crack It:
This is a Quant Comp question with geometry, so begin by drawing the figure and labeling any information from the problem on the figure. The question only states that lines l1 and l2 are parallel. Now work with the quantities. Quantity A is the value of a + b. The parallel lines in the figure are intersected by the same line, which creates big angles and small angles at each intersection. The rule of parallel lines dictates that when two parallel lines are crossed by a third line, the big angles are equal and the small angles are equal. Additionally, the sum of any big angle and any small angle is 180 degrees, as there are 180 degrees in a line. Angle a is a small angle and angle b is a large angle, so the value of a + b is 180. Quantity B is also 180. The quantities are equal. The correct answer is choice (C).

Knowing the properties of parallel lines helps answer the previous question. Occasionally, the GRE asks about lines or angles independently of any other figure or concept, such as in the previous question. However, most of the time the GRE asks about degrees, lines, and angles in relationship to other figures. How could knowing the properties of parallel lines, plus a little knowledge about parallelograms, help to answer this more complex question?


|
Quantity A |
Quantity B |
|
120 + x |
a + b |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It:
This is a Quant Comp question with geometry, so begin by drawing the figure and labeling any information from the problem on the figure. The problem states that the figure is a parallelogram, so the sides opposite each other are parallel. There is no additional information in the problem, so begin working with the quantities. Quantity A is 120 + x. The angle marked as 120 is the large angle created by a line intersecting two parallel sides. The angle marked x is the small angle created by the same line. When two parallel lines are intersected by the same line, the large and small angles that are formed have a sum of 180. Therefore, x = 180 – 120 = 60 and Quantity A is 120 + 60 = 180. Now work with Quantity B. Quantity B is a + b. For any parallelogram, angles on the same side add up to 180°. Therefore, Quantity B is 180. The quantities are equal. The correct answer is choice (C).

The previous example shows how the GRE combines concepts from two different knowledge bases to make a more difficult problem. In that example, if you do not know about the big and small angles of parallel lines or about parallelograms you may struggle to determine the correct answer.
Let’s try another example of how the GRE could test degrees. But, this time let’s consider an example that only involves vertical angles and lines.


In the figure above, what is the value of a + b ?
 145
145
 155
155
 180
180
 200
200
 225
225
Here’s How to Crack It:
This is a geometry question, so begin by drawing the figure and labeling any information from the problem on the figure. The question stem provides no additional information, so work the problem. The question asks for the value of a + b. Determine the value of these variables independently. Angle a is adjacent to a 35-degree angle that is created by the intersection of two lines. Therefore, angle a is the difference between the degrees in the line and 35, which is 180 – 35 = 145. Angle b is adjacent to a 125-degree angle that is created by a different intersection of two lines. So, angle b is the difference between the degrees in the line and 125, which is 180 – 125 = 55. The value of a + b is 145 + 55 = 200. The correct answer is choice (D).

There were several ways to solve the problem above. For instance, you could have noticed that the two lines are each 180 degrees, so the total degrees for both lines is 360 degrees. Then, it would have been reasonable to write the equation a + b + 35 + 125 = 360 and solve to find that a + b = 200.
Much like with parallel lines, vertical angles are often paired with another domain of knowledge. Take, for example, the following question that works with circles.

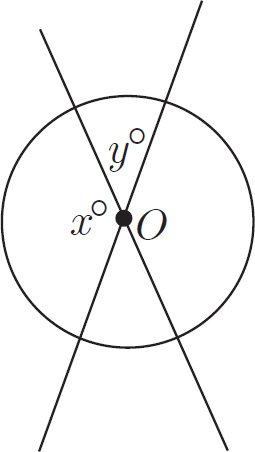
In the figure above, the circle has center O and the two lines intersect at point O. If the length of the arc of the circle opposite angle y is  the total circumference of the circle, then what is the measure of angle x ?
the total circumference of the circle, then what is the measure of angle x ?
 45
45
 90
90
 120
120
 135
135
 150
150
Here’s How to Crack It:
While this problem appears to be predominantly about circles, it is primarily about vertical angles with only a little circle knowledge required. This is a geometry question, so begin by drawing the figure and labeling any information from the problem on the figure. The question states that the arc opposite angle y is  the total circumference of the circle. Because the length of an arc is proportional to its corresponding angle, angle y is
the total circumference of the circle. Because the length of an arc is proportional to its corresponding angle, angle y is  the total angle of the circle. A circle has 360 degrees, so angle y is 360 ×
the total angle of the circle. A circle has 360 degrees, so angle y is 360 ×  = 60 degrees. Because angle y was created by two intersecting lines, angle y has a vertical angle pair with the angle directly below it. Therefore, the angle directly below angle y is also 60 degrees. The total value of these two angles is 120 degrees. Angle x and the angle opposite angle x are also vertical angles, so they are also equal. Because the vertical pair with angle y makes up 120 of the 360 degrees in a circle, the vertical angle pair with angle x makes up 360 – 120 = 240 degrees. Because the angles are equal, both angle x and the angle opposite it are 240 + 2 = 120 degrees. The correct answer is choice (C).
= 60 degrees. Because angle y was created by two intersecting lines, angle y has a vertical angle pair with the angle directly below it. Therefore, the angle directly below angle y is also 60 degrees. The total value of these two angles is 120 degrees. Angle x and the angle opposite angle x are also vertical angles, so they are also equal. Because the vertical pair with angle y makes up 120 of the 360 degrees in a circle, the vertical angle pair with angle x makes up 360 – 120 = 240 degrees. Because the angles are equal, both angle x and the angle opposite it are 240 + 2 = 120 degrees. The correct answer is choice (C).

Beginning this chapter’s specific discussions with degrees, lines, and angles serves a few valuable purposes. First, the line is the simplest form of a geometric figure. Maybe more critically, this topic illustrates how the GRE often pairs more than one concept together. If you had an in-depth understanding of lines and angles, but only a cursory understanding of circles or parallelograms, you may have missed one of these questions.
The most common way the GRE increases the difficulty of a question is by pairing it with another figure. This allows them to test domain knowledge from two shapes instead of one.
The GRE does not stop pairing concepts with degrees, lines, and angles. They pair all sort of figures together–circles, squares, triangles, coordinate planes, polygons, etc. Always keep your eye open for figures or descriptions that indicate more than one shape. If you see these types of figures, take the problem one shape at a time. Typically, something about one of the shapes leads to opportunities to uncover missing information about the other.
The GRE often tries to ask for the area of a triangle, or the length of one of the sides of a triangle, by hiding the fact that it is asking about a triangle at all. Don’t be fooled! Take the following problem, for example:

Adam’s house is 3 kilometers due west of the local high school and 7 kilometers due north of the local grocery store.
|
Quantity A |
Quantity B |
|
The straight-line distance, in kilometers, between the local high school and the local grocery store. |
8 kilometers |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It:
The question begins by describing the location of three places: Adam’s house, the local high school, and the local grocery store. Draw each of these places and label any information. Place a point and label it A for Adam’s house. Draw a line from point A directly to the right to another point labeled H, for the local high school. Label the length of that line 3 kilometers. Draw another line directly down from point A to another point labeled G, for the local grocery store. Label the length of this line 7 kilometers. This is all the information in the problem, so now work with the quantities. Quantity A is the straight-line distance, in kilometers, between the local high school and the local grocery store. Draw the line between points G and H and label it x. This creates triangle AGH. Because point A is directly to the right of point H and directly north of point G, this creates a right angle. So, triangle AGH is a right triangle. Determine the length of the missing side by using the Pythagorean Theorem. The length of the missing side is between 32 + 72 = 58, so c2 = 58 and c =  . Quantity B is 8 kilometers. Because
. Quantity B is 8 kilometers. Because 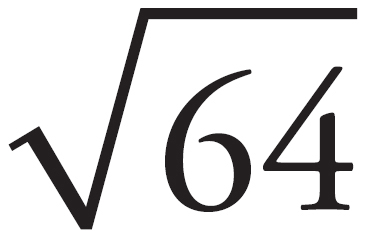 = 8, Quantity B is greater than Quantity A. The correct answer is choice (B).
= 8, Quantity B is greater than Quantity A. The correct answer is choice (B).

Do you notice anything interesting about the previous triangle question? How about the fact that at no point during the question stem or the quantities did the word “triangle” ever appear? The only reasonable way we know this is a triangle question is if we draw the figure described, label the information in the problem, and recognize the presence of the triangle.
Now work with the following question:

A right triangle has legs of length x and y such that 3 ≤ x ≤ 5 and 4 ≤ y ≤ 8. Which of the following could be the length of the hypotenuse?
Indicate all such lengths.
 5
5
 6
6
 7
7
 8
8
 9
9
Here’s How to Crack It:
This is an All that Apply question, so make sure to evaluate each answer choice. The question describes a right triangle with leg lengths 3 ≤ x ≤ 5 and 4 ≤ y ≤ 8 and asks for the length of the hypotenuse. The hypotenuse of a right triangle is found using the Pythagorean Theorem, so find the range of possible values of the hypotenuse. The least possible length of the hypotenuse is when x = 3 and y = 4, so use the Pythagorean Theorem to find that the hypotenuse is 9 + 16 = c2 and c2 = 25. Therefore, c = 5 and the least length of the hypotenuse is 5. The greatest possible length of the hypotenuse is when x = 5 and y = 8, so that length is 25 + 64 = c2 and c2 = 89. So, 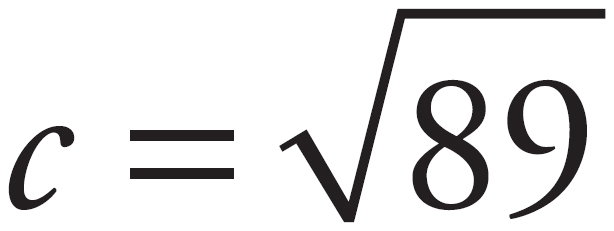 . While it may not be apparent what
. While it may not be apparent what  is as a decimal or fraction, it can be determined that it is greater than 9 but less than 10 because
is as a decimal or fraction, it can be determined that it is greater than 9 but less than 10 because  and
and  . All the answer choices are integer lengths, so the range for the length of the hypotenuse is 5 ≤ hypotenuse < 10. All of the answer choices fall within this range, so the correct answer is choices (A), (B), (C), (D), and (E).
. All the answer choices are integer lengths, so the range for the length of the hypotenuse is 5 ≤ hypotenuse < 10. All of the answer choices fall within this range, so the correct answer is choices (A), (B), (C), (D), and (E).

The preceding question is an example of combining two concepts into one question using geometry and one of the other GRE math topics. In the case above, we needed to use knowledge of triangles and knowledge of working with inequalities to find a range in order to answer the question.
Which leads us to another important point for how GRE geometry questions are made more difficult–they are not always paired with another figure. They are occasionally paired with a concept from another discipline. This means that GRE geometry questions are more chameleon-like than algebra and arithmetic–they can take on different styles.
Nonetheless, the difficulty of a GRE geometry question is usually increased by pairing two figures. This is especially true of triangles. The hypotenuse of a triangle is a natural pair for the diameter of a circle of the diagonal length of a rectangle. Take the following question for example:

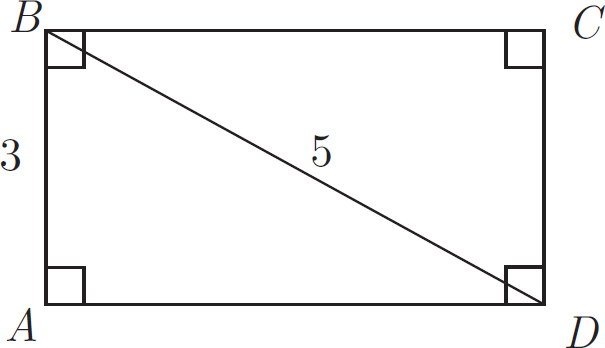
In the rectangle above, what is the area of triangle ABD ?
Here’s How to Crack It:
This is a geometry question, so redraw the figure and label any information from the problem. The problem states that figure ABCD is a rectangle. This was apparent from the presence of the small squares at the corners of the rectangle, which indicate a right angle. The question asks for the area of triangle ABD, which can be found by the expression 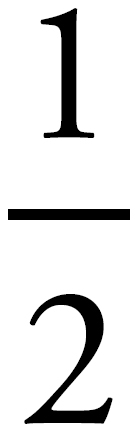 (base)(height). The figure provides the height, which is 3. The figure also provides the length of the hypotenuse, 5, so solve for the length of the base using the Pythagorean Theorem. Alternatively, recognize that 3 and 5 are both members of a 3:4:5 special right triangle. Either way, the length of the base is 4. Therefore, the area of triangle ABD is
(base)(height). The figure provides the height, which is 3. The figure also provides the length of the hypotenuse, 5, so solve for the length of the base using the Pythagorean Theorem. Alternatively, recognize that 3 and 5 are both members of a 3:4:5 special right triangle. Either way, the length of the base is 4. Therefore, the area of triangle ABD is 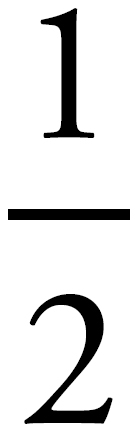 (4)(3) = 6. The correct answer is 6.
(4)(3) = 6. The correct answer is 6.

The previous question makes it apparent that ABD is a triangle and that BD is both the hypotenuse of the triangle and the diagonal of the rectangle. The same is true about the hypotenuse of the triangle and the side of the square in the following figure. For practice, try to use the information provided to determine the area of square ABDE.

Because the legs of the triangle are both 7 and the angle opposite the hypotenuse is a right angle, this is a 45:45:90 triangle. The sides of a 45:45:90 triangle have a relationship of x : x : x so the hypotenuse, which is also a side of the square, is 7
so the hypotenuse, which is also a side of the square, is 7 . The area of the square is (7
. The area of the square is (7 )2 = 49 × 2 = 98.
)2 = 49 × 2 = 98.
While the previous two figures made it obvious what role the sides of the triangle play in the relationship to the other figure, oftentimes the GRE does not provide for you all the necessary lines. Instead, they may expect you to draw them in yourself. An example of this is in the next question, which tests another special right triangle.


Triangle XYZ in the figure above is an equilateral triangle. If the perimeter of the triangle is 12, what is its area?




 8
8
 12
12


Here’s How to Crack It:
This is a geometry question, so begin by drawing the figure and labeling any information from the problem on the figure. The question states that triangle XYZ is an equilateral triangle, so each of the angles is 60 degrees. The question also states that the perimeter of the triangle is 12, so the length of each side of the triangle is 4. The question asks for the area of the triangle, which is found by the equation area = 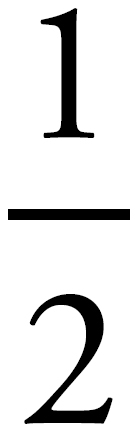 (base)(height). The base of the triangle is the length of one of the sides, so the base is 4. However, to determine the height, it is necessary to drop a line from one of the points straight down to intersect the opposite side. Because the triangle is equilateral, this line bisects the angle it originated from, creating two 30-degree angles, as shown below:
(base)(height). The base of the triangle is the length of one of the sides, so the base is 4. However, to determine the height, it is necessary to drop a line from one of the points straight down to intersect the opposite side. Because the triangle is equilateral, this line bisects the angle it originated from, creating two 30-degree angles, as shown below:

This creates two 30:60:90-degree special right triangles, each with a side relationship of x : x : 2x, respectively. The length of the hypotenuse of the triangle is 4 and that corresponds to the side of 2x, so 2x = 4 and x = 2. This means the short leg of the triangle (the one opposite the 30-degree angle) is 2 and the middle side of the triangle, which is also the height of the triangle, is 2
: 2x, respectively. The length of the hypotenuse of the triangle is 4 and that corresponds to the side of 2x, so 2x = 4 and x = 2. This means the short leg of the triangle (the one opposite the 30-degree angle) is 2 and the middle side of the triangle, which is also the height of the triangle, is 2 . The lengths of this right triangle are labeled in the figure below:
. The lengths of this right triangle are labeled in the figure below:

The height of the triangle is 2 , so the area of the triangle is
, so the area of the triangle is  . The correct answer is choice (B).
. The correct answer is choice (B).

If you see square root 2 or square root 3 in the answer choices, it’s a tip off that the problem is testing special right triangles.
The previous question did not make it explicit that it was testing 30:60:90 triangles. Instead, getting the question correct relied on you to draw the height, recognize that the height creates two 30:60:90 triangles, and know the relationship between the sides and angles of a 30:60:90 triangle. While that question only tested one figure—a single triangle—the most difficult triangle questions include a relationship between a triangle and another figure while concealing the presence of the relationship. This requires that you be capable of parsing out the missing information. And here’s the real kicker–the question may not even appear to include a triangle at all!
Knowing the relationships between the sides and angle measurements of right triangles is essential to answering some GRE questions, so make sure to know these cold.


In the figure above, a circle is inscribed in a square and another square is inscribed in the circle. If the area of the smaller square is 36, what is the straight-line distance between points A and C ?
 6
6
 12
12
 24
24
 36
36
 72
72
Here’s How to Crack It:
This is a geometry question, so begin by drawing the figure and labeling any information from the problem on the figure. The problem states that a circle is inscribed in a square and a square is inscribed in that circle. The area of the smaller square is 36, which means that the length of the sides of the smaller square is 6. If the length of each of the sides is 6, then the smaller square is made up of two 45:45:90-degree triangles that have legs of length 6. The side relationship of a 45:45:90 triangle is x : x : x , so the length of the hypotenuse is 6
, so the length of the hypotenuse is 6 . The hypotenuse of the smaller square is the same length as the diameter of the circle. Because a circle’s diameter is constant for all lines that pass through the center of the circle, this figure could be redrawn as follows:
. The hypotenuse of the smaller square is the same length as the diameter of the circle. Because a circle’s diameter is constant for all lines that pass through the center of the circle, this figure could be redrawn as follows:

Considering this, the diameter of the circle is the same length as the sides of the larger square. This is also described by the word inscribed in the question stem, which means that the circle touches the square at the ends of the diameter. The question asks about the distance between points A and C. Square ABCD is also made up of two 45:45:90 triangles with legs of length 6 . Therefore, the length of the diagonal of the larger square is 6
. Therefore, the length of the diagonal of the larger square is 6 (
( ) = 12. The correct answer is choice (B).
) = 12. The correct answer is choice (B).

One common way for the GRE to test relationships between figures is by shading portions of a figure, such as can be seen in the next question:


In the figure above, a square is placed inside of a rectangle.
|
Quantity A |
Quantity B |
|
The area of the shaded region |
40 |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It:
This is a Quant Comp question with geometry, so begin by drawing the figure and labeling any information from the problem on the figure. The problem states that a square is placed inside a rectangle, so the larger quadrilateral is a rectangle and the smaller quadrilateral is a square. Now work with the quantities. Quantity A is the area of the shaded region. The area of the shaded region is found by the expression area of the entire figure – area of the unshaded region (that is, area of the entire figure minus area of the unshaded region). The area of the entire figure is the area of the rectangle, which is 8 × 7 = 56. The area of the unshaded region is the area of the square, which is 42 = 16. So, the area of the shaded region is 56 – 16 = 40. Quantity A is 40. Quantity B is also 40. The quantities are equal. The correct answer is choice (C).

If you look closely, there is something curious about the figure in the previous problem. The larger quadrilateral certainly looks like a square, but the problem states it’s a rectangle and the lengths of the sides are not the same, which means it is not a square. What gives?
The GRE is under no obligation to draw figures to scale. The GRE occasionally uses this fact to trip students up. Consider the following problem:


In the figure above, BC = CF.
|
Quantity A |
Quantity B |
|
The area of ABCF |
The area of FCDE |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It:
This is a Quant Comp question with geometry, so begin by drawing the figure and labeling any information from the problem on the figure. The figure states that BC = CF, so mark both BC and CF as x. Now there is a variable in the question, so be prepared to Plug In more than once. There is no further information in the problem, so work with the quantities. Quantity A is the area of ABCF. Because BC = CF and the angles of ABCF are right angles, ABCF is a square. The area of a square is found by the expression side2. The side of ABCF is x, so Plug In. If x = 2, then the area of ABCF is 4. Now work with Quantity B. Quantity B is the area of FCDE. The length of side CF is x = 2. If the length of side CD equals the length of side BC, then CD is also 2 and the area of FCDE is 4. In this case, the quantities are equal and choices (A) and (B) can be eliminated. However, the problem gives no indication that BC = CD or that CF = CD. Therefore, it is possible that the length of CD is 3, for example. If that is the case, then FCDE is a rectangle with area 3 × 2 = 6. Quantity B is now greater than Quantity A. Eliminate choice (C). The correct answer is choice (D).

When the GRE asks about quadrilaterals, it tends to test the area or the perimeter. Much like it does for every other topic, the GRE increases the difficulty of questions that involve common concepts by obscuring the fact that they are testing something basic by cloaking it with other concepts.
The area of quadrilaterals is one of the knowledge bases the GRE likes to ask about unfamiliar contexts. Check out the following problem:


If AD = 6, what is the area of parallelogram ABCD ?
Here’s How to Crack It:
This is a geometry question, so begin by drawing the figure and labeling any information from the problem on the figure. The problem states that AD = 6, so write that on the figure. The question asks for the area of parallelogram ABCD. The area of a parallelogram is found by the expression base × height. The height of the parallelogram is 5 and the base is 6, so the area is 6 × 5 = 30.

The last question is a straightforward area question, so long as you know the formula for the area of a parallelogram. If you don’t know the formula for the area of a parallelogram, you may be at a loss for how to find an answer to the question. Next, let’s look at an example of how the GRE may obfuscate the concept of quadrilaterals.

A rectangular patio is 6 feet wide by 15 feet long. The rectangular bricks used to make the patio are 6 inches by 12 inches. How many bricks were used to make this patio? (Note: 1 foot = 12 inches)
 45
45
 90
90
 120
120
 180
180
 200
200
Here’s How to Crack It:
Start by converting the dimensions of the patio into inches so that both the patio and the bricks are measured using the same units. Because 1 foot is equivalent to 12 inches, the dimensions of the patio are 72 inches wide (6 × 12) by 180 inches long (15 × 12). The area of the patio, in square inches, is A = lw = (72)(180) = 12,960. The area of each brick, in square inches, is A = lw = 6 × 12 = 72. To find the number of bricks needed for the patio, divide the area of the patio by the area of one brick: 12,960/72 = 180. The correct answer is choice (D).

There are many ways the GRE can test the area or perimeter of quadrilaterals. The best way to prepare for this figure type is to know the equations, be familiar with the different types of quadrilaterals, and understand the relationship between the dimensions that make up the area and the dimensions that make up the perimeter. The area and the perimeter of quadrilaterals are derived from the same dimensions (length and width). If you have the necessary information to solve for one of either the area or perimeter of a quadrilateral, it’s often the case that you have the necessary information to solve for both. This tactic can often be combined with less familiar quadrilaterals to really up the difficulty of a problem.
Unsure of all these formulas and relationships? Check out the previous chapter.


If the area of the trapezoid above is 108, what is the perimeter?

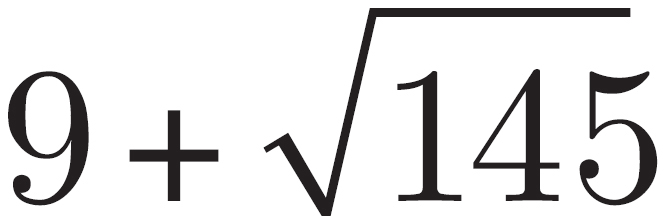

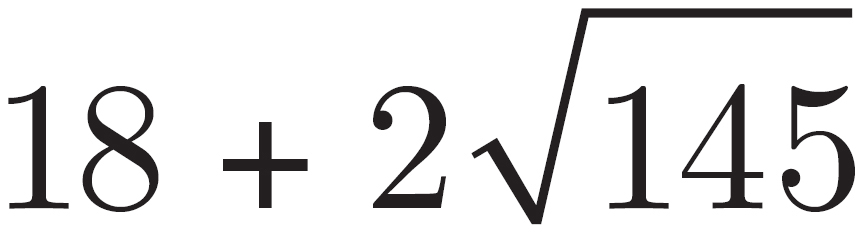






Here’s How to Crack It:
This is a geometry question, so begin by drawing the figure and labeling any information from the problem on the figure. The problem states that the area of the trapezoid is 108. The area of the trapezoid can be found by splitting the trapezoid into 3 familiar figures—a rectangle and two right triangles, as shown below.

By splitting this figure, it’s easier to recognize the right triangles that are created by the heights. Because each right triangle has a right angle and an angle of 50 degrees, the right triangles are identical. Therefore, the length of the base of each triangle is half the difference between the length of the top and the bottom of the trapezoid. The difference between the top and the bottom is 10 – 8 = 2, so the length of the base for each triangle is 1. There are two identical right triangles, and the area of each is found by the expression 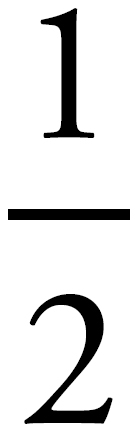 (base)(height). Because the triangles are identical, the combined area of the triangles is
(base)(height). Because the triangles are identical, the combined area of the triangles is  = base × height. The base of the triangles is 1, so the combined area of the triangles is equal to whatever the height is. The area of the rectangle is found by the expression length × width. The width of the rectangle is 8 and the length is the same as the height of the triangles. Therefore, it is possible to write the equation for the area of the trapezoid as 108 = height + 8(height) = 9(height) and height = 12.
= base × height. The base of the triangles is 1, so the combined area of the triangles is equal to whatever the height is. The area of the rectangle is found by the expression length × width. The width of the rectangle is 8 and the length is the same as the height of the triangles. Therefore, it is possible to write the equation for the area of the trapezoid as 108 = height + 8(height) = 9(height) and height = 12.
The question asks for the perimeter of the figure. The perimeter of the figure is the sum of the top of the trapezoid, the bottom of the trapezoid, and the hypotenuse of each of the triangles created above. The top and bottom of the trapezoid are given by the problem. The triangles are right triangles and the legs of the triangles are known, so use the Pythagorean Theorem. The hypotenuse is 12 + 122 = c2 and c2 = 145. Thus, c =  . So, the perimeter of the trapezoid is 8 + 10 +
. So, the perimeter of the trapezoid is 8 + 10 +  +
+  = 18 + 2
= 18 + 2 . The correct answer is choice (B).
. The correct answer is choice (B).

The GRE asks about a multitude of characteristics of circle—area, circumference, central angles, sectors, arcs, diameter, radius, etc. Finding the correct answer for difficult circle questions on the GRE is often about understanding the relationship between these different characteristics. For instance, it’s important to know that if you’re given the radius of a circle, you can calculate the area or circumference. Similarly, if you know radius and the length of an arc, you can calculate the central angle or sector area. Take a look at the following problems that illustrate some of the common ways that the GRE tests circles.


In the wheel above, with center O, the area of the entire wheel is 169π. If the area of the shaded hubcap is 144π, then t =
Here’s How to Crack It:
This is a geometry question, so begin by drawing the figure and labeling any information from the problem on the figure. The problem states that the area of the entire wheel is 169π. The area of a circle is found by the expression πr2, so πr2 = 169π. This means r2 = 169 and r = 13. The radius of the entire circle with center O is 13. The problem then states that the area of the shaded hubcap is 144π. The radius of the shaded area is found by the equation πr2 = 144π, which means r2 = 144 and r = 12. The problem asks for the value of t, which is the difference between the radius of the circle with center O and the radius of the shaded area, which is 13 – 12 = 1. The correct answer is 1.

Let’s try another one:


In the figure above, a circle with the center O is inscribed in square WXYZ. If the circle has radius 3, then PZ =
 6
6

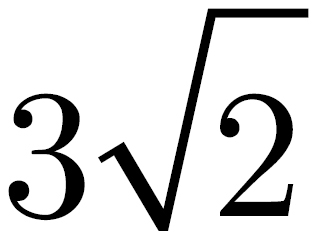






Here’s How to Crack It:
This is a geometry question, so begin by drawing the figure and labeling any information from the problem on the figure. The problem states that the circle is inscribed in the square and the circle has a radius of 3. Because the circle is inscribed in the square, the diameter of the circle is the same length as a side of the square. The radius of the circle is 3, so the diameter of the circle is 6, which means that each of the sides of the square are also 6. The question asks for the value of PZ. The length of PZ is the diameter of the circle plus the distance between the end of the circle and the corner of the square. The value for the distance between the edge of the circle and the corner of the square is the difference between the diameter of the circle and the diagonal of the square divided by two. The difference is divided by two because both PX and the distance between Z and the perimeter of the circle are equal. Begin by solving for the value of the diagonal of the square. The diagonal of the square splits the square in half, forming two 45:45:90-degree right triangles. The lengths of the sides of a 45:45:90-degree right triangle are is x : x : x , respectively. If two sides of the square are 6, then the diagonal is 6
, respectively. If two sides of the square are 6, then the diagonal is 6 . The diameter of the circle is 6. Therefore, the distance between the edge of the circle and the corner of the square is
. The diameter of the circle is 6. Therefore, the distance between the edge of the circle and the corner of the square is  . Add this distance to the diameter of the circle to find that the length of PZ is 3
. Add this distance to the diameter of the circle to find that the length of PZ is 3 – 3 + 6 = 3
– 3 + 6 = 3 + 3. The correct answer is choice (E).
+ 3. The correct answer is choice (E).

Solving the previous two questions involves using the diameter and radius of a circle to yield other information about the circle, such as the area. This diameter and radius of a circle can also be used to determine information about other figures, such as a triangle or a square. But there is more about circles that the GRE can test besides area, diameter, and radius. The following question is a good example of two other measures of circles that are related: arc length and central angle.


In the circle with center O shown above, what is the length of minor arc AB ?



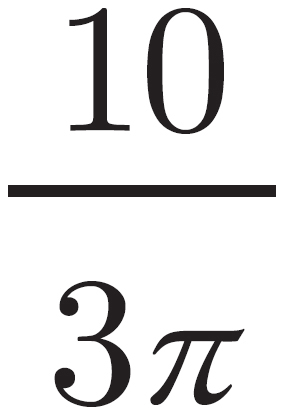
 3π
3π

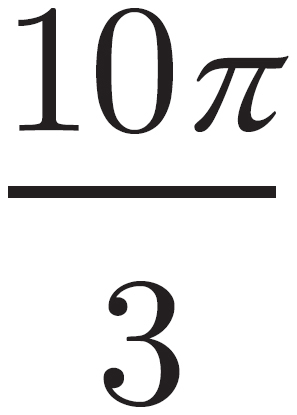
 10π
10π
Here’s How to Crack It:
This is a geometry question, so begin by drawing the figure and labeling any information from the problem on the figure. The problem states that angle AOB is 120 degrees. The question asks about the length of arc AB, which is a portion of the circumference of the circle. Begin by determining the circumference of the circle. The circumference of a circle is found by the expression 2πr. The radius of the circle is 5, so the circumference is 10π. The length of an arc of the circle is proportional to the degree measure of the angle with which it is associated. In this case, arc AB is associated with angle AOB, which is 120 degrees. The circumference of the circle is associated with the degree measure of the entire circle, so the circumference is related to all 360 degrees in the circle. In order to find the length of the arc, set up a proportion that states 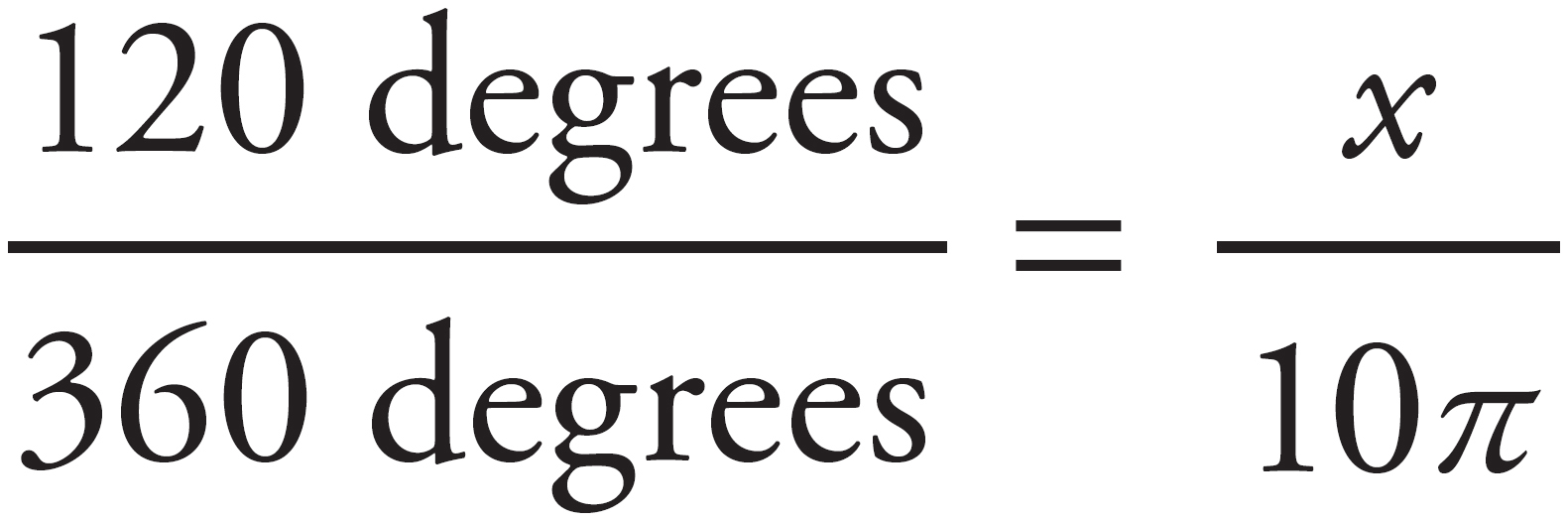 . Cross-multiply and divide to find that 1200π = 360x and =
. Cross-multiply and divide to find that 1200π = 360x and = 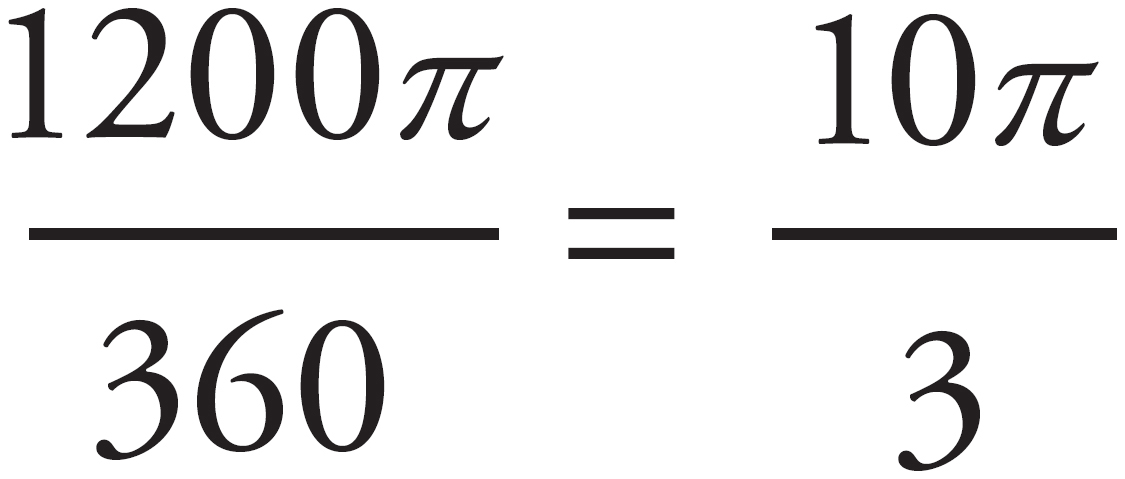 . The correct answer is choice (E).
. The correct answer is choice (E).

The previous problem provided the radius and a central angle and asked to solve for the length of an arc. However, the problem could have given the radius and the length of the arc and asked for the central angle. In that case, the process to find the central angle is the same as the process to find the arc length. Instead of using the central angle to find the proportion, find the relationship between the arc and the circumference. Once that fraction is determined, set that equal to the fraction of the missing angle and 360 degrees.
A similar process could be used if the question asked for the area of a shaded segment, such as seen in the figure below.

The shaded area of the circle (called a sector) can be calculated if you can determine the area of the entire circle and the central angle that is associated with the shaded region.
Let’s try a version of this kind of problem:


In the circle with center O shown above, if the shaded region has an area of 8ϖ and the measure of angle AOB is 60 degrees, what is the radius of the circle?
 2
2
 4
4
 6
6
 8
8
 10
10
Here’s How to Crack It:
This is a geometry question, so begin by drawing the figure and labeling any information from the problem on the figure. The problem states that the area of the shaded region is 8π and the measure of angle AOB is 60 degrees, so set up a proportion to find the area of the entire circle.
That proportion is  . Cross-multiply and divide to find that 60x = 2,880π and x = 48π. The area of the circle is 48π, so use this and the equation for the area of a circle to calculate the radius as πr2 = 48π and
. Cross-multiply and divide to find that 60x = 2,880π and x = 48π. The area of the circle is 48π, so use this and the equation for the area of a circle to calculate the radius as πr2 = 48π and  . The correct answer is choice (B).
. The correct answer is choice (B).

There are many iterations of how circles can be tested on the GRE. Circles can be tested alone or with other figures. Covering all these iterations is beyond the scope of this chapter. But, if you take the practice tests and drills, you’ll see a good sampling of the different ways the GRE can ask about this versatile shape.
The types of questions that the GRE constructs regarding coordinate geometry may be best thought of as falling into one of two primary buckets: questions about concepts specific to coordinate geometry and questions that marry concepts of coordinate geometry with the other types of figures we’ve seen in this chapter thus far.
Let’s begin our discussion of coordinate geometry questions on the GRE with the first group, starting with a question about the quadrants of the coordinate system.


Points (x, 5) and (–6, y), not shown in the figure above, are in Quadrants I and III, respectively. If xy ≠ 0, in which quadrant is point (x, y) ?
 IV
IV
 III
III
 II
II
 I
I
 It cannot be determined from the information given.
It cannot be determined from the information given.
Here’s How to Crack It:
If point (x, 5) is in Quadrant I, that means x is positive. If point (–6, y) is in Quadrant III, then y is negative. The quadrant that contains coordinate points that have a positive x and a negative y is Quadrant IV. The correct answer is choice (A).

Another basic concept that is specific to coordinate geometry is the slope of a line. Occasionally the GRE asks about the slope of a given line directly. More commonly, the GRE asks about slope as part of the equation of a line. The equation of a line is sometimes provided by the problem. However, the GRE can also ask that the equation be derived by using a line drawn on the coordinate plane that has clearly defined points. An example of this can be seen in the following problem:


The line  is graphed on the rectangular coordinate axes.
is graphed on the rectangular coordinate axes.
|
Quantity A |
Quantity B |
|
OR |
OP |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It:
This is a Quant Comp question with coordinate geometry. The question stem provides a figure and the equation of the line on the figure. Determine the different elements of the equation of the line. The y-intercept, or b, is 1. That means the line crosses the y-axis at 1. So, the coordinates of point P are (0, 1). Now determine the coordinates of point R. We know the y-coordinate is 0 because point R is on the x-axis. Let’s use that information along with the equation of the line in the question stem to determine the x-coordinate value of R.
y = mx + b

Now let’s solve for x.

So the coordinates of point R are ( , 0). That means OR, in Quantity A, is equal to
, 0). That means OR, in Quantity A, is equal to  , and OP, in Quantity B, is equal to 1. The answer is (B).
, and OP, in Quantity B, is equal to 1. The answer is (B).
Another approach to this question would be to focus on the meaning of slope. Because the slope is 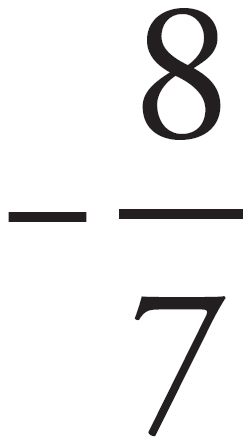 , that means the vertical change is 8 and the horizontal change is 7. In other words, you count up 8 and over 7. Clearly the rise is more than the run; thus OP is more than OR.
, that means the vertical change is 8 and the horizontal change is 7. In other words, you count up 8 and over 7. Clearly the rise is more than the run; thus OP is more than OR.

Another way the coordinate plane is tested on the GRE is a question that asks to find a point on a line. Knowing the rise over run equation for computing the slope can help solve these problems.


In the rectangular coordinate system above, q = 9. If the line passes through the origin, what is the value of p ?
 6
6
 8
8
 9
9
 12
12
 13
13
Here’s How to Crack It:
The question states the line passes through the origin and the figure shows that the line passes through point (8, 6). Therefore, the slope of the line is 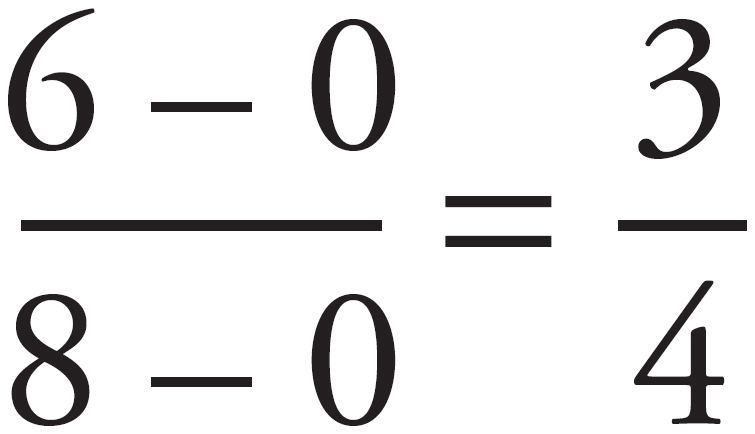 . Now that the slope of the line is known, use this information to determine the value of p when q = 9 by pairing these points with one of the other points on the line and setting it equal to the slope. The equation is
. Now that the slope of the line is known, use this information to determine the value of p when q = 9 by pairing these points with one of the other points on the line and setting it equal to the slope. The equation is 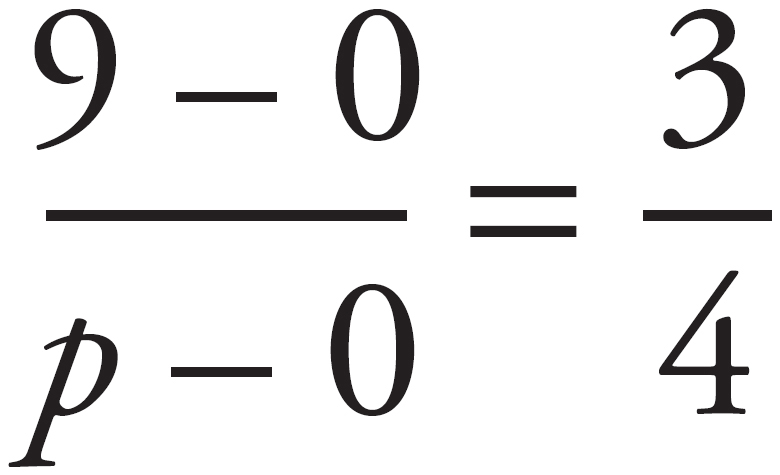 and 3p = 36, so p = 12. The correct answer is choice (D).
and 3p = 36, so p = 12. The correct answer is choice (D).

Coordinate system questions may also ask you to solve for the intercept of a line. The intercept of a line is the point at which the line crosses another. Typically, on the GRE, the intercept is where the line crosses the x- or y-axis.
Knowing the slope-intercept form of a linear equation can help to solve these types of questions.
Take a look at a question that involves solving for the intercepts:

What is the x-intercept of the line defined by the equation y = 2x + 3 ?









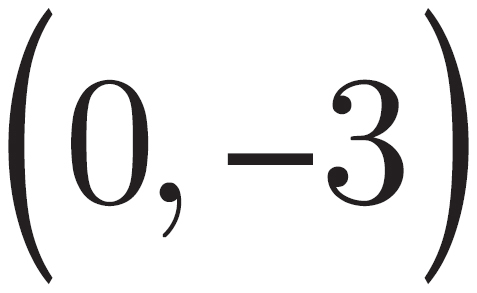
Here’s How to Crack It:
The x-intercept is the point at which the line crosses the x-axis. The line crosses the x-axis when y = 0. To solve for the x-intercept, set y = 0 in the equation and solve for x: 0 = 2x + 3 and x =  . The answer choices are shown as the points of the x-intercept, so find the one where x =
. The answer choices are shown as the points of the x-intercept, so find the one where x =  and y = 0. The correct answer is choice (C).
and y = 0. The correct answer is choice (C).

Coordinate systems sometimes have more than two lines on a single plot. The GRE may ask you to determine the relationship between the two lines.
Many times, the relationship is determined by the slope of the lines. Parallel lines have the same slope. Perpendicular lines have slopes that are negative reciprocals of each other. In other words, if the slope of one line is 2, then the slope of a line perpendicular to it is  .
.

Points C and D are located at (–3, 4) and (5, –12), respectively. Line m passes through points C and D. What is the slope of a line that is perpendicular to line m ?
 –4
–4
 –2
–2
 –
–


 2
2
Here’s How to Crack It
The slope of line m is equal to 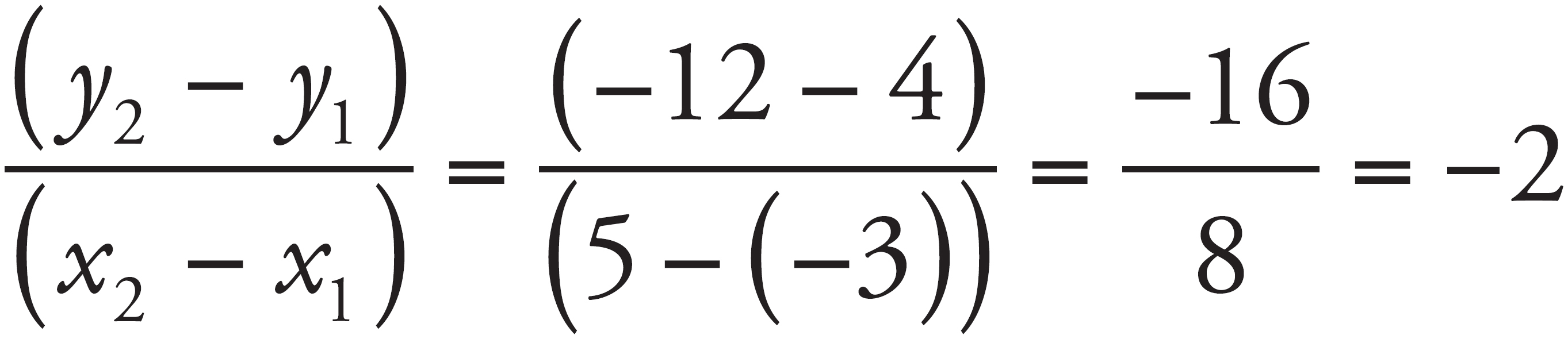 . The negative reciprocal of –2 is
. The negative reciprocal of –2 is 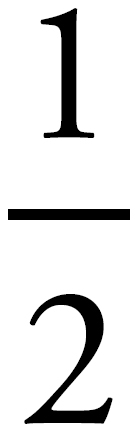 , so the correct answer is (D). Another way to solve this would be to plot line m using points C and D.
, so the correct answer is (D). Another way to solve this would be to plot line m using points C and D.
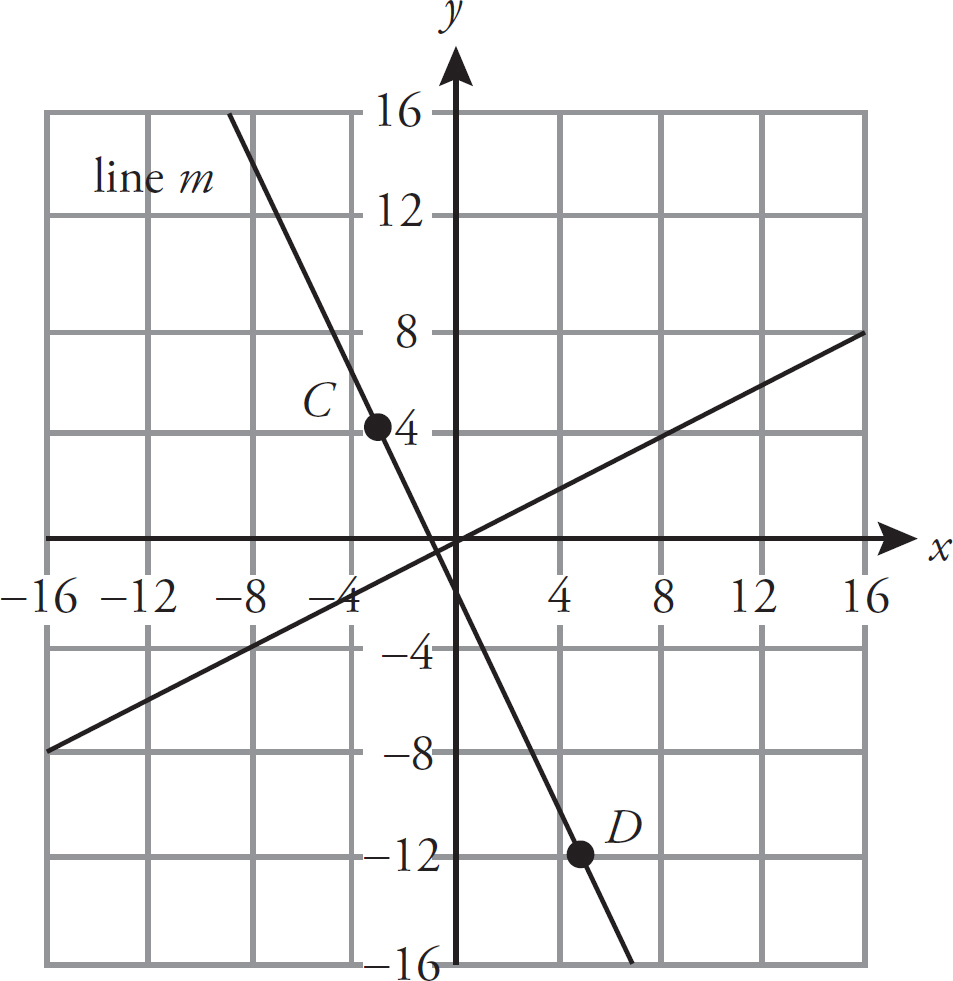
Line m slopes rather sharply down from left to right, so it has a negative slope. A line perpendicular to line m would have a positive slope, so (A), (B), and (C) can be eliminated. Finally, a line perpendicular to line m would have a rather gradual positive slope, so eliminate (E).
Coordinate geometry questions on the GRE test:
Quadrants
Slope
Points on a line
Intercepts of a line
Parallel or Perpendicular lines
To recap, the types of coordinate geometry questions that are specific to coordinate geometry involve quadrants, slopes, points on a line, intercepts, and parallel and perpendicular lines.
But, one of the primary ways to ramp up the difficulty of coordinate geometry questions is to involve other figures. The next question is an example of this, which pairs circles and coordinate geometry concepts.

A circle with center (2, 5) and a radius of 4 sits on the coordinate plane. Which of the following points are inside the circle?
Indicate all such points.
 (5, 6)
(5, 6)
 (6, 9)
(6, 9)
 (–1, 5)
(–1, 5)
 (0, 3)
(0, 3)
Here’s How to Crack It:
In order to determine if a point is inside the circle, it’s necessary to determine the number of units that the point is away from the center of the circle. If the number of units is less than the radius of the circle then the point sits inside the circle. The distance between the center of the circle and a point can be considered the hypotenuse of a right triangle that is created by the intersection between the extension of the center and the point. Consider the following example:

So, for each answer choice, find the intersection of the point from the answer choice and the center of the circle extended and apply the Pythagorean Theorem to determine the length of the hypotenuse.
For choice (A), the distance along the x-axis is 5 – 2 = 3 and the distance along the y-axis is 6 – 5 = 1. Therefore, the hypotenuse is 32 + 12 = c2 and c2 = 10, so c =  . Because 4 =
. Because 4 =  , the distance from the center of the circle to the point is less than the radius. Therefore, this point lies within the circle. Keep choice (A). Apply this to each of the remaining points. The hypotenuse of choice (B) is 42 + 42 = c2 and c =
, the distance from the center of the circle to the point is less than the radius. Therefore, this point lies within the circle. Keep choice (A). Apply this to each of the remaining points. The hypotenuse of choice (B) is 42 + 42 = c2 and c = 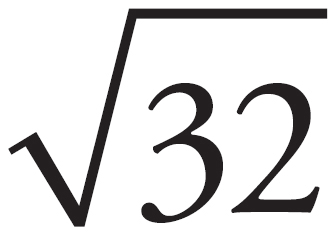 , which is greater than the radius, so eliminate choice (B). Choice (C) is a straight horizontal line that has a length of 3. This is less than the radius, so keep choice (C). The hypotenuse of choice (D) is 22 + 22 = c2 and c =
, which is greater than the radius, so eliminate choice (B). Choice (C) is a straight horizontal line that has a length of 3. This is less than the radius, so keep choice (C). The hypotenuse of choice (D) is 22 + 22 = c2 and c =  , which is less than the radius, so keep choice (D). The correct answer is choices (A), (C), and (D).
, which is less than the radius, so keep choice (D). The correct answer is choices (A), (C), and (D).

The GRE could pair any figure along with the coordinate plane–triangles, squares, rectangles, etc. The key to these questions is to look for common relationships between the concepts of coordinate geometry and the dimensions of the figures.
The final section of this chapter on GRE geometry focuses on 3D figures and polygons. The GRE asks about these types of questions in only a handful of ways. We’ll discuss each below, starting with basic questions about volume and surface area.

A right circular cylinder with height 2 inches has volume 16 cubic inches.
|
Quantity A |
Quantity B |
|
The radius of the base of the cylinder, in inches |
4 inches |
Here’s How to Crack It:
This is a Quant Comp geometry problem, so begin by drawing the figure and labeling any information from the problem on the figure. The problem describes a right circular cylinder with a height of 2 inches and a volume of 16. Draw this figure. The volume of a cylinder is found by the equation volume = area of the base × height. The height is 2 and the volume is 16, so rewrite this equation as 16 = area of the base × 2. The area of the base is the area of the circle at the bottom of the cylinder, so this is found by the expression πr2. Now work with the quantities. Quantity A is the radius of the base of the cylinder and Quantity B is 4 inches. Instead of solving for the radius, use the value in Quantity B as the radius and compare the result to the volume provided by the problem. In this case 42(π)(2) = 32π and 32π > 16, so the radius of the cylinder is less than 4. Quantity B is greater. The correct answer is choice (B).

Here’s another example:

What is the volume of a rectangular box, expressed in terms of its length, l, that is four times as long as it is high, and twice as wide as it is long?
 l3
l3



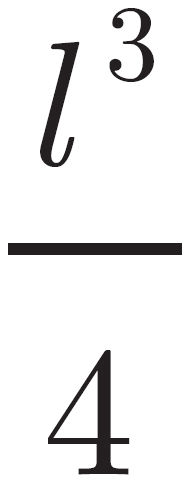




Here’s How to Crack It:
This is a geometry problem, so begin by drawing the figure and labeling any information from the problem on the figure. The question describes a rectangular box. The volume of a rectangular box is from by the expression length × width × height. The problem provides information about the height and width in terms of the length, so rewrite these. The problem says the box is four times as long as it is high, so height =  . The problem states that the box is twice as wide as it is long, so width = 2(length). Now rewrite the equation for volume in terms of length, so volume = length × 2(length) ×
. The problem states that the box is twice as wide as it is long, so width = 2(length). Now rewrite the equation for volume in terms of length, so volume = length × 2(length) ×  . The correct answer is choice (B).
. The correct answer is choice (B).

Sometimes, the GRE can combine the concepts of surface area and volume into the same question, as shown below:

What is the volume of a cube with a surface area of 96 inches2 ?
 64 inches3
64 inches3
 70 inches3
70 inches3
 74 inches3
74 inches3
 78 inches3
78 inches3
 82 inches3
82 inches3
Here’s How to Crack It:
This is a geometry problem, so begin by drawing the figure and labeling any information from the problem on the figure. The problem gives the surface area of a cube. The surface area of a cube is found by the expression 6(s2), where s is the length of one of the sides. This is true because a cube is a three-dimensional square and the surface area is the sum of the areas of each of the faces of the cube. Therefore, 96 = 6(s2) and s2 = 16. Thus, s = 4. The volume of a cube is found by the expressions s3, so the volume of this cube is 43 = 64. The correct answer is choice (A).

One of the ways in which the GRE makes these types of problems more difficult is by adding an additional element to the description of the figure, such as shown below:

A right circular tank with a height of 6 is halfway filled with water. If the volume of water in the tank is 27π, then what is the radius of the base of the tank?
Here’s How to Crack It:
The problem states that the tank is halfway filled with water. The volume of water in the tank is 27π, so the total volume of the tank is 54π. The volume of a cylinder is found by the expression πr2(height). The height is 6, so solve for the radius: 54π = πr2(6) and r2 = 9. Therefore, r = 3. The correct answer is 3.

There’s a special formula that you can use if you are ever asked to find the length of a diagonal (the longest distance between any two corners) inside a three-dimensional rectangular box. It is a2 + b2 + c2 = d2, where a, b, and c are the dimensions of the figure.
Take a look:

What is the length, in inches, of the longest distance between any two corners in a rectangular box with dimensions 3 inches by 4 inches by 5 inches?
 5
5


 12
12


 50
50
Questions that ask about the length of the diagonal of a rectangular box sometimes ask about the longest length of an object that could be placed inside the box. These questions are solved in the same way—the GRE is just trying to mask what it is asking about!
Here’s How to Crack It:
Let’s use our formula, a2 + b2 = c2. The dimensions of the box are 3, 4, and 5.
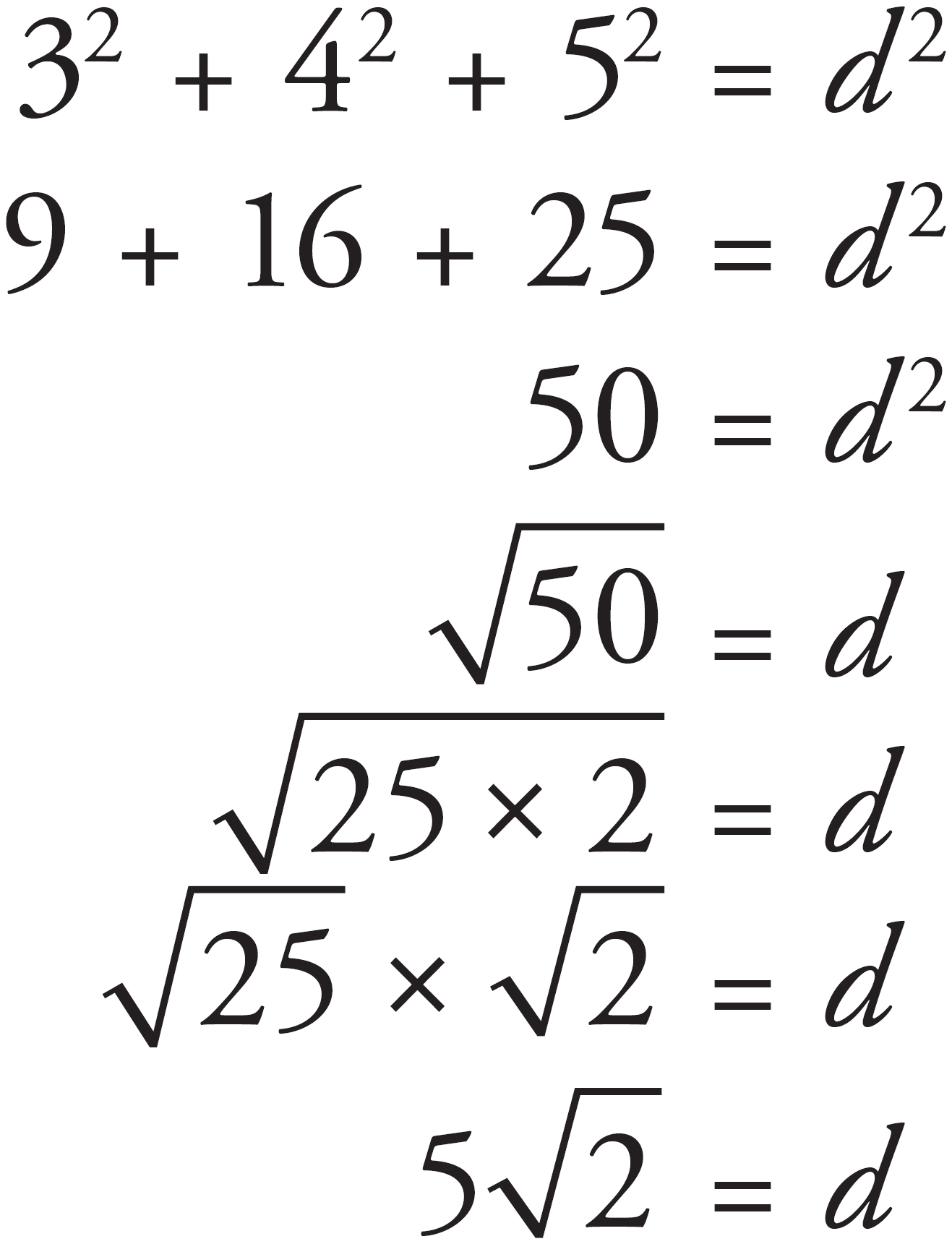
The correct answer is choice (B).

The GRE also asks about figures with more than four sides. For the purpose of this chapter, we are going to refer to these as polygons. These questions can come in all shapes and sizes, but they mostly boil down to one of two calculations: the degree measure of the angles or the area of the figure. Take a look at the following question that tests both concepts.
A polygon is technically a figure with at least three straight sides and angles, and typically five or more. A triangle is a polygon, as well as a rectangle and square.

If the length of one side of a regular hexagon is 8, what is the area of the hexagon?
 24
24
 36
36
 46
46
 64
64
 96
96
Here’s How to Crack It:
This is geometry problem, so begin by drawing the figure and labeling any information from the problem on the figure. The problem describes a hexagon with the length of one side equal to 8. Because the problem describes the hexagon as a regular hexagon, all the sides are the same length. Draw this figure and label one of the sides as 8. The problem asks for the area of the hexagon. When solving for the area of an unfamiliar figure, begin by breaking the figure down into recognizable figures. In this case, a straight line drawn from the center of the hexagon to two adjacent corners on the perimeter of the hexagon creates a triangle with two sides of equal length. The angles opposite those sides are also equal. Determine the value of these angles by finding the value of the central angle created by the two lines from the center. This is the value of x in the figure below.

The central angle of the figure is found by dividing 360 degrees by the number of sides. In this case, there are 6 sides, so the interior angle is 360 ÷ 6 = 60 degrees. Because there are 180 degrees in a triangle, the remaining two angles have a sum of 180 – 60 = 120 degrees. Because this is a regular hexagon, the distances between the center of the figure and the corners are equal. Therefore, each of the angles opposite the lengths are also equal. So, each additional angle in the triangle is 60 degrees. All the angles are equal, so this is an equilateral triangle and the length of all the sides is 8. Now solve for the area of the triangle. The area is 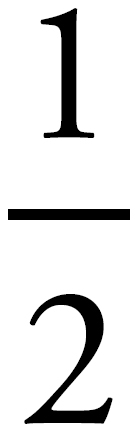 (base)(height) and base = 8. When drawn in, the height bisects one of the 60 degree angles and cuts the base in half. This creates two 30:60:90 right triangles. The side relationship of a 30:60:90 is x : x
(base)(height) and base = 8. When drawn in, the height bisects one of the 60 degree angles and cuts the base in half. This creates two 30:60:90 right triangles. The side relationship of a 30:60:90 is x : x : 2x. The value of x is half of the base, so x = 4. The height is the side opposite the 60-degree angle, so the height of the triangle is 4
: 2x. The value of x is half of the base, so x = 4. The height is the side opposite the 60-degree angle, so the height of the triangle is 4 . Therefore, the area of the triangle is
. Therefore, the area of the triangle is 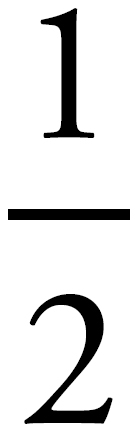 (4)(4
(4)(4 ) = 8
) = 8 . There are six such triangles that make up the area of the hexagon, so the area of the hexagon is 6 × 8
. There are six such triangles that make up the area of the hexagon, so the area of the hexagon is 6 × 8 = 48
= 48 . The correct answer is choice (C).
. The correct answer is choice (C).

In the problem above, you had to solve for the area of a hexagon by using the length of a side, the central angle, the length from the center of the figure to the corners, the properties of equilateral triangles, the side relationships of a 30:60:90 triangle, and the area of a triangle. That’s a lot to cover in one problem!
However, consider how different drawing the figure for the problem above would have been if the problem read:
If the length of one side of a hexagon is 8, what is the area of the hexagon?
This new question stem removes the word “regular.” The word “regular” indicates that the sides and angles are all equal length. Without that word, it is impossible to accurately draw this figure, let alone solve for the area.
This is an example of how the GRE uses precise wording to create questions. While the GRE may occasionally include information that is unnecessary to answer the question, it will never leave anything out.
There is one additional aspect of working with polygons that was not covered in the previous problem. When asked about these types of figures, you may be asked to find the measure of the interior angles, or the sum of certain interior angles. For instance, consider the following problem, which is a derivative of the problem you just worked through.

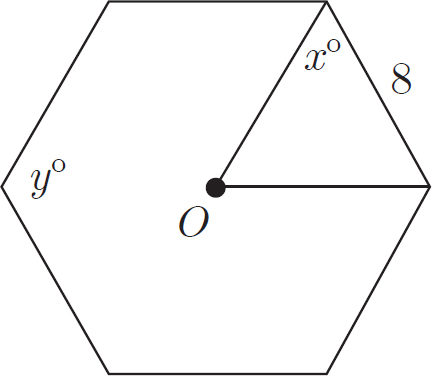
In the regular hexagon with center O shown above, what is the value of x + y ?
 60
60
 120
120
 150
150
 180
180
 240
240
Here’s How to Crack It:
This is geometry problem, so begin by drawing the figure and labeling any information from the problem on the figure. You know from the previous problem that the measure of x is 60. The process to find this degree measure is the same no matter what the problem is ultimately asking for, so we are not going to run through that explanation again. If you are unsure, check out the previous problem. However, this problem introduces another variable, y, which is the measure of the interior angle of the hexagon. The formula to solve for the interior angle of a hexagon is  , where n is the number of sides in the figure. In this case, there are 6 sides in the figure, so the interior angle of a single corner is
, where n is the number of sides in the figure. In this case, there are 6 sides in the figure, so the interior angle of a single corner is 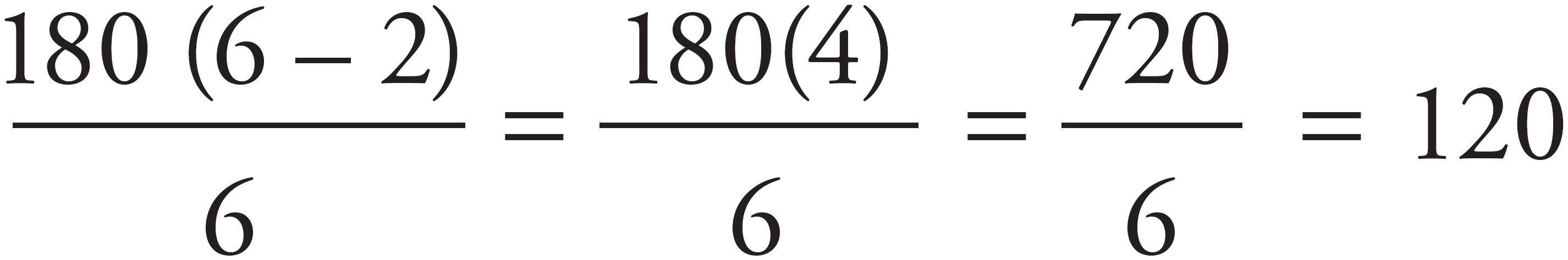 degrees. The question asks for the value of x + y, which is 60 + 120 = 180. The correct answer is choice (D).
degrees. The question asks for the value of x + y, which is 60 + 120 = 180. The correct answer is choice (D).

Remember, whenever you have a question that has answer choices, like a regular multiple-choice question or a multiple-choice, multiple-answer question that has variables in the answer choices, Plug In. On geometry problems, you can Plug In values for angles or lengths as long as the values you plug in don’t contradict either the wording of the problem or the laws of geometry (you can’t have the interior angles of a triangle add up to anything but 180, for instance).
Here’s an example:


In the drawing above, if AC = CD, then r =
 45 – s
45 – s
 90 – s
90 – s
 s
s
 45 + s
45 + s
 60 + s
60 + s
Key Formulas and Rules
Here is a review of the key rules and formulas to know for the GRE Math section.
Lines and angles
All straight lines have 180 degrees.
A right angle measures 90 degrees.
Vertical angles are equal.
Parallel lines cut by a third line have two kinds of angles: big angles and small angles.
All of the big angles are equal and all of the small angles are equal. The sum of a big angle and a small angle is 180 degrees.
Triangles
All triangles have 180 degrees.
The angles and sides of a triangle are in proportion—the largest angle is opposite the largest side and the smallest side is opposite the smallest angle.
The Pythagorean Theorem is c2 = a2 + b2, where c is the length of the hypotenuse.
The area formula for a triangle is A =  .
.
Quadrilaterals
All quadrilaterals have 360 degrees.
The area formula for squares and rectangles is bh.
Circles
All circles have 360 degrees.
The radius is the distance from the center of the circle to any point on the edge.
The area of a circle is πr2.
The circumference of a circle is 2πr.
Here’s How to Crack It
See the variables in the answer choices? Let’s Plug In. First of all, we’re told that AC and CD are equal, which means that ACD is an isosceles right triangle. So both angles A and D have to be 45 degrees. Now it’s Plugging In time. The smaller angles, r and s, must add up to 45 degrees, so let’s make r = 40 degrees and s = 5 degrees. The question asks for the value of r, which is 40, so that’s our target answer. Now eliminate answer choices by plugging in 5 for s.
(A) 45 – 5 = 40. Bingo! Check the other choices to be sure.
(B) 90 – 5 = 85. Nope.
(C) 5. Nope.
(D) 45 + 5 = 50. Eliminate it.
(E) 60 + 5 = 65. No way.
By the way, we knew that the correct answer couldn’t be greater than 45 degrees, because that’s the measure of the entire angle D, so you could have eliminated (D) and (E) right away.

When ETS doesn’t include a drawing with a geometry problem, it usually means that the drawing, if supplied, would make ETS’s answer obvious. In cases like this, you should just draw it yourself. Here’s an example of a time when ETS doesn’t provide a drawing because it would make the correct answer too obvious—so go ahead and draw one yourself!

|
Quantity A |
Quantity B |
|
The diameter of a circle with area 49π |
14 |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It
Visualize the figure. If the area is 49π, what’s the radius? Right: 7. And if the radius is 7, what’s the diameter? Right: 14. The answer is (C).

On tricky quant comp questions, you may need to draw the figure once, eliminate two answer choices, and then draw it another way to try to disprove your first answer and to see if the answer is (D). Here’s an example of a problem that might require you to do this:

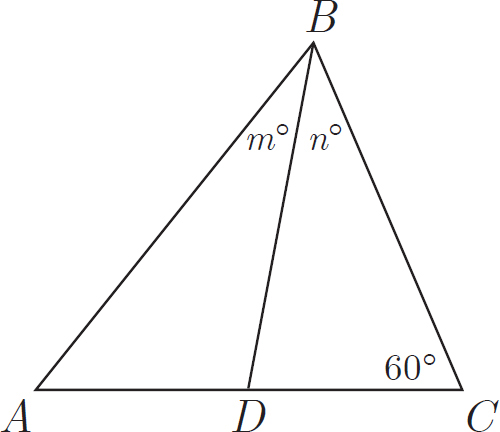
D is the midpoint of AC.
|
Quantity A |
Quantity B |
|
m |
n |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It
Are you sure that the triangle looks exactly like this? Nope. We know only what we are told—that the lengths of AD and DC are equal; from this figure, it looks like angles m and n are also equal. Because this means that it’s possible for them to be, we can eliminate (A) and (B). But let’s redraw the figure to try to disprove our first answer.

Try drawing the triangle as stretched out as possible. Notice that n is now clearly greater than m, so you can eliminate (C), and the answer is (D).

Click here to download a PDF of Geometry Drill.
Think you have mastered these concepts? Try your hand at the following problems and check your work after you have finished. You can find the answers in Part V.
1 of 15
Which of the following could be the degree measures of two angles in a right triangle?
Indicate all such angles.
 20° and 70°
20° and 70°
 30° and 60°
30° and 60°
 45° and 45°
45° and 45°
 55° and 55°
55° and 55°
 75° and 75°
75° and 75°
2 of 15

What is the perimeter of the figure above?
 51
51
 64
64
 68
68
 77
77
 91
91
3 of 15

AB = BC = EG
FG = 8
|
Quantity A |
Quantity B |
|
The area of square ABCD |
32 |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
4 of 15

(a, 6) is a point (not shown) in Quadrant I.
(–6, b) is a point (not shown) in Quadrant II.
|
Quantity A |
Quantity B |
|
a |
b |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
5 of 15
A piece of twine with length of t is cut into two pieces. The length of the longer piece is 2 yards greater than 3 times the length of the shorter piece. Which of the following is the length, in yards, of the longer piece?



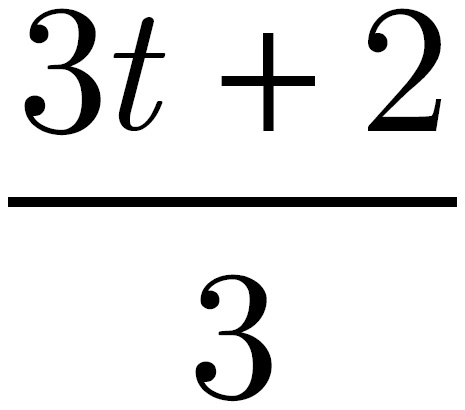

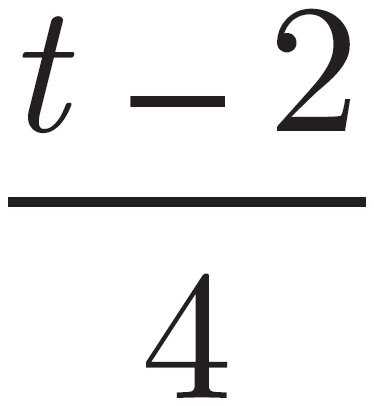




6 of 15

The circle with center D is drawn inside the circle with center C, as shown in the figure above. If CD = 3, what is the area of semicircle EAB ?

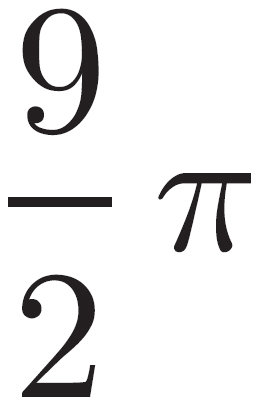








7 of 15
For the final exam in a scuba diving certification course, Karl navigates from one point in a lake to another. Karl begins the test x meters directly beneath the boat and swims straight down toward the bottom of the lake for 8 meters. He then turns to his right and swims in a straight line parallel to the surface of the lake and swims 24 meters, at which point he swims directly from his location, in a straight line, back to the boat. If the distance that Karl swims back to the boat is 26 meters, what is the value of x ?
8 of 15
|
Quantity A |
Quantity B |
|
The circumference of a circular region with radius r |
The perimeter of a square with side r |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
9 of 15
Triangle ABC is contained within a circle with center C. Points A and B lie on the circle. If the area of circle C is 25π, and the measure of angle ACB is 60°, which of the following are possible lengths for side AB of triangle ABC ?
Indicate all such lengths.
 3
3
 4
4
 5
5
 6
6
 7
7
10 of 15
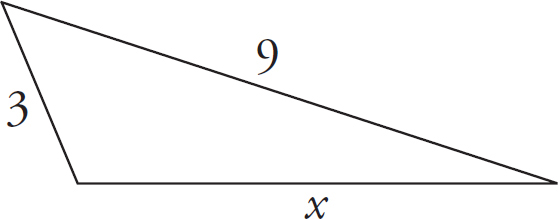
|
Quantity A |
Quantity B |
|
x |
5.9 |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
11 of 15

|
Quantity A |
Quantity B |
|
x |
y |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
12 of 15

Given points A(2, 3) and B(x, y) in the rectangular coordinate system above, if y = 4.2, then x =
 2.6
2.6
 2.8
2.8
 2.9
2.9
 3.0
3.0
 3.2
3.2
13 of 15

In rectangle ABCD above, which of the following is the area of the triangle ABD ?
 6
6
 7.5
7.5
 10
10
 12
12
 15
15
14 of 15

The circle above has a center O.
∠AOB = ∠BOC
|
Quantity A |
Quantity B |
|
The area of triangle AOB |
The area of the shaded region |
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
15 of 15

The circumference of the circle with center O shown above is 15π. LMNO is a parallelogram and ∠OLM = 108°. What is the length of minor arc AB ?
 15π
15π
 9π
9π
 3π
3π
 2π
2π
 π
π
1. V = Length × width × height
2. 16π
3. y = mx + b
4. 180
5. 720
6. P = 2(length) + 2(width)
7. Right triangle
8. 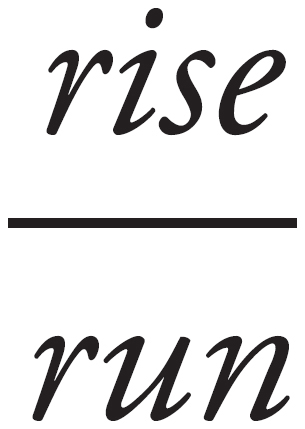 or
or 
9. 360
There may be only a handful of geometry questions on the GRE, but you’ll be expected to know a fair number of rules and formulas.
Line and angle problems typically test your knowledge of vertical angles, parallel lines, right angles, and straight angles.
Make sure you know your triangle basics, including the total degrees of a triangle, the relationship between the angles and sides of a triangle, the third side rule, and right triangles.
Know the area formulas for triangles, rectangles, and circles.
Problems involving the xy-coordinate plane can test common geometry concepts, such as the area of a triangle or a square, or other coordinate geometry concepts, such as slope and the equation of a line.
Understand how to solve for the volume and surface area of 3D figures and the interior angle and area of figures with more than four sides.
Don’t forget to Plug In on geometry problems!