Merge Sort: A Faster Sorting Algorithm

There are several well-known, fast sorting algorithms; merge sort, quick sort, and heap sort are the ones you are most likely to encounter in a future computer science course. Most of them involve techniques that we haven’t taught you yet, but merge sort can be written to be more accessible. Merge sort is built around the idea that taking two sorted lists and merging them is proportional to the number of items in both lists. The running time for merge sort is N log₂ N.

We’ll start with very small lists and keep merging them until we have a single sorted list.

Merging Two Sorted Lists

Given two sorted lists L1 and L2, we can produce a new sorted list by running along L1 and L2 and comparing pairs of elements. (We’ll see how to produce these two sorted lists in a bit.)

Here is the code for merge:

​	​def​ merge(L1: list, L2: list) -> list:
​	​"""Merge sorted lists L1 and L2 into a new list and return that new list.​
​	​ >>> merge([1, 3, 4, 6], [1, 2, 5, 7])​
​	​ [1, 1, 2, 3, 4, 5, 6, 7]​
​	​ """​
​
​	newL = []
​	i1 = 0
​	i2 = 0
​
​	​# For each pair of items L1[i1] and L2[i2], copy the smaller into newL.​
​	​while​ i1 != len(L1) ​and​ i2 != len(L2):
​	​if​ L1[i1] <= L2[i2]:
​	newL.append(L1[i1])
​	i1 += 1
​	​else​:
​	newL.append(L2[i2])
​	i2 += 1
​
​	​# Gather any leftover items from the two sections.​
​	​# Note that one of them will be empty because of the loop condition.​
​	newL.extend(L1[i1:])
​	newL.extend(L2[i2:])
​	​return​ newL

i1 and i2 are the indices into L1 and L2, respectively; in each iteration, we compare L1[i1] to L2[i2] and copy the smaller item to the resulting list. At the end of the loop, we have run out of items in one of the two lists, and the two extend calls will append the rest of the items to the result.

Merge Sort

Here is the header for mergesort:

​	​def​ mergesort(L: list) -> None:
​	​"""Reorder the items in L from smallest to largest.​
​
​	​ >>> L = [3, 4, 7, -1, 2, 5]​
​	​ >>> mergesort(L)​
​	​ >>> L​
​	​ [-1, 2, 3, 4, 5, 7]​
​	​ """​

Function mergesort uses merge to do the bulk of the work. Here is the algorithm, which creates and keeps track of a list of lists:

• Take list L and make a list of one-item lists from it.

• As long as there are two lists left to merge, merge them, and append the new list to the list of lists.

The first step is straightforward:

​	​# Make a list of 1-item lists so that we can start merging.​
​	workspace = []
​	​for​ i ​in​ range(len(L)):
​	workspace.append([L[i]])

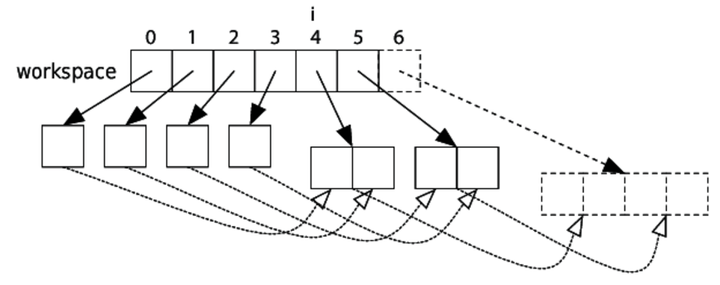
The second step is trickier. If we remove the two lists, then we’ll run into the same problem that we ran into in bin_sort: all the following lists will need to shift over, which takes time proportional to the number of lists.

Instead, we’ll keep track of the index of the next two lists to merge. Initially, they will be at indices 0 and 1, and then 2 and 3, and so on:

Here is our refined algorithm:

• Take list L and make a list of one-item lists from it.
• Start index i off at 0.
• As long as there are two lists (at indices i and i + 1), merge them, append the new list to the list of lists, and increment i by 2.

With that, we can go straight to code:

​	​def​ mergesort(L: list) -> None:
​	​"""Reorder the items in L from smallest to largest.​
​
​	​ >>> L = [3, 4, 7, -1, 2, 5]​
​	​ >>> mergesort(L)​
​	​ >>> L​
​	​ [-1, 2, 3, 4, 5, 7]​
​	​ """​
​
​	​# Make a list of 1-item lists so that we can start merging.​
​	workspace = []
​	​for​ i ​in​ range(len(L)):
​	workspace.append([L[i]])
​
​	​# The next two lists to merge are workspace[i] and workspace[i + 1].​
​	i = 0
​	​# As long as there are at least two more lists to merge, merge them.​
​	​while​ i < len(workspace) - 1:
​	L1 = workspace[i]
​	L2 = workspace[i + 1]
​	newL = merge(L1, L2)
​	workspace.append(newL)
​	i += 2
​
​	​# Copy the result back into L.​
​	​if​ len(workspace) != 0:
​	L[:] = workspace[-1][:]

Notice that since we’re always making new lists, we need to copy the last of the merged lists back into the parameter L.

Merge Sort Analysis

Merge sort, it turns out, is N log₂ N, where N is the number of items in L. The following diagram shows the one-item lists getting merged into two-item lists, then four-item lists, and so on until there is one N-item list:

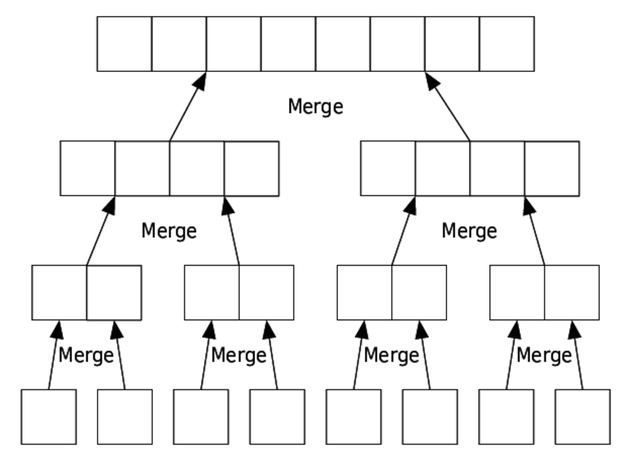
The first part of the function, creating the list of one-item lists, takes N iterations, one for each item.

The second loop, in which we continually merge lists, will take some care to analyze. We’ll start with the very last iteration, in which we are merging two lists with about N/2 items. As we’ve seen, function merge copies each element into its result exactly once, so with these two lists, this merge step takes roughly N steps.

On the previous iteration, there are four lists of size N/4 to merge into two lists of size N/2. Each of these two merges takes roughly N/2 steps, so the two merges together take roughly N steps total.

On the iteration before that, there are a total of eight lists of size N/8 to merge into the four lists of size N/4. Four merges of this size together also take roughly N steps.

We can subdivide a list with N items a total of log₂ N times using an analysis much like we used for binary search. Since at each “level” there are a total of N items to be merged, each of these log₂ N levels takes roughly N steps. Hence, merge sort takes time proportional to N log₂ N.

That’s an awful lot of code to sort a list! There are shorter and clearer versions—but again, they rely on techniques that we haven’t yet introduced.

Despite all the code and our somewhat messy approach (it creates a lot of sublists), merge sort turns out to be much faster than selection sort and insertion sort. More importantly, it grows at the same rate as the built-in sort:

---

Table 25. Running Times for Selection, Insertion, Merge, and list.sort (in milliseconds)

List Length	Selection Sort	Insertion Sort	Merge Sort	list.sort
1000	148	64	7	0.3
2000	583	268	15	0.6
3000	1317	594	23	0.9
4000	2337	1055	32	1.3
5000	3699	1666	41	1.6
10000	14574	6550	88	3.5

---

Big-Oh and All That

Our method of analyzing the performance of searching and sorting algorithms might seem like hand-waving, but there is actually a well-developed mathematical theory behind it. If f and g are functions, then the expression f(x) = O(g(x)) is read “f is big-oh of g” and means that for sufficiently large values of x, f(x) is bounded above by some constant multiple of g(x), or equivalently that function g gives us an upper bound on the values of function f. Computer scientists use this to group algorithms into families, such as those sorting functions that execute in N² time and those that execute in N log₂ N time.

These distinctions have important practical applications. In particular, one of the biggest puzzles in theoretical computer science today is whether two families of algorithms (called P and NP for reasons that we won’t go into here) are the same or not. Almost everyone thinks they aren’t, but no one has been able to prove it (despite the offer of a million-dollar prize for the first correct proof). If it turns out that they are the same, then many of the algorithms used to encrypt data in banking and military applications (as well as on the web) will be much more vulnerable to attack than expected.