Problem 84 (Geometry, Level 1)
What is the measure of angle b° shown in the figure above if a° = 58°?
(A) 60
(B) 78
(C) 52
(D) 50
(E) not enough information
Mathematics is the door and key to the sciences.
—Roger Bacon
SAT problems are currently assigned by the College Board three difficulty levels: easy, medium, and hard. In this chapter, on a scale from Level 1 (easiest) to Level 5 (hardest), which is also used for SAT math questions/problems, I have mapped Levels 1 and 2 to easy, Levels 3 and 4 to medium, and Level 5 to hard. Of the three math sections contained on an SAT test, two consist of multiple-choice questions and one of multiple-choice and open-ended questions/problems.
To allow students to pick and choose problems by content, each problem in this chapter was assigned a qualifier to designate the main area of math in which knowledge is required in order to solve the problem as well as whether the problem is a word problem or not. The latter qualifier was added to allow students not only to practice the factual knowledge in a particular field but also select problems that emphasize analytic/critical thinking skills. The qualifiers are: arithmetic skills (including numbers, operations, etc.), algebra (including functions), geometry (including measurements), miscellaneous (including data analysis, statistics, probability, etc.), and word (for word problems).
The function shown below is used to predict the number of adults (A) accompanying their children to a water park:
A(T) = 2(120 – T)(T – 75)
where T° F is the expected high temperature for that day. The expected temperatures for Saturday and Sunday are 80° F and 85° F, respectively. Based on this model, calculate how many more adults are expected to come to the park on Sunday than on Saturday.
(A) 300
(B) 260
(C) 600
(D) 165
(E) 360
If x is 7 less than twice the product of y and z, calculate an expression for x in terms of y and z.
(A) 7 – 2yz
(B) 7 – (2y + z)
(C) 7 – 2(y + z)
(D) 2(y + z) –7
(E) 2yz –7
All 15 students in a music class completed the study of 4 required classic piano concerts. In addition, 3 of them completed the study of 5 contemporary piano compositions, and 5 students gave a recital during which they played a piano work by an American composer. Calculate the total number of assignments completed by the students in this music class.
(A) 20
(B) 23
(C) 33
(D) 80
(E) 225
Consider two circles, one having a radius that is 3 times the radius of the other. What is the greatest possible number of points of intersection of the two circles?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
What is the measure of angle b° shown in the figure above if a° = 58°?
(A) 60
(B) 78
(C) 52
(D) 50
(E) not enough information
Assuming Michael runs at a constant pace and needs 15 minutes to complete a lap around his school’s football field, calculate how much of a lap he will cover in 6 minutes.
(A)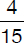 
(B) 
(C)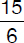 
(D) 
(E) 
Jessica needs to buy tomatoes. She finds that her neighborhood supermarket sells them in boxes that contain t tomatoes each. She ends up buying b boxes for which she pays d dollars. Assuming the tomatoes are equal in size and weight, which of the following formulas gives the price of a tomato?
(A)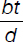 
(B)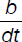 
(C) btd
(D)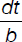 
(E)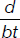 
Calculate the value of x3y2 if x = y and y = 2.
(A) 8
(B) 32
(C) 16
(D) 24
(E) 36
Which of the following values could be equal to x if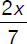 
is an integer?
(A) 3
(B) 
(C) –5
(D) 4
(E) –14
Calculate the number of positive integers less than 25 that are equal to 3 times an odd integer.
(A) 6
(B) 3
(C) 5
(D) 2
(E) 4
The degree measures of three of the four angles of a quadrilateral are in the ratio of 2:3:5. The fourth angle measures 60°. Calculate the degree measure of the largest angle of the quadrilateral.
(A) 150°
(B) 240°
(C) 180°
(D) 90°
(E) 120°
The size of a rectangular closet is 1 ft × 2 ft. If the floor is to be covered with square tiles of side length equal to 4 in, how many tiles will be needed?
(A) 16
(B) 24
(C) 36
(D) 18
(E) 32
Calculate a possible value of an integer given that if divided by 2 and 3, the remainders are 0 and 1, respectively.
(A) 19
(B) 22
(C) 23
(D) 24
(E) 21
If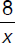 
= y and x = 2, calculate the expression x2(y – 1).
(A) 10
(B) 8
(C) 16
(D) 12
(E) 24
There are 16 boys and 8 girls in a class. The day before Thanksgiving, all girls showed up at school but the number of boys who were present represented 25% of the total student population. How many boys were absent that day?
(A) 16
(B) 18
(C) 20
(D) 10
(E) 14
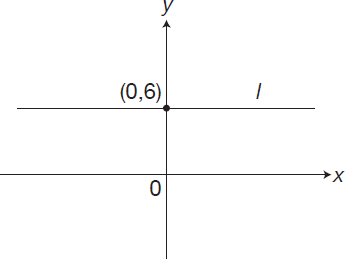
In the figure above, line l is perpendicular to the y-axis and intersects it 6 units away from the x-axis. Which one of the following points is on line l?
(A) (6, 1)
(B) (6, 0)
(C) (1, 0)
(D) (2, 6)
(E) (1, 3)
If 32x = 729, then x =
(A) 1
(B) 2
(C) 3
(D) 6
(E) 12
When 250 pigeons raised and trained on a farm were released, only 50 did not reach the destination 50 miles away. What fraction of the pigeons that were released reached the destination?
(A) 
(B) 
(C)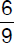 
(D) 
(E) 
A 56 centimeter-long piece of tape is 8 centimeters longer than 3 times the length of a shorter piece of tape. Calculate the length of the shorter piece of tape.
(A) 48
(B) 24
(C) 16
(D) 28
(E) 12
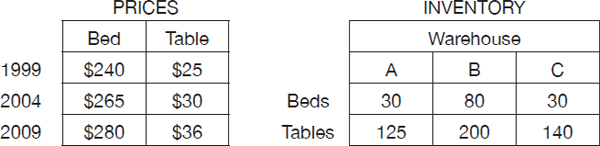
The table above gives the prices of the most popular styles of beds and tables manufactured by a furniture company in 3 different years. The second table gives the maximum number of beds and tables that can be stocked in each of the three warehouses (A, B, and C) owned by the manufacturer. Calculate the maximum possible value of the bed and table inventory in warehouse B in 1999.
(A) $21,600
(B) $24,400
(C) $22,200
(D) $24,200
(E) $26,300
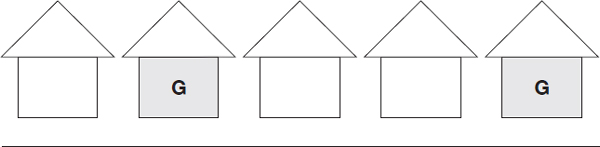
Eastside Blvd.
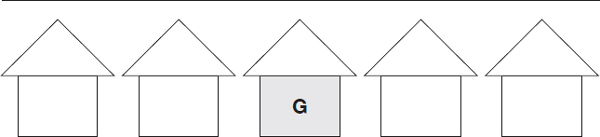
Five houses on each side of Eastside Blvd. are shown in the above figure. A town ordinance requires that no two houses directly across from each other on opposite sides of the street and no two houses next to each other on the same side of the street be painted the same color. If the houses labeled “G” in the figure above are painted gray, how many of the remaining houses can be painted gray?
(A) 6
(B) 4
(C) 1
(D) 5
(E) 3
Calculate x if 2x – y = 7 and 3x + 2y = 35.
(A) 4
(B) 21
(C) 7
(D) 5
(E) 14
Which of the following statements must be true given that Monica is older than John, who’s older than Briana but younger than Luke?
(A) Luke is younger than Briana
(B) Luke is older than Monica
(C) Briana is younger than Luke
(D) Briana is older than Luke
(E) Monica is older than Luke
Calculate the value of 5a given that 3a – 2b = 4b and 2b = 3.
(A) 15
(B) 8
(C) 25
(D) 10
(E) 5
Running at constant rate, it takes Bobby 3 hours to finish a 15-mile race. George runs at a rate that is 
of Bobby’s. How many minutes would it take George to finish a 10-mile race?
(A) 300
(B) 600
(C) 500
(D) 150
(E) 60
There are 60 brownies in a box to be distributed in a 1:2:4:5 ratio among four children. What is the second largest number of brownies that any one child can receive?
(A) 10
(B) 5
(C) 50
(D) 20
(E) 60
What is the area of a square obtained by joining two congruent triangles, given that the longest side of each triangle is 4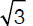
?
(A) 16
(B) 36
(C) 16
(D) 16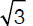
(E) 24
If N and M are single-digit integers used to represent the numbers 18N, N5, and 1M9, calculate M given that
18N – N5 = 1M9
(A) 4
(B) 3
(C) 9
(D) 8
(E) 5
A student planned to spend an hour and a half working on the homework for three subject areas: math, social studies, and science. If 
of this time was used for the math homework 
and of the remaining time is used for the social studies project, how many minutes does the student have left for his science homework?
(A) 20
(B) 35
(C) 45
(D) 55
(E) 60
Michelle gets to keep a marble she will chose at random from a jar. The jar contains 23 white, 15 black, and 37 yellow marbles. Calculate the probability that Michelle picks out a black marble.
300, 150, 75, 226, 113, 340, 170, …
Calculate the 10th term of the sequence above given that its first term is 300 and each term thereafter is obtained (1) dividing by 2, if the previous term is even, or (2) multiplying by 3 and then adding 1, if the previous term is odd.
In a small town, a member of the Board of Education resigned and a new member was appointed. As a result, the ages of 8 of the 9 members are: 54, 66, 49, 57, 59, 62, 55, and 63. The youngest member of the new board happens to be 25 years younger than the oldest member. If the median age of the members is 57, what is the age of the newly appointed board member?
In a right triangle, the difference between the measures of the two smaller angles is 30°. Calculate the measure (in degrees) of the largest of the two angles.
The number of bears in a national park has tripled during every 3-year period since the beginning of 2000. If there were 8,100 bears in the park at the beginning of 2009, how many bears were in the same park at the beginning of 2000?
The clay needed to make a brick is contained in a spherical ball of clay with a radius of 3 inches. If a spherical ball of clay with a radius equal to 9 inches is delivered to the brick factory, how many bricks can be made out of it—given that the volume (V) of a sphere with radius r is given by the following formula:
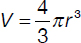
Grades are often computed using a weighted average. Suppose that homework counts 10%, quizzes 20%, and tests 70%. Calculate a student’s overall grade if his or her average/total grades in homework, quizzes, and tests were 92, 68, and 81, respectively.
In the figure below, AB = 7, AD = 4, DC = 10. What is the perimeter of the trapezoid ABCD?
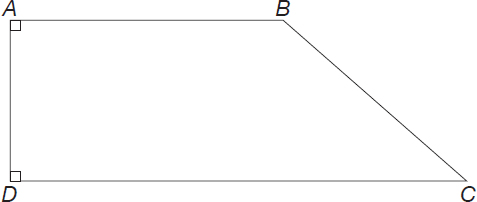
Note: Figure not drawn to scale
In a clock factory, Mike assembles—on the average—15 clocks while his older and more experienced colleague, Steve, assembles 24 clocks in an hour. If the two workers were assigned two identical orders of 48 clocks, how many more minutes does it take Mike to assemble the clocks than it takes Steve?
(A) 48
(B) 72
(C) 24
(D) 15
(E) 60
In a metropolitan area, the standard charge for a speeding ticket is $60. An additional $10 charge is added for every mile per hour a driver travels above the speed limit. On a street where the speed limit was 30 miles per hour, a driver was fined $250 for speeding. Calculate the speed recorded by the police radar.
(A) 54
(B) 65
(C) 50
(D) 49
(E) 55
At a used-camera shop, a customer could choose among 12 digital cameras of a certain brand. Nine of them were in perfect condition and 3 were defective or slightly damaged. The customer picked a camera that was supposed to be in perfect condition but shortly thereafter discovered that it was scratched. What is the probability that the second camera chosen is in perfect condition?
(A)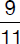 
(B)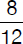 
(C)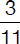 
(D)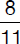 
(E) 
An auto plant in Michigan—currently under construction—is predicted to manufacture approximately 5 million cars in 2025. This number represents a 25% increase from the previous year. Which of the following best describes the number of cars manufactured in 2024?
(A) 1.25 million
(B) 2 million
(C) 4 million
(D) 5.25 million
(E) 3.75 million
Samantha’s choice for a four-digit number to be her computer password met the following rules:
• the last digit had to be a divisor of 30
• the greatest common factor of the middle two digits had to be 2
• the leftmost/first digit was a prime number.
Which of the following numbers could be Samantha’s password?
(A) 1216
(B) 7456
(C) 9463
(D) 5863
(E) 2687
A bag contains blue, white, and red marbles. The number of white marbles is 2 more than the number of blue marbles, and the number of red marbles is 4 times the number of white marbles. Which of the following could be the total number of marbles in the bag?
(A) 53
(B) 48
(C) 26
(D) 46
(E) 35
Three years ago, the average (arithmetic mean) number of rare coins owned by 20 collectors was 90. Today, 3 collectors updated their numbers as in the past 3 years, they acquired additional coins. The original numbers, 65, 58, and 55, were replaced by 85, 88, and 105, respectively. Calculate the correct average number of rare coins owned by the 20 collectors today.
(A) 85
(B) 105
(C) 100
(D) 95
(E) 93
An ice-cream shop offers 6 different toppings for its ice cream cakes. The regular/standard price includes 2 different combinations. Calculate how many different combinations of toppings are available for no additional cost.
(A) 12
(B) 15
(C) 36
(D) 6
(E) 64
If x2 – y2 = 55 and x – y = 5, what is the value of y?
(A) 8
(B) 11
(C) 3
(D) 6
(E) 10
Let the operation Δ be defined as x Δ y = x + 2xy–y. How much greater is 5 Δ 7 than 3 Δ 4?
(A) 38
(B) 45
(C) 23
(D) 6
(E) 10
If x and y are odd integers, which of the following is NOT an odd integer?
I. (x – 1)(y + 2)
II. (x + 1) + 2y–1
III. (x – 1) – y
(A) I only
(B) II only
(C) III only
(D) I and II
(E) II and III
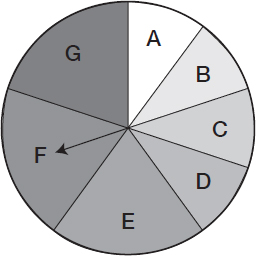
In the figure above, the regions A, B, C, and D have an equal area. Each of the equal regions E, F and G has twice the area of each of the equal regions A, B, C or D. What is the probability that the tip of a spinner would stop at random into the F region?
(A)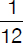 
(B) 
(C) 
(D) 
(E) 
In the xy-plane, the line with equation y = 7x – 28 crosses the x-axis at the point with coordinates (a, b). What is the value of a?
(A) –28
(B) –2
(C) 0
(D) 4
(E) 5
If f(x) = 4 + 2x2, find the value of a positive integer k for which f(2k) = 18k
(A) –2
(B) 0
(C) 1
(D) 2
(E) 3
There are 75 more men than women enrolled in a college. If the total number of student enrolled is 225, what percent of the students enrolled are women?
(A) 20%
(B) 33.33%
(C) 50%
(D) 66.66%
(E) 75%
The area of a rectangle is 125. What is its perimeter given that it can be divided into five equal squares?
(A) 25
(B) 60
(C) 75
(D) 50
(E) not enough information
If 2x + 3 is 5 less than 2y–6, calculate by what amount x–4 is less than y.
(A) 16
(B) 8
(C) 13
(D) 11
(E) 12
By definition, (x)* = 2x2–3. Find an expression for [(y–z)*] – [(y + z)*].
(A) y2–8yz + z2
(B) 8yz
(C) y2–z2
(D) 2y2 + 2z2
(E) –8yz
30 less than 20% of 500 is equal to a number increased by 40% of its value. Calculate the number in question.
(A) 70
(B) 45
(C) 80
(D) 50
(E) 40
The slope of a line is 
. Calculate a if the line passes through points (0, a) and (2a, 1).
(A) 1
(B) 2
(C)
(D) –
(E) –1
If Mike is not a member of the local swim and tennis club, indicate from which of the following statements it can be determined whether or not Mike is a member of the local golf club.
(A) Some people who are not in the swim and tennis club are not in the golf club.
(B) Anyone who is not in the swim and tennis club is not in the golf club.
(C) No one is in both the swim and tennis club and the golf club.
(D) Everyone in the swim and tennis club is in the golf club.
(E) Everyone in the swim and tennis club is not in the golf club.
On the playground of a nursery school, there is a box containing building blocks of different colors and shapes. If all of the cubes are blue, which of the following statements must be true?
I. If a block is blue, then it is a cube.
II. If a block is not a cube, then it is not blue.
III. If a block is not blue, then it is not a cube.
(A) I only
(B) I and III only
(C) III only
(D) II only
(E) II and III only
Pairs of Sneakers
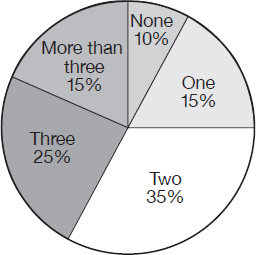
The figure above shows the percentages of players in a basketball camp who own the indicated number of sneakers. If 80 players own at least three pairs of sneakers, how many players own one pair or less?
(A) 80
(B) 48
(C) 52
(D) 50
(E) 20
Consider the sequence
3, 9, 27,...
Its first term is 3, and each term thereafter is three times the preceding term—making this a geometric sequence. Calculate the kth term of the sequence.
(A) 3k
(B) k2
(C) 3k
(D) 3k–1
(E) (k–1)3
Calculate the average value of 25, a, b, 31, c, and d if the arithmetic mean of a and c is 15 and that of b and d is 23.
(A) 23
(B) 25
(C) 16
(D) 22
(E) 28
The average (arithmetic mean) score received by a team of 15 members at a school competition was 87. When additional 5 members were added to the group, the average score of the team of 20 became 90. What is the average score of the 5 additional members to the team?
(A) 100
(B) 85
(C) 95
(D) 90
(E) 99
Let three numbers be a, b, and c. Their average is 2 less than 5 times the median. Calculate an expression for the average of a and c in terms of b given that 0 < a < b < c .
(A) 7b –3
(B)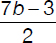 
(C) 5b –2
(D)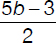 
(E) 3 –7b
The degree measures of the interior angles in a triangle are x°, 2x°, and 90°. Its longest leg is 20. What is the length of the leg opposing the angle with degree measure 2x°?
(A) 20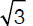
(B) 10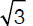
(C) 15
(D) 10
(E) 20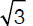
Lara and Matt borrowed 45 books from the library and had to return them the next day. If Lara returns 5 fewer books than four times as many books as Matt does, calculate the number of books Matt returns.
The average (arithmetic mean) of five integers is the same as the median of the same numbers. If four of the five numbers are
13, 1, 7, 11
and the 5th is x, calculate all possible values for x.
Each term after the second term of a sequence is the product of the two preceding terms. If the 5th and 6th terms are 16 and 256, respectively, calculate the first term of the sequence.
A cafeteria has a lunch special consisting of soup or salad, a sandwich, coffee, tea, or a nonalcoholic beverage, and a dessert. If the menu lists 2 soups, 3 salads, 6 sandwiches, and 10 desserts, how many different lunches can one choose?
The first two terms in the sequence above are 1 and k, and each term thereafter is the sum of the two preceding terms. If the sum of the first 6 terms is 116, what is the value of k?
In rectangle ABCD below,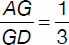 
and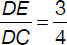 
. What is the value of the ratio
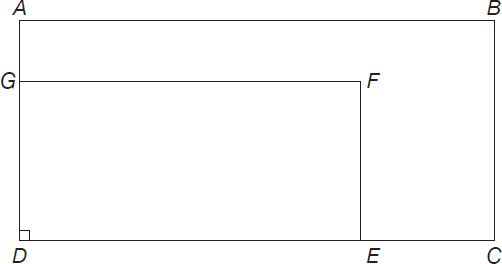
Note: Figure not drawn to scale
A certain triangle has two angles with the same degree measure. If the lengths of two sides of the triangle are 5 and 7, what is the maximum value for the perimeter of the triangle?
At the end of the season, team A won 
and lost 
of the games it played against team B. During the entire season, the teams were tied in 32 games. Calculate the total number of games the teams played against each other.
In Angelo’s Restaurant, the daily menu features 4 kinds of omelets. The first kind were made with 4 eggs each and they represented 
of the total number. The second kind used only 3 eggs each and they represented 
of the rest of the omelets. The remaining 80 omelets were equally split between the last two categories and only used 2 eggs each. Calculate the total number of eggs Angelo needs to make a daily supply of omelets.
Seven friends played two rounds of a board game and each time accumulated an integer score. The two scores for each player were added together and the resulting numbers were 86, 98, 59, 48, 68, 72, and x. The 7th player, whose total score was x, obtained a score of 40 in the first round. Calculate one possible value of the 7th player’s second round score, given that x is the median of the seven total scores.
A jar contains 15 red and 15 blue marbles. Calculate the least number of marbles that would have to be removed from the jar such that the ratio of blue to red marbles left in the jar will be 2 to 3.
Jane has four times as many marbles as Mike. If Jane gives Mike eight marbles, she will be left with four fewer marbles than him. What is the total number of marbles that Jane and Mike have?
Given three consecutive integers, if the sum of the first and third integers is increased by 8, the result is 5 less than triple the second integer. Find the first of the three consecutive integers.
At a parent-teacher association meeting, the ratio of women to men is 3 to 5. Six women had to leave the meeting earlier and, as a result, the ratio of women to men becomes 1 to 2. How many women are in the room at the end of the meeting?
Anna joined her best friend and her family on a day trip and spent 30% and 45% of her daily allowance on breakfast and lunch, respectively. As a result, she’s left with $15 to cover her dinner. How much money did she spend for breakfast?
The president of a college decided to retire in December 2009. He served in that capacity for 11 consecutive complete terms. Given that one complete term lasts 4 years—from the beginning of January of the 1st year through the end of December of the 4th year—calculate the year in which the president began to serve his first term.
(A) 1966
(B) 1965
(C) 1955
(D) 1956
(E) 1962
In isosceles triangle ABC, side BC is shorter than the other two sides. If the degree measure of ∠A is a multiple of 22, calculate the greatest possible measure of ∠C.
(A) 78
(B) 88
(C) 75
(D) 86
(E) 79
A certain call—lasting more than a minute—costs $1.23. The telephone company calculates the charges according to the following formula: first minute costs m cents; each additional minute costs n cents. Of the expressions shown below, identify the one representing the length in minutes of the $1.23 call.
(A)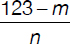 
(B)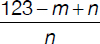 
(C)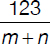 
(D)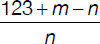 
(E)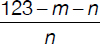 
Two sets of numbers, X and Y, are defined as the set of prime numbers and the set of two-digit, positive integers whose unit digit is 5, respectively. Calculate how many numbers are common to both sets.
(A) 0
(B) 2
(C) 3
(D) 1
(E) 5
x is a positive, odd integer. Calculate 20% of the value of the expression 3x + 8, given that it satisfies the following double inequality:
60 < 3x + 8 < 70
(A) 52
(B) 57
(C) 13
(D) 60
(E) 62
Two identical 300-degree arcs are joined together to enclose the area shown in the figure above (not drawn to scale.) Both arcs are part of identical circles with radius equal to 12. Calculate the area of the shape shown in the figure.
(A) 120π + 72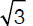
(B) 240π + 72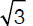
(C) 240π + 3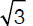
(D) 300π + 60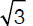
(E) 60π + 300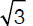
Consider a geometric sequence of positive numbers. After the first term, the ratio of each term to the term immediately preceding it is 3 to 1. Calculate the ratio of the 9th term in this sequence to the 6th term.
(A) 9:1
(B) 27:1
(C) 81:1
(D) 243:1
(E) 729:1
Express 73z+2 in terms of n, given that 7z = n?
(A) 7n3
(B) 49n
(C) 7n2
(D) 49n2
(E) 49n3
Two numbers, a and b, are selected at random from the set A and B, respectively, where
A = {2, 5}
B = {1, 3, 6}
Indicate which of the following statements must be true.
I. The probability that a + b is a prime number is
II. The probability that a + b > 8 is 
III. The probability that ab > a + b is 
(A) I only
(B) II only
(C) I and II only
(D) I and III only
(E) II and III only
Four cheetahs were brought to a national park in an effort to reverse their extinction. At the time this experiment started, there were none left in the park. Through the care of the rangers, it is expected that this population will double its size every 5 years. Assuming the trend continues, how many more cheetahs will be in the park after 25 years than are in the park after 15 years?
(A) 24
(B) 300
(C) 120
(D) 100
(E) 96
Calculate the values of x for which the expression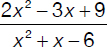 
is undefined.
(A) 0, 6
(B) –3, 2
(C) –2, 3
(D) 0, 2
(E) 0, 3
Calculate the range of function f(x) = 3x2 – 5 given that its domain of definition is restricted to –1 ≤ x ≤ 7.
(A) –1 ≤ f(x) ≤ 142
(B) –5 ≤ f(x) ≤ 43
(C) –1 ≤ f(x) ≤ 43
(D) –5 ≤ f(x) ≤ 142
(E) –5 ≤ f(x) ≤ 103
Two triangles, T1 and T2, have sides of lengths 15 and 25. The length of the third side of each triangle is an integer. Calculate the greatest possible difference between the perimeters of the triangles T1 and T2.
Let A be a set consisting of n integers such that the difference between the greatest and the least integers is 225. Consider a second set of integers, B, formed by multiplying each integer in A by 6 and then subtracting 7 from the product. Calculate the difference between the greatest and the least integer in B.
An opaque jar contains 5 red, 4 yellow, and 6 green candies. A child is allowed to pick two candies. What is the probability (1) of getting a green followed by a red candy or (2) of getting a red followed by a green or a yellow candy?
Lines l and n are parallel and their equations are: 3x – 2y = 8 and y = mx + b respectively. Knowing that in the xy-plane, line n passes through the point (–1, 2), calculate the value of m + b.
N and a are positive integers. Knowing that
1. N = a3 and
2. N is divisible by 15 and 20,
calculate the smallest possible value of N.
By what percent will the area of a circle increase, if its radius is quadrupled?
Calculate the greatest possible perimeter of a triangle when the lengths of two of its sides are 7 and 11 and given that the third side is also an integer.
In a class of 25 students, the average score on a final test calculated for 20 students was 75. Five students missed the test day with cold symptoms and were scheduled for a make-up. Their average score was eventually 80. What is the average score of the class?