Chapter 4: Quadratic Equations and Functions

As you saw in Chapter 8, algebraic functions not only produce straight lines but curved ones too. A special type of curved function is called a parabola. Perhaps you have seen the shape of a parabola before:

The shape of the water from a drinking fountain
The path a football takes when thrown
The shape of an exploding firework
The shape of a satellite dish
The path a diver takes into the water
The shape of a mirror in a car’s headlamp

Many real life situations model a quadratic equation. This chapter will explore the graph of a quadratic equation and how to solve such equations using various methods.

Graphs of Quadratic Functions

Chapter 9 introduced the concept of factoring quadratic trinomials of the form $0=ax^2+bx+c$ . This is also called the standard form for a quadratic equation. The most basic quadratic equation is $y=x^2$ . The word quadratic comes from the Latin word quadrare, meaning “to square.” By creating a table of values and graphing the ordered pairs, you find that a quadratic equation makes a $U$ -shaped figure called a parabola.

$x$	$y$
–2	4
–1	1
0	0
1	1
2	4

The Anatomy of a Parabola

A parabola can be divided in half by a vertical line. Because of this, parabolas have symmetry. The vertical line dividing the parabola into two equal portions is called the line of symmetry. All parabolas have a vertex, the ordered pair that represents the bottom (or the top) of the curve.

The vertex of a parabola has an ordered pair $(h, k)$ .

Because the line of symmetry is a vertical line, its equation has the form $y=h$ , where $h=$ the $x-$ coordinate of the vertex.

An equation of the form $y=ax^2$ forms a parabola.

If $a$ is positive, the parabola will open upward. The vertex will be a minimum.

If $a$ is negative, the parabola will open downward. The vertex will be a maximum.

The variable $a$ in the equation above is called the leading coefficient of the quadratic equation. Not only will it tell you if the parabola opens up or down, but it will also tell you the width.

If $a>1$ or $a<-1$ , the parabola will be narrow about the line of symmetry.

If $-1<a<1$ , the parabola will be wide about the line of symmetry.

Example 1: Determine the direction and shape of the parabola formed by $y=-\frac{1}{2} x^2$ .

Solution: The value of $a$ in the quadratic equation is –1.

Because $a$ is negative, the parabola opens downward.
Because $a$ is between –1 and 1, the parabola is wide about its line of symmetry.

Domain and Range

Several times throughout this textbook, you have experienced the terms domain and range. Remember:

Domain is the set of all inputs ( $x-$ coordinates).
Range is the set of all outputs ( $y-$ coordinates).

The domain of every quadratic equation is all real numbers $(\mathbb{R})$ . The range of a parabola depends upon whether the parabola opens up or down.

If $a$ is positive, the range will be $y \ge k$ .

If $a$ is negative, the range will be $y \le k$ , where $k=y-$ coordinate of the vertex.

Vertical Shifts

Compare the five parabolas to the right. What do you notice?

The five different parabolas are congruent with different $y-$ intercepts. Each parabola has an equation of the form $y=ax^2+c$ , where $a=1$ and $c=y-$ intercept. In general, the value of $c$ will tell you where the parabola will intersect the $y-$ axis.

The equation $y=ax^2+c$ is a parabola with a $y-$ intercept of $(0, c)$ .

The vertical movement along a parabola’s line of symmetry is called a vertical shift.

Example 1: Determine the direction, shape, and $y-$ intercept of the parabola formed by $y=\frac{3}{2} x^2-4$ .

Solution: The value of $a$ in the quadratic equation is $\frac{3}{2}$ .

Because $a$ is positive, the parabola opens upward.
Because $a$ is greater than 1, the parabola is narrow about its line of symmetry.
The value of $c$ is –4, so the $y-$ intercept is (0, –4).

Projectiles are often described by quadratic equations. When an object is dropped from a tall building or cliff, it does not travel at a constant speed. The longer it travels, the faster it goes. Galileo described this relationship between distance fallen and time. It is known as his kinematical law. It states the “distance traveled varies directly with the square of time.” As an algebraic equation, this law is:

$d=16t^2$

Use this information to graph the distance an object travels during the first six seconds.

$t$	$d$
0	0
1	16
2	64
3	144
4	256
5	400
6	576

The parabola opens upward and its vertex is located at the origin. The value of $a>1$ , so the graph is narrow about its line of symmetry. However, because the values of the dependent variable $d$ are very large, the graph is misleading.

Example 2: Anne is playing golf. On the fourth tee, she hits a slow shot down the level fairway. The ball follows a parabolic path described by the equation, $y=x-0.04x^2$ , where $x=$ distance in feet from the tee and $y=$ height of the golf ball, in feet.

Describe the shape of this parabola. What is its $y-$ intercept?

Solution: The value of $a$ in the quadratic equation is –0.04.

Because $a$ is negative, the parabola opens downward.
Because $a$ is between –1 and 1, the parabola is wide about its line of symmetry.
The value of $c$ is 0, so the $y-$ intercept is (0, 0).

The distance it takes a car to stop (in feet) given its speed (in miles per hour) is given by the function $d(s)=\frac{1}{20} \ s^2+s$ . This equation is in standard form $f(x)=ax^2+bx+c$ , where $a=\frac{1}{20}, b=1$ , and $c=0$ .

Graph the function by making a table of speed values.

$s$	$d$
0	0
10	15
20	40
30	75
40	120
50	175
60	240

The parabola opens upward with a vertex at (0, 0).
The line of symmetry is $x=0$ .
The parabola is wide about its line of symmetry.

Using the function to find the stopping distance of a car travelling 65 miles per hour yields:

$d(65)=\frac{1}{20} (65)^2+65=276.25 \ feet$

Multimedia Link: For more information regarding stopping distance, watch this CK-12 Basic Algebra: Algebra Applications: Quadratic Functions

video_image

Forensics. The distance a car travels even after the brakes are applied can be described through a quadratic function. But there is also the reaction time, the split second before the brakes are applied. The total distance is known as the stopping distance and this segment analyzes the quadratic function. (Click here to watch the video)

- YouTube video.

Practice Set

Sample explanations for some of the practice exercises below are available by viewing the following video. Note that there is not always a match between the number of the practice exercise in the video and the number of the practice exercise listed in the following exercise set. However, the practice exercise is the same in both. CK-12 Basic Algebra: Graphs of Quadratic Functions (16:05)

video_image

Graphs of Quadratic Functions (Click here to watch the video)

Define the following terms in your own words.
1. Vertex
2. Line of symmetry
3. Parabola
4. Minimum
5. Maximum

}

Without graphing, how can you tell if $y=ax^2+bx+c$ opens up or down?
Using the parabola below, identify the following:
1. Vertex
2. $y-$ intercept
3. $x-$ intercepts
4. Domain
5. Range
6. Line of symmetry
7. Is $a$ positive or negative?
8. Is $a$ $-1<a<1$ or $a<-1$ or $a>1$ ?

Use the stopping distance function from the lesson to find:
1. $d(45)$
2. What speed has a stopping distance of about 96 feet?

Using Galileo’s law from the lesson, find:
1. The distance an object has fallen at 3.5 seconds
2. The total distance the object has fallen in 3.5 seconds

Graph the following equations by making a table. Let $-3 \le x \le 3$ . Determine the range of each equation.

$y=2x^2$
$y=-x^2$
$y=x^2-2x+3$
$y=2x^2+4x+1$
$y=-x^2+3$
$y=x^2-8x+3$
$y=x^2-4$

Which has a more positive $y-$ intercept?

$y=x^2$ or $y=4x^2$
$y=2x^2+4$ or $y=\frac{1}{2} x^2+4$
$y=-2x^2-2$ or $y=-x^2-2$

Identify the vertex and $y-$ intercept. Is the vertex a maximum or a minimum?

$y=x^2-2x-8$
$y=-x^2+10x-21$
$y=2x^2+6x+4$

Does the graph of the parabola open up or down?

$y=-2x^2-2x-3$
$y=3x^2$
$y=16-4x^2$

Which equation has a larger vertex?

$y=x^2$ or $y=4x^2$
$y=-2x^2$ or $y=-2x^2 -2$
$y=3x^2-3$ or $y=3x^2-6$

Graph the following functions by making a table of values. Use the vertex and $x-$ intercepts to help you pick values for the table.

$y=4x^2-4$
$y=-x^2+x+12$
$y=2x^2+10x+8$
$y=\frac{1}{2} x^2-2x$
$y=x-2x^2$
$y=4x^2-8x+4$
Nadia is throwing a ball to Peter. Peter does not catch the ball and it hits the ground. The graph shows the path of the ball as it flies through the air. The equation that describes the path of the ball is $y=4+2x-0.16x^2$ . Here, $y$ is the height of the ball and $x$ is the horizontal distance from Nadia. Both distances are measured in feet. How far from Nadia does the ball hit the ground? At what distance, $x$ , from Nadia, does the ball attain its maximum height? What is the maximum height?
Peter wants to enclose a vegetable patch with 120 feet of fencing. He wants to put the vegetable patch against an existing wall, so he needs fence for only three of the sides. The equation for the area is given by $a=120 x-x^2$ . From the graph, find what dimensions of the rectangle would give him the greatest area.

Mixed Review

Factor $6u^2 v-11u^2 v^2-10u^2 v^3$ using its GCF.
Factor into primes: $3x^2+11x+10$ .
Simplify $- \frac{1}{9} (63) \left(- \frac{3}{7} \right)$ .
Solve for $b: |b+2|=9$ .
Simplify $(4x^3 y^2 z)^3$ .
What is the slope and $y-$ intercept of $7x+4y=9?$

Solving Quadratic Equations by Graphing

Isaac Newton’s theory for projectile motion is represented by the equation:

$h(t)=- \frac{1}{2} (g) t^2+v_0 t+h_0$

$t=$ time (usually in seconds)
$g=$ gravity due to acceleration; either 9.8 m/s or 32 ft/s
$v_0=$ initial velocity
$h_0=$ initial height of object

Consider the following situation: “A quarterback throws a football at an initial height of 5.5 feet with an initial velocity of 35 feet per second.”

By substituting the appropriate information:

$g=32$ because the information is given in feet
$v_0=35$
$h_0=5.5$

The equation becomes $h(t)=-\frac{1}{2} (32) t^2+35t+5.5 \rightarrow h(t)=-16t^2+35t+5.5$ .

Using the concepts from the previous lesson, we know

The value of $a$ is negative, so the parabola opens downward.
The vertex is a maximum point.
The $y-$ intercept is (0, 5.5).
The graph is narrow about its line of symmetry.

At what time will the football be 6 feet high? This equation can be solved by graphing the quadratic equation.

Solving a Quadratic Using a Calculator

Chapter 7 focused on how to solve systems by graphing. You can think of this situation as a system: $\begin{cases} y=-16t^2+35t+5.5\ y=6 \end{cases}$ . You are looking for the appropriate $x-$ coordinates that give a $y-$ coordinate of 6 feet. Therefore, you are looking for the intersection of the two equations.

Begin by typing the equations into the $[Y=]$ menu of your calculator. Adjust the window until you see the vertex, $y-$ intercept, $x-$ intercepts, and the horizontal line of 6 units.

By looking at the graph, you can see there are two points of intersection. Using the methods from chapter 7, find both points of intersection.

$(0.014,6) \ and \ (2.172,6)$

At 0.014 seconds and again at 2.17 seconds, the football is six feet from the ground.

Using a Calculator to Find the Vertex

You can also use a graphing calculator to determine the vertex of the parabola. The vertex of this equation is a maximum point, so in the [CALCULATE] menu of the graphing option, look for [MAXIMUM].

Choose option #4. The calculator will ask you, “LEFT BOUND?” Move the cursor to the left of the vertex and hit [ENTER].

The calculator will ask, “RIGHT BOUND?” Move the cursor to the right of the vertex and hit [ENTER].

Hit [ENTER] to guess.

The maximum point on this parabola is (1.09, 24.64).

Example 1: Will the football reach 25 feet high?

Solution: The vertex represents the maximum point of this quadratic equation. Since its height is 24.64 feet, we can safely say the football will not reach 25 feet.

Example 2: When will the football hit the ground, assuming no one will catch it?

Solution: We know want to know at what time the height is zero. $\begin{cases} y=-16t^2+35t+5.5 \ y=0 \end{cases}$ . By repeating the process above and finding the intersection of the two lines, the solution is (2.33, 0). At 2.33 seconds, the ball will hit the ground.

The point at which the ball reaches the ground $(y=0)$ represents the $x-$ intercept of the graph.

The $x-$ intercept of a quadratic equation is also called a root, solution, or zero.

Example: Determine the number of solutions to $y=x^2+4$ .

Solution: Graph this quadratic equation, either by hand or with a graphing calculator. Adjust the calculator’s window to see both halves of the parabola, the vertex, the $x-$ axis, and the $y-$ intercept.

The solutions to a quadratic equation are also known as its $x-$ intercepts. This parabola does not cross the $x-$ axis. Therefore, this quadratic equation has no real solutions.

Example: Andrew has 100 feet of fence to enclose a rectangular tomato patch. He wants to find the dimensions of the rectangle that encloses the most area.

Solution: The perimeter of a rectangle is the sum of all four sides. Let $w=$ width and $l=$ length. The perimeter of the tomato patch is $100=l+l+w+w \rightarrow 100=2l+2w$ .

The area of a rectangle is found by the formula $A=l(w)$ . We are looking for the intersection between the area and perimeter of the rectangular tomato patch. This is a system.

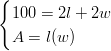
$\begin{cases} 100 = 2l+2w \ A = l(w) \end{cases}$

Before we can graph this system, we need to rewrite the first equation for either $l$ or $w$ . We will then use the Substitution Property.

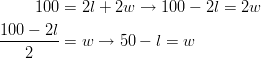
$100 &= 2l+2w \rightarrow 100-2l=2w\ \frac{100-2l}{2} &= w \rightarrow 50-l=w$

Use the Substitution Property to replace the variable $w$ in the second equation with the express $50-l$ .

$A=l(50-l)=50l-l^2$

Graph this equation to visualize it.

The parabola opens downward so the vertex is a maximum. The maximum value is (25, 625). The length of the tomato patch should be 25 feet long to achieve a maximum area of 625 square feet.

Practice Set

video_image

Solving Quadratic Equations by Graphing (Click here to watch the video)

What are the alternate names for the solution to a parabola?
Define the following variables in the function
$h(t)=-\frac{1}{2} (g) t^2+v_0 t+h_0$ .
1. $h_0$
2. $t$
3. $v_0$
4. $g$
5. $h(t)$

A rocket is launched from a height of 3 meters with an initial velocity of 15 meters per second.
1. Model the situation with a quadratic equation.
2. What is the maximum height of the rocket? When will this occur?
3. What is the height of the rocket after four seconds? What does this mean?
4. When will the rocket hit the ground?
5. At what time will the rocket be 13 meters from the ground?

How many solutions does the quadratic equation have?
$-x^2+3=0$
$2x^2+5x-7=0$
$-x^2+x-3=0$

Find the zeros of the quadratic equations below. If necessary, round your answers to the nearest hundredth.

$y=-x^2+4x-4$
$y=3x^2-5x$
$x^2+3x+6=0$
$-2x^2+x+4=0$
$x^2-9=0$
$x^2+6x+9=0$
$10x^2-3x^2=0$
$\frac{1}{2}x^2-2x+3=0$
$y=-3x^2+4x-1$
$y=9-4x^2$
$y=x^2+7x+2$
$y=-x^2-10x-25$
$y=2x^2-3x$
$y=x^2-2x+5$
Andrew is an avid archer. He launches an arrow that takes a parabolic path, modeled by the equation $y=-4.9t^2+48t$ . Find how long it takes the arrow to come back to the ground.

For questions 24 – 26,

(a) Find the roots of the quadratic polynomial.

(b) Find the vertex of the quadratic polynomial.

$y=x^2+12x+5$
$y=x^2+3x+6$
$y=-x^2-3x+9$
Sharon needs to create a fence for her new puppy. She purchased 40 feet of fencing to enclose three sides of a fence. What dimensions will produce the greatest area for her puppy to play?
An object is dropped from the top of a 100-foot-tall building.
1. Write an equation to model this situation.
2. What is the height of the object after 1 second?
3. What is the maximum height of the object?
4. At what time will the object be 50 feet from the ground?
5. When will the object hit the ground?

Mixed Review

Factor $3r^2-4r+1$ .
Simplify $(2+\sqrt{3})(4+\sqrt{3})$ .
Write the equation in slope-intercept form and identify the slope and $y-$ intercept: $9-3x+18y=0$ .
The half life of a particular substance is 16 days. An organism has 100% of the substance on day zero. What is the percentage remaining after 44 days?
Multiply and write your answer in scientific notation: $0.00000009865 \times 123564.21$
A mixture of 12% chlorine is mixed with a second mixture containing 30% chlorine. How much of the 12% mixture is needed to mix with 80 mL to make a final solution of 150 mL with a 20% chlorine concentration?

Solving Quadratic Equations Using Square Roots

Suppose you needed to find the value of $x$ such that $x^2=81$ . How could you solve this equation?

Make a table of values.
Graph this equation as a system.
Cancel the square using its inverse operation.

The inverse of a square is a square root.

By applying the square root to each side of the equation, you get:

$x &= \pm \sqrt{81}\ x &= 9 \ or \ x=-9$

In general, the solution to a quadratic equation of the form $0=ax^2-c$ is:

$x=\sqrt{\frac{c}{a}} \ \text{or} \ x=- \sqrt{\frac{c}{a}}$

Example 1: Solve $(x-4)^2-9=0$ .

Solution: Begin by adding 9 to each side of the equation.

$(x-4)^2=9$

Cancel square by applying square root.

$x-4=3 \ or \ x-4=-3$

Solve both equations for $x: x=7 \ or \ x=1$

In the previous lesson, you learned Newton’s formula for projectile motion. Let’s examine a situation in which there is no initial velocity. When a ball is dropped, there is no outward force placed on its path; therefore, there is no initial velocity.

A ball is dropped from a 40-foot building. When does the ball reach the ground?

Using the equation from the previous lesson, $h(t)=-\frac{1}{2} (g) t^2+v_0 t+h_0$ , and substituting the appropriate information, you get:

$&& 0 &=-\frac{1}{2} (32)t^2+(0)t+40\ \text{Simplify} && 0 &= -16t^2+40\ \text{Solve for} \ x: && -40 &= -16t^2\ && 2.5 &= t^2\ && t & \approx 1.58 \ and \ t \approx -1.58$

Because $t$ is in seconds, it does not make much sense for the answer to be negative. So the ball will reach the ground at approximately 1.58 seconds.

Example: A rock is dropped from the top of a cliff and strikes the ground 7.2 seconds later. How high is the cliff in meters?

Solution: Using Newton’s formula, substitute the appropriate information.

$&& 0 &= -\frac{1}{2} (9.8)(7.2)^2+(0)(7.2)+ h_0\ \text{Simplify:} && 0 &= -254.016+h_0\ \text{Solve for} \ h_0: && h_0 &= 254.016$

The cliff is approximately 254 meters tall.

Practice Set

video_image

Solving Quadratic Equations by Square Roots (Click here to watch the video)

Solve each quadratic equation.

$x^2=196$
$x^2-1=0$
$x^2-100=0$
$x^2+16=0$
$9x^2-1=0$
$4x^2-49=0$
$64x^2-9=0$
$x^2-81=0$
$25x^2-36=0$
$x^2+9=0$
$x^2-16=0$
$x^2-36=0$
$16x^2-49=0$
$(x-2)^2=1$
$(x+5)^2=16$
$(2x-1)^2-4=0$
$(3x+4)^2=9$
$(x-3)^2+25=0$
$x^2-6=0$
$x^2-20=0$
$3x^2+14=0$
$(x-6)^2=5$
$(4x+1)^2-8=0$
$(x+10)^2=2$
$2(x+3)^2=8$
How long does it take a ball to fall from a roof to the ground 25 feet below?
Susan drops her camera in the river from a bridge that is 400 feet high. How long is it before she hears the splash?
It takes a rock 5.3 seconds to splash in the water when it is dropped from the top of a cliff. How high is the cliff in meters?
Nisha drops a rock from the roof of a building 50 feet high. Ashaan drops a quarter from the top-story window, which is 40 feet high, exactly half a second after Nisha drops the rock. Which hits the ground first?
Victor drops an apple out of a window on the $10^{th}$ floor, which is 120 feet above ground. One second later, Juan drops an orange out of a $6^{th}$ -floor window, which is 72 feet above the ground. Which fruit reaches the ground first? What is the time difference between the fruits’ arrival to the ground?

Mixed Review

Graph $y=2x^2+6x+4$ . Identify the following:
1. Vertex
2. $x-$ intercepts
3. $y-$ intercepts
4. axis of symmetry

What is the difference between $y=x+3$ and $y=x^2+3$ ?
Determine the domain and range of $y=-(x-2)^2+7$ .
The Glee Club is selling hot dogs and sodas for a fundraiser. On Friday the club sold 112 hot dogs and 70 sodas and made $154.00. On Saturday the club sold 240 hot dogs and 120 sodas and made $300.00. How much is each soda? Each hot dog?

Solving Quadratic Equations by Completing the Square

There are several ways to write an equation for a parabola:

Standard form: $y=ax^2+bx+c$
Factored form: $y=(x+m)(x+n)$
Vertex form: $y=a(x-h)^2+k$

Vertex form of a quadratic equation: $y=a(x-h)^2+k$ , where $(h,k)=$ vertex of the parabola and $a=$ leading coefficient

Example 1: Determine the vertex of $y=-\frac{1}{2} (x-4)^2-7$ . Is this a minimum or a maximum point of the parabola?

Solution: Using the definition of vertex form, $h=4, k=-7$ .

The vertex is (4, –7).
Because $a$ is negative, the parabola opens downward.
Therefore, the vertex (4, –7) is a maximum point of the parabola.

Once you know the vertex, you can use symmetry to graph the parabola.

$x$	$y$
2
3
4	–7
5
6

Example 2: Write the equation for a parabola with $a=3$ and vertex (–4, 5) in vertex form.

Solution: Using the definition of vertex form $y=a(x-h)^2+k, h=-4$ and $k=5$ .

$y &= 3(x-(-4))^2+5\ y &= 3(x+4)^2+5$

Consider the quadratic equation $y=x^2+4x-2$ . What is its vertex? You could graph this using your calculator and determine the vertex or you could complete the square.

Completing the Square

Completing the square is a method used to create a perfect square trinomial, as you learned in the previous chapter.

A perfect square trinomial has the form $a^2+2(ab)+b^2$ , which factors into $(a+b)^2$ .

Example: Find the missing value to create a perfect square trinomial: $x^2+8x+?$ .

Solution: The value of $a$ is $x$ . To find $b$ , use the definition of the middle term of the perfect square trinomial.

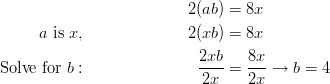
$&& 2(ab) &= 8x\ a \ \text{is} \ x, && 2(xb) &= 8x\ \text{Solve for} \ b: && \frac{2xb}{2x} &= \frac{8x}{2x} \rightarrow b=4$

To complete the square you need the value of $b^2$ .

$b^2=4^2=16$

The missing value is 16.

To complete the square, the equation must be in the form: $y=x^2+\left(\frac{1}{2} b \right )x+b^2$ .

Looking at the above example, $\frac{1}{2}(8)=4$ and $4^2=16$ .

Example 3: Find the missing value to complete the square of $x^2+22x+$ ?. Then factor.

Solution: Use the definition of the middle term to complete the square.

$\frac{1}{2} (b)=\frac{1}{2} (22)=11$

Therefore, $11^2=121$ and the perfect square trinomial is $x^2+22x+121$ . Rewriting in its factored form, the equation becomes $(x+11)^2$ .

Solve Using Completing the Square

Once you have the equation written in vertex form, you can solve using the method learned in the last lesson.

Example: Solve $x^2+22x+121=0$ .

Solution: By completing the square and factoring, the equation becomes:

$&& (x+11)^2 &= 0\ \text{Solve by taking the square root:} && x+11 &= \pm0\ \text{Separate into two equations:} && x+11 &=0 \ or \ x+11=0\ \text{Solve for} \ x: && x &= -11$

Example: Solve $x^2+10x+9=0$ .

Solution: Using the definition to complete the square, $\frac{1}{2}(b)=\frac{1}{2}(10)=5$ . Therefore, the last value of the perfect square trinomial is $5^2=25$ . The equation given is

$x^2+10x+9=0, \ and \ 9 \neq 25$

Therefore, to complete the square, we must rewrite the standard form of this equation into vertex form.

Subtract 9: $x^2+10x=-9$

Complete the square: Remember to use the Addition Property of Equality.

$&& x^2+10x+25 &= -9+25\ \text{Factor the left side.} && (x+5)^2 &= 16\ \text{Solve using square roots.} && \sqrt{(x+5)^2} &= \pm \sqrt{16}\ && x+5 &=4 \ or \ x+5=-4\ && x &= -1 \ or \ x=-9$

Example: An arrow is shot straight up from a height of 2 meters with a velocity of 50 m/s. What is the maximum height that the arrow will reach and at what time will that happen?

Solution: The maximum height is the vertex of the parabola. Therefore, we need to rewrite the equation in vertex form.

$\text{We rewrite the equation in vertext form.} && y &= -4.9t^2+50t+2\ && y-2 &= -4.9t^2+50t\ && y-2 &= -4.9(t^2-10.2t)\ \text{Complete the square inside the parentheses.} && y-2-4.9(5.1)^2 &= -4.9(t^2-10.2t+(5.1)^2)\ && y-129.45 &= -4.9(t-5.1)^2$

The maximum height is 129.45 meters.

Multimedia Link: Visit the http://www.mathsisfun.com/algebra/completing-square.html - mathisfun webpage for more explanation on completing the square.

Practice Set

video_image

Solving Quadratic Equations by Completing the Square (Click here to watch the video)

What does it mean to “complete the square”?
Describe the process used to solve a quadratic equation by completing the square.
Using the equation from the arrow in the lesson,
1. How high will an arrow be four seconds after being shot? After eight seconds?
2. At what time will the arrow hit the ground again?

Write the equation for the parabola with the given information.

$a=a$ , vertex $=(h, k)$
$a=\frac{1}{3}$ , vertex $=(1, 1)$
$a=-2$ , vertex $=(-5, 0)$
Containing (5, 2) and vertex (1, –2)
$a=1$ , vertex $=(-3, 6)$

Complete the square for each expression.

$x^2+5x$
$x^2-2x$
$x^2+3x$
$x^2-4x$
$3x^2+18x$
$2x^2-22x$
$8x^2-10x$
$5x^2+12x$

Solve each quadratic equation by completing the square.

$x^2-4x=5$
$x^2-5x=10$
$x^2+10x+15=0$
$x^2+15x+20=0$
$2x^2-18x=0$
$4x^2+5x=-1$
$10x^2-30x-8=0$
$5x^2+15x-40=0$

Rewrite each quadratic function in vertex form.

$y=x^2-6x$
$y+1=-2x^2-x$
$y=9x^2+3x-10$
$y=32x^2+60x+10$

For each parabola, find:

The vertex
$x-$ intercepts
$y-$ intercept
If it opens up or down
The graph the parabola

$y-4=x^2+8x$
$y=-4x^2+20x-24$
$y=3x^2+15x$
$y+6=-x^2+x$
$x^2-10x+25=9$
$x^2+18x+81=1$
$4x^2-12x+9=16$
$x^2+14x+49=3$
$4x^2-20x+25=9$
$x^2+8x+16=25$
Sam throws an egg straight down from a height of 25 feet. The initial velocity of the egg is 16 ft/sec. How long does it take the egg to reach the ground?
Amanda and Dolvin leave their house at the same time. Amanda walks south and Dolvin bikes east. Half an hour later they are 5.5 miles away from each other and Dolvin has covered three miles more than the distance that Amanda covered. How far did Amanda walk and how far did Dolvin bike?
Two cars leave an intersection. One car travels north; the other travels east. When the car traveling north had gone 30 miles, the distance between the cars was 10 miles more than twice the distance traveled by the car heading east. Find the distance between the cars at that time.

Mixed Review

A ball dropped from a height of four feet bounces 70% of its previous height. Write the first five terms of this sequence. How high will the ball reach on its $8^{th}$ bounce?
Rewrite in standard form: $y=\frac{2}{7} x-11$ .
Graph $y=5 \left( \frac{1}{2} \right)^x$ . Is this exponential growth or decay? What is the growth factor?
Solve for $r: |3r-4| \le 2$ .
Solve for $m:-2m+6=-8(5m+4)$ .
Factor $4a^2+36a-40$ .

Quick Quiz

Graph and identify:
1. The vertex
2. The axis of symmetry
3. The domain and range
4. The $y-$ intercept
5. The $x-$ intercepts estimated to the nearest tenth

Solve $y=x^2+9x+20$ by graphing.
Solve for $x: 74=x^2-7$ .
A baseball is thrown from an initial height of 5 feet with an initial velocity of 100 ft/sec.
1. What is the maximum height of the ball?
2. When will the ball reach the ground?
3. When is the ball 90 feet in the air?

Solve by completing the square: $v^2-20v+25=6$

Solving Quadratic Equations Using the Quadratic Formula

This chapter has presented three methods to solve a quadratic equation:

By graphing to find the zeros;
By solving using square roots; and
By using completing the square to find the solutions

This lesson will present a fourth way to solve a quadratic equation: using the Quadratic Formula.

History of the Quadratic Formula

As early as 1200 BC, people were interested in solving quadratic equations. The Babylonians solved simultaneous equations involving quadratics. In 628 AD, Brahmagupta, an Indian mathematician, gave the first explicit formula to solve a quadratic equation. The Quadratic Formula was written as it is today by the Arabic mathematician Al-Khwarizmi. It is his name upon which the word “Algebra” is based.

The solution to any quadratic equation in standard form $0=ax^2+bx+c$ is

$x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$

Example: Solve $x^2+10x+9=0$ using the Quadratic Formula.

Solution: We know from the last lesson the answers are $x=-1$ or $x=-9$ .

By applying the Quadratic Formula and $a=1, b=10$ , and $c=9$ , we get:

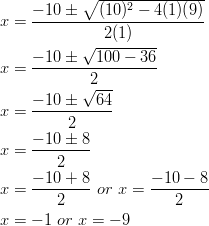
$x &= \frac{-10 \pm \sqrt{(10)^2-4(1)(9)}}{2(1)}\ x &= \frac{-10 \pm \sqrt{100-36}}{2}\ x &= \frac{-10 \pm \sqrt{64}}{2}\ x &= \frac{-10 \pm 8}{2}\ x &= \frac{-10 + 8}{2} \ or \ x=\frac{-10-8}{2}\ x &= -1 \ or \ x=-9$

Example 1: Solve $-4x^2+x+1=0$ using the Quadratic Formula.

Solution:

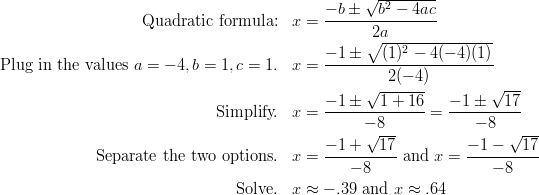
$\text{Quadratic formula:} && x & =\frac{-b \pm \sqrt{b^2-4ac}}{2a}\ \text{Plug in the values} \ a=-4, b=1, c=1. && x& =\frac{-1 \pm \sqrt{(1)^2-4(-4)(1)}}{2(-4)}\ \text{Simplify.} && x & =\frac{-1 \pm \sqrt{1+16}}{-8}=\frac{-1 \pm \sqrt{17}}{-8}\ \text{Separate the two options.} && x&=\frac{-1+\sqrt{17}}{-8} \ \text{and} \ x=\frac{-1-\sqrt{17}}{-8}\ \text{Solve.} && x & \approx -.39 \ \text{and} \ x \approx .64$

Multimedia Link For more examples of solving quadratic equations using the Quadratic Formula, see Khan Academy Equation Part 2 (9:14).

video_image

2 more examples of solving equations using the quadratic equation (Click here to watch the video)

Figure 2 provides more examples of solving equations using the quadratic equation. This video is not necessarily different from the examples above, but it does help reinforce the procedure of using the Quadratic Formula to solve equations.

Finding the Vertex of a Quadratic Equation in Standard Form

The $x-$ coordinate of the vertex of $0=ax^2+bx+c$ is $x=-\frac{b}{a}$

Which Method to Use?

Usually you will not be told which method to use. You will have to make that decision yourself. However, here are some guidelines to which methods are better in different situations.

Graphing – a good method to visualize the parabola and easily see the intersections. Not always precise.
Factoring – best if the quadratic expression is easily factorable
Taking the square root – is best used of the form $0=ax^2-c$
Completing the square – can be used to solve any quadratic equation. It is a very important method for rewriting a quadratic function in vertex form.
Quadratic Formula – is the method that is used most often for solving a quadratic equation. If you are using factoring or the Quadratic Formula, make sure that the equation is in standard form.

Example: The length of a rectangular pool is 10 meters more than its width. The area of the pool is 875 square meters. Find the dimensions of the pool.

Solution: Begin by drawing a sketch. The formula for the area of a rectangle is $A=l(w)$ .

$A &= (x+10)(x)\ 875 &= x^2+10x$

Now solve for $x$ using any method you prefer.

The result is $x=25$ . So, the length of the pool is 35 meters and the width is 25 meters.

Practice Set

The following video will guide you through a proof of the Quadratic Formula. CK-12 Basic Algebra: Proof of Quadratic Formula (7:44)

video_image

Proof of Quadratic Formula (Click here to watch the video)

video_image

Using the Quadratic Formula (Click here to watch the video)

What is the Quadratic Formula? When is the most appropriate situation to use this formula?
When was the first known solution of a quadratic equation recorded?

Find the $x-$ coordinate of the vertex of the following equations.

$x^2-14x+45=0$
$8x^2-16x-42=0$
$4x^2+16x+12=0$
$x^2+2x-15=0$

Solve the following quadratic equations using the Quadratic Formula.

$x^2+4x-21=0$
$x^2-6x=12$
$3x^2-\frac{1}{2}x=\frac{3}{8}$
$2x^2+x-3=0$
$-x^2-7x+12=0$
$-3x^2+5x=0$
$4x^2=0$
$x^2+2x+6=0$

Solve the following quadratic equations using the method of your choice.

$x^2-x=6$
$x^2-12=0$
$-2x^2+5x-3=0$
$x^2+7x-18=0$
$3x^2+6x=-10$
$-4x^2+4000x=0$
$-3x^2+12x+1=0$
$x^2+6x+9=0$
$81x^2+1=0$
$-4x^2+4x=9$
$36x^2-21=0$
$x^2+2x-3=0$
The product of two consecutive integers is 72. Find the two numbers.
The product of two consecutive odd integers is 11 less than 3 times their sum. Find the integers.
The length of a rectangle exceeds its width by 3 inches. The area of the rectangle is 70 square inches. Find its dimensions.
Suzie wants to build a garden that has three separate rectangular sections. She wants to fence around the whole garden and between each section as shown. The plot is twice as long as it is wide and the total area is 200 square feet. How much fencing does Suzie need?
Angel wants to cut off a square piece from the corner of a rectangular piece of plywood. The larger piece of wood is $4 \ \text{feet} \times 8 \ \text{feet}$ and the cut off part is $\frac{1}{3}$ of the total area of the plywood sheet. What is the length of the side of the square?
Mike wants to fence three sides of a rectangular patio that is adjacent the back of his house. The area of the patio is $192 \ ft^2$ and the length is 4 feet longer than the width. Find how much fencing Mike will need.

Mixed Review

The theatre has three types of seating: balcony, box, and floor. There are four times as many floor seats as balcony. There are 200 more box seats than balcony seats. The theatre has a total of 1,100 seats. Determine the number of balcony, box, and floor seats in the theatre.
Write an equation in slope-intercept form containing (10, 65) and (5, 30).
120% of what number is 60?
Name the set() of numbers to which $\sqrt{16}$ belongs.
Divide $6 \frac{1}{7} \div - 2 \frac{3}{4}$ .
The set is the number of books in a library. Which of the following is the most appropriate domain for this set: all real numbers; positive real numbers; integers; or whole numbers? Explain your reasoning.

The Discriminant

You have seen parabolas that intersect the $x-$ axis twice, once, or not at all. There is a relationship between the number of real $x-$ intercepts and the Quadratic Formula.

Case 1: The parabola has two $x-$ intercepts. This situation has two possible solutions for $x$ , because the value inside the square root is positive. Using the Quadratic Formula, the solutions are $x=\frac{-b+\sqrt{b^2-4ac}}{2a}$ and $x=\frac{-b-\sqrt{b^2-4ac}}{2a}$ .

Case 2: The parabola has one $x-$ intercept. This situation occurs when the vertex of the parabola just touches the $x-$ axis. This is called a repeated root, or double root. The value inside the square root is zero. Using the Quadratic Formula, the solution is $x=\frac{-b}{2a}$ .

Case 3: The parabola has no $x-$ intercept. This situation occurs when the parabola does not cross the $x-$ axis. The value inside the square root is negative, therefore there are no real roots. The solutions to this type of situation are imaginary, which you will learn more about in a later textbook.

The value inside the square root of the Quadratic Formula is called the discriminant. It is symbolized by $D$ . It dictates the number of real solutions the quadratic equation has. This can be summarized with the Discriminant Theorem.

If $D>0$ , the parabola will have two $x-$ intercepts. The quadratic equation will have two real solutions.
If $D=0$ , the parabola will have one $x-$ intercept. The quadratic equation will have one real solution.
If $D<0$ , the parabola will have no $x-$ intercepts. The quadratic equation will have zero real solutions.

Example 1: Determine the number of real solutions to $-3x^2+4x+1=0$ .

Solution: By finding the value of its discriminant, you can determine the number of $x-$ intercepts the parabola has and thus the number of real solutions.

$D &= b^2-4(a)(c)\ D &= (4)^2-4(-3)(1)\ D &= 16+12=28$

Because the discriminant is positive, the parabola has two real $x-$ intercepts and thus two real solutions.

Example: Determine the number of solutions to $-2x^2+x=4$ .

Solution: Before we can find its discriminant, we must write the equation in standard form $ax^2+bx+c=0$ .

Subtract 4 from each side of the equation: $-2x^2+x-4=0$ .

$\text{Find the discriminant.} && D &= (1)^2-4(-2)(-4)\ && D &= 1-32=-31$

The value of the discriminant is negative; there are no real solutions to this quadratic equation. The parabola does not cross the $x-$ axis.

Example 2: Emma and Bradon own a factory that produces bike helmets. Their accountant says that their profit per year is given by the function $P=0.003x^2+12x+27,760$ , where $x$ represents the number of helmets produced. Their goal is to make a profit of $40,000 this year. Is this possible?

Solution: The equation we are using is $40,000=0.003x^2+12x+27,760$ . By finding the value of its discriminant, you can determine if the profit is possible.

Begin by writing this equation in standard form:

$0 &= 0.003x^2+12x-12,240\ D &= b^2-4(a)(c)\ D &= (12)^2-4(0.003)(-12,240)\ D &= 144+146.88=290.88$

Because the discriminant is positive, the parabola has two real solutions. Yes, the profit of $40,000 is possible.

Multimedia Link: This http://sciencestage.com/v/20592/a-level-maths-:-roots-of-a-quadratic-equation-:-discriminant-:-examsolutions.html - video, presented by Science Stage, helps further explain the discriminant using the Quadratic Formula.

Practice Set

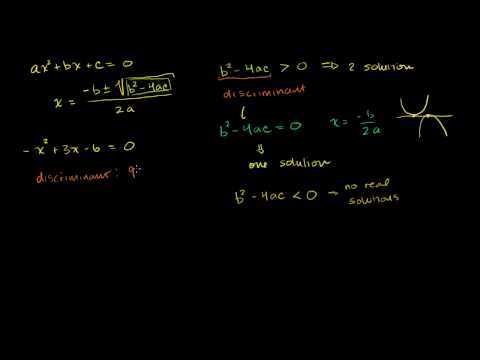
video_image

Discriminant of Quadratic Equations (Click here to watch the video)

What is a discriminant? What does it do?
What is the formula for the discriminant?
Can you find the discriminant of a linear equation? Explain your reasoning.
Suppose $D=0$ . Draw a sketch of this graph and determine the number of real solutions.
$D=-2.85$ . Draw a possible sketch of this parabola. What is the number of real solutions to this quadratic equation.
$D>0$ . Draw a sketch of this parabola and determine the number of real solutions.

Find the discriminant of each quadratic equation.

$2x^2-4x+5=0$
$x^2-5x=8$
$4x^2-12x+9=0$
$x^2+3x+2=0$
$x^2-16x=32$
$-5x^2+5x-6=0$

Determine the nature of the solutions of each quadratic equation.

$-x^2+3x-6=0$
$5x^2=6x$
$41x^2-31x-52=0$
$x^2-8x+16=0$
$-x^2+3x-10=0$
$x^2-64=0$

A solution to a quadratic equation will be irrational if the discriminant is not a perfect square. If the discriminant is a perfect square, then the solutions will be rational numbers. Using the discriminant, determine whether the solutions will be rational or irrational.

$x^2=-4x+20$
$x^2+2x-3=0$
$3x^2-11x=10$
$\frac{1}{2}x^2+2x+\frac{2}{3}=0$
$x^2-10x+25=0$
$x^2=5x$
Marty is outside his apartment building. He needs to give Yolanda her cell phone but he does not have time to run upstairs to the third floor to give it to her. He throws it straight up with a vertical velocity of 55 feet/second. Will the phone reach her if she is 36 feet up? (Hint: The equation for the height is given by $y=-32t^2+55t+4$ .)
Bryson owns a business that manufactures and sells tires. The revenue from selling the tires in the month of July is given by the function $R=x(200-0.4x)$ where $x$ is the number of tires sold. Can Bryson’s business generate revenue of $20,000 in the month of July?
Marcus kicks a football in order to score a field goal. The height of the ball is given by the equation $y=-\frac{32}{6400}x^2+x$ , where $y$ is the height and $x$ is the horizontal distance the ball travels. We want to know if Marcus kicked the ball hard enough to go over the goal post, which is 10 feet high.

Mixed Review

Factor $6x^2-x-12$ .
Find the vertex of $y=-\frac{1}{4} x^2-3x-12=y$ by completing the square.
Solve using the Quadratic Formula: $-4x^2-15=-4x$ .
How many centimeters are in four fathoms? (Hint: 1 fathom = 6 feet)
Graph the solution to $\begin{cases} 3x+2y \le -4\ x-y>-3 \end{cases}$ .
How many ways can 3 toppings be chosen from 7 options?

Linear, Exponential, and Quadratic Models

So far in this text you have learned how to graph three very important types of equations.

Linear equations in slope-intercept form $y=mx+b$
Exponential equations of the form $y=a(b)^x$
Quadratic equations in standard form $y=ax^2+bx+c$

In real-world applications, the function that describes some physical situation is not given. Finding the function is an important part of solving problems. For example, scientific data such as observations of planetary motion are often collected as a set of measurements given in a table. One job for the scientist is to figure out which function best fits the data. In this lesson, you will learn some methods that are used to identify which function describes the relationship between the dependent and independent variables in a problem.

Using Differences to Determine the Model

By finding the differences between the dependent values, we can determine the degree of the model for the data.

If the first difference is the same value, the model will be linear.
If the second difference is the same value, the model will be quadratic.
If the number of times the difference has been taken exceeds five, the model may be exponential or some other special equation.

Example: The first difference is the same value (3). This data can be modeled using a linear regression line.

The equation to represent this data is $y=3x+2$

When we look at the difference of the $y-$ values, we must make sure that we examine entries for which the $x-$ values increase by the same amount.

For example, examine the values in the following table.

At first glance, this function might not look linear because the difference in the $y-$ values is not always the same.

However, we see that the difference in $y-$ values is 5 when we increase the $x-$ values by 1, and it is 10 when we increase the $x-$ values by 2. This means that the difference in $y-$ values is always 5 when we increase the $x-$ values by 1. Therefore, the function is linear.

The equation is modeled by $y=5x+5$ .

An example of a quadratic model would have the following look when taking the second difference.

Using Ratios to Determine the Model

Finding the difference involves subtracting the dependent values leading to a degree of the model. By taking the ratio of the values, one can obtain whether the model is exponential.

If the ratio of dependent values is the same, then the data is modeled by an exponential equation, as in the example below.

Determine the Model Using a Graphing Calculator

To enter data into your graphing calculator, find the [STAT] button. Choose [EDIT].

[L1] represents your independent variable, your $x$ .
[L2] represents your dependent variable, your $y$ .

Enter the data into the appropriate list. Using the first set of data to illustrate yields:

You already know this data is best modeled by a linear regression line. Using the [CALCULATE] menu of your calculator, find the linear regression line, linreg.

Look at the screen above. This is where you can find the quadratic regression line [QUADREG], the cubic regression line [CUBICREG], and the exponential regression line, [EXPREG].

Practice Set

video_image

Linear, Quadratic, and Exponential Models (Click here to watch the video)

The second set of differences have the same value. What can be concluded?
Suppose you find the difference five different times and still don't come to a common value. What can you safely assume?
Why would you test the ratio of differences?
If you had a cubic ( $3^{rd}$ -degree) function, what could you conclude about the differences?

Determine whether the data can be modeled by a linear equation, a quadratic equation, or neither.

$& x && -4 && -3 && -2 && -1 && 0 && 1\ & y && 10 && 7 && 4 && 1 && -2 && -5$
$& x && -2 && -1 && 0 && 1 && 2 && 3\ & y && 4 && 3 && 2 && 3 && 6 && 11$
$& x && 0 && 1 && 2 && 3 && 4 && 5\ & y && 50 && 75 && 100 && 125 && 150 && 175$
$& x && -10 && -5 && 0 && 5 && 10 && 15\ & y && 10 && 2.5 && 0 && 2.5 && 10 && 22.5$
$& x && 1 && 2 && 3 && 4 && 5 && 6\ & y && 4 && 6 && 6 && 4 && 0 && -6$
$& x && -3 && -2 && -1 && 0 && 1 && 2\ & y && -27 && -8 && -1 && 0 && 1 && 8$

Can the following data be modeled with an exponential function?

$& x && 0 && 1 && 2 && 3 && 4 && 5\ & y && 200 && 300 && 1800 && 8300 && 25,800 && 62,700$
$& x && 0 && 1 && 2 && 3 && 4 && 5\ & y && 120 && 180 && 270 && 405 && 607.5 && 911.25$
$& x && 0 && 1 && 2 && 3 && 4 && 5\ & y && 4000 && 2400 && 1440 && 864 && 518.4 && 311.04$

Determine whether the data is best represented by a quadratic, linear, or exponential function. Find the function that best models the data.

$& x && 0 && 1 && 2 && 3 && 4\ & y && 400 && 500 && 625 && 781.25 && 976.5625$
$& x && -9 && -7 && -5 && -3 && -1 && 1\ & y && -3 && -2 && -1 && 0 && 1 && 2$
$& x && -3 && -2 && -1 && 0 && 1 && 2 && 3\ & y && 14 && 4 && -2 && -4 && -2 && 4 && 14$
As a ball bounces up and down, the maximum height it reaches continually decreases. The table below shows the height of the bounce with regard to time.
1. Using a graphing calculator, create a scatter plot of this data.
2. Find the quadratic function of best fit.
3. Draw the quadratic function of best fit on top of the scatter plot.
4. Find the maximum height the ball reaches.
5. Predict how high the ball is at 2.5 seconds.

Time (seconds)	Height (inches)
2	2
2.2	16
2.4	24
2.6	33
2.8	38
3.0	42
3.2	36
3.4	30
3.6	28
3.8	14
4.0	6

A chemist has a 250-gram sample of a radioactive material. She records the amount remaining in the sample every day for a week and obtains the following data.
1. Draw a scatter plot of the data.
2. Which function best suits the data: exponential, linear, or quadratic?
3. Find the function of best fit and draw it through the scatter plot.
4. Predict the amount of material present after 10 days.

Day	Weight(grams)
0	250
1	208
2	158
3	130
4	102
5	80
6	65
7	50

The following table show the pregnancy rate (per 1000) for U.S. women aged 15 – 19 (source: US Census Bureau). Make a scatter plot with the rate as the dependent variable and the number of years since 1990 as the independent variable. Find which model fits the data best. Use this model to predict the rate of teen pregnancy in the year 2010.

Year	Rate of Pregnancy (per 1000)
1990	116.9
1991	115.3
1992	111.0
1993	108.0
1994	104.6
1995	99.6
1996	95.6
1997	91.4
1998	88.7
1999	85.7
2000	83.6
2001	79.5
2002	75.4

Mixed Review

Cam bought a bag containing 16 cups of flour. He needs $2 \frac{1}{2}$ cups for each loaf of bread. Write this as an equation in slope-intercept form. When will Cam run out of flour?
A basketball is shot from an initial height of 7 feet with an velocity of 10 ft/sec.
1. Write an equation to model this situation.
2. What is the maximum height the ball reaches?
3. What is the $y-$ intercept? What does it mean?
4. When will the ball hit the ground?
5. Using the discriminant, determine whether the ball will reach 11 feet. If so, how many times?

Graph $y=|x-2|+3$ . Identify the domain and range of the graph.
Solve $6 \ge -5(c+4)+10$ .
Is this relation a function? $\{(-6,5),(-5,-3),(-2,-1),(0,-3),(2,5)\}$ . If so, identify its domain and range.
Name and describe five problem-solving strategies you have learned so far in this chapter.

Problem-Solving Strategies: Choose a Function Model

As you learn more and more mathematical methods and skills, it is important to think about the purpose of mathematics and how it works as part of a bigger picture. Mathematics is used to solve problems that often arise from real-life situations. Mathematical modeling is a process by which we start with a real-life situation and arrive at a quantitative solution.

Modeling involves creating a set of mathematical equations that describes a situation, solving those equations, and using them to understand the real-life problem.

Often the model needs to be adjusted because it does not describe the situation as well as we wish.

A mathematical model can be used to gain understanding of a real-life situation by learning how the system works, which variables are important in the system, and how they are related to each other. Models can also be used to predict and forecast what a system will do in the future or for different values of a parameter. Lastly, a model can be used to estimate quantities that are difficult to evaluate exactly.

Mathematical models are like other types of models. The goal is not to produce an exact copy of the “real” object but rather to give a representation of some aspect of the real thing. The modeling process can be summarized as a flow chart:

Notice that the modeling process is very similar to the problem-solving format we have been using throughout this book. One of the most difficult parts of the modeling process is determining which function best describes a situation. We often find that the function we choose is not appropriate. Then we must choose a different one.

Consider an experiment regarding the elasticity of a spring.

Example: A spring is stretched as you attach more weight at its bottom. The following table shows the length of the spring in inches for different weights in ounces.

$& \text{Weight (oz)} && 0 && 2 && 4 && 6 && 8 && 10 && 12 && 14 && 16 && 18 && 20\ & \text{Length (in)} && 2 && 2.4 && 2.8 && 3.2 && 3.5 && 3.9 && 4.1 && 4.4 && 4.6 && 4.7 && 4.8$

a) Find the length of the spring as a function of the weight attached to it.

b) Find the length of the spring when you attach 5 ounces.

c) Find the length of the spring when you attach 19 ounces.

Solution: Begin by graphing the data to get a visual of what the model may look like.

This data clearly does not fit a linear equation. It has a distinct curve that will not be modeled well by a straight line.
Nor does this graph seem to fit a parabolic shape; thus it is not modeled by a quadratic equation.
The curve does not fit the exponential curves studied in Chapter 8.
By taking the third set of differences, the value is approximately equal. Use the methods learned in the previous lesson to find a cubic regression equation. Check by graphing to see if this model is a good fit.

Example: A golf ball is hit down a straight fairway. The following table shows the height of the ball with respect to time. The ball is hit at an angle of $70^\circ$ with the horizontal with a speed of 40 meters/sec.

$& \text{Time (sec)} && 0 && 0.5 && 1.0 && 1.5 && 2.0 && 2.5 && 3.0 && 3.5 && 4.0 && 4.5 && 5.0 && 5.5 && 6.0 && 6.5 && 7.0\ & \text{Height (meters)} && 0 && 17.2 && 31.5 && 42.9 && 51.6 && 57.7 && 61.2 && 62.3 && 61.0 && 57.2 && 51.0 && 42.6 && 31.9 && 19.0 && 4.1$

a) Find the height of the ball as a function of time.

b) Find the height of the ball when $t=2.4 \ \text{seconds}$ .

c) Find the height of the ball when $t=6.2 \ \text{seconds}$ .

Solution: Begin by graphing the data to visualize the model.

This data fits a parabolic curve quite well. We can therefore conclude the best model for this data is a quadratic equation.

To solve part a), use the graphing calculator to determine the quadratic regression line.

$y=-4.92 x^2+34.7 x+1.2$

b) The height of the ball when $t=2.4 \ seconds$ is:

$y=-4.92(2.4)^2+34.7(2.4)+1.2=56.1 \ meters$

c) The height of the ball when $t=6.2 \ seconds$ is

$y=-4.92(6.2)^2+34.7(6.2)+1.2=27.2 \ meters$

Practice Set

Sample explanations for some of the practice exercises below are available by viewing the following videos. Note that there is not always a match between the number of the practice exercise in the videos and the number of the practice exercise listed in the following exercise set. However, the practice exercise is the same in both.

CK-12 Basic Algebra: Identifying Quadratic Models (8:05)

video_image

Using y=x^2 to give a sense of why the change in the change of y (or the change in the slope) is constant (Click here to watch the video)

CK-12 Basic Algebra: Identifying Exponential Models (4:00)

video_image

Identifying Exponential Models (Click here to watch the video)

CK-12 Basic Algebra: Quadratic Regression (9:17)

video_image

Using a calculator to perform a quadratic regression (Click here to watch the video)

A thin cylinder is filled with water to a height of 50 centimeters. The cylinder has a hole at the bottom that is covered with a stopper. The stopper is released at time and allowed to empty. The following data shows the height of the water in the cylinder at different times.
$& \text{Time (sec)} && 0 && 2 && 4 && 6 && 8 && 10 && 12 && 14 && 16 && 18 && 20 && 22 && 24\ & \text{Height (cm)} && 50 && 42.5 && 35.7 && 29.5 && 23.8 && 18.8 && 14.3 && 10.5 && 7.2 && 4.6 && 2.5 && 1.1 && 0.2$
1. What seems to be the best model for this situation?
2. Find the linear regression line and determine the height of the water at 4.2 seconds.
3. Find a quadratic equation and determine the height of the water at 4.2 seconds.
4. Find a cubic regression line and determine the height of the water at 4.2 seconds.
5. Which of these seems to be the best fit?
6. Using the function of best fit, find the height of the water when $t=5 \ \text{seconds}$ .
7. Using the function of best fit, find the height of the water when $t=13 \ \text{seconds}$ .

A scientist counts 2,000 fish in a lake. The fish population increases at a rate of 1.5 fish per generation but the lake has space and food for only 2,000,000 fish. The following table gives the number of fish (in thousands) in each
generation.

$& \text{Generation} && 0 && 4 && 8 && 12 && 16 && 20 && 24 && 28\ & \text{Number (thousands)} && 2 && 15 && 75 && 343 && 1139 && 1864 && 1990 && 1999$
1. Which function seems to best fit the dataL linear, quadratic, or exponential?
2. Find the model for the function of best fit.
3. Find the number of fish as a function of generation.
4. Find the number of fish in generation 10.
5. Find the number of fish in generation 25.

Using the golf ball example, find the maximum height the ball reaches.
Using the golf ball example, evaluate the height of the ball at 5.2 seconds.

Mixed Review

Evaluate $2 \div 6 \cdot 5+3^2-11 \cdot 9^{\frac{1}{2}}$ .
60 shirts cost $812.00 to screen print. 115 shirts cost $1,126.00 to screen print. Assuming the relationship between the number of shirts and the total cost is linear, write an equation in point-slope
form.
1. What is the start-up cost (the cost to set up the screen)?
2. What is the slope? What does it represent?

Solve by graphing: $y=x^2+3x-1$ .
Simplify $\frac{\frac{6}{7}}{\frac{1}{2}}$ .
Newton’s Second Law states $F=m \cdot a$ . Rewrite this equation to solve for $m$ . Use it to determine the mass if the force is 300 Newtons and the acceleration is 70 m/sec.
The area of a square game board is 256 square inches. What is the length of one side?
Write as a percent: $\frac{3}{1000}$ .

Chapter 10 Review

Define each term.

Vertex
Standard form for a quadratic equation
Model
Discriminant

Graph each function. List the vertex (round to the nearest tenth, if possible) and the range of the function.

$y=x^2-6x+11$
$y=-4x^2+16x-19$
$y=-x^2-2x+1$
$y=\frac{1}{2} x^2+8x+6$
$y=x^2+4x$
$y=- \frac{1}{4} x^2+8x-4$
$y=(x+4)^2+3$
$y=-(x-3)^2-6$
$y=(x-2)^2+2$
$y=-(x+5)^2-1$

Rewrite in standard form.

$x-24=-5x$
$5+4a=a^2$
$-6-18a^2=-528$
$y=-(x+4)^2+2$

Solve each equation by graphing.

$x^2-8x+87=9$
$23x+x^2-104=4$
$13+26x=-x^2+11x$
$x^2-9x=119$
$-32+6x^2-4x=0$

Solve each equation by taking its square roots.

$x^2=225$
$x^2-2=79$
$x^2+100=200$
$8x^2-2=262$
$-6-4x^2=-65$
$703=7x^2+3$
$10+6x^2=184$
$2+6x^2=152$

Solve each equation by completing the square then taking its square roots.

$n^2-4n-3=9$
$h^2+10h+1=3$
$x^2+14x-22=10$
$t^2-10t=-9$

Determine the maximum/minimum point by completing the square.

$x^2-20x+28=-8$
$a^2+2-63=-5$
$x^2+6x-33=4$

Solve each equation by using the Quadratic Formula.

$4x^2-3x=45$
$-5x+11x^2=15$
$-3r=12r^2-3$
$2m^2+10m=8$
$7c^2+14c-28=-7$
$3w^2-15=-3w$

In 45-50, for each quadratic equation, determine:

(a) the discriminant

(b) the number of real solutions

$4x^2-4x+1=0$
$2x^2-x-3=0$
$-2x^2-x-1=-2$
$4x^2-8x+4=0$
$-5x^2+10x-5=0$
$4x^2+3x+6=0$
Explain the difference between $y=x^2+ 4$ and $y=-x^2+4$ .
Jorian wants to enclose his garden with fencing on all four sides. He has 225 feet of fencing. What dimensions would give him the largest area?
A ball is dropped off a cliff 70 meters high.
1. Using Newton’s equation, model this situation.
2. What is the leading coefficient? What does this value tell you about the shape of the parabola?
3. What is the maximum height of the ball?
4. Where is the ball after 0.65 seconds?
5. When will the ball reach the ground?

The following table shows the number of hours spent per person playing video games for various years in the United States.
$& x && 1995 && 1996 && 1997 && 1998 && 1999 && 2000\ & y && 24 && 25 && 37 && 43 && 61 && 70$
1. What seems to be the best function for this data?
2. Find the best fit function.
3. Using your equation, predict the number of hours someone will spend playing video games in 2012.
4. Does this value seem possible? Explain your thoughts.

The table shows the amount of money spent (in billions of dollars) in the U.S. on books for various
years.

$& x && 1990 && 1991 && 1992 && 1993 && 1994 && 1995 && 1996 && 1997 && 1998\ & y && 16.5 && 16.9 && 17.7 && 18.8 && 20.8 && 23.1 && 24.9 && 26.3 && 28.2$
1. Find a linear model for this data. Use it to predict the dollar amount spent in 2008.
2. Find a quadratic model for this data. Use it to predict the dollar amount spent in 2008.
3. Which model seems more accurate? Use the best model to predict the dollar amount spent in 2012.
4. What could happen to change this value?

The data below shows the number of U.S. hospitals for various
years.

$& x && 1960 && 1965 && 1970 && 1980 && 1985 && 1990 && 1995 && 2000\ & y && 6876 && 7123 && 7123 && 6965 && 6872 && 6649 && 6291 && 5810$
1. Find a quadratic regression line to fit this data.
2. Use the model to determine the maximum number of hospitals.
3. In which year was this?
4. In what years were there approximately 7,000 hospitals?
5. What seems to be the trend with this data?

A pendulum’s distance is measured and recorded in the following
table.

$& swing && 1 && 2 && 3 && 4 && 5 && 6\ & length && 25 && 16.25 && 10.563 && 6.866 && 4.463 && 2.901$
1. What seems to be the best model for this data?
2. Find a quadratic regression line to fit this data. Approximate the length of the seventh swing.
3. Find an exponential regression line to fit this data. Approximate the length of the seventh swing.

Chapter 10 Test

True or false? The vertex determines the domain of the quadratic function.
Suppose the leading coefficient $a=-\frac{1}{3}$ . What can you conclude about the shape of the parabola?
Find the discriminant of the equation and determine the number of real solutions: $0=-2x^2+3x-2$ .
A ball is thrown upward from a height of four feet with an initial velocity of 45 feet/second.
1. Using Newton’s law, write the equation to model this situation.
2. What is the maximum height of the ball?
3. When will the ball reach 10 feet?
4. Will the ball ever reach 36.7 feet?
5. When will the ball hit the ground?

In 5–9, solve the equation using any method.

$2x^2=2x+40$
$11j^2=j+24$
$g^2=1$
$11r^2-5=-178$
$x^2+8x-65=-8$
What is the vertex of $y=-(x-6)^2+5$ ? Does the parabola open up or down? Is the vertex a maximum or a minimum?
Graph $y=(x+2)^2-3$ .
Evaluate the discriminant. How many real solutions do the quadratic equation have? $-5x^2-6x=1$
Suppose $D=-14$ . What can you conclude about the solutions to the quadratic equation?
Rewrite in standard form: $y-7=-2(x+1)^2$ .
Graph and determine the function's range and vertex: $y=-x^2+2x-2$ .
Graph and determine the function's range and $y-$ intercept: $y=\frac{1}{2} x^2+4x+5$ .
The following information was taken from USA Today regarding the number of cancer deaths for various years.

Year	Number of Deaths Per 100,000 men
1980	205.3
1985	212.6
1989	217.6
1993	212.1
1997	201.9

Cancer Deaths of Men (
Source: USA Today
)
1. Find a linear regression line to fit this data. Use it to predict the number of male deaths caused by cancer in 1999.
2. Find a linear regression line to fit this data. Use it to predict the number of male deaths caused by cancer in 1999.
3. Find an exponential regression line to fit this data. to predict the number of male deaths caused by cancer in 1999.
4. Which seems to be the best fit for this data?

Texas Instruments Resources

In the CK-12 Texas Instruments Algebra I FlexBook, there are graphing calculator activities designed to supplement the objectives for some of the lessons in this chapter. See http://www.ck12.org/flexr/chapter/9620.