4
Segmenting Customers and Markets – Intuition Behind Clustering, Classification, and Language Analysis
As always, there’s good news and there’s bad news. The bad news is, we seem incapable of solving our more pressing or persistent problems. The good news is, we’re getting closer to building a machine that might do it for us.
– Jim Vibert, “If Artificial Intelligence Is the Answer, What’s the Question?,” The ChronicleHerald, January 1, 2018
Intuition Behind Clustering and Classification Algorithms
Let’s start from scratch. What’s the most basic thing intelligence is good for? Telling things apart, that’s what. If we have a bunch of data and we want to make sense out of it, the simplest thing we can do is make distinctions: put some of the stuff over here, and other stuff over there. More formally, we want to “partition” a collection of data items into groups or classes or boxes or buckets or bins or subsets or categories or whatever word you want to use to represent a top-level fundamental division.
That’s easy enough, but if we want to perform well at this we need some way of measuring how well we have done it. The basic concept here is called “metric” or “distance function.” It means that, given two things, you have a number that represents how close together or far apart they are. We will denote the distance between two data points a and b by the notation d(a,b). This is a mathematical function that, in order to qualify as a metric, has to satisfy the following four properties:
- d(a,a) = 0 (everything is zero distance away from itself – obvious, but if you don’t remember to say this, dumb computers will get into trouble)
- d(a,b) >= 0 (distances are always positive or zero)
- d(a,b) = d(b,a) (the distance between two things doesn’t depend on which direction you are going – not true for traffic, but good enough for what we’re doing)
- d(a,b) + d(b,c) >= d(a,c), which is called the “triangle inequality”
The triangle inequality is what makes the math work – it says that getting from a to c can’t be any harder than getting from a to b and then getting from b to c (and it might be easier if there is a different way to get there that doesn’t pass through b).
So what we want is for all the things we group together to be “close.” In other words, to have a small distance between each pair of them, and for the things we put in different groups to be “distant.”
This gives us a “goodness of fit” measure. A partition of data into subgroups is better than another partition into the same number of subgroups, if the average distance between things in the same group is smaller.
For example, politicians think differently from other people. If we are drawing a map, or subdividing a territory into townships or counties or whatever, we will think about the distance between two people as how far away their houses are from each other, so we will draw circles around dense concentrations of houses and call them towns, and so on.
But to a politician, people who vote for the same party are similar and people who vote for different parties are far apart, so they like to draw district lines for electoral purposes in a way that groups together voters with similar views, even if the district ends up being shaped like a salamander or something even more bizarre. This process is called “gerrymandering,” because the first guy to do it was named Elbridge Gerry, who, although he signed the Declaration of Independence and was vice president, is probably embarrassed to be remembered mostly for cutting up the map of Massachusetts into weird shapes when he was governor so that his party would win more seats.
Whether a partition is good or bad depends on how you measure how far apart things are.
If your data is represented by a list of numbers (how many? “n” of them), then there are three common distance functions that are used:
- Euclidean distance – how far apart the points are in space. Of course, the “space” might have n dimensions rather than two or three and be hard for sane humans to visualize, but the formula of Pythagoras still works: the Euclidean distance between the points (a1, a2, a3, . . . , a_n) and (b1, b2, . . . , b_n) is given by the following equation:
sqrt((a1 – b1)^2 + (a2 – b2)^2 + (a3 – b3)^2 + . . . + (a_n – b_n)^2)
- Taxicab distance – if the “dimensions” are unrelated attributes so that the concept of “diagonal” is silly, for example in midtown Manhattan where “vacant lot” is a mythological thing, just add up the distance in each dimension as follows:
|a1 – b1| + |a2 – b2| + . . . + |a_n – b_n|
- What do those vertical bars mean? That’s called the “absolute value” function, and it just means to “erase minus signs,” so that the distance from 14th Street to 23rd Street is 9 blocks and not negative 9 blocks. The taxi’s meter doesn’t run backward when the cab turns around.
- Max distance – focuses on the largest of the individual distances for each dimension.
Okay, so obviously we can just look at all possible ways to divide up the data, measure the average distances between things, and pick the best one, right?
Well, maybe you can, if you are willing to run your program for a few trillion years, but “all possible ways” is a big number of things to try. So there are various tricks to cut down the amount of work we have to do but still come close enough to the best answer.
Also, we don’t just want to divide things up into blobs that don’t make any sense, and we may already know something about the data that we want to take advantage of. For example, if we are drawing lines for Congressional districts, these things called “towns” already exist, and even if they’re not all equal in population so we have to split them up a little, we might want to still make the districts match up with existing boundaries wherever possible.
This brings us to the distinction we’ll see over and over in this book, between “supervised” and “unsupervised” learning. In this context, unsupervised learning means to just minimize the average distance, and is called “clustering” because the groups it finds are things that are closer together.
Supervised learning is called “classification” because we start with a pre-existing list of categories and things we know belong to those categories that can be used for training data, and then try to see which category fits each data point best.
Clustering is simpler, so we’ll look at that first. Assume you have a distance function you like, and you know how many different groups you want to divide the data into (obviously if every point is in its own group, your total average distance is 0, but that’s not a very helpful way to look at things). Then “all possible ways” to cluster things is a lot of ways. For example, if you have 100 unique things and you want to divide them into 10 groups, the number of ways to do this is about (10^100)/(10!), which is more than the number of atoms in the universe.
Technically, it’s possible that there is a faster way to find the best partition than looking at all the ways, but probably not very much faster, because this problem is known to be “NP-complete,” which is a fancy computer science word meaning “we can’t prove it’s hard but we think it’s really really hard.” However, we can find a pretty good solution, though not necessarily the best, by using a method called the “k centers algorithm.”
What does this approximate solution method do? We decide that every one of our clusters (or blobs or categories or whatever) will have a specific point called the “center,” and any data point will belong to whichever cluster whose center it is closest to. That turns out to be easier to calculate, because after you start with a bunch of centers and calculate the goodness of fit, you push them around a little bit and see which directions improve things, and so on until you can’t improve things any more.
If you were paying attention, the previous sentence will remind you of the tool AlphaZero used in Chapter 3: gradient descent!
Here is a more detailed, five-step outline:
- k-centers algorithm pseudo code (Euclidean distance in this example)
- Start with k random points in n-dimensional space – need n * k parameters.
- Calculate goodness of fit = sum of distances.
- For each of the nk directions, perturb and recalculate to get directional derivative.
- Move along path of steepest descent until it stops decreasing.
- Repeat.
However, this method has the problem that it sometimes gets stuck at a “local optimum” where you can’t improve by taking small steps, even though there is a better place further away. So you try again with different random start points and after a bunch of these pick the winner!
Doing this perfectly is a hard problem, but doing it approximately is usually good enough and there are several algorithms that have performed well. Much more than you want to know can be found here:
https://cran.r-project.org/web/views/Cluster.html
For each center, the collection of all places that are closer to it than to any other center is called its “Voronoi cell.” If the centers are equally spaced horizontal and vertical grid points on a plane, the cells look like squares, but as bees have discovered, or rather as evolution has discovered for them, if you stagger the centers so that the cells are shaped like hexagons, you can reduce the average distance and economize on beeswax.
If they’re not equally spaced, some cells will be bigger than others, but that’s okay, we don’t have to have all the cells the same size – if the underlying data is clumpy, small and large cells might make sense. On average, though, the interior cells will still be hexagons of some kind if the space of data points is two-dimensional (shown in Figure 4.1) – this is a mathematical theorem that follows from Euler’s formula “V – E + F = 2.”

Figure 4.1 Two-dimensional Voronoi cells.
In this two-dimensional picture, you can see that the interior boundary lines are segments of the perpendicular bisectors of the segments connecting the centers.
In three dimensions, they will look sort of like squashed spheres if the centers are roughly equally spaced (see Figure 4.2).
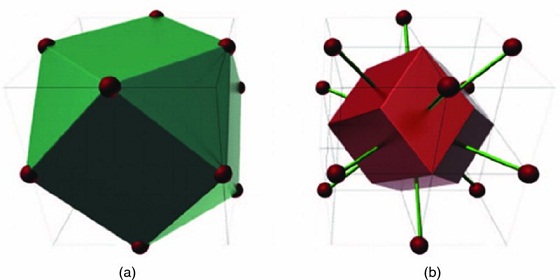
Figure 4.2 Three-dimensional Voronoi cells.
Classification is quite different from clustering, because you are imposing a pre-existing set of groups on new data, rather than letting the data tell you what the groups should be.
If you want, you can use a similar technique and make Voronoi cells – for example, in an election, you could say that all the schools in the city will be the polling places, and the voting precincts will be defined so that everyone has to vote at whichever school they are closest to. Unlike with clustering, this minimizes the average distance of voters to polling places, rather than the average distance of voters to each other, but it works pretty similarly.
However, you might know a lot more about what you want the classes to be, and you might also not be sure how to best measure the distance between things, you just want them to be in the right class. So you can use deep learning AI systems to do this in a more generalized way – let the system come up with its own distance function that is “tuned” on the training data, so that the classification scheme performs close to correctly on the training data. Because of anomalies and outliers, you will have a tradeoff between how good the performance is and how complicated the computation is.
In between a simple distance minimization and a general learning scheme are rule-based systems that incorporate expert knowledge by using decision trees (every flowchart meme you’ve ever seen is implementing a decision tree). Rule-based systems can be considered a special case of “Bayesian classifiers” that work with probabilities. In a decision tree, all probabilities are 0 or 1, but a Bayesian classification algorithm starts with a probability distribution and then adjusts the probabilities based on the same kind of criteria; at the end, each data item has a probability of being in each class that is hopefully more concentrated than the starting probability distribution was.
A simple example of a Bayesian classifier: You want to classify adults into “male” and “female” and start with a 50–50 probability distribution, then add data on how tall they are. Someone who is 5 feet tall has the probability of being female adjusted upward and the probability of being male adjusted downward, but if the person’s first name is Richard, then there is going to be an even larger adjustment toward “male,” because most adults named Richard who are 5 feet tall are men.
Bayes’ theorem makes exact how you update on evidence. It is represented by the following formula:
P(A|B) = P(B|A)P(A)/P(B)
Here P means “probability of” and | means “given the information.”
Thus: Suppose 52% of adults are women, 5% of women are 5 feet tall, and 1% of men are 5 feet tall. So the probability that a random adult is 5 feet tall is (5% × 52% + 1% × 48%) = 3.08%. Let A = “Female” and B = “5 feet tall.” Then, given that an adult is 5 feet tall, the probability that the person is a woman is
(5%)(52%)/3.08% = 2.6%/3.08% = 65/77 = 84.4%
To make this more intuitive: Start with 10,000 people and assume they are a representative group; 5200 are women and 4800 are men. Since 5% of 5200 is 260 and 1% of 4800 is 48, there are 260 women and 48 men who are 5 feet tall, so if you know someone is 5 feet tall their chance of being a woman is 260/(260 + 48) = 260/308 = 65/77 = 84.4%.
It is very easy for people to mess this kind of calculation up, even very smart people like doctors. A typical example: Let’s say 1% of people in a certain population have a certain cancer. A test is 90% accurate – if you have the cancer it is positive 90% of the time, and if you don’t have the cancer it is positive 10% of the time. You take the test and the result is positive. How worried should you be?
Well, in a population of 1000 people, there will be 10 with cancer of whom 9 are correctly diagnosed and 1 who is incorrectly found to be healthy, and there will be 990 without cancer of whom 99 will be told their test was positive. So there will be 108 positive tests – 99 false positives and only 9 true positives. Your chances of having cancer have increased from 1 in 100 to 1 in 12 – scary but not terrifying! This is why they always do follow-up tests.
85% of all customer interactions won’t require human customer service reps by the end of this decade.
– “Gartner Customer 360 Summit 2011”
Intuition Behind Forecasting and Prediction Algorithms
A fundamental polarity in understanding systems is static versus dynamic. “Dynamic” means in motion, and changing over time. “Static” means stationary, and not changing over time.
We have learned about classification and clustering, which are static ways of looking at data. But very often, we will care about how data changes over time, because we want to know something about the future. You can know about the past by remembering stuff, and you can know about the present by looking around, but we don’t know how to time travel. So we need to be smarter about figuring out what the future holds, the point being not simply to know what it will be like, but to prepare for it.
We have two words for trying to figure out what the future will be like, which are pretty similar, but it’s useful to make a distinction between them. “Forecasting” is when we attempt to describe the future based on historical data. “Prediction,” on the other hand, is a more general process, which includes forecasting as a special case. Prediction models the future based not only on past data but also on additional understandings and insights we might have that aren’t directly represented by past data.
A key concept here is “model.” In science, a model is a representation of features we think are important about some phenomenon, usually involving structured data representing those features, and rules about how that data is expected to change over time, given various inputs. Models are oversimplifications of reality that we hope still take into account enough of what is important to tell us what we want to know.
When we are forecasting, the numbers we care about have some history, and in the simplest case the history is all we have. Even in this case, we have mathematical tools to help. The data is in the form of a time series, which are sequences of values corresponding to particular points or periods in time. Common examples include prices measured daily, temperature measured hourly, population measured annually. The time interval matters – weather fluctuates from hour to hour and we may care about this, but we have to average daily temperatures to take out these fluctuations in order to understand the seasons, and we have to average annual temperatures to take out seasonal fluctuations in order to understand long-term climate trends.
Normally, a time series will be expected to have some periodic components (such as hourly temperature fluctuations within a day, or seasonal fluctuations within a year), as well as some trends, which represent a directional movement. There may also be some degree of random change which, if it is not represented in the model, is regarded as “noise.”
For centuries, mathematical tools have been used to identify the following simple features:
- Fourier analysis to identify periodicities.
This involves expressing a function in terms of basic functions called “sine waves,” with varying frequencies and heights and shifts.
Figure 4.3 shows a randomly picked location from the online climate database maintained by the National Centers for Environmental Information, a division of the Department of Commerce.
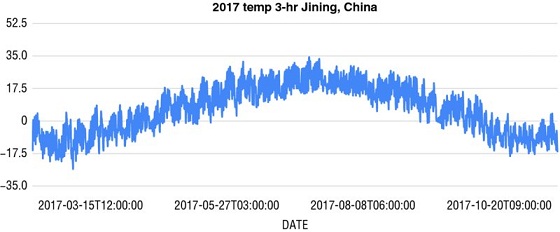
Figure 4.3 A graph of temperature taken every three hours at a China weather station in 2017.
It shows the temperature taken every three hours at a weather station in China for the year 2017: an annual periodicity is apparent, and when you look at the closeup of the data from the first few weeks (Figure 4.4), a daily periodicity is also.
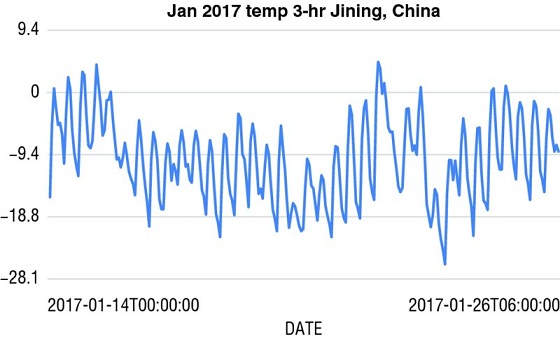
Figure 4.4 Temperatures for January 2017.
Applying Fourier analysis to the data set would quickly find these regularities: the first term would be a peak in July at 20 degrees Celsius and a trough in January at –10 degrees Celsius representing average daily temperature over the year, and the next most important term would have a 24-hour periodicity and vary between about +8 and –8 representing the daytime and nighttime variation above and below the average temperature, peaking at about 0600 Greenwich Mean Time (midafternoon in Jining).
- Regression models to identify linear relationships and trends (possibly after some kind of algebraic transformation: prices change by multiplicative factors so logarithms can be used to change a geometrically changing function into a linearly changing one).
The example of this model that everyone has seen is finding the best-fit straight line through a set of points. If you have points (x1, y1), (x2, y2), . . . , (x_n, y_n) in the coordinate plane, where x is the independent variable and y is the dependent variable, you want the “best” line with the equation y = ax + b. What is “best”? Well, your line will pass through the points (x1, ax1 + b), (x2, ax2 + b), . . . , (x_n, ax_n + b) and you will have a sequence of “errors” representing the vertical distance of the actual data points from the line:
e1 = y1– (ax1 + b), e2 = y2 – (ax2 + b), . . .
The “best” line in a “least-squares regression” is the one which minimizes the sum of the squares of the errors: e1^2 + e2^2 + . . .
We find this by calculus.
Then the slope of the regression line, a, is given by
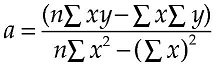
(the Σ symbol means “sum of,” you add up the value for all the points), and the intercept of the regression line, b, is given by
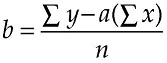
- Stochastic models to measure and characterize noise, random fluctuation, and error.
An example of a stochastic model would be a “random walk” – if you imagine tossing a coin 200 times, and moving up or down 1 each time you get heads or tails respectively, you get something that looks like Figure 4.5 (This data was created using a random number generator).
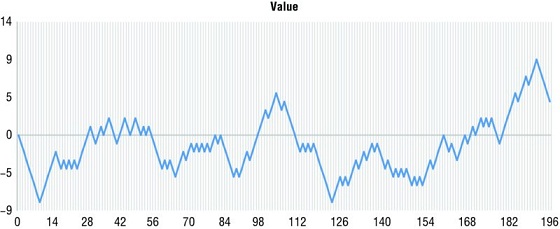
Figure 4.5 A stochastic model of tossing a coin and moving according to the results.
Figure 4.6 represents another which was a biased coin, 40% heads and 60% tails.
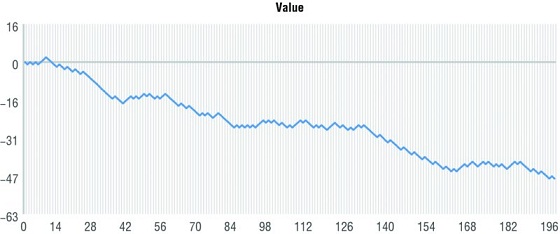
Figure 4.6 Using a biased coin of 40% heads and 60% tails.
But patterns in time-series data can be more complicated than can be easily captured by these classical tools.
There is a whole sector of the financial industry devoted to “technical analysis,” which looks only at price data over time and ignores the underlying properties of the securities, on the assumption that these underlying properties are already taken into account in the prices, and the changes in the prices and what they indicate about investor psychology and attitudes are what need to be understood.
The patterns they seek can be much more complicated than linear, periodic, and stochastic components; some can be represented by geometric features of the graphs of prices over time, while others are more subtle but might be represented implicitly by neural network models trained using deep learning techniques.
Weather can also be “forecasted” simply by looking at past data almanacs do okay using long-term historical averages taking seasonality into account, while “trends” in temperature or other variables like precipitation and pressure and wind velocity can be extrapolated in simple ways.
But the development of scientific weather models that use physics to directly (but probabilistically) calculate future values of these variables go beyond forecasting to prediction, because the models use more data than the time series of past values at a particular place to estimate future values: they take data at other places and factor in geographical data to do calculations based on established mathematical relationships.
In short: for AI purposes, forecasting can be seen as supervised learning where no assumptions are made beyond the historical sequences of past data; and that forecasting is presumed to contain sufficient information to allow estimation of future data based on patterns discovered in the past data.
Scientists and practitioners (on Wall Street the word “scientist” might be a bit too flattering) came up with simple tools for this type of forecasting centuries ago, and continue to develop more sophisticated pattern recognition tools, some using deep learning techniques.
Prediction can be seen as supervised learning where we have additional quantities other than the ones whose values we are trying to predict, representing the state of the system and inputs to the system. We have models expressed in terms of math which say how the variables relate to each other and change over time (differential equations are the major kind of time-dependent model). These models have “parameters” that can be tuned based on data, but impose a structure that isn’t present in the raw time series data.
When you don’t have a model, but you do have data other than time series data, then it gets trickier! You are contributing your judgment of which other types of data are relevant, but you want the system to be smart enough to make the best use of them. The theoretical way to do this uses the scientific principle called Occam’s razor (“the simplest explanation is the best”) and the computer science concept known as Kolmogorov complexity (“data is as complex as the shortest program which produces it”) and says “whatever the shortest program is that produces the output data given the input data is what you should use on new input data.” As long as you have enough data to show the key patterns, this works, in theory. In practice it’s impossible to tell what the shortest working program is because it might take a really long time to finish. So you have to use other techniques, like using deep learning on lots of training data, but what you get will be less understandable.
People worry that computers will get too smart and take over the world, but the real problem is that they’re too stupid and they’ve already taken over the world.
– Pedro Domingos, The Master Algorithm (Basic Books, 2015)
Intuition Behind Natural Language Processing Algorithms and Word2Vec
We’ve talked about numerical data and algorithms and how to make sense out of them. But most of the data we actually deal with is in the form of words, and to have computers be able to do things that involve interacting with people, we have to get them to understand what the words mean.
This is a very hard problem.
In fact, it is what is jokingly called an “AI-complete” problem, meaning if we could do it, we could do anything else we wanted to, because we could just tell the computer, in English, what we wanted.
But that involves building a machine that can pass the Turing Test: In other words, fool people who talk with it via texting into thinking that it is a real person for at least a minute. Or maybe we just want the machine to understand words in a limited enough way to be useful, even if they can’t be friends with us. Google’s most recent demo is scarily close.
This is also hard. But progress has been made. Here are four major things we want computers to be able to do with words, in increasing order of difficulty:
- Auto-complete when someone types (saves us time, despite the occasional annoyance of incorrect auto-complete guesses).
- Find something we are looking for (saves us even more time).
- Answer questions (makes us smarter, or solves our problems).
- Translate text into a different language (helps expand our world to be able to communicate in any language).
Why is this so hard? Because language is one of the most complicated things our brain does (maybe even the most complicated, except for whatever your job is). It is so hard that you have to be a little kid, in fact, to learn it quickly!
Not kidding here. Remember the fundamental principle of AI difficulty: “the hard stuff is easy, but the easy stuff is hard.” This seems insane until you look at it the right way, and then it is obvious: the things that we learn in school, or as adults, are things we are taught, and which we already have words to understand them with, so we can teach it to a computer too, theoretically.
But things we learned as infants, or even as instinct that evolution taught our species (visual processing of light into images is a big example), are things that we know, but don’t know how we know them.
It’s been understood since ancient times that adults are smarter than kids, at least in many respects. However, one thing kids can do much better than adults (aside from playing video games) is learning new languages. This is because a child’s brain is very flexible, somewhat like a clay sculpture that hasn’t dried yet.
Languages can be quite different from each other. As we get older, the brain gets less flexible and a lot of the switches that are never altered get stuck in place (kinda like when you don’t do anything with the pipes under your sink for a few years and then when you have to fix them the valve has gotten stuck because you didn’t wiggle it every now and then).
What’s really cool is that if you learn more than one language while you are very young, the switches corresponding to the different languages stay loose, and it is easier for you to learn additional languages, even as an adult.
Okay. So teachers figured out lots and lots and lots of rules that supposedly explained what is really going on, but the rules have exceptions, and the exceptions have exceptions, and that’s just the spoken part.
If the language has been written down for a long time there’s all sorts of additional trouble related to the fact that the language evolved while the old texts didn’t, which is why English spelling doesn’t make much sense, and why a “spelling bee” is even a thing (which many non-English speakers consider a ridiculous thing to make a contest out of).
A good example of the funky nature of English is that the previous sentence can actually be constructed and understood. That’s because it’s a mashup of old German and old French, and Latin, and a bunch of other local things the natives of Britain spoke before getting stomped by the Romans and the Anglos and the Saxons and the Danes, and finally the French.
The last time the English got stomped was 1066, but then they got clever and adventurous and (most importantly) nautical. They sailed all around the world trading and colonizing, and because their language was already flexible enough because of the previous stompings, they borrowed and borrowed from dozens of other languages around the world.
English swallowed everything, and as a result it became the default language that everyone used to communicate with the rest of the world because there were people who knew English everywhere, and if you needed to communicate with someone with whom you didn’t share a language, the easiest language to find translators for was English.
All human languages have some things in common. The most fundamental distinction is between syntax (the sequences of symbols that are spoken or written, and the vocabulary of which sequences are legal words, and the structure of grammar that governs how the words relate to each other) and semantics (what these utterances actually mean). What we care about is meaning, but what we have to work with is syntax: vocabulary and grammar.
The problem is that stuff that makes sense syntactically can be meaningless semantically. For example, grammar says that “Adjective adjective noun verb adverb” is a valid sentence structure: “Little brown foxes jump quickly” makes sense, right? But how about “colorless green ideas sleep furiously”? Same structure, but what does it mean?
And even the syntactic structure can be impossible to interpret without semantic cues. For example, Buffalo buffalo buffalo buffalo buffalo.
You heard that right. The word “Buffalo” is a place name of a city in New York that can serve as an adjective, and a noun describing the animal also known as bison, and a verb meaning “to thwart.” Let’s use all-caps to make it harder. There are lots of good ways to parse
BUFFALO BUFFALO BUFFALO BUFFALO BUFFALO.
For example: New York bison thwart New York bison.
Or, Bison bison thwart thwart New York (that is, buffaloes who are buffaloed by other buffaloes themselves buffalo the city of Buffalo).
With a string of six or seven “buffaloes” the number of possibilities explodes.
We’ll skip over all the relatively ineffective efforts that attempted to use an advanced understanding of syntax and a complicated model of the world to provide semantics, and get to the point: it turned out that what worked best was getting lots and lots and lots of data and being simple about it. How did our four applications fare?
First, “auto-complete” got good simply by keeping a big dictionary of everything people ever typed and seeing what letters and words and sequences of words tended to follow what other letters or words or sequences of words. Meaning was superfluous!
For example, you can use Google to find the frequency of various word sequences, or n-grams, and this gets particularly interesting when you look at it as a time series. Check out the Google Ngram Viewer in Figure 4.7.
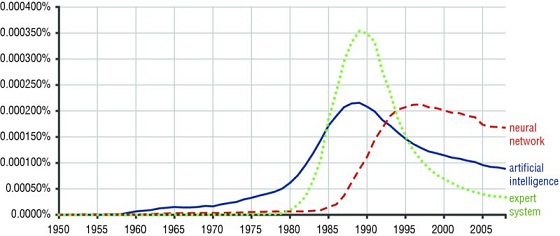
Figure 4.7 The Google Ngram Viewer shows the frequency of word sequences.
Second, search applications didn’t have to understand the meaning of the texts directly – it turned out to be very useful already just to see what things were connected or linked to what other things. This allowed the development of a metric that ranked the relevance of web pages to each other.
As it turns out, that was enough, because even though the first bunch of search results you got might not be exactly what you were looking for, there would be some stuff that was getting closer to what you wanted, and you could then use that to refine your search with words or phrases that you hadn’t previously tried, but which you got reminded of by the relatively good results you did get. The bigger the internet got, the better search engines got at estimating relevance.
The folks at Google went even further and developed a tool called “Word2Vec,” which looked not only at which pages linked where, but at which words in the relevant texts were used in close proximity to which other words. This way, they could learn about contexts.
A simple two-layer neural network is used to give every word a “vector” score, which represents its position in a multidimensional context space. Although people could examine the network and guess things like the reason the words “Ronaldo” and “Messi” are close together is they’re the two biggest soccer stars, so that if you search for one you can also be given results about the other, human supervision was not involved.
The network figured it out from being trained on 20 million words of text. Each dimension might have some semantic interpretation that we could come up with pretty good labels for, but we wouldn’t have chosen the particular set of dimensions and weights that the algorithm did.
There are various choices that can be made when implementing Word2Vec: context could be represented by a “bag of words” where order doesn’t matter, or by weighting nearby words more heavily, the number of dimensions could be 100 or 1000, the number of surrounding words in the context window might be 5 or 10, high and low frequency words can be handled differently in the training set, and so on.
But the philosophy remains the same: A word is characterized by the company it keeps. Word2Vec has been shown to capture both syntactic and semantic relationships better than previous methods which were more “supervised.”
Here are some tips from Google on how to use their tool (they are freely available at: https://code.google.com/archive/p/word2vec)
The word2vec tool takes a text corpus as input and produces the word vectors as output. It first constructs a vocabulary from the training text data and then learns vector representation of words. The resulting word vector file can be used as features in many natural language processing and machine learning applications.
A simple way to investigate the learned representations is to find the closest words for a user-specified word. The distance tool serves that purpose. For example, if you enter ‘france’, distance will display the most similar words and their distances to ‘france’, which should look like:
Word Cosine distance
| 1 | spain | 0.678515 |
| 2 | belgium | 0.665923 |
| 3 | netherlands | 0.652428 |
| 4 | italy | 0.633130 |
| 5 | switzerland | 0.622323 |
| 6 | luxembourg | 0.610033 |
| 7 | portugal | 0.577154 |
| 8 | russia | 0.571507 |
| 9 | germany | 0.563291 |
| 10 | catalonia | 0.534176 |
There are two main learning algorithms in word2vec: continuous bag-of-words and continuous skip-gram. The switch -cbow allows the user to pick one of these learning algorithms. Both algorithms learn the representation of a word that is useful for prediction of other words in the sentence. These algorithms are described in detail in [1,2].
Interesting properties of the word vectors
It was recently shown that the word vectors capture many linguistic regularities, for example vector operations vector(‘Paris’) vector(‘France’) + vector(‘Italy’) results in a vector that is very close to vector(‘Rome’), and vector(‘king’) – vector(‘man’) + vector(‘woman’) is close to vector(‘queen’) [3, 1]. You can try out a simple demo by running demo-analogy.sh.
To observe strong regularities in the word vector space, it is needed to train the models on large data set, with sufficient vector dimensionality as shown in [1]. Using the word2vec tool, it is possible to train models on huge data sets (up to hundreds of billions of words).
From words to phrases and beyond
In certain applications, it is useful to have vector representation of larger pieces of text. For example, it is desirable to have only one vector for representing ‘san francisco’. This can be achieved by pre-processing the training data set to form the phrases using the word2phrase tool, as is shown in the example script ./demo-phrases.sh. The example output with the closest tokens to ‘san_francisco’ looks like:
Word Cosine distance
| 1 | los_angeles | 0.666175 |
| 2 | golden_gate | 0.571522 |
| 3 | oakland | 0.557521 |
| 4 | california | 0.554623 |
| 5 | san_diego | 0.534939 |
| 6 | pasadena | 0.519115 |
| 7 | seattle | 0.512098 |
| 8 | taiko | 0.507570 |
| 9 | houston | 0.499762 |
| 10 | chicago_illinois | 0.491598 |
Third, answering questions was harder than search because questions had more structure than search strings. But with the development of neural networks that were trained using massive databases of almost everything people had ever put on the internet, the most common kinds of questions people asked came to be understood implicitly, without any need for an explicit model of the world or very sophisticated grammatical analysis.
Nuances could be missed leading to silly mistakes, but the results were “good enough” for most uses. When combining this with massive databases of knowledge, IBM’s Watson program was able to defeat Jeopardy’s all-time champions, and annoy Alex Trebek.
Fourth, automatic translation is the biggie, and the same techniques described above work pretty well for simple dialogues, but the more complex the subject matter and the writing, the weirder the translations get.
It remains an open question just how accurately difficult material can be processed, but people familiar with the quirks of their smartphone translator programs can usually communicate effectively with people they don’t share a language with by patient retrying. One useful trick is to go back and forth until you find something that translates reversibly so that both directions think the two texts are equivalent. If the text in your language is close enough, then it’s safe to assume the text of the other language won’t be embarrassingly bad.
The best work here is done in China, because Chinese is a very hard language to translate into English, and China has a great need for translation services, and China has lots of really smart computer people. Chinese could have been a contender for the default language, because it has a simple and flexible grammatical structure, but for a couple of fatal flaws.
For instance, the use of tones is an element so foreign to Western languages that even polyglots can find that the switch got stuck and they can’t easily handle tones. What’s more, the refusal until recently to create a Roman alphabetic representation of Chinese made the language much harder for Westerners to learn. Even the Chinese have a hard time remembering all the characters!
Getting information off the Internet is like taking a drink from a firehose.
– Mitchell Kapor, quoted in “Information Quotes,” The Data Governance Institute, www.datagovernance.com
Intuition Behind Data and Normalization Methods
Brains are squishy and computers are hard and pointy, but the reason we can get computers to do useful thinking work is that there is something called “language” which is the in-between thing that we both can use.
Unfortunately, even though human children can be tortured in classrooms until they are capable of translating the vocal utterances that they learn effortlessly as toddlers into symbols that can be read and written and typed into a computer keyboard, there are still extremely annoying differences between natural languages and computer languages, which even relatively smart human adults struggle with. Not everyone can program, because it requires an artificial, fussy, and incredibly unforgiving type of language use that just isn’t natural for most people.
However, there are enough people who can program that tools have been created which allow ordinary folks to do useful things with computers, and even though many of those programmers are nerds, enough of them have good social skills and understanding of how the rest of us think that some of these tools are pretty awesome.
A good example is the “spreadsheet.” The most common of these is Microsoft Excel, but they go back a lot further than that. In fact, they go back as far as Dan Bricklin and Bob Frankston, who created VisiCalc, the first “killer app” for PCs, in 1978. In a way, they go back even further, to Edward F. (Ted) Codd, who invented the idea of a relational database at IBM in 1969.
The basic concept here is a table, which consists of rows and columns. Traditionally, we think of each row of the table as corresponding to some kind of item, and each column of the table as corresponding to an attribute or feature of that item, but it’s really more flexible than that. A spreadsheet consists of a large grid of rows and columns, within which are formulas linking cells (specified by rows and columns) to other cells, and which may contain rectangular subsets defined by intervals of rows and columns that may be regarded as tables. There is also the concept of “workbook,” which contains several spreadsheets that can be linked to each other by formulas, yielding what is technically a 3-D structure, but the third dimension is not really essential.
Even before computers, people organized data into tables, but the magical thing about spreadsheets is that you can use them to automatically link tables together. This means that if you change some important piece of information in the right place, it automatically changes everywhere else it needs to, if you have set things up correctly.
Here’s a simple example. Every postal address in the United States has a five-digit zip code, which corresponds to a “post office,” and which also has a town name and a state associated with it. Suppose your company has a big list of customers with names and addresses. You could store the “City,” “State,” and “ZIP” categories independently for each customer, but if a town changes its name, you have to go in and change the “City” field for each customer in that town.
If you have a separate table that stores zip codes and the city and state for each one, then you only have to change this in one place, and a table you create in the spreadsheet can have the “City” column contain, not independent data, but a link to the zip code table. Then it will automatically show the updated town name for all customers, and if you send out a mass mailing the envelopes will all get addressed correctly.
Of course, customers who have their own private misspelling of their town’s name will not get to have your company store this additional information for them, but the mail will get to them anyway so they probably won’t notice or complain.
The relationships between data items are captured by what is known as a “data model.” This is basically a list of tables, each of which links certain rows or columns to other tables. Some tables are intended to have unique identifiers called “keys,” and the database enforces this condition. If you set things up correctly, the zip code table will not let you enter the same zip code twice with different data for city and state.
On the other hand, there may be a separate table to keep track of the fact that, although states are always unique and have standard names, sometimes there are different names for places that have the same zip code, for example different sections of the same small town that only has one post office.
The trick is to make sure that redundancy is eliminated, so that when something changes, the change propagates, and all tables are updated correctly.
Some tables may have more complicated keys: Although it is common to impose unique identifiers like social security numbers for people or VINs for cars, a wireless phone provider may track all the transactions for a given account by a key that combines the phone number, date, and time the phone call was initiated.
Another example: The Census Bureau will have a unique identifier for individual people (which is not supposed to be the social security number, because of privacy protection laws), and another identifier for “households”; each household will have a list of people who belong to it, but one of those people will be defined as “householder” (that person used to be called “head of household,” until too many couples got into fights over who would be it). The table of “householders” will link to both the table of households and the table of individuals.
More advanced databases come with tools to check and maintain data integrity. A special programming language called SQL (Structured Query Language) allows you to ask complicated questions and have the system figure out the best way to calculate the answer. As it turns out, although people have a hard time learning how to program, they can learn how to ask precise questions more easily than they can learn how to make the machine find the answers to the questions efficiently. But you can do a lot with just spreadsheets.
Just for fun, here’s some sample SQL code from a US government website, operated by the National Institute of Standards and Technology here: https://www.itl.nist.gov/div897/ctg/dm/sql_examples.htm
create a table to store information about weather observation stations:
No duplicate ID fields allowed
CREATE TABLE STATION
(ID INTEGER PRIMARY KEY,
CITY CHAR(20),
STATE CHAR(2),
LAT_N REAL,
LONG_W REAL);
populate the table STATION with a few rows:
INSERT INTO STATION VALUES (13, ‘Phoenix’, ‘AZ’, 33, 112);INSERT INTO STATION VALUES (44, ‘Denver’, ‘CO’, 40, 105);INSERT INTO STATION VALUES (66, ‘Caribou’, ‘ME’, 47, 68);
query to look at table STATION in undefined order:
SELECT * FROM STATION;
| ID | CITY | STATE | LAT_N | LONG_W |
| 13 | Phoenix | AZ | 33 | 112 |
| 44 | Denver | CO | 40 | 105 |
| 66 | Caribou | ME | 47 | 68 |
query to select Northern stations (Northern latitude > 39.7):
selecting only certain rows is called a “restriction.”
SELECT * FROM STATION WHERE LAT_N > 39.7;| ID | CITY | STATE | LAT_N | LONG_W |
| 44 | Denver | CO | 40 | 105 |
| 66 | Caribou | ME | 47 | 68 |
query to select only ID, CITY, and STATE columns:
selecting only certain columns is called a “projection.”
SELECT ID, CITY, STATE FROM STATION;
| ID | CITY | STATE |
| 13 | Phoenix | AZ |
| 44 | Denver | CO |
| 66 | Caribou | ME |
query to both “restrict” and “project”:
SELECT ID, CITY, STATE FROM STATION WHERE LAT_N > 39.7;
| ID | CITY | STATE |
| 44 | Denver | CO |
| 66 | Caribou | ME |
Q: How do you keep a computer programmer in the shower all day long?
A: Give them a shampoo with a label that says “[lather, rinse, repeat].”
– Network World, https://www.networkworld.com