
As an example of the sort of thing which mathematicians do with numbers, suppose we set ourselves the following problem: to calculate the difference between the square of any number, and the square of the number next after it.
In the first few cases, this is quite easy to do. We have
22 − l2 = 4 − 1 = 3
32 − 22 = 9 − 4 = 5
42 − 32 = 16 − 9 = 7
52 − 42 = 25 − 16 = 9
and so on. To go on very far with this would be extremely tiresome. Also, the results written down on the right-hand side suggest that some sort of rule is operating, and that, if we could find out what it was, we could by-pass a lot of arithmetic.
Let us examine one case more closely, to find out if possible what is really characteristic about it. Take for example the third case written down above. It can also be written as
(3 + l)2 − 32 = 7,
where (3 + l)2 means that the numbers in the bracket are to be added together, and then the result is to be squared. But actually we could do the squaring without doing the addition first. This would go as follows

To get the first row of figures under the line, I multiply each of 1 and 3 by 1; to get the second line, I multiply each by 3, and set out the results one step to the left, for convenience of addition. Then add, and we get the answer as written.
Our example now takes the form
32 + (2 × 3) + 1 − 32 = 7.
This shows where the result really comes from. It is made up as (2 × 3) + 1, the 32 terms cancelling out. Now exactly the same argument could be used in any other case. For example in the next case we have

and that gives the result, 9; and so in all the other cases.
I hope the reader agrees that it would be intolerable to have to write out separately a lot of different sums of this kind, each of which is really quite similar to all the others. The question arises whether we cannot find some wholesale method, by which we can in some sense do them all at once.
The method actually consists of using a letter, for example n, to denote each of a class of numbers. For example, in the above case let n denote in turn each of the numbers 1, 2, 3, and so on. At any moment we can of course focus our attention on one particular number, e.g., 20, and say “let n be 20.”
If n denotes any number, the next number is n + 1. The squares of these numbers are written n2 and (n + l)2. Our problem then takes the form, what is the value of (n + l)2 − n2, where n has any of the values 1,2,3, …. To solve it, we proceed exactly as in the case n = 3. To calculate (n + l)2, we write
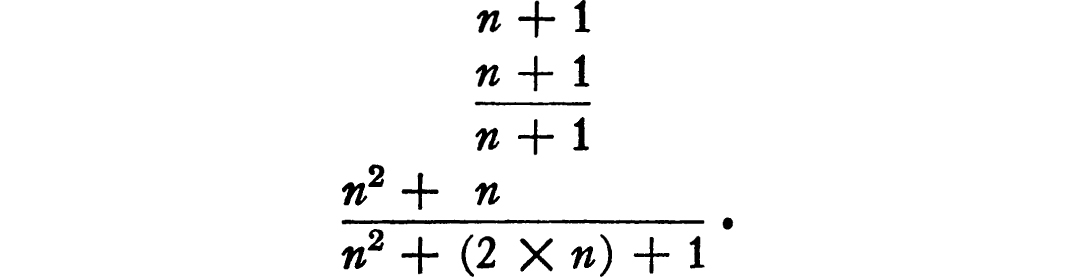
Subtracting n2, what is left is (2 × n) + 1. The result can be written in the form
(n + l)2 − n2 = (2 × n) + l.
In products involving letters, the sign of multiplication × is usually omitted. Thus we write 2n instead of 2 × n, and we should write the above formula as
(n + l)2 − n2 = 2n + 1.
It is easily seen that this formula gives the above arithmetical results as particular cases, when we take n to be 1, 2, 3 or 4. But now any number of other cases can also be derived from it; for example 862 − 852 = 2 × 85 + 1 = 170 + 1 = 171.
The branch of mathematics in which classes of numbers are denoted by symbols, such as letters, in the above way, is called algebra. The expression just written down is an example of an algebraical formula. It is equivalent to a whole class—usually (as in this case) an infinite class of arithmetical formulae. Not only so, but it exhibits what is really characteristic about the arithmetical formulae. The algebra goes to the root of the matter, and ignores the casual oddities of particular cases.
In many formulae we use two or more letters at the same time. The classes of numbers from which the letters are to take their values may be the same or different. For example, we might say “let a and b each denote any positive integer.” A formula involving such a and b is for example
(a + b)2 = a2 + 2ab + b2.
This can be proved in exactly the same way as the above particular case, in which a was 3 and b was 1.
This is actually the simplest of a chain of formulae, which are together known as the binomial theorem. The next such formula is an expression for the cube of the sum of two numbers, and is
(a + b)3 = a3 + 3a2b + 3ab2 + b3.
There are some kinds of algebra which are so complicated that they use up the whole alphabet, both capital and small letters, and the Greek alphabet too. A few years ago a mathematical paper was published in which a Chinese character was used as one of the algebraical symbols. Actually the possibilities are endless, since we can also attach suffixes to letters as additional labels, and write for example, m1, m2, … mn, … as algebraical symbols.
A few letters have come to be used in a different way, so that they always (unless there is a local rule to the contrary) mean the same number. The letter e and the Greek letter π are used in this way to denote specially important numbers.
As an example of algebra, let us multiply together the two expressions a + b and a − b. I call these expressions rather than numbers, because, though they represent numbers, they do not just do that. When I write “a + b” or “a − b” I mean “think of any two numbers you like, and then think of their sum or difference.” The particular numbers thought of will not matter in what follows. This is really the essence of algebra, that the particular values of such expressions rather fall into the background; it is the way in which the numbers occur in the expressions that is of interest.
The multiplication goes in the same way as in the previous section; we can write it as
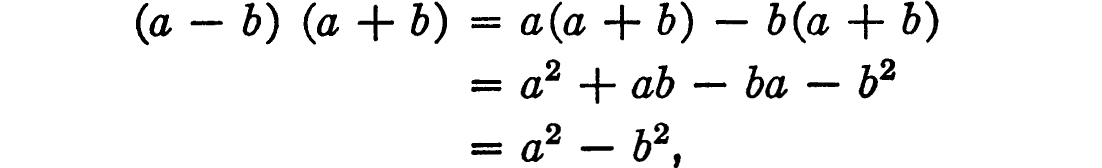
the ab and − ba cancelling out.
Hence the product of a − b and a + b is a2 − b2. Conversely, we can say that the factors of a2 − b2 are a − b and a + b. This is really just another way of saying the same thing.
It is important to notice that the problem of finding the factors of a2 − b2 in algebra is quite different from that of finding the factors of particular values of this expression in arithmetic. Consider for example the factors of 52 − 42, i.e. 25 − 16 = 9. The algebra gives the formula
52 − 42 = (5 − 4) (5 + 4).
This is correct arithmetic too, but in arithmetic it has not got us anywhere, because in fact 5 − 4 = 1 and 5 + 4 = 9, so that the first factor is trivial, and the second can itself be factorized again. From the point of view of algebra, this is just an accident due to the particular values of a and b chosen. In algebra, a − b and a + b are the ultimate factors of a2 − b2. You cannot factorize a + b any further, though you can, as it happens, factorize 5 + 4.
The algebra books are full of examples of factors of algebraic expressions. Here we shall recall just a few of them, which the reader should be able to verify quite easily. We have
a3 + b3 = (a + b) (a2 − ab + b2)
a3 − b3 = (a − b) (a2 + ab + b2)
and a4 − b4 = (a − b) (a + b) (a2 + b2).
None of these expressions can be reduced down any further into factors.
All these formulae are examples of algebraical identities; that is, they are equations in which the two sides are equal for all values of the numbers a, b, …, and not because they have any particular values.
As another illustration of algebra, let us consider what is meant by an inequality in algebra. In arithmetic, an inequality is just a relation between particular numbers, such as 2 < 3. In algebra, an inequality involves letters such as a, b, … which represent whole classes of numbers, and an inequality is a relation of “greater than” or “less than” which is true for all numbers belonging to these classes.
As an example of an inequality in algebra, we shall show that the square of the sum of any two numbers can never be less than four times their product. Let us denote the two numbers by a and b. Then in symbols the theorem to be proved is (a + b)2 ≥ 4ab.
This is easily seen to be true in particular cases; for example (2 + 3)2 = 52 = 25, which is greater than 4 × 2 × 3 = 24; and (3 + 4)2 = 72 = 49, which is greater than 4 × 3 × 4 = 48. What is wanted however is a proof that the inequality is true independently of the particular values of the numbers concerned. Such a proof must depend merely on the way in which the a and b occur in the formula.
If one of the numbers, say a, is positive, and the other, b, is negative, the result is trivial. This is an expression often used by mathematicians, and it means that the result is so obvious that no formal proof is needed. The standard of triviality of course tends to alter as we become more experienced mathematicians. In this case, if a is positive and b is negative, the left-hand side of the proposed inequality, (a + b)2, is positive or zero, and the right-hand side, 4ab, is negative. The inequality then merely asserts that a certain positive or zero number is greater than a certain negative number, and this is trivial.
If a and b were both negative, the inequality would amount to the same thing as the corresponding formula involving −a and −b instead of a and b. Hence it is sufficient to consider the case where a and b are both positive.
To prove it in this case, we observe that
(a + b)2 = a2 + 2ab + b2;
the difference between this and 4ab is a2 − 2ab + b2, and we have therefore to prove that this expression is necessarily positive or at least zero; and it is so, because it is equal to (a − b)2, by the same rule for squaring an algebraic expression involving two numbers; and the square of any number, positive or negative, is positive. This gives the required proof.
We have been careful to write the inequality with ≥ instead of >, because it may happen that the two numbers (a + b)2 and 4ab are actually equal. This will be so if the numbers a and b are equal, since each side of the proposed inequality is then 4a2; and a little consideration of the argument will show that this is the only case in which equality can occur.
As another example of an inequality, we shall prove that if a, A, b and B represent any four numbers, then
(aA + bB)2 ≤ (a2 + b2) (A2 + B2).
For example, if a = 1, b = 2, A = 3 and B = 4, then the left-hand side is (3 + 8)2 = ll2 = 121, and the right-hand side is

There is no case in which this inequality is trivial, since both sides of it are obviously positive.
To prove it, multiply out both sides in full; it takes the form
a2A2 + 2aAbB + b2B2 ≤ a2A2 + a2B2 + b2A2 + b2B2.
The difference between the right-hand side and the left-hand side is a2B2 − 2aAbB + b2A2, and by the formula for squares this is equal to (aB − 2bA)2. As a square, this is necessarily positive, or at least zero. Hence the right-hand side is at least as great as the left-hand side, which was to be proved.
The subject of inequalities has occupied the attention of many mathematicians in recent times, and many remarkable results of the above kind have been proved.
As another example of algebraical formulae, we shall next sum the arithmetical and geometrical progressions. These will be required later in the book, and anyhow they are good examples of the way in which letters are used to represent whole classes of numbers.
A number is said to be the arithmetical mean of two other numbers, if it is equal to half their sum, i.e. if twice the first number is equal to the sum of the other two. Thus 2 is the arithmetical mean of 1 and 3, since 2 × 2 = 1+3; similarly 5 is the arithmetical mean of 3 and 7, and 10 of 8 and 12.
An arithmetical progression is a sum, such as 1 + 2 + 3 + 4, or 3 + 5 + 7 + 9 + 11, in which each term is the arithmetical mean of those on each side of it. It is of course easy to write down the values of these sums—they are in fact 10 and 35 respectively. But what we now want is a general rule by which the values of all such sums can be written down at once, however many terms they contain. As the simplest case of this problem, consider the sum
1 + 2 + 3 + 4 + · · · + (n − 1) + n
containing n terms, where n is any positive number. The problem of summing this for every n is no longer a problem of arithmetic. It is one of algebra, since what we have to look for is a general formula expressing the sum of the progression in terms of n, valid whatever particular number n may represent.
This problem can be solved in the following way. Suppose first that n is an even number, i.e., n has 2 as a factor. Let n = 2m, say. Let us begin by adding the first term of the progression to the last; the result is n + 1. Next, add the second term of the progression to the last but one; the result is 2 + n − 1, which is again n + 1; next the third term and the last but two make n + 1, and clearly this is a general rule. It is on the recognition of the existence of such general rules that proofs in algebra depend.
Now all the terms can be paired off in this way, since we have supposed that there is an even number of terms. The number of pairs is half the total number of terms, i.e., it is m; each pair is equal to n + 1; consequently the whole sum is equal to m(n + 1).
This solves the problem if n is an even number. If n is an odd number, then n − 1 is an even number, and consequently the sum of the terms as far as n − 1 can be obtained from the above formula. Let n − 1 = 2l, say. Then the sum of the terms as far as n − 1 is ln. Hence the total sum is ln + n = n(l + 1). The problem is therefore solved in all cases. For example, the sum of 1 + 2 + ··· + 100 is 50 × 101 = 5050, and the sum of 1 + 2 + ··· + 149 is 149 × 75 = 11175.
Any other arithmetical progression can be summed by using the formulae already obtained. For example 3 + 5 + ··· + 25 is equal to 3 + 3 + ··· + 3 (twelve terms) + 2(1 + 2 + ··· + 11) = 36 + 2 × 66 = 36 + 132 = 168.
It is also easy to obtain general formulae for all such sums in a similar way.
There is another sort of progression called a geometrical progression. A number is said to be the geometrical mean of two other numbers, if its square is equal to the product of the other two numbers; for example, 4 is the geometrical mean of 2 and 8, and 6 is the geometrical mean of 4 and 9. The origin of the use of the words “arithmetical” and “geometrical” in the sense given here seems to be rather obscure, but the ideas involved are very simple.
A geometrical progression is a sum such as 1 + 2 + 4 + 8 or 2 + 6 + 18 + 54 in which each term is the geometrical mean of its two neighbours. The general form of a geometrical progression beginning with 1 and containing n terms is 1 + a + a2 + ··· + an − 2 + an − 1. The problem of summing the geometrical progression consists of finding a formula for this sum, depending of course both on n, the number of terms, and on a, the quotient of each term by the one before.
In this case it is no use adding pairs of terms, and a different device has to be thought of. Suppose that we multiply the whole progression by a (the same a of course, as occurs in the progression). The result is a + a2 + ··· + an − 1 + an. Now subtract the original progression from this. The result is an − 1, since all the other terms cancel in pairs. Now what we have obtained in this way is a − 1 times the original sum. The value of the original sum is therefore (an − 1) ÷ (a − 1). For example, 1 + 2 + 4 + 8 is (24 − 1) ÷ (2 − 1), i.e. 16 − 1 = 15. Naturally the formula shows to more advantage when it is applied to longer sums, in which direct addition is not so easy.
There is another way in which letters are used in mathematics to represent numbers. We sometimes write a letter instead of a number, not because we want to represent a whole class of numbers, but because we do not know what the number in question is. An unknown number is often represented by the letter x.
An equation is a formula which asserts that two numbers, arrived at by different processes of calculation, are in fact equal. An equation differs from an identity in the fact that it is not usually true for all values of the symbols which occur in it, but merely for some particular values of these symbols, or even for only one such value. It is then a question of finding out what these particular values are. This is known as solving the equation.
If the numbers on the two sides of an equation involve an unknown number x, to solve the equation is to find the value or values of x for which the equation is true. Such values are called the roots of the equation. Simple examples of equations are 2x + 3 = 11, and x + 1 = 2x + 4. The technique of solving such equations is taught in algebra books. It can at once be verified that the solutions of these equations are x = 4 and x = − 3 respectively.
Equations are often presented to us as practical problems. Suppose that I have 3d., and that two people each give me the same sum, and that then I have lid. What sum did they each give me? Suppose that they each gave me x pence. Then the situation is precisely represented by the former of the above equations. Each, of course, gave me 4d.
Readers will probably remember being asked at school to solve problems of this kind: “A father is four times as old as his son. In twenty years time, he will be only twice as old. Find their ages.” Here there are two unknowns, the ages of the father and of the son. Let us denote them by x and y. The first statement is then expressed by the algebraic equation x = 4y. After twenty years, their respective ages will have become x + 20 and y + 20. Consequently the second statement is expressed by the equation x + 20 = 2(y + 20). These two equations are called “simultaneous equations,” since they are both true for the same x and y. It can easily be verified that the solution is x = 40, y = 10. For the method of getting this I must again refer to algebra books.
Now consider the following problem: “A father is three times as old as his son. In ten years time the son will be twice as old as his father. How old are they now?”
This problem is obviously an idiotic one; but the algebra goes along quite happily. If the father’s age now is x and the son’s is y, the two statements are represented by the equations
x = 3y, y + 10 = 2(x + 10)
and the solution is x = − 6, y = − 2. The point is that the algebra is a machine which does just what it is asked to do, and no more. As we have forgotten to mention that there cannot be negative ages, the data are actually quite consistent, and the answer, though absurd if related to real life, is perfectly correct mathematically.
This name is given to that part of algebra in which we ask questions about factors, the divisibility of certain numbers by other numbers, the possibility of expressing numbers by means of algebraic expressions of certain kinds, and other things of that sort. It is a very ancient subject, which was studied particularly by Diophantus, a mathematician of the 3rd century A.D. It has this peculiarity, that many of its problems are very easy to state, but very difficult to solve.
Some examples, involving prime numbers, have already been considered in Chapter II. As another example, consider the following problem: to find numbers x, y, and z such that x2 + y2 = z2. This has an obvious connection with the famous theorem of Pythagoras, that the square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides. A well-known solution is obtained by taking x = 3, y = 4, and z = 5, since then x2 = 9, y2 = 16, z2 = 25, and 9 + 16 = 25. Another solution is x = 5, y = 12 and z = 13, since 25 + 144 = 169.
What we ask in the theory of numbers is whether it is possible to manufacture such solutions indefinitely; or, what comes to the same thing, whether there is a general formula which always gives solutions. The result is as follows. Let a and b be any two positive numbers, of which a is the greater; and let x = a2 − b2, y = 2ab and z = a2 + b2. Then the equation is satisfied, whatever the values of a and b. This is easily seen from the rule for squaring the sum of two numbers. We have (a2 − b2)2 = a4 − 2a2b2 + b4 and (2ab)2 = 4a2b2; adding, the result is a4 + 2a2b2 + b4, and this is (a2 + b2)2. This proves the general rule. The 3, 4, 5 example is formed by taking a = 2 and b = 1, and the 5, 12, 13 example by taking a = 3 and b = 2. As another example, let a = 5 and b = 2. Then x = 21, y = 20 and z = 29; and it is easily verified that 212 + 202 = 292.
This is merely an example of a large class of problems which were considered by Diophantus and other mathematicians.
This particular problem had a remarkable sequel. Fermat, the celebrated French mathematician already mentioned, was very much interested in these questions. He possessed a copy of Bachet’s Diophantus, in the margin of which he noted some of his own discoveries or conjectures. One of these marginal notes asserted that it is impossible to solve the equation xn + yn = zn when n is any number greater than 2; that is, that there are no numbers x, y, z such that x3 + y3 = z3 or x4 + y4 = z4 and so on. This assertion has become known as Fer-mat’s last theorem. The remarkable thing about it is that to this day no other mathematician has been able either to prove or to disprove it. It is not even known with certainty whether Fermat had a proof, or whether he was only guessing. As he made other conjectures, some of which have turned out to be false, we may think that it was a guess. If so, it was a remarkably good guess, since the theorem has been verified for a great many values of n, though not, as Fermat said, for all values.
Another theorem of Fermat, this time not very difficult to prove, is that, if p is a prime number, and a is another number not divisible by p, then ap − 1 − 1 is divisible by p. For example, take p = 7 and a = 2. Then 26 − 1 = 64 − 1 = 63, which is divisible by 7. On the other hand, if p = 9, which is not a prime number, and a = 2, then 28 − 1 = 256 − 1 = 255, which is not divisible by 9.
Another celebrated theorem in the theory of numbers, due to Lagrange (1736–1813) asserts that every positive number is the sum of four squares. For example 5 = 22 + l2 + 02 + 02, and 12 = 32 + l2 + l2 + l2. The point of the theorem is that, however large the number concerned may be, it is never necessary to use more than four squares to express it. Compared with the proofs of many theorems in this subject, the proof of this cannot be called very difficult, but it is beyond the scope of this book. This theorem has suggested many others of the same kind, involving cubes, fourth powers and so on.