There are many operations of mathematics in which we give our attention in succession to one number, then to another, then to a third number, and so on indefinitely. In ordinary counting, for example, we think of 1, 2, 3, and so on, where “and so on” means “it is clear how to proceed in this way indefinitely.” Such a succession of numbers is called a sequence. Other examples are
where “…” means the same as “and so on.” More examples of such sequences will be given later.
In most cases it is in the ultimate behaviour of a sequence, the “and so on,” that the main interest lies. The above examples show that there are various different possibilities. The sequence 1, 2, 3, … goes on increasing beyond all bounds; in technical language, we say that “it tends to infinity.” The reader should not try to analyse this phrase too closely. It means just what we have said, and no more. It does not imply that there is a place “infinity” at which the sequence ultimately arrives.
The sequence 1,0,1,0, … is said to oscillate. There is nothing particular to explain about this.
The terms of the sequence 
become smaller and smaller as we go along; and in fact they become indefinitely small, passing on their way any small boundary which we like to set up beforehand. Such a sequence is said to “tend to the limit 0.” The number 0 is not a term of the sequence, but it is that number to which the sequence points unmistakably. The sequence 
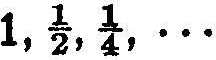obviously has the same property.
There is a technical notation for all this. For “tends to” we draw an arrow, →; “tends to infinity” is written “→∞“ (again ∞ should not be thought of as a number, but merely as a symbol occurring in this expression). We usually denote a typical integer by n (n for number). The property of the sequence which has just been explained is then written as
and read “as n tends to infinity, 
tends to 0.”
We can of course easily make up sequences with limits other than 0; for example, the sequence 
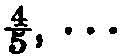tends to the limit 1; in technical notation as
The relation of all this to the theory of irrationals is not made clear by these examples, because all the numbers and limits concerned happen to be rational. But there is a very important connection. The situation is briefly as follows. Suppose that we have a sequence of numbers a1, a2, a3, … such that each is greater than the one before, but such that they do not increase beyond all bounds; suppose for example that we have a fixed number M which is greater than every number of the sequence. Then an important theorem says that the sequence does tend to a limit; i.e., that there is a number A such that an → A as n → ∞. But this theorem depends entirely on the theory of irrational numbers. The number A may be irrational, and then the theorem would not be true if “number” merely meant “rational number.”
In this subject too we think of a number, then think of another number, and so on, but now at each stage we add the new number to the total of those that came before. Suppose, for example, that the numbers concerned are 
. Then the operation is indicated by the formula
ending with the inevitable + …, or “and so on.” This means that we first take the number 1; then take the number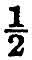 
, and form the sum 1 + 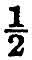; then take the number 
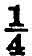and form the sum 
, and so on. These sums are called the partial sums of the series. To consider the series amounts to the same thing as considering the sequence of its partial sums. Of course we cannot add all the terms of such a series. What we can do is to think about the sequence of the partial sums. If this sequence tends to a limit, the series is said to converge, or to be convergent. Otherwise, it is said to diverge, or to be divergent. In the case of convergence, the limit to which the partial sums of the series tend is called the “sum” of the series. It is in this case only that the series taken as a whole can be said to have a definite “value,” namely its sum.
Let us examine the above example a little more closely. A geometrical illustration would probably help the reader in doing this. Think of the terms of a series as measurements made along a foot rule, graduated in inches. “1” means “one inch from the end.” “ + 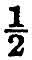” means “add another half-inch.” This takes us half-way from the one-inch mark to the two-inch mark. “ + 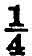” means “add another quarter-inch.” This again takes us half-way from where we were before to the two-inch mark. And in fact it is easily seen that the addition of every term of the series has precisely the same effect. We always get half-way towards 2, without ever getting quite there. However, the number 2 clearly has a special relation to this series, and in fact it is its sum in the sense which has been defined above. The result is expressed by the formula
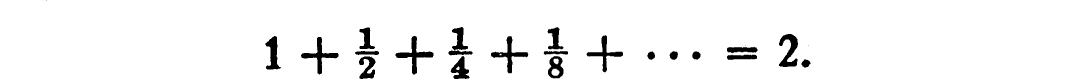
The reader who has succeeded in following this argument to its conclusion has summed his first infinite series. Or is it the first? I seem to remember learning at quite an early age something about recurring decimals. Suppose that I try to express the fraction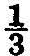 
as a decimal. I must carry out the operation of dividing 3 into 1.000 …; 3 into 1 won’t go; 3 into 10 goes 3 with remainder 1; so again I have to divide 3 into 10, and again it goes 3 with the remainder 1; and so on indefinitely. It is natural to write the result of the process in the form .333 …, but in fact the division never really comes out to a final result. Of course .333 … is nothing more nor less than the infinite series
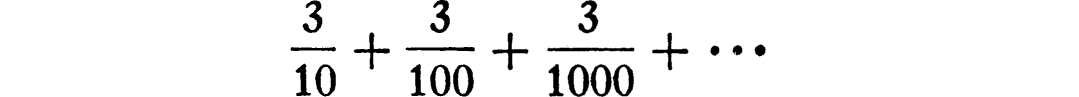
and it will be shown later that the sum of this series really is .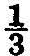
Apparently it is possible to sum an infinite series without knowing it.
The notation which mathematicians use for series is as follows. We use ∑, the Greek capital sigma or “s,” to mean “the sum of” whatever is written after it. Thus ∑n means “the sum of all numbers such as n,” belonging to some specified class. For example, by
we should mean the sum of all the integers from 1 to 4, that is 1 + 2 + 3 + 4 = 10. As another example, the reader may verify that
In the case of an infinite series, the symbol “∞” is written at the top of the ∑. The two infinite series which we have just summed would be written as
and
These two series are examples of what are called infinite geometrical progressions. We have already explained what a finite geometrical progression is; it is a sum of terms in which each term is the geometrical mean of its two neighbours. If the first term is 1, and the next term is x, such a progression is of the form 1 + x + ··· + xn. Now we can go on adding such terms indefinitely, and if we do so we obtain the infinite series 
It is easy to see that such a series can have no meaning if x is 1 or any larger number; for example, if x is 1, it is simply
1 + 1 + 1 + ….
The partial sums are 1,2,3, … which just go on getting larger and larger; in other words, the series is divergent.
On the other hand, if x lies between 0 and 1 we can sum the series. To do this, we have to consider the behaviour of the “partial sums” 1 + x + ··· + xn−1 when n is large. We have already obtained a convenient expression for this sum, namely 
. Now, as we have explained in a previous section, the numbers xn which occur in the numerator here become smaller and smaller, beyond all small bounds, when n is increased indefinitely; or, as we say, xn tends to 0 as n tends to infinity. The limit of the right-hand side is therefore simply obtained by omitting this term; i.e., it is
The sum of the series to infinity is therefore 
, or, as we may write it,
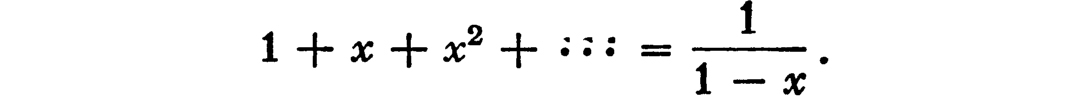
We have already had some examples of this formula. In the case x = 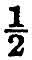, the formula gives
In the case 
, it gives
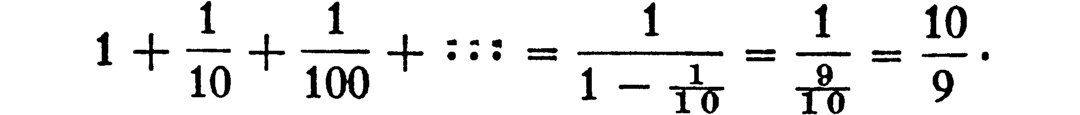
This is equivalent to the formula used above for evaluating the recurring decimal .333 … (to get it exactly, multiply throughout by 
).
As another example of an infinite series which can be summed, consider the series
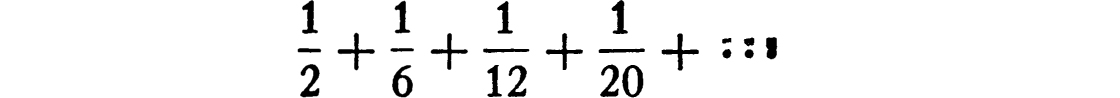
or as we may write it (to show the rule by which the terms are formed)
The nth term of this series is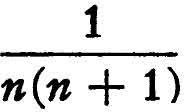 
. Now it is easily seen from the rule of subtraction of fractions that this is equal to 
. Applying this formula to each of the terms of the series, we see that the partial sum as far as the nth term is equal to
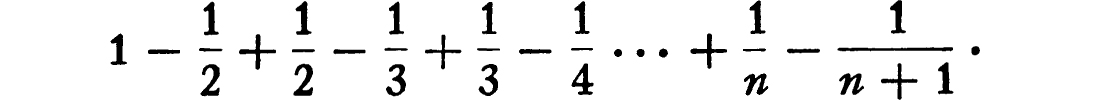
Here all the terms cancel in pairs except the first and the last, so that the whole sum is equal to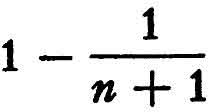 
. Now when n tends to infinity the term 
tends to 0. It follows that the series is convergent, and that its sum is 1.
There is a certain conclusion to which many people who have studied up to this point the subject of infinite series have jumped. Is it not true that, if the terms of the series tend to 0, the series is convergent? It seems as if this may be so, since the addition of small terms makes little difference to the sum. Actually the suggested theorem is false. The best-known example of this is the series of the reciprocals of all the integers,
To prove that this series is divergent we do not do anything particular with the first two terms, which are together equal to 
. Now take the next two terms, 
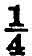and . The latter is the smaller, so that we have two terms, neither of which is less than 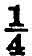. Their sum is therefore not less than .
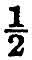Next take the next four terms, 
. Of this the last is the smallest. Consequently we have four terms, none of which is less than 
. Their sum is therefore not less than
At the next stage we take eight terms, each not less than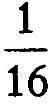 
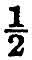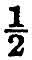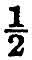; and so on and so on. As many times as we like we can find a block of terms to add, the sum of which is not less than . But if we go on adding and and 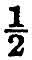indefinitely the total sum will increase beyond all bounds. We have thus proved that the series which we have been discussing is divergent.
This proof has some useful lessons for the beginner in mathematics. It shows, what the reader may by this time be ready to grant anyhow, that the truths of mathematics are often not obvious ones. We are constantly coming upon questions which are quite easy to put, but not at all easy to answer. It often requires a very ingenious argument to decide what the truth is. In this lies much of the fascination of mathematics. It is like an endless game against a skilled opponent. If we can think of the right move, we win. Once we have made the right move, we gain some definite piece of knowledge which is never afterwards in doubt.
How to think of the right move is another question. It is largely a matter of experience. Mathematical technique consists of the accumulated bright ideas of thousands of years. Let us examine our bright idea about the series 
to see what it really amounted to. It was like a gambit in chess, in which a piece is sacrificed to gain what turns out to be a winning advantage of position. We want to prove that the partial sums of the series are ultimately very large. We do it by replacing them by something smaller. I said “
is greater than 
.” Of course we could simply add, and get 
, which is larger still. The point is that, by simply adding, we get more and more complicated sums as we go along the series, until we are finally lost in hopeless arithmetic. But replacing each block of terms by the same number of terms, each equal to the last of the block, is something which we can go on doing endlessly without getting lost. It is a winning move.
Infinite series were used by many mathematicians before they had any clear idea of what we call convergence or divergence. It may seem surprising that it was possible to do this; but what the old-time mathematicians were really doing was to use infinite series as if they were finite sums, and since this is often justifiable they usually got the right answer. In other cases they obtained results which seem strange to us. One of Euler’s papers contains the formula
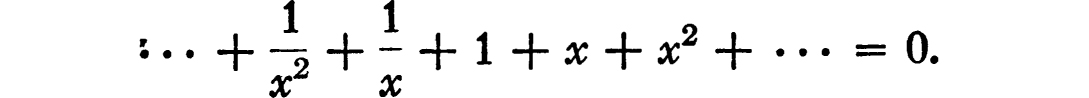
This is a series infinite in both directions. The “proof” simply consists of combining the formulae
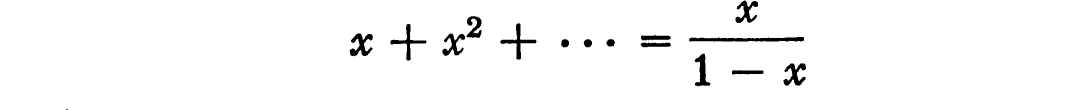
and
The objection to this is that, while each of these formulae is correct for some value of x, there is no value of x for which they are both correct; the former is true when x is less than 1, and the latter when x is greater than 1.
Some of the formulae used by writers of that time are not open to such obvious objections. The formula 1 − 1 + 1 − 1 + … = 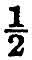was used by Leibnitz and John Bernoulli, and Euler gave 1 − 3 + 5 − 7 + … = 0. These series are not convergent, according to our definitions. We might call them oscillatory. In the former, for example, the partial sums are alternately 1 and 0. These numbers have no definite limit, but the number 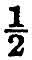does happen to be their average value. In modern times methods have been given of attaching a definite meaning to, or “summing*’ such series, according to which the above formulae are actually correct.
In the above sections we have referred several times to decimals. We must now put down our ideas on this subject in a more systematic way.
In an expression such as 23.781, the figures to the left of the dot, or decimal point, represent an integer, which has been sufficiently discussed. The first figure to the right of the dot, here 7, means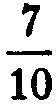 
; the next to the right again, here 8, means 
; the next, 1, means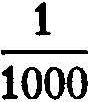 
; and so on, if there are any more figures. Thus the above expression means 23 + 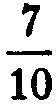+ + 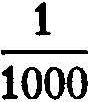. Clearly this is a rational number.
We call such an expression a finite decimal. We can also think of infinite decimals, in which the sequence of numbers after the decimal point never terminates. An infinite decimal may be formed by endlessly repeating one figure, or a block of figures. Examples are .333 … or .141414 …, or .23111 … in which repetition starts after a certain point. These are called recurring decimals. Other infinite decimals (such as those for π or e) are formed in a less obvious way.
Now an infinite decimal is just a particular kind of infinite series. We have already pointed this out in some simple cases, and the same thing holds in every case. Also it can be proved without difficulty that every infinite decimal is a convergent series, and consequently that it has a definite “sum.” Thus every decimal, finite or infinite, corresponds to a certain number, either rational or irrational. There is also a simple rule to show which sort of number the sum is. If the decimal is finite or recurring, the sum is rational; otherwise it is irrational.
It can also be proved without much difficulty that the converse of this theorem is true; every number can be expressed as a decimal, finite or infinite; and for each number there is only one expression as a decimal, provided that we agree not to use recurring 9. The necessity of this arises as follows. Consider for example the decimal .0999 …, where the 9 recurs. This is equivalent to the series
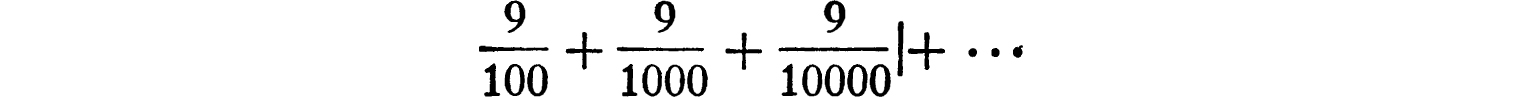
or to
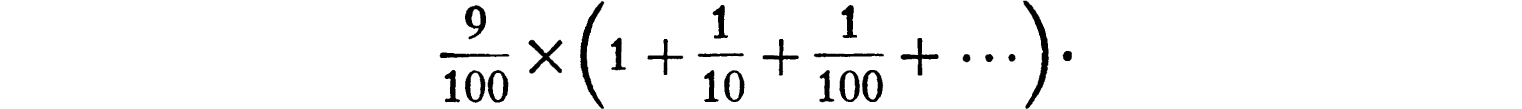
The sum of the series in brackets has already been found; it is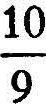 
. Hence the value of the decimal is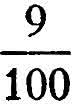 
. But 
can also be expressed as .1, and this is obviously a simpler and more natural way of doing it. The use of a recurring 9 is therefore superfluous and can be ruled out.
The fact that any irrational number can be thought of as a decimal, even if it does end with the inevitable “+ …” gives the irrational numbers a sort of concreteness. We can operate with these decimals just as we do in ordinary finite arithmetic, and with use the irrationals soon acquire a familiarity equal to that of the rationals.
This must seem at first a senseless question, because you can make up as many irrational numbers as you like; as we say, there are an infinity of them. The point is that it is possible to distinguish between some kinds of infinite aggregates and others. Some are, so to speak, more infinite than others. This may seem a surprising and even nonsensical statement, but examples show that it can be given a definite meaning.
The standard infinite set is the set of positive integers 1,2,3, …. This is the material out of which our whole system has been built, and it is natural to compare any other infinite set with it. Given any other infinite set (say for example, the set of rational numbers, or the set of irrational numbers) we ask whether it is possible to number off the members of this set, so that each member corresponds to just one of the positive integers. Suppose for example that the set is the set of even numbers, 2, 4, 6, …. In this the typical number is 2n, and if we make this correspond to the integer n, the “numbering off” is achieved at once.
A set for which this can be done is called an enumerable set.
Consider next the set of all rational numbers between 0 and 1. These also can be “enumerated,” in the following way. Take first the number 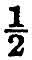, because its denominator, 2, is the smallest possible. Next take the numbers 
and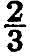 
, their denominators being the next smallest, 3, and their numerators running through the numbers less than 3 in order. As fourth and fifth in the list take the numbers 
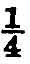and 
, for similar reasons, 
being omitted since it is equal to 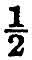. As sixth, seventh and eighth in the list we take 
, and 
, and so on, increasing the denominator by 1 each time, and then taking the numerators in order of size, omitting fractions already expressed in a simpler way. Clearly every fraction finds a definite place in this list, though it is not quite easy to write down the place taken by a given fraction m/n. It will be noticed, however, that we do not say “arrange all the rational numbers between 0 and 1 in order of magnitude, and count them off in that order.” This would not work, because, if you take any particular rational number, it is impossible to fix on any other one as being the next greater. There would always actually be others in between.
We have thus shown that the set of the rational numbers between 0 and 1 is enumerable. Now consider the same problem for all the numbers between 0 and 1, both rational and irrational. In the case of the irrational numbers there are no denominators to start work on, so that the method used above is not available; and of course an order-of-magnitude arrangement will not help, any more than it does with the rational numbers. We are at a loss to know what to do.
In fact, the problem is insoluble. This is a remarkable result, first proved by the German mathematician Cantor. It can be proved as follows. Suppose that the desired result had been achieved, and that all numbers between 0 and 1 had been enumerated in a definite way. Since each such number can be expressed as a decimal, this amounts to an enumeration of all the decimals. For the sake of writing down something definite, suppose that the first three decimals in the list were
.3427 …
.2981 …
.0446 …
to four decimal places. Now the point is that, if we could make such a list of all the decimals, we could derive from this list another decimal, different from every one in the list. The first decimal in the list begins .3 …. Very well, let the proposed new one begin .4 …. The second one in the list has a 9 in the second place; very well, let the new one go on .40 …. The third one has a 4 in the third place; very well, let the new one go on .405 …. The rule of operation consists of adding 1 to the nth figure in the nth decimal, except that, to avoid a possible recurring 9, we replace 8 by 7, not by 9.
The new decimal thus constructed differs in the nth place from the nth decimal in the list, and so it is different from every one of them. The assumption that it is possible to arrange all the numbers between 0 and 1 in such a list is therefore proved to be false.
The theorem shows that the “infinity” of irrational numbers is of a different kind from the “infinity” of rational numbers. There are in a sense many more of them. If we can imagine a situation in which we could pick out a number at random from all the numbers between 0 and 1, it is infinitely improbable that this number would be rational. This of course is not the same thing as being asked to think of a number “at random.” We should presumably think of one of the most familiar ones, and it would turn out to be rational.