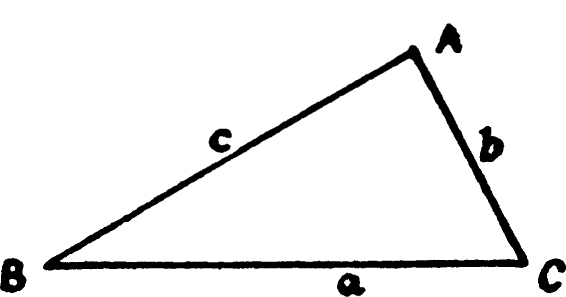
Trigonometry is mostly about measuring triangles. It is an art whereby, if certain parts of a triangle are known, the others can be calculated. A triangle has three sides and three angles. Let us denote the sides by a, b, and c, and the angles opposite to them by A, B, and C.
If the lengths of all the sides are known, then the shape of the triangle is fixed, and the angles can be determined. Again, suppose that two sides, say a and
b, and the angle C included between them, are given. Then again the triangle is fixed, and the third side c and the other two angles A and B can be found. Still another case is that in which one side, say a, and the two angles B and C at its ends are given. Then again the triangle is fixed, and the other two sides b and c, and the third angle A can be found. This process of finding the remaining parts from those which are known is called solving the triangle.
Trigonometry has applications well known to surveyors and men who map out the world. Suppose for example that the line BC is measured out on land, and that A is a point at the same level which we can see in the distance. Let us stand at B and measure the angle there, and then at C and measure the angle there. Then the triangle can be solved, and so the distance of A from either B or C can be found.
In another case, A is a distant mountain top. Suppose that the horizontal distance a of the mountain from an observer at B is known, and the angle B through
which we have to raise our eyes to look at A can be measured. The angle at C is also known (it is a right angle). Hence the triangle can be solved, and the height b of the mountain can be found.
If we can suppose that the familiar geometry of objects on earth is true also for those which we see out in space, these methods can also be used to find the distance of the heavenly bodies. BC can be a base-line measured on the earth, or even the distance between a point on the earth at two different places in its orbit. The distance of a heavenly body A can then be determined by observation of the angles at B and C.
Reader, do not despise these studies. They solaced the youth of Wordsworth’s “Wanderer.”*
Lore of a different kind
The annual savings of a toilsome life
The purer elements of truth involved
In lines and numbers, and by charm severe
(Especially perceived where nature droops
And feeling is suppressed) preserve the mind
Busy in solitude and poverty.
These occupations oftentimes deceived
The listless hours, while in the hollow vale
Hollow and green, he lay on the green turf
In pensive idleness. What could he do
With blind endeavours, in that lonesome life,
Thus thirsting daily? let still uppermost
Nature was at his heart as if he felt—
Though yet he knew not how—a wasting power
In all things which from her sweet influence
Might tend to wean him. Therefore with her lines,
Her forms, and with the spirit of her forms,
He clothed the nakedness of austere truth,
While yet he lingered in the rudiments
Of science, and among her simplest laws,
His triangles—they were the stars of heaven,
The silent stars! Oft did he take delight
To measure th’ altitude of some tall crag
That is the eagle’s birthplace, or some peak
Familiar with forgotten years, that shews
Inscribed, as with the silence of the thought,
Upon its bleak and visionary sides
The history of many a winter storm,
Or obscure records of the path of fire.
We have spoken above of measuring the sides and angles of a triangle. According to the system of geometry which we have explained, the vertices of a triangle are points in the Cartesian plane defined by co-ordinates (x, y), and the distance between two of them (x, y) and (x′, y′) is defined by the formula 
given before. We have not yet said what is meant by measuring an angle, and this problem must now be faced.
Suppose that the vertex of the angle is made the centre of a circle of radius 1. Then a measure of the size of the angle is the length of the part of the circle lying between the arms of the angle. That this length exists can be proved in the same way as was used to prove that the whole circle has a length.
The measure assigned to an angle in this way is called its circular measure. The circular measure of a complete turn (e.g., facing north round to facing north again) is the whole circumference of the circle, and so it is equal to 2π. The circular measure of a right angle is a quarter of that of a complete turn, and so is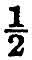 
π. At any rate, it is fairly obvious that this is the measure of the angle in the Cartesian plane between any of the axes of co-ordinates and the next one round beyond it. We defined perpendicular lines in general as two lines lx + my = 0 and l′x + m′y = 0 such that ll′ + mm′ = 0, and strictly speaking we ought to prove that the circular measure of the angle between any two such lines is 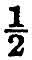π. This is not difficult to do, and we shall assume here that all such results, involving the direction in which the angle sticks out, are correct.
There are a few other angles of which the circular measure can easily be written down. It is known that the angles of any triangle together make up two right angles, i.e., an angle of circular measure π. The angle of an equilateral triangle must be one-third of this, and so its circular measure is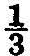 
π.
The unit of circular measure is known as a radian; that is, a radian is an angle such that the length of the arc of a circle of radius 1 drawn across it is also equal to 1.
The traditional way of measuring an angle is rather different from this. It originated with the Babylonians, who counted in the scale of sixty, and consequently found one-sixtieth to be a specially convenient fraction. According to this system, the whole circle is divided up into 360 equal parts, and the angle subtended by each part at the centre is called a degree. One sixtieth part of a degree is called a minute, and one sixtieth part of a minute is called a second (i.e., second-sixtieth). Thus the circular measure of a degree is 
, that of a minute is 
, and that of a second is 
. an angle of 7 degrees, 6 minutes and 5 seconds, for example, is written 7° 6′ 5′′.
The difficulty about this is, how to divide a circle into 360 equal parts, if we have not already defined the measure of an angle in some other way? It can be done of course, by methods of repeated bisection and approximation, but this comes to much the same thing as the definition by means of circular measure already used.
Apparently the construction of a single degree by Euclidean methods (ruler and compasses) is not possible. The problem is the same as that of constructing a regular polygon of 360 sides, since there are 360 degrees in a complete turn. Since there is a simple Euclidean method of bisecting any angle, it would be sufficient to begin by constructing a regular polygon of 45 sides; for we could then use the bisection method three times to construct in turn polygons of 90,180 and 360 sides. But the regular polygon of 45 sides is not one of those which can be constructed.
Euclid gave constructions for regular polygons of 3, 4, 5, 6, 8, 10, 12 and 15 sides. The construction is also possible for any number of sides which can be formed from these by multiplication by any power of 2. There are also some other regular polygons which can be constructed, the most interesting being that of 17 sides.
It was proved by Gauss that the construction is possible for any polygon with 22k + 1 sides, where k is any integer, provided that this is a prime number. The numbers 3, 5, 17, 257 and 66537 correspond to k = 0, 1, 2, 3, 4, and all these are prime numbers, so that all such regular polygons can (in theory) be constructed. Several mathematicians have actually worked out the construction for 17 sides, and this is complicated enough. The case of 257 sides has been worked out.
There is a story that a student at Gottingen once asked his professor for a subject on which to write a thesis. The professor, who thought that in any case he would do no good, told him (as a joke) to construct the regular polygon of 66537 sides. The student went away. Many years afterwards, an old man tottered into the university, carrying a heavy trunk. He had come back with the construction of his polygon.
Actually it is quite possible to measure angles without using the lengths of circles, or any sophisticated ideas of that kind. For example, instead of drawing a circle across our angle, and measuring an arc of that, we could
erect a perpendicular to one of the arms, say at unit distance along it from the vertex. The angle can then be measured by the length BC cut off on this perpendicular by the other arm of the angle. This way of measuring an angle involves nothing more than the measurement of distances between points.
We might start by taking a point B on one arm of the angle at a distance from A different from 1. In virtue of the properties of similar triangles, the ratio of BC to AB, i.e., the fraction (length BC) ÷ (length AB), is the same, whatever point B we start from. The same measurement of the angle is therefore given by this ratio, which is independent of the actual lengths of AB and BC. For this reason, this measure of the angle is called a trigonometrical ratio.
This particular measure of the angle A is called the tangent of the angle, and is written for short as tan A. This name arose as follows. It was customary to consider an angle as part of the following figure.
Here POR is twice the angle to be considered, and it is bisected by OQ, so that we really consider the angle POQ. The circular measure of this angle is denoted by the Greek letter θ (theta = th). PR is an arc of a circle with centre O and radius 1, and OQ produced meets it in S. PT is the tangent to the circle at P, i.e., the straight line which touches the circle at P. It is known that this makes a right angle with OP.
The tangent of the angle θ, tan θ, is then equal to the length of the tangent PT, since it is equal to PT/OP, and OP is 1.
As examples, we may give the following values of the tangents of angles:
A right-angle, 90° or 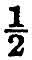π radians, has no finite value for its tangent. If we think of P, in the above figure, travelling round the circle until it is vertically above O, T travels farther and farther away to the right. Ultimately the tangent at P is parallel to OQ, so that they never meet, and the point T does not exist. Since the length PT increases beyond all bounds in this process, we express the result in the picturesque phrase “the tangent of a right angle is infinite.”
Another way of measuring the angle O is by means of the length of the line PQ. This is called the sine of the angle, and is written sin θ (but sin is pronounced sine). The sine is another trigonometrical ratio, and is an alternative way of measuring an angle. Some examples of the sines of angles are:
Still another way of measuring the angle θ is by means of the length OT. This is called the secant, and is written sec θ.
The ratios 1/tan θ, 1/sec θ, and 1/sin θ are called the cotangent, cosine and cosecant of the angle, and are written cot θ, cos θ, and cosec θ.
Naturally all these ways of measuring the angle θ are related. If ABC is a triangle with a right angle at B, and the angle at A is θ, then sin θ = BC/AC, cos θ = AB/AC, and tan θ = BC/AB. Consequently tan θ = sin θ/cos θ. Another important relation is
Here sin2 θ means sin θ × sin θ, i.e., the square of sin θ (sin θ2 would mean the sine of the square of θ, which would be quite different): and similarly cos2 θ means cos θ × cos θ. The relation is equivalent to
or
This is true by Pythagoras’ theorem (or of course in Cartesian geometry by the definition of distance).
Trigonometry books are full of formulae relating the sides and angles of a triangle. Here we can mention two of the simplest only. Suppose that we have a triangle ABC. Let the lengths of the sides opposite to the vertices A, B, C, be a, b, and c respectively, and suppose the three angles measured by their sines, sin A, sin B, and sin C. Then the sine of the three angles are proportional to the length of the opposite sides; in formulae
This is a pleasing and elegant result which should appeal to anyone with an eye for a nice formula. Apart from this, it happens to be useful. Suppose that we know the length of the side a of the triangle, and the measures of the angles B and C. Then since the angles of a triangle add up to two right angles, we can at once determine the angle A. We can therefore find the values of sin A, sin B, and sin C; and then the lengths b and c of the other two sides can be found from the formula. In fact they are
This is just what we need to determine the distance of an inaccessible point, if we can measure out a base line, and get the bearings of the point from each end of the base line. As another example of the solution of a triangle, suppose that we are given the lengths of the three sides, a, b, and c. Then it is required to find the angles, A, B and C. The formula actually determines the cosines of these angles. It is
with similar formulae for cos B and cos C. Having determined the cosines, the angles can be found, e.g., in degrees, minutes and seconds.
As another example of the use of trigonometry, suppose that we wish to measure the altitude of a tall crag, whose altitude and distance from us are both unknown.
We can measure its elevation θ from the point where we stand. Now walk towards it a distance d. The elevation will now be greater; call it θ′. We are now at an unknown distance x from a point on the same level as the observer, vertically below the top. However, the various parts of the figure are connected by the formulae
On subtracting we obtain
Since d, θ and θ′ are known, and the cotangents can be calculated, the value of h can be found from this formula.
In the previous section, we have made statements such as “An angle A is known; therefore its sine can be determined.” How is this to be done? The answer usually is, by getting someone else to do the work. In other words, we quote the value printed in a table.
Here is a small specimen taken out of a table of sines.
The numbers 30, 31, 32, on the left-hand side are angles measured in degrees. Those along the top are minutes (one sixtieth of a degree). The entries in the table are the values of the sines of the angles, so that for example the second entry from the left in the top row, .50252, is the value of the sine of the angle of 30° 10′ (thirty degrees and ten minutes). These values are of course not exact. They are the best we can do with only five decimal places at our disposal; that is, we write down the rational number with denominator 100000 which is nearest to the actual value of the sine. The complete table runs from 0° to 90°. It is quite a simple and crude table. Many more accurate ones exist, both as regards the number of decimal places used and the closeness between the entries, which here is 10.
How did the man who made the table calculate these values? The methods are too complicated to describe here in detail. For some angles, the exact value of the sine is known. For example, sin 30° is exactly 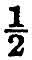, and this appears as the first entry, .50000, in the above table. For most angles there is no exact formula, but there are approximate formulae, and these are used to fit in the values of the sines of such angles.
Similar tables are published giving the values of the tangents of angles. It is such a table that would be used in the problem of the crag referred to above, since cot θ = 1/tan θ, so that the cotangent can easily be deduced from the tangent. We also often require the values of cosines, but these can be deduced from a table of sines, since the cosine of an angle is equal to the sine of 90° minus the angle. The reader should be able to verify this without difficulty from a figure.
I will record here, without attempting to prove them, some formulae which play a very important part in trigonometry. Suppose that we have any two angles, which we may denote by A and B. Then the sine or cosine of A + B can be expressed in terms of the sines and cosines of the separate angles A and B. The formulae are
and
These are called the addition formulae for the sine and cosine. Proofs of them are to be found in every book on trigonometry.
As a particular case we might take the two angles equal, say B = A. The formulae in this case reduce to
and
We can thus find the sine or cosine of twice an angle, if we know the sine or cosine of the angle. A more interesting step is usually in the other direction. In view of the relation sin2 A + cos2 A = 1, the formula for cos 2A can be written in the form cos 2A = 2 cos2A − 1, or in the form cos 2A = 1− 2 sin2 A. These formulae enable us to find the sine or cosine of half an angle from the cosine of the angle. For example from 
we deduce that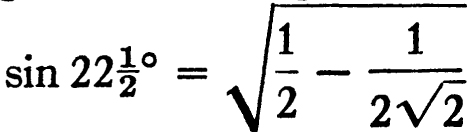 
.
There is a remarkable connection between the formulae of trigonometry and the formulae in the theory of the complex numbers considered in the last chapter. The original result in this order of ideas is called after its discoverer Abraham de Moivre or Demoivre (1667—1754), a mathematician of French birth who lived in London. It is:
where i is the “square root of minus one.” It is not difficult to derive this from the addition formulae, at any rate when n is a positive integer. For example, when n is 2, the left-hand side is
According to the rule for interpreting i2, this is equal to
and, by the above formulae for the sine and cosine of twice an angle, this is cos 2θ + i sin 2θ, which is Demoivre’s theorem.
There is another sort of trigonometry in which we measure triangles, not in a plane, but on the surface of a sphere. On a sphere there are of course no straight lines, and the simplest curves on a sphere are circles. Any plane intersects the sphere in a circle, and a plane through the centre of the sphere intersects the sphere in the greatest possible circle. Such a circle is called a great circle, and great circles play the same part on a sphere as straight lines do on a plane. The earth is roughly spherical; on the earth, the equator and the meridians are examples of great circles. The situation on a sphere is of course not quite the same as on a plane, because two great circles intersect in two points (e.g., two meridians intersect at the north pole and also at the south pole), whereas two straight lines intersect in at most one point. Still, it is usually possible to concentrate our attention on one of these intersections.
A spherical triangle is a figure on a sphere bounded by arcs of three great circles. A spherical triangle has three sides and three angles, just as a plane triangle has; but the sides are measured, not by their lengths, but by the angles which they subtend at the centre of the sphere. So in spherical trigonometry the angles are angles, and the sides are angles too. If we wish to survey the surface of the earth, taking into account its curvature, it is spherical trigonometry which we have to use. The problems of spherical trigonometry, solution of triangles and so forth, are similar to those of plane trigonometry, but naturally the formulae are more complicated. I will quote only one of them. Suppose that we have a spherical triangle, whose angles are A, B, and C, and whose sides are a, b, and c (i.e., the side opposite to the angle A subtends an angle a at the centre of the sphere). Then
This is an elegant formula, which obviously has some connection with the corresponding formula of plane trigonometry.
* The Excursion, Bk 1.
