Chapter 2
Form
“Architectural form is the point of contact between mass and space … Architectural forms, textures, materials, modulation of light and shade, color, all combine to inject a quality or spirit that articulates space. The quality of the architecture will be determined by the skill of the designer in using and relating these elements, both in the interior spaces and in the spaces around buildings.”
Edmund N. Bacon
The Design of Cities
1974
FORM
Form is an inclusive term that has several meanings. It may refer to an external appearance that can be recognized, as that of a chair or the human body that sits in it. It may also allude to a particular condition in which something acts or manifests itself, as when we speak of water in the form of ice or steam. In art and design, we often use the term to denote the formal structure of a work—the manner of arranging and coordinating the elements and parts of a composition so as to produce a coherent image.
In the context of this study, form suggests reference to both internal structure and external outline and the principle that gives unity to the whole. While form often includes a sense of three-dimensional mass or volume, shape refers more specifically to the essential aspect of form that governs its appearance—the configuration or relative disposition of the lines or contours that delimit a figure or form.
Shape
The characteristic outline or surface configuration of a particular form. Shape is the principal aspect by which we identify and categorize forms.
In addition to shape, forms have visual properties of:
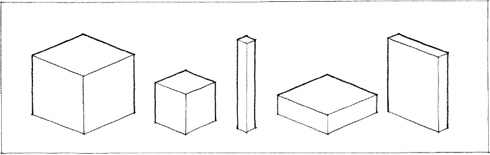
Size
The physical dimensions of length, width, and depth of a form. While these dimensions determine the proportions of a form, its scale is determined by its size relative to other forms in its context.
Color
A phenomenon of light and visual perception that may be described in terms of an individual’s perception of hue, saturation, and tonal value. Color is the attribute that most clearly distinguishes a form from its environment. It also affects the visual weight of a form.
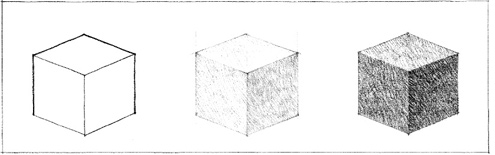
Texture
The visual and especially tactile quality given to a surface by the size, shape, arrangement, and proportions of the parts. Texture also determines the degree to which the surfaces of a form reflect or absorb incident light.
PROPERTIES OF FORM
Forms also have relational properties that govern the pattern and composition of elements:
Position
The location of a form relative to its environment or the visual field within which it is seen.
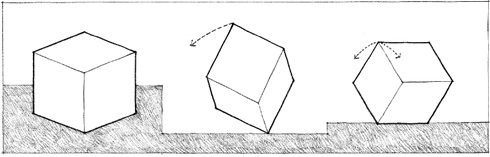
Orientation
The direction of a form relative to the ground plane, the compass points, other forms, or to the person viewing the form.
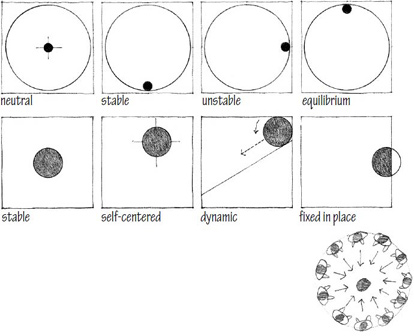
Visual Inertia
The degree of concentration and stability of a form. The visual inertia of a form depends on its geometry as well as its orientation relative to the ground plane, the pull of gravity, and our line of sight.
All of these properties of form are in reality affected by the conditions under which we view them.
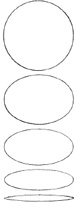
• A changing perspective or angle of view presents different shapes or aspects of a form to our eyes.
• Our distance from a form determines its apparent size.
• The lighting conditions under which we view a form affects the clarity of its shape and structure.
• The visual field surrounding a form influences our ability to read and identify it.
SHAPE
Shape refers to the characteristic outline of a plane figure or the surface configuration of a volumetric form. It is the primary means by which we recognize, identify, and categorize particular figures and forms. Our perception of shape depends on the degree of visual contrast that exists along the contour separating a figure from its ground or between a form and its field.
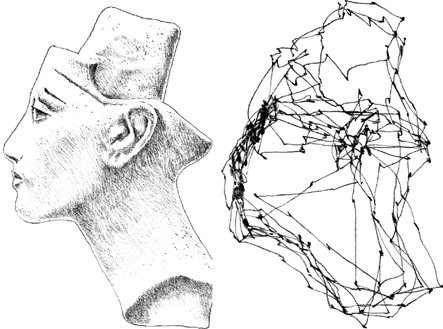
Bust of Queen Nefertiti
The pattern of eye movement of a person viewing the figure, from research by Alfred L. Yarbus of the Institute for Problems of Information Transmission in Moscow.
In architecture, we are concerned with the shapes of:
• floor, wall, and ceiling planes that enclose space
• door and window openings within a spatial enclosure
• silhouettes and contours of building forms
These examples illustrate how shaping the juncture between mass and space expresses the manner in which the contours of a building mass rise from the ground plane and meet the sky.
Central Pavilion, Horyu-Ji Temple, Nara, Japan, A.D. 607
Villa Garches, Vaucresson, France, 1926–27, Le Corbusier. This architectural composition illustrates the interplay between the shapes of planar solids and voids.
Suleymaniye Mosque,
Constantinople (Istanbul), 1551–58, Sinan
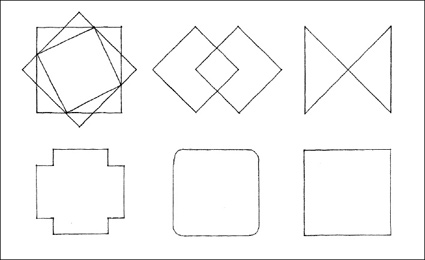
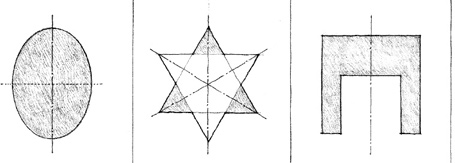
PRIMARY SHAPES
Gestalt psychology affirms that the mind will simplify the visual environment in order to understand it. Given any composition of forms, we tend to reduce the subject matter in our visual field to the simplest and most regular shapes. The simpler and more regular a shape is, the easier it is to perceive and understand.
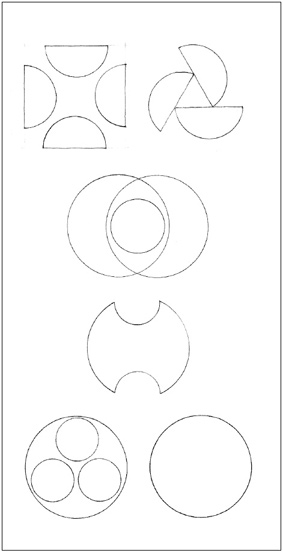
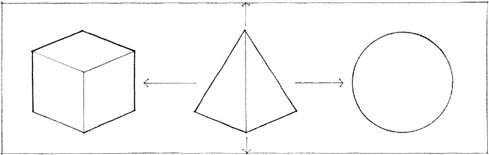
From geometry we know the regular shapes to be the circle, and the infinite series of regular polygons that can be inscribed within it. Of these, the most significant are the primary shapes: the circle, the triangle, and the square.
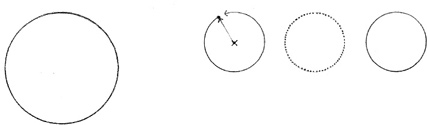
Circle
A plane curve every point of which is equidistant from a fixed point within the curve
Triangle
A plane figure bounded by three sides and having three angles
Square
A plane figure having four equal sides and four right angles
CIRCLE
Compositions of circles and circular segments
The circle is a centralized, introverted figure that is normally stable and self-centering in its environment. Placing a circle in the center of a field reinforces its inherent centrality. Associating it with straight or angular forms or placing an element along its circumference, however, can induce in the circle an apparent rotary motion.
Plan of the Ideal City of Sforzinda, 1464, Antonio Filarete
Roman Theater according to Vitruvius
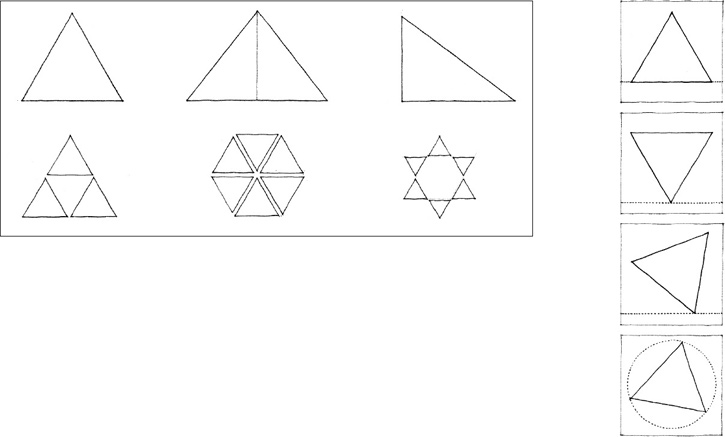
TRIANGLE
The triangle signifies stability. When resting on one of its sides, the triangle is an extremely stable figure. When tipped to stand on one of its vertices, however, it can either be balanced in a precarious state of equilibrium or be unstable and tend to fall over onto one of its sides.
Modern Art Museum, Caracas, Venezuela, 1955, Oscar Niemeyer
Vigo Sundt House, Madison, Wisconsin, 1942, Frank Lloyd Wright
Great Pyramid of Cheops at Giza, Egypt, c. 2500 B.C.
SQUARE
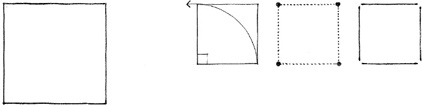
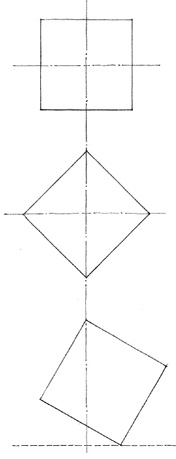
Compositions resulting from the rotation and modification of the square
The square represents the pure and the rational. It is a bilaterally symmetrical figure having two equal and perpendicular axes. All other rectangles can be considered variations of the square – deviations from the norm by the addition of height or width. Like the triangle, the square is stable when resting on one of its sides and dynamic when standing on one of its corners. When its diagonals are vertical and horizontal, however, the square exists in a balanced state of equilibrium.
Bathhouse, Jewish Community Center, Trenton, New Jersey, 1954–59, Louis Kahn
Agora of Ephesus, Asia Minor, 3rd century B. C.
SURFACES
In the transition from the shapes of planes to the forms of volumes is situated the realm of surfaces. Surface first refers to any figure having only two dimensions, such as a flat plane. The term, however, can also allude to a curved two-dimensional locus of points defining the boundary of a three-dimensional solid. There is a special class of the latter that can be generated from the geometric family of curves and straight lines. This class of curved surfaces include the following:
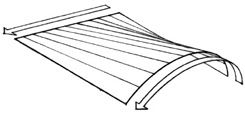
• Cylindrical surfaces are generated by sliding a straight line along a plane curve, or vice versa. Depending on the curve, a cylindrical surface may be circular, elliptic, or parabolic. Because of its straight line geometry, a cylindrical surface can be regarded as being either a translational or a ruled surface.
• Translational surfaces are generated by sliding a plane curve along a straight line or over another plane curve.
• Ruled surfaces are generated by the motion of a straight line. Because of its straight line geometry, a ruled surface is generally easier to form and construct than a rotational or translational surface.
• Rotational surfaces are generated by rotating a plane curve about an axis.
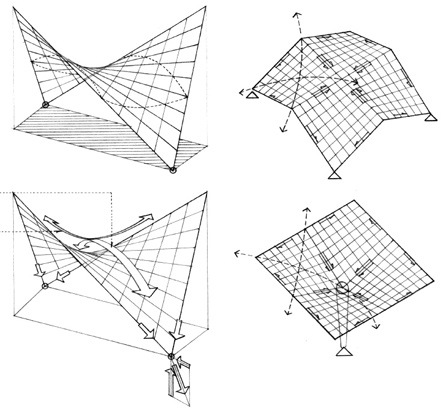
• Paraboloids are surfaces all of whose intersections by planes are either parabolas and ellipses or parabolas and hyperbolas. Parabolas are plane curves generated by a moving point that remains equidistant from a fixed line and a fixed point not on the line. Hyperbolas are plane curves formed by the intersection of a right circular cone with a plane that cuts both halves of the cone.
• Hyperbolic paraboloids are surfaces generated by sliding a parabola with downward curvature along a parabola with upward curvature, or by sliding a straight line segment with its ends on two skew lines. It can thus be considered to be both a translational and a ruled surface.
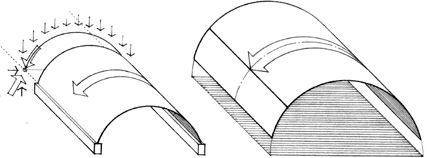
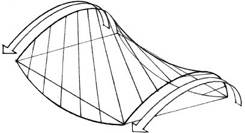
CURVED SURFACES
Saddle surfaces have an upward curvature in one direction and a downward curvature in the perpendicular direction. Regions of downward curvature exhibit archlike action while regions of upward curvature behave as a cable structure. If the edges of a saddle surface are not supported, beam behavior may also be present.
The geometric basis for these curved surfaces can be effectively utilized in digital modeling as well as in the description, fabrication and assembly of curvilinear architectural elements and components. The fluid quality of curved surfaces contrasts with the angular nature of rectilinear forms and are appropriate for describing the form of shell structures as well as nonloadbearing elements of enclosure.
Symmetrical curved surfaces, such as domes and barrel vaults, are inherently stable. Asymetrical curved surfaces, on the other hand, can be more vigorous and expressive in nature. Their shapes change dramatically as we view them from different perspectives.
Walt Disney Concert Hall, Los Angeles, California, 1987–2003, Frank O. Gehry & Partners
PRIMARY SOLIDS
“ … cubes, cones, spheres, cylinders, or pyramids are the great primary forms that light reveals to advantage; the image of these is distinct and tangible within us and without ambiguity. It is for this reason that these are beautiful forms, the most beautiful forms.” Le Corbusier
The primary shapes can be extended or rotated to generate volumetric forms or solids that are distinct, regular, and easily recognizable. Circles generate spheres and cylinders; triangles generate cones and pyramids; squares generate cubes. In this context, the term solid does not refer to firmness of substance but rather to a three-dimensional geometric body or figure.
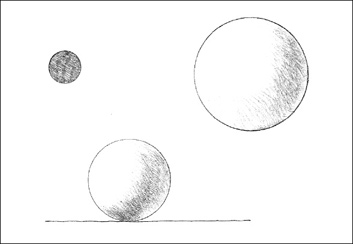
Sphere
A solid generated by the revolution of a semicircle about its diameter, whose surface is at all points equidistant from the center. A sphere is a centralized and highly concentrated form. Like the circle from which it is generated, it is self-centering and normally stable in its environment. It can be inclined toward a rotary motion when placed on a sloping plane. From any viewpoint, it retains its circular shape.
Cylinder
A solid generated by the revolution of a rectangle about one of its sides. A cylinder is centralized about the axis passing through the centers of its two circular faces. Along this axis, it can be easily extended. The cylinder is stable if it rests on one of its circular faces; it becomes unstable when its central axis is inclined from the vertical.
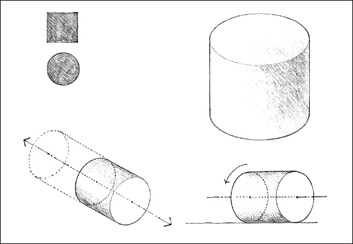
Cone
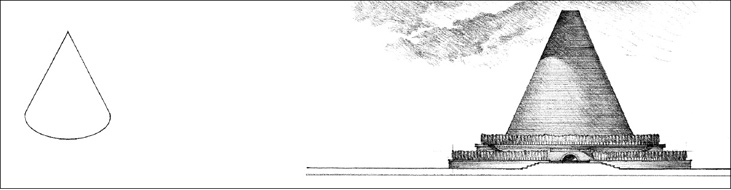
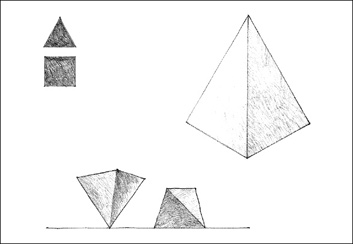
A solid generated by the revolution of a right triangle about one of its sides. Like the cylinder, the cone is a highly stable form when resting on its circular base, and unstable when its vertical axis is tipped or overturned. It can also rest on its apex in a precarious state of balance.
Pyramid
A polyhedron having a polygonal base and triangular faces meeting at a common point or vertex. The pyramid has properties similar to those of the cone. Because all of its surfaces are flat planes, however, the pyramid can rest in a stable manner on any of its faces. While the cone is a soft form, the pyramid is relatively hard and angular.
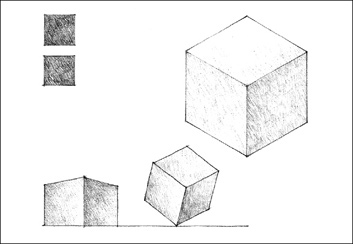
Cube
A prismatic solid bounded by six equal square sides, the angle between any two adjacent faces being a right angle. Because of the equality of its dimensions, the cube is a static form that lacks apparent movement or direction. It is a stable form except when it stands on one of its edges or corners. Even though its angular profile is affected by our point of view, the cube remains a highly recognizable form.
Maupertius, Project for an Agricultural Lodge, 1775, Claude-Nicolas Ledoux
Chapel, Massachusetts Institute of Technology, Cambridge, Massachusetts, 1955, Eero Saarinen and Associates
Project for a Conical Cenotaph, 1784, Étienne-Louis Boulée
Pyramids of Cheops, Chephren, and Mykerinos at Giza, Egypt, c. 2500 B.C.
Hanselmann House, Fort Wayne, Indiana, 1967, Michael Graves
Diwan-i-Khas, Fatehpur Sikri, Palace Complex of Akbar the Great Mogul Emperor of India, 1569–74
REGULAR & IRREGULAR FORMS
Regular forms refer to those whose parts are related to one another in a consistent and orderly manner. They are generally stable in nature and symmetrical about one or more axes. The sphere, cylinder, cone, cube, and pyramid are prime examples of regular forms.
Forms can retain their regularity even when transformed dimensionally or by the addition or subtraction of elements. From our experiences with similar forms, we can construct a mental model of the original whole even when a fragment is missing or another part is added.
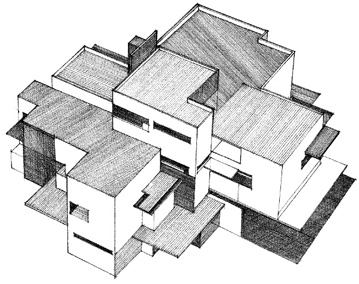
Irregular forms are those whose parts are dissimilar in nature and related to one another in an inconsistent manner. They are generally asymmetrical and more dynamic than regular forms. They can be regular forms from which irregular elements have been subtracted or result from an irregular composition of regular forms.
Since we deal with both solid masses and spatial voids in architecture, regular forms can be contained within irregular forms. In a similar manner, irregular forms can be enclosed by regular forms.
Irregular Forms:
Philharmonic Hall, Berlin, 1956–63, Hans Scharoun
An Irregular Composition of Regular Forms:
Katsura Imperial Villa, Kyoto, Japan, 17th century
Regular Forms within an Irregular Composition:
Mosque of Sultan Hasan, Cairo, Egypt, 1356–63
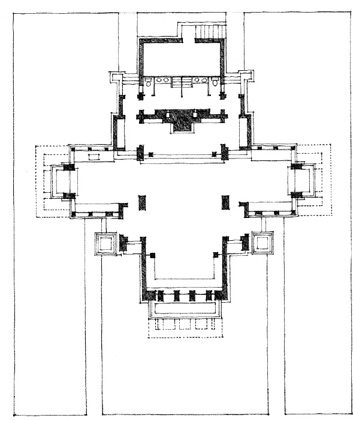
A Regular Composition of Regular Forms:
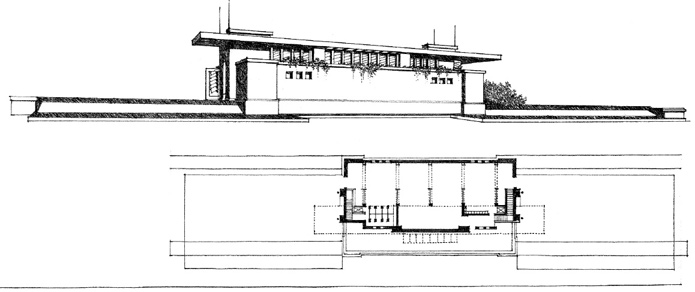
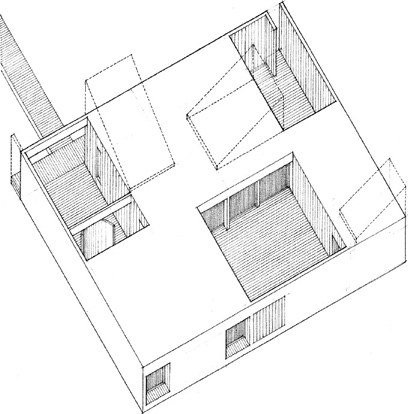
Coonley Playhouse, Riverside, Illinois, 1912, Frank Lloyd Wright
Irregular Forms within a Regular Field:
Courtyard House Project, 1934, Mies van de Rohe
TRANSFORMATION OF FORM
All other forms can be understood to be transformations of the primary solids, variations which are generated by the manipulation of one or more dimensions or by the addition or subtraction of elements.
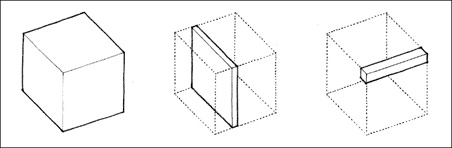
Dimensional Transformation
A form can be transformed by altering one or more of its dimensions and still retain its identity as a member of a family of forms. A cube, for example, can be transformed into similar prismatic forms through discrete changes in height, width, or length. It can be compressed into a planar form or be stretched out into a linear one.
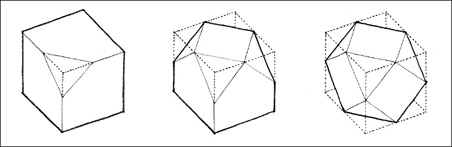
Subtractive Transformation
A form can be transformed by subtracting a portion of its volume. Depending on the extent of the subtractive process, the form can retain its initial identity or be transformed into a form of another family. For example, a cube can retain its identity as a cube even though a portion of it is removed, or be transformed into a series of regular polyhedrons that begin to approximate a sphere.
Additive Transformation
A form can be transformed by the addition of elements to its volume. The nature of the additive process and the number and relative sizes of the elements being attached determine whether the identity of the initial form is altered or retained.
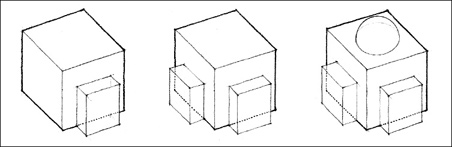
Dimensional Transformation of a Cube into a Vertical Slab:
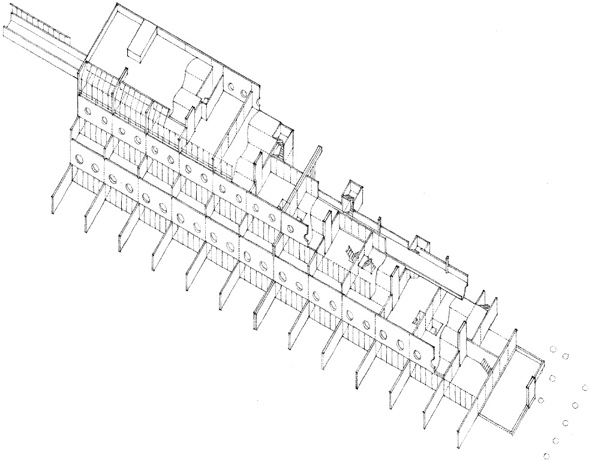
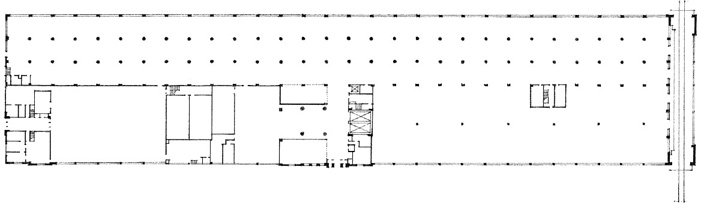
Unité d’Habitation, Firminy-Vert, France, 1963–68, Le Corbusier
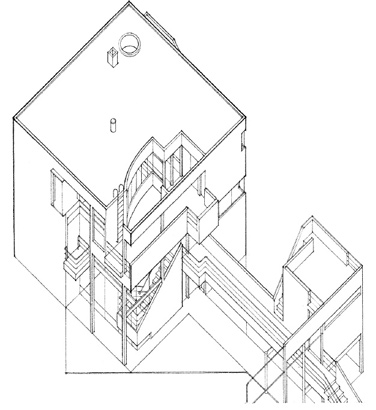
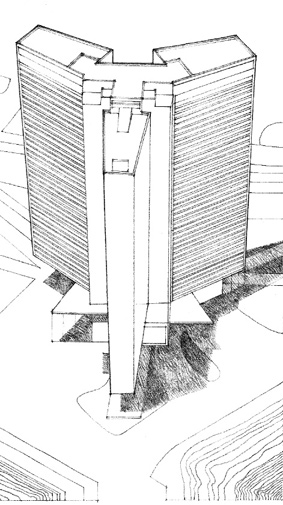
Subtractive Transformation Creating Volumes of Space:
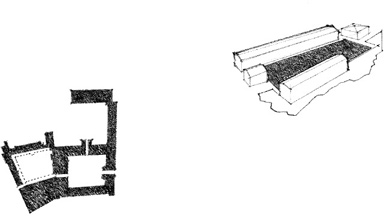
Gwathmey Residence, Amagensett, New York, 1967, Charles Gwathmey/Gwathmey Siegel
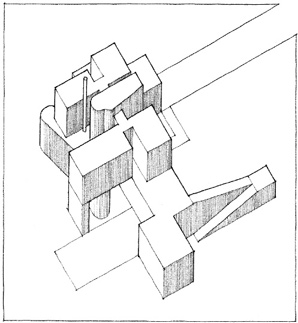
Additive Transformation of a Parent Form by the Attachment of Subordinate Parts:
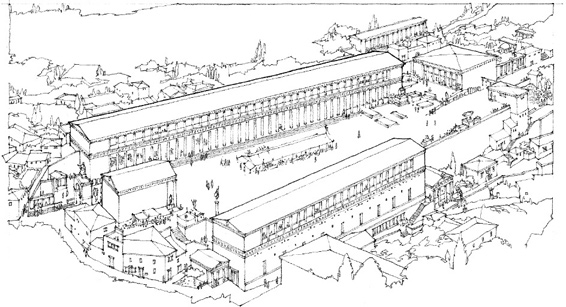
Il Redentore, Venice, 1577–92, Andrea Palladio
DIMENSIONAL TRANSFORMATION
A sphere can be transformed into any number of ovoid or ellipsoidal forms by elongating it along an axis.
A pyramid can be transformed by altering the dimensions of the base, modifying the height of the apex, or tilting the normally vertical axis.
A cube can be transformed into similar prismatic forms by shortening or elongating its height, width, or depth.
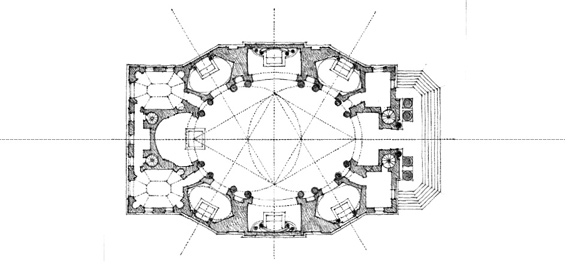
Plan of an Elliptical Church, Pensiero Della Chiesa S. Carlo, Project, 17th century, Francesco Borromini
St. Pierre, Firminy-Vert, France, 1965, Le Corbusier
Project for Yahara Boat Club, Madison, Wisconsin, 1902, Frank Lloyd Wright
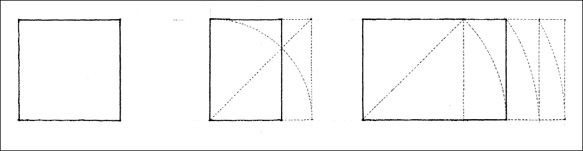
SUBTRACTIVE FORM
We search for regularity and continuity in the forms we see within our field of vision. If any of the primary solids is partially hidden from our view, we tend to complete its form and visualize it as if it were whole because the mind fills in what the eyes do not see. In a similar manner, when regular forms have fragments missing from their volumes, they retain their formal identities if we perceive them as incomplete wholes. We refer to these mutilated forms as subtractive forms.
Because they are easily recognizable, simple geometric forms, such as the primary solids, adapt readily to subtractive treatment. These forms will retain their formal identities if portions of their volumes are removed without deteriorating their edges, corners, and overall profile.
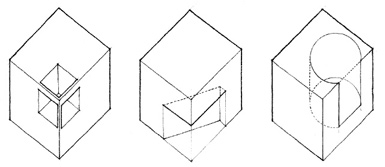
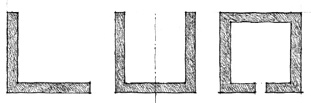
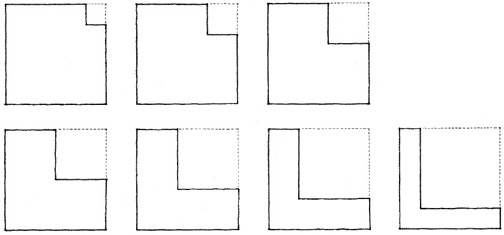
Ambiguity regarding the original identity of a form will result if the portion removed from its volume erodes its edges and drastically alters its profile.
In the series of figures below, at what point does the square shape with a corner portion removed become an L- shaped configuration of two rectangular planes?
House at Stabio, Switzerland, 1981, Mario Botta
Spatial volumes may be subtracted from a form to create recessed entrances, positive courtyard spaces, or window openings shaded by the vertical and horizontal surfaces of the recess.
Gorman Residence, Amagansett, New York, 1968, Julian and Barbara Neski
Khasneh al Faroun, Petra, 1st century A.D.
Gwathmey Residence, Amagansett, New York, 1967, Charles Gwathmey/Gwathmey Siegel & Associates
Shodhan House, Ahmedabad, India, 1956, Le Corbusier
Benacerraf House Addition, Princeton, New Jersey, 1969, Michael Graves
SUBTRACTIVE & ADDITIVE FORMS
After a sketch, Four House Forms, by Le Corbusier for the cover of Volume Two of the Oeuvre Complète, published in 1935.
ADDITIVE FORM
While a subtractive form results from the removal of a portion of its original volume, an additive form is produced by relating or physically attaching one or more subordinate forms to its volume.
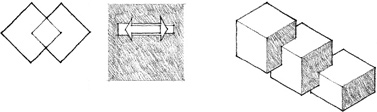
The basic possibilities for grouping two or more forms are by:
Spatial Tension
This type of relationship relies on the close proximity of the forms or their sharing of a common visual trait, such as shape, color, or material.
Edge-to-edge Contact
In this type of relationship, the forms share a common edge and can pivot about that edge.
Face-to-face Contact
This type of relationship requires that the two forms have corresponding planar surfaces which are parallel to each other.
Interlocking Volumes
In this type of relationship, the forms interpenetrate each other’s space. The forms need not share any visual traits.
Additive forms resulting from the accretion of discrete elements can be characterized by their ability to grow and merge with other forms. For us to perceive additive groupings as unified compositions of form—as figures in our visual field—the combining elements must be related to one another in a coherent manner.
These diagrams categorize additive forms according to the nature of the relationships that exist among the component forms as well as their overall configurations. This outline of formal organizations should be compared with a parallel discussion of spatial organizations in Chapter 4.
Lingaraja Temple, Bhubaneshwar, India, c. A.D. 1100
Centralized Form
A number of secondary forms clustered about a dominant, central parent-form
Linear Form
A series of forms arranged sequentially in a row
Radial Form
A composition of linear forms extending outward from a central form in a radial manner
Clustered Form
A collection of forms grouped together by proximity or the sharing of a common visual trait
Grid Form
A set of modular forms related and regulated by a three-dimensional grid
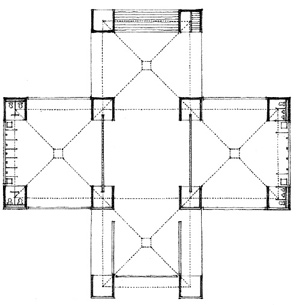
CENTRALIZED FORM
S. Maria Della Salute, Venice, 1631–82, Baldassare Longhena
Beth Sholom Synagogue, Elkins Park, Pennsylvania, 1959, Frank Lloyd Wright
Villa Capra (The Rotunda), Vicenza, Italy, 1552–67, Andrea Palladio
Centralized forms require the visual dominance of a geometrically regular, centrally located form, such as a sphere, cone, or cylinder. Because of their inherent centrality, these forms share the self-centering properties of the point and circle. They are ideal as freestanding structures isolated within their context, dominating a point in space, or occupying the center of a defined field. They can embody sacred or honorific places, or commemorate significant persons or events.
Yume-Dono, Eastern precinct of Horyu-Ji Temple, Nara, Japan, A.D. 607
Tempietto, S. Pietro in Montorio, Rome, 1502, Donato Bramante
LINEAR FORM
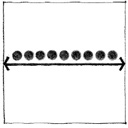
A linear form can result from a proportional change in a form’s dimensions or the arrangement of a series of discrete forms along a line. In the latter case, the series of forms may be either repetitive or dissimilar in nature and organized by a separate and distinct element such as a wall or path.
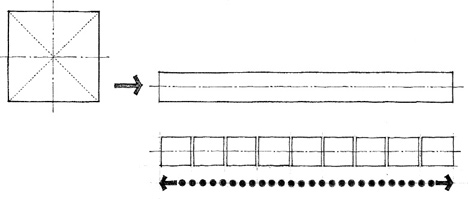
• A linear form can be segmented or curvilinear to respond to topography, vegetation, views, or other features of a site.
• A linear form can front on or define an edge of an exterior space, or define a plane of entry into the spaces behind it.
• A linear form can be manipulated to enclose a portion of space.
• A linear form can be oriented vertically as a tower element to establish or denote a point in space.
• A linear form can serve as an organizing element to which a variety of secondary forms are attached.
Runcorn New Town Housing, England,1967, James Stirling
Linear Growth through the Repetition of Forms
Linear Form Expressing Procession or Movement
Burroughs Adding Machine Company, Plymouth, Michigan, 1904, Albert Kahn
Agora of Assos, Asia Minor, 2nd Century B.C.
Linear Forms Fronting on or Defining Exterior Space
Queen’s College, Cambridge, England, 1709–38, Nicholas Hawksmoor
18th-century buildings fronting a tree-lined canal in Kampen, Holland
Henry Babson House, Riverside, Illinois, 1907, Louis Sullivan
Linear Organizations of Space
The Mile-high Illinois, Skyscraper Project, Chicago, Illinois, 1956, Frank Lloyd Wright
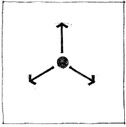
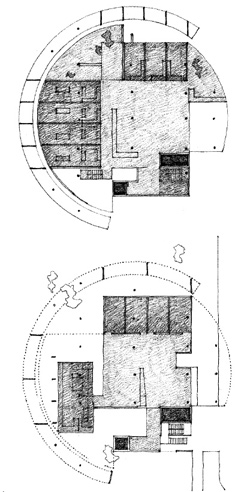
RADIAL FORM
A radial form consists of linear forms that extend outward from a centrally located core element in a radiating manner. It combines the aspects of centrality and linearity into a single composition.
Radial forms can grow into a network of centers linked by linear arms.
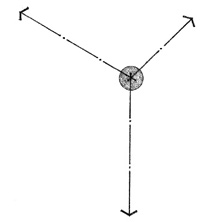
The core is either the symbolic or functional center of the organization. Its central position can be articulated with a visually dominant form, or it can merge with and become subservient to the radiating arms.
The radiating arms, having properties similar to those of linear forms, give a radial form its extroverted nature. They can reach out and relate to or attach themselves to specific features of a site. They can expose their elongated surfaces to desirable conditions of sun, wind, view, or space.
Secretariat Building, UNESCO Headquarters, Place de Fontenoy, Paris, 1953–58, Marcel Breuer
The organization of a radial form can best be seen and understood from an aerial viewpoint. When viewed from ground level, its central core element may not be clearly visible and the radiating pattern of its linear arms may be obscured or distorted through perspective foreshortening.
Skyscraper by the Sea, Project for Algiers, 1938, Le Corbusier
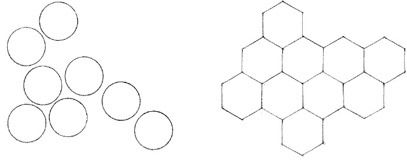
CLUSTERED FORM
While a centralized organization has a strong geometric basis for the ordering of its forms, a clustered organization groups its forms according to functional requirements of size, shape, or proximity. While it lacks the geometric regularity and introverted nature of centralized forms, a clustered organization is flexible enough to incorporate forms of various shapes, sizes, and orientations into its structure.
Considering their flexibility, clustered organizations of forms may be organized in the following ways:
• They can be attached as appendages to a larger parent form or space.
• They can be related by proximity alone to articulate and express their volumes as individual entities.
• They can interlock their volumes and merge into a single form having a variety of faces.
A clustered organization can also consist of forms that are generally equivalent in size, shape, and function. These forms are visually ordered into a coherent, nonhierarchical organization not only by their close proximity to one another, but also by the similarity of their visual properties.
A Cluster of Forms Attached to a Parent Form:
Vacation House, Sea Ranch, California, 1968, MLTW/Moore
A Cluster of Interlocking Forms:
G.N. Black House (Kragsyde), Manchester-by-the Sea, Massachusetts, 1882–83, Peabody & Stearns
A Cluster of Articulated Forms:
House Study, 1956, James Stirling & James Gowan
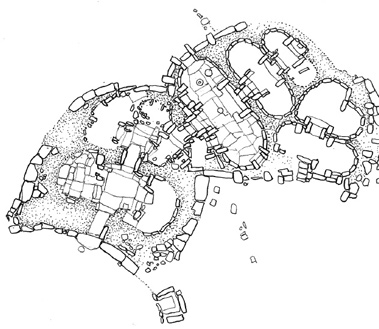
Trulli Village, Alberobello, Italy Traditional dry-stone shelters in existence since the 17th century.
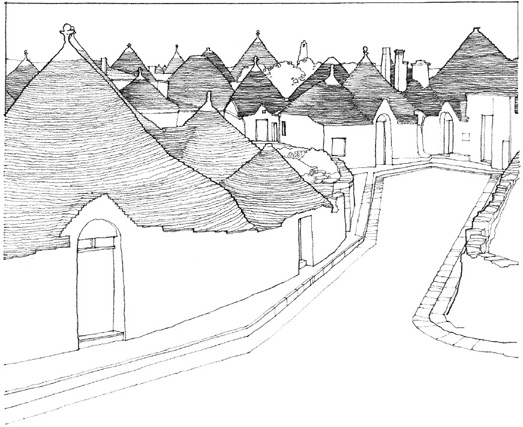
Numerous examples of clustered housing forms can be found in the vernacular architecture of various cultures. Even though each culture produced a unique style in response to differing technical, climatic, and sociocultural factors, these clustered housing organizations usually maintained the individuality of each unit and a moderate degree of diversity within the context of an ordered whole.
Dogon Housing Cluster, Southeastern Mali, West Africa, 15th century–present
Taos Pueblo, New Mexico, 13th century
Ggantija temple complex, Malta, c. 3000 B.C.
Vernacular examples of clustered forms can be readily transformed into modular, geometrically ordered compositions which are related to grid organizations of form.
Habitat Israel, Jerusalem, 1969, Moshe Safdie
Habitat Montreal, 1967, Moshe Safdie
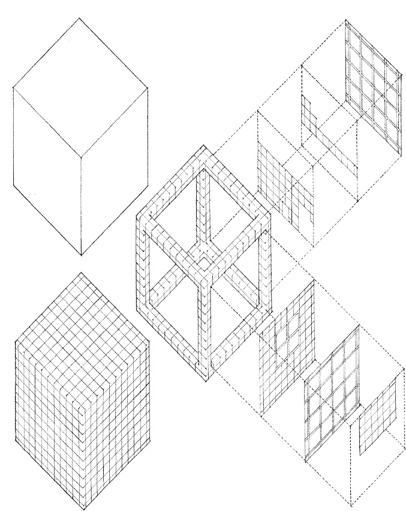
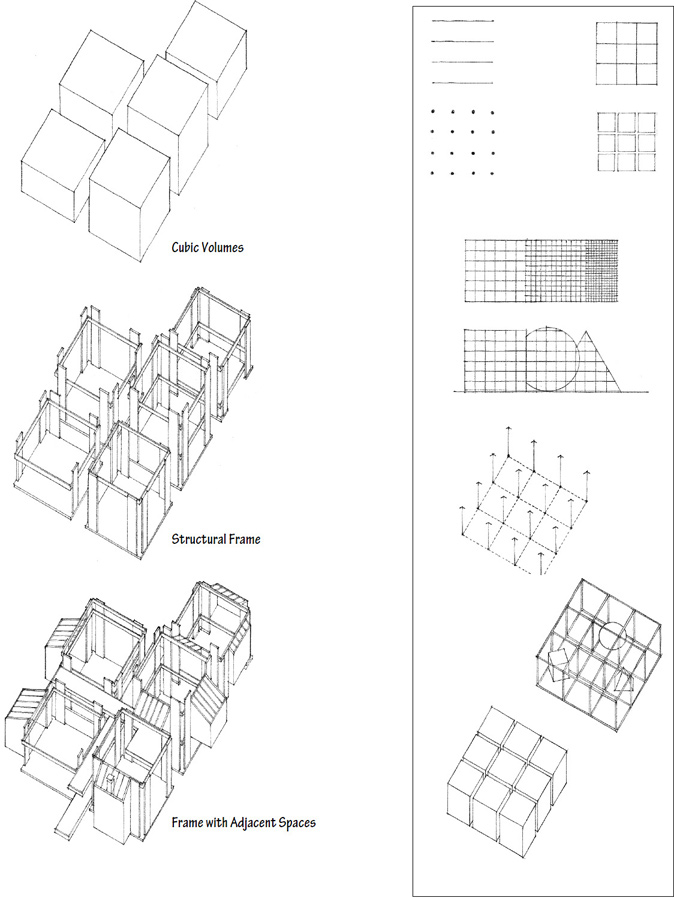
GRID FORM
Conceptual Diagram, Gunma Prefectural Museum of Fine Arts, Japan, 1974, Arata Isozaki
A grid is a system of two or more intersecting sets of regularly spaced parallel lines. It generates a geometric pattern of regularly spaced points at the intersections of the grid lines and regularly shaped fields defined by the grid lines themselves.
The most common grid is based on the geometry of the square. Because of the equality of its dimensions and its bilateral symmetry, a square grid is essentially nonhierarchical and bidirectional. It can be used to break the scale of a surface down into measurable units and give it an even texture. It can be used to wrap several surfaces of a form and unify them with its repetitive and pervasive geometry.
The square grid, when projected into the third dimension, generates a spatial network of reference points and lines. Within this modular framework, any number of forms and spaces can be visually organized.
Nakagin Capsule Building, Tokyo, 1972, Kisho Kurokawa
Hattenbach Residence, Santa Monica, California, 1971–73, Raymond Kappe
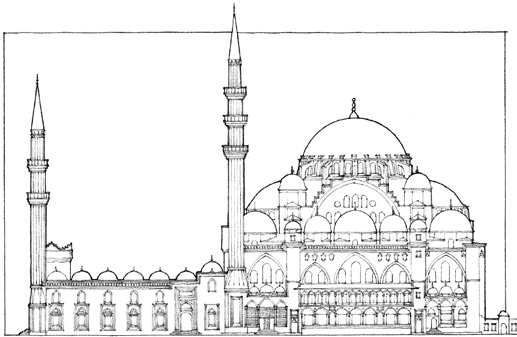
FORMAL COLLISIONS OF GEOMETRY
When two forms differing in geometry or orientation collide and interpenetrate each other’s boundaries, each will vie for visual supremacy and dominance. In these situations, the following forms can evolve:
• The two forms can subvert their individual identities and merge to create a new composite form.
• One of the two forms can receive the other totally within its volume.
• The two forms can retain their individual identities and share the interlocking portion of their volumes.
• The two forms can separate and be linked by a third element that recalls the geometry of one of the original forms.
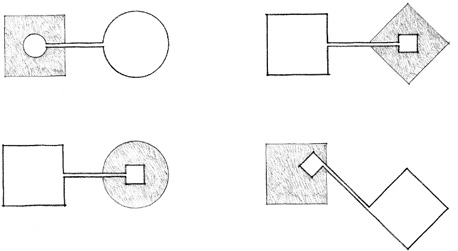
Forms differing in geometry or orientation may be incorporated into a single organization for any of the following reasons:
• To accommodate or accentuate the differing requirements of interior space and exterior form
• To express the functional or symbolic importance of a form or space within its context
• To generate a composite form that incorporates the contrasting geometries into its centralized organization
• To inflect a space toward a specific feature of a building site
• To carve a well-defined volume of space from a building form
• To express and articulate the various constructional or mechanical systems that exist within a building form
• To reinforce a local condition of symmetry in a building form
• To respond to contrasting geometries of the topography, vegetation, boundaries, or existing structures of a site
• To acknowledge an already existing path of movement through a building site
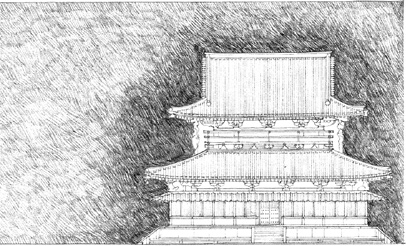
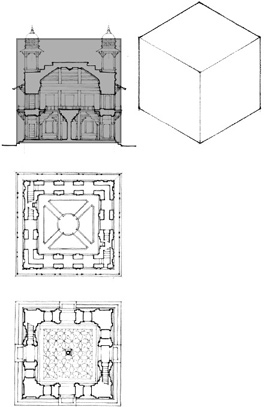
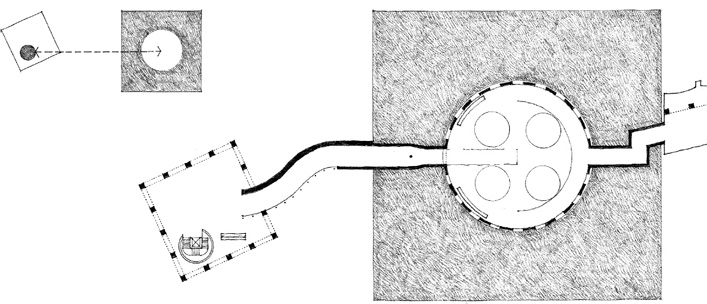
CIRCLE & SQUARE
Plan for an Ideal City, 1615, Vincenzo Scamozzi
A circular form can be freestanding in its context to express its ideal shape and still incorporate a more functional, rectilinear geometry within its boundaries.
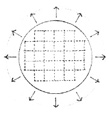
The centrality of a circular form enables it to act as a hub and unify forms of contrasting geometry or orientation about itself.
Chancellery Building, French Embassy, Brasilia, 1964–65, Le Corbusier
The Island Villa (Teatro Marittimo), Hadrian’s Villa, Tivoli, Italy, A.D. 118–125
Museum for North Rhine–Westphalia, Dusseldorf, Germany, 1975, James Stirling & Michael Wilford
Lister County Courthouse, Solvesborg, Sweden, 1917–21, Gunnar Asplund
A circular or cylindrical space can serve to organize the spaces within a rectangular enclosure.
Murray House, Cambridge, Massachusetts, 1969, MLTW/Moore-Turnbull
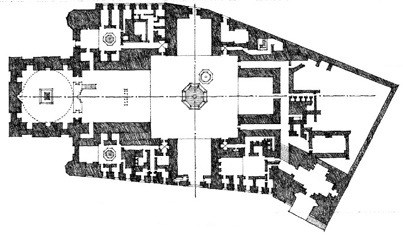
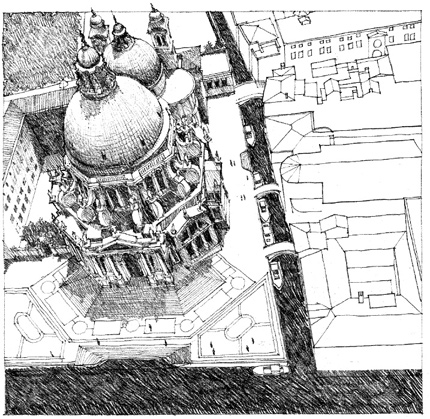
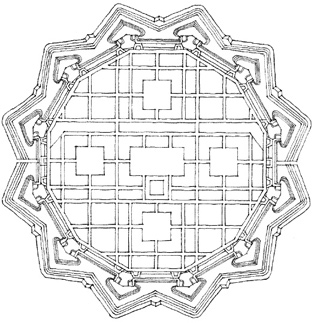
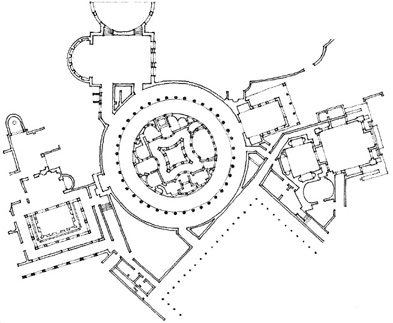
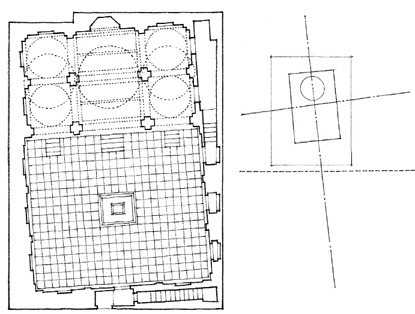
ROTATED GRID
Plan of the Ideal City of Sforzinda, 1464, Antonio Filarete
St. Mark’s Tower, Project, New York City, 1929, Frank Lloyd Wright
Pearl Mosque, within the Red Fort, an imperial palace at Agra, India, 1658–1707. The interior space of this mosque is oriented exactly with the cardinal points so that the quibla wall faces in the direction of the holy city of Mecca, while its exterior conforms to the existing layout of the fort.
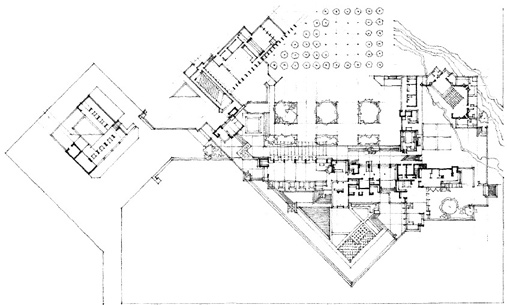
National Museum of Roman Art, Mérida, Spain, 1980–6, Rafael Moneo. The structural grid of the lower level of the museum floats over and contrasts with the geometry of the ancient Roman remains of Mérida.
A Diagram of Architecture:
Taliesin West, near Scottsdale, Arizona, 1938–59, Frank Lloyd Wright
A diagram by Bernhard Hoesli of the geometry regulating the layout of Taliesin West
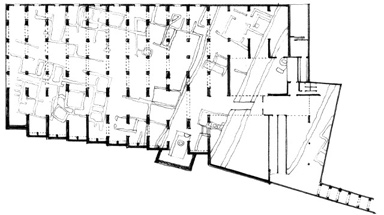
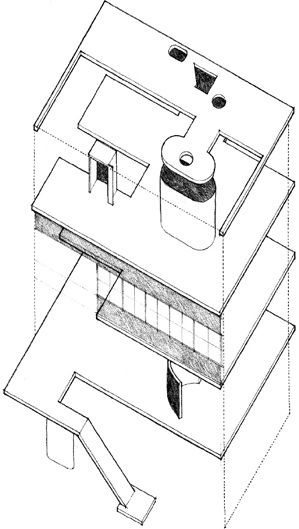
Diagram as Architecture:
House III for Robert Miller, Lakeville, Connecticut, 1971, Design Development Drawings, Peter Eisenman
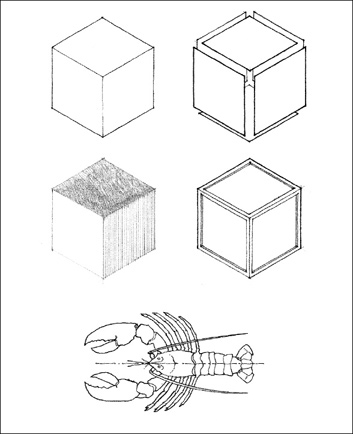
ARTICULATION OF FORM
Palacio Güell, Barcelona, 1885–89, Antonio Gaudi
Articulation refers to the manner in which the surfaces of a form come together to define its shape and volume. An articulated form clearly reveals the precise nature of its parts and their relationships to each other and to the whole. Its surfaces appear as discrete planes with distinct shapes and their overall configuration is legible and easily perceived. In a similar manner, an articulated group of forms accentuates the joints between the constituent parts in order to visually express their individuality.
A form can be articulated by:
• differentiating adjoining planes with a change in material, color, texture, or pattern
• developing corners as distinct linear elements independent of the abutting planes
• removing corners to physically separate neighboring planes
• lighting the form to create sharp contrasts in tonal value along edges and corners
In opposition to the emphasis on joints and joinery, the corners of a form can be rounded and smoothed over to emphasize the continuity of its surfaces. Or a material, color, texture, or pattern can be carried across a corner onto the adjoining surfaces to de-emphasize the individuality of the surface planes and emphasize instead the volume of a form.
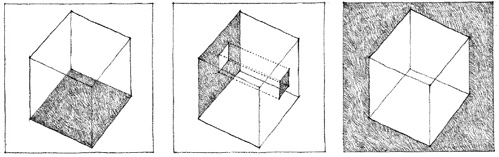
EDGES & CORNERS
Since the articulation of a form depends to a great degree on how its surfaces meet each other at corners, how these edge conditions are resolved is critical to the definition and clarity of a form.
While a corner can be articulated by simply contrasting the surface qualities of the adjoining planes, or obscured by layering their joining with an optical pattern, our perception of its existence is also affected by the laws of perspective and the quality of light that illuminates the form.
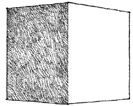
For a corner to be formally active, there must be more than a slight deviation in the angle between the adjoining planes. Since we constantly search for regularity and continuity within our field of vision, we tend to regularize or smooth out slight irregularities in the forms we see. For example, a wall plane that is bent only slightly will appear to be a single flat plane, perhaps with a surface imperfection. A corner would not be perceived.
At what point do these formal deviations become an acute angle? … a right angle?
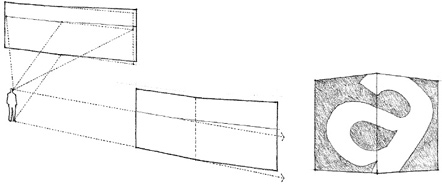
a segmented line? … a straight line?
a circular segment? … a change in a line’s contour?
CORNERS
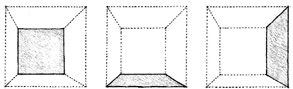
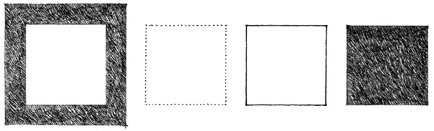
Corners define the meeting of two planes. If the two planes simply touch and the corner remains unadorned, the presence of the corner will depend on the visual treatment of the adjoining surfaces. This corner condition emphasizes the volume of a form.
A corner condition can be visually reinforced by introducing a separate and distinct element that is independent of the surfaces it joins. This element articulates the corner as a linear condition, defines the edges of the adjoining planes, and becomes a positive feature of the form.
If an opening is introduced to one side of the corner, one of the planes will appear to bypass the other. The opening diminishes the corner condition, weakens the definition of the volume within the form, and emphasizes the planar qualities of the neighboring surfaces.
If neither plane is extended to define the corner, a volume of space is created to replace the corner. This corner condition deteriorates the volume of the form, allows the interior space to leak outward, and clearly reveals the surfaces as planes in space.
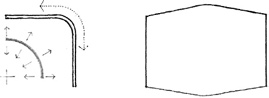
Rounding off the corner emphasizes the continuity of the bounding surfaces of a form, the compactness of its volume, and softness of its contour. The scale of the radius of curvature is important. If too small, it becomes visually insignificant; if too large, it affects the interior space it encloses and the exterior form it describes.
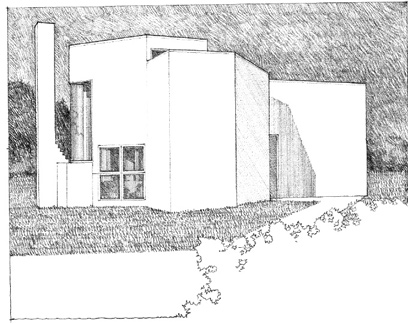
Everson Museum, Syracuse, New York, 1968, I.M. Pei
The unadorned corners of the forms emphasize the volume of their mass.
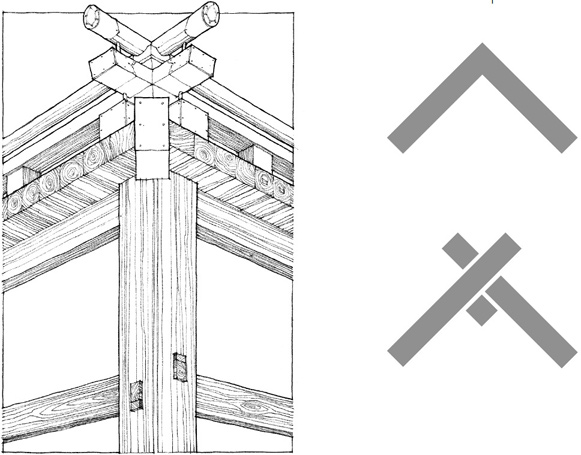
Corner Detail, Izumo Shrine, Shimane Prefecture, Japan, A.D. 717 (last rebuilt in 1744).
The timber joinery articulates the individuality of the members meeting at the corner.
Corner Detail, Commonwealth Promenade Apartments, Chicago, 1953–56, Mies van der Rohe. The corner member is recessed to be independent of the adjoining wall planes.
Corner Detail, The Basilica, Vicenza, Italy, 1545, Andrea Palladio. The corner column emphasizes the edge of the building form.
Einstein Tower, Potsdam, Germany, 1919, Eric Mendelsohn
Rounded corners express continuity of surface, compactness of volume, and softness of form.
Laboratory Tower, Johnson Wax Building, Racine, Wisconsin, 1950, Frank Lloyd Wright
Kaufmann Desert House, Palm Springs, California, 1946, Richard Neutra
Openings at corners emphasize the definition of planes over volume.
Architectural Design Study, 1923, Van Doesburg and Van Esteren
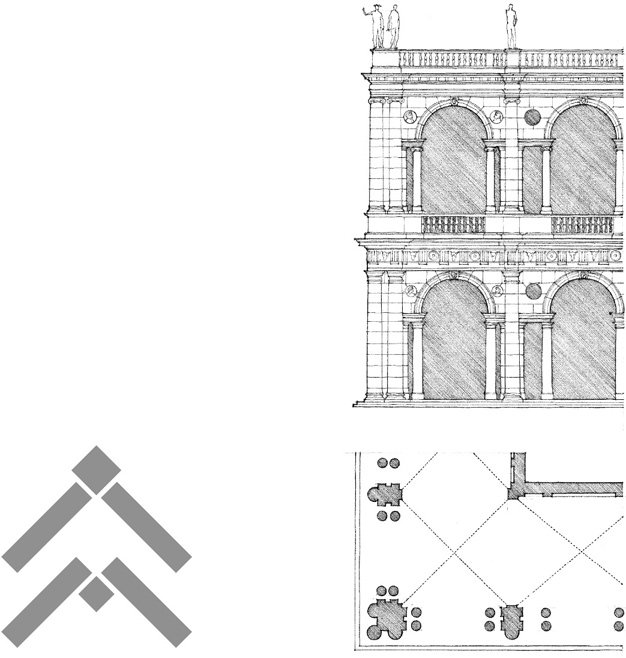
SURFACE ARTICULATION
Our perception of the shape, size, scale, proportion, and visual weight of a plane is influenced by its surface properties as well as its visual context.
• A distinct contrast between the surface color of a plane and that of the surrounding field can clarify its shape, while modifying its tonal value can either increase or decrease its visual weight.
• A frontal view reveals the true shape of a plane; oblique views distort it.
• Elements of known size within the visual context of a plane can aid our perception of its size and scale.
• Texture and color together affect the visual weight and scale of a plane and the degree to which it absorbs or reflects light and sound.
• Directional or oversized optical patterns can distort the shape or exaggerate the proportions of a plane.
Vincent Street Flats, London, 1928, Sir Edwin Lutyens
Palazzo Medici-Ricardo, Florence, Italy, 1444–60, Michelozzi
The color, texture, and pattern of surfaces articulate the existence of planes and influence the visual weight of a form.
Hoffman House, East Hampton, New York, 1966–67, Richard Meier
John Deere & Company Building, Moline, Illinois, 1961–64, Eero Saarinen & Associates. The linear sun-shading devices accentuate the horizontality of the building form.
CBS Building, New York City,1962–64, Eero Saarinen & Associates. Linear columnar elements emphasize the verticality of this high-rise structure.
Linear patterns have the ability to emphasize the height or length of a form, unify its surfaces, and define its textural quality.
Fukuoka Sogo Bank, Study of the Saga Branch, 1971, Arata Isozaki. A grid pattern unifies the surfaces of the three-dimensional composition.
A transformation from a pattern of openings in a plane to an open facade articulated by a linear framework.
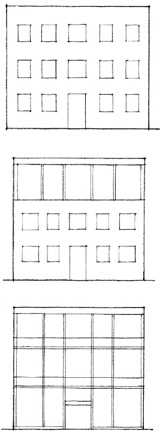
IBM Research Center, La Guade, Var, France, 1960–61, Marcel Breuer.
The three-dimensional form of the openings creates a texture of light, shade, and shadows.
First Unitarian Church, Rochester, New York, 1956–67, Louis Kahn.
The pattern of openings and cavities interrupts the continuity of the exterior wall planes.
