Chapter 6: Proportion & Scale

Chapter 6

Proportion & Scale

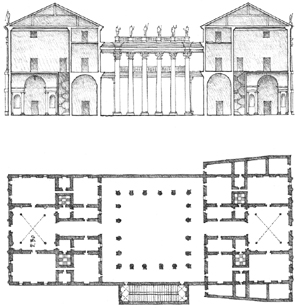
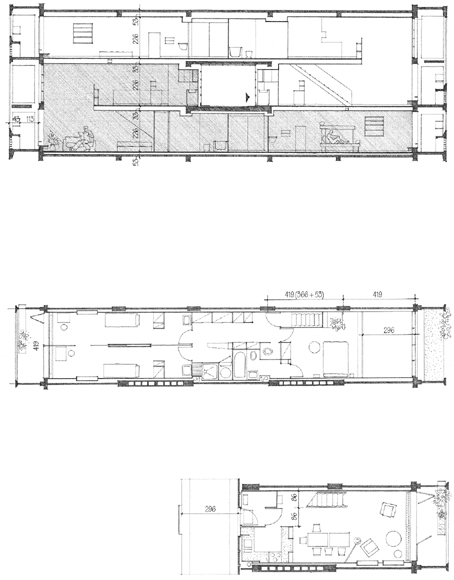
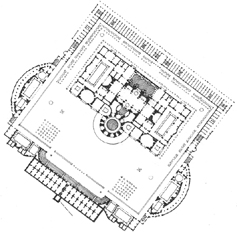
“… Within the Villa Foscari you are aware of the thickness of the walls that separate the rooms, each of which has been given definitive and precise form. At either end of the cross-arm of the central hall is a square room measuring 16 x 16 feet. It lies between a larger and a smaller rectangular room, the one 12 x 16, the other 16 x 24 feet, or twice as large. The smaller has its longer wall, the larger its shorter, in common with the square room. Palladio placed great emphasis on these simple ratios: 3:4, 4:4, and 4:6, which are those found in musical harmony. The width of the central hall is also based on 16. Its length is less exact because the thickness of the walls must be added to the simple dimensions of the rooms. The special effect of the hall in this firmly interlocked composition is produced by its great height, the barrel-vaulted ceiling towering high above the side rooms into the mezzanine. But, you may ask, does the visitor actually experience these proportions? The answer is yes—not the exact measurements but the fundamental idea behind them. You receive an impression of a noble, firmly integrated composition in which each room presents an ideal form within a greater whole. You also feel the the rooms are related in size. Nothing is trivial—all is great and whole.”

Steen Eiler Rasmussen
Experiencing Architecture
1962

PROPORTION & SCALE

This chapter discusses the interrelated issues of proportion and scale. While scale alludes to the size of something compared to a reference standard or to the size of something else, proportion refers to the proper or harmonious relation of one part to another or to the whole. This relationship may not only be one of magnitude, but also of quantity or degree. While the designer usually has a range of choices when determining the proportions of things, some are given to us by the nature of materials, by how building elements respond to forces, and by how things are made.

MATERIAL PROPORTIONS

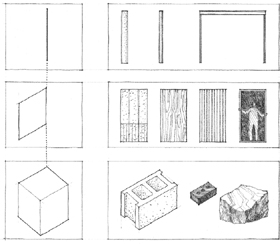
All building materials in architecture have distinct properties of elasticity, hardness, and durability. And they all have an ultimate strength beyond which they cannot extend themselves without fracturing, breaking, or collapsing. Since the stresses in a material resulting from the force of gravity increase with size, all materials also have rational dimensions beyond which they cannot go. For example, a stone slab that is four-inches thick and eight-feet long can be reasonably expected to support itself as a bridge between two supports. But if its size were to increase fourfold, to sixteen-inches thick and thirty-two-feet long, it would probably collapse under its own weight. Even a strong material like steel has lengths beyond which it cannot span without exceeding its ultimate strength.

All materials also have rational proportions that are dictated by their inherent strengths and weaknesses. Masonry units like brick, for example, are strong in compression and depend on their mass for strength. Such materials are therefore volumetric in form. Materials like steel are strong in both compression and tension and can therefore be formed into linear columns and beams as well as planar sheet materials. Wood, being a flexible and fairly elastic material, can be used as linear posts and beams, planar boards, and as a volumetric element in log cabin construction.

STRUCTURAL PROPORTIONS

In the construction of architecture, structural elements are called upon to span spaces and transmit their loads through vertical supports to the foundation system of a building. The size and proportion of these elements are directly related to the structural tasks they perform and can therefore be visual indicators of the size and scale of the spaces they help enclose.

Beams, for example, transmit their loads horizontally across space to their vertical supports. If the span or load of a beam were doubled, its bending stresses would likewise double, possibly causing it to collapse. But if its depth were doubled, its strength would increase fourfold. Depth, therefore, is the critical dimension of a beam and its depth-to-span ratio can be a useful indicator of its structural role.

In a similar manner, columns become thicker as their loads and unsupported height increase. Together, beams and columns form a skeletal structural framework that defines modules of space. By their size and proportion, columns and beams articulate space and give it scale and a hierarchical structure. This can be seen in the way joists are supported by beams, which in turn are supported by girders. Each element increases in depth as its load and span increase in size.

South gateway of the third fence of Naigu, the inner shrine, Ise Shrine, Mie Prefecture, Japan, A.D. 690

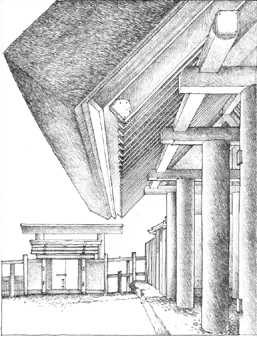
The proportions of other structural elements, as bearing walls, floor and roof slabs, vaults, and domes, also give us visual clues to their role in a structural system as well as the nature of their material. A masonry wall, being strong in compression but relatively weak in bending, will be thicker than a reinforced concrete wall doing the same work. A steel column will be thinner than a wood post supporting the same load. A four-inch-thick reinforced concrete slab will span farther than four-inch wood decking.

As a structure depends less on the weight and stiffness of a material and more on its geometry for stability, as in the case of a membrane structure or a space frame, its elements will get thinner and thinner until they lose their ability to give a space scale and dimension.

Wood and Brick
Schwartz House, Two Rivers, Wisconsin, 1939, Frank Lloyd Wright

Membrane
Roof of Olympic Swimming Arena, Munich, Germany, 1972, Fred Otto

Steel
Crown Hall, Illinois Institute of Technology, Chicago, 1956, Mies van der Rohe

MANUFACTURED PROPORTIONS

Many architectural elements are sized and proportioned not only according to their structural properties and function, but also by the process through which they are manufactured. Because these elements are mass-produced in factories, they have standard sizes and proportions imposed on them by the individual manufacturers or by industry standards.

Concrete block and common brick, for example, are produced as modular building units. Although they differ from each other in size, both are proportioned on a similar basis. Plywood and other sheathing materials also are manufactured as modular units with fixed proportions. Steel sections have fixed proportions generally agreed upon by the steel manufacturers and the American Institute of Steel Construction. Windows and doors have proportions that are set by the individual manufacturers of the units.

Standard Casement Window Units

Since these and other materials must ultimately come together and achieve a high degree of fit in the construc-tion of a building, the standard sizes and proportions of factory-produced elements affect the size, proportion, and spacing of other materials as well. Standard door and window units are sized and proportioned to fit into modular masonry openings. Wood or metal studs and joists are spaced to accept modular sheathing materials.

PROPORTIONING SYSTEMS

Even considering the proportional constraints imposed on a form by the nature of its material, its structural function, or by the manufacturing process, the designer still has the ability to control the proportion of the forms and spaces within and around a building. The decision to make a room square or oblong in plan, intimate or lofty in scale, or to endow a building with an imposing, higher-than-normal facade, legitimately falls to the designer. But on what basis are these decisions made?

If a space 400 square feet in area were required, what dimensions—what ratios of width-to-length and length-to-height—should it have? Of course, the functioning of the space and the nature of the activities to be accommodated will influence its form and proportion.

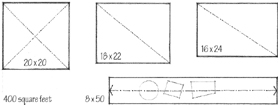
A technical factor, such as its structure, might limit one or more of its dimensions. Its context—the exterior environment or an adjacent interior space—might pressure its form. The decision might be to recall a space from another time and place and to simulate its proportions. Or the decision might be based finally on an aesthetic, visual judgment of the “desirable” relationships among the dimensions of the parts and the whole of a building.

A square space, having four equal faces, is static in nature. If its length expands and dominates its width, it becomes more dynamic. While square and oblong spaces define places for activity, linear spaces encourage movement and are susceptible to subdivision into a number of zones.

Woodland Chapel, Stockholm, Sweden, 1918–20, Erik Gunnar Asplund

Proportion is the equality between two ratios in which the first of the four terms divided by the second equals the third divided by the fourth.

In truth, our perception of the physical dimensions of architecture, of proportion and scale, is imprecise. It is distorted by the foreshortening of perspective and distance, and by cultural biases, and is thus difficult to control and predict in an objective and precise manner.

Small or slight differences in the dimensions of a form are especially difficult to discern. While a square, by definition, has four equal sides and four right angles, a rectangle can appear to be exactly square, almost a square, or very much unlike a square. It can appear to be long, short, stubby, or squat, depending on our point of view. We use these terms to give a form or figure a visual quality that is largely a result of how we perceive its proportions. It is not, however, an exact science.

If the precise dimensions and relationships of a design that is regulated by a proportioning system cannot be objectively perceived in a similar manner by everyone, why are proportioning systems useful and of particular significance in architectural design?

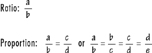
The intent of all theories of proportions is to create a sense of order and harmony among the elements in a visual construction. According to Euclid, a ratio refers to the quantitative comparison of two similar things, while proportion refers to the equality of ratios. Underlying any proportioning system, therefore, is a characteristic ratio, a permanent quality that is transmitted from one ratio to another. Thus, a proportioning system establishes a consistent set of visual relationships between the parts of a building, as well as between the parts and the whole. Although these relationships may not be immediately perceived by the casual observer, the visual order they create can be sensed, accepted, or even recognized through a series of repetitive experiences. Over a period of time, we might begin to see the whole in the part, and the part in the whole.

Proportioning systems go beyond the functional and technical determinants of architectural form and space to provide an aesthetic rationale for their dimensions. They can visually unify the multiplicity of elements in an architectural design by having all of its parts belong to the same family of proportions. They can provide a sense of order in, and heighten the continuity of, a sequence of spaces. They can establish relationships between the exterior and interior elements of a building.

A number of theories of “desirable” proportions have been developed in the course of history. The notion of devising a system for design and communicating its means is common to all periods. Although the actual system varies from time to time, the principles involved and their value to the designer remain the same.

Theories of Proportion:

• Golden Section

• Classical Orders

• Renaissance Theories

• Modulor

• Ken

• Anthropometry

• Scale

A fixed proportion used in determining measurements and dimensions

Types of Proportion:

GOLDEN SECTION

The geometric construction of the Golden Section, first by extension, and then by division.

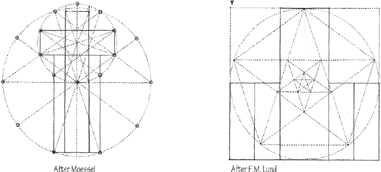
Mathematical systems of proportion originate from the Pythagorean concept of ‘all is number’ and the belief that certain numerical relationships manifest the harmonic structure of the universe. One of these relationships that has been in use ever since the days of antiquity is the proportion known as the Golden Section. The Greeks recognized the dominating role the Golden Section played in the proportions of the human body. Believing that both humanity and the shrines housing their deities should belong to a higher universal order, they utilized these same proportions in their temple structures. Renaissance architects also explored the Golden Section in their work. In more recent times, Le Corbusier based his Modulor system on the Golden Section. Its use in architecture endures even today.

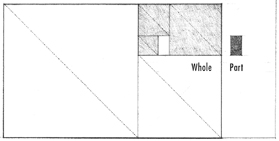
The Golden Section can be defined as the ratio between two sections of a line, or the two dimensions of a plane figure, in which the lesser of the two is to the greater as the greater is to the sum of both. It can be expressed algebraically by the equation of two ratios: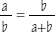

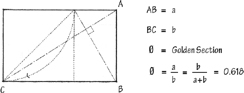
The Golden Section has some remarkable algebraic and geometric properties that account for its existence in architecture as well as in the structures of many living organisms. Any progression based on the Golden Section is at once additive and geometrical.

Another progression that closely approximates the Golden Section in whole numbers is the Fibonacci Series: 1, 1, 2, 3, 5, 8, 13 …. Each term again is the sum of the two preceding ones, and the ratio between two consecutive terms tends to approximate the Golden Section as the series progresses to infinity.

In the numerical progression: 1, θ 1, θ 2, θ 3 … θn, each term is the sum of the two preceding ones.

A rectangle whose sides are proportioned according to the Golden Section is known as a Golden Rectangle. If a square is constructed on its smaller side, the remaining portion of the original rectangle would be a smaller but similar Golden Rectangle. This operation can be repeated indefinitely to create a gradation of squares and Golden Rectangles. During this transformation, each part remains similar to all of the other parts, as well as to the whole. The diagrams on this page illustrate this additive and geometrical growth pattern of progressions based on the Golden Section.

The Parthenon, Athens, 447–432 B.C., Ictinus and Callicrates

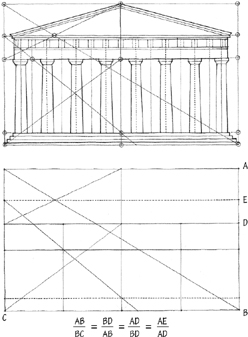
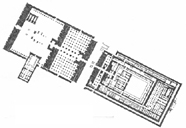
These two graphic analyses illustrate the use of the Golden Section in the proportioning of the facade of the Parthenon. It is interesting to note that while both analyses begin by fitting the facade into a Golden Rectangle, each analysis then varies from the other in its approach to proving the existence of the Golden Section and its effect on the dimensions and distribution of elements across the facade.

Tempietto of S. Pietro in Montorio, Rome, 1502—10, Donato Bramante

World Museum (Project), Geneva, 1929, Le Corbusier

Standard Gothic Plan and Section

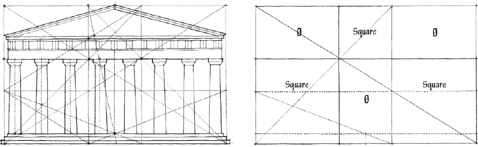
REGULATING LINES

Palazzo Farnese, Rome, 1515, Antonio da Sangallo the Younger

The Pantheon, Rome, A.D. 120–124

If the diagonals of two rectangles are either parallel or perpendicular to each other, they indicate that the two rectangles have similar proportions. These diagonals, as well as lines that indicate the common alignment of elements, are called regulating lines. They were seen previously in the discussion of the Golden Section, but they can also be used to control the proportion and placement of elements in other proportioning systems as well. Le Corbusier, in Towards a New Architecture, stated the following:

“A regulating line is an assurance against capriciousness; it is a means of verification which can ratify all work created in fervour … It confers on the work the quality of rhythm. The regulating line brings in this tangible form of mathematics which gives the reassuring perception of order. The choice of a regulating line fixes the fundamental geometry of the work … It is a means to an end; it is not a recipe.”

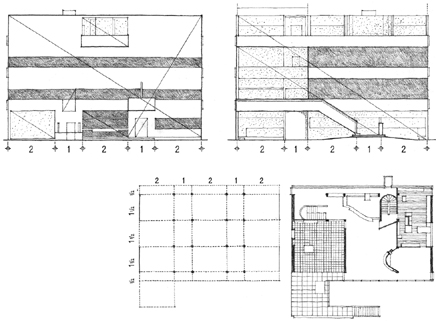
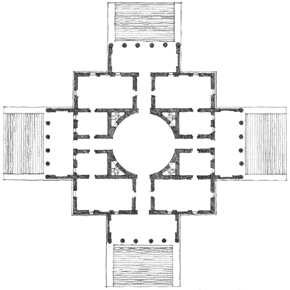
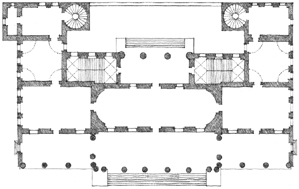
In his essay, The Mathematics of the Ideal Villa, 1947, Colin Rowe pointed out the similarity between the spatial subdivision of a Palladian villa and the structural grid of a villa by Le Corbusier. While both villas shared a similar proportioning system and a relationship to a higher mathematical order, Palladio’s villa consisted of spaces with fixed shapes and harmonic interrelationships. Le Corbusier’s villa was composed of horizontal layers of free space defined by the floor and roof slabs. The rooms varied in shape and were asymmetrically arranged at each level.

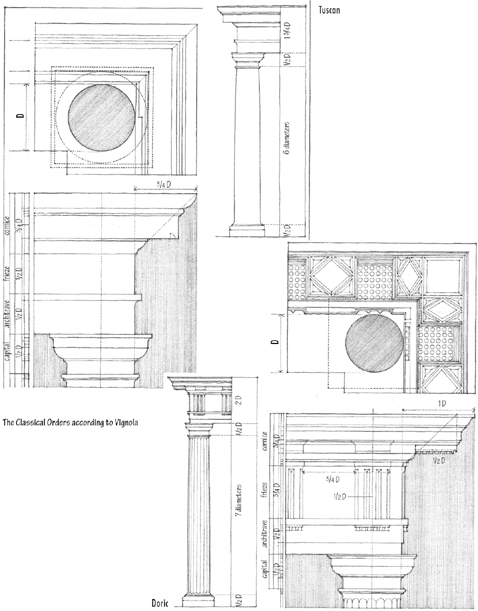
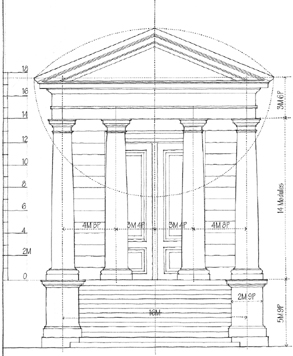
Villa Garches, Vaucresson, France, 1926–27, Le Corbusier

Villa Foscari, Malcontenta, Italy, 1558, Andrea Palladio

CLASSICAL ORDERS

Ionic Order, from the Temple on the Ilissus, Athens, 449 B.C., Callicrates. After a drawing by William R. Ware.

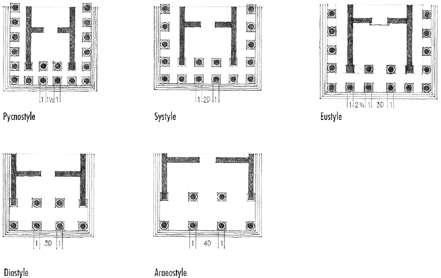
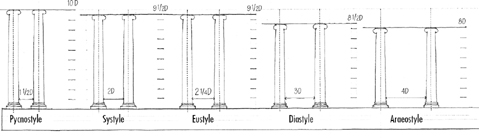
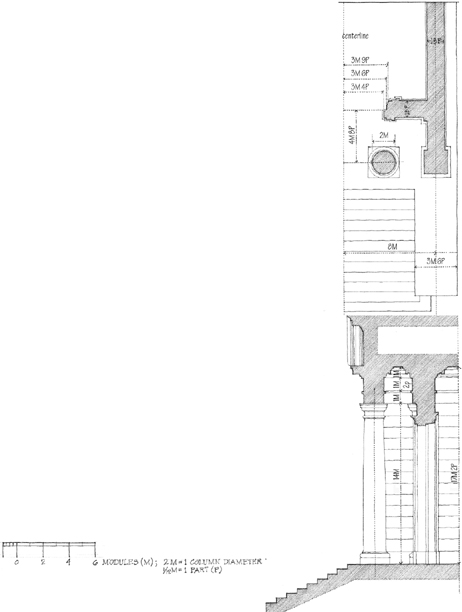
To the Greeks and Romans of classical antiquity, the Orders represented in their proportioning of elements the perfect expression of beauty and harmony. The basic unit of dimension was the diameter of the column. From this module were derived the dimensions of the shaft, the capital, as well as the pedestal below and the entablature above, down to the smallest detail. Intercolumniation—the system of spacing between columns—was also based on the diameter of the column.

Because the sizes of columns varied according to the extent of a building, the Orders were not based on a fixed unit of measurement. Rather, the intention was to ensure that all of the parts of any one building were proportionate and in harmony with one another.

Vitruvius, in the time of Augustus, studied actual examples of the Orders and presented his ‘ideal’ proportions for each in his treatise, The Ten Books on Architecture. Vignola recodified these rules for the Italian Renaissance and his forms for the Orders are probably the best known today.

Classification of Temples according to their Intercolumniation

Vitruvius’ Rules for the Diameter, Height, and Spacing of Columns

Temple Front in the Tuscan Order

RENAISSANCE THEORIES

S. Maria Novella, Florence, Italy.
Alberti designed the Renaissance facade (1456–70) to complete a Gothic church (1278–1350).

Diagram by Francesco Giorgi, 1525, illustrating the series of interlocking ratios that results from applying Pythagoras’ theory of means to the intervals of the Greek musical scale.

Pythagoras discovered that the consonances of the Greek musical system could be expressed by the simple numerical progression—1, 2, 3, 4—and their ratios, 1:2, 1:3, 2:3, 3:4. This relationship led the Greeks to believe they had found the key to the mysterious harmony that pervaded the universe. The Pythagorean creed was “Everything is arranged according to numbers.” Plato later developed Pythagoras’ aesthetics of numbers into an aesthetics of proportion. He squared and cubed the simple numerical progression to produce the double and triple progressions, 1, 2, 4, 8, and 1, 3, 9, 27. For Plato, these numbers and their ratios not only contained the consonances of the Greek musical scale but also expressed the harmonic structure of his universe.

The architects of the Renaissance, believing that their buildings had to belong to a higher order, returned to the Greek mathematical system of proportions. Just as the Greeks conceived music to be geometry translated into sound, Renaissance architects believed that architecture was mathematics translated into spatial units. Applying Pythagoras’ theory of means to the ratios of the intervals of the Greek musical scale, they developed an unbroken progression of ratios that formed the basis for the proportions of their architecture. These series of ratios manifested themselves not only in the dimensions of a room or a facade, but also in the interlocking proportions of a sequence of spaces or an entire plan.

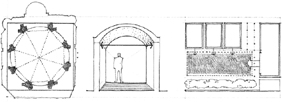
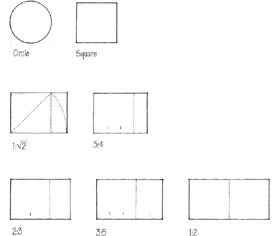
Seven Ideal Plan Shapes for Rooms.
Andrea Palladio (1508–80) was probably the most influential architect of the Italian Renaissance. In The Four Books on Architecture, first published in Venice in 1570, he followed in the footsteps of his predecessors, Alberti and Serlio, and proposed these seven “most beautiful and proportionable manners of rooms.”

Determining the Heights of Rooms.
Palladio also proposed several methods for determining the height of a room so that it would be in proper proportion to the room’s width and length. The height of rooms with flat ceilings would be equal to their width. The height of square rooms with vaulted ceilings would be one-third greater than their width. For other rooms, Palladio used Pythagoras’ theory of means to determine their heights. Accordingly, there were three types of means: arithmetic, geometric, and harmonic.

Arithmetic:

Geometric: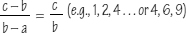

Harmonic:

In each case, the height of a room is equal to the mean (b) between the two extremes of the width (a) and length (c) of the room.

“Beauty will result from the form and correspondence of the whole, with respect to the several parts, of the parts with regard to each other, and of these again to the whole; that the structure may appear an entire and complete body, wherein each member agrees with the other, and all necessary to compose what you intend to form.”
Andrea Palladio, The Four Books on Architecture, Book I, Chapter 1.

Villa Capra (The Rotunda), Vicenza, Italy, 1552–67, Andrea Palladio 12 x 30, 6 x 15, 30 x 30

Palazzo Chiericati, Vicenza, Italy, 1550, Andrea Palladio 54 x 16 (18), 18 x 30, 18 x 18, 18 x 12

Villa Thiene, Cicogna, Italy, 1549, Andrea Palladio
18 x 36, 36 x 36, 36 x 18, 18 x 18, 18 x 12

Palazzo Iseppo Porto, Vicenza, Italy, 1552, Andrea Palladio
30 x 30, 20 x 30, 10 x 30, 45 x 45

MODULOR

Le Corbusier developed his proportioning system, the Modulor, to order “the dimensions of that which contains and that which is contained.” He saw the measuring tools of the Greeks, Egyptians, and other high civilizations as being “infinitely rich and subtle because they formed part of the mathematics of the human body, gracious, elegant, and firm, the source of that harmony which moves us, beauty.” He therefore based his measuring tool, the Modulor, on both mathematics (the aesthetic dimensions of the Golden Section and the Fibonacci Series), and the proportions of the human body (functional dimensions).

Le Corbusier began his study in 1942, and published The Modulor: A Harmonious Measure to the Human Scale Universally Applicable to Architecture and Mechanics in 1948. A second volume, Modulor II, was published in 1954.

The basic grid consist of three measures, 113, 70, and 43 centimeters, proportioned according to the Golden Section.

43 + 70 = 113

113 + 70 = 183

113 + 70 + 43 = 226 (2 x 113)

113, 183, and 226 define the space occupied by the human figure. From 113 and 226, Le Corbusier developed the Red and Blue series, diminishing scales of dimensions that were related to the stature of the human figure.

Le Corbusier saw the Modulor not merely as a series of numbers with an inherent harmony, but as a system of measurements that could govern lengths, surfaces, and volumes, and “maintain the human scale everywhere.” It could “lend itself to an infinity of combinations; it ensures unity with diversity … the miracle of numbers.”

The principal work of Le Corbusier that exemplified the use of the Modulor was his Unité d’Habitation at Marseilles. It uses 15 measures of the Modulor to bring human scale to a building that is 140 meters long, 24 meters wide, and 70 meters high.

Le Corbusier used these diagrams to illustrate the diversity of panel sizes and surfaces that could be obtained with the proportions of the Modulor.

Facade Detail, Unité d’Habitation, Firminy-Vert, France, 1965–68, Le Corbusier

Plans and Section of Typical Apartment Unit,
Unité d’Habitation, Marseilles, 1946–52, Le Corbusier

KEN

Traditional Japanese House

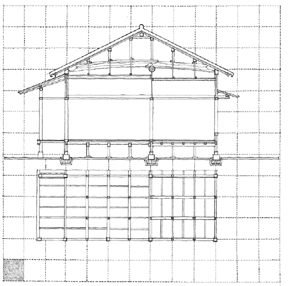
The traditional Japanese unit of measure, the shaku, was originally imported from China. It is almost equiva lent to the English foot and divisible into decimal units. Another unit of measure, the ken, was introduced in the latter half of Japan’s Middle Ages. Although it was originally used simply to designate the interval between two columns and varied in size, the ken was soon standardized for residential architecture. Unlike the module of the Classical Orders, which was based on the diameter of a column and varied with the size of a building, the ken became an absolute measurement.

The ken, however, was not only a measurement for the construction of buildings. It evolved into an aesthetic module that ordered the structure, materials, and space of Japanese architecture.

The tokonoma (picture recess) is a shallow, slightly raised alcove for the display of a kakemono or flower arrangement. As the spiritual center of a traditional Japanese house, the tokonoma is located in its most formal room.

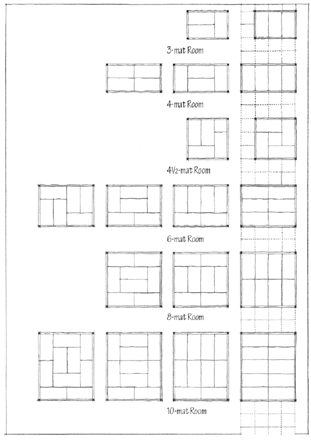
Two methods of designing with the ken modular grid developed that affected its dimension. In the Inaka-ma method, the ken grid of 6 shaku determined the center-to-center spacing of columns. Therefore, the standard tatami floor mat (3 x 6 shaku or 0.5 x 1 ken) varied slightly to allow for the thickness of the columns.

In the Kyo-ma method, the floor mat remained con-stant (3.15 x 6.30 shaku) and the column spacing (ken module) varied according to the size of the room and ranged from 6.4 to 6.7 shaku.

The size of a room is designated by the number of its floor mats. The traditional floor mat was originally proportioned to accommodate two persons sitting or one person sleeping. As the ordering system of the ken grid developed, however, the floor mat lost its dependence on human dimensions and was subjected to the demands of the structural system and its column spacing.

Because of their 1:2 modularity, the floor mats can be arranged in a number of ways for any given room size. And for each room size, a different ceiling height is established according to the following: height of the ceiling (shaku), measured from the top of the frieze board = number of mats x 0.3.

In a typical Japanese residence, the ken grid orders the structure as well as the additive, space-to-space sequence of rooms. The relatively small size of the module allows the rectangular spaces to be freely arranged in linear, staggered, or clustered patterns.

Elevations of a Traditional Japanese Residence

ANTHROPOMETRY

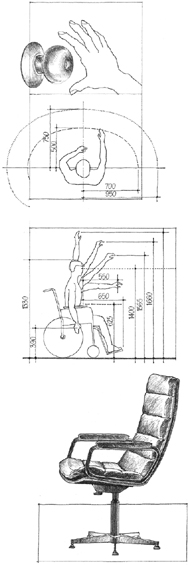
Anthropometry refers to the measurement of the size and proportions of the human body. While the architects of the Renaissance saw the proportions of the human figure as a reaffirmation that certain mathematical ratios reflected the harmony of their universe, anthropometric proportioning methods seek not abstract or symbolic ratios, but functional ones. They are predicated on the theory that forms and spaces in architecture are either containers or exten-sions of the human body and should therefore be determined by its dimensions.

The difficulty with anthropometric proportioning is the nature of the data required for its use. For example, the dimensions given here in millimeters are average measurements and are merely guidelines that should be modified to satisfy specific user needs. Average dimensions must always be treated with caution since variations from the norm will always exist due to the difference between men and women, among various age and racial groups, even from one individual to the next.

The dimensions and proportions of the human body affect the proportion of things we handle, the height and distance of things we try to reach, and the dimensions of the furnishings we use for sitting, working, eating, and sleeping. There is a difference between our structural dimensions and those dimensional requirements that result from how we reach for something on a shelf, sit down at a table, walk down a set of stairs, or interact with other people. These are functional dimensions and will vary according to the nature of the activity engaged in and the social situation.

A special field that has developed from a concern with human factors is ergonomics—the applied science that coordinates the design of devices, systems, and environments with our physiological and psychological capacities and requirements.

In addition to the elements that we use in a building, the dimensions of the human body also affect the volume of space we require for movement, activity, and rest. The fit between the form and dimensions of a space and our own body dimensions can be a static one as when we sit in a chair, lean against a railing, or nestle within an alcove space. There can also be a dynamic fit as when we enter a building’s foyer, walk up a stairway, or move through the rooms and halls of a building. A third type of fit is how a space accommodates our need to maintain appropriate social distances and to have control over our personal space.

SCALE

While proportion pertains to an ordered set of mathematical relationships among the dimensions of a form or space, scale refers to how we perceive or judge the size of something in relation to something else. In dealing with the issue of scale, therefore, we are always comparing one thing to another.

The entity an object or space is being compared to may be an accepted unit or standard of measurement. For example, we can say that a table is, according to the U.S. Customary System, 3 feet wide, 6 feet long, and 29 inches high. Using the International Metric System, the same table would measure 914 mm wide, 1829 mm long, and 737 mm high. The physical dimensions of the table have not changed, just the system used to calculate its size.

In drawing, we use a scale to specify the ratio that determines the relationship between an illustration to that which it represents. For example, the scale of an architectural drawing notes the size of a depicted building in comparison to the real thing.

VISUAL SCALE

How large is this square?

Mechanical scale: the size or proportion of something relative to an accepted standard of measurement.
Visual scale: the size or proportion an element appears to have relative to other elements of known or assumed size.

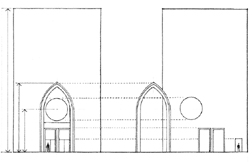
Of particular interest to designers is the notion of visual scale, which refers not to the actual dimensions of things, but rather to how small or large something appears to be in relation to its normal size or to the size of other things in its context.

When we say something is small-scale or miniature, we usually mean that thing appears to be smaller than its usual size. Likewise, something that is large-scale is perceived as being larger than what is normal or expected.

We speak of urban scale when we refer to the size of a project in the context of a city, or neighborhood scale when we judge a building appropriate to its locale within a city, or street scale when we note the relative sizes of elements fronting a roadway.

At the scale of a building, all elements, no matter how plain or unimportant they may be, have a certain size. Its dimensions may be predetermined by the manufacturer, or they may be selected by the designer from a range of choices. Nevertheless, we perceive the size of each element in relation to other parts or to the whole of a composition.

For example, the size and proportion of windows in a building facade are visually related to one another as well as to the spaces between them and the overall dimensions of the facade. If the windows are all of the same size and shape, they establish a scale relative to the size of the facade.

If, however, one of the windows is larger than the others, it would create another scale within the composition of the facade. The jump in scale could indicate the size or significance of the space behind the window, or it could alter our perception of the size of the other windows or the overall dimensions of the facade.

Many building elements have sizes and characteristics that are familiar to us and which we use to gauge the sizes of other elements around them. Such elements as residential window units and doorways help give us an idea of how large a building is and how many stories it has. Stairs and certain modular materials, such as brick and concrete block, help us measure the scale of a space. Because of their familiarity, these elements, if oversized, can also be used to deliberately alter our perception of the size of a building form or space.

Some buildings and spaces have two or more scales operating simultaneously. The entrance portico of the library at the University of Virginia, modeled after the Pantheon in Rome, is scaled to the overall building form while the doorway and windows behind it are scaled to the size of the spaces within the building.

University of Virginia, Charlottesville, 1817–26, Thomas Jefferson

The recessed entry portals of Reims Cathedral are scaled to the dimensions of the facade and can be seen and recognized at a distance as the entrances to the interior space of the church. As we get closer, however, we see that the actual entrances are really simple doors within the larger portals and are scaled to our dimensions, to a human scale.

Reims Cathedral, 1211–90

HUMAN SCALE

Human scale in architecture is based on the dimensions and proportions of the human body. It has already been mentioned in the section on anthropometric proportioning that our dimensions vary from individual to individual and should not be used as an absolute measuring device. We can, however, gauge a space whose width is such that we can reach out and touch its walls. Similarly, we can judge its height if we can reach up and touch the ceiling plane overhead. Once we can no longer do these things, we must rely on visual rather than tactile clues to give us a sense of the scale of a space.

For these clues, we can use elements that have human meaning and whose dimensions are related to the dimensions of our posture, pace, reach, or grasp. Such elements as a table or chair, the risers and treads of a stairway, the sill of a window, and the lintel over a doorway, not only help us judge the size of a space but also give it a human scale.

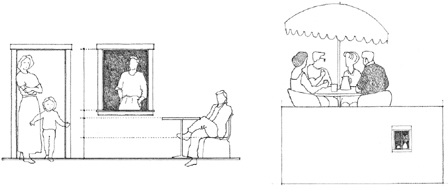
While something that is monumental in scale makes us feel small in comparison, a space that is intimate in scale describes an environment in which we feel comfortable, in control, or important. Intimate settings of tables and lounge chairs in a large hotel lobby tell us something about the expansiveness of the space as well as define comfortable, human-scale areas within it. A stairway leading up to a second-story balcony or loft can give us an idea of the vertical dimension of a room as well as suggest a human presence. A window in a blank wall conveys something about the space behind it and also leaves the impression that it is inhabited.

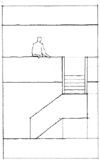
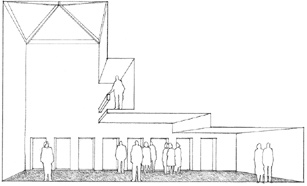
Of a room’s three dimensions, its height has a greater effect on its scale than either its width or length. While the walls of the room provide enclosure, the height of the ceiling plane overhead determines its qualities of shelter and intimacy.

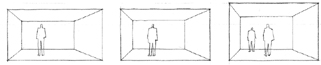
Raising the ceiling height of a 12 X 16-foot room from 8 to 9 feet will be be more noticeable and affect its scale more than if its width were in-creased to 13 feet or its length to 17 feet. While the 12 X 16-foot room with a 9-foot ceiling might feel comfortable to most people, a 50 X 50 foot space with the same ceiling height would begin to feel oppressive.

In addition to the vertical dimension of a space, other factors that affect its scale are:
• the shape, color, and pattern of its bounding surfaces
• the shape and disposition of its openings
• the nature and scale of the elements placed within it

A SCALAR COMPARISON

On these two pages are architectural structures from various historic periods and places drawn to the same or similar scale. Our perception of how big something or someplace is is always relative to its context and to the size of what we are familar with, such as the length of a Boeing 747 airliner.

Plan of Civic Center, Isfahan, Capital of Persia, 1628