-
If y = −x − 15 and
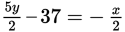, then what is the value of 2x + 6 ?
Now you’ll have a chance to try a few more test-like questions. Use the scaffolding as needed to guide you through the question and get the right answer.
Some guidance is provided, but you’ll need to fill in the missing parts of explanations or the step-by-step math to get to the correct answer. Don’t worry—after going through the examples at the beginning of this chapter, these questions should be completely doable. If you find yourself struggling, however, review the worked examples again.
A bead shop sells wooden beads for $0.20 each and crystal beads for $0.50 each. If a jewelry artist buys 127 beads total and pays $41 for them, how much more did she spend on crystal beads than wooden beads?
The following table can help you structure your thinking as you go about solving this problem. The Kaplan strategic thinking is provided, as are bits of structured scratchwork. If you’re not sure how to approach a question like this, start at the top and work your way down.
| Strategic Thinking | Math Scratchwork |
|---|---|
| Step 1: Read the question, identifying and organizing important information as you go | |
| You’re asked how much more the jewelry artist spent on crystal beads than on wooden beads. | |
| Step 2: Choose the best strategy to answer the question | |
| Use the Kaplan Strategy for Translating English into Math. | wooden: crystal: |
| Variables are easy to pick for this question. Think about what letters the words start
with. |
per wooden per crystal |
| total bought spent |
|
| Separate each numerical piece into its own phrase, then convert to math. |
per wooden → per crystal → |
| total bought → spent → |
|
| Assemble a system of equations, then solve. You can use either substitution or combination to solve for the quantity of each bead type. Remember to think critically about which approach would be faster in this situation. |
+ = + = = = |
| Determine how much the jewelry artist spent on each type of bead, then take the difference. |
$ on wooden $ on crystal |
| − = | |
| Step 3: Check that you answered the right question | |
| If you came up with (A), you’re absolutely correct. |
If y = −x − 15 and
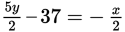, then what is the value of 2x + 6 ?
Larger numbers don’t make this question any different; just be careful with the arithmetic. Again, the following table can help you structure your thinking as you go about solving this problem. Kaplan's strategic thinking is provided, as are bits of structured scratchwork. If you’re not sure how to approach a question like this, start at the top and work your way down.
| Strategic Thinking | Math Scratchwork |
|---|---|
| Step 1: Read the question, identifying and organizing important information as you go | |
| You’re asked to find the value of 2x + 6y. | |
| Step 2: Choose the best strategy to answer the question | |
| Start by rearranging the equations so that they’re in the same general format. Because you’re asked for an expression, look for a shortcut. Don’t bother trying to solve for either x or y individually. |
|
|
+ = |
|
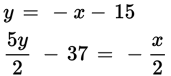
| A good strategy: Clear the fractions from the second equation so you can use combination.
Once the fractions are gone, confirm that adding the second equation to the first
will yield the expression you need. |
( + = ) |
| Step 3: Check that you answered the right question | |
| If your answer is 59, you’re correct! | _____ |