Chapter 1
Introduction

Tom Gleeson¹ and Steven E. Ingebritsen²

¹Department of Civil Engineering, University of Victoria, Victoria, BC, Canada; ²U.S. Geological Survey, Menlo Park, CA, USA

Permeability is the primary control on fluid flow in the Earth's crust. Thus, characterization of permeability is a central concern of many Earth scientists; hydrogeologists and petroleum engineers recognize it as their most essential parameter. More broadly considered, permeability is the key to a surprisingly wide range of geological processes, because it also controls the advection of heat and solutes and generation of anomalous pore pressures (Fig. 1.1). The practical importance of permeability – and the potential for large, dynamic changes in permeability – is highlighted by ongoing issues associated with hydraulic fracturing for hydrocarbon production (“fracking”), enhanced geothermal systems, and geologic carbon sequestration.

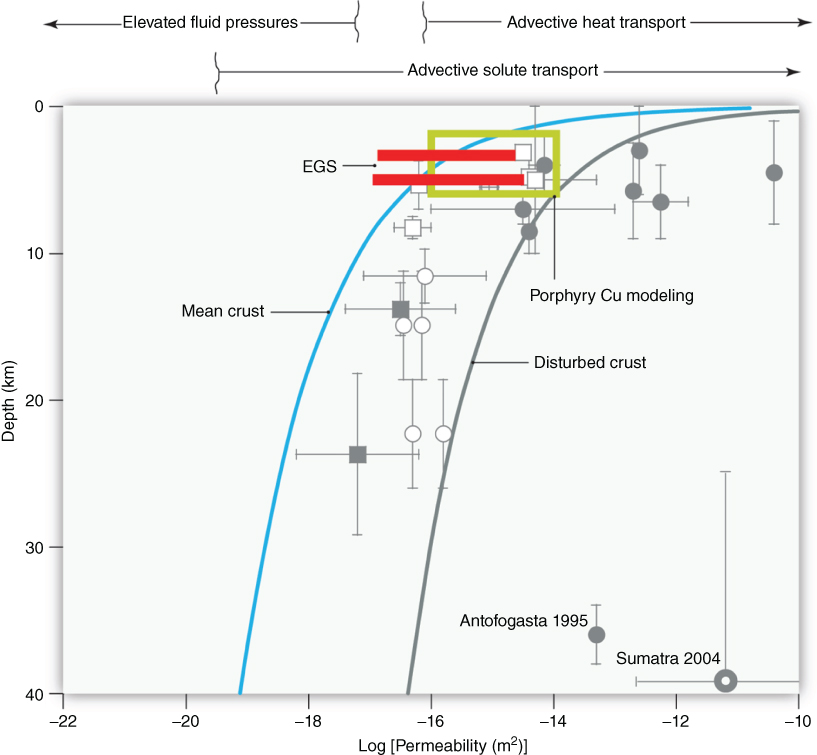
Fig. 1.1 Crustal-scale permeability (k) data. Arrows above the graph indicate approximate ranges of k over which certain geologically significant processes are likely. The “mean crust” k curve is based on k estimates from hydrothermal modeling and the progress of metamorphic reactions (Manning and Ingebritsen 1999). However, on geologically short timescales, k may reach values significantly in excess of these mean crust values (Ingebritsen and Manning 2010). The power-law fit to these high-k data – exclusive of the Sumatra datum (Waldhauser et al. 2012) – is labeled “disturbed crust.” The evidence includes rapid migration of seismic hypocenters (solid circles), enhanced rates of metamorphic reaction in major fault or shear zones (open circles), recent studies suggesting much more rapid metamorphism than had been canonically assumed (solid squares), and anthropogenically induced seismicity (open squares); bars depict the full permissible range for a plotted locality and are not Gaussian errors. Red lines indicate k values before and after enhanced geothermal systems reservoir stimulation at Soultz (upper line) (Evans et al. 2005) and Basel (lower line) (Häring et al. 2008) and green rectangle is the k-depth range invoked in modeling the formation of porphyry-copper ores (Weis et al. 2012). (See color plate section for the color representation of this figure.)

The measured permeability of the shallow continental crust is so highly variable that it is often considered to defy systematic characterization. Nevertheless, some order has been revealed in globally compiled data sets, including postulated relations between permeability and depth on a whole-crust scale (i.e., to approximately 30 km depth; e.g., Manning & Ingebritsen 1999; Ingebritsen & Manning 2010) and between permeability and lithology in the uppermost crust (to approximately 100 m depth: Gleeson et al. 2011). The recognized limitations of these empirical relations helped to inspire this book.

Although there are many thousands of research papers on crustal permeability, this is the first book-length treatment. Here, we have attempted to bridge the historical dichotomy between the hydrogeologic perspective of permeability as a static material property that exerts control on fluid flow and the perspective of economic geologists, crustal petrologists, and geophysicists who have long recognized permeability as a dynamic parameter that changes in response to tectonism, fluid production, and geochemical reactions.

This book is based in large part on a special thematic issue of the Geofluids journal published in early to mid-2015 (Geofluids 15:1–2). Several changes and improvements differentiate the book from the thematic issue: the authors of the 22 original Geofluids papers have had the opportunity to revise and update their respective chapters, and three additional chapters have been added to fill gaps in the topical coverage (Ishibashi et al., this book; Taron et al., this book; Yardley, this book); the introductory material has been revised and expanded; the reference list has been consolidated and updated; an index has been added; and a complementary website (http://crustalpermeability.weebly.com/) has been built to house permeability data and other supporting information. Much of this introduction, and much of the bridging material between topical sections of the book, is derived from the introduction to the Geofluids thematic issue, with changes and additions where appropriate.

Motivation and background

This book is motivated by the controlling effect of permeability on diverse geologic processes; by practical challenges associated with emerging technologies such as hydraulic fracturing, enhanced geothermal systems, and geologic carbon sequestration; and by the historical dichotomy between the hydrogeologic concept of permeability as a static material property that exerts control on fluid flow and the perspective of other Earth scientists who have long recognized permeability as a dynamic parameter. Issues associated with hydraulic fracturing, enhanced geothermal systems, and geologic carbon sequestration have already begun to promote a constructive dialog between the static and dynamic views of permeability, and here we have made a conscious effort to include both viewpoints. We focus on the quantification of permeability, encompassing both direct measurement of permeability in the uppermost crust and inferential permeability estimates, mainly for the deeper crust.

The directly measured permeability (k) of common geologic media varies by approximately 16 orders of magnitude, from values as low as 10²³ m² in intact crystalline rock, intact shales, and fault gouge, to values as high as 10⁻⁷ m² in well-sorted gravels. Permeability can be regarded as a process-limiting parameter in that it largely determines the feasibility of advective solute transport (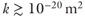), advective heat transport (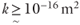), and the generation of elevated fluid pressures (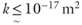) (Fig. 1.1) – processes which in turn are essential to ore deposition, hydrocarbon migration, metamorphism, tectonism, and many other fundamental geologic phenomena.

In the brittle upper crust, topography, magmatic heat sources, and the distribution of recharge and discharge dominate patterns of fluid flow, and externally derived (meteoric) fluids are common (e.g., Howald et al., this book). In contrast, the hydrodynamics of the ductile lower crust are dominated by devolatilization reactions and internally derived fluids (e.g., Connolly & Podladchikov, this book). The brittle–ductile transition between these regimes occurs at 10–15 km depth in typical continental crust. Permeability below the brittle–ductile transition is non-negligible, at least in active orogenic belts (equivalent to mean bulk k of order l0⁻¹⁹ to l0⁻¹⁸ m²) so that the underlying ductile regime can be an important fluid source to the brittle regime (e.g., Ingebritsen & Manning 2002).

The objective of this book is to synthesize the current understanding of static and dynamic permeability through representative contributions from multiple disciplines. In this introduction, we define crucial nomenclature, discuss the “static” and “dynamic” permeability perspectives, and very briefly summarize the contents of the book. Additional summary and synthesis can be found before and after the three main sections of the book, which are labeled “the physics of permeability,” “static permeability,” and “dynamic permeability.”

Nomenclature: porosity, permeability, hydraulic conductivity, and relative permeability

Here, we define some of the key hydrogeologic parameters that are repeatedly used in this book, namely porosity, permeability, hydraulic conductivity, and relative permeability. These are conceptually related but distinct concepts.

First, we note that all of these parameters are continuum properties that are only definable on a macroscopic scale. Perhaps most obviously, at any microscopic point in a domain, porosity (V_void/V_total = n) will be either 0 in the solid material or 1 in a pore space. As one averages over progressively larger volumes, the computed value of n will vary between 0 and 1 and, if the medium is sufficiently homogeneous, the volume-averaged value of n will eventually become nearly constant over a volume range, which has been termed the representative elementary volume (REV) (Bear 1972, 1979). Figure 1.2 shows, for example, a hypothetical section of volcanic ash-flow tuff; note the distinctly different porosity of the flow center relative to the flow top and bottom.

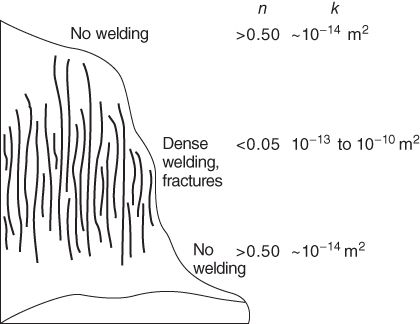
Fig. 1.2 Cross section through a hypothetical ash-flow tuff unit showing typical values of porosity (n) and permeability (k). The thickness of individual ash-flow tuff sheets ranges from a few meters to more than 300 m. Tertiary ash-flow tuffs are widespread in the western United States, particularly in the Basin and Range province.

(Adapted from Winograd 1971.)

The concept of permeability – the ability of a material to transmit fluid – also applies only at an REV scale and can be regarded as reflecting detailed solid–fluid geometries that we cannot map and thus wish to render as macroscale properties. Exact analytical expressions for permeability can be obtained for simple geometries such as bundles of capillary tubes or parallel plates (constant-aperture fractures), but actual pore-fracture geometries are never known.

Porosity (n)–permeability (k) relations have been the subject of many studies (e.g., Luijendijk & Gleeson, this book), and there is often a positive correlation between these two essential quantities. However, even in the case of classical porous media, a correlation between n and k cannot be assumed for mixed-size grains, or when comparing media with greatly different grain sizes. For instance, although there is a positive correlation between n and k for clays themselves, clays are 10⁴–10¹⁰ times less permeable than well-sorted sands (e.g., Freeze & Cherry 1979), despite having generally higher porosities. Furthermore, positive correlation between n and k cannot be assumed in more complex media. Consider again our ash-flow tuff example (Fig. 1.2): the top and bottom of an ash flow cool relatively rapidly, retaining their original high porosities (approximately 0.50), but the permeability of this “unwelded” material is relatively low, because the pores are small and not well connected. If the ash flow is sufficiently thick, pores deform and collapse in the slowly cooling interior, where the final value of porosity can be quite low (<0.05). However, the flow interior also tends to fracture during cooling, and the interconnected fractures transmit water very effectively despite the low overall porosity. The net result of the cooling history is that flow interiors typically have up to 10⁴ times higher permeability than “unwelded” flow tops and bottoms, despite their much lower porosities (0.05 vs. 0.50).

Both laboratory and in situ (borehole) testing normally return values of hydraulic conductivity (K) rather than permeability (k), and this parameter reflects both rock and fluid properties:

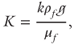
where 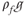is the specific weight of the fluid and μ_f is its dynamic viscosity. In order to compare rock properties among different geothermal conditions, or different fluids (e.g., hydrocarbons vs. aqueous fluids), it is necessary to convert measured values of K to values of k (e.g., Stober & Bucher, this book). Considering once again our ash-flow tuff example: if the surficial outcrop depicted in Figure 1.2 could somehow be translated from standard temperature and pressure (STP = 15°C, 1 bar) to 300°C and approximately 1000 bars (approximately 10 km depth), without any changes in its physical morphology, its permeability k would not change, but its hydraulic conductivity would be approximately 10 times larger because of the increase in the ρ_f/μ_f ratio.

Finally, the empirically based concept of relative permeability is used to extend the linear flow law for viscous fluids (i.e., Darcy's law) to multiphase systems. Relative permeability (k_r) represents the reduction in the mobility of one fluid phase due to the interfering presence of another fluid phase in the pore space and is treated as a scalar varying from 0 to 1, usually as some function of volumetric fluid saturation (e.g., V_liquid/V_void, where for instance [V_vapor + V_liquid]/V_void = 1). This concept is widely invoked in the context of hydrocarbon migration and production (oil–gas–liquid water) and unsaturated flow above the water table (air–liquid water), but is also applied to multiphase flow in hydrothermal systems – for instance by Weis (this book), who allows for the presence of three distinct phases in the void space (vapor + liquid + solid NaCl). Because methane-saturated shales can have very low permeabilities to basinal brines, some studies have used relative permeability effects to explain anomalous pressure in mature sedimentary basins (e.g., Deming et al. 2002).

Static versus dynamic permeability

Some economic geologists, geophysicists, and metamorphic petrologists have long recognized permeability as a dynamic parameter that changes in response to dewatering, fluid production, and seismicity (e.g., Sibson et al. 1975; Walder & Nur 1984; Yardley 1986; Hanson 1995; Connolly 1997). For the purposes of this book, we consider “dynamic permeability” to include any transient variation in permeability, regardless of timescale. However, as pointed out by Huber & Su (this book), “dynamic permeability” also has a traditional and much narrower technical definition as frequency-dependent permeability.

The view of permeability as a dynamic parameter varying with time is in stark contrast to the hydrogeologic concept of permeability as a static material property that exerts control on fluid flow. Indeed, the term “intrinsic permeability,” widely used in the hydrogeologic and petroleum engineering literature, seems to imply an immutable property.

However, there is abundant evidence that permeability varies in time as well as space, and that temporal variability in permeability is particularly pronounced in environments characterized by strong chemical and thermal disequilibrium. Laboratory experiments involving hydrothermal flow in crystalline rocks under pressure, temperature, and chemistry gradients often result in order-of-magnitude permeability decreases over daily to subannual timescales due to water–rock interaction (e.g., Morrow et al. 1981; Moore et al. 1994; Yasuhara et al. 2006), and field observations of continuous, cyclic, and episodic hydrothermal-flow transients at various timescales also suggest transient variations in permeability (e.g., Baker et al. 1987; Hill et al. 1993; Haymon 1996; Fornari et al. 1998; Sohn 2007). The occurrence of active, long-lived (10³–10⁶ years) hydrothermal systems (Cathles et al. 1997), despite the tendency for permeability to decrease with time due to water–rock interaction, implies that other processes such as hydraulic fracturing and earthquakes regularly create new flow paths (e.g., Rojstaczer et al. 1995). Indeed, in the past decade, coseismic permeability enhancement and subsequent permeability decay have been directly observed (Elkhoury et al. 2006; Kitagawa et al. 2007; Xue et al. 2013). It is also clear that sufficiently overpressured fluids cannot be contained in the crust and will create the permeability necessary to escape (e.g., Cathles & Adams 2005; Connolly & Podladchikov 2015; Weis, 2015). These various observations have inspired suggestions that crustal-scale permeability is a dynamically self-adjusting or even emergent property (e.g., Townend & Zoback 2000; Rojstaczer et al. 2008; Weis et al. 2012), reflecting a dynamic competition between permeability creation by processes such as fluid sourcing and tectonic fracturing and permeability destruction by processes such as compaction, diagenesis, hydrothermal alteration, and retrograde metamorphism. An important caveat is that there is likely a fundamental difference between permeability structure and evolution between prograde and retrograde metamorphism (Yardley, this book). Whereas pervasively wet rocks and near-lithostatic fluid pressures may accompany prograde metamorphism, localized hydration of dry rocks by fluid flow under near-hydrostatic fluid pressures is likely characteristic of retrograde metamorphism.

Contents of this book

The following chapter of this book proposes a data structure to embrace and extend the existing knowledge of crustal permeability. The remainder of this book can be broadly categorized as dealing with the physics of permeability (5 chapters), static permeability (6 chapters), and dynamic permeability (13 chapters). Additional summary and synthesis sections are provided before and after these three main sections of the book.

Data structures to integrate and extend existing knowledge

We live in an era of exploding information technology. Thus, the initial chapter in this book, by Fan et al., outlines a vision for the “DigitalCrust”: a community-governed, four-dimensional data system of the Earth's crustal structure. The DigitalCrust concept calls for a particular emphasis on crustal permeability and porosity, which have not been synthesized elsewhere and play an essential role in crustal dynamics. The Crustal Permeability data portal associated with this book at http://crustalpermeability.weebly.com/ is a complementary effort intended to unearth permeability data currently tucked away in many dusty corners of the web and in even dustier reports, books, and theses. The intent is to provide links to online, peer-reviewed permeability data that are globally accessible. In contrast to DigitalCrust, the Crustal Permeability data portal will not host data, and data do not have to be spatially located. Data requirements are simply that the data be peer reviewed (published in a peer-reviewed journal, book, or report); include permeability or other related fluid flow and transport parameters; and be hosted and publicly available on an online data repository such as figshare or institutional web pages such as the those of the United States Geological Survey (USGS).

Acknowledgments

We thank the USGS Powell Center for hosting two workshops that led to the Geofluids thematic issue and this book; the USGS Geothermal and Volcano Hazards programs (SEI) and the Natural Sciences and Engineering Research Council (TG); and Erick Burns, Hedeff Essaid, Paul Hsieh, Christian Huber, Jennifer Lewicki, Michael Manga, Craig Manning, Mark Person, and Richard Worden for thoughtful comments that helped to improve the introductory and bridging material. Mark Ranjram compiled the permeability–depth relations depicted in Figure 1.1 of Chapter 30. We also thank all the authors for their persistence and for their substantial contributions to the Geofluids thematic issue and this book; the 65 or so referees who helped to evaluate and improve those contributions; and the Editors and staff of Geofluids for their advice and support. Chapters coauthored by TG and SEI were handled with editorial independence.