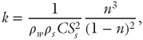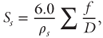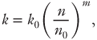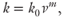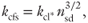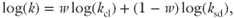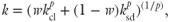Chapter 10
How well can we predict permeability in sedimentary basins? Deriving and evaluating porosity–permeability equations for noncemented sand and clay mixtures

Elco Luijendijk¹ and Tom Gleeson²

¹Geoscience Centre, Georg-August-Universität Göttingen, Göttingen, Germany; ²Department of Civil Engineering, University of Victoria, Victoria, BC, Canada

Abstract

The permeability of sediments is a major control on groundwater flow and the associated redistribution of heat and solutes in sedimentary basins. While porosity–permeability relationships of pure clays and pure sands have been relatively well established at the laboratory scale, the permeability of natural sediments remains highly uncertain. Here, we quantify how well existing and new porosity–permeability equations can explain the permeability of noncemented siliciclastic sediments. We have compiled grain size, clay mineralogy, porosity, and permeability data on pure sand and silt (n=126), pure clay (n=148), and natural mixtures of sand, silt, and clay (n=92). The permeability of pure sand and clay can be predicted with high confidence (R²≥0.9) using the Kozeny–Carman equation and empirical power law equations, respectively. The permeability of natural sediments is much higher than predicted by experimental binary mixtures and ideal packing models. Permeability can be predicted with moderate confidence (R²=0.26–0.48) and a mean error of 0.6 orders of magnitude as either the geometric mean or arithmetic mean of the permeability of the pure clay and sand components, with the geometric mean providing the best measure of the variability of permeability. We test the new set of equations on detailed well-log and permeability data from deltaic sediments in the southern Netherlands, showing that permeability can be predicted with a mean error of 0.7 orders of magnitude using clay content and porosity derived from neutron and density logs.

Key words: permeability, sediments

Introduction

Fluid flow in sedimentary basins and the associated redistribution of heat and solutes depends strongly on the permeability of sediments. However, data on the permeability of sediments are scarce and tend to be restricted to permeable units that form shallow aquifers or deeper geothermal or hydrocarbon reservoir units (Neuzil 1994; Ehrenberg & Nadeau 2005; Gleeson et al. 2011). Permeability of pure granular material or clays can be relatively well approximated using porosity–permeability equations that have been calibrated to experimental data (Mesri & Olson 1971; Bourbie & Zinszner 1985; Revil & Cathles 1999). However, the permeability of mixed sand, silt, and clay materials that form the bulk of sediments in most sedimentary basins remains difficult to predict.

The high variability of permeability of natural sand and clay sediments is illustrated by the permeability data shown in Figure 10.1. The relatively well-constrained porosity–permeability trends for pure quartz sand and the clay minerals kaolinite, illite, and smectite contrast with the high variability of permeability of sand–clay mixtures based on shallow (<2 km deep) samples from the Roer Valley Graben in the Netherlands and the Beaufort-Mackenzie Basin in Canada (Heederik 1988; Hu & Issler 2009; Luijendijk 2012).

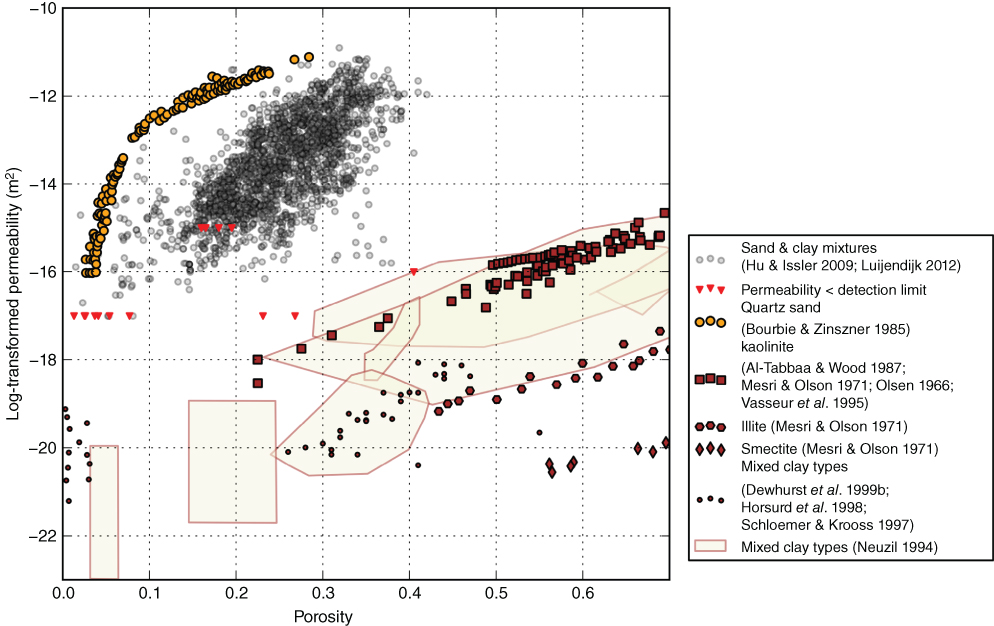
Fig. 10.1 Porosity and permeability data of sand–clay mixtures and pure sands and clays. (See color plate section for the color representation of this figure.)

A number of previous studies that predominantly focus on clay-rich lithologies have found a linear correlation between log-transformed permeability and clay content (Yang & Aplin 1998; Dewhurst et al. 1999a; Schneider et al. 2011). In contrast, Koltermann & Gorelick (1995) and Revil & Cathles (1999) derive equations for the porosity and permeability of ideal mixtures of sand and clay that predict a rapid decrease of permeability with increasing clay content, with a minimum at clay contents of approximately 40%. These two models create very different predictions of permeability. However, they have each only been tested on a limited range of natural sediments. The Koltermann & Gorelick (1995) and Revil & Cathles (1999) models are based on mainly laboratory-scale binary mixtures of sand and clay (Marion 1990; Knoll & Knight 1994), while the log-linear relation between clay content and permeability is mainly based on clay-rich sediments. Therefore, the extent to which porosity–permeability equations can be used to predict permeability of natural sediments at larger scales remains uncertain.

A number of studies have demonstrated that permeability can be successfully predicted using data on pore-size distributions (Marshall 1958; Yang & Aplin 1998; Dewhurst et al. 1999b; Schneider et al. 2011). However, such data are rarely available, and thus, pore-size distributions presently offer little opportunity to characterize sediment permeability at larger scales (Walderhaug et al. 2012).

Our objective was to quantify how well permeability of sand–clay mixtures can be predicted using simple mixing models and information on porosity, grain size, and clay content that are frequently available in sedimentary basins or can be inferred from sample descriptions or well-log data. We first evaluate how well a number of existing porosity–permeability equations such as the Kozeny–Carman equation fit a compilation of data on the permeability of pure sands and clays. We then use existing and new data sets of mixed siliciclastic sediments to evaluate how permeability relates to the permeability of the pure sand and clay end members. We also use these data sets to evaluate existing permeability equations and develop and test a new approach based on the power mean. Previous studies have used power mean equation to explore the effective permeability of heterogeneous distributions of permeability at reservoir scales (Gómez-Hernández & Gorelick, 1989; McCarthy 1991; de Dreuzy et al. 2010), but this approach has to our knowledge not yet been combined with permeability equations of pure sands and clays to study the permeability of sediment mixtures at sample scale. We focus most of our analysis on core-plug (0.1 m) scale, which is the scale of most of the permeability data available in the literature. In the last section, we combine the power mean porosity–permeability equation with well-log data to scale-up permeability estimates from core plug to formation (50 m) scale.

Our analysis focuses exclusively on noncemented sediments. Note that throughout this chapter, the term sand is used to denote any granular siliciclastic material, that is, sand and silts. Clay refers to clay minerals. For data sets where there was no direct information on the percentage of clay minerals in sediment mixtures, we used a grain size cutoff of 2 µm to estimate clay content, which follows the cutoff values used for the main data sets that were included in our analysis (Heederik 1988; Dewhurst et al. 1999a).

Data and methods

We apply existing and new equations for the permeability of pure sand and clay and sand–clay mixtures using several permeability data sets. The data sets consist of a compilation of published experimental and field data on the permeability of pure sands and clays and a combination of published and newly compiled data on the permeability of sand–clay mixtures from sedimentary basins.

Permeability data sets

Pure sands and clays

Permeability data for pure quartz sand were obtained from Bourbie & Zinszner (1985), who report permeability data for the Oligocene Fontainebleau sandstone in the Paris Basin. Permeability was measured using a falling-head permeameter. The porosity varies from 2% to 30% as a function of burial depth. The median grain size is constant for all samples at 250 µm.

Data on the permeability of pure clays were obtained from several experimental studies in which porosity and permeability were measured during compaction experiments (Olsen 1966; Mesri & Olson 1971; Al-Tabbaa & Wood 1987; Vasseur et al. 1995). Permeability was measured in these studies using either consolidation (Olsen 1966; Mesri & Olson 1971), steady-state flow (Vasseur et al. 1995), or falling-head tests (Al-Tabbaa & Wood 1987). Al-Tabbaa & Wood (1987) measured permeability normal and perpendicular to the normal stress, while for the remainder of studies the anisotropy of permeability was not discussed. Descriptions of experimental procedures suggest that the measured permeability likely represents permeability parallel to the applied stress for the Olsen (1966) and Vasseur et al. (1995) data sets, whereas for the Mesri & Olson (1971) data set, the exact test setup is unknown.

Sand–clay mixtures

The relation of the permeability of sand–clay mixtures to porosity and clay content was examined using two data sets: one consisting of Cenozoic shallow marine sands in the Roer Valley Graben in the southern Netherlands and the second consisting of unconsolidated marine clays and silts of the Eocene London Clay formation in southeast England. While large compilations of permeability data have been published (Neuzil 1994; Nelson & Kibler 2001; Ehrenberg & Nadeau 2005; Wilson et al. 2008; Yang & Aplin 2010), the Roer Valley Graben and London Clay data sets are to our knowledge the only available data sets that combine detailed porosity, permeability, grain size, and clay content data, as well as some constraints on the mineralogy of the clay fraction. Both data sets consist of sediments that were buried less than 2 km deep and, therefore, have not been affected significantly by diagenesis.

The first data set from the Roer Valley Graben consists of 67 core samples from the geothermal exploration well AST-02 (Heederik 1988). The samples were derived from the Paleocene Reusel Member and the Eocene/Oligocene Vessem Member, which both consist of shallow marine (deltaic) fine sand and silt deposits with low clay contents. Detailed permeability and grain size data were reported separately in industry reports (Jones 1987; Anonymous 1988) that are available on the website of the Dutch Geological Survey (http://www.nlog.nl). Porosity and permeability were measured on 0.1-m-long core plugs with a diameter of 0.025 m. Porosity was measured by helium porosimetry. Both horizontal and vertical permeabilities were measured using nitrogen as a flowing fluid, with a detection limit of 1.0 × 10⁻¹⁷ m². The grain size data are shown in Figure 10.2A. Clay mineralogy data were available for 24 samples in these members and an adjacent stratigraphic unit; see Table 10.1. Note that while the permeability data were derived from a geothermal exploration well, geothermal gradients in the area are moderate, approximately 35 °C km⁻¹ (Luijendijk et al. 2011). The grain size, porosity, and permeability for this data set are available as supplemental information (Table SI), from the authors' web page (http://wwwuser.gwdg.de/eluijen) and on http://www.figshare.com.

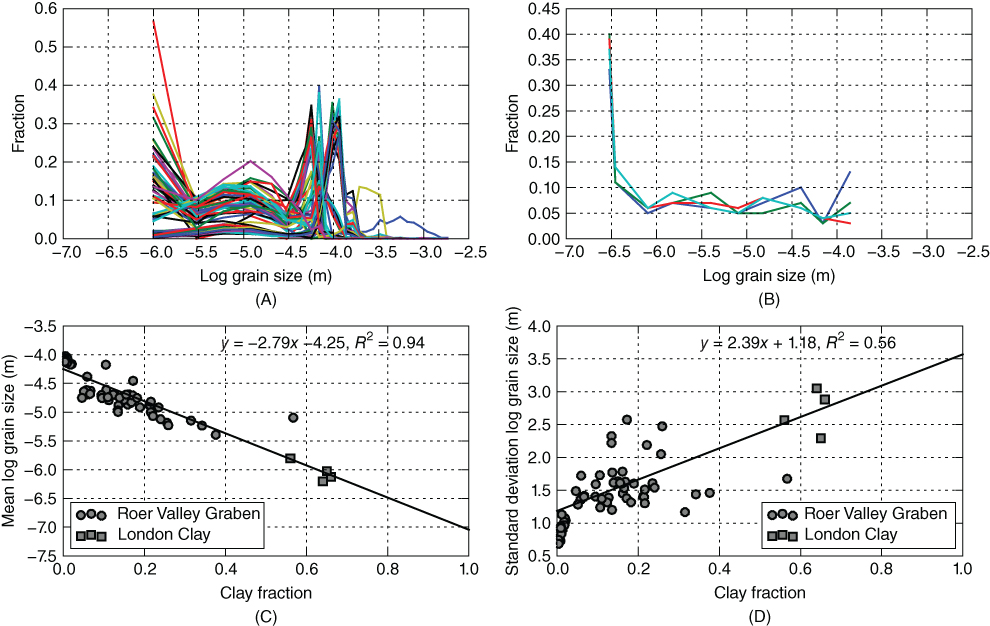
Fig. 10.2 Grain size distribution data for samples from (A) well AST-02 in the Roer Valley Graben (Heederik 1988) and (B) the London Clay data set (Dewhurst et al. 1999a). (C) Good correlation (R² = 0.94) between mean grain size and clay content suggests that independent information on clay content can be used to provide rough estimates of mean grain size. In general, the standard deviation of the distribution of grain size increases with increasing clay content, although clay content only explains 56% of the variation of the grain size distribution (D).

Table 10.1 Clay mineralogy data for Cenozoic sediments in the Roer Valley Graben (Heederik 1988) and the London Clay formation (Kemp & Wagner 2006)

Data set	Sample id.	Depth	Unit	Kaolinite	Illite	Smectite	Mixed layer illite–Smectite	Chlorite
Roer Valley Graben	1	875	Breda Formation	0.20	0.50	0.20	0.10	0.00
	2	875	Breda Formation	0.20	0.50	0.15	0.15	0.00
	3	875	Breda Formation	0.20	0.60	0.10	0.10	0.00
	4	876	Breda Formation	0.15	0.70	0.10	0.05	0.00
	5	876	Breda Formation	0.25	0.45	0.20	0.10	0.00
	6	876	Breda Formation	0.20	0.50	0.20	0.10	0.00
	7	1204	Voort Sand Member	0.00	0.50	0.40	0.10	0.00
	8	1201	Voort Sand Member	0.00	0.45	0.45	0.10	0.00
	9	1217	Voort Sand Member	0.00	0.65	0.25	0.10	0.00
	10	1213	Voort Sand Member	0.00	0.40	0.45	0.15	0.00
	11	1210	Voort Sand Member	0.00	0.60	0.30	0.10	0.00
	12	1458	Rupel Clay Member	0.40	0.50	0.05	0.05	0.00
	13	1453	Rupel Clay Member	0.35	0.45	0.10	0.10	0.00
	14	1462	Rupel Clay Member	0.30	0.50	0.10	0.10	0.00
	15	1466	Vessem Member	0.35	0.35	0.15	0.15	0.00
	16	1479	Vessem Member	0.15	0.35	0.30	0.20	0.00
	17	1476	Vessem Member	0.40	0.45	0.10	0.05	0.00
	18	1474	Vessem Member	0.45	0.45	0.05	0.00	0.05
	19	1484	Vessem Member	0.05	0.40	0.40	0.15	0.00
	20	1488	Vessem Member	0.05	0.20	0.65	0.10	0.00
	21	1491	Vessem Member	0.00	0.20	0.65	0.15	0.00
	22	1496	Vessem Member	0.00	0.30	0.60	0.10	0.00
	23	1492	Vessem Member	0.00	0.25	0.65	0.10	0.00
	24	1502	Vessem Member	0.00	0.30	0.65	0.05	0.00
London Clay	Arithmetic mean			0.15	0.44	0.30	0.10	0.00
	Min. k			0.00	0.20	0.65	0.15	0.00
	Max. k			0.45	0.45	0.05	0.00	0.05
	Arithmetic mean			0.25	0.26	0.38	n/a	0.12
	Min. k			0.09	0.17	0.65	n/a	0.09
	Max k			0.33	0.34	0.15	n/a	0.19

A second data set consists of four samples from the Eocene London Clay deposit (Dewhurst et al. 1999a). The London Clay contains sizeable fractions of silt and fine sand, with clay contents ranging from 56% to 67%. Compared with Dewhurst et al. 1999b, we did not use a number of samples with low clay contents due to insufficient grain size distribution data. The samples were compacted experimentally with pressures up to 33 × 10⁶ Pa. Permeability was measured parallel to the applied stress using steady-state flow tests. Porosity and permeability were measured at various stages of experimental compaction of the four samples, resulting in a total of 25 porosity and permeability data. Information on the clay mineralogy of the London Clay was derived from Kemp & Wagner (2006); see Table 10.1 for a summary of the clay mineralogy data and Figure 10.2B for the grain size data.

We compare both natural sediment data sets to a third data set of experimental binary mixtures of kaolinite clay and quartz sand published by Knoll (1996), who measured porosity and permeability in seven samples consisting of homogeneous mixtures with a uniform grain size of 7 × 10⁻⁴ to 8 × 10⁻⁴ m. Permeability was measured using steady-state flow tests. The specific surface of the sand component was reported as 39 m² kg⁻¹.

In addition to the three main data sets, we use an additional data set of siliciclastic sediments from the Beaufort-Mackenzie Basin in Canada (Hu & Issler 2009) to explore the variation of permeability anisotropy in natural sediments. This data set contains n = 2112 porosity and permeability data of noncemented siliciclastic sediments from Cenozoic formations that were already shown in Figure 10.1. For n = 224 samples, both horizontal (bedding-parallel) and vertical permeability data were available. Detailed clay content and grain size data were not available for this data set. Sample descriptions show that lithology ranges from clay to coarse sand and predominantly consists of very-fine to medium-sized sand.

Permeability equations

Kozeny–Carman equation

Permeability of granular material such as sand and silt was calculated using the Kozeny–Carman equation (Kozeny 1927; Carman 1937, 1956):

10.1

where C is a constant, ρ_w and ρ_s are the density of the fluid and solid phase (kg m⁻³), S_s is the specific surface (m² kg⁻¹) of the solid phase, and n is porosity. The Kozeny–Carman equation was derived from the Hagen–Poiseuille equation (Poiseuille 1844) and calculates flow through a series of cylindrical pipes that represent the connected pore space. The empirical Kozeny–Carman constant C was introduced by Carman (1937) to account for the tortuosity of flow paths and was reported to equal five for uniform spheres (Carman 1956). Previous authors have shown that, while successful at high porosities, the Kozeny–Carman equation overestimates permeability at lower values of porosity (Bourbie & Zinszner 1985), perhaps due to the disproportional closure of pore throats at low porosities (Doyen 1988). Mavko & Nur (1997) demonstrated that permeability can be more successfully predicted by replacing total porosity (n) in the Kozeny–Carman equation with the effective or connected porosity n_e = n–n_t, where n_t is the percolation threshold.

For granular material, the specific surface (S_s) in Eq. 10.1 was calculated as a function of the grain size distribution (Holdich 2002; Chapuis & Aubertin 2003):

10.2

where f is the mass fraction of grain size D (m). Previous research has shown that this equation can estimate the specific surface of a range of sediments with an error of 20% or less and that using the specific surface provides better predictions of permeability than modified formulations of the Kozeny–Carman equation that use a representative grain size instead of specific surface (Chapuis & Aubertin 2003; Chapuis 2012).

For cases where detailed grain size distribution data were absent, but median grain size was known, the specific surface was calculated assuming a log-normal distribution of grain size. A log-normal distribution is a good first estimate for the grain size distribution of sediments (Tanner 1964; Folk 1966; Weltje & Prins 2003).

No data were available on the specific surface or the grain size distribution for the Fontainebleau sand data set. Instead, the value of specific surface S_s of the Fontainebleau sandstone was calibrated. The median grain size of the Fontainebleau sandstone is known (250 µm, Bourbie & Zinszner 1985), and therefore, the corresponding grain size distribution could be calculated to ensure that the S_s value was realistic. Typical values of specific surface for kaolinite, illite, and smectite used for estimating permeability using the Kozeny–Carman equation were estimated as 14 × 10³, 116 × 10³, and 600 × 10³ m² kg⁻¹ (Mesri & Olson 1971; Ames et al. 1983).

Empirical power law equations

As noted by previous authors (Taylor 1948; Michaels & Lin 1954; Freeze & Cherry, 1979), the Kozeny–Carman equation is less successful in predicting the permeability of clays than sands. As an alternative, previous studies have proposed empirical porosity–permeability relationships, in which permeability is calculated as a log-linear or power law function of porosity or void ratio (Mesri & Olson 1971; Tavenas et al. 1983; Al-Tabbaa & Wood 1987; Tokunaga et al. 1998; Yang & Aplin 1998; Revil & Cathles 1999; Schneider Reece et al. 2012). Here, we test two proposed empirical power law equations.

Revil & Cathles (1999) and Tokunaga et al. (1998) suggest that clay permeability can be calculated as a power law function of porosity:

10.3

where k₀ is the permeability at a reference porosity n₀ (m²) and m is an empirical coefficient. Following Revil & Cathles (1999), we choose a reference porosity of 0.5. Al-Tabbaa & Wood (1987), Mesri & Olson (1971), Tavenas et al. (1983), and Vasseur et al. (1995) suggest that permeability can be approximated as a power law function of the void ratio:

10.4

where k₀ is permeability at a void ratio of 1 (m²), v is the void ratio, and m is an empirically determined coefficient. The void ratio (v) is the ratio of the volume of the void space to the volume of solids and is related to porosity (n) by v = n/(l − n).

Ideal packing model

Given the strong contrast between the permeability behaviors of granular material (sands and silts) and clays, previous workers have developed methods to calculate sediment permeability by treating sediments as binary mixtures of sand or silt and clay and estimating permeability from the permeability of the sand and clay components. Revil & Cathles (1999) developed a model based on ideal packing of sand–clay mixtures in which clays are dispersed homogeneously in the sand pores. Following Revil & Cathles (1999) and Revil (2002), permeability of sand–clay mixtures is calculated as

10.5

10.6

10.7

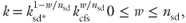
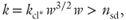
where w is the fraction of clay, k_cl* and k_sd* are the permeability of the sand and clay fraction of the sediment (m²), k_cfs is the permeability of sand of which the pore space is completely filled by clay (m²), and n_sd is the porosity of the sand fraction, that is, the theoretical porosity if one would remove all the clay from the sediment. Revil & Cathles (1999) and Revil (2002) used a modified Kozeny–Carman equation to calculate the permeability of the sand fraction (k_sd*) and a power law equation similar to Eq. 10.3 to calculate the permeability of the clay fraction (k_cl*). In both cases, the permeability is not calculated using the observed porosity of the sample (n), but using a theoretical porosity of the sand fraction or the clay fraction only. We refer to the porosity of the clay fraction as n_cl.

To evaluate the ideal packing model, we calculated permeability for two of the three mixed sediment data sets, the binary sand–kaolinite and the Roer Valley data sets. For the kaolinite–sand data set by Knoll (1996), we follow Revil & Cathles (1999) and use a value of k_sd* = 4.4 × l0⁻¹⁰ m² and k_cl* = 1.5 × l0⁻¹⁵ m² for the permeability of the sand and clay fraction. For the Roer Valley Graben data set, k_sd* and k_cl* were calculated using the Kozeny–Carman equation (Eq. 10.1) and power law–void ratio equation (Eq. 10.4), respectively. The porosity of the sand fraction (n_sd) was estimated to be 0.4 for the Roer Valley Graben data set based on observed porosity of clay-free sands in this data set. The porosity of the clay fraction (n_cl) was set to 0.2, given the 1500 m burial depth of this data set and clay compaction curves by Revil (2002). For the London Clay data set, we could not estimate the porosity of the sand and clay end members with sufficient confidence, as this data set contained no data close to the pure clay or sand end members. In addition, permeability was measured on experimentally compacted samples. For each new compacted permeability measurement, one would need to recalculate n_sd and n_cl, which cannot be easily derived from the observed porosity. Therefore, this data set was not used to evaluate the ideal packing model.

Power mean model

As an alternative to the ideal packing model, we estimate the permeability of sediment mixtures using the geometric, arithmetic, and harmonic mean of the clay and sand or silt components. Warren & Price (1961) have shown that the effective permeability of randomly distributed components is equal to the geometric mean of the components, which for a random mixture of sand and clay yields:

10.8

where w is the fraction of clay, and k_cl and k_sd are the permeability of the sand and clay fraction of the sediment (m²). Note that, in contrast to k_sd* and k_cl* in the ideal packing model (Eqs 10.7), the permeability of the clay and sand fractions are based on the observed porosity (n) of each sample, instead of the porosity of the sand and clay end members. If the clay is distributed in a laminar manner in a sand matrix, the effective permeability for flow parallel to the layers is given by the arithmetic mean, and the effective permeability for flow perpendicular to a layered sequence is given by the harmonic mean (Cardwell & Parsons 1945). These three different means describe different relations between clay content and permeability, which can be generalized using the power mean or Holder mean of the sand and clay fractions:

10.9

where P is the power mean exponent, which can vary between −1 and 1. For P = 1, Eq. 10.9 is equal to the arithmetic mean, and for P = −1, Eq. 10.9 reduces to the harmonic mean. For lim_P→0, Eq. 10.9 equals the geometric mean (Eq. 10.8).

We quantify which values of P are able to describe the permeability of sand–clay mixtures for two data sets with detailed porosity, permeability, clay content, and grain size distribution data (see “Sand–clay mixtures”). The range between the harmonic and arithmetic means (−1 < P < 1) is expected to capture the full variation of permeability in natural sand–clay mixtures. The harmonic mean results in a permeability that is close to that of the clay component and represents samples in which flow is dominated by the clay fraction. Conversely, the arithmetic mean represents samples in which flow is dominated by the most permeable fraction.

Evaluating permeability equations

We analyze the relation between the observed permeability of mixed siliciclastic sediments and the permeability of pure sand and clay end members using a new metric, the normalized permeability difference:

10.10

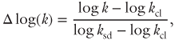
where Δlog(k) is the normalized permeability difference, the difference between the observed permeability and the theoretical permeability of the pure clay component, normalized by the difference between the pure sand and clay components. Here, k denotes the observed permeability, and k_sd and k_cl are the permeability of sand and clay components, respectively (m²). The permeability of pure sand and clay was calculated using Eqs 10.1 and 10.4, respectively, using the available porosity and grain size data for each sample. Specific surface (S_s) of the sand and silt fraction of each sample was calculated from the grain size distribution using Eq. 10.2.

The permeability of the clay component was calculated as the geometric mean of the permeability of each clay mineral, which is justified by experimental results from Mondol et al. (2008). Direct information on the clay mineralogy for each sample was not available. However, Heederik (1988) and Kemp & Wagner (2006) report clay mineralogy for the formations that were sampled to obtain the Roer Valley Graben and London Clay data sets, respectively (Table 10.1). The uncertainty of the permeability of the clay component (k_cl) was taken into account by calculating minimum and maximum estimates of the permeability using the clay samples with the highest and lowest kaolinite contents. A best estimate was calculated using the average clay mineral content.

The performance of the permeability equations was evaluated by calculating the coefficient of determination (R²) and the mean absolute error (MAE) of the predicted permeability. The coefficient of determination was calculated as (Anderson-Sprecher 1994):

10.11

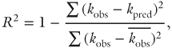
where k_obs is the observed and k_pred is the predicted permeability (m²), respectively. Note that for nonlinear models such as those used in this chapter, R² can be negative if the variance of the prediction error is greater than the variance of the data set.

Estimating porosity and clay content using well-log data

Detailed core-plug measurements are typically only available for relatively permeable formations that are of interest for hydrocarbon or geothermal energy exploration. An alternative way to estimate permeability on larger scales is to utilize information from well logs. We explore how well core-scale permeability can be estimated from well-log data using estimates of porosity and clay content derived from well logs to calculate permeability for the Roer Valley Graben data set. We subsequently compare the calculated values and their uncertainty to the measured permeability. Porosity was calculated from the bulk density log using

10.12

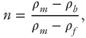
where ρ_m and ρ_f are the density of the sediment matrix and pore fluid, respectively (kg m⁻³), and ρ_b is the bulk density as measured using the gamma–gamma ray log tool. The matrix density and fluid density in the analyzed section of well AST-02 are 2660 kg m⁻³ and 1025 kg m⁻³ (Heederik 1988).

The clay content of sediments was estimated by comparing the porosity calculated from bulk density logs with neutron logs. The neutron log detects the presence of water in the formation. Water is located in the pore space but also occurs as part of the mineral formula of clay minerals and as water bound to the mineral surface. If the porosity is known, the percentage of clay minerals, w, can be determined as

10.13

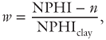
where NPHI is porosity measured by a neutron log and NPHI_clay is neutron porosity of a pure clay. Typical values of neutron porosity for kaolinite, illite, and smectite are 0.37, 0.30, and 0.44 neutron porosity units, respectively (Serra 1982; Rider 2002).

The permeability of the sand and clay components was calculated using Eqs 10.1 and 10.4, respectively. For the sand component, the specific surface was calculated from the grain size distribution, which was estimated using an empirical correlation between grain size and observed clay content shown in Figure 10.2C,D. For both the Roer Valley Graben and London Clay data sets, the median grain size decreases and the standard deviation of the log-transformed grain size distribution increases with increasing clay content. We use the linear correlation as best estimates for grain size distribution. These relations are likely to be slightly specific to these formations, although consistent with general trends in the grain size literature. For basins where such correlations are not available, several sources in the literature provide rough estimates of grain size distribution (Spencer 1963).

Given the high uncertainty of the correlation between clay fraction and grain size distribution (Fig. 10.2), all further calculations were performed using the lowest and highest values of the standard deviation of the log-transformed grain size in Figure 10.2 (0.7 and 3.0 m) as an uncertainty range.

Results

Comparison predicted and observed permeability pure sands and clays

The comparison of permeability data in Figure 10.3 confirms that while the Kozeny–Carman equation can successfully predict the permeability of sands (Fig. 10.3A), it fails to predict the permeability of clays (Fig. 10.3B). The Kozeny–Carman equation is reasonably close for kaolinite (R² = 0.51, mean absolute error log(k) = 0.39), but overpredicts permeability by an order of magnitude for the clay minerals illite and smectite. When the value of the Kozeny–Carman constant (C) is calibrated to the clay permeability data, the predicted values of permeability are much closer to the observed values. However, the equation still overestimates permeability at low porosity. In contrast, the empirical power law relation of permeability to the void ratio is able to closely match the observed values of permeability with a mean absolute error of log-transformed permeability ranging between 0.1 and 0.2 and a coefficient of determination (R²) between 0.90 and 0.99 for kaolinite, illite, and smectite. The difference between observed and calculated permeability values and the calibrated model parameters is listed in Tables 10.2 and 10.3.

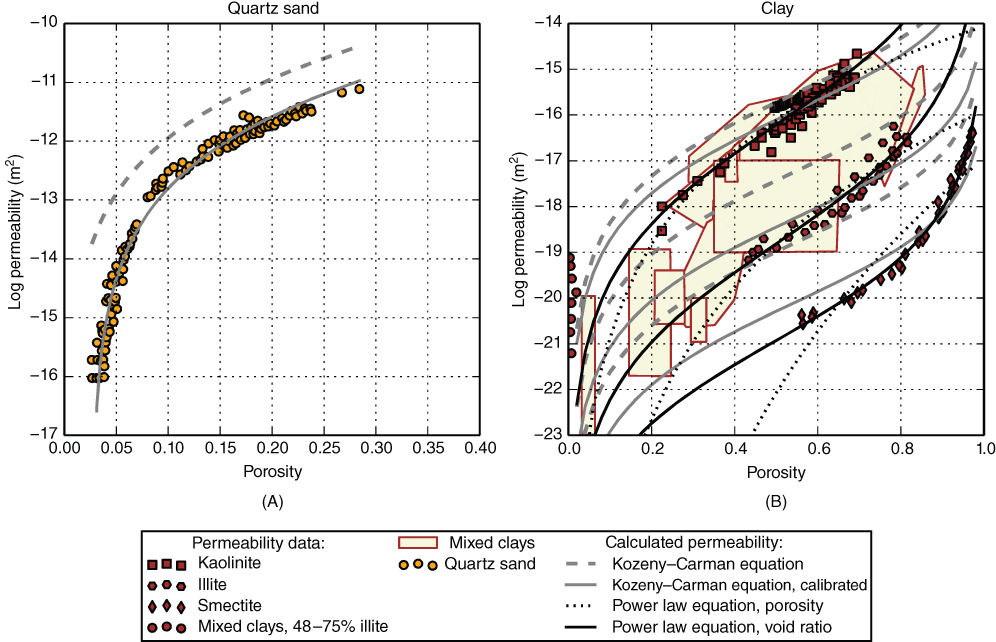
Fig. 10.3 Comparison of calculated and observed permeability for (A) quartz sand and (B) pure clays. For sands, the Kozeny–Carman equation (Eq. 10.1) reproduces the data well, but only when the equation includes a percolation threshold and the value of the specific surface is calibrated. For clays, the permeability data are closely matched when permeability is calculated as a power law function of the void ratio (Eq. 10.4). Data for sands were reported by Bourbie & Zinszner (1985). Permeability data for pure clays were obtained from Al-Tabbaa & Wood (1987), Mesri & Olson (1971), Olsen (1966), and Vasseur et al. (1995). The figure also shows data on mixed clay types from Schloemer & Krooss (1997) and Neuzil (1994) that were not used to calibrate the porosity–permeability equations. See Table 10.2 for the fit statistics of the permeability equations and Table 10.3 for calibrated parameter values. (See color plate section for the color representation of this figure.)

Table 10.2 Performance of permeability equations for pure clays and sands

Material	n	Equation	Equation number	Mean absolute error log(k)	R2
Sand	126	Kozeny–Carman	1	1.16	0.26
		Kozeny–Carman, calibrated	1	0.19	0.97
Kaolinite	79	Kozeny–Carman	1	0.39	0.51
		Kozeny–Carman, calibrated	1	0.22	0.82
		Power law, porosity	4	0.17	0.90
		Power law, void ratio	5	0.17	0.90
Illite	33	Kozeny–Carman	1	1.01	−0.65
		Kozeny–Carman, calibrated	1	0.30	0.81
		Power law, porosity	4	0.25	0.87
		Power law, void ratio	5	0.20	0.92
Smectite	36	Kozeny–Carman	1	1.29	−0.04
		Kozeny–Carman, calibrated	1	0.37	0.91
		Power law, porosity	4	0.43	0.86
		Power law, void ratio	5	0.10	0.99

Table 10.3 Calibrated parameter values for the permeability equations of pure sands and clays

Equation	Eq. number	Parameter	Units	Calibrated parameter values
				Sand	Kaolinite	Illite	Smectite
Kozeny–Carman	10.1	Ss	m2 kg−1	14.80
		C	Dimensionless		12	51	100
		nt	Dimensionless	0.027	0.0016	0.0025	0.0025
Power law, porosity	10.4	k0	m2		7.65 × 10−17	1.53 × 10−19	8.44 × 10−23
		m	Dimensionless		6.82	9.65	17.02
Power law, void ratio	10.5	k0	m2		6.16 × 10−17	1.54 × 10−19	1.18 × 10−21
		m	Dimensionless		3.61	3.58	3.01

As discussed by Tokunaga et al. (1998), experimental permeability data for pure clays for porosities lower than 0.2 are scarce. Comparing calculated permeabilities to data on natural mixed clay types (Neuzil 1994) and mudstones predominantly composed of illite (Schloemer & Krooss 1997) shows that neither the power law permeability–void ratio equation nor the Kozeny–Carman equation can match the data at low porosities. The porosity–permeability equations still underestimate permeability. However, the natural clays included in the Neuzil (1994) and Schloemer & Krooss (1997) data sets include a sizeable silt fraction and may therefore have a higher permeability than pure clays.

The permeability of the Fontainebleau sands shown in Figure 10.3A can be calculated with a mean absolute error of log(k) of 0.19 provided that both the value of specific surface (S_s) and the percolation threshold (n_t) are calibrated. When specific surface is estimated using a uniform grain size (i.e., σ = 0) and the median grain size of 250 µm reported by Bourbie & Zinszner (1985), permeability is overestimated by up to 1 order of magnitude. The calibrated value of the specific surface is 14.8 m² kg⁻¹. Following Eq. 10.2, this value of specific surface corresponds to a standard deviation of log-transformed grain size of 1.0, which conforms to the literature values for well-sorted sands. The misfit of the calculated permeability when using a uniform grain size shows the importance of taking into account grain size distributions for calculating permeability using the Kozeny–Carman equation (Chapuis & Aubertin 2003). The calibrated value of the percolation threshold n_t is 0.027.

Predicting the permeability of sand–clay mixtures

The permeabilities of natural sand–clay mixtures from the London Clay and the Roer Valley Graben data sets show strong correlations with porosity, clay content, and grain size (Fig. 10.4A–C). The permeabilities of the sand and clay fractions of each sample as calculated using Eqs 10.2, and 10.4 are shown in Figure 10.4A. The difference between the permeability of the sand and clay fraction is six orders of magnitude, while the internal variation for the sand and clay components due to grain size distribution and clay mineralogy is two orders of magnitude. This illustrates that clay content is the dominant factor determining the permeability of noncarbonate sediments (Dewhurst et al. 1999b).

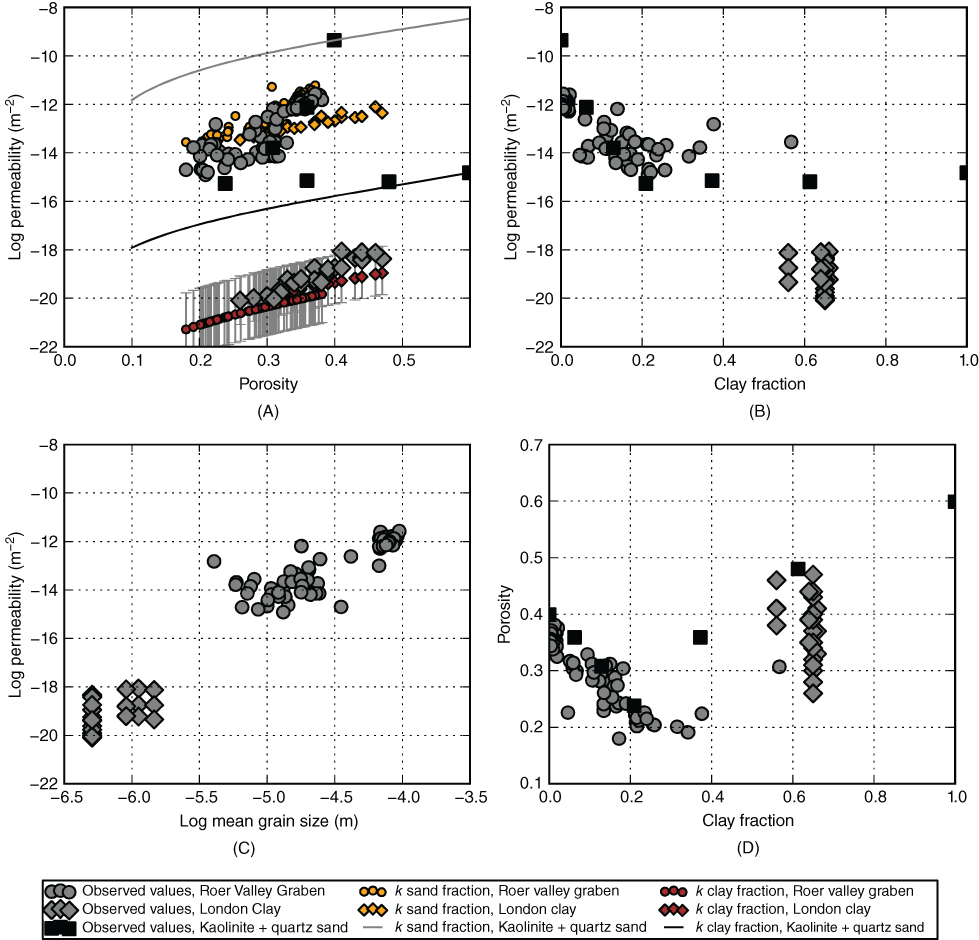
Fig. 10.4 Relation of permeability to (A) porosity, (B) clay content, and (C) mean grain size and (D) the relation between clay content and porosity for two data sets of natural sand–clay mixtures and one experimental data set that consists of a mixture of kaolinite and quartz sand with a uniform grain size. The data for natural sediments were derived from unconsolidated shallow marine sands in the Roer Valley Graben (Heederik 1988) and the London Clay in southeast England (Dewhurst et al. 1999a). The experimental data were reported by Knoll (1996). The calculated permeabilities of the clay and sand fraction of each sample of the Roer Valley Graben and London Clay data sets are also shown in (A). The permeabilities of the Roer Valley Graben and the London Clay data sets are relatively close to the calculated permeabilities of their sand and clay fractions, respectively. The error bars for the clay fraction reflect the uncertainty in the mineral composition. (See color plate section for the color representation of this figure.)

Figure 10.5 shows how the three data sets compare with the permeability of pure sand and clay at the same porosity. The three data sets show markedly different relations between clay content and permeability. The experimental homogeneous sand–clay mix by Knoll (1996) shows a rapid decline of permeability with increasing clay content. The London Clay shows similar low permeability values at clay contents of 50–70%. In contrast, deltaic sands from the Roer Valley Graben retain high values of permeability at clay contents up to 60%. Even at moderate clay contents, the permeability remains several orders of magnitude higher than the estimated permeability of the clay fraction (see also Fig. 10.4A).

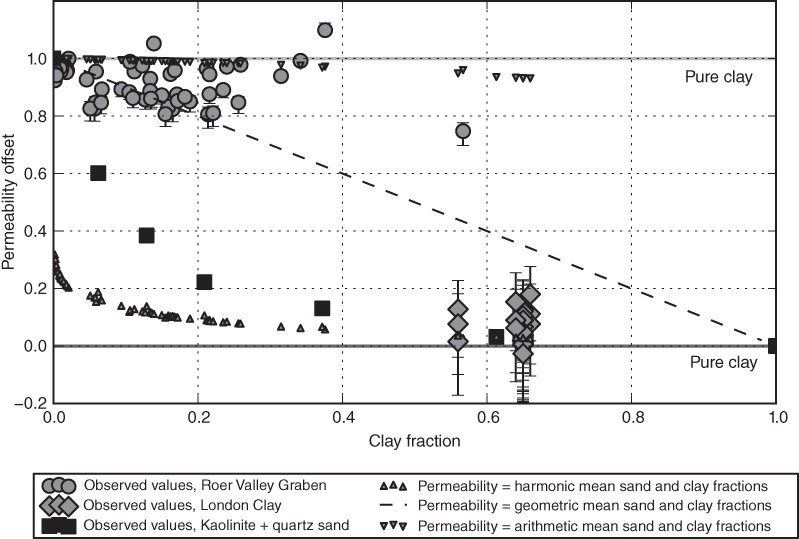
Fig. 10.5 Normalized permeability difference for two natural and one experimental data sets of sand–clay mixtures. The normalized permeability difference is calculated as the difference between the log-transformed permeability and the calculated permeability of the pure clay fraction, normalized by the difference in permeability between pure sand and clay. The three data sets show markedly different behavior. The fine-sand and silt-dominated samples of the Roer Valley Graben data set maintain relatively high permeability over the entire range of clay contents of 0–60%. In contrast, the experimental data set shows permeability decreasing rapidly with increasing clay content. The London Clay data set shows relatively low values of permeability that are close to the predicted permeability of the clay fraction, even though the samples also contain a silt fraction of 35–45%. The permeabilities calculated as the harmonic, geometric, or arithmetic mean of the sand and clay components are also shown for reference. Note that, due to the normalized log scale on the y-axis, the harmonic mean and arithmetic mean permeability cannot be shown as a single line.

Comparisons between the data sets and the ideal packing model and the power mean permeability equation are also shown in Figure 10.5 and model error statistics are shown in Table 10.4. The ideal packing model underestimates the permeability of the Roer Valley Graben data set by up to 2 orders of magnitude. The negative value of R² indicates that the variance of the model error is greater than the variance of the observed permeability data. The ideal packing model is much more successful in predicting the permeability of the London Clay data set. Note that due to the difficulty of estimating n_sd and n_cl, we could not calculate the model error of the ideal packing model for this data set.

Table 10.4 Performance of permeability equations for mixed sand and clay sediments

Permeability equation	Parameter	Roer Valley Graben data set	London Clay data set
Ideal packing	R2	−4.8	n/a
Ideal packing	MAE	1.7	n/a
Harmonic mean	R2	−33.5	0.39
Harmonic mean	MAE	6.0	0.40
Geometric mean	R2	0.26	−8.4
Geometric mean	MAE	0.57	1.9
Arithmetic mean	R2	0.48	−84.1
Arithmetic mean	MAE	0.61	5.8

The permeability of the Roer Valley Graben data set is much better predicted by the power mean model than by the ideal packing model. The modeled permeability is close to the observed permeability for either a power mean exponent (p) of 0 or 1, which corresponds to the geometric and arithmetic mean, respectively (see Fig. 10.6B,C). The predictive power is moderate; coefficients of determination (R²) of 0.26–0.48 show that approximately a quarter to half of the variance of the data set can be explained by the power mean equation with a fixed exponent of 0 or 1. The calculated value of the power mean exponent p for each sample is shown in Figure 10.6D. The mean value of p for the Roer Valley Graben data set is 0.01 and ranges from −0.25 to 0.8 (Fig. 10.6D).

Fig. 10.6 Comparison between observed permeability of natural sediments and permeability calculated as the harmonic, geometric, and arithmetic mean of the sand and clay fractions (A–C) and calculated values of the power mean exponent (P) for each sediment sample (D). Calculated values of the power mean exponent (P) for each sediment sample. For the Roer Valley Graben data set, the calculated power mean exponent clusters around a value of 0 (D). For the London Clay data set, permeability is best predicted using a value of P that lies approximately halfway between the geometric and harmonic means, with a mean calculated value of P of −0.4.

In contrast, the power mean exponents for the London Clay data set all fall between the values for harmonic mean and geometric mean, with a mean of −0.39. Permeability is well predicted by the harmonic mean equation, with R² of 0.39 and a mean absolute error of 0.4 m² (see Fig. 10.6A and Table 10.4).

The lower permeability of the London Clay samples may be attributed in part to the fact that this data set represents permeability perpendicular to the normal stress, while permeability for the Roer Valley Graben data set was measured parallel to the subhorizontal bedding. The vertical permeability is likely to be lower. A compilation of anisotropy for siliciclastic sediments of the Beaufort-Mackenzie data set shows that the anisotropy (the ratio of horizontal to vertical permeability, k_h/k_v) in 90% of the core-plug samples lies between 0 and 10 (Fig. 10.7). Assuming that this database is representative of natural sand–clay mixtures, the vertical permeability of the Roer Valley Graben data set could be up to 1 order of magnitude lower than the horizontal permeability shown in Figure 10.4. A decrease of 1 order of magnitude would shift the normalized permeability difference values (Fig. 10.5) down by approximately 20%, which results in values that are still much higher than the experimental sand–kaolinite mixture or the London Clay data sets.

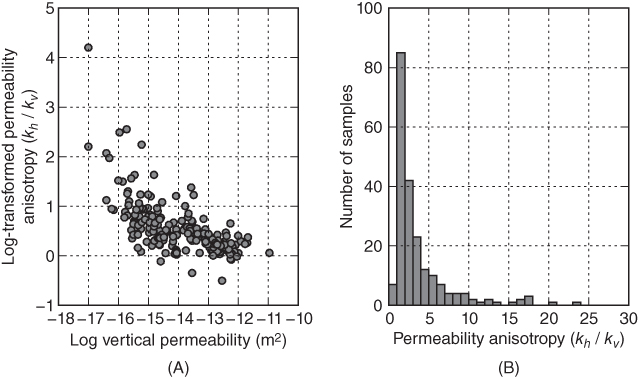
Fig. 10.7 Permeability anisotropy in n = 224 sediment samples from the Beaufort-Mackenzie Basin (Hu & Issler 2009); k_h and k_v denote horizontal and vertical permeability, respectively.

Predicting permeability using well logs

We used only well-log-derived estimates of porosity, grain size distribution, and clay content to calculate permeability for a section of well AST-02, from which the Roer Valley Graben data set was derived. We first derived clay content from neutron and density log data as explained in estimating porosity and clay content using well-log data. Figure 10.8 shows that the observed clay content for well AST-02 is best matched using an apparent neutron porosity of 0.42. The correlation coefficient is relatively low (R² = 0.52), possibly due to lithological variation, such as minor carbonate and organic matter contents or minor offsets between the depths of core samples and well logs. In addition, samples may contain a minor portion of nonclay minerals smaller than 2 µm, and, conversely, some clay particles may be larger than 2 µm.

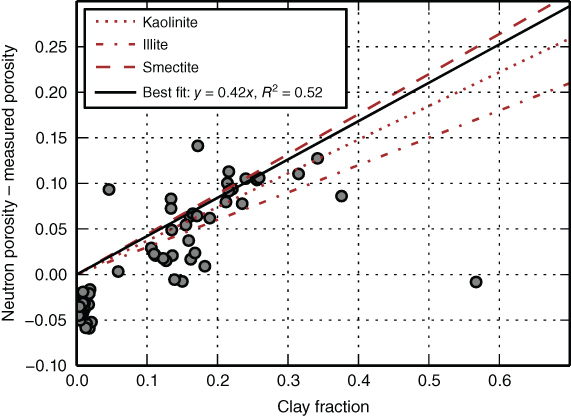
Fig. 10.8 Clay content measured in core samples versus the difference between neutron porosity and observed porosity for the Roer Valley Graben data set. Neutron porosity includes water bound to clay minerals and is higher than the actual porosity in clay-rich sediments. The theoretical neutron porosity of kaolinite, illite, and smectite is shown for comparison (Rider 2002). The clay content of the core samples was calculated as the fraction of grain sizes smaller than 2 µm.

A comparison between the well-log and core data and calculated and observed permeability is shown in Figure 10.9. The clay content and grain size calculated from well-log data match the observed data from core-plug samples and correctly show the transition between moderate clay content and small grain sizes of the Reusel Member to the clay-free sediments of the overlying Vessem Member. The calculated permeability curves show that the permeability calculated as the geometric mean of the sand and clay components is close to the observed values and shows a similar sensitivity to clay content.

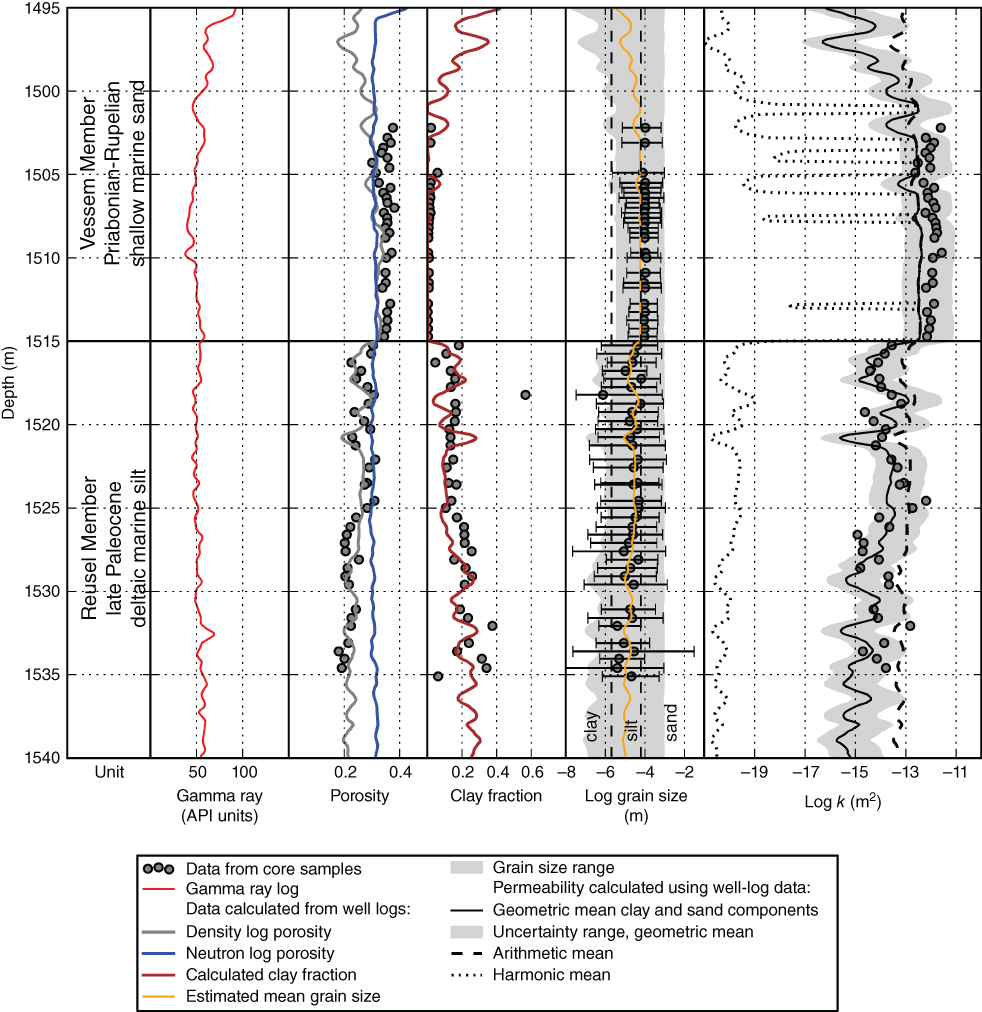
Fig. 10.9 Comparison of well-log data with porosity, clay content, and permeability from core samples in well AST-02. Permeability was calculated using well-log-derived estimates of porosity, clay content, and grain size distribution. Grain size distribution was calculated using the empirical correlations between clay content and grain size distributions shown in Figure 10.2C and D. The calculated permeability shows a relatively good match with observed permeability and estimates permeability within 1 order of magnitude for 80% of the samples. The uncertainty range of the calculated permeability averages ±1.0 orders of magnitude and was calculated using minimum and maximum estimates of clay mineralogy and grain size distribution. (See color plate section for the color representation of this figure.)

A comparison of the error between the observed and calculated values of permeability is shown in Figure 10.6 and the model error statistics are shown in Table 10.5. Using observed data on porosity, clay content, and grain size, the permeability can be estimated with a mean absolute error of log k of 0.57–0.61 m² for the geometric and arithmetic mean equations. When only density and neutron log data are used, the permeability can still be predicted with a mean absolute error of 0.72–0.75 and an R² value of 0.23 and 0.33 for the geometric mean and arithmetic mean permeability, respectively (see Table 10.5).

Table 10.5 Performance of permeability equations for the Roer Valley Graben data set using well-log data as an input

Permeability equation	R2	MAE
Harmonic mean	−26.0	4.7
Geometric mean	0.23	0.72
Arithmetic mean	0.33	0.75

The higher value of the coefficient of determination for the arithmetic mean permeability (R² = 0.33) compared with the geometric mean (R² = 0.23) is caused by a number of outliers (e.g., see Fig. 10.6A–C) and a higher variance of the model error for the geometric mean equation. However, the arithmetic mean model results in a much lower sensitivity of permeability to clay content than is observed in the data. The range of log-transformed permeability predicted by the arithmetic mean equation is −13.5 to −12.4 m², while the range of the observed values of log(k) is −14.9 to −11.6 m² (see Fig. 10.9). While overall underpredicting permeability, the geometric mean predicts a similar variation in permeability as observed in the data, with a range of −15.6 to −12.4 m². Therefore, in this case, the geometric mean is a better measure for the variability of permeability in a siliciclastic formation.

Conclusions

We have compiled n = 148 data on the permeability of pure clays (kaolinite, illite, and smectite) and n = 126 data on clay-free sand from published data sets, as well as detailed data on porosity, permeability, and grain size distribution of shallow (<2 km) sediments from an existing data set of London Clay (n = 29) and a newly compiled data set of deltaic silts and fine sands (n = 67). In addition, we compare permeability of the natural sediments with an experimental data set consisting of homogeneous mixture of kaolinite and quartz sand with a uniform grain size.

The Kozeny–Carman equation was able to predict permeability of quartz sands with a mean absolute error of log(k) of 0.19 and an R² value of 0.97, but only if a percolation threshold was introduced that accounts for the difference between connected and total pore space at low porosity. The Kozeny–Carman equation was less successful in predicting permeability of pure clays. However, an empirical function that calculates permeability as a power law function of void ratio was able to match the observed permeability closely with a mean absolute error of 0.1–0.2 orders of magnitude and R² values exceeding 0.90.

The permeability of sand–clay mixtures shows a strong contrast between the behavior of natural sediments and experimental homogeneous sand–clay mixtures. The permeability of the experimental binary sediment mixture showed a rapid decrease with increasing clay content, with permeability decreasing to minimum values at clay contents of approximately 20%. However, the permeability of a data set consisting of natural silts and fine sands retained relatively high values of permeability at clay contents ranging from 0% to 60%. The comparison between these data sets suggests that permeability equations developed for ideally packed sediment mixtures have limited applicability to natural sediments.

For the deltaic sand and silt data set, log-transformed permeability can be estimated with mean absolute errors of 0.57 and 0.61 and moderate predictive power (R² = 0.26 to R² = 0.48) using either the geometric mean or arithmetic mean value for the power mean exponent, the Kozeny–Carman equation for the permeability of the pure sand component, and a power law equation for the clay component. In contrast, a second data set consisting of shallow marine clays and silts showed much lower values of permeability, which fall in between the geometric and harmonic means of permeability of their clay fraction and the sand or silt fraction.

The contrast in permeability trends of the two data sets may be related to the internal structure of the core-plug-sized (0.1 m) samples. Clay particles are not likely to be distributed homogeneously in deltaic sediments and are therefore not able to block all pore throats throughout the sample, even at high clay contents. The comparatively low permeability of the shallow marine clays and silts of the London Clay may be due to a more homogeneous distribution of clays in these sediments. The contrast between the two data sets points to a nonlinear relation between permeability and clay content that has been suggested by several previous studies (Dewhurst et al. 1999b).

The comparison of anisotropy and permeability of siliciclastic sediments shown in Figure 10.7A points to the importance of sediment structure in core-plug samples. The permeability anisotropy increases with decreasing vertical permeability, which presumably correlates with increasing clay contents. This may reflect a laminar distribution of clays, which would decrease vertical permeability, while the horizontal permeability is maintained by relatively clay-free intervals in the sample. An additional explanation for the correlation between anisotropy and permeability could be that compaction and the realignment of clay minerals increases anisotropy and reduces porosity and permeability for clay-rich samples.

For the deltaic sediment data set, the model error only increases in minor amounts if neutron and density log data are used to estimate porosity, clay content, and grain size distribution, instead of core-plug data. The mean error increases to 0.72 and 0.75 and the R² decreases to 0.23 and 0.33 for power mean exponents of 0 and 1, respectively. The relatively accurate prediction of permeability from widely available neutron and density log data provides new opportunities for estimating permeability for formations where no core samples are available and for determining the variation of permeability at larger scales.

A comparison of well-log-derived permeability shows that, while the model error is slightly higher, the geometric mean equation replicates the variability of permeability much better than the arithmetic mean. Thus, the geometric mean equation would be the best first estimate for the variability of permeability in heterogeneous siliciclastic sediments.

Acknowledgments

We would like to thank Michael Cardiff and three anonymous reviewers for their excellent and very thorough reviews that helped us improve the manuscript considerably.

Supporting information

Additional supporting information may be found in the online version of this chapter, Geofluids (2015) 15, 67–83:

1. Table SI.Grain size, porosity, and permeability data for core-plug samples of Cenozoic sediments from geothermal well AST-02 in the Roer Valley Graben, southern Netherlands.