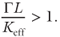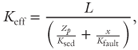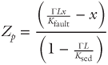Chapter 18
The permeability of active subduction plate boundary faults
Demian M. Saffer
Department of Geosciences, Center for Geomechanics, Geofluids, and Geohazards, The Pennsylvania State University, University Park, PA, USA
Abstract
At subduction zones, continuous influx of fluids drives a dynamic system in which fault slip, fluid flow, and advective transport are tightly coupled. Field and numerical modeling studies have provided insight into the nature and rates of flow in these systems and illustrated that active subduction faults, including the master décollement and splay faults cutting the upper plate, are important conduits. Observations of in situ fracture dilation, modeling studies, and direct measurements documenting strong pressure dependence of fault permeability collectively suggest that permeability varies in time, perhaps due to pore pressure cycling. However, mechanical and fluid budget considerations dictate that increased fault permeability cannot be sustained, nor can it be present across the entire fault surface at a given time. The emerging conceptual model is that permeable patches or channels occupy only a fraction of the fault surface and shift transiently. Fault zone permeabilities obtained by several approaches are consistent between margins, with time-averaged values of approximately 10−15 to 10−14m2, several orders of magnitude higher than for the sediment matrix. Higher, transiently increased values of approximately 10−13 to 10−11m2 are required to explain geochemical and thermal signals and observed focused flow rates. Although faults accommodate significant fluid fluxes from dewatering of the surrounding sediment, they have little effect on pore pressures within the wall rock, where drainage is limited by low matrix permeability. However, fault permeability is a key control on the transport and preservation of localized geochemical and thermal anomalies from depths where temperatures are higher and low-temperature metamorphic reactions are underway. Despite significant recent progress, several key aspects of hydrologic behavior in these active faults remain incompletely understood, including the nature and timescale of transience, the causes of permeability enhancement and its relationship to fault slip and pore pressure fluctuations, and the depths and distances from which deeply sourced fluids are captured, mixed, and transported up-dip.
Key words: advective transport, dewatering, fault permeability, fluid flow, subduction zones
Introduction
Fault zone permeability, its spatial distribution, relationship to fault zone structural architecture, and variation in time are primary controls on the magnitude and distribution of fluid, heat, and solute fluxes in the Earth's crust (e.g., Faulkner et al. 2010; Bense et al. 2013). At subduction zones in particular, the combination of rapid fluid delivery and dewatering, tectonic deformation, and earthquakes leads to a dynamic environment in which fault zone processes and fluid flow are tightly linked. Fault permeability in these systems exerts a first-order control on pore-fluid pressure distribution, and thus the effective normal stress that governs the absolute strength of fault zones and immediately adjacent wall rock (e.g., Rice 1992; Townend & Zoback 2000), the overall geometry of the forearc (e.g., Davis et al. 1983; Saffer & Bekins 2002), and the nature of fault slip (e.g., Scholz 1998; Kodaira et al. 2004; Liu & Rice 2007; Saffer & Tobin 2011; Kitajima & Saffer 2012). Subduction fault permeability is also a fundamental control on heat transport and elemental and volatile refluxes to the oceans (e.g., Chan & Kastner 2000; Hacker 2008).
Focused Ocean Drilling Program (ODP) and Integrated Ocean Drilling Program (IODP) efforts have enabled detailed investigations into fault zone structure, architecture, frictional properties, in situ pore pressure, and permeability at several subduction margins (Fig. 18.1) (e.g., Screaton et al. 1990, 1995, 2000; Tobin et al. 2001; Skarbek & Saffer 2009; Bekins et al. 2011; Saffer & Tobin 2011). These investigations have provided important new insights into fault zone hydraulic behavior (e.g., Mascle et al. 1988; Westbrook et al. 1994; Shipley et al. 1995; Moore et al. 2001; Kinoshita et al. 2009), based on diverse approaches that include laboratory experiments (e.g., Zwart et al. 1997); drilling, logging, and well testing (e.g., Screaton et al. 2000; Bourlange et al. 2003; Bekins et al. 2011; Conin et al. 2013); analyses of down-hole geochemical and thermal observations (e.g., Fisher & Hounslow 1990; Saffer & Screaton 2003); seafloor study of seep distributions, rates, and chemistry (e.g., Moore et al. 1990; Carson et al. 1994); imaging of gas hydrate bottom-simulating reflector geometry (Davis et al. 1995; Zwart et al. 1996); and regional-scale modeling studies constrained by field and laboratory data (e.g., Bekins et al. 1995; Saffer & Bekins 1998a; Spinelli et al. 2006) (Fig. 18.2).
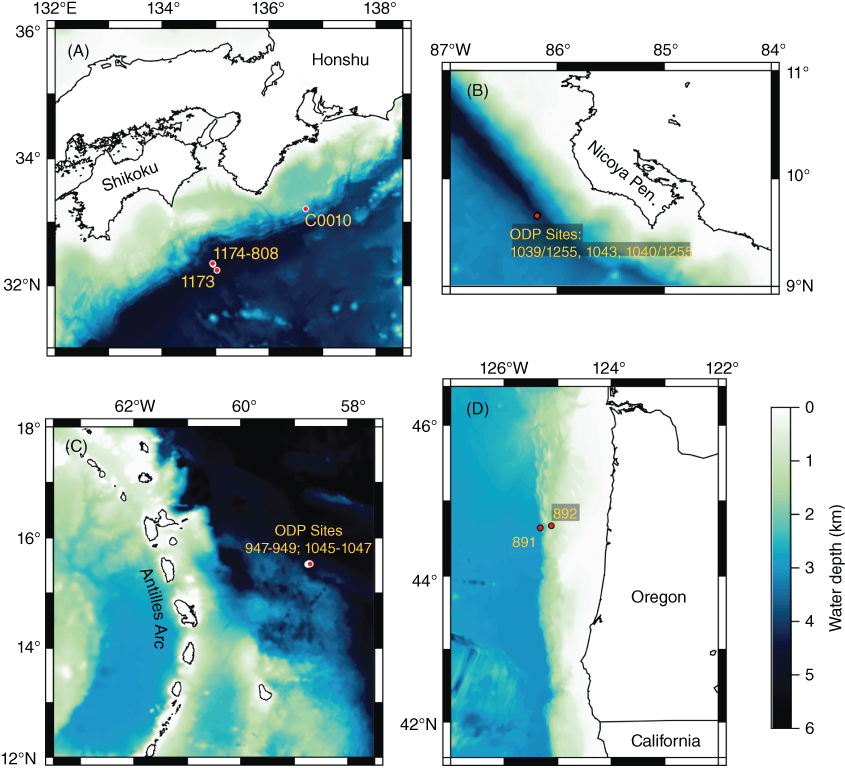
Fig. 18.1 Maps showing study areas for the (A) Nankai, (B) Costa Rica, (C) Barbados, and (D) Cascadia subduction zones. Locations of ODP and IODP boreholes discussed in the text are shown in red. (See color plate section for the color representation of this figure.)
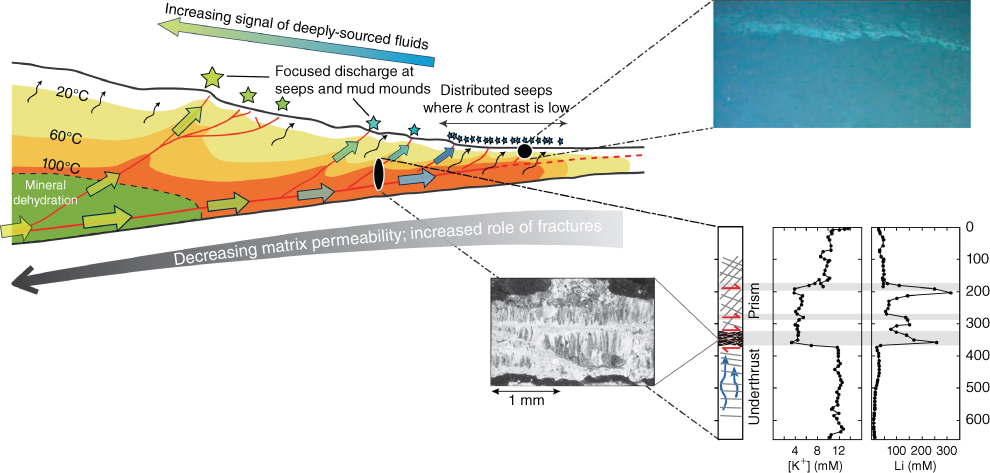
Fig. 18.2 Schematic subduction zone cross section synthesizing hydrologic, geologic, and geochemical observations indicating focused fluid flow along fault zones. Colors indicate temperature distribution and illustrate the role of faults in advecting heat (after Vrolijk et al. (1991)). Arrows indicate fluid flow; colors represent the relative contributions of deeply sourced fluids derived from diagenetic and metamorphic reactions (green) and initial pore water with seawater composition (blue). Stars at seafloor indicate sites of focused seepage, with the same color scheme as flow arrows. Inset at bottom right shows schematic structural column spanning the décollement at ODP Site 1040 (Costa Rican margin) and pore-water geochemical data indicating active or recent flow in the décollement and a splay fault in the hanging wall (Chan & Kastner 2000; Morris et al. 2003b). Photograph shows example of an antitaxial vein from the Barbados décollement (Vrolijk & Sheppard 1987). Photograph at the top right shows approximately 50-cm-high authigenic carbonate crust formed at the outcrop of the décollement at the Costa Rican margin. (See color plate section for the color representation of this figure.)
Recent major reviews of fault zone permeability have summarized conceptual aspects of fault zone permeability, the state of knowledge of fault zone hydraulic architecture (Bense et al. 2013), and the interplay between fault structure and mechanical and hydrological behaviors (Faulkner et al. 2010) across a wide range of geologic and tectonic settings. Other recent work has synthesized data and modeling studies for particular well-studied localities (e.g., Bekins & Screaton 2007). To date, there has not been a comprehensive review of fault permeability that integrates information from multiple subduction zones needed to parameterize numerical models, provide a framework for comparison and interpretation of flow rate and geochemical data, and interpret data sets from ongoing borehole observatory deployments.
The goal of this paper is to synthesize a wide range of analyses and observations across several subduction margins and to summarize current knowledge about the permeability of active subduction zone faults. Discussion is restricted primarily to observations and constraints on flow rates, advective transport, and fault physical properties; although chemical processes associated with cementation and healing are likely to play a role in the evolution of fault permeability, there are few relevant observations at the shallow depths where active subduction faults have been accessed. I focus specifically on: (i) quantitative constraints on fault zone permeability, its links to observed fault zone architecture, structure, and seismic reflection character, and its variation with depth and effective normal stress; (ii) evidence for temporal and spatial variations in permeability and fluid fluxes; and (iii) the implications of existing observations for drainage of excess fluid pressure and the transport of heat and solutes.
Fault zone architecture: inferences about hydraulic properties and behavior
A wide range of field observations suggest that tectonically active fault zones act as permeable conduits, with significant anisotropy associated with fault architecture that leads to higher permeability along structure than across it (e.g., Arch & Maltman 1990; Caine et al. 1996; Faulkner & Rutter 2001; Tobin et al. 2001; Bense et al. 2013). At subduction zones, observations are generally consistent with conceptual models of fault architecture that include one or more zones of fine-grained fault gouge where slip is localized, surrounded by damaged and fractured wall rock (e.g., Caine et al. 1996; Faulkner et al. 2010).
Structural descriptions of drill core, down-hole logging data, and regional-scale geophysical observations at shallow depths (less than approximately 2 km below sea floor, bsf) all indicate that major subduction zone thrust faults – including the master décollement, splay faults, and out-of-sequence thrusts – are characterized by tens-of-meters-thick zones of brecciated sediment and sedimentary rock with intense shear fabrics. These faults commonly include thin zones of localized shear bounded by deformed and fractured, brecciated, and possibly dilated fault rock (e.g., Bourlange et al. 2003; Ujiie et al. 2003; Vannucchi & Leoni 2007). Fracturing is primarily focused in the hanging wall, with an increased intensity of brecciation downward, and a sharp basal contact with relatively less deformed underthrust sediments below (Fig. 18.3) (Shipboard Scientific Party 1994; Tobin et al. 2001; Ujiie et al. 2003; Vannucchi & Leoni 2007). Field observations also suggest that with increasing depth and decreasing porosity in the sedimentary and metasedimentary wall rock, fault zone permeability should become increasingly fracture dominated and localized (e.g., Moore 1989), whereas in high-porosity sediments at shallow depths, fracture networks are likely to be more distributed and complex (e.g., Maltman et al. 1997) (Figs 18.2 and 18.3).
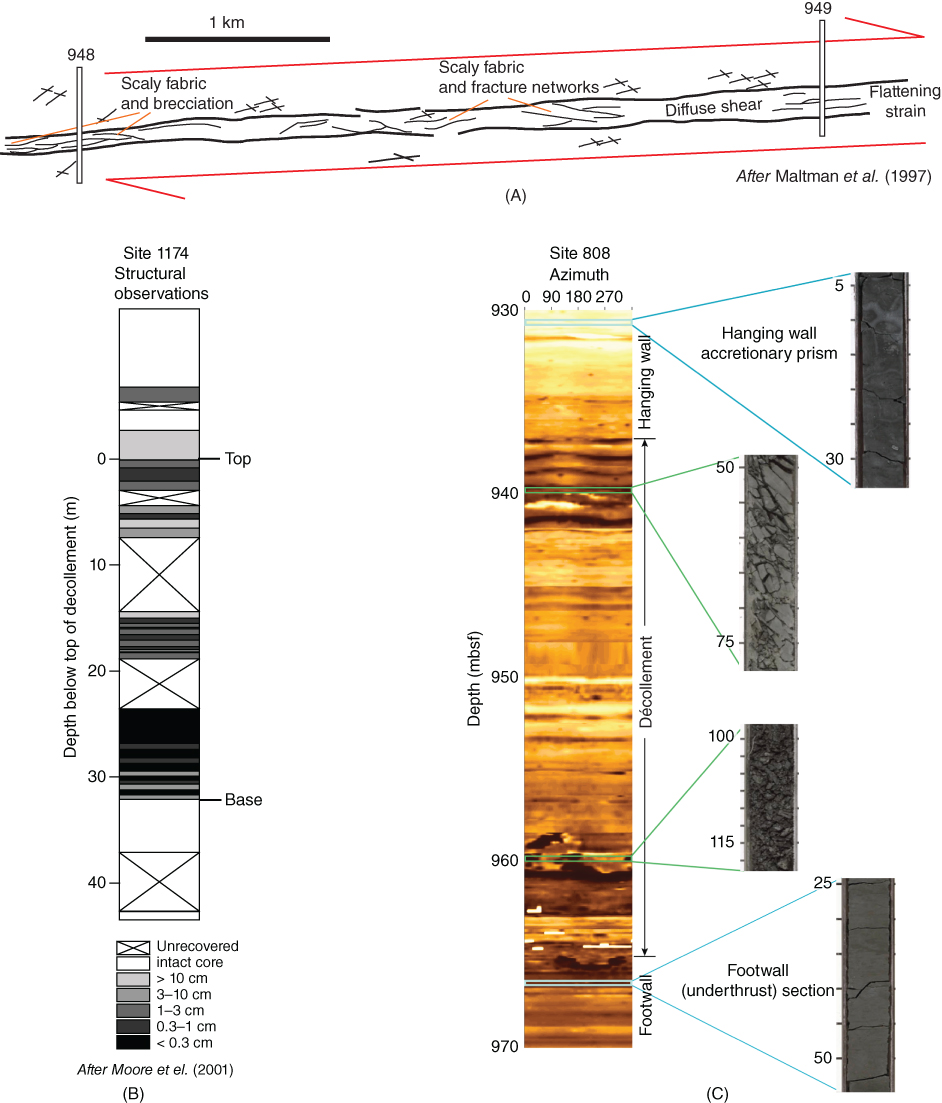
Fig. 18.3 Summary of structural and logging observations across the décollement zone at the Barbados (A) and Nankai (B and C) subduction zones. The décollement is commonly defined as a tens-of-meters-thick zone of brecciated and fractured scaly mudstone, with increasing intensity of brecciation downward, and a sharp basal contact with relatively undeformed underthrust sediment. (A) Synthesis of logging and structural observations from core at several ODP sites at the Barbados margin (after Maltman et al. (1997)). (B) Summary structural section across the décollement at ODP Site 1174, located approximately 2 km landward of the trench in the Nankai Trough (after Moore et al. (2001)). (C) Logging while drilling resistivity image across the décollement zone at ODP Site 808 in the Nankai Trough, located approximately 1 km landward of Site 1174. Core photographs are from ODP Site 1174 with equivalent locations at Site 808 estimated based on relative depth from the top of the décollement (after Ienaga et al. (2006)). (See color plate section for the color representation of this figure.)
For example, at the Costa Rica subduction zone, the active décollement was sampled by drilling at four ODP sites – two located approximately 500 m landward of the trench that sampled the fault at approximately 150 m below seafloor (mbsf) (Sites 1043 and 1255) and two located approximately 1.6 km from the trench where the fault depth is approximately 350 mbsf (Sites 1040 and 1254) (Fig. 18.1) (e.g., Tobin et al. 2001; Vannucchi & Leoni 2007). At these sites, the décollement zone comprises brecciated mudstone derived primarily from the hanging wall and ranges in thickness from 12 to 35 m. Brecciation generally increases in intensity with depth, with fragment sizes decreasing from 1 to 10 cm near the top of the fault zone to <0.3 mm at its base (Vannucchi & Leoni 2007). The base of the décollement is marked by an approximately 10-cm-thick zone of interpreted highly localized shear that separates the damage zone above and the relatively undeformed underthrust sediment below.
The décollement at the Nankai Trough is characterized by a similar pattern of brecciation within an approximately 30- to 40-m-thick damage zone, composed of millimeter- to centimeter-scale overconsolidated mudstone fragments bounded by striations (Fig. 18.3) (e.g., Mikada et al. 2002; Ujiie et al. 2003). Coring across the frontal thrust of the Oregon accretionary prism sampled zones of intense shear fabrics, consisting of 1–5 mm polished angular chips of clay and siltstone that are more consolidated than the adjacent wall rock, and zones of well-developed scaly fabric, characterized by pervasive shear and highly polished parting surfaces (Shipboard Scientific Party 1994). Similar scaly fabrics are also a defining characteristic of the Barbados décollement zone (Fig. 18.3) (e.g., Maltman et al. 1997).
Textural and structural analyses, in situ measurements and images obtained by wireline logging or logging while drilling, and detailed study of veins suggest that these brecciated fault zones may be dilated by near-lithostatic pore pressures (Fig. 18.3) (e.g., Labaume et al. 1997a; Bourlange et al. 2003; Conin et al. 2013). For example, resistivity images and logging measurements through the décollement zone at the Nankai Trough document an approximately 30-m-thick zone containing abundant electrically conductive fractures. This, in combination with a contrast between the high bulk density of cored material and low bulk density measured by logging while drilling at a scale of tens of centimeters, has been interpreted to reflect a zone of dilated fractures bounding intact and densified (overconsolidated) breccia fragments (e.g., Bourlange et al. 2003; Ienaga et al. 2006). This is consistent with the observation that while fractures are abundant throughout the drilled and logged section, most conductive fractures are associated with major fault zones (e.g., McNeill et al. 2004; Ienaga et al. 2006; Conin et al. 2013). It is also consistent with waveform modeling of seismic reflections from active subduction zone faults, which suggest that they represent discrete zones of fractured and compliant rock with low P-wave velocity relative to the surrounding wall rock, and which are characterized by increased – although not necessarily lithostatic – pore-fluid pressures (e.g., Cloos 1984; Shipley et al. 1994; Tobin et al. 1994; Moore et al. 1995). At larger scales, the heterogeneous distribution of fault zone seismic reflection amplitude has been interpreted to represent fluid-enriched ‘channels’ within the fault where pore pressures are highest and permeability is enhanced due to dilation (e.g., Shipley et al. 1994).
Carbonate and mud-filled vein textures record growth and filling synchronous with deformation, providing additional evidence for both increased pore pressure and permeability, in both active and exhumed fault zones (e.g., Vrolijk & Sheppard 1987; Sample 1996; Labaume et al. 1997a,b; Kondo et al. 2005; Vannucchi & Leoni 2007; Rowe et al. 2009). Textural evidence and vein structures in the décollement at both Barbados and Nankai further suggest that increased pore pressure within the faults is episodic, leading to overconsolidation relative to surrounding sediments at times when pore pressure is decreased, and postconsolidation embrittlement, fracturing, and vein formation at times when pore pressure is increased (e.g., Karig 1990; Ujiie et al. 2003; Vannucchi & Leoni 2007).
Observations of fluid flow, advective transport, and simple models
Indicators of focused fluid flow along fault zones include veins and thermal and geochemical anomalies centered at faults sampled by drilling (e.g., Vrolijk & Sheppard 1987; Blanc et al. 1991; Kastner et al. 1991), observations of seeps and mud mounds at the seafloor where faults outcrop (e.g., Carson et al. 1994; Henry et al. 2002; Hensen et al. 2004), and shoaling of the gas hydrate bottom-simulating reflector where it intersects faults in the subsurface (Zwart et al. 1996). Patterns of consolidation and inferred pore pressure within the underthrusting sediment section suggest upward drainage and thus also provide clear evidence for a permeable décollement or fractured hanging wall overlying the subducted sediment package (Fig. 18.4) (e.g., Moore 1989; Saffer 2003, 2007; Screaton & Saffer 2005; Skarbek & Saffer 2009). For the most part, these observations do not yield detailed quantitative constraints on fault zone permeability or flow rate, but do provide first-order estimates of hydraulic properties and key evidence for focused and transient flow.
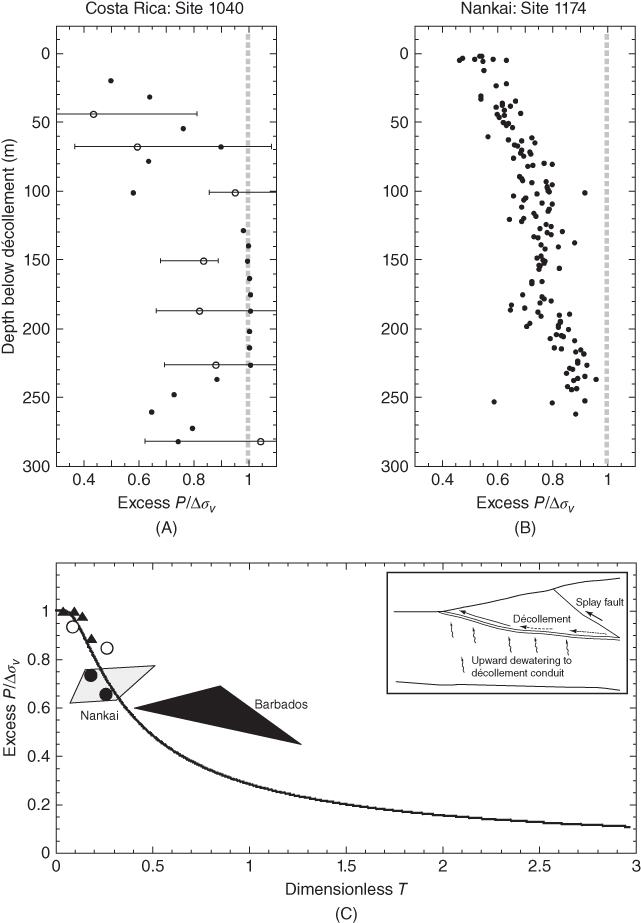
Fig. 18.4 Excess pore pressures within the underthrust sediment sections at (A) Costa Rica (ODP Site 1040) and (B) Nankai (Site 1174), normalized to the increase in overburden from burial by subduction (after Saffer (2007)). Small circles are from measured shipboard porosity; open circles and error bars are from reconsolidation tests. Values of unity indicate undrained behavior, whereas values of zero indicate fully drained (hydrostatic) conditions. At both margins, the pressure profiles suggest upward drainage. (C) Synthesis of normalized excess pore pressures at several drill sites from the Costa Rica (open circles), Barbados (triangles), and Nankai (filled circles) margins, and pressures estimated from seismic reflection interval velocities at the Nankai and Barbados margins (polygons, as labeled) (from Saffer 2007). Line shows predicted pore pressure in a top-drained layer (i.e., inset, top right) (Wissa et al. 1971; von Huene & Lee 1982). The agreement between model and observations at multiple margins suggests that underthrust sediments commonly dewater upward to a permeable décollement.
The common observation of seafloor seeps and active mud mounds localized near outcrops of major fault zones illustrates that the master décollement, out-of-sequence thrusts, and splay faults are important pathways for the focused transport of fluids, as well as the advection of dissolved solutes that support chemosynthetic communities and form authigenic carbonate deposits (cf Fig. 18.2) (Moore et al. 1990; Carson et al. 1994; Henry et al. 2002; Hensen et al. 2004; Ranero et al. 2008; Sahling et al. 2008). Flow rates associated with fault zones are consistently 3–6 orders of magnitude higher than measured or modeled background rates (e.g., Carson & Screaton 1998; Sahling et al. 2008). Sites of seafloor seepage at or near fault outcrops, and geochemical and thermal indicators of active focused flow at faults sampled by drilling have been correlated with negative seismic polarity fault zone reflections at the Nankai (Henry et al. 2002), Cascadia (Moore et al. 1990, 1995), Costa Rica (e.g., Chan & Kastner 2000; Spinelli et al. 2006; Ranero et al. 2008), and Barbados (Gieskes et al. 1990; Shipley et al. 1994) subduction zones, consistent with hypothesized links between subsurface overpressure, fault zone dilation, and enhanced permeability (Fig. 18.5) (e.g., Brown et al. 1994; Saffer & Bekins 1999; Bourlange & Henry 2007).
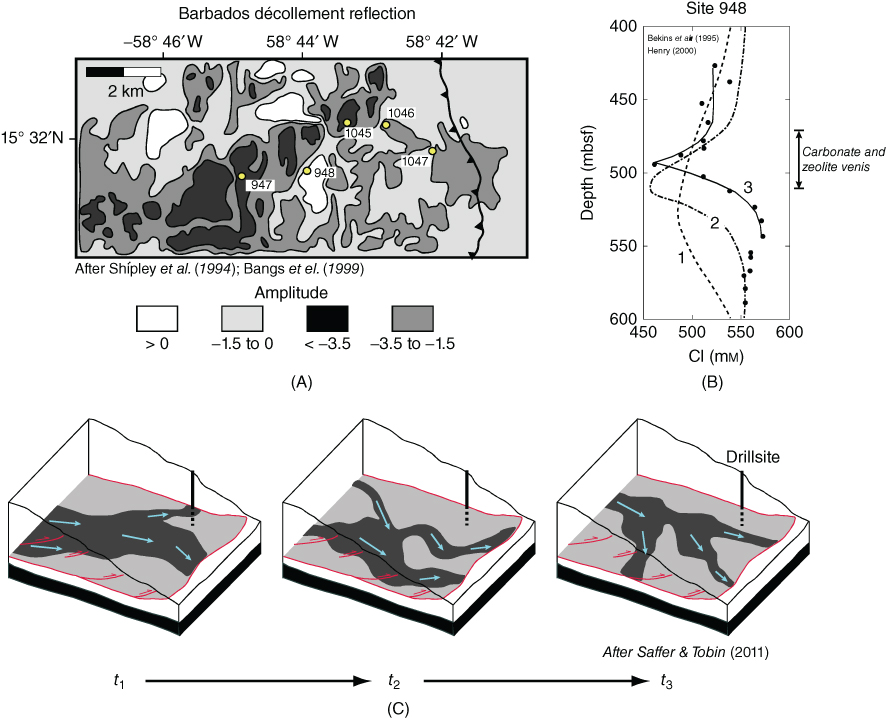
Fig. 18.5 (A) Seismic reflection amplitude of the Barbados décollement zone (from Shipley et al. (1994)), showing locations of trench (barbed line; teeth facing subduction direction) and ODP drill sites (circles). (B) Pore-water chloride profile at Site 948, with freshening centered at the décollement. Curves show model results from Bekins et al. (1995) for transiently increased décollement permeability of 10−13 m2 (1; duration 30 kyr) and 10−11 m2 (2; duration 300 year) and transient diffusion model from Henry (2000) (3; duration approximately 11 kyr). Distribution of veining within the décollement is shown at right. (C) Schematic showing conceptual model in which permeable channels along the décollement shift over time, leading to transient behavior at a given location, and spatially distributed zones of high permeability and flow (after Saffer & Tobin (2011)). (See color plate section for the color representation of this figure.)
Pore-water geochemical anomalies observed at shallow fault zones (less than approximately 1 km below seafloor) commonly include increased concentrations of B and Li, increased δ18 O, decreased CI and K concentrations attributed to clay transformation and other dehydration reactions at greater depth (i.e., pore-water freshening), and increased concentrations of thermogenic hydrocarbons (e.g., Kastner et al. 1991; Vrolijk et al. 1991; Chan & Kastner 2000; Morris et al. 2003b; Hensen et al. 2004; Ranero et al. 2008; Solomon et al. 2009). Collectively, these geochemical signatures require migration of fluids along permeable and hydraulically connected faults over lateral distances of 20 km or more, from source regions where temperatures are 80–150°C (Figs 18.2 and 18.5) (e.g., Moore et al. 1987; Vrolijk et al. 1991; Spinelli et al. 2006; Saffer & McKiernan 2009; Solomon et al. 2009). The finite width of the anomalies provides evidence for transient flow focused along fault zones, combined with outward diffusion (e.g., Blanc et al. 1991). Thermal anomalies centered at fault zones penetrated by drilling provide further evidence for time-varying and localized flow from depths of at least a few kilometers, although the depth of fluid origin is not as well constrained as for geochemical anomalies (e.g., Vrolijk et al. 1991; Davis et al. 1995). The drilling and seep site observations also suggest that splay faults, in addition to the master décollement, are important pathways for solute and fluid transport (Cloos 1984; Vrolijk et al. 1991; Hensen et al. 2004; Teichert et al. 2005; Lauer & Saffer 2012).
Simple one-dimensional (1D) analyses of observed flow rates at seep sites and of thermal anomalies encountered during drilling have provided first-order estimates of transmissivity and permeability along subduction thrusts at several margins (Table 18.1; Fig. 18.6). For example, at the Costa Rican margin, Ranero et al. (2008) estimate the permeabilities required to accommodate observed flow rates at seafloor mud mounds and seeps correlated with splay faults cutting the upper plate. Assuming steady-state and 1D flow along fault or fracture conduits that feed the vents, a minimum estimated permeability of 1.3 × 10−14 to 2 × 10−12 m2 is obtained by assuming a lithostatic (maximum) pressure gradient driving flow (Table 18.1; Fig. 18.6). At the Barbados margin, Fisher & Hounslow (1990) used a simple model to demonstrate that transient fluid flow along the décollement is required to explain thermal observations at a suite of ODP boreholes. The estimated flow rates are consistent with a fault-parallel décollement permeability of approximately 10−12 m2. Davis et al. (1995) conducted a similar analysis of a down-hole temperature anomaly centered at the frontal thrust in the Oregon accretionary prism (ODP Site 892) and showed that it requires transient fluid flow that initiated in approximately the last 400 years at rates of approximately 6 × 10−5 m s−1, corresponding to permeabilities of approximately 1.9 × 10−12 m2. Davis et al. (1995) also estimated a regional background flow rate of approximately 1 × 10−6 m s−1 along the frontal thrust required to perturb subsurface temperatures and deflect the gas hydrate bottom-simulating reflector upward (e.g., Zwart et al. 1996); this corresponds to a permeability of approximately 3 × 10−14 m2. Henry et al. (1992) report comparable flow rates (approximately 100 m year−1, or 3.2 × 10−6 m s−1) based on the analysis of shallow temperature probe measurements at the eastern Nankai accretionary prism.
Table 18.1 Reported permeabilities of active subduction faults
| Location | Depth (mbsf) | Permeability (m2) | Type of flow/in situ conditions | Technique | Source(s) |
| Barbados décollement | 398–463 m | 1 to 1.2 × 10−14 | In situ; σv′ of approximately 1.7 MPa | Two-well test | Screaton et al. (2000) |
| Barbados décollement | 398–538 m | Approximately 8 × 10−16 to 6 × 10−13 | In situ; at σv′ from 0.1 to 2 MPa | Single-well injection tests | Fisher & Zwart (1996, 1997) |
| Barbados décollement | 398–463 m | 5 × 10−18 to 2 × 10−17 | In situ; at σv′ from 2.25 to 2.7 MPa | Single-well, low-volume injection tests | Screaton et al. (1997) |
| Barbados décollement | 398–538 m | log(k) = −14.8–log(σv′) | In situ; as f(σv′) | Synthesis of well tests | Bekins et al. (2011) |
| Barbados décollement | 250–1200 m | 10−13 to 10−15 | Steady state | Numerical modeling | Screaton et al. (1990) |
| 250–6800 m | Approximately 10−14 | Steady state | Bekins et al. (1995) | ||
| Approximately 0.2–20 km | Approximately 10−14 | Steady state | Cutillo et al. (2003) | ||
| Approximately 0.2–5000 m | Approximately 10−15 to 10−14 | Steady state* | Henry & Le Pichon (1991) | ||
| 250–6800 m | 10−13 to 10−11 | Transient | Bekins et al. (1995) | ||
| Approximately 0.2–20 km | Approximately 10−12 | Transient | Cutillo et al. (2003) | ||
| 250–2000 m | Approximately 3 × 10−13 to 10−14 | Transient† | Henry (2000) | ||
| Barbados décollement | 190–280 m | Approximately 10−12 | Transient | Analysis of thermal anomaly | Fisher & Hounslow (1990) |
| Barbados décollement | 399–429 m | 1.1 × 10−18 to 1.1 × 10−17 | At effective stresses approximately 0.1–0.8 MPa | Laboratory measurements on cores | Zwart et al. (1997) |
| Costa Rica décollement | 133–371 m | 2.5 × 10−16 to 7 × 10−15 | Background/steady state | Geochemical mixing constraint | Saffer & Screaton (2003) |
| Costa Rica décollement | 0–19 km | >4 × 10−15 10−13 to 10−11 | Steady-state transient | Numerical modeling | Spinelli et al. (2006) |
| 0–300 m | >10−17 | Steady state | Screaton & Saffer (2005) | ||
| Costa Rica shallow splay fault | 281 m | 6 × 10−19 to 2 × 10−15 | At effective stresses 0.05–0.9 MPa | Laboratory measurements on core | Bolton et al. (1999) |
| Costa Rica splay faults | 0–10 km | 1.3 × 10−14 to 2 × 10−12 | Focused discharge; unclear if steady or transient | Analysis of seep flow rates | Ranero et al. (2008) |
| Costa Rica splay faults | 0–13 km | Approximately 10−12 to 10−14 | Steady state | Numerical modeling | Lauer & Saffer (2012) |
| Nankai décollement | 800–4600 m | 10−15 to 10−17 | Steady state | Numerical modeling | Saffer & Bekins (1998a,b) |
| 5 × 10−14 to 10−12 | Transient | ||||
| 940–7400 m | 10−19 to 3 × 10−14‡ | Steady state | Saffer (2010) | ||
| Nankai décollement | 700–5000 m | Approximately 7 × 10−16 to 8 × 10−14§ | Steady state | Underthrust dewatering; numerical modeling | Skarbek & Saffer (2009) |
| Nankai megasplay | 389–407 m | >2 × 10−17 | In situ; background | Response to tidal loading | Hammerschmidt et al. (2013) |
| Oregon décollement | 10−16 to 10−14 | Steady state | Numerical modeling | Saffer & Bekins (1998b) | |
| Oregon frontal thrust | 92–116 m | 1.9 × 10−12 | Transient | Analysis of thermal anomaly | Davis et al. (1995) |
| 3 × 10−14 | Background | Bottom-simulating reflector shoaling | |||
| Oregon frontal thrust | 92–116 m | 6 × 10−13 to 6 × 10−12 | Transient | Thermal disequilibrium from vein fill | Sample (1996) |
| Oregon frontal thrust | 92–116 m | 6.3 × 10−14 to 5.7 × 10−13 | In situ; as f(σv′); approximately 0.30–0.35 MPa | Single-well injection tests | Screaton et al. (1995) |
| Oregon frontal thrust | 92–116 m | 2.5 × 10−16 to 1.8 × 10−15 | In situ; as f(σv′); approximately 0.59 MPa | Single-well, low-volume injection tests | Screaton et al. (1995) |
| Oregon frontal thrust | 105–165 m | Approximately 6 × 10−17 to 3.5 × 10−15 | At estimated in situ σv′ | Laboratory measurements on cores; fault-normal orientation | Brown (1995) |
* Varies systematically from approximately 10−14 m2 at the trench to 10−15 m2 by 100 km landward.
† Model of solitary wave propagation based on permeability–effective stress relationship from packer tests reported by Fisher & Zwart (1997).
‡ Assigned to vary linearly with depth from 3 × 10−14 m2 at the trench to 10−19 m2 at 60 km landward.
§ Decreases systematically from approximately 6 to 8 × 10−14 m2 at the trench to 7 × 10−16 m2 at 38 km landward.
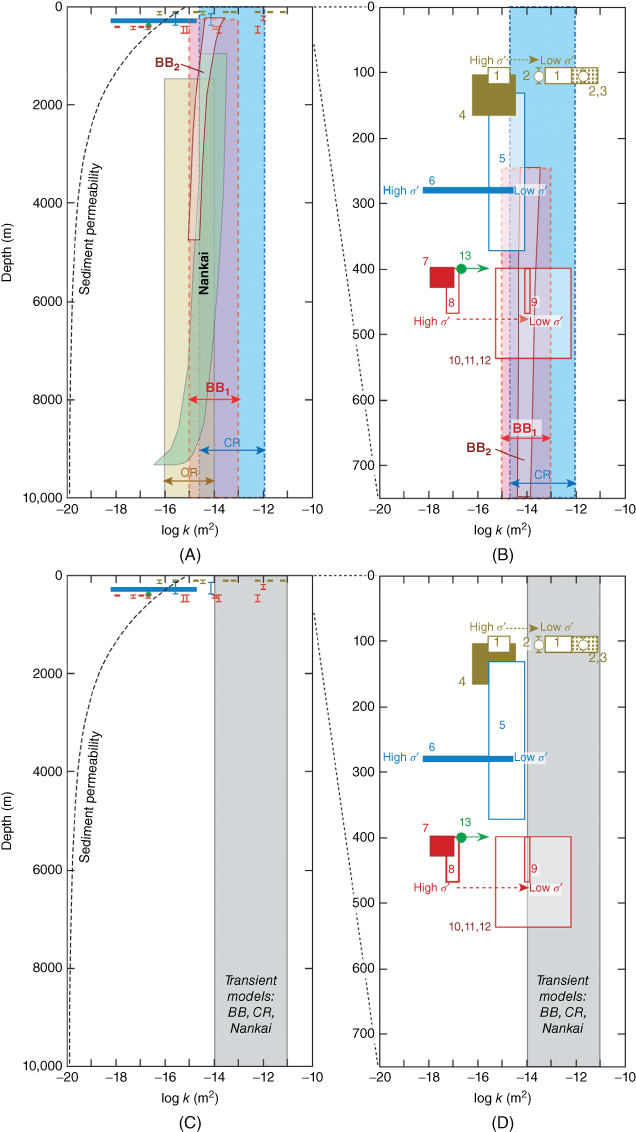
Fig. 18.6 Synthesis of published constraints on fault permeability reported in Table 18.1, shown as functions of depth below seafloor (mbsf). (A) and (B) show in situ permeability measurements or estimates described in the text and in Table 18.1, with permeability ranges derived from steady-state numerical modeling studies for the Barbados (BB1: Bekins et al. (1995) and Screaton et al. (1990); BB2: Henry & Le Pichon (1991)), Nankai (green; Saffer (2010); Skarbek & Saffer (2009)), Oregon (light brown; Saffer & Bekins (1998b)), and Costa Rican (blue; Spinelli et al. (2006)) margins. Mudstone sediment matrix permeability from Skarbek & Saffer (2009) (dashed line) is shown for comparison. (C) and (D) show the in situ permeabilities with transiently increased permeabilities from numerical models for the Nankai, Barbados, and Costa Rican margins (gray-shaded region). The in situ and laboratory measurements are blown up in panels (B) and (D). These include laboratory measurements (filled squares), in situ determinations from well testing (open squares), analyses of thermal anomalies and tidal responses in borehole observatories (open and closed circles, respectively), and analysis of vein chemistry (stippled square). These follow the same color scheme as for model results: brown = Oregon; maroon = Barbados; blue = Costa Rica; green = Nankai. Arrows show the range of permeabilities obtained over ranges of effective stress in well tests at the Oregon frontal thrust (1), Barbados décollement (8–9), and in laboratory measurements of fault zone core from Costa Rica (6). 1 = Screaton et al. (1995); 2 = Davis et al. (1995); 3 = Sample (1996); 4 = Brown (1995); 5 = Bolton et al. (1999); 6 = Saffer & Screaton (2003); 7 = Zwart et al. (1997); 8 = Screaton et al. (1997); 9 = Screaton et al. (2000); 10 = Bekins et al. (2011); 11 = Fisher & Zwart (1997); 12 = Fisher & Hounslow (1990); 13 = Hammerschmidt et al. (2013). (See color plate section for the color representation of this figure.)
Additional constraints on fault zone permeability have been extracted from detailed analyses of veins. Carbonate veins found within scaly shear zones in the Barbados décollement zone are characterized by O, Sr, and C isotope ratios indicative of a deep source, where temperatures are higher than those in situ (Vrolijk & Sheppard 1987; Labaume et al. 1997b). Similar observations from carbonate veins along the frontal thrust at the Oregon margin (Sample 1996) also suggest chemical and thermal disequilibrium between vein-forming fluids and the current thermal structure of the upper plate, with excess temperatures of up to approximately 100°C. To advect fluids along the fault zone and preserve this thermal signal, the flow rate must have been sufficiently high to limit diffusive heat loss to the wall rock during flow; Sample (1996) estimates that a linear water particle velocity (v) of approximately 1–10 km year−1 is required. For an assumed head gradient of unity driving flow (i.e., significant overpressure as suggested by Screaton et al. (1995) and Brown (1995)) and a porosity of 20%, these flow rates correspond to a permeability of approximately 6 × 10−13 to 6 × 10−12 m2 (Table 18.1). These inferred permeabilities and flow rates are similar to those estimated by Davis et al. (1995) for the same fault.
At the Costa Rican margin, two boreholes that sample décollement fluids at different locations document a systematic increase in the magnitude of pore-water freshening with a distance from the trench (Morris et al. 2003b). Saffer & Screaton (2003) combined this observation with the known dewatering flux from underthrusting sediment to estimate the fluid flux in the décollement using a simple mixing model. Because the fluids entering the décollement via dewatering of the consolidating underthrust section below (i.e., Fig. 18.4C, inset) have a seawater composition, the change in décollement fluid composition (freshening) between the two drill sites defines the mixing between contributions from the décollement and underthrust fluid reservoirs and, thus, constrains the flux along the fault. Their analysis indicates flow rates of 4 × 10−3 to 1.1 × 10−1 m year−1. For a 10-m-thick fault zone conduit and a head gradient driving flow defined by pore-fluid pressure measurements in a long-term borehole observatory (Solomon et al. 2009), these rates correspond to a permeability of approximately 2.5 × 10−16 to 7 × 10−15 m2. A thinner flow conduit would result in proportionally higher permeability values.
The suite of observations from drilling, seafloor campaigns, and geophysical surveys underpin a conceptual model of fault zone hydrogeology in which permeability enhancement and pore pressure fluctuations are transient and potentially linked to fault slip events (e.g., Bekins et al. 1995; Solomon et al. 2009; Saffer & Tobin 2011). As discussed in more detail later (constraints from regional-scale numerical models), this is consistent with the magnitude and width of geochemical and thermal profiles centered at fault zones that suggest transient focused flow (Fig. 18.5) (e.g., Fisher & Hounslow 1990; Gieskes et al. 1990; Blanc et al. 1991; Davis et al. 1995), and with analyses of fluid budgets showing that the high flow rates observed at seepage sites or required to explain geochemical and thermal anomalies cannot be sustained (e.g., Le Pichon et al. 1990; Carson & Screaton 1998; Saffer & Bekins 1999; Bekins & Screaton 2007).
Quantitative constraints on fault zone permeability from measurements and flow models
Direct quantitative constraints on fault zone permeability have come from active perturbation testing and passive monitoring at sealed ODP and IODP boreholes, and from numerical modeling studies that define plausible fault hydraulic properties through comprehensive sensitivity analyses. In general, these quantifications of fault zone permeability treat the fault itself as an effective porous medium over the scales of interest, typically a few to tens of meters in thickness and several kilometers along structure (e.g., Screaton et al. 1990; Bekins et al. 1995; Bense et al. 2013). Results from constant injection rate and slug testing at wells are well matched by solutions for Darcian flow in radial coordinates, supporting this general assumption (e.g., Fisher & Zwart 1997; Screaton et al. 2000). The geometry of perturbation tests and passive monitoring (vertical boreholes intersecting shallowly dipping faults) yield effective fault-parallel hydraulic properties and are insensitive to fault-normal permeability. In general, constraints derived from numerical modeling studies are also primarily sensitive to the permeability along structure.
Insights from well testing and borehole observatories
The most direct constraints on fault zone hydraulic properties have come from well testing in sealed boreholes that are either screened across fault zones or access them via an open hole below casing (e.g., Davis et al. 1995). Such direct constraints are generally scarce, but ODP and IODP drilling efforts have enabled targeted hydrologic experiments that have accessed fault zones in the Cascadia, Barbados, and Nankai subduction zones, and chemical/hydraulic monitoring at the décollement zone offshore Costa Rica (Table 18.1; Fig. 18.6) (e.g., Screaton et al. 1995, 1997, 2000; Fisher & Zwart 1997; Solomon et al. 2009; Bekins et al. 2011). Although these tests are limited to shallow depths (<1 km), where faults have formed within relatively high-porosity and poorly consolidated sediments and where total and effective stresses are low, they represent the best and only direct measurements of in situ fault zone permeability. These measurements have provided essential ground truth for numerical models that extend constraints to greater depths and larger scales, as described later (constraints from regional scale numerical models).
At the frontal thrust of the Oregon accretionary prism at ODP Site 892, a suite of shipboard packer injection tests was conducted immediately after drilling, and the site was visited approximately 1 year later by submersible to conduct low-volume pumping tests (Screaton et al. 1995). These tests were all conducted in an interval of open hole from 93.6 to 178.5 mbsf. On the basis of structural features described in cores and down-hole thermal data that identify an active flow zone, the thickness of the fault conduit sampled by the down-hole hydraulic tests was assumed to extend from 92 to 116 mbsf (24 m thickness). The tests provided an opportunity to measure fault zone hydraulic properties at high in situ pore pressure (pore pressures of approximately 65% of lithostatic; shipboard packer tests) and at low in situ pressures (near hydrostatic) during the follow-up submersible tests. The packer injection tests included both slug testing and constant rate injection tests and yielded permeabilities of 6.3 × 10−14 to 5.7 × 10−13 m2. In contrast, the low-volume pump and recovery tests yielded permeabilities of 1.2 to 1.8 × 10−15 m2. An additional permeability estimate of 2.5 × 10−16 m2 was obtained from the formation pressure recovery following shut-in of the well. The large discrepancy between the two sets of tests indicates a strong sensitivity of permeability to effective normal stress (e.g., Rice 1992); the fault zone permeability is approximately 2–3 orders of magnitude higher at elevated in situ fluid pressures than at hydrostatic pore pressure. Observed seafloor seepage fluxes and flow rates inferred from shoaling of the gas hydrate bottom-simulating reflector are most consistent with the in situ permeabilities measured under increased pore pressure conditions, and suggest that the undisturbed fault zone in the subsurface is both overpressured and permeable (e.g., Tobin et al. 1994; Brown 1995; Davis et al. 1995; Screaton et al. 1995).
A similar set of tests was conducted in cased boreholes at the Barbados subduction zone that provided access to the décollement at ODP Sites 948 and 949, and monitored the formation over a depth range from 481 to 538 and from 398 to 463 mbsf, respectively (Fisher & Zwart 1996; Fisher & Zwart 1997; Screaton et al. 1997). Shortly after drilling and casing the borehole across the fault zone at each site, a series of packer tests – including pulse (slug) tests and constant flow rate injection tests – were carried out over a several-hour period. Over the course of each test, the background pore pressure in the tested depth interval rose such that the suite of packer tests provided permeability measurements over a range of effective vertical normal stress (σv′) from approximately 0.1 to 1.6 MPa at Site 948 (Fisher & Zwart 1996) and approximately 0.3–2.0 MPa at Site 949 (Fisher & Zwart 1997). These tests yielded fault zone permeabilities that increased systematically from approximately 8 × 10−16 to 6 × 10−13 m2 as pore pressure increased and σv′ decreased. An additional suite of low-volume slug and recovery tests were conducted approximately 1.5 years later by submersible (Screaton et al. 1997). During these low-volume tests, pore pressures were lower than in the previous injection tests, and the effective normal stress was concomitantly higher, ranging from 2.25 to 2.7 MPa. These tests yielded permeabilities of 5 × 10−18 to 2 × 10−17 m2, consistent with laboratory measurements on core samples (Zwart et al. 1997).
Monitoring of the pressure response at Site 949 to drilling of a nearby borehole approximately 2.5 years later provided additional constraints on fault zone permeability via an inadvertent two-well test (Screaton et al. 2000). Forward modeling of the pressure response yielded a best-fit hydraulic diffusivity of approximately 0.008 m2 s−1 for the décollement zone, with the primary uncertainty associated with the exact distance between the two holes. For storativity values estimated from formation pressure response to seafloor tidal loading (e.g., Wang & Davis 1996), this diffusivity corresponds to a décollement permeability of 1 to 1.2 × 10−14 m2, approximately 1 order of magnitude higher than expected from the relationship between permeability and effective stress defined by the suite of single-well tests (Screaton et al. 2000; Bekins et al. 2011). Bekins et al. (2011) revisited the analysis of the single-well tests to account for erroneously high reported permeabilities by invoking hydraulic fracturing induced by near-wellbore stress perturbations in the injection tests at low effective stresses, and by attributing erroneously low permeabilities reported for the low-volume slug tests to partial infilling of the borehole and screens. After accounting for these effects, the range of permeabilities is narrowed significantly from approximately 10−15 to 10−14 m2; a best fit to the corrected well tests is defined by log(k) = −14.8 − log(σv′).
At the Nankai margin, Hammerschmidt et al. (2013) estimated formation hydraulic properties from the pressure response to ocean tidal loading in a sealed borehole (IODP Site C0010) spanning the megasplay, a major out-of-sequence thrust that reaches the surface approximately 30 km from the trench. For their analysis, pressures were monitored continuously within an isolated interval spanning the fault from 389 to 407 mbsf. Based on the minimal phase lag of measured pressures relative to the ocean tidal loading, combined with estimates of formation and wellbore storage, Hammerschmidt et al. (2013) show that the fault zone permeability is >2 × 10−17 m2. This calculation is based on a wellbore storage effect (Sawyer et al. 2008), whereby if formation hydraulic diffusivity is sufficiently low, a phase lag will be introduced because a finite mass of fluid must move from the formation to the instrument to sense pressure changes. The analysis provides only a lower bound, however, because (i) larger permeability (or hydraulic diffusivity) would also result in a zero phase lag, and (ii) the estimate of instrument compliance includes only the borehole volume and the compressibility of pure water; if the instrument compliance is higher than reported, for example, due to damaged or remolded sediment in the annulus or within the rock volume in the near field of the hole, higher hydraulic diffusivity would be required.
Constraints from regional-scale numerical models
Steady-state models: temporally and spatially averaged permeability
Numerical modeling studies at individual margins have provided constraints on fault zone hydrogeologic properties through detailed analyses relating pore pressure to sediment and fault permeabilities (e.g., Screaton et al. 1990; Bekins et al. 1995; Saffer & Bekins 1998a; Spinelli et al. 2006). These models account for the distribution of fluid sources driven by sediment compaction and mineral dehydration, and incorporate constraints on sediment matrix permeability defined by laboratory experiments (e.g., Skarbek & Saffer 2009; Daigle & Screaton, 2015a). Model simulations define bounds on time-averaged regional-scale fault permeability that are consistent with a range of observations including (i) measured flow rates (e.g., Lauer & Saffer 2012), (ii) down-hole temperatures (e.g., Henry 2000), and (iii) pore-fluid pressures measured in boreholes, predicted from seismic interval velocities, or required at a regional scale to explain a narrowly tapered wedge geometry that reflects low absolute shear strength along the base of the accretionary wedge (e.g., Davis et al. 1983; Matmon & Bekins 2006; Saffer & Bekins 2006).
Several 2D numerical hydrologic models of the Barbados accretionary complex have defined bounds on the décollement permeability across the forearc. Screaton et al. (1990) and Bekins et al. (1995) used a steady-state model driven by fluid sources from a prescribed sediment compaction field, computed from an estimated porosity distribution (Bray & Karig 1985; Bekins & Dreiss 1992), and illustrated that the time-averaged décollement permeability should lie between 10−15 and 10−13 m2 and must be >103–105 times higher than the surrounding sediment matrix to channelize flow (Table 18.1; Fig. 18.6). Although overall simulated pore pressures in the accretionary complex are not as sensitive to the décollement permeability as to that of the matrix (pore pressures are sensitive to décollement permeability only in the immediately adjacent wall rock; Fig. 18.7), flow directions are strongly sensitive to décollement permeability. Higher fault permeability would lead to substantial downward drainage from the accretionary prism inconsistent with Cl− and CH4 profiles observed at drill sites, whereas lower permeabilities would lead to unrealistically high overpressures in the décollement zone and adjacent sediments (Screaton et al. 1990).
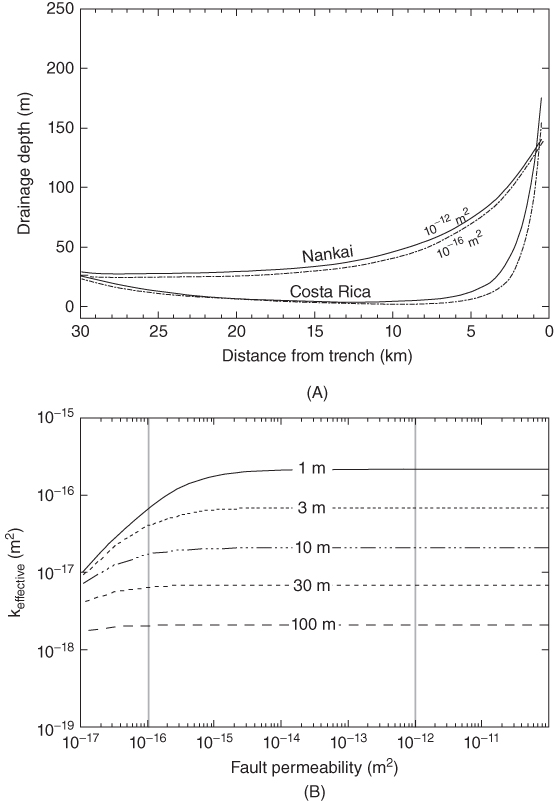
Fig. 18.7 (A) Drainage penetration depth (defined in text) as a function of distance from the trench for the Nankai and Costa Rican margins and for décollement permeabilities of 10−12 m2 (solid curves) and 10−16 m2 (dashed curves). (B) Effective permeability for a flow path from the matrix sediments 30 km landward of the trench to the trench at Costa Rica (cf. Fig. 18.4C, inset) as a function of fault conduit permeability, shown for sediment located at different distances away from the fault (as labeled). Vertical gray lines mark values of fault permeability shown by curves in panel (A). Both the drainage of adjacent sediments and the effective conductivity for flow paths to the seafloor are independent of fault permeability except in cases of low fault permeability or for sediments within several meters of the fault.
Henry & Le Pichon (1991) simulated flow in the Barbados prism using a 2D model explicitly coupling loading, sediment consolidation, and fluid flow and obtained a similar result: the décollement permeability required to accommodate the dewatering flux from adjacent sediments should decrease from 10−14 m2 at the toe of the margin to 10−15 m2 by 100 km landward, where the décollement is ∼5 km deep (Fig. 18.6). They also showed that to explain channelized flow along the décollement without significant vertical leakage, the décollement permeability must be approximately 104 times larger than that of the adjacent sediment.
Similar modeling studies have also been conducted for the Nankai (Saffer & Bekins 1998a; Bourlange & Henry 2007; Skarbek & Saffer 2009; Saffer 2010), Costa Rican (Spinelli et al. 2006), and Cascadia (Wang 1994; Saffer & Bekins 1998b) subduction zones (Fig. 18.6; Table 18.1). At the Nankai margin, a detailed study designed to explore the pore pressure distribution and patterns of pore-water freshening showed that steady-state décollement permeability should be at least 10−17 to 10−15 m2 in the outermost 50 km of the accretionary complex (Saffer & Bekins 1998a). More recent work by Saffer (2010) explored the effects of sandy layers in the accreted and underthrust sediment sections and showed that décollement permeabilities in a similar range, decreasing from 3 × 10−14 m2 near trench to approximately 10−17 m2 60 km landward, yield pore pressures consistent with the observed wedge taper angle. Models that couple loading, sediment consolidation, and fluid flow (following a similar approach to that of Henry & Le Pichon (1991)) illustrate that to accommodate the dewatering flux from underthrusting sediments while also sustaining pore pressures required to match both large-scale mechanical constraints from critical taper theory and those inferred along the wedge base from porosity and seismic wave speeds, the décollement permeability must decrease systematically from approximately 6 to 8.2 × 10−14 m2 near trench to 7 × 10−16 m2 by 40 km landward (Table 18.1; Fig. 18.6) (Skarbek & Saffer 2009).
A similar, although less extensive, suite of models have defined bounds on décollement zone permeability at the Costa Rican and Oregon margins, including coupled 2D simulations of consolidation and dewatering focused on the seaward-most 2.5 km of the Costa Rican margin (Screaton & Saffer 2005), and regional-scale models of both the Costa Rican (Spinelli et al. 2006) and Cascadia margins (Saffer & Bekins 1998b) (Table 18.1; Fig. 18.6). Coupled models of loading and sediment consolidation demonstrate that décollement permeabilities >10−17 m2 can match observed porosity and inferred pore pressure profiles in the subducting section. The regional studies yield ranges of décollement permeability of 10−14 to 10−12 m2 and 10−16 to 10−14 m2 for the Costa Rican and Oregon margins, respectively, required to accommodate dewatering fluid sources driven by porosity reduction (sediment transport through a prescribed porosity field; e.g., Bekins & Dreiss (1992)) while maintaining fluid pressures consistent with mechanical constraints from critical taper theory.
Modeling efforts at different locations yield steady-state décollement permeabilities in a strikingly similar range (10−15 to 10−13 m2) (Fig. 18.6), despite the fact that the geometries, rates of accretion and dewatering, and sediment matrix permeabilities differ substantially between margins. These permeability values are consistent with many of the in situ measurements at shallow depths (Fig. 18.6B). Values of décollement permeability at the Costa Rican margin extend above this range (to 10−12 m2), likely because (i) the steeply tapered upper plate increases the flow path length for fluids to escape diffusely through the prism and therefore confines larger fluxes in décollement than at other margins, and (ii) the combined effects of complete sediment subduction and a higher convergence rate (approximately 9 cm year−1 vs approximately 4 cm year−1 at Nankai and Cascadia) lead to larger dewatering fluxes from the subducting sediments that must be accommodated (e.g., Henry & Le Pichon 1991; Saffer & Bekins 2006). The lower permeability range for the Cascadia system can be explained by a similar logic. The Cascadia margin is characterized by a large overall sediment thickness (approximately 3–4 km), of which only a few hundred meters are subducted. As a result, the subducted section is mostly dewatered before reaching the trench, and a smaller dewatering flux is available to drive flow and elevated pore-fluid pressure along the décollement.
Modeling studies also illustrate the importance of major splay faults at some margins as agents of dewatering and solute or heat transport, as indicated qualitatively by geochemical and thermal signals of focused flow (e.g., Henry et al. 2002; Hensen et al. 2004; Teichert et al. 2005; Ranero et al. 2008). At the Costa Rican margin, where seafloor seepage associated with faults cutting the upper plate is well characterized, Lauer & Saffer (2012) used a 2D model to show that for realistic compaction- and dehydration-driven fluid source distributions at depth, reported flow rates in areas of focused discharge require splay fault permeabilities of approximately 10−14 to 10−12 m2 (Table 18.1). These permeabilities are generally consistent with those estimated by first-order analyses of thermal and geochemical anomalies in splay faults at both the Costa Rican and Oregon margins (e.g., Sample 1996; Ranero et al. 2008).
Time dependence and heterogeneous distribution of permeability
Models of coupled heat or solute transport and fluid flow illustrate that transiently increased permeability is required to explain observed geochemical and thermal profiles (e.g., Bekins et al. 1995; Henry 2000; Spinelli et al. 2006), down-hole temperature data (e.g., Fisher & Hounslow 1990), and seafloor seepage measurements (e.g., Saffer & Bekins 1998a) (Fig. 18.6C,D, Table 18.1). For example, to explain pore-water freshening anomalies centered at the décollement and other major fault zones at the Costa Rican, Nankai, and Barbados subduction zones, fluids must flow from zones of mineral dehydration at depth to the near-trench region where boreholes have been drilled, and flow must be rapid enough to preserve a chemical signature of the deeply seated fluids (cf., Figs 18.2 and 18.5) (e.g., Bekins et al. 1995; Spinelli et al. 2006). Similarly, rapid transient flow is needed to explain localized thermal anomalies spanning fault zones in the Cascadia and Barbados accretionary prisms (e.g., Fisher & Hounslow 1990; Davis et al. 1995; Sample 1996; Cutillo et al. 2003).
In 2D numerical models that simulate clay dehydration and coupled fluid flow and solute transport, décollement permeabilities of approximately 10−11 to 10−13 m2 are required to reproduce observed profiles of pore-water freshening at drill sites near the trench at the Barbados, Nankai, and Costa Rican margins (e.g., Bekins et al. 1995; Saffer & Bekins 1998a; Henry 2000; Spinelli et al. 2006). The 2D and 3D models of coupled fluid flow and heat transport at the Barbados margin illustrate that fault-centered thermal anomalies observed in shallow boreholes are best reproduced by transient flow with fault permeabilities of approximately 10−12 m2 (Cutillo et al. 2003). These permeabilities are approximately 1–3 orders of magnitude higher than those estimated from steady-state models (e.g., Screaton et al. 1990; Henry & Le Pichon 1991; Bekins et al. 1995; Saffer & Bekins 1998a,b; Spinelli et al. 2006) and are most consistent with in situ measurements conducted at increased pore pressure and low effective stress conditions (e.g., Davis et al. 1995; Screaton et al. 1995; Bekins et al. 2011) (Table 18.1; Fig. 18.6).
To explain the width of the anomalies, the modeling results also suggest that flow along the fault conduit must have been continuous (or quasi-continuous) over timescales of several hundred to thousands of years (Bekins & Screaton 2007) to as long as approximately 100 kyr (Saffer & Bekins 1998a, 1999; Henry 2000). Detailed recent studies of pore-water freshening at the Nankai (Brown et al. 2001; Saffer & McKiernan 2009) and Barbados (Fitts & Brown 1999; Bekins & Screaton 2007) subduction zones have accounted for the potential effects of in situ clay transformation or artifacts caused by pore-water extraction on reported pore-water geochemical profiles. The resulting corrected anomalies are shifted and more clearly centered on the décollement zone at both margins, but their widths are comparable to those originally reported.
As suggested on the basis of structural observations, analyses of vein textures and compositions, and theoretical arguments (e.g., Rice 1992), strong effective stress dependence of permeability is one likely mechanism to explain transient permeability enhancement, potentially associated with solitary pressure waves or seismic activity that generates an initial perturbation to pressure or permeability at depth (e.g., Rice 1992; Henry 2000; Bourlange & Henry 2007). This interpretation is consistent with recent work by Thorwart et al. (2013), who estimated the permeability of the Costa Rican subduction plate interface at approximately 15 km depth from time-dependent migration of seismicity swarms, based on the assumption that their migration is linked to diffusion of fluid pressure along the fault (e.g., Shapiro et al. 2003). Their analysis yields fault zone permeabilities of 3.2 × 10−14 to 1.06 × 10−12 m2, comparable to those required in transient models to explain pore-water freshening profiles at boreholes near the trench (Spinelli et al. 2006). Transient pulses of pore-fluid pressure at shallower depths are also required to satisfy mechanical constraints at the Nankai and Barbados subduction zones (e.g., Henry 2000; Skarbek & Saffer 2009), where measured or inferred present-day pressures near the trench are approximately 0.5–3 MPa lower than is needed for sliding along the décollement. This concept has been explored by modeling of pressure and permeability “fronts” migrating up-dip as predicted by models of solitary wave propagation in fault zones with strongly effective stress-dependent permeability (Henry 2000; Bourlange et al. 2003) and is consistent with the idea that regions of high seismic reflectivity and interpreted dilation along the décollement represent the leading edge of a migrating pulse of near-lithostatic pore pressure (Shipley et al. 1994).
Modeling of coupled consolidation and fluid flow at Barbados has further shown that the volume fluxes of fluid needed to maintain dilated faults greatly exceed those available within the incoming sedimentary section, implying that if migration of pressurized fluids is responsible for increased fault permeability, the permeable zones must be transient, heterogeneously distributed, or both (cf. Fig. 18.5) (Stauffer & Bekins 2001; Bekins & Screaton 2007). A similar argument arises at other locations, including Nankai and Costa Rica, from consideration of the fluid budget in combination with observed focused flow rates or those required in numerical models to explain chemical and thermal anomalies. These fluxes are approximately 10–500 times greater than the inventory of fluids, implying that increased permeability is present only approximately 0.2–10% of the time or that permeable channels occupy only this fraction of the fault surface at any given time (Fig. 18.5) (e.g., Le Pichon et al. 1990; Brown et al. 1994; Saffer & Bekins 1999; Spinelli et al. 2006).
Laboratory measurements
Laboratory measurements of permeability on intact fault zone core samples are scarce, owing to the difficulty of coring, recovering, and preserving intensely fractured and brecciated materials (Brown 1995; Zwart et al. 1997; Bolton et al. 1999). Additional insights have come from permeability measurements on experimentally sheared synthetic analogs or remolded sediment (e.g., Arch & Maltman 1990; Dewhurst et al. 1996; Ikari & Saffer 2012). In general, the laboratory measurements yield permeabilities at the lower bound or below those obtained from in situ testing or derived from numerical modeling studies.
For core samples obtained from the active frontal thrust in the Oregon accretionary prism, Brown (1995) measured permeabilities ranging from approximately 6 × 10−17 to 3.5 × 10−15 m2 under effective stresses similar to those estimated in situ (Table 18.1; Fig. 18.6). These values are below or at the lower end of the range obtained by well testing at the same fault (Screaton et al. 1995), and as much as 3 orders of magnitude lower than values of enhanced – and presumably transiently increased – fault permeability estimated on the basis of observed down-hole temperatures and vein chemistry (Davis et al. 1995; Sample 1996). Permeability measurements on core samples from the décollement zone at Barbados yield values of approximately 10−18 to 10−17 m2, over a range of effective stresses of 96–768 kPa (Brückmann et al. 1997; Zwart et al. 1997). As is the case for the Oregon frontal thrust, these values fall below (Bekins et al. 2011) or overlap only the lower bound (Screaton et al. 1997) of permeabilities obtained by well testing.
Bolton et al. (1999) report on a series of triaxial tests conducted on cores from the toe of the Costa Rican margin, including one friable claystone from an active splay fault in the upper plate. Their tests illustrate that under normal consolidation conditions up to 900 kPa mean effective stress, the fault zone permeability is less than 10−18 m2, whereas in an overconsolidated state achieved by reduction in effective mean stress to <100 kPa following initial consolidation to 900 kPa, its permeability is increased by more than 3 orders of magnitude to 2 × 10−15 m2. As described earlier (fault zone architecture: inferences about hydraulic properties and behavior), geologic evidence suggests that similar processes may operate in situ; fracture networks within the décollement are interpreted to dilate due to shearing of overconsolidated mudstone under conditions of increased pore pressure and reduced effective stress (e.g., Karig 1990; Ujiie et al. 2003; Uehara & Shimamoto 2004).
The differences between laboratory measurements of permeability and those obtained from in situ well testing and regional-scale modeling are most likely explained by two effects. First, in most cases, the laboratory samples do not sample the most disturbed and intensely fractured or brecciated portions of the fault zone (cf. Fig. 18.3). This leads to a sampling bias due to preferential core recovery and a potential scale dependence because the core samples do not include the largest and most conductive fractures. As a result, the laboratory measurements are most compatible with in situ tests conducted at high effective normal stresses, during which connected fracture networks in the fault zone are partly closed (e.g., Screaton et al. 1995) (Fig. 18.6). Second, the core samples used in laboratory tests are oriented vertically (i.e., at a high angle to the fault); if the fault permeability is strongly anisotropic (e.g., Brown et al. 1994; Faulkner & Rutter 2001), then the in situ well tests, which sample permeability parallel to the fault, should yield higher values.
Permeability measurements on synthetic analogs, and on remolded or sheared sedimentary protolith and wall rock, also provide additional basic insights into the hydraulic behavior of subduction faults (e.g., Arch & Maltman 1990; Brown et al. 1994; Dewhurst et al. 1996; Ikari & Saffer 2012). These tests generally demonstrate an overall decrease in permeability and increase in permeability anisotropy (higher permeability parallel to the shearing direction) as a function of shearing, due to clay particle alignment, development of microstructures, and consolidation. The shear-parallel permeability is similar to that measured in unsheared sediments (e.g., Dewhurst et al. 1996) or in some cases slightly enhanced by alignment of fabric elements (e.g., Arch & Maltman 1990), whereas fault-normal permeability is reduced by one-half to as much as 3 orders of magnitude, with fault-normal permeability values as low as 10−21 to 10−20 m2 (e.g., Dewhurst et al. 1996; Ikari & Saffer 2012).
This result may be relevant to the behavior of clay-rich fault cores that accommodate large localized shear strains (e.g., Vannucchi & Leoni 2007), but is probably not representative of regional-scale fault permeability that is dominated by connected fracture networks in the damage zone, as indicated by structural observations and logging data. If low-permeability sheared clays form a spatially continuous fault core, décollements could act as combined conduit – barriers with high permeability parallel to structure and low permeability across it (e.g., Tobin et al. 2001), leading to isolation of flow systems above and below the fault (e.g., Silver et al. 2000). However, there is little direct evidence for such continuity of sheared clays, in part, because direct sampling is restricted to a small number of boreholes. Moreover, both the drainage pattern in underthrusting sediments (Fig. 18.4) and geochemical observations (Saffer & Screaton 2003) indicate fluid communication between the subjacent sediment section and the fault zone, and therefore suggest that low-permeability zones of localized shear are not ubiquitous or continuous.
Implications and key outstanding questions
The nature of fault zone permeability and flow paths
Temporally and spatially averaged fault zone permeabilities (i.e., those represented by steady-state models and a subset of in situ measurements) are consistent across several margins worldwide and range from approximately 10−13 to 10−15 m2. The similarity between margins is striking, considering that they are characterized by different convergence rates, wedge geometries, sediment thicknesses, thermal structures, and partitioning of sediment between accretion and underthrusting at the trench. Permeabilities above this range would lead to well-drained conditions within the fault and immediately adjacent wall rocks, inconsistent with a wide range of observations that indicate increased pore-fluid pressure and mechanical weakness along the décollement and in the uppermost subducted sediments (e.g., Davis et al. 1983). Lower permeabilities lead to décollement zone pore pressures in excess of lithostatic or which are inconsistent with predictions from critical taper theory (e.g., Brown et al. 1994; Bekins et al. 1995; Saffer & Bekins 1998a).
The fault zone permeabilities required to explain geochemical and thermal anomalies observed in drill holes and to match measured flow rates at focused seepage sites are higher than the range defined by steady-state models. They are also consistent between margins and range from approximately 10−11 to 10−13 m2 (e.g., Fisher & Hounslow 1990; Bekins et al. 1995; Davis et al. 1995; Saffer & Bekins 1998a; Spinelli et al. 2006) (Fig. 18.6; Table 18.1). The shape of advective signals centered at fault zones is most consistent with transient permeability enhancement and flow, likely driven by pulses of increased pore pressure that reduce effective normal stress and drive dilation of fracture networks (e.g., Blanc et al. 1991; Henry 2000). However, these increased pressures and permeabilities cannot be continuous in time, nor can they be present across the entire fault surface at a given time; the former would violate the overall fluid budget (Le Pichon et al. 1990; Saffer & Bekins 1999; Bekins & Screaton 2007), whereas the latter would be inconsistent with the maintenance of a tapered wedge geometry (e.g., Brown et al. 1994). As an additional consideration, if permeable regions on the fault are heterogeneously distributed, to access fluids and allow dewatering of the subducted section, they cannot be stationary (e.g., Bekins & Screaton 2007). The emerging picture is that increased fault permeability is both transient and heterogeneous, with overpressured and permeable patches or “channels” restricted to only a portion of the fault surface and shifting over time (cf. Fig. 18.5C) (e.g., Carson & Screaton 1998; Saffer & Bekins 1999; Bekins & Screaton 2007).
The transiently increased permeabilities defined by numerical modeling studies overlap the upper range of measured values obtained at low effective normal stresses (Fig. 18.6C,D), consistent with the idea that transient flow is linked to the pressure dependence of permeability and dilation of fracture networks. Although lower, permeabilities estimated from steady-state models are most consistent with the middle to upper range of in situ borehole measurements, and are generally higher than the lowest point measurements (Fig. 18.6A,B). This may suggest that the long-term average fault permeability reflects modestly increased in situ pore pressure.
Recent work has also shown that in addition to the master décollement, splay faults cutting the upper plate are important egress pathways for fluids derived from sediment consolidation and dehydration reactions (e.g., Ranero et al. 2008; Sahling et al. 2008). Although focused studies have been limited to a few margins, mounting evidence from seafloor sampling, drilling, and numerical modeling demonstrates that these structures efficiently tap deep fluids by intercepting them from the décollement or deep interior of the wedge (Sample 1996; Teichert et al. 2005; Lauer & Saffer 2012). One implication is that fluids sampled at seafloor seep sites or by drilling into upper plate faults should exhibit a systematic increase in the deeply sourced contribution with distance landward (Fig. 18.2) (Mottl et al. 2004; Teichert et al. 2005). Translation of pore pressure from the plate interface to the base of layered slope sediments capping the upper plate wedge may also provide a mechanism to explain the locations of active mud volcanoes and mud mounds (Hensen et al. 2004).
Faults and the plumbing of subduction complexes
Dewatering and drainage state: the role of faults
Because faults are permeable, they carry focused fluxes of fluid derived from dewatering and drainage of underthrust and accreted sediments (e.g., Screaton et al. 1990; Saffer & Bekins 1998a). Yet despite their key role in carrying dewatering fluxes, the drainage state of the accretionary wedge and underthrusting section remains primarily controlled by the sediment matrix permeability (Screaton et al. 1990; Saffer & Bekins 2006). To simply and directly quantify the effect of fault permeability on drainage of the adjacent wall rock, I define a dewatering “penetration depth” (Zp) as the distance into the wall rock (away from a fault conduit) at which the effective hydraulic diffusivity along a flow path to the trench allows pressure dissipation at a rate comparable to the tectonic loading rate.
To define the penetration depth, I adopt the criterion for maintenance of abnormal pressure introduced by Neuzil (1995), relating the strength of geologic forcing (Γ) to the characteristic path length for fluid escape (L) and the effective hydraulic conductivity (Keff) along the flow path:
The geologic forcing (Γ; units of fluid volume per rock volume per time) results from processes that act as sources or sinks of fluid; these may represent actual fluid volume production (e.g., from hydrocarbon generation or dehydration reactions) or virtual sources that act to increase pressure (e.g., disequilibrium compaction or thermal pressurization). Although not a strict threshold for the generation or maintenance of increased pore pressure, the criterion given by Eq. 18.1 provides a framework to evaluate the potential for overpressures in a wide range of geologic settings, including subduction zones (e.g., Neuzil 1995; Saffer & Bekins 2006).
Assuming a drainage path through the sediment matrix and to the fault (cf. Fig. 18.4C, inset), L is given by (x + Zp), where x is the distance along the fault to the seafloor. For the case of the décollement, x is the distance from the trench. The effective hydraulic conductivity (Keff) from the penetration depth to the seafloor is given by:
where Ksed and Kfault are the hydraulic conductivity of the sediment matrix and the fault zone, respectively. Rearranging Eq. 18.2 and combining with Eq. 18.1 defines an expression for the penetration depth:
I solve Eq. 18.3 for Zp as a function of distance from the trench (x) for a suite of fault permeabilities, using the Nankai and Costa Rican subduction zones as example cases (Fig. 18.7). The geologic forcing is defined on the basis of porosity loss with increasing depth and distance into the subduction zone (e.g., Spinelli et al. 2006). Sediment matrix permeability is defined by permeability–porosity relationships reported for sediments at each margin (Skarbek & Saffer 2009; Gamage et al. 2011; Daigle & Screaton 2015a). In computing both fault and sediment hydraulic conductivity from permeability, I account for variation in fluid viscosity with temperature (where dynamic viscosity μ = 2.4 × 10−5[10248.37/(T+133.15)] and T is temperature in degrees Celsius) (Smith & Chapman 1983).
Penetration depth decreases systematically with burial and consolidation (from approximately 130 to 175 m near the trench to only tens of meters by 10 km landward), as sediment matrix permeability decreases (e.g., Daigle & Screaton 2015a) (Fig. 18.7A). A highly permeable fault (k = 10−12 m2; consistent with reported transient permeabilities) drains the adjacent sediments only very slightly more efficiently than a fault 4 orders of magnitude less permeable (k = 10−16 m2; consistent with the lower bound on reported steady-state permeabilities). At distances beyond approximately 25 km landward of the trench, the penetration depth increases slightly because with progressive burial and porosity loss the effects of decreasing geologic forcing and fluid viscosity outpace the decrease in sediment permeability.
Although simplified, this approach illustrates that permeable faults (or other conduits) will be efficient in dewatering sediments only locally over most of the outer forearc. This is because the matrix permeability at depths greater than a few kilometers is several orders of magnitude lower than fault permeability (cf. Fig. 18.6). As a result, fluid access to the permeable conduit is controlled by the matrix permeability. This is also illustrated by considering the sensitivity of effective permeability for drainage to the seafloor to conduit permeability (Fig. 18.7B; example for a location 30 km from the trench). For fault permeabilities >10−15 m2, further increases in fault permeability have no effect on the effective permeability. For lower fault permeabilities, the effective permeability is sensitive to variations in fault permeability only within less than 30 m of the fault. This behavior is also noted in 1D and 2D numerical modeling studies for individual margins (Barbados, Costa Rica, and Nankai) (Screaton et al. 1990; Saffer & Bekins 1998a; Spinelli et al. 2006; Skarbek & Saffer 2009) and those designed to explore the hydrologic behavior of subduction complexes more generally (Saffer & Bekins 2006), both of which show that permeable faults are in hydraulic communication with only the upper tens of meters of the underthrusting section, and that simulated overall pore-fluid pressures are far less sensitive to fault permeability than to the bulk sediment permeability.
Advection and preservation of localized anomalies along faults
In contrast to the drainage of pore-fluid pressures, faults, including both the master décollement and splay faults, are clearly key pathways for focused advective transport of heat and solutes. Commonly, first-order evaluation of transport behavior is framed in terms of the Peclet number, which relates rates of advection and diffusion in one dimension in the transport direction. However, for localized thermal or geochemical signals transported along conduits sufficiently rapidly that they cannot diffuse laterally (fundamentally a 2D problem), a slightly more restrictive formulation is appropriate (e.g., Fisher & Hounslow 1990; Sample 1996). In this case, the dissipation of an initial pulse localized in a flow conduit can be described by
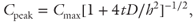
where Cpeak is the maximum concentration at the center of the conduit at any time t; Cmax is the initial maximum concentration at the center of the conduit; D is the diffusivity; and h is the conduit width (Carslaw & Jaeger 1959). Adopting the simple criterion that to preserve observed anomalies centered at fault zones, flow must transport a pulse faster than it can be dissipated by diffusion, the problem can then be defined by the ratio of timescales required for fluid flow and chemical or thermal diffusion (Fig. 18.8) (e.g., Sample 1996). This approach may slightly overestimate the timescale of dissipation where matrix permeability is high enough to allow significant advection of solute or heat away from the potentially overpressured fault conduit; thus, the flow rates shown in Fig. 18.8 should be considered minima. However, the effect of fault-normal solute or heat advection is likely to be small (e.g., Henry 2000; Bekins & Screaton 2007) and restricted to shallow depths where sediment matrix permeability is greater than approximately 10−16 m2.
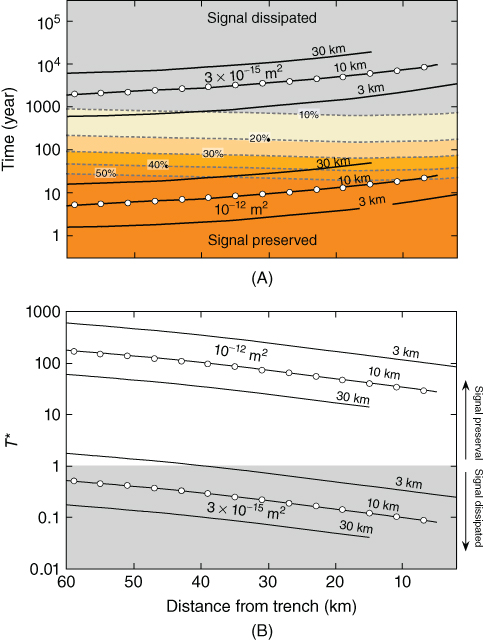
Fig. 18.8 (A) Time required for up-dip fluid migration over distances of 3, 10, or 30 km (black curves, as labeled) as a function of distance landward of the trench, for fault permeabilities of 10−12 m2 (bottom, as labeled) and 3 × 10−15 m2 (top, as labeled). Flow rates are computed assuming a fault zone porosity of 0.05, a hydraulic gradient equivalent to a pore pressure ratio (λ = Pfiuid/Plithostatic) of 0.80, and accounting for varying fluid viscosity as a function of temperature. Times required for the dissipation of a 1-m-wide initial solute concentration pulse are shown by color shading, computed assuming a molecular diffusivity (D) of 10−9 m2 s−1, and with effective diffusivity defined as a function of sediment matrix porosity by D* = D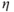 /2 and accounting for the effects of temperature and fluid viscosity by the Stokes–Einstein equation (Helfferich 1966). Dashed contours show the times at which the peak concentration of the pulse has decreased to a particular percentage of the initial peak value. (B) The ratio (T*) of the times shown in panel (A) (Tdiffusion/Tflow) as a function of distance from the trench, where Tdiffusion is defined as the time by which the pulse is reduced to 10% of its initial amplitude. For a fault zone permeability of 10−12 m2, localized concentration pulses would dissipate by <50% over transport distances of <10 km, regardless of location. For fault permeability of 3 × 10−15 m2, signals would dissipate by >90% in most scenarios. Thermal structure, geometry, and sediment matrix porosity distribution are defined using the Nankai accretionary complex as an example (Skarbek & Saffer 2009). (See color plate section for the color representation of this figure.)
/2 and accounting for the effects of temperature and fluid viscosity by the Stokes–Einstein equation (Helfferich 1966). Dashed contours show the times at which the peak concentration of the pulse has decreased to a particular percentage of the initial peak value. (B) The ratio (T*) of the times shown in panel (A) (Tdiffusion/Tflow) as a function of distance from the trench, where Tdiffusion is defined as the time by which the pulse is reduced to 10% of its initial amplitude. For a fault zone permeability of 10−12 m2, localized concentration pulses would dissipate by <50% over transport distances of <10 km, regardless of location. For fault permeability of 3 × 10−15 m2, signals would dissipate by >90% in most scenarios. Thermal structure, geometry, and sediment matrix porosity distribution are defined using the Nankai accretionary complex as an example (Skarbek & Saffer 2009). (See color plate section for the color representation of this figure.)
This simple formulation yields basic insights into the conditions that favor rapid advection and preservation of focused anomalies along faults. In general, for realistic hydraulic gradients driving flow, fault zone permeability must be greater than approximately 10−14 m2 to maintain focused pore-water geochemical signals as they are transported up-dip (Fig. 18.8). The required permeability scales inversely with flow distance: for longer migration paths, higher permeability is needed to deliver a pulse before it is dissipated by diffusion (Fig. 18.8, compare curves).
Geochemical anomalies observed in shallow fault zones generally indicate source regions located several tens of kilometers down-dip, where temperatures are >80–150°C (e.g., Kastner et al. 1991; You et al. 1996). To preserve focused anomalies over these migration distances requires fault zone permeabilities of approximately 10−12 to 10−13 m2. This is in excellent agreement with the results of detailed 2D modeling studies at numerous margins, which suggest that (i) transiently increased permeabilities >10−13 m2 are needed to match the magnitude and shape of geochemical and thermal profiles, and (ii) steady-state permeabilities of approximately 10−15 to 10−14 m2 lead to simulated profiles that are both too small in magnitude and too broad to match observations (e.g., Bekins et al. 1995; Saffer & Bekins 1998a; Spinelli et al. 2006). The simple approach illustrated in Figure 18.8 provides a useful and simple framework to derive constraints from field observations, without requiring construction and parameterization of a full 2D or 3D model of flow and transport. Because thermal diffusivity is approximately 3 orders of magnitude higher than chemical diffusivity, preservation of temperature anomalies would require permeabilities > 10−12 m2. This may also explain why most thermal signals observed in shallow boreholes are considered to reflect flow from only a few kilometers depth (i.e., short migration distances) (Fisher & Hounslow 1990; Sample 1996).
From Figure 18.8, it is also evident that the rates of both flow and diffusion vary with depth. As a consequence, advection of focused anomalies should be increasingly efficient with increased depth. This results from the combined effects of reduced effective diffusivity with depth, and decreased fluid viscosity that leads to faster flow rates for a given fault permeability. Fluid viscosity decreases by approximately 1 order of magnitude over the temperature range from 0 to 100°C. In contrast, the effective diffusivity decreases only modestly with depth because there is a trade-off between reduction in diffusivity due to porosity decrease and an increase in diffusivity as fluid viscosity decreases (i.e., as described by the Stokes–Einstein equation).
Key outstanding questions
Despite wide-ranging observations that constrain fault zone architecture, physical properties, flow rates, distances of flow and transport, and a basic model of temporally and spatially variable flow (e.g., Carson & Screaton 1998), the timescale and causes of permeability variations remain enigmatic (Saffer & Tobin 2011). Direct observations of geochemical and flow rate changes associated with earthquakes and slow slip events, both in borehole observatories (e.g., Solomon et al. 2009; Davis et al. 2011) and at the seafloor (e.g., Brown et al. 2005; Tsuji et al. 2013), document unequivocally that seismic activity drives pulses of fluid flow. Yet, the timescale of transient flow interpreted from the width of geochemical and thermal anomalies is as long as tens to hundreds of kyr – far longer than earthquake recurrence intervals.
This apparent discrepancy could be explained if permeability variations associated with fault slip and healing are superimposed on a longer-term cycle of permeability enhancement driven by pore-fluid pressure buildup and release or by chemical precipitation and sealing. Alternatively, the width of the down-hole geochemical profiles may simply document the initiation of continuous focused flow. This initiation time could reflect the point at which the fault is buried deeply enough and has low enough porosity to host brittle deformation that would lead to the generation of discrete fractures and conduit behavior (cf., Fig. 18.3A) (Caine et al. 1996; Saffer & Bekins 1999). In both of these scenarios, seismicity-driven flow pulses would result in quasi-continuous flow since the time of fault localization or superimposed on longer-timescale flow cycles, but would not be resolvable from down-hole profiles that record only the integrated signal from many events.
The details of feedbacks and causal relationships between permeability enhancement, pore pressure translation, and fault slip in subduction zones are also incompletely understood. Numerical and analytical models of perturbations in fault zones with strongly effective stress-dependent permeability demonstrate the possibility of solitary waves, in which pressure pulses migrate up-dip and modify fault permeability as they pass (e.g., Rice 1992; Bourlange & Henry 2007), raising the prospect that this process could also trigger the migration of seismicity or propagation of slow slip (e.g., Thorwart et al. 2013). Models specific to the Nankai subduction zone show that migration of pressure pulses by this mechanism is more than 500 times too slow to directly explain slip propagation inferred from migration of small earthquake swarms at rates of kilometers per day (Bourlange & Henry 2007). This suggests that pressure pulse migration may not explain triggering of fault slip. However, the propagation velocity of the pressure pulse depends strongly on the maximum value and form of the stress–permeability relation; thus, the parameter space explored by modeling may simply warrant further investigation. Sealing via cementation or vein filling and subsequent rupture of seals (i.e., by hydraulic fracturing or seismic slip) may also be important controls on permeability cycling. However, at shallow depths where faults have been cored most extensively, veining is noted but generally sparse (e.g., Labaume et al. 1997a,b; Vrolijk & Sheppard 1987); at greater depths where pressure and temperature are higher, chemical sealing may become increasingly important (e.g., Sibson 1981b).
Ultimately, better defining the sensitivity of permeability to effective stress (e.g., Bekins et al. 2011) and its variation as functions of depth and fault zone architecture is essential to better quantify the nature and magnitude of permeability changes in response to hypothesized perturbations in pressure or permeability. These include continuous processes of metamorphic fluid release, tectonic loading, and chemically driven porosity reduction that could drive a cyclic buildup and release of pressure (e.g., Sibson 1981b), as well as seismicity or slow slip events that perturb pressure or permeability at depth (e.g., Bourlange & Henry 2007). Direct measurements are limited to shallow depth (<1 km); down-hole experiments in deeper (5–6 km) boreholes will extend the range of effective stresses and P–T conditions where fault properties are sampled (e.g., Tobin & Kinoshita 2006). At depths beyond the reach of drilling, modeling studies constrained by shallow observations, or by the (presumed fluid-driven) migration of seismicity (Shapiro et al. 2003; Thorwart et al. 2013), provide a promising approach to quantify fault permeability behavior.
Finally, although advective signals measured at the seafloor and in the shallow subsurface have yielded clear evidence for long-distance migration of fluids, significant uncertainty remains in precisely defining fluid source regions, documenting the mixing of fluids derived from different dehydration reactions or diagenetic processes, and quantifying the behavior of nonconservative solute tracers. Considerably tighter constraints on the depth of origin for migrating fluids, and on the relative contributions from distinct source regions, may be possible with the use of multiple tracers that originate at different depths and temperatures (e.g., You et al. 1996; Mottl et al. 2004). Ultimately, multitracer numerical simulations of coupled flow and transport will lead to a refined and more quantitative understanding of volatile budgets, fluid migration pathways, flow rates, and the associated fault permeabilities.
Acknowledgments
This research used data obtained as part of the ODP and IODP. This work was supported by postexpedition funding from the Consortium for Ocean Leadership (US-SSP) and NSF awards 0451602, 0623633, 1049591, and 0752114. Detailed discussions with Elizabeth Screaton, Barbara Bekins, and J. Casey Moore were instrumental in conceiving and developing this review. I also thank Katelyn Huffman (Fig. 18.3C), Tom Shipley (Fig. 18.5A), Peter Vrolijk (micrograph; Fig. 18.2), and Miriam Kastner (data for Fig. 18.5B) for providing graphics and data used in figures.