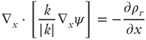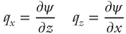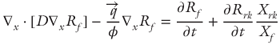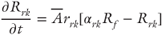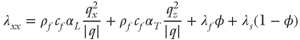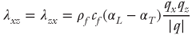Chapter 21
Evidence for long-timescale (>103 years) changes in hydrothermal activity induced by seismic events
Trevor Howald1, Mark Person1, Andrew Campbell1, Virgil Lueth2, Albert Hofstra3, Donald Sweetkind3, Carl W. Gable4, Amlan Banerjee5, Elco Luijendijk6, Laura Crossey7, Karl Karlstrom7, Shari Kelley2 and Fred M. Phillips1
1Department of Earth & Environmental Science, New Mexico Institute of Mining and Technology, Socorro, NM, USA; 2New Mexico Bureau of Geology and Mineral Resources, Socorro, NM, USA; 3U.S. Geological Survey, Denver, CO, USA; 4Los Alamos National Laboratory, Los Alamos, NM, USA; 5Indian Statistical Institute, Kolkata, India; 6Department of Structural Geology and Geodynamics, Georg-August-Universität Göttingen, Göttingen, Germany; 7Department of Earth and Planetary Sciences, University of New Mexico, Albuquerque, NM, USA
Abstract
The pollen 14C age and oxygen isotopic composition of siliceous sinter deposits from the former Beowawe geyser field reveal evidence of two hydrothermal discharge events that followed relatively low-magnitude (<M5) earthquakes of Holocene and Late Pleistocene age along the Malpais fault zone in Whirlwind Valley, Nevada, USA. The observed 20‰ trend of decreasing δ18O over about a 5000–7000-year period following each earthquake is consistent with a fault-controlled groundwater flow system that, following initial discharge of deep and hot groundwater, contains increasing amounts of cool meteoric water through time. Model simulations of this hydrothermal system can only match trends in the isotope data if we include a 1000-fold increase in fault permeability (from <10−14m2 to >10−11m2) following each earthquake. However, the timescale for the onset of thermal convection implied by an overturned temperature profile in a geothermal well 300m from the Malpais fault is much shorter: 200–1000 years. We speculate that individual segments of the Malpais fault become clogged on shorter timescales and that upward flow of groundwater subsequently follows new routes to the surface.
Key words: fault, hydrothermal, oxygen isotope, permeability, sinter
Introduction
Numerous studies have reported centimeter- to meter-scale water-level fluctuations in wells (King et al. 1999; Wang et al. 2004a; Chia et al. 2001; Manga et al. 2012), temperature changes (Dziak et al. 2003), increases in stream flow (Muir-Wood & King 1993), and changes in geyser periodicity (Husen et al. 2004a) in response to seismic events. The hydrologic response to seismic waves is thought to be due to either deep-seated fracture closure/dilation (Muir-Wood & King 1993; Sibson 1996) or shallower crustal permeability changes (Rojstaczer & Wolf 1992; Brodsky et al. 2003; Elkhoury et al. 2006; Manga et al. 2012). Both mechanisms call upon significant permeability changes. The hydrogeologic response to seismicity can be complex (Wang et al. 2004a) with water levels rising or falling in different locations of the stress field proximal to the earthquake foci. Hydrologic changes have been observed to occur at great lateral distances from the earthquake epicenter (103 km; Husen et al. 2004a). In the vast majority of the aforementioned studies, the hydrologic system responded to seismic events are on timescales no greater than several years (Manga et al. 2012). Curewitz & Karson (1994) proposed that stress changes at fault tips and fault kinematics could induce transient hydrothermal behavior on much longer timescales. Quantitative paleohydrologic reconstructions of ore-deposit formation and diagenesis have also supported hydrologic transients associated with seismicity and fault-permeability changes on timescales of 103 years (e.g., Garven et al. 2001; Appold et al. 2007). The objective of this study is to constrain seismicity-induced fault-permeability changes and their effects on hot-spring/geyser isotopic composition over timescales of 103 years within the Beowawe geothermal system, Nevada. The unique contribution of this study is a new data set of sinter-deposit ages and isotopic compositions over timescales of thousands of years.
Within Whirlwind Valley, Nevada, a large sinter terrace about 65 m high and 1600 m long (Rimstidt & Cole 1983) crops out along the Malpais fault zone, which is a high-angle normal fault with an east–northeast strike (Fig. 21.1A, B, D). The sinter deposits document geothermal discharge of the former Beowawe geyser field. The Malpais fault zone forms the southeastern edge of a graben that underlies Whirlwind Valley; the Muleshoe fault forms the northwestern edge (Fig. 21.1A). The sinter deposit formed within an area of exceptionally high heat flow at shallow depth (dashed orange lines, Fig. 21.2A). Zoback (1979) estimated that the sinter deposits contain 1.76 × 1010 kg of silica and that the time required to form the Beowawe sinter deposits was 210,000 years assuming a constant flow rate (Renner et al. 1975) and concentration of dissolved silica.
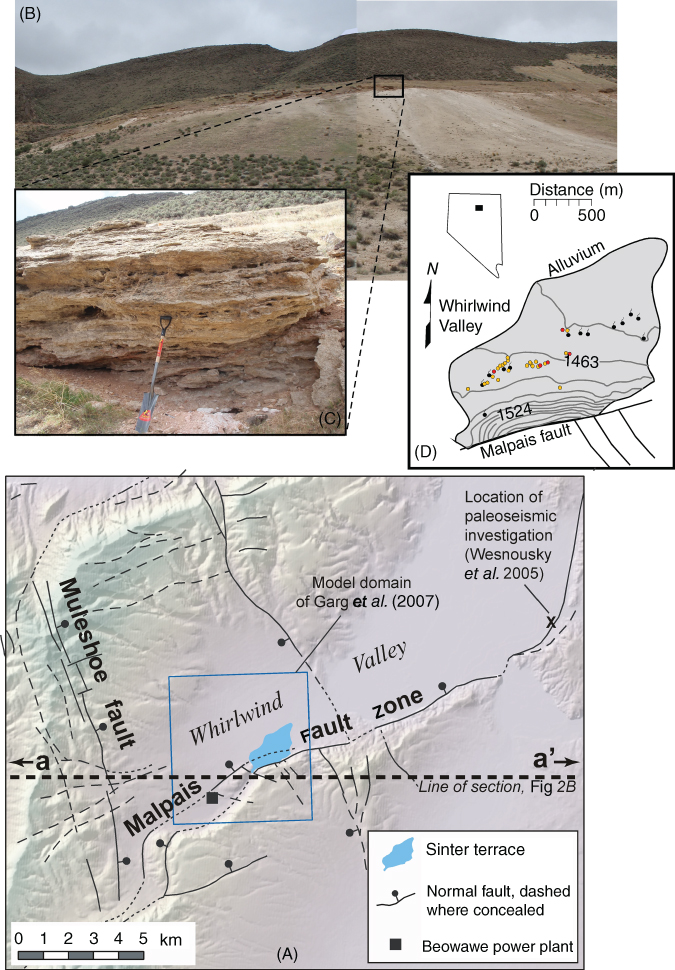
Fig. 21.1 (A) Structural map showing location of Beowawe sinter deposits, paleoseismic investigation of Wesnousky et al. (2005) along the Malpais fault zone, the Beowawe power plant (black square). (B) Photo mosaic of Beowawe sinter deposits, Whirlwind Valley, Nevada. The photo was taken looking southeast. (C) Outcrop scale photo of sinter deposits. (D) Sinter topographic map with locations of historic and paleo hot springs (black circles, as well as locations of sinter samples (red and yellow circles). Multiple samples were collected at locations with yellow dots. (See color plate section for the color representation of this figure.)
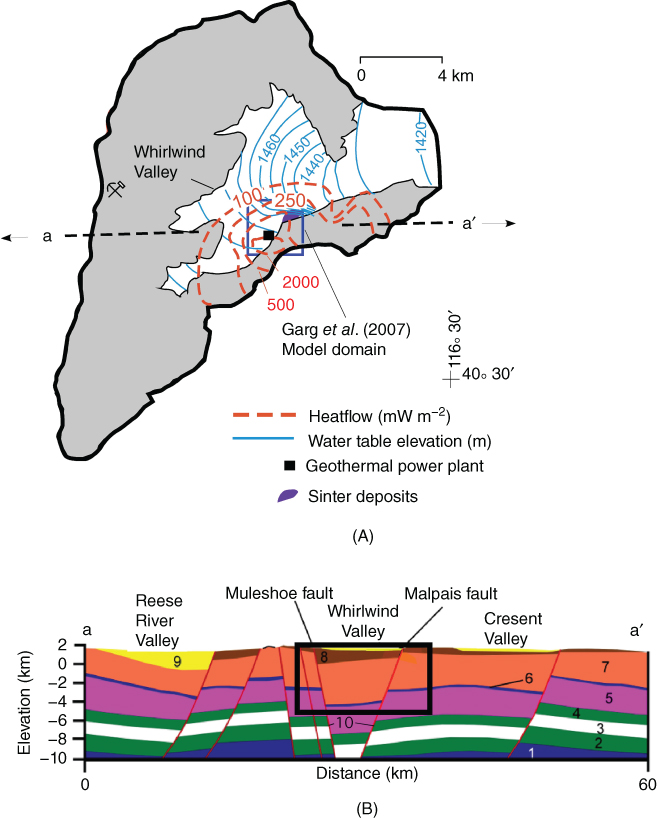
Fig. 21.2 (A) Heat flow (orange dashed contour lines; in mW m−2) and water-table elevation (solid light blue lines; m) contour map across Whirlwind Valley, Nevada. Location of regional hydrothermal model cross section is depicted by a–a'. Dark blue box indicates the location of the Beowawe sinter terrace shown in Figure 21.1B. Heat-flow and water-table contour maps from Olmsted & Rush (1987) and Faulder et al. (1997). (B) Hydrogeologic cross section across Reese, Whirlwind, and Crescent Valleys. The inset (solid black rectangle) denotes the portion of the hydrothermal model domain presented in Figure 21.3A–F. Permeability data for the different numbered units in Figure 21.1C are presented in Table 21.1 and described in the supplemental materials section. (See color plate section for the color representation of this figure.)
As part of this study, we analyzed 63 sinter samples from the Beowawe geyser field for δ18O (red and yellow dots in Fig. 21.1D). Pollen extracted from a subset of the sinter-deposit samples were dated using 14C (Fig. 21.3). The dated samples revealed isotopic depletion in fluid δ18O of about 20‰ over 5000–7000 years that appear to be correlated with Holocene and Late Pleistocene seismic activity along the Malpais fault (Fig. 21.3). Isotopic fractionation associated with boiling can only produce approximately a 2‰ shift in composition (Harris 1989) and cannot be called upon to explain the 20‰ depletion. Similarly, the effects of Quaternary climate change on the isotopic composition of precipitation in the southwestern United States are only on the order of 4‰ (Asmerom et al. 2010). We believe the simplest explanation for these isotopic trends is that seismicity along the Malpais fault increased fracture permeability, initiating rapid discharge of geothermal water within a single-pass hydrothermal system that, as time passed, received an increasing proportion of isotopically light meteoric water. The system gradually shut down due to mineralization and incursion of cool, dense meteoric water. One of the main goals of this study is to use thermal and isotopic modeling to test this hypothesis.
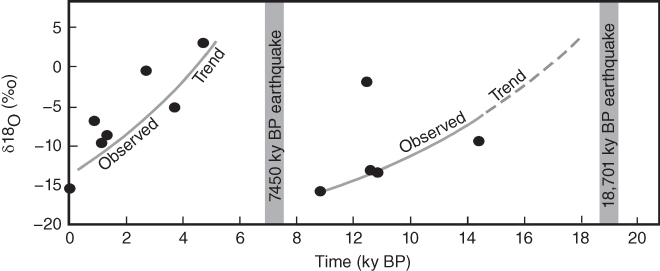
Fig. 21.3 Reconstructed temporal evolution of fluid compositions based on calculated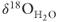 
(at 93°C) in equilibrium with sinter and radiocarbon dates on pollen in sinter (circles). The best-fit dashed gray lines drawn through the sample points show that 
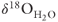progressively decreased during two distinct episodes of fluid flow through the Beowawe geothermal system. Timing of earthquakes reported by Wesnousky et al. (2005) suggests that each episode of fluid flow was triggered by seismicity. Initially, hot fluids are in isotopic equilibrium with the carbonate reservoir rocks at 5 km depth discharge. Introduction of isotopically depleted meteoric water through time results in the progressive decrease in isotopic composition of discharging fluids along the Malpais fault. Sample point on the origin of the Y-axis (−15‰) is the present-day average 
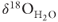value at Beowawe for precipitation (John et al. 2003).
Linkages between seismicity and geyser/hot-spring activity have been documented in modern geothermal systems (Wang & Manga 2010b). Husen et al. (2004a) documented temporal changes in Yellowstone geyser eruption periodicity and linked them to distant earthquakes. However, no linkages between seismicity and surface water geochemistry have been found within the Yellowstone National Park watershed (Hurwitz et al. 2007). Mogi et al. (1989) were among the first to report geothermal temperature increases in response to seismic events: a 1–2°C increase following seismic activity at Usami Hot Springs, Izu Peninsula in Japan. More recently, King et al. (1994a) and Manga & Rowland (2009) proposed that permeability increases following an M 5.5 earthquake led to a 1–2°C temperature decrease in Alum Rock spring, California. Diagenetic studies have also suggested episodic fluid flow events associated with seismicity along shallow fault systems. Boles & Grivetti (2000) and Boles et al. (2004) reported relatively high fluid-inclusion homogenization temperatures (80–125°C) at shallow depths (<300 m) along faults that crop out on the onshore region of the Santa Barbara Basin. These authors hypothesize that Pleistocene paleoseismicity increased the permeability associated with a series of faults, resulting in an episodic hydrothermal system. Paleohydrologic modeling by Appold et al. (2007) indicated that the combination of pressure declines with a deep overpressured reservoir and permeability changes associated with calcite cementation led to the eventual decline of hydrothermal activity over a period of about 100–1000 years. However, we are unaware of any seismicity study that has provided a high-resolution temporal record of changes in hydrothermal activity over geologic timescales.
Our study is one of the first to assess the isotopic evolution of hydrothermal fluids within a geothermal system using pollen-dated sinter deposits. We are only aware of one other study that has applied 14C dating in the study of sinter deposits within the Great Basin (Lynn et al. 2008). They document changes in silica mineralogy (Opal-A to quartz) as a function of sinter age from the Steamboat Springs sinter deposits, NV. They analyzed terrace and distal apron samples as well as a 13.1 m-deep drill core. AMS 14C pollen ages from the drill core revealed discordant ages with depth. The authors suggested that this was the result of physical mixing of older and younger sinter fragments.
Study area
Background
The Beowawe geothermal system is one of the highest temperature geothermal reservoirs in the Basin and Range physiographic province (Fig. 21.2A), with a temperature of about 220°C at 3 km depth (Olmsted & Rush 1987). The system is liquid dominated; boiling is localized at very shallow depths. The most recent volcanism in the area occurred during the middle-Miocene and is not considered a feasible heat source. The low helium R/RA value of 0.46 reported by Welhan et al. (1988) is also indicative of an amagmatic system. The Beowawe geothermal system is located within the Battle Mountain heat-flow high, which has a background heat flow of about 110 mW m−2 (Smith 1983). This is believed to be partially due to a thinned crust (19–23 km; Heimgartner et al 2006). Shallow temperature-gradient measurements indicate heat flow greater than 2000 mW m−2 (Olmsted & Rush 1987). The large shallow heat flow is thought to be associated with deep-seated and permeable normal faults that allow hot fluids to be brought up to the surface quickly. Geothermal waters discharge at a high rate (18 kg s−1) along the Malpais fault zone, where volumetrically significant sinter deposits have accumulated (Zoback 1979).
The permeability of the Malpais fault zone has been estimated by several prior studies. Faulder et al. (1997) reported well pressure tests that were used to estimate the Malpais fault-zone permeability. They reported the fault-zone conductance to be between about 6 × 10−11 and 1.2 × 10−10 m3. Person et al. (2008) developed a paleohydrothermal model of gold mineralization to assess the plumbing of the Miocene-age Mule Canyon gold deposits in Whirlwind Valley. They assigned a vertical permeability of 10−11 m2 to the Muleshoe and Malpais faults in their basin-scale, cross-sectional hydrothermal model of Whirlwind Valley. Garg et al. (2007) developed a three-dimensional, single-phase, fault-scale (about 3 km × 3 km × 3.5 km; blue box in Fig. 21.1A) hydrothermal and solute-transport model of the Malpais fault zone to reproduce direct-current resistivity, magnetotelluric, and well temperature surveys. Two of the six wells studied by these authors, those closest to the Malpais fault zone (Balz-1, 85-15; see Fig. 21.4B,C) displayed pronounced temperature overturns with depth consistent with a transient geothermal flow system (Ziagos & Blackwell 1986). In order to match observed temperature data (Fig. 21.4A–D), Garg et al. (2007) assigned a permeability of 2 × 10−13 m2 to a 1.2-km-long and 3-km-deep section of the Malpais fault zone, while the remaining segments of the Malpais fault were assigned 10−15 m2. The model included a specified fluid flux of 20 kg s−1 along the base of the Malpais fault (at about 3 km depth) to match observed geothermal discharge and was run for 25,000 years, sufficiently long to approach quasi-steady-state thermal conditions. While the Garg et al. (2007) model was able to simulate temperatures that were a good match to four of the six wells, the observed thermal overturns (Fig. 21.4B,C) in the wells closest to the Malpais fault zone could not be reproduced. This may be because the model represents late time (25,000 years), quasi-steady-state conditions, and the overturned temperature profiles are likely the result of a short-term transient fluid pulse (Ziagos & Blackwell 1986).
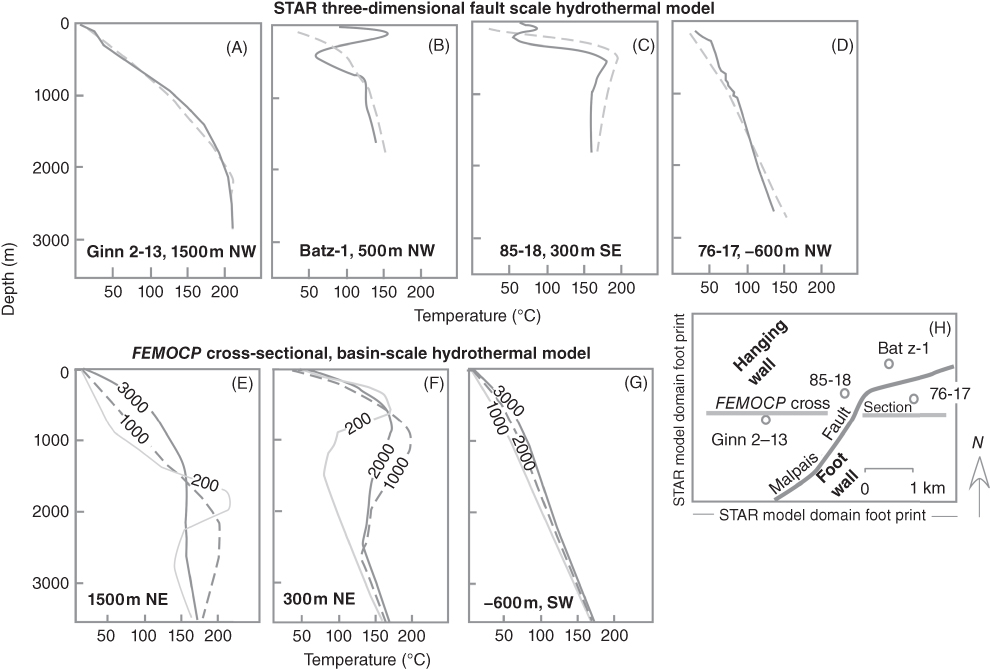
Fig. 21.4 (A–D) Observed (solid black lines) and computed (red dashed lines) temperature profiles from three-dimensional, fault-scale, hydrothermal STAR model of Malpais fault zone. Well distances from Malpais fault and well names are listed in the lower left-hand corner of each plot. All computed temperatures are after 25,000 years (Adapted from Garg et al. (2007)). (E–G) Time-dependent evolution of computed temperature profiles extracted from FEMOCP cross-sectional, basin-scale hydrothermal model at different distances from the Malpais fault zone using “best-fit” Malpais zone fault permeability of 10−12 m2. Location of wells and the STAR model footprint are shown in Figure 21.2H along with the location of the FEMOCP cross-sectional transect.
History of geothermal development at Beowawe
The Beowawe geothermal system has been under scientific investigation since 1934. Detailed reports on the geology, structure, and hypothesized hydrothermal fluid flow pathways can be found in Zoback (1979) and Struhsacker (1980). Both these papers provide detailed geologic maps of the area, lithologic descriptions of the rock units, cross sections derived from geothermal wells, and summaries of the geologic history.
The Beowawe geothermal system was once the second-largest site in the United States for active geyser, fumarole, and hot-spring activity, second only to Yellowstone National Park. Today, these geothermal discharges have subsided and Beowawe is host to only a large sinter terrace and a few fumaroles (Fig. 21.1B,C). This change is likely due to geothermal fluid production, which began in 1985 with a 16.7 MW dual-flash power plant (square, Fig. 21.1A).
White (1998) published a detailed report on the Beowawe geothermal system before, during, and after geothermal drilling and development. The report includes pictures of the formerly active geysers and springs, geologic and hydrologic maps of the geysers and Whirlwind Valley area, and a table summarizing water geochemistry from previous studies of the Beowawe geothermal system. This report, along with the article published by Nolan & Anderson (1934), provides a detailed characterization of the Beowawe geothermal system before geothermal development.
Conceptual model of transient hydrothermal flow within the Beowawe geothermal system
We propose that the isotopic trends presented in Figure 21.3 are the result of a transient, single-pass hydrothermal system of the type described by Lowell (1991) (Fig. 21.5). We hypothesize that within the discharge area (Malpais fault, Figs 21.1A and 21.2B), initially hot, isotopically enriched fluids discharged at the surface following a seismic event. Discharge temperature and isotopic composition peaked shortly after the onset of flow. The brief lag time is required for deep reservoir fluids to make their way up to the surface. In the recharge area, in response to temporarily enhanced fault permeability, we hypothesize that isotopically depleted meteoric water flowed downward along fault conduits (here the Muleshoe fault zone, Figs 21.1A and 21.2B), moved laterally through the karst reservoir (thin dark blue unit in Fig. 21.2B) picking up heat, and then discharged at the surface along the Malpais fault. The δ18O of the meteoric water increased along the flow path due to mixing with geothermal reservoir fluids (karst aquifer, see unit 6, Fig. 21.2B) and fluid–rock isotope exchange. However, as the flow system evolved over time, the discharging fluids trended toward a meteoric composition. Lowell et al. (1993) showed that discharge temperature is controlled by the product of fault-zone width and permeability or conductance (kb), and showed that hot-spring temperature peaks at intermediate values of fault conductance. This is because at the highest flow rates (or widest fault zones), the recharge increases to the point that it has a net cooling effect on the hydrothermal system. For lower permeability conditions, heat conduction dominates. In the conceptual model presented in Figure 21.5, the groundwater flow is driven by the water-table topographic gradient. It is likely that density effects also contribute significantly to driving fluid flow up the Malpais fault zone at Beowawe (Person et al. 2008).
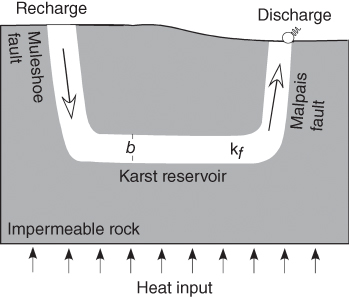
Fig. 21.5 Conceptual diagram depicting single-pass model of a hydrothermal system having a conduit width of “b” and a fault-zone permeability of kf. In this diagram, circulation is driven by a hydraulic head gradient between the uplands and lowlands.
(Adapted from Lowell (1991)).
Another independent line of evidence that argues for transient hydrothermal fluid flow within the Beowawe geothermal system comes from the analysis of borehole temperature profiles. Present-day borehole temperature profiles proximal to the Malpais fault zone show temperature overturns (solid black lines in Fig. 21.4B,C). Ziagos & Blackwell (1986) showed that such temperature overturns result from transient lateral flows of geothermal fluids (Fig. 21.6). These authors developed analytical and numerical solutions for transient temperature profiles associated with lateral fluid flow into a shallow aquifer. They considered the consequences of hydrothermal fluids moving up a fault zone and then laterally into a shallow aquifer (Fig. 21.6A), and showed that after the onset of lateral flow temperature profiles in wells displayed a distinctive thermal overturn that decreased with increasing distance from the fault zone (Fig. 21.6B). At late time, however, the overturns dissipate due to downward heat conduction (Fig. 21.6C). Ziagos & Blackwell (1986) also presented numerical results using the fast Fourier transform method to investigate time-dependent changes in the enthalpy of the discharging fluids. In this scenario, high enthalpy fluids were input for 1000 years, followed by lower enthalpy fluid input. Fluid temperatures within the water-table aquifer rose quickly at first, followed by a more gradual temperature increase. Once cool fluids were introduced after 1000 years, the opposite pattern developed: rapid cooling followed by a more gradual temperature decline. We argue later that the post-1000-year temperature declines shown in Figure 21.6D are analogous to time-dependent changes in isotopic composition of geothermal fluids within the Beowawe geothermal system (Fig. 21.3). One issue we must address in this study is that the onset of convection we estimate from the temperature profile data in Figure 21.4B,C is considerably shorter than the duration of flow revealed by the isotopic data in Figure 21.3.
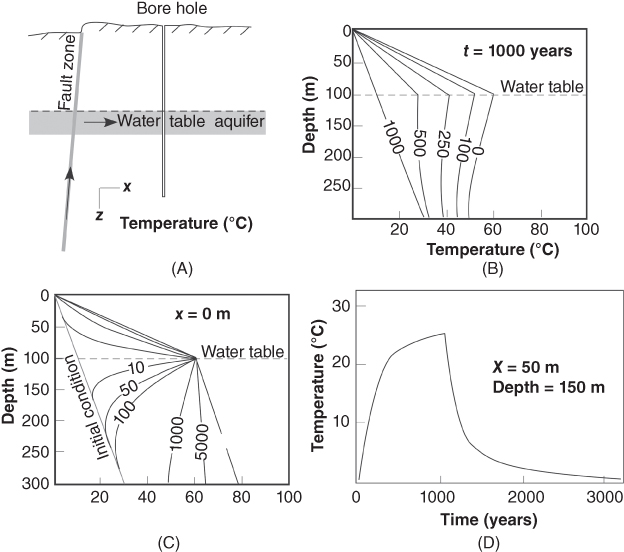
Fig. 21.6 (A) Schematic diagram depicting conceptual model for time-dependent analytical solution of thermal transients presented by Ziagos & Blackwell (1986). The Laplace-transform analytical solution was developed to represent temperature changes in wells resulting from lateral outflow of hot geothermal fluids that move up a fault zone and out into a shallow water-table aquifer. (B) Changes in temperature along a well bore after 1000 years of lateral flow rate at 1 myear−1. The initial geothermal gradient was 100°C km−1. Profile labels are the distance of the well bores from the fault zone in meters. (C) Temperature changes through time at a well bore located at the fault zone (x = 0 m). Profile labels denote time since the onset of flow. Note that at early times, temperature overturns. At late time, the temperature inversions are erased by downward heat conduction. (D) Fast Fourier transform solution for time-dependent changes in temperature 50 m from the fault zone at a depth of 150 m below the water table. Changes in temperature are due to time-dependent changes in the temperature of the fluid entering the shallow water-table aquifer. A step function is used to represent the inflow of initially hot water for 1000 years followed by cooler water inflow.
(Adapted from Ziagos & Blackwell (1986)).
The onset of convection appears to be correlated with Holocene and Late Pleistocene seismic events along the Malpais fault zone (see X, Fig. 21.1A), which hosts the sinter deposits (Fig. 21.3; Wesnousky et al. 2005). The age of each paleoseismic event along the Malpais fault was estimated using 14C dates on carbonaceous material in soil layers that are truncated by the fault (Wesnousky et al. 2005). The small size (<0.5 m) of the offsets between colluvium layers along the fault (Wesnousky et al. 2005) suggests that these were low-energy earthquakes (<M5) (Friedrich et al. 2004). We hypothesize that flow commences following permeability increases along subvertical faults following seismicity (Wang & Manga 2010b; Fig. 21.5). Hot, silica-rich fluids within a deep (∼5 km depth) carbonate geothermal reservoir move up the Malpais fault and discharge at the surface (Fig. 21.2B). Progressive silica mineralization and influx of cool meteoric fluids along the fault zone eventually shut the convective flow system down or at least reduces rates of sinter formation (Lowell et al. 1993). To test the aforementioned hypotheses, we constructed a series of geologically referenced hydrothermal models that include fluid–rock oxygen-isotope transport and exchange (Bowman et al. 1994) within the Beowawe geothermal system. We systematically vary the permeability of the fault zones in order to constrain the magnitude of permeability changes following a seismic event in a manner that is consistent with the sinter-deposit data. We address the following questions: (i) What fault permeability is consistent with present-day conditions within the Beowawe geothermal system? (ii) How large of a permeability increase is required to enhance hydrothermal activity within Beowawe geothermal system? (iii) Does a single-pass geothermal system with progressive influx of meteoric water produce a trend of decrease isotopic composition consistent with the sinter data we collected? (iv) Over what timescales does this occur? (v) Assuming that the flow system shuts down at late time, how long does it take for the isotopic fluid composition in the deep carbonate reservoir to recover?
Methods
Sample preparation
We collected 63 sinter samples between 2009 and 2012 along the Beowawe siliceous sinter terrace within Whirlwind Valley (Fig. 21.1D) to establish the periodicity of hydrothermal activity in the Beowawe geothermal field. Almost all the samples were collected at the surface and along a single road cut. All the sinter samples were analyzed for mineralogy, crystallinity, and oxygen-isotope composition. Pollen and charcoal extracted from 11 sinter samples were dated using radiocarbon methods (Table 21.1).
Table 21.1 Radiocarbon dates of pollen taken from sinter deposits
| Sample number | Age (yrs) | Con. int. (yr) | δ13C (‰) | Primary minerals | Latitude | Longitude | δ18Osinter | δ18Ofluid @ 90°C |
| B-1c | 10,454 | ±40 | −25.3 | Opal, Qtz, kaolinite | N40°33′'44.5″ | W116°35′25.9″ | 20.10 | −2.20 |
| B-8 | 4,706 | ±25 | −20 | Opal | N40°33′41.4″ | W116°35′29.4″ | 24.93 | 2.63 |
| B-14a | 893 | ±25 | −23.6 | Opal, plagioclase | N40°33′36.4″ | W116°35′40.8″ | 15.1 | −7.2 |
| B-15 | 2,684 | ±25 | −24.5 | Opal | N40°33′38.0″ | W116°35′34.2″ | 21.4 | −0.9 |
| B-19c | 1,137 | ±20 | −22.3 | Opal, Qtz | N40°33′43.1″ | W116°35′10.7″ | 12.5 | −9.8 |
| B-3 | 8,797 | ±60 | −29.2 | Opal, Qtz, kaolinite | N40°33′42.8″ | W116°35′26.9″ | 6.93 | −15.37 |
| B-5 | 14,375 | ±70 | −29.6 | Opal | N40°33′38.7″ | W116°35′29.1″ | 12.56 | −9.74 |
| B-6 btm | 10,774 | ±50 | −29.1 | Opal | N40°33′40.50″ | W116°35′33″ | 8.77 | −13.54 |
| B-7 | 10,580 | ±50 | −29.3 | Opal | N40°33′41.5″ | W116°35′29.3″ | 8.90 | −13.41 |
| B-11 wht | 3,693 | ±30 | −26.3 | Calcite, cristobalite, sanidine | N40°33′30.29″ | W116°35′21″ | 16.90 | −5.40 |
| B-10b | 1,322 | ±40 | −26.1 | Opal | N40°33′38.7″ | W116°35′29.1″ | 13.4 | −8.9 |
In order to separate organic matter from mineral grains, the sinter was treated with a 50% hydrogen peroxide solution to remove any organic material trapped in pores and outer surfaces. The samples were rinsed with water, oven-dried, and crushed. The crushed material was treated in 10% HCl to remove carbonates and then in 50% HF to remove silicates. The sinter material was then washed three times in 10% HCl and then in water. The remaining material was separated using a 150 µm sieve. The organic matter larger than 150 µm was collected in a centrifuge tube. The material <150 µm was sieved at 6 µm and particle sizes between 6 µm < X < 150 µm were collected. Multiple gravity separations were also performed using sodium polytungstate (density 2.0 g ml−1) to remove remaining insoluble minerals. Plant fragments that floated at 2.0 g ml−1 were then sieved using a 6 µm filter and rinsed with water. The float material was loaded into a combustion tube. The radiocarbon activity of the pollen/charcoal samples were then analyzed at Rafter Radiocarbon Laboratory in New Zealand using an accelerator mass spectrometry.
Sinter mineralogy analysis
The mineralogy and crystallinity of the sinter samples were determined using X-ray diffraction. Samples were dried in an oven at 60°C to remove any water present and then hand ground to pass through a 150 µm mesh sieve. The composition of the sinter deposits was determined using a PanAnalytical XPert Pro diffractometer and methods outlined in Herdianita et al. (2000). The sinter samples were analyzed using CuKα radiation for 15 minutes each over a range of 10°–40° 2Θ and a step size of 0.0170°. X-ray diffraction patterns were interpreted using PANalytical X'Pert HighScore Plus software to determine the crystallinity (order/disorder) of the opaline phase of the sinters. Crystallinity can be measured as the full-width half-maximum (FWHM) by manually fitting a profile and baseline to the diffraction pattern and then measuring the width of the band at half intensity (Herdianita et al. 2000). The sinter terrace at the Beowawe geothermal system consists primarily of Opal-A, Opal-A/CT, Opal-CT/A, or Opal-CT and indicates that geothermal fluids were saturated with respect to amorphous silica. Rimstidt & Cole (1983) argue that the amorphous silica comprising the sinter deposits at Beowawe precipitated at temperatures of 88–98°C. Measured temperatures of geothermal fluids in the “Frying Pan” geyser and another small geyser were about 95 and 98°C, respectively, prior to exploitation (Mariner et al. 1983; Nolan & Anderson 1934).
Sinter oxygen-18 analysis
Stable-isotope analysis of oxygen from the opal samples was performed using New Mexico Tech's fluorination line following Borthwick & Harmon (1982) and Baertschi & Silverman (1951). Powdered samples were reacted with dilute HCl to remove any carbonate, then rinsed with distilled water, and dried in an oven at 60°C for 12 hours. Samples were prefluorinated with ClF3 in nickel reaction vessels for 10 minutes at room temperature to ensure that all remaining water was removed from the samples and reaction chambers, and then reacted with ClF3 at 500°C for 8 hours. The liberated oxygen gas was converted into CO2 with a carbon electrode. The CO2 gas was analyzed via dual inlet on the Delta XP IRMS spectrometer for δ18O using an OZ-Tech CO2 gas standard. Samples that produced yields below 60% were not used for interpretation. Samples that produced yield values between 60% and 80% were analyzed two or three times and then averaged with a reproducibility of ±0.8. The isotopic composition of water (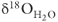
) was calculated from that of sinter (δ18Osinter) at 93°C using the equilibrium fractionation factor of Kita et al. (1985) (
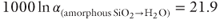). The temperature selected is within the limits of the fractionation equation and the reported range of fluid temperatures in the geyser field where sinter was deposited.
Single-phase, single-pass hydrothermal model description
In order to interpret the stable-isotope history of the sinter deposit and the present-day temperature trends, we constructed a relatively simple, cross-sectional, single-phase hydrothermal model of the Beowawe geothermal system. In this model, permeability is instantaneously increased along the Muleshoe and Malpais fault zones (unit 10, Fig. 21.2B) to create a single-pass hydrothermal system. Manga et al. (2012) argued that this type of permeability change can be caused by the removal of small particles that block fault apertures. The faults are connected to permeable geothermal reservoir at depth, a karst subunit within the Great Basin Paleozoic aquifer system (unit 6, Fig. 21.2B). Based on geophysical, geologic, and drilling information, the source reservoir for the geothermal fluids is interpreted to be Paleozoic carbonate 3–5 km below the surface (Watt et al. 2007). This interpretation is confirmed by the δ13C compositions of dissolved inorganic carbon in Beowawe geothermal fluids (−2 to 1‰), which is typical of Paleozoic marine limestones (Day 1987). The isotopic compositions of water and dissolved inorganic carbon at Beowawe reported by Day (1987) were further discussed by John and coworkers (2003, p. 460–461). The δD of the water (−115‰) is about 10‰ less than modern meteoric water in the area. Such values are common in active hot springs across the Basin and Range Province, USA, and have been interpreted to reflect the involvement of Pleistocene meteoric water in these systems (Smith et al. 2002). Day (1987) attributed the high δ13C values (−2 to 1‰) to dissolution of Paleozoic limestone (−2.5 to 3‰) situated at deep levels (∼3000 m) below siliciclastic rocks of the Roberts Mountains thrust. Given the high reservoir temperature (∼220°C), the small δ18O shift from the meteoric water line (<3‰) requires large water–rock ratios (∼10; John et al. 2003) and a permeable fault and/or karst-controlled flow system. Early Paleozoic marine carbonate rocks in Nevada have δ18O values that range from ∼20‰ to 30‰ (Hofstra & Cline 2000). Over time, fluids in a high-temperature reservoir will equilibrate with the surrounding rocks and shift to higher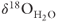 
values. The aforementioned range of carbonate rock compositions and the fractionation equation of Kim & O'Neil (1997) (
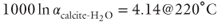) show that an equilibrated reservoir fluid will have 
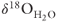values between 16‰ and 26‰, comparable to the higher 
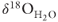values from the sinter deposits (Fig. 21.3). The lowest 
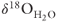values in Figure 21.3 appear to require a component of meteoric water.
Our paleohydrologic model includes calculations of groundwater flow rates, temperatures, and fluid–rock isotopic interactions/transport. The Beowawe hydrogeologic cross section was constructed along an east–west transect across the southern part of Whirlwind Valley (a–a′, Figs 21.1A and 21.2A,B). It extends to the adjacent Reese River and Crescent Valleys, which enables us to consider the possibility of interbasin transfers of groundwater. These were found to be negligible (Person et al. 2008). Model results presented here are focused on Whirlwind Valley, which hosts the Beowawe geyser field.
The governing transport equations are presented in Table 21.2. Similar to that of Garg et al. (2007), our model is not capable of representing boiling conditions. In addition, mineral dissolution–precipitation reactions and their effects on fault permeability are not considered (e.g., Lowell et al. 1993). A detailed stratigraphy along this section was generalized into a limited number of hydrogeologic units comprised of stratigraphic units inferred to have similar hydrologic properties. Geologic structure was similarly generalized such that the only structures portrayed on the sections are either those that have sufficient offset to juxtapose different hydrogeologic units or structures that were explicitly included as part of the flow scenario being tested. In certain cases, structures that were subparallel to the section were omitted or generalized as a fault more nearly perpendicular to the section trace. Although based on surface and subsurface geologic and geophysical data, the hydrogeologic cross sections are intended to represent generalized scenarios that contain the salient geologic features needed to test a flow hypothesis; they are not intended to be literal representations of all that is known concerning the subsurface geology.
Table 21.2 Governing transport equations
| Stream functions |
| Cauchy–Riemann equations |
| Heat transport |
|
21.3  |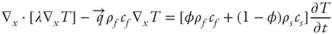
| Fluid–rock isotope transport |
| Kinetic fluid–rock isotope exchange |
|
21.5b
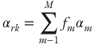 21.5c  |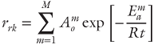
| Thermal conduction–dispersion tensor |
|
21.6
|
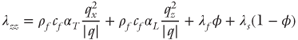
| Solute diffusion–dispersion tensor |
|
21.7  |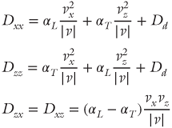
k is permeability tensor;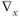 
is the gradient operator; ρr is the relative density (ρr = (ρf − ρo)/ρo); ρo is the reference fluid density; ρf is fluid density at elevated temperature and pressure; x, z are the spatial coordinates; Ψ is the stream function;|k| is the determinant of the permeability tensor; T is temperature; qx, qz are the components of Darcy flux in x- and z-directions; cf is the specific heat capacity of the fluid; cs is the specific heat capacity of the solid; ϕ is porosity; λxx, λzx, λxz, λzz are the components of the thermal conductivity–dispersion tensor of the porous medium; Dxx, Dzx, Dxz, Dzz are the components of dispersion–diffusion; |v| is the magnitude of velocity, vx and vz are the components of specific discharge in the x- and z-directions; Dd is the molecular diffusion coefficient for porous media; qx and qz are the components of Darcy flux in the x- and z-directions, respectively; αL and αT are the longitudinal and transverse dispersivities, respectively; Rf is the fluid isotopic ratio; Rrk is the bulk rock isotopic ratio (averaged over all mineral phases present); t is time; Xrk is the fractional abundance of oxygen in the bulk rock phase; Xf is the fractional abundance of oxygen in water; 
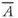is the bulk rock reactive surface area; rrk is the bulk rock reaction rate for fluid–rock isotope exchange; αrk is the bulk fluid–rock equilibrium isotope-exchange factor averaged over all oxygen-bearing mineral phases; M is the total number of oxygen-bearing mineral phases for a given rock; 
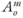is the preexponenital factor of the mth mineral phase; 
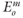is the activation energy for the exchange reaction; and R is the ideal law constant. Note that temperature is in Kelvin for isotope-exchange reactions.
The hydrothermal model used in this study considered the effects of both topography- and density-driven single-phase groundwater flow (Raffensperger & Garven 1995). The fluid flow (Eq. 21.1, Table 21.2) and heat-transport equations (Eq. 21.2, Table 21.2) were coupled using temperature- and pressure-dependent density and viscosity relations from Batzle & Wang (1992). In this study, the transients are driven mainly by permeability changes. We represented advective–dispersive isotope transport and fluid–rock isotope exchange (Eqs 21.4 and 21.5, Table 21.2) using a kinetic-based approach described by Bowman et al. (1994). We assumed that each lithologic unit was composed of seven different minerals, each having its own isotopic fluid–rock exchange parameters and initial isotopic composition (Tables 21.3 and 21.4). Temperature-dependent equilibrium isotope fractionation factors, preexponential factor (Ao), and the activation energy (Ea) for each of the mth mineral phases were taken from experimental data reported by Zhang et al. (1994), Zheng (1999), and Sheppard & Gilg (1996).
Table 21.3 Mineral isotopic parameters
| Xm | cm | dm | em | fm | ρm | δ0 | Ao | Ea | Initial δ18O composition | Mineral |
| 0.5325 | 0.0 | 3.306 | 0.0 | −2.71 | 2650 | 18 | 3.46E-05 | 11 | 10 | Quartz# |
| 0.13 | −0.388 | 5.538 | −11.35 | 3.132 | 2850 | −2 | 4.50E-08 | 6.5 | 26 | Dolomite$ |
| 0.48 | −0.891 | 8.557 | −18.11 | 8.27 | 2710 | 1 | 4.50E-08 | 6.5 | 26 | Calcite$ |
| 0.1343 | 0.0 | 2.76 | 0.0 | −6.75 | 2600 | 16 | 0.0000047 | 9.5 | 16 | Kaolinite* |
| 0.2747 | 0.0 | 3.904 | −5.47 | 1.86 | 4500 | 20 | 0.0475 | 13.4 | 20 | Barite |
| 0.4180 | 0.0 | 4.12 | −7.5 | 2.24 | 2700 | 20 | 1.39E-07 | 26.2 | 20 | Anorthite |
Ao is the preexponential factor in moles m−2 s−1; Ea is the activation energy in kcal mol−1; Xm is the fraction of oxygen in a given mineral phase; cm–fm are empirical constants used to estimate the equilibrium temperature-dependent fractionation factor for the mth oxygen-bearing mineral phase using the following relationship: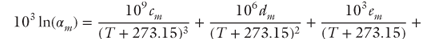 
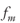. The bulk equilibrium fractionation factor for a given lithologic unit (αrk) in our model is given by 
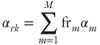, where frm is the fraction of the mth oxygen-bearing mineral phase that occurs within a given lithologic unit.
# Zhang et al. (1994)et al.
$ Zheng (1999).
* Sheppard & Gilg (1996).
Table 21.4 Initial percentages of oxygen-bearing minerals in each stratigraphic layer
| Unit numbers | Unit name | Qtz | Dol | Cal | Kaol | Bar | Anor |
| 10 | Fault zone | 75 | 5 | – | 10 | 10 | – |
| 9 | Quaternary basin fill | 36 | 5 | 50 | – | – | 9 |
| 8 | Volcanoclastics (tuffs, alluvium) | 36 | 5 | 50 | – | – | 9 |
| 7 | Middle Miocene volcanics | 70 | – | – | 20 | – | 10 |
| 6 | High-permeability karst unit | – | 10 | 80 | 10 | – | – |
| 5 | Low-permeability carbonates | – | 10 | 80 | 10 | – | – |
| 4 | Low-permeability Proterozoic siliciclastics | 75 | 5 | – | 19 | 1 | – |
| 3 | High-permeability Proterozoic siliciclastics | 75 | 5 | – | 19 | 1 | – |
| 2 | Low-permeability Proterozoic siliciclastics | 75 | 5 | – | 19 | 1 | – |
| 1 | Proterozoic metamorphic rocks | 80 | – | – | 5 | – | 15 |
Abbreviations: Qtz – quartz, Dol – dolomite, Cal – calcite, Kaol – kaolinite, Bar – barite, Anor – anorthite.
For the groundwater flow equation, we specified a constant value (Ψ = 0) stream-function boundary along the sides and base of the domain consistent with a no-flux boundary condition. We specified a flux (dΨ/dz) boundary condition across the top of the model domain with the magnitude of the flux being proportional to the lateral water-table gradient (Fogg & Senger 1985). For heat transfer, a specified temperature of 10°C was imposed along the top boundary except at the Malpais fault zone, where groundwater discharges. Here, a no-flux boundary condition was imposed (dT/dz = 0). This boundary condition implies that vertical flow rates are high enough that heat is not lost by conduction at the water table. This boundary condition was used by Appold et al. (2007) to emulate spring discharge along Refugio-Carneros and Coast faults in the Santa Barbara Basin. A basal heat flux was also imposed at the base of the solution domains (80 mW m−2), based on heat flux estimates from the northern Nevada rift (Blackwell 1983). We fixed the δ18O composition of meteoric recharge at −15‰ at the water table. A no-flux boundary condition was imposed (dRf/dz = 0) at the Malpais fault zone for these two tracers. No-flux boundary conditions were imposed along the sides and base of the solution domain for isotope transport.
Thermal conductivity, solute diffusivity, and longitudinal and transverse dispersivities were fixed (Table 21.5) for all lithological units. We assumed a conductive geothermal gradient as an initial condition (about 40°C km−1). Initial fluid isotope composition (Rf) values were assigned using these initial conductive temperatures. Each stratigraphic unit was assigned an initial rock isotope composition depending on its mineral assemblages (Table 21.3).
Table 21.5 Rock thermal and transport properties
| Variable | Symbol | Value/units |
| Thermal conductivity of fluid | λs | 0.58 W m °C−1 |
| Thermal conductivity of solids | λs | 2.5 W m °C−1 |
| Heat capacity of the fluid phase | cf | 4180 J kg−1 |
| Heat capacity of the solid phases | cs | 800 J kg−1 |
| Longitudinal dispersivity | αL | 1.0 m |
| Transverse dispersivity | αT | 0.1 m |
| Solute diffusivity | Dd | 10−10 m2 s−1 |
| Reactive surface areas |  |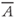
10−4 m2 mol−1 |
Hydrostratigraphic framework model
The permeabilities of the hydrostratigraphic units shown in Figure 21.2B are listed in Table 21.6. The permeability values used in our model are consistent with values reported in the literature for Basin and Range sedimentary rocks (Blankennagel & Weir 1973; Winograd & Thordarson 1975; Plume & Carlton 1988; Maurer et al. 1996; Bredehoeft 1997; Belcher 2004; Welch et al. 2007). We used published permeability data sets for crustal rocks as a guide in selecting these values (Brace 1980, 1984; Clauser 1992, Manning & Ingebritsen 1999). Because these data sets present a range of permeability conditions for a given lithologic unit, we relied on model calibration to match Beowawe heat-flow and temperature profiles (Person et al. 2008). The hydrogeologic section includes the following hydrogeologic units: a deep, low-permeability unit that includes Proterozoic crystalline basement rocks (Unit 1; dark blue strata in Fig. 21.2B); two low-permeability intervals of Upper Proterozoic to Early Cambrian siliciclastic rocks (Units 2, 4; green strata in Fig. 21.2B) that bracket a middle 1.5-km-thick interval of higher permeability, highly fractured quartz sandstone (Unit 3; white unit in Fig. 21.2B); Cambrian–Devonian dominantly carbonate rocks (Unit 5, purple strata in Fig. 21.2B); low-permeability strata of the Roberts Mountain allochthon (Unit 7, orange strata in Fig. 21.2B); Miocene volcanic rocks, including lava flows and ash-flow tuff (Unit 8, brown strata in Fig. 21.2B); alluvial-basin fill (Unit 9, yellow strata in Fig. 21.2B); and fault zones (Unit 10, red lines in Fig. 21.2B). A 100-m-thick interval of potentially enhanced horizontal permeability was added at the top of the Paleozoic carbonate unit (Unit 6, blue interval in Fig. 21.2B). This interval represents a sequence boundary that commonly contains karst features and is highly permeable. Such sequence boundaries are present at various stratigraphic levels within the Paleozoic section (Cook & Corboy 2004). The inferred subsurface structural geometry portrayed on section a–a′ is generalized from published sections presented in John & Wrucke (2003) and Watt et al. (2007). Major structural elements include west-dipping range-bounding faults on the west side of the Shoshone Range, and steep faults in the vicinity of the Mule Canyon deposit that proxy for the east-dipping Muleshoe fault (John et al. 2003) and for highly anisotropic permeability within dike swarms of the northern Nevada rift (John & Wrucke 2003). A single steep west-dipping fault is portrayed in the vicinity of Beowawe and generalizes the Malpais fault and other ENE-trending and NNW-trending faults that localize geothermal fluids (Zoback 1979; Struhsacker 1980). All of these faults are portrayed as cutting both low-permeability strata of the Roberts Mountain allochthon and underlying Cambrian–Devonian dominantly carbonate rocks. Gentle dips result in the most permeable part of the Paleozoic carbonate rock section, only attaining maximum depths of about 6 km below land surface.
Table 21.6 Hydrologic rock properties
| Unit | log10(k) | Description |
| 10 | −11 to −13 | Faults (black lies) |
| 9 | −16 | Basin fill (yellow) |
| 8 | −17 | Tuffs (brown) |
| 7 | −17 | Volcanics (orange) |
| 6 | −10 | Karst zone (blue) |
| 5 | −17 | Carbonates (purple) |
| 4 | −17 | Proterozoic siliciclastics (green) |
| 3 | −14 | Proterozoic shales (white) |
| 2 | −17 | Proterozoic sandstones (green) |
| 1 | −17 | Proterozoic bed rocks (dark blue) |
kx (horizontal permeability, m2), unit numbers are listed in Figure 21.1C.
The subvertical faults are relatively thin (∼40 m) and are assigned isotropic fault properties. Subvertical faults are connected hydrologically to a thin aquifer unit at the top of the Paleozoic carbonates and, potentially, by a deep, thick, more porous aquifer in the middle of the siliciclastic sequence (10−13 m2). Practical considerations regarding simulation time restricted our ability to represent the fault zones using grid refinement on the submeter scale, which would have been desirable.
Sensitivity study
We conducted a sensitivity study to assess what values of fault permeability could explain both the modern temperature overturns and the isotopic evolution of geothermal discharge. We ran the simulations using fault permeabilities ranging from 10−14 to 10−11 m2. Computed temperatures simulated using fault permeability less than 10−13 m2 were clearly too low and are not presented. Computational limitations prevented us from running simulations with fault permeabilities greater than 10−11 m2. After 5000 years of hydrothermal fluid flow, we lowered the subvertical fault and karst reservoir permeability to 10−19 m2 in order to allow the system to return to conductive equilibrium. This was done to represent the effects of fault clogging by silica mineralization. We then monitored the thermal and isotopic recovery for an additional 5000 years. The rationale for including a thermal-recovery phase was to see whether the fluids could return to isotopic equilibrium after 5000 years. We monitored simulated temperatures at the base of the Muleshoe fault in the recharge area and at the water table along the Malpais fault within the discharge area.
Results
Isotopic composition and age of the sinter deposits
Calculated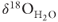 
values and 14C dates on pollen recovered from sinter samples provide evidence for two periods of geothermal fluid discharge that each exhibit a progressive decrease in 
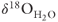through time (Fig. 21.3). Some of our data are from a single flowstone layer extending down slope from a vent lacks the progressive changes that might be expected if Rayleigh fractionation during progressive precipitation of silica was important. The highest 
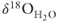values reflect isotopic exchange between fluid and sedimentary rocks in a geothermal reservoir at low water/rock ratios (e.g., 0.1) and temperatures in excess of 200°C (Sheppard 1986). The trends of decreasing 
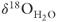through time suggest increasing contributions of unexchanged meteoric water. Modern geothermal fluids at Beowawe have an isotopic composition (
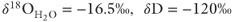) (John et al. 2003) that is representative of unexchanged meteoric water and that plots near (within 4‰ δ18O) the meteoric water line.
Model results
For a fault permeability of 10−12 m2, computed temperatures after 200 years (Fig. 21.7A) show strong convective cooling within the recharge area along the Muleshoe fault. By 1000 years, temperature declines extend into the karst aquifer and pronounced thermal overturns developed (Fig. 21.7B). The rate of cooling within the Muleshoe fault is strongly controlled by fault permeability (Fig. 21.8A). Within the discharge area along the Malpais fault, temperatures increased to a peak value about 180°C before declining (Fig. 21.8C). The timing of peak discharge temperature along the Malpais fault zone is quite sensitive to fault permeability (Fig. 21.8C). For a fault permeability of 10−13 m2, the temperatures peaked after about 5000 years, whereas for a fault permeability of 10−11 m2, they peaked in less than 100 years. A fault permeability of 10−12.3 m2 (5.0 × 10−13 m2) produced peak temperatures of about 180°C after 1000 years. The highest permeability fault zone did not correspond to the highest discharge temperature because of the cooling effect of low-temperature meteoric water (Forster & Smith 1989). Vertical flow rates along the Malpais fault varied between about 60 and 3 m year−1 for the range of permeabilities considered (10−11 to 10−13 m2). We estimate that for this range of fault permeabilities, the time required for groundwater to pass through the single-pass system by pure advection is between 300 and 4500 years.
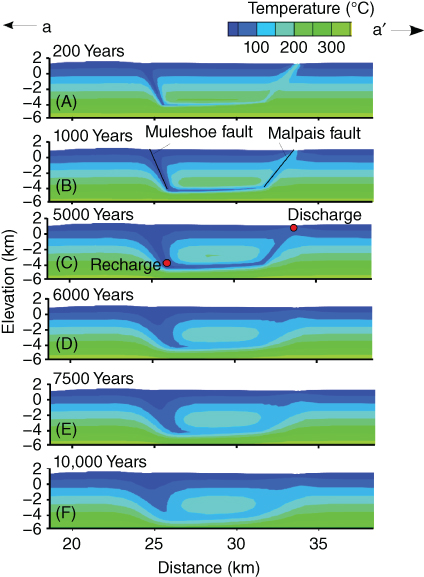
Fig. 21.7 Computed temperature contour maps illustrating thermal evolution along the Malpais fault, Muleshoe fault, and karst aquifer. Fault zones were assigned a uniform permeability of 10−12 m2. Fluid flow is active for 5000 years (A-C) followed by 5000 years (6000–10,000 years; D-F) of conductive cooling. Shallow meteoric fluid infiltration occurs down the Muleshoe fault zone and then along a thin, permeable karst zone. Upflow occurs along the Malpais fault zone. Points labeled “recharge” and “discharge” are the locations within the Beowawe geothermal system where temperature and δ18Ofluid were plotted through time in Figure 21.8A,C. (See color plate section for the color representation of this figure.)
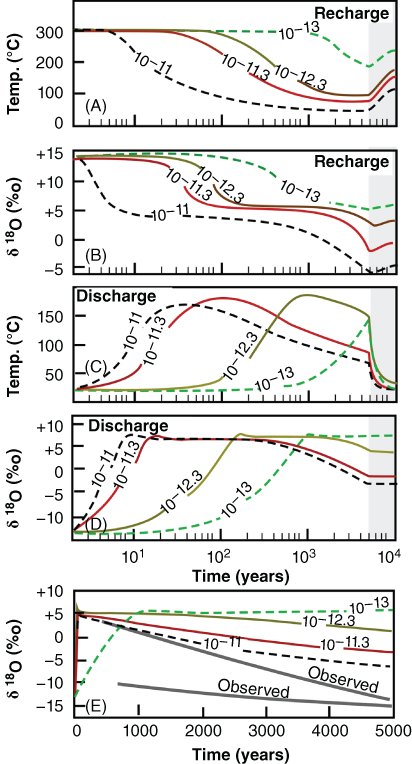
Fig. 21.8 Effect of fault permeability variations on simulated temporal temperature changes (A) and (B) oxygen isotopic composition along the Muleshoe fault zone at a depth of about 5 km. The numbers on the lines denote the permeability assigned to the Muleshoe and Malpais faults (in m2). Effect of fault permeability variations on simulated temporal changes in temperature (C) and (D) oxygen isotopic composition along the Malpais fault zone at the water table. The shaded area of the graphs represents conductive recovery following 5000 years of convection and cooling of fluids moving through the system. Locations within the recharge and discharge area are shown in Figure 21.2c (red circles). (E) Comparison of observed trends (gray dashed lines) and computed changes in 
versus time for the Beowawe sinter terrace. (See color plate section for the color representation of this figure.)
When the flow system is shut off at 5000 years, a relatively cool region with a vertical width of 1000 m is present above and below the karst zone (Fig. 21.7C). Conductive thermal recovery occurs at a much slower rate than the advective cooling (Figs 21.7D–F and 21.8A). This prevented the recovery back to initial thermal conditions over a 5000-year period and slows temperature-dependent isotopic exchange rates (Fig. 21.8B,D). Based on the vertical thickness of the thermally disturbed region above and below the karst zone (1000 m), we estimate that it would require at least 104 additional years to approach initial conductive conditions, assuming a thermal diffusivity of 1.25 × 10−6 m2 s−1. If the flow system were reinitiated following the 5000-year period of conductive recovery, the discharging fluid along the Malpais fault zone would be only moderately enriched.
Figure 21.5E–G presents computed, time-dependent evolution of temperature profiles extracted from our cross-sectional model at different distances from the Malpais fault. Early-time (200–1000 years since the onset of flow) temperature profiles within the hanging wall close to the Malpais fault resulted in temperature overturns that are similar in form to the observed conditions within the Batz-1 and 85-15 wells (Fig. 21.5E–G). The timescale is much shorter than the geochemical transients inferred from the sinter deposits (Fig. 21.3).
By 5000 years, fluid temperatures were below 100°C at a depth of 5 km for the most permeable fault scenarios (Fig. 21.8A). These lower temperatures restrict isotopic fluid–rock interactions. Once the flow system ceased at 5000 years, computed temperatures within the recharge area along the Muleshoe fault rebounded toward their initial conditions (Figs 21.7 D–F and 21.8A,C). Computed 
composition within the recharge area along the Muleshoe fault underwent rapid initial depletion as meteoric water began to descend (Fig. 21.8B). As progressively lighter fluids invaded the fault zone, reaction rates increased under isothermal conditions, causing stabilization in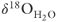 
levels. The amount of isotopic depletion depends strongly on permeability. The isotopic composition of fluids entering the karst aquifer was lightest for the most permeable conditions. Isotopic enrichment between the bottom of the Muleshoe fault zone and the discharge area at the top of the Malpais fault was only slight (∼2‰ Fig. 21.8D). Enrichment in the isotopic composition in the discharge area (Fig. 21.8D) along the Malpais fault peaked earlier than computed temperatures (Fig. 21.8C). Computed δ18OH2O composition dropped from about +6 to −3‰ but never reached the meteoric-water end member (−15 δ18O). The slight bump in the initial peak of 
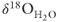is due to a downward tilt in the karst reservoirs to the west; the initial isotopic composition along the west edge of the karst zone was slightly enriched relative to the east side.
The time required for the simulated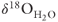 
composition within the Malpais fault zone to peak (+7‰) ranged between 10 and 1000 years after the onset of flow, for the permeability conditions considered (Fig. 21.8D). These values are more depleted than the initial equilibrium conditions with the karst reservoir at 5 km depth (+13‰), likely because of mixing of relatively unexchanged meteoric water and carbonate reservoir fluids along the flow path. Simulated oxygen-isotope composition of the discharging fluids decreased from about +7 to −3‰ for fault permeabilities between 10−12 and 10−11 m2 (Fig. 21.8D). This is about 50% of the decline observed (Figs 21.3 and 21.8E). Once flow terminated, recovery of computed temperatures (Fig. 21.8A) and 
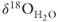began (Fig. 21.8B). However, the fluid isotopic composition did not return to equilibrium levels over the simulated time frame due to the slow rates of thermal recovery.
Discussion and conclusions
Our cross-sectional, single-pass model is clearly too idealized to account for all features of the observed thermal and isotopic data. In order to match the observed thermal overturns in temperature profiles near the Malpais fault (Fig. 21.5B,C), the model requires that hydrothermal fluid flow persist for only 1000 years or less. This is much briefer than the duration of declining isotopic composition within the sinter deposits we sampled (5000–7000 years). How can these two observations be reconciled? We propose that the Malpais fault zone is composed of several pathways to the surface, each pathway having different fault-zone apertures. As the most permeable conduit is sealed off by mineralization, alternative conduits are accessed along the Malpais fault. This is slightly analogous to channel avulsion in braided river systems. Published timescale estimates for fault clogging by Lowell et al. (1993) support this conceptual model. These authors developed simple analytical models for fault sealing by silica precipitation using a wide range of fault permeabilities (10−10 to 10−16 m2) and geothermal reservoir temperatures (50°C and 300°C). For these two temperatures, the time required for fault sealing ranged from less than 1 year (300°C) to more than 300 years (50°C) for a fault permeability of 10−12 m2. The notion of changes in the locus of hot-spring discharge is supported, in part, by the observation that peak shallow heat flow today is to the south of the Beowawe sinter deposits, which was clearly the locus of discharge in the past (Fig. 21.2A). This conceptual model of fault clogging and rerouting of flow through fault zones is not a new idea. Saffer (this issue) presents thermal/geochemical data from the Barbados and Nankai accretionary prism to argue that relatively high rates of fluid fluxes through permeable fault systems could only be active between 0.2 and 10% of the time due to clogging by fluid–rock geochemical reactions (Saffer, Fig. 21.4C, this issue).
Another complexity that is not accounted for in our single-pass model is the observed abrupt shift from nearly meteoric fluid composition (−15‰ δ18O) at about 7.5 ka to isotopically enriched discharge at 4.5 ka. We speculate that different reservoirs may be tapped during different seismic events. Alternatively, the conflict between modeled and measured values might be resolved if the discharging geothermal fluids are actually part of a two-component mixture of a deeper, slowly circulating, hot fluid with enriched δ18O and a shallow-circulating, warm meteoric fluid with lighter δ18O. The fault rupture might preferentially alter the permeability of the deeper part of the fault, and thus increase the amount of deeper fluid in discharging water. After fault slip, the deeper portion of the fault might “heal up” and gradually decrease the deeper fluid contribution to very low levels, while the shallow fluid contribution might remain more constant. Thus, the deeper fluid temperature and δ18O oscillates only moderately with time (and could perhaps fully recover between earthquakes).
Our interpretation of the thermal and isotopic evolution of the Beowawe geothermal system must be tempered by parameter uncertainty. There is a significant uncertainty in the reactive surface area and kinetic coefficients used in our fluid–rock isotope-exchange models. Surface area for fluid–rock isotope-exchange models can be computed using mineral grain size (Brantley & Mellott 2000) or fracture spacing (Rimstidt & Barnes 1980). Surface areas based on mineral grains can be as high as 1 m2 mol−1. The value we used (10−4 m2 mol−1) was based on fracture spacing and would be representative of a fracture spacing of about 70 cm (assuming the rock is comprised entirely of feldspar). Our model of fault permeability was static. Other studies (Roberts et al. 1996; Garven et al. 2001; Appold et al. 2007) have allowed fault permeability to decay through time due to changes in fault stress, mineralization, and fluid pressure decline.
For a fault permeability of 10−12 m2, our model results indicate that discharge peaked at temperatures of 180°C along the Malpais fault about 30 years after the onset of convection. Then, discharge temperatures began to cool. The most isotopically enriched discharge fluids break through in about 10 years. The finding of transient heat pulses at hot springs is not new. Numerous researchers have observed similar phenomena in their models of fault-controlled hydrothermal systems (e.g., Forster & Smith 1989; Lopez & Smith 1995). This is due to the high rate of enthalpy extraction allowed by the high fault permeability and consequent high flow rates. It is worth noting that the magnitude of the temperature change presented in this study is far larger than that observed in studies of modern earthquake-influenced hot springs (e.g., Mogi et al. 1989; Manga & Rowland 2009). This may be due to the extraordinary high extensional deformation rates along the Basin and Range faults (Kennedy & Van Soest 2007).
Our oxygen isotope analysis of 14C-dated sinter deposits (Fig. 21.3) show that large (up to 20‰) time-dependent decreases in the isotopic composition of the geothermal fluids occurred along the Malpais fault zone over geologic timescales. We interpret this decline as the result of progressive influx of meteoric fluids into a single-pass, liquid-dominated, geothermal system. Other potential mechanisms that could account for isotopic changes (e.g., boiling, climate-driven changes in precipitation composition and isotopic composition during the Late Pleistocene, or Rayleigh distillation of the geothermal fluids during sinter-deposit formation) cannot account for such a large shift in δ18O. The single-pass hydrothermal/isotope transport model of the Beowawe geothermal system seems to be the most plausible mechanism for the observed data, although it is clearly too idealized. If our conceptual model of the Beowawe geothermal system is correct, our analysis provides insights into how transient permeability changes occur along fault zones over geological timescales. Estimated rates of silica clogging of faults (as fast as 10 years; Lowell et al. 1993) are much shorter than those indicated by the sinter-deposit isotope data.
Groundwater flow must be three-dimensional in nature. Person et al. (2012) showed how hydrothermal flow frequently focuses at relatively high-permeability intersections of fault zones, as observed across the Basin and Range Province by Coolbaugh et al. (2005). Furthermore, Garg et al. (2007) found that only narrow regions of the Malpais fault zone were permeable. Nevertheless, any three-dimensional model must still incorporate downward fluid movement on the Muleshoe or some other fault system, lateral flow through a reservoir, and upward flow along the Malpais fault.
Our studies have described transient hydrothermal systems within the Basin and Range Province. McKenna et al. (2005) concluded that the high temperatures (280°C at 3.8 km depth) along the base of the Dixie Valley fault within the Dixie Valley geothermal system must be due to hydrothermal flow transients in the order of 30,000–50,000 years. These authors also speculated that the time-dependent fault permeability was related to seismicity. Temperature profiles from wells at Dixie Valley, however, show little evidence of thermal overturns.
Low-magnitude earthquakes result in slip increments of millimeters to centimeters along faults. Hill (1977) and Sibson (1996) proposed that low-magnitude (<4M) earthquake swarms can induce significant amounts of fluid movement capable of generating economic gold deposits along fracture networks. Varying the permeability of the fault zones in our model provided some insight into the magnitude of permeability change following each seismic event. While none of the models produced the full 20‰ range observed in Figure 21.3, the fault permeability had to have been on the order of 10−11 m2 or greater. The highest permeability scenario (5 × 10−11 m2) produced about a 10‰ decrease in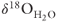 
over a few thousand years, while a permeability of 10−13 m2 produced almost no decrease (Fig.21.8D). Numerical considerations prevented us from assigning higher fault permeability to the Muleshoe and Malpais faults. It is possible that representing isotope transport through distinct fractures, or greater mesh refinement, would have improved the model fit to observed data. Extrapolating the trends in the rate of decline in computed 
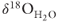in Figure 21.8E, we suspect that a fault permeability of 10−9 m2 would likely produce a close match with observed data. Prior to the onset of hydrothermal circulation, the permeability of the Malpais and/or Muleshoe fault must have been at or below 10−14 m2, producing low-temperature discharge that could not have carried much dissolved silica to form sinter deposits. Fault conductance controls the magnitude of convective heat flow, so our reported fault permeabilities are to some degree nonunique. A wider fault zone would require a lower fault permeability in order to produce the same convective thermal anomaly.
Isotope data collected as part of this study suggest that Holocene geothermal systems in the Basin and Range Province are episodic in nature on timescales of about 5000–7000 years. Zoback (1979) estimated that about 210,000 years were required to account for all of the silica (1.28 × 1011 kg) along the Beowawe geyser field terrace. She assumed continuous flow at modern Beowawe geyser field discharge rates (61 l s−1) and modern silica concentrations. In our model, each hydrothermal flow event discharged about 9.1 × 109 kg of silica (Person et al. 2008). Assuming a fault-zone width of 40 m, a length of 2 km, and that 10% of the dissolved silica is available for sinter formation, more than 100 episodic flow events would be required to form the 1.28 × 1011 kg Beowawe geyser field sinter terrace.
Acknowledgments
We thank Andy Manning of the USGS and two anonymous reviewers for their constructive criticism of an earlier draft of this manuscript. This work was supported by an NSF grant to Mark Person and Albert Hofstra (NSF-EAR 0809644). We also acknowledge the support of the National Science Foundation (EPSCoR) under Grant No. IIA-1301346 to Mark Person and Laura Crossey.