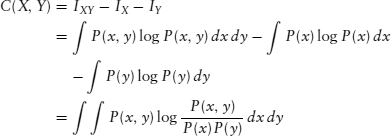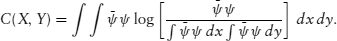CHAPTER 5
Minipaper: Quantitative Measure of Correlation (1955)
Prof. Wheeler
H. Everett
Quantitative Measure of Correlation
If one makes the statement that two variables, X and Y, are correlated, what is basically meant is that one learns something about one variable when he is told the value of the other. By utilizing some of the concepts of information theory this notion can be made to yield a natural and satisfactory quantitative measure of the correlation of two variables. In information theory one defines the quantity of information contained in a probability distribution for a random variable X, with density P(x), to be:
IX= ∫ P(x) log P(x)dx,
a quantity which agrees quite closely with our intuitive ideas about information.j
Suppose now that we are given a joint distribution P(x, y) over two random variables X and Y, for which we seek a measure of the correlation between the two variables. Let us focus our attention upon the variable X. If we are not informed of the value of Y, then the probability distribution of X (marginal or a priori distribution) is P(x) = ∫ P(x, y)dy, and our information about X is given by IX = ∫ P(x) log P(x) dx. However, if we are now told that Y has the value y, the probability distribution for X changes to the conditional distribution Py(x) = P(x, y)/P(y), with information  = ∫ Py(x) log Py(x) dx. According to what has been said we wish the correlation to measure how much we learn about X by being informed of the value of y, that is, the change in information. However, since this change may depend upon the particular value of Y which we are told, the natural thing to do is to consider the expected change in information about X, given that we are to be told the value of Y. This quantity we shall call the correlation of X with Y, denoted by C(X, Y). Thus:
= ∫ Py(x) log Py(x) dx. According to what has been said we wish the correlation to measure how much we learn about X by being informed of the value of y, that is, the change in information. However, since this change may depend upon the particular value of Y which we are told, the natural thing to do is to consider the expected change in information about X, given that we are to be told the value of Y. This quantity we shall call the correlation of X with Y, denoted by C(X, Y). Thus:
C(X, Y) = ∫P(y) [ – IX] dy
– IX] dy
It turns out that this quantity is also the expected change in information about Y given that we are to be informed of the value of X, so that the correlation is symmetric in X and Y, and it is in fact equal to the information of the joint distribution less the sum of the information for the two a priori distributions:
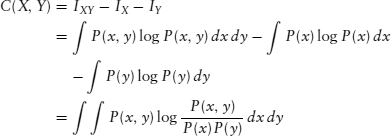
It has the further property that it is zero if and only if the two variables are independent, and is otherwise strictly positive, ranging to +∞ in the case of a functional dependence of x on y (perfect correlation).
It is in several respects superior to the usual correlation coefficient of statistics, which can be zero even when the variables are not independent, and which can assume both positive and negative values. A negative correlation can give, after all, quite as much information as a positive correlation.
Finally, it is invariant to changes of scale, i.e., if z = ax then C(Z, Y) = C(X, Y), so that if we decided to measure x in meters instead of inches, for example, the correlation with Y would be unchanged, so that it is in some sense an absolute measure.k
These notions can be easily extended to distributions over more than two variables by introducing further “correlation numbers,” a process which leads to a simple and elegant algebra for these quantities.
Extending to wave mechanics, we define the correlation between observables X and Y, with wave function in x, y representation ψ(x, y), to be:
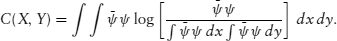
 = ∫ Py(x) log Py(x) dx. According to what has been said we wish the correlation to measure how much we learn about X by being informed of the value of y, that is, the change in information. However, since this change may depend upon the particular value of Y which we are told, the natural thing to do is to consider the expected change in information about X, given that we are to be told the value of Y. This quantity we shall call the correlation of X with Y, denoted by C(X, Y). Thus:
= ∫ Py(x) log Py(x) dx. According to what has been said we wish the correlation to measure how much we learn about X by being informed of the value of y, that is, the change in information. However, since this change may depend upon the particular value of Y which we are told, the natural thing to do is to consider the expected change in information about X, given that we are to be told the value of Y. This quantity we shall call the correlation of X with Y, denoted by C(X, Y). Thus: