i}, in which case the state ψ will be changed to the state j with probability |(ψ, j)|2.This minipaper develops the basic premise of Everett’s thesis stripped of its formalism but laced with explanatory metaphors, such as splitting amoebas that share overlapping memories until diverging into separate futures recorded as consistent histories. There are several handwritten drafts of this minipaper and two typed versions, one turned into Wheeler. Wheeler made handwritten notes on his copy of this minipaper. These notes are presented here in the lettered footnotes.l
Prof. Wheeler
H. Everett
Probability in Wave Mechanicsm
In present formulations of quantum mechanics there are two essentially different ways in which the state of a system changes, one continuous and causal, and the other discontinuous and probabilistic. Let ψ be the state of a system with energy operator H, then the two processes are:
i}, in which case the state ψ will be changed to the state j with probability |(ψ, j)|2.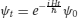
The question arises as to whether these two rules are compatible; in particular what occurs in the event that (2) is applied to the measurement process itself (i.e., to the state of the combined system of the original system plus apparatus and observer). In this case nothing like the discontinuity of (1) can occur, and one has to decide whether to abandon (1), and the statistical interpretation of quantum mechanics in favor of the purely causal description (2), or to limit the applicability of (2) to systems within which “measurements” are not taking place. If we were to deny the applicability of (2) to the measurement process, however, we are faced with the difficulty of how to distinguish a measurement process from other natural processes. For what n might a group of n particles be construed as forming a measuring apparatus or observer, and cease to be governed by (2)? We would be faced with the task of dividing all processes into two categories, the usual ones which are governed by (2), and the mysterious type called measurements which are immune to (2) and follow (1) instead. Still another alternative would be to attempt some sort of deterministic “hidden parameter” theory in which probabilities would arise as a result of the ignorance of the observer concerning the values of the hidden parameters.o
It is our purpose here to indicate that a purely causal theory which postulates the existence of some sort of wave function for the entire universe, and for which (2) alone holds, forms an adequate theory. That is, that by assuming the general validity of pure wave mechanics, without any initial statistical interpretation, we obtain a theory which is in principle applicable to all natural processes, and furthermore one which even leads to probabilistic aspects on a subjective level in a rather novel way (i.e., that we are able to deduce that (1) will appear to hold to observers).
We turn now to the formalism of quantum mechanics. We shall assume a particle model, in which we envisage the universe to be composed of a large number of elementary particles, possessing a single total wave function, which we assume to obey the Schrödinger equation. (No results will depend upon this, however, they will hold for field theories as well, and any wave equation, that is, any system of “quantum mechanics”.)
The first question that arises is “What actually does happen in the process of measurement?” Several authors (Von Neumann, Bohm, etc.) treat this question to some degree.p Assume that we have a system, S, and an apparatus, A, and that the system variable of interest is x, while the apparatus variable of interest is y (position of a meter needle, spot on photographic film, etc.) and that prior to making a measurement the system is in a definite state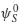 
and the apparatus in a state 
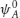, and furthermore that they are initially independent, so that the wave function of the whole system before the measurement begins is simply the product wave function. The measurement is then brought about by allowing the two systems to interact, by “turning on” a suitable interaction hamiltonian HI (x, y), which is chosen so as to introduce a correlation between the system variable x and the apparatus variable y. However, in order that the measurement be “good”, HI must be chosen so that the system state will not be disturbed (except in phase) if it is an eigenstate of the measurement.
Now, the measurement is arranged so that corresponding to each system eigenstate i, with value xi, there will be a definite apparatus state with value yi after the measurement. However, if the system is originally not in an eigenstate of x, but in a state of the form 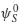= ∑i ai i then after the measurement the apparatus state will be indefinite to the same extent. This follows from the linearity of the wave equation and the superposition principle. In short, nothing discontinuous has happened, the system has not been forced to jump into an eigenstate, and, indeed, the relative amplitudes for the various eigenstates of the system remain unaltered. Nothing remotely resembling process (1) has taken place.
What has happened, however, is that the apparatus has become correlated to the system, even though neither is in a definite eigenstate of the variable under discussion. (Reminiscent of the example of Einstein, Rosen, and Podolsky.) This is possible because after the measurement the wave function for S + A is in a higher dimensional space than that of S or A alone. If we look at a “cross section”q of the total wave function for which the variable x has the definite value xi, we find that the apparatus has the definite value yi, which corresponds, while if we choose to consider the “cross section” for xj definite, we immediately find that y has the definite value yj, etc.r
So we see that from the viewpoint of wave mechanics that when a measuring apparatus interacts with a system which is not in an eigenstate of the variable being measured that the apparatus itself “smears out” and is indefinite, no matter how large or “classical” it is.s Nevertheless, it is correlated with the system in the above sense, and it is this correlation which allows us to give an adequate interpretation of the theory.
How is it possible, this “smearing out” of even classical objects which is implied by wave mechanics, and which is seemingly so contrary to our experience? Does this mean that we must abandon our quantum mechanical description and say that it fails at a classical level? We shall see that all that is necessary is to carry the theory to its logical conclusion to see that it is consistent after all.
Suppose that a human observer sets up his apparatus and makes a measurement on a system not in an eigenstate of the measurement, the result to appear as the position of a meter needle. According to what we have said, the meter needle itself will be “smeared out” after the measurement, but correlated to the system.t Why doesn’t our observer see a smeared out needle?u The answer is quite simple. He behaves just likev the apparatus did. When he looks at the needle (interacts), he himself becomes smeared out,w but at the same time correlated to the apparatus, and hence to the system. If we reflect for a moment upon the total wave function of the situation system-apparatus-observer, and again consider “cross sections”, we see that for the definite system value xj the needle has definite position yj, and there is a definite observer who perceives that the needle has the definite position yj, and, of course, similarly for all the other values. In other words, the observer himself has splitx into a number of observers, each of which sees a definite result of the measurement.y Furthermore, should our observer call over his lab assistant to look at the needle, the assistant would also split,z but be correlated in such a manner as always to agree with the first observer as to the position of the needle, so that no inconsistencies would ever arise.
In order to better illustrate the central role of correlations in quantum mechanics we consider the following example: In a box, say a one centimeter cube, we place a proton and an electron, each in momentum eigenstates, so that the position amplitude of each is uniform over the whole box. After a period of time we would expect a hydrogen atom to have formed.aa Nevertheless the position amplitude of the electron is still uniform over the whole box, just as that of the proton. All that has occurred is that the position densities have become correlated. All that is meant by the statement “There is a hydrogen atom in the box” is the existence of this correlation.ab, ac
In fact, it is clear from the circumstance that the wave equation is in 3N dimensional space, rather than 3 dimensional, that whenever several systems interact some degree of correlation is produced. Consider a large number of interacting particles. If we suppose them to be initially independent, then throughout the course of time the position amplitude of any single particle spreads out farther and farther, approaching uniformity over the whole universe, while at the same time, due to interactions, strong correlations will be built up, so that we might say that the particles have coalesced to form a solid object.ad That is, even though the position amplitude of any single particle would be “smeared out” over a vast region, if we consider a “cross section” of the total wave function for which one particle has a definite position, then we immediately find all the rest of the particles nearby, forming our solid object. It is this phenomenon which accounts for the classical appearance of the macroscopic world, the existence of definite solid objects, etc., since we ourselves are strongly correlated to our environment. Even though it is possible for a macroscopic object to “smear out”, particularly if it is connected to an amplification device whose operation depends upon microscopic events, we would never be aware of it due to the fact that the interactionsae between the object and our senses are so strong that we become correlated almost instantly.af
We now see that the wave mechanical description is really compatible with our ideas about the definiteness on a classical level, due to the existence of strong correlations.
We must now turn around and try to see why process (1) has been so successful. Imagine an observer making a series of quantum mechanical measurements (such as the sequence of measuring the z component of spin of an electron, then its x component, then again its z component, etc.). From the point of view of wave mechanics he is splittingag each time a measurement is made, so that after a number of measurements we could speak of his “life tree”. If we focus our attention on any single “branch” of this tree we see an observer who always perceives definite (and unpredictable)ah results of his measurements, and to whom the system has, with each measurement, apparently popped discontinuously into an eigenstate of the measurement. (Whereas from our point of view the observer himself has simply split into a number of observers, one for each eigenstate of the system, a process which is quite continuous and causal.)ai Furthermore, for almost all of the “branches” of his “life tree” which we might consider, the frequencies with which the observer sees the various results of his measurements will follow the probabilistic law of (1).aj Therefore, for practical considerations, an observer is justified in using (1) for calculations; not because the system undergoes any such probabilistic jumps, but simply because he himself will split into a number of observers, to each of which it appears that the system underwent a probabilistic jump.
We have, then, a theory which is objectively causal and continuous, while at the same time subjectively probabilistic and discontinuous. It can lay claim to a certain completeness, since it applies to all systems, of whatever size, and is still capable of explaining the appearance of the macroscopic world. The price, however, is the abandonment of the concept of the uniqueness of the observer, with its somewhat disconcerting philosophical implications.ak
As an analogy one can imagine an intelligent amoeba with a good memory. As time progresses the amoeba is constantly splitting, each time the resulting amoebas having the same memories as the parent.al Our amoeba hence does not have a life line, but a life tree. The question of the identity or non identity of two amoebas at a later time is somewhat vague. At any time we can consider two of them, and they will possess common memories up to a point (common parent) after which they will diverge according to their separate lives thereafter.
We can get a closer analogy if we were to take one of these intelligent amoebas, erase his past memories, and render him unconscious while he underwent fission, placing the two resulting amoebas in separate tanks, and repeating this process for all succeeding generations, so that none of them would be aware of their splitting. After a while we would have a large number of individuals, sharing some memories with one another, differing in others, each of which is completely unaware of his “other selves” and under the impression that he is a unique individual. It would be difficult indeed to convince such an amoeba of the true situation short of actually confronting him with his “other selves”. The same is true if one accepts the hypothesis of the universal wave function. Each time an individual splits he is unaware of it, and any single individual is at all times unaware of his “other selves” with which he has no interaction from the time of splitting.
We have indicated that it is possible to have a complete, causal theory of quantum mechanics, which simultaneously displays probabilistic aspects on a subjective level, and that this theory does not involve any new postulates, but in fact results simply by taking seriously wave mechanics and assuming its general validity. The physical “reality” is assumed to be the wave function of the whole universe itself. By properly interpreting the internal correlations in this wave function it is possible to explain the appearance of the macroscopic world to us, as well as the apparent probabilistic aspects.am
l See also the discussion of the minipapers in the biographical introduction (chapter 2, pg. 17). Digital scans of the earlier versions of this minipaper can be found at UCIspace (pg. xi).
m Everett’s copy of this document has handwritten marginal notes from his advisor John Wheeler. These are included here as notes with minimal editing in their approximate location.
n Wheeler writes in the margin:
o This would be something like Bohmian mechanics (Bohm, 1952), which Everett understood well and discussed in the long thesis (chapter 8, pgs. 153–54).
p Everett took von Neumann (1932, 1955) and Bohm (1952) as canonical texts on this topic.
q Wheeler writes in the margin: “image unclear.”
r This notion of the cross section of the total wave function is the basis for Everett’s notion of relative states in the long and short theses. Here the object system has definite value xi relative to the measuring apparatus recording the corresponding outcome yi. Cross sections, relative states, elements, and branches provided Everett with a language for talking about correlations between subsystems of a larger composite system. That is, they provided alternative ways to talk about the correlation structure that models pure wave mechanics.
s Wheeler writes in the margin: “meaning of smear-out example showing how compatible with class. nature of meas & associated amplification.”
t Wheeler writes in the margin: “X”.
u Wheeler writes in the margin: “X”.
v Wheeler changed “like” to “as.”
w Wheeler writes in the margin: “X”.
x Wheeler writes in the margin: “X”.
y This passage suggests that the measurement process involves a physical splitting of the observer. Here Everett clearly describes the process as one where a single observer splits into multiple observers, each of which has a definite measurement outcome. One clear advantage of this line is that it makes the explanation for why an observer perceives a determinate measurement outcome entirely straightforward: each postmeasurement observer actually has a single determinate outcome.
z Wheeler writes in the margin: “X”.
aa Wheeler writes in the margin: “X By radiation? What about the lack of correlation it introduces”.
ab Wheeler writes in the margin: “X”.
ac This example later plays a central role in the long thesis in explaining by analogy with the hydrogen atom what a composite physical object is in pure wave mechanics (pgs. 134–37).
ad Wheeler writes in the margin: “rad’n assumed? Analog to H2? If so, caution on radiation uncertainties. A complication in the discussion. But without it, particles escape those [?] position correlations”.
ae Wheeler writes in the margin: “spell out”.
af Perhaps the best sense of what Everett had in mind is given by how he reworked and filled in the arguments here in the long thesis. See the discussion beginning on (pg. 134).
ag Wheeler writes in the margin: “Split? Better words needed. Do first an unconscious object to show ideas more objectively.” From the earliest manuscripts both Wheeler and Everett were in search of appropriate words to describe pure wave mechanics. While he spoke most often in terms of elements, branches, and relative states, Everett changed his language regularly. For a few examples of language problems see pgs. 121, 206, 209–10, and 222.
ah Wheeler writes in the margin: “Elucidate details to show doubter how expt’lly to convince himself.”
ai Wheeler writes in the margin: “Amplifier necessary for validity of what is said here, it seems to me.”
aj Everett provides no argument for this point here nor is there an explanation of the specific sense of “almost all” or typicality for which this is true. It is likely, however, that Everett knew how he would argue for this later. See, for example, the discussions following pgs. 189 and 123.
ak Wheeler writes in the margin: “Careful examination needed of all the important apparent paradoxes”.
al Wheeler writes in the margin: “This analogy seems to me quite capable of misleading readers in what is a very subtle point. Suggest omission”.
am Wheeler writes at the bottom of the page: “Have to discuss questions of knowability of the universal ψ f’n.—And latitude with which we can ever determine it. Question of pooling of data by diff. observers. Question whether new view has any practical consequences. Also its implications for machinery of the world. Any special simplicity to be expected for the wave f’n? If not, why not? If so, what kind of simplicity? Any explanation then why world doesn’t look simple?” The questions of how observers pool data in pure wave mechanics and the complex appearance of the world became central questions for Everett in the long thesis. See for example the discussions starting on pp. 194, 130, and 134.