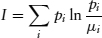
In May 1957, the first of a pair of related papers by E. T. Jaynes appeared in the journal Physical Review. In these papers Jaynes sought to apply Shannon information theory to statistical mechanics with the aim, in part, of providing an account of thermodynamic probabilities.
Everett saw a direct connection between Jayne’s project of providing probabilities for classical statistical mechanics and his own project of providing probabilities for pure wave mechanics, but he disagreed with Jaynes on the proper way to carry out such a project. Everett argued that Jaynes’ subjectivist approach did not avoid the problem of having to postulate special a priori probabilities. In particular, Everett pointed out that Jayne’s proposed measure of information was only one of a class of suitable information measures—a fact that Everett explicitly acknowledged in his own work. For Everett, the class of potential information measures was, in part, determined by the specific character of the system being considered; from which Everett concluded that Jaynes’ principle of maximum entropy cannot be construed as providing an a priori or canonical standard for statistical inference. Concerning his own work, while Everett held that the norm-squared probability measure was special in pure wave mechanics, he also knew that this measure represented one option among many.jv
Jaynes wrote a lengthy reply to Everett’s letter, dated 17 June 1957. He thanked Everett for his comments, but firmly defended his position. In particular, Jaynes argued that the special character of an object system may always be accounted for in terms of learned information which causes one to update their subjective probabilities from earlier prior probabilities. Hence, Jaynes concluded, “You claim that my theory is only a special case of your theory, with one particular information measure. I can, with equal justice claim that your theory is a special case of mine.”
It seems that Everett did not respond to Jaynes’ letter nor to a subsequent letter Jaynes wrote after reading the short version of Everett’s thesis when it was published in the Review of Modern Physics. Copies of these letters can be found in the archive of Jaynes’ papers at Washington University in St. Louis.
Hugh Everett, III
Institute for Defense Analyses
The Pentagon
Washington, D.C.
June 11, 1957
Dr. E.T. Jaynes
Department of Physics
Stanford University
Stanford, California
Dear Dr. Jaynes,
I am writing with respect to your article, “Information Theory and Statistical Mechanics” in the May 15 Physical Review.
While I fully sympathize with the “subjectivist” view of statistical mechanics that you express, I must point out a rather fundamental and inescapable difficulty with the principle of maximum entropy as you have stated it. It occurred to me also several years ago that one might take such an approach—that one might be able to circumvent the reliance on dynamical laws by basing deductions on a minimum information principle, with the subjectivist interpretation of probabilities as the justification. This is indeed an appealing idea.
The difficulty is that one is seduced by this method into believing, as you apparently do and I did, that one has circumvented the problem of assigning a priori probabilities when one has in fact done no such thing, but has tacitly admitted a particular a priori distribution.
Briefly, the trouble lies in using the expression ∑ pi ln pi to measure information. I shall demonstrate shortly that this choice is highly prejudicial and is equivalent to merely assuming equal a priori probabilities for each state.
It has occurred independently to several people, myself included, that the proper definition of information is a relative one, the information of a probability distribution relative to some underlying (basic) measure (or probability distribution) already given.
Thus for a discrete set of states {Si}, with basic measure {µi} (simply a set of weights in the discrete case), the relative information of a distribution {pi} over the states is defined as:
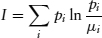
The reasons for this more general definition will become clear shortly. First, it enables one to define information for any probability distribution, i.e., for arbitrary probability measures over completely arbitrary sets of unrestricted cardinality. (Judging by your footnote, you are aware of the difficulties of even the continuous case for the ordinary definition.) This general definition comes about as follows: Consider an arbitrary set X, with probability measure p and underlying (I call it an information measure) measure µ. Now consider a finite partition P of X into subsets Xi. We then have a finite distribution over these sets and an information (in the relative sense) defined:
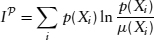
Now it is an easily proved theorem that any refinement of P will never decrease the information (i.e., P′ is a refinement of P implies that IP′ ≥ IP). Hence IP is a monotone function on the directed set of all finite partitions, and always has a limit, which we define as the information of P relative to µ. Thus this relative definition generalizes, while the usual one doesn’t, as you know.
A second advantage lies in the application to stochastic processes. If one defines the information of a distribution relative to a stationary distribution of the process, one can prove the theorem that information never increases with time (entropy never decreases).
Example: Two state Markov process with transition probabilities Ti→j:
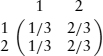
has the stationary distribution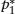 
= 1/3, 
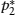= 2/3. For this process the information of a distribution p1, p2 should be:
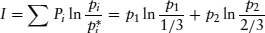
It is only for doubly-stochastic processes (where ∑i Tij = 1 as well as ∑i Tij = 1) that the stationary measure is uniform, and one can get away with the old definition ∑ Pi ln pi.
But notice that to determine the stationary measure, one must know the dynamics of the system. If you try to make predictions about this example using a minimum ∑ pi ln pi you will make worse predictions about this example than I, who use ∑ pi ln pi/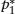 since I take into account the known fact that this system is not equally likely to be in any of its states.
Similarly in the case of statistical mechanics of gases. Only after one has established that the measure one is using is stationary (Liouville’s Theorem) is one justified in using it. The central problem is, as always, discovering the basic measure (or a priori probabilities, if you will). It is just fortuitous 1) that Lebesgue measure is the proper one for phase space so that ∫p ln pdt, which is really information relative to Lebesgue measure, is correct, and 2) that for doubly-stochastic processes, the type almost always encountered in physics, the uniform measure is stationary and hence ∑ pi ln pi correct. These two circumstances are, I believe, what cause people to be seduced into believing a special case can be regarded as a general principle.
I really have a lot more to say on the subject, but time doesn’t permit. I hope this rather hastily written letter conveys adequately the nature of my objection that you have not really sidestepped the fundamental problem of assigning a priori probabilities—which does depend on dynamical laws, ergodic properties, etc.—but have only camouflaged it.
Nevertheless, I sympathize with your viewpoint, and believe a lot can be done in this line. I hope you will continue, and that my remarks on the more general definition of information may be of help to you.
Sincerely yours,
Hugh Everett, III
P.S. Re the axioms which “uniquely” determine the definition of information (or entropy):
It is, then, on quite as firm ground as the more restricted form, and your statement, “Therefore one expects that deductions made from any other information measure, if carried far enough, will eventually lead to contradictions,” is a bit too strong.
HE:ne
jv See, for example, Everett’s presentation of his prior typicality measure for pure wave mechanics in the long thesis (pgs. 123–30). However, the proper status of probabilities in pure wave mechanics remains an open question.