One of the principal objects of theoretical research is to find the point of view from which the subject appears in the greatest simplicity.

—Josiah Willard Gibbs1

HEAT AND MOTION

As mentioned in chapter 3, in 1738 Daniel Bernoulli proposed that a gas is composed of particles that bounce around and collide with one another and with the walls of the container. Applying Newtonian mechanics, he was able to prove Boyle's law, which said that the pressure of a gas at constant temperature is inversely proportional to its volume.

Other scientists who early anticipated kinetic theory included the polymath scientist and poet Mikhail Lomonosov (1711–1765) in Russia, physicist Georges-Louis Le Sage (1724–1803) in Switzerland, and amateur scientist John Herapath (1790–1868) in England.

Lomonosov, born a poor fisherman's son in Archangel, was an incredible genius—far ahead of his time. He rejected the phlogiston theory of combustion, realized that heat is a form of motion, discovered the atmosphere of Venus, proposed the wave theory of light, and experimentally confirmed the principle of conservation of matter that had confounded Robert Boyle and other better-remembered Western scientists. He presaged William Thomson (Lord Kelvin, 1824–1907) in the concept of absolute zero. He also showed that Boyle's law would break down at high pressure. In all this, he assumed matter was composed of particles. Lomonosov's story, unfamiliar to most in the West, has been told in a recent article in the magazine Physics Today.2

Le Sage invented an electric telegraph and proposed a mechanical theory of gravity. While he independently proposed kinetic theory, it made no improvement on that of Bernoulli and was wrong in several ways.

Herapath's paper was rejected by the Royal Society in 1820, and although he managed to have his ideas published elsewhere, they were generally ignored. But he was on the right track.³

Despite the largely unrecognized success of Bernoulli's model and these other tentative, independent proposals, the professional physics community centered in western Europe was slow to further develop the atomic model of matter because of its fundamental misunderstanding of the nature of heat. The majority view was that heat was a fluid called caloric that flowed from one body to another. However, this was mistaken, and the story of that discovery is a great tale in itself.

As has often happened in the history of physics, military applications provided both an incentive for research and a source of crucial knowledge from that research. During the American Revolutionary War, a New England physicist named Benjamin Thompson (1753–1814) served with the Loyalist forces. After the war, he moved to London and in 1784 was knighted by King George III. From there, Thompson moved to the royal court of Bavaria and was named Count Rumford of the Holy Roman Empire. Rumford is the name of the town in New Hampshire where he had lived prior to the war, now known as Concord.

While supervising the boring of cannon for the Bavarian army, Thompson noticed that as long as he kept boring away, heat was continuously generated. If heat were a fluid contained in the cannon, then at some point it should have been all used up. In a paper to the Royal Society in 1798, Rumford argued against the caloric theory and proposed a connection between heat and motion. It would be a while before the physics community would accept this connection.

THE HEAT ENGINE

In France, another military engineer, Nicolas Léonard Sadi Carnot (1796–1832), who had served under Napoleon, made the first move toward what would become the science of thermodynamics. Steam engines were just coming into use and it was imperative to understand how they worked. With amazing insight, Carnot proposed an abstract heat engine, now called the Carnot cycle, which enabled calculations to be made without the complications of any specific working design.

The Carnot cycle is composed of four processes:

1. Heat from a high temperature reservoir causes a gas to expand at constant temperature (isothermally). The expanding gas is used to drive a piston and do work.
2. The gas is expanded further with no heat in or out (adiabatically) and more work is done.
3. Then the piston moves back (say it is attached to a flywheel), compresses the gas isothermally, and heat is exhausted to the low temperature reservoir.
4. The gas returns to its original state with an adiabatic compression.

The final two steps require work to be done on the gas, but the amount is less than the work done during the two expansions, so a net amount of work is done in the cycle.

An idealized heat engine, not necessarily a Carnot engine, is diagrammed in figure 5.1.

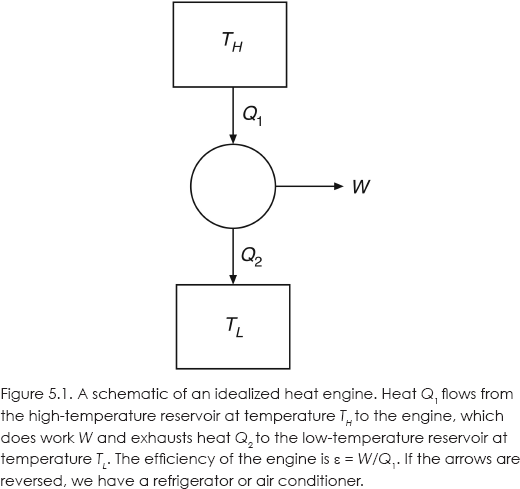
The efficiency of this idealized engine is ε = W/Q₁, that is, the work done as a fraction of the heat in. Carnot showed that for the Carnot cycle, ε depends on only the temperatures of two heat reservoirs: ε = 1 – T_L / T_H. The higher-temperature reservoir provides the heat, and waste heat is exhausted into the lower-temperature reservoir. In a steam engine, a furnace provides the heat and the environment acts as the exhaust reservoir. Carnot argued that no practical heat engine operating between the same two temperatures could be more efficient than the Carnot cycle.

The Carnot cycle and other idealized engines can be reversed so that work is done on the gas while heat is pumped from the lower-temperature reservoir to the higher-temperature one. In that case, the cycle acts as a refrigerator or air conditioner.

Carnot realized that neither a perfect heat engine, nor a perfect refrigerator or air conditioner, was possible. Consider a perfect air conditioner. That would be one that moves heat from a lower-temperature area, such as a room, to a higher-temperature area, such as the environment outside the room, without requiring any work being done. Such a device could be used to produce a heat engine with 100 percent efficiency, that is, a perpetual-motion machine, by taking the exhaust heat from the engine and pumping it back to its higher-temperature source.

However, heat is never observed to flow from a lower temperature to a higher temperature in the absence of work being done on the system. This principle would later become the simplest statement of the second law of thermodynamics. But physicists had still to come up with the first law.

CONSERVATION OF ENERGY AND THE FIRST LAW

According to historian Thomas Kuhn, the discovery of the fundamental physics principle of conservation of energy was simultaneous among several individuals.4 The term vis viva, which means “living force” in Latin, is an early expression for energy. It was used by Leibniz to refer to the product of the mass and square of the speed of a body, mv². He observed that, for a system of several bodies, the sum m₁v₁² + m₂v₂² + m₃v₃² +…was often conserved. Later it was shown that the kinetic energy of a particle (for speeds much less than the speed of light) is ½mv². This was perhaps the first quantitative statement of conservation of energy. He also noticed that mgh + mv² was conserved, thus introducing what was later shown to be the gravitational potential energy of a body of mass m at a height h above the ground, where g is the acceleration due to gravity.

In 1841, Julius Robert von Mayer (1814–1878) made the first clear statement of what is perhaps the most important principle in physics:

Energy can be neither created nor destroyed.5

Mayer received little recognition at the time, although he was eventually awarded the German honorific “von,” equivalent to knighthood.

In 1850, Rudolf Clausius (1822–1888) formulated the first law of thermodynamics:

In a thermodynamic process, the increment in the internal energy of a system is equal to the difference between the increment of heat accumulated by the system and the increment of work done by it.⁶

This wording is still used today. In the case of the heat engine diagrammed in figure 5.1, Q₁ = W + Q₂.

In 1847, Hermann von Helmholtz published a pamphlet titled Über die Erhaltung der Kraft (On the Conservation of Force).⁷ Here it must be understood that by “force,” Helmholtz was referring to energy. Although rejected by the German journal Annalen der Physik, an English translation was published that received considerable notice from English scientists.

The first law of thermodynamics makes the connection between energy, heat, and work explicit. A physical system has some “internal energy,” that is yet to be identified. That internal energy can change only if heat is added or subtracted, or if work is done on or by the system. Once again, this is more easily seen with a simple equation:

 

ΔU = Q – W,

where ΔU is the change in internal energy of the system, Q is the heat input, and W is the work done by the system. These are algebraic quantities that can have either sign. Thus, if Q is negative, heat is output; if W is negative, work is done on the system.

Note that conservation of energy can still be applied in the caloric theory of heat. Caloric is conserved the same way the amount of a fluid, such as water, is conserved when pumped from one point to another. However, caloric is not conserved in a heat engine because mechanical work is done and heat is lost. Recognizing that heat was mechanical and not caloric was the big step that had to be taken in order to understand thermodynamics.

THE MECHANICAL NATURE OF HEAT

Carnot's work on heat engines was not immediately recognized. However, starting in 1834, the new science of thermodynamics was developed more definitively by Benoît Paul Émile Clapeyron (1799–1864) and others.

In England, James Prescott Joule (1818–1889) raised a theological objection to the notion of Carnot and Clapeyron that heat can be lost. In 1843 he wrote:

I conceive that this theory…is opposed to the recognised principles of philosophy because it leads to the conclusion that vis viva may be destroyed by an improper disposition of the apparatus: Thus Mr Clapeyron draws the inference that “the temperature of the fire being 1000°C to 2000°C higher than that of the boiler there is an enormous loss of vis viva in the passage of the heat from the furnace to the boiler.” Believing that the power to destroy belongs to the Creator alone I affirm…that any theory which, when carried out, demands the annihilation of force, is necessarily erroneous.8

Joule was thinking of conservation of energy, but he was attributing it to deity. He believed that whatever God creates as a basic agent of nature must remain constant for all time.

Although Joule's motivation was at least partly theological, he had the data to demonstrate that heat was not a fluid but a form of energy. In a whole series of experiments, Joule showed how different forms of mechanical and electrical energy generate heat and measured their equivalence. His most significant experiment, which is discussed in most elementary physics textbooks, was published in 1850.⁹ An 1869 engraving of his apparatus is given in figure 5.2.¹⁰

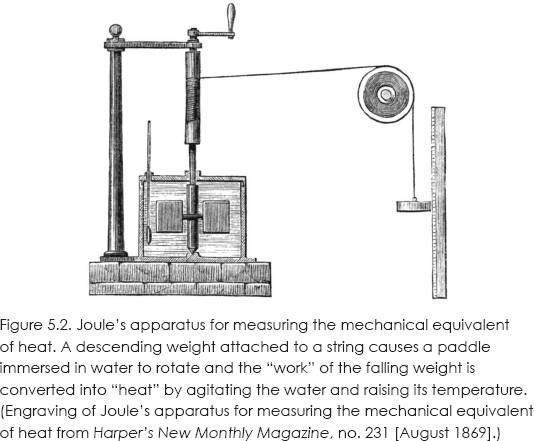
Shown is a paddle wheel immersed in water that is turned by a falling weight. Multiplying the value of the weight and the distance it falls gives you the work done in stirring the water. A thermometer measures the rise in temperature of the water, from which you can obtain the heat generated. One calorie is the heat needed to raise the temperature of one gram of water one degree Celsius.11 In the modern International System of Units, the unit of energy and work is named in Joule's honor. He determined the mechanical equivalent of heat to be 4.159 Joules/calorie (the current value is 4.186).

ABSOLUTE ZERO

Another important step in the development of thermodynamics was the notion of absolute temperature, introduced by William Thomson, later made Lord Kelvin, in 1848.12 Thomson sought an absolute temperature scale that applied for all substances rather than being specific to a particular substance. Carnot's abstract heat engine provided Thomson with the means by which absolute differences in temperature could be estimated by the mechanical effect produced. As he writes,

The characteristic property of the scale which I now propose is, that all degrees have the same value; that is, that a unit of heat descending from a body A at the temperature T° of this scale, to a body B at the temperature (T-1)°, would give out the same mechanical effect, whatever be the number T. This may justly be termed an absolute scale, since its characteristic is quite independent of the physical properties of any specific substance.

Kelvin considered a common thermometer in use at the time, called an air thermometer, in which a temperature change is measured by the change in volume of a gas under constant pressure. He then argued that a heat engine operating in reverse (as a refrigerator) could be used to reduce the temperature of a body. However, at some point the volume of the gas in the thermometer would be reduced to zero. Thus, infinite cold can never be reached but some absolute zero of temperature must exist. Using experimental data from others, Kelvin estimated this to be –273 degrees Celsius, that is, –273 C. Pretty good. Today we define the absolute temperature in Kelvins (K) to be the Celsius temperature plus 273.15.

THE SECOND LAW OF THERMODYNAMICS

Clausius was also responsible for the first clear statement of the second law of thermodynamics, about which we will have much more to say. Energy conservation does not forbid a perfect refrigerator in which no work is needed to move heat from low temperature to high temperature. But it is an empirical fact that we never see this happening. Heat is always observed to flow from higher to lower temperatures. This is perhaps the simplest way to state the second law of thermodynamics. The other versions just follow. As mentioned previously, if you had a perfect refrigerator, you could use it to cool the low-temperature reservoir of a heat engine below ambient temperature so it could operate with heat from the environment, which would then be serving as the high-temperature reservoir.

Clausius found a way to describe the second law quantitatively. He proposed that there was a quantity that he called entropy (“inside transformation” in Greek) that for an isolated system must either stay the same or increase. In the case of two bodies in contact with one another but otherwise isolated, the heat always flows from higher temperature to lower temperature because that is the direction in which the total entropy of the system increases.

KINETIC THEORY

Once the mechanical nature of heat as a form of energy was understood and absolute temperature was defined, the kinetic theory of gases could be developed further. The particulate model provided a simple way to understand physical properties of gases and other fluids described by macroscopic thermodynamics, and the related dynamics of fluids, purely in terms of Newtonian mechanics.

In 1845, the Royal Society rejected a lengthy manuscript submitted by a navigation and gunnery instructor working in Bombay for the East India Company named John James Waterston. Although not correct in all of its details, the paper contained the essentials of kinetic theory, as better-known scientists would develop it a few years later. In particular, Waterston made the important connection between temperature and energy of motion.

One better-known scientist was Rudolf Clausius. In 1857, he published The Kind of Motion We Call Heat, in which he describes a gas as composed of particles. Clausius proposed that the absolute temperature of the gas, as anticipated by Waterston, was proportional to the average kinetic energy of the particles. The particles of the gas had translational, rotational, and vibrational energies, and the internal energy was the sum of these.

Although he wasn't the first to propound the kinetic model, Clausius had the skill and reputation needed to spark interest in the subject. In 1860, a brilliant young Scotsman named James Clerk Maxwell (1831–1879) derived an expression for the distribution of speeds of molecules in a gas of a given temperature, although his proof was not airtight. Clausius had assumed all the speeds were equal.

In 1868, an equally brilliant and even younger physicist in Austria named Ludwig Boltzmann (1844–1906) provided a more convincing proof of what became known as the Maxwell-Boltzmann distribution, although the two never met. Boltzmann would be the primary champion of the atomic theory of matter and provide its theoretical foundation based on statistical mechanics against the almost-uniform skepticism of others, including Maxwell, and downright harsh opposition from some, notably Ernst Mach.13

However, before we get to that, let us consider an example of how kinetic theory is applied. The simplest application of kinetic theory is to what is called an ideal gas, which is circularly (but not illogically) defined as any gas that obeys the ideal gas equation.

Let P be the pressure, V be the volume, and T be the absolute temperature of a container of gas. The ideal gas law, formulated by Clapeyron, combines Boyle's law and Gay-Lussac's law, which is better known as Charles's law, and was proposed by Joseph Louis Gay-Lussac (1778–1850). For a fixed mass of gas:

Boyle's law	PV = constant for constant T
Charles's law	V/T = constant for constant P
Ideal gas law	PV/T = constant

In freshman physics classes today, a model in which an ideal gas is just a bunch of billiard-ball-type particles bouncing around inside a container is used to prove that

 

PV = NkT,

where N is the number of particles in the container and k is Boltzmann's constant (which is just a conversion factor between energy and temperature). This is the precise form of the ideal gas law.

HOW BIG ARE ATOMS?

A key issue in the atomic theory of matter is the scale of atoms. The first step in the direction of establishing the size of atoms was made by the Italian physicist Lorenzo Romano Amedeo Carlo Avogadro, Count of Quaregna and Cerreto (1776–1856). Avogadro proposed what is now called Avogadro's law, which states that equal volumes of all gases at the same conditions of temperature and pressure contain the same number of molecules.

At the time, the terms atoms and molecules were used interchangeably. Avogadro recognized that there were two types of submicroscopic ingredients in matter, the first being elementary molecules, which we now call atoms (or, in my designation, “chemical atoms,” which are identified with the chemical elements), and the second being assemblages of atoms, which today we simply call molecules.14

Avogadro's number (or Avogadro's constant) is the number of molecules in one mole of a gas. The number of moles in a sample of matter is the total mass of the sample divided by the atomic weight of the element or compound that makes up the sample. Allow me to use some simple mathematics that will be easier to understand than anything I can say with words alone. Let's make the following definitions:

NA	Avogadro's number
N	the number of molecules (or atoms) in a sample of matter
M	the mass of that sample in grams
n	the number of moles in that sample
A	the atomic weight of the element or compound in the sample
m	the actual mass of the atom or molecule in grams

Consider hydrogen, where we make the approximation A = 1 (actual value 1.00794). Let the mass of the hydrogen atom be m = m_H in grams. Then,

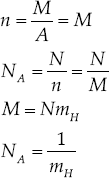
That is, Avogadro's number, to an approximation sufficient for our purposes, is simply the reciprocal of the mass of a hydrogen atom in grams.

Avogadro did not know the value of N_A. The first estimate, which was reasonably close to the more accurate value later established, was made in 1865 by an Austrian scientist named Johann Josef Loschmidt (1821–1895). He actually estimated another number now called Loschmidt's number, but it was essentially the same quantity.

Using the current best value, N_A = 6.022 × 10²³, we get m_H = 1.66 × 10^–24 grams.

To find the number of molecules in M grams of any substance, simply multiply M by N_A/A. Since the density of water is 1 gram per cubic centimeter (by definition) and its molecular weight is A = 18, a cubic centimeter of water contains N = 3.3 × 10²² water molecules.

Until scientists had an estimate for Avogadro's number, they had no idea that the number of molecules in matter was so huge and that the molecules themselves had such small masses. Many chemists thought atoms were balls rubbing against each other, like oranges in a basket. In the next chapter, we will see how the substructure of the chemical atoms was revealed in nuclear physics.

STATISTICAL MECHANICS

Kinetic theory is the simplest example of the application of statistical mechanics, developed by Clausius, Maxwell, Max Planck (1858–1947), and Josiah Willard Gibbs (1839–1903), but whose greatest architect was Ludwig Boltzmann. By assuming the atomic picture of matter for all situations, not just an ideal gas, statistical mechanics uses the basic principles of particle mechanics and laws of probability to derive all the principles of macroscopic thermodynamics and fluid mechanics. With statistical mechanics, atoms and the void came home to stay.

Boltzmann had a difficult time convincing others, including Maxwell, that statistical mechanics was a legitimate physical theory. Boltzmann had been a good friend of fellow Austrian Loschmidt, who, as we have seen, had made an estimate of the size of atoms. So Boltzmann knew that the volumes of gas dealt with in the laboratory contained many trillions of atoms. Obviously, it was impossible to keep track of the motion of each, so he was necessarily led to statistical methods. However, at the time, statistics was not to be found in the physicist's toolbox.

Probability and statistics was already a mathematical discipline, thanks mainly to the efforts of Blaise Pascal (1623–1662) and Carl Friedrich Gauss (1777–1855). It was mostly used to calculate betting odds, although there is no record of Pascal using it to determine the odds for Pascal's wager.15

In any case, the mathematics for calculating probabilities was available to Boltzmann. No one before Boltzmann had ever thought to apply statistics to physics, where the laws were assumed to be certain and not subject to chance. Even Maxwell did not immediately grasp that the Maxwell-Boltzmann distribution, which assumes random motion, was just the probability for a molecule having a speed of a certain value within a certain range. Boltzmann did not appreciate that at first, either. But he nevertheless initiated a revolution in physics thinking that reverberates to this very day.

Boltzmann's monumental work occurred in 1872, when he was twenty-eight years old. He derived a theorem, which was called the H-theorem by an English physicist who mistook Boltzmann's German script uppercase E for an H. This theorem was essentially a proof of the second law of thermodynamics.

In Boltzmann's H-theorem, a large group of randomly moving particles will tend to reach a state where a certain quantity H is minimum. Boltzmann identified H with the negative of the entropy of the system, and so the H-theorem said that the entropy tends to a maximum, which is just what is implied by the second law of thermodynamics.

Boltzmann's equation for entropy is engraved on his gravestone:

 

S = klogW,

where log is the natural logarithm (the inverse of the exponential function), usually written today as log_e or ln, and W is the number of accessible states of the system.

What exactly do we mean by the “number of accessible states”? Basically, it is the number of microstates needed to give a particular macrostate. Let me give a simple example. Consider the toss of a pair of dice. Each possible outcome of the toss constitutes a separate accessible microstate of the system of two dice. Now, suppose the “energy” of the system is defined as the sum of the number of dots that turn faceup. Each energy is a different macrostate. The lowest energy is 2, which can occur only one way, “snake eyes,” 1 and 1. So the system has one accessible microstate of energy 2. Similarly, the highest energy of 12 has only one accessible microstate, “boxcars,” 6 and 6.

Now, energy 3 can occur two ways, so there are two accessible states of that energy. Energy 7 has the most accessible states: 6 and 1, 1 and 6, 5 and 2, 2 and 5, 4 and 3, 3 and 4, for a total of six states. And so on. Figure 5.3 shows the number of accessible microstates for each possible value of energy.

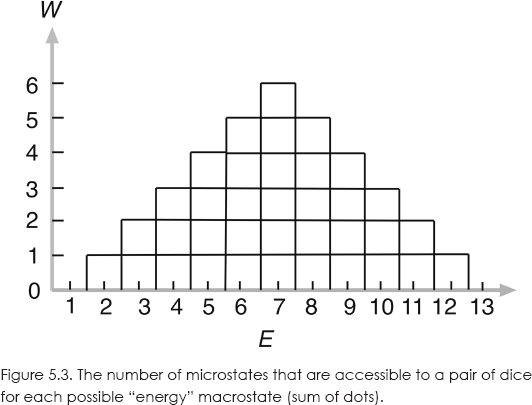
To get the entropy of the dice as a function of energy, just pick off W from the graph and calculate it from the previous equation. Recall that Boltzmann's constant, k, just coverts temperature units to energy units. Let k = 1, in which case entropy is dimensionless. So, for example, for E = 10, W = 3 and S = log(3) = 1.09.

Note that the lower the value of W—that is, the lower the entropy—the more information we have about the microstates of the system of a given energy. When E = 7, the system can be in any of six possible microstates, which is the lowest information state. When E = 1 or 12, we have only one possible microstate and maximum information. Communications engineer Claude Shannon made the connection between entropy and information in 1948, thus founding the now vitally important field of information theory that is fundamental to communications and computer science.16

This example also makes clear the statistical nature of entropy. The probability of obtaining any particular energy with a toss of the dice is W divided by the total area of the graph, which is 36 for our particular example. Thus, the probability of E = 7 (tossing a 7) is 6/36 = 1/6. The probability of E = 4 is 3/36 = 1/12.

Here the number of samples is small, so we have a wide probability distribution. As the number of samples increases, the probability distribution becomes narrower and narrower so that the outcome becomes more and more predictable. This is known as the law of large numbers, or the central limit theorem in probability theory.

Most physicists at the time were not convinced by Boltzmann's H-theorem. His friend Loschmidt posed what is called the irreversibility paradox. The laws of mechanics are time reversible, so if a set of particle interactions results in H decreasing, the reversed processes will result in H increasing. Maxwell had made a similar argument with a device called “Maxwell's demon,” an imaginary creature that can redirect particles so that they flow from cold to hot.

It took Boltzmann a while to realize that his theorem was not a hard-and-fast rule but rather a matter of probabilities. It was not that the system would reach minimum H and stay there forever, as it seems he originally thought, but it can fluctuate away from it. This is what made the H-theorem so hard to accept for great thinkers like Maxwell and Thomson. The second law is just a statistical law. Who had ever heard of a law of physics that was just based on probabilities? What took everyone, including Boltzmann, a long time to realize was that entropy does not always have to increase. It can decrease.

However, all the familiar, macroscopic applications of entropy deal with systems of great numbers of particles, where the probability of entropy decreasing is infinitesimally small. So the second law of thermodynamics is generally considered inviolate. For example, in his 1971 book, Bioenergetics; the Molecular Basis of Biological Energy Transformations, Albert L. Lehninger has a diagram showing several processes such as the flow of heat between regions of different temperature and the movement of molecules from regions of different pressure or different concentrations. In the caption he says, “Such flows never reverse spontaneously.”17

What never?
No, never.
What never?
Well, hardly ever.¹⁸

Consider the flow of heat between two bodies in contact with one another. Picture what happens microscopically, which I have emphasized is always the best way to view any physical process to really understand what is going on. In figure 5.4, the body with black particles is at lower temperature, as indicated by the shorter arrows, on average, that represent their velocity vectors. The body with the white particles is higher temperature, indicated by longer arrows. Energy is transferred between the two bodies by collisions in the separating wall. On average, more energy is transferred from the higher-temperature body to the lower-temperature one because, in a collision between two bodies, the one with the higher energy will transfer more of its energy to the other body. However, when the number of particles is small, there is some chance that occasionally energy will be transferred in the opposite direction, in apparent violation of the second law.

Now, in principle, this can happen no matter how many particles are involved. Indeed, all the so-called irreversible processes of thermodynamics are, in principle, reversible. Open the door of a closed room and all the air in the room can rush out the door, leaving behind a vacuum. All that has to happen is that at the instant you open the door, all the air molecules need to be moving in that direction. However, this is very, very unlikely because of the huge number of molecules involved. If a room contained just three molecules, no one would be surprised to see them all exit the room when the door was opened.

Thus, Loschmidt's paradox is no paradox. Regardless of the number of particles, every process is, in principle, reversible, exactly as predicted by Newtonian mechanics. This is also true in modern quantum theories.

THE ARROW OF TIME

As Boltzmann eventually realized, there is no inherent direction to time. The second law of thermodynamics, which some physicists have termed the most important law of physics, is not a law at all. It is simply a definition of what Arthur Eddington in 1927 dubbed the arrow of time. Rather than saying that the entropy of a closed system must increase, or at best stay constant, with time, the proper statements of the second law is as follows.

Second Law of Thermodynamics

The arrow of time is specified by the direction in which the total entropy of the universe increases.

As we will see in chapter 10, in the twentieth century, it was found that not all elementary particle processes run in both time directions with equal probability. Some authors have trumpeted this as the source of a fundamental arrow of time. However, this is incorrect. The processes observed still are reversible, with the differences in probability being only on the order of one in a thousand. They are time asymmetric but not time irreversible. The arrow of time defined by the second law of thermodynamics is of little use when the number of particles involved is small, which is why you never see it used in particle physics.

THE ENERGETIC OPPOSITION

Perhaps the best-known of the late nineteenth- and early twentieth-century antiatomists was the Austrian physicist and philosopher Ernst Mach. Along with chemists Wilhelm Ostwald (1853–1932) and George Helm (1851–1923) in Germany, and physicist/historian Pierre Duhem (mentioned in chapter 3) in France, Mach advocated a physical theory called energeticism.19 This theory was based on the hypothesis that everything is composed of continuous energy. In this scheme, there are no material particles. Thermodynamics is the principle science of the physical world and energy is the governing agent.²⁰ The goal of science, then, is to “describe and codify the conditions under which matter reacts without having to make any hypothesis whatsoever about the nature of matter itself.”²¹

We have seen how, with the rise of the Industrial Revolution in the nineteenth century, the science of thermodynamics developed as a means of describing phenomena involving heat, especially heat engines. Thermodynamics became a remarkably advanced science with enormous practical value.

The nineteenth-century science of thermodynamics was based solely on macroscopic observations and made no assumptions about the structure of matter. Furthermore, it was very sophisticated mathematically. It contained great, general principles such as the zeroth, first, second, and third laws of thermodynamics. Indeed, energy was the key variable that could appear as the heat into or out of a system, the mechanical work done on or by a system, or the internal energy contained inside the system itself. A remarkable set of equations was developed relating the various measurable variables of system such as pressure, temperature, and volume, to other abstract variables such as entropy, enthalpy, and free energy.

At the same time, the atomic theory of matter suffered from the problems we have already discussed, in particular, as Mach especially continued to emphasize, that no one had ever seen an atom. He insisted that science should only concern itself with the observable.

The figure who did the most to promote the general theory of macroscopic thermodynamics was a reclusive American physicist, Josiah Willard Gibbs (1839–1903), with a series of publications in the Transactions of the Connecticut Academy of Sciences in 1873, 1876, and 1878. While this was not, to say the obvious, a widely read journal, Gibbs sent copies to all the notable physicists of the time, even translating them into German. Ostwald seized on Gibbs's work as support for energeticism, but Gibbs wasn't in that camp. He was not against atoms; he just did not need them to develop the mathematics of thermodynamics.22 Indeed, his work provided a foundation for statistical mechanics as well as for physical chemistry, and a year before his death in 1903, he wrote a definitive textbook, Elementary Statistical Mechanics.

In any event, the energeticists had good reasons to view thermodynamics as the foundation of physics. Ostwald even denied the existence of matter outright. All was energy. He saw advantages in science adopting energeticism:

First, natural science would be freed from any hypothesis. Next, there would no longer be any need to be concerned with forces, the existence of which cannot be demonstrated, acting on atoms that cannot be seen. Only quantities of energy involved in the relevant phenomena would matter. Those we can measure, and all we need to know can be expressed in those terms.²³

Ostwald gained great prominence in chemistry, including an eventual Nobel Prize in 1909. He founded what is called physical chemistry, which combines chemistry with thermodynamics in order to understand the role of energy exchanges in chemical reactions. Boltzmann had met Ostwald when the younger man was still getting started, and they kept up a friendly interaction—at least for a while.

However, Ostwald was influenced by Mach and, like many chemists, did not see the particulate theory as particularly convincing or useful. The matter came to a head on September 16, 1895, when Boltzmann and mathematician Felix Klein (1849–1925) debated Ostwald and Helm in front of a large audience in Lübeck. Ostwald was the far better debater, but Boltzmann easily won the day by arguments alone (which shows it can be done).

The chemists tried to argue that all the laws of mechanics and thermodynamics follow from conservation of energy alone. Boltzmann pointed out that Newtonian mechanics was more than energy conservation, and thermodynamics was more than the first law. In particular, as we have seen, the second law had to be introduced precisely because the first law did not forbid certain processes that are observed not to occur.

The famous Swedish chemist Svante Arrhenius (1859–1927), who attended the debate, wrote later, “The energeticists were thoroughly defeated at every point, above all by Boltzmann, who brilliantly expounded the elements of kinetic theory.” Also in attendance was the young Arnold Sommerfeld (1868–1951), who would become a major figure in the new quantum mechanics of the twentieth century. He wrote, “The arguments of Boltzmann broke through. At the time, we mathematicians all stood on Boltzmann's side.”24

THE POSITIVIST OPPOSITION

Mach's opposition was not so much based on his support for energeticism as his commitment to a philosophy that was fashionable at the time called positivism, which was put forward by French philosopher Auguste Comte (1798–1857). Comte, who was mainly interested in applying science to society and is regarded as the founder of sociology, believed that science must “restrict itself to the study of immutable relations that effectively constitute the laws of all observable events.” He dismissed any hope to gain “insight into the intimate nature of any entity or into the fundamental way phenomena are produced.”²⁵ Comte summarizes his position:

The sole purpose of science is, then, to establish phenomenological laws, that is to say, constant relationships between measurable quantities. Any knowledge about the nature of their substratum remains locked in the province of metaphysics.²⁶

Mach insisted that the atomic theory was not science, that physicists should stick to describing what they measure—temperature, pressure, heat—and not deal with unobservables. Atoms are, at best, a useful fiction.

Mach's name is well known because of the definition of the Mach number as the ratio of a speed to the speed of sound, and he make major contributions to the theory of sound and supersonic motion. He is also recognized for Mach's principle, a vague notion that has many different forms but basically says that a body all alone in the universe would have no inertia, so inertia must be the consequence of the other matter in the universe. Einstein made Mach's principle famous by referring to it in developing his general theory of relativity, although he does not seem to have used it anyplace in his derivations. Furthermore, the principle has never been placed on a firm philosophical or mathematical foundation.

After producing poorly received physics books titled The Conservation of Energy (1872) and The Science of Mechanics (1883), Mach turned increasingly toward writing and lecturing on philosophy, meeting there with greater success. In the 1890s, he crossed paths with Boltzmann as they both settled down in Vienna.

In Vienna, Boltzmann found himself decidedly in the minority as students and the general public flocked to Mach's lectures while few were interested in the demanding work of mathematical physics. Mach continued to assert that there is no way to prove that atoms are objectively real. Before the Viennese Academy of Sciences, Mach stated unequivocally, “I don't believe atoms exist!”27

The dispute between Mach and Boltzmann was clearly not over physics but over the philosophy of science. What is it that science tells us about reality? This question is not settled today. Mach's positivism continued into the early twentieth century as the philosophical doctrine of logical positivism that was also centered in Vienna with a group called the Vienna Circle. The logical positivists were led by Moritz Schlick and included many of the top philosophers of the period, such as Otto Neurath, Rudolf Carnap, A. J. Ayer, and Hans Reichenbach.

The goal of the logical positivists was to apply formal logic to empiricism. In their view, theology and metaphysics, neither of which had any empirical basis, were meaningless. Mathematics and logic were tautologies. Only the observable was verifiable knowledge. So far, so good.

While logical positivism held the center stage of philosophy for a while, it eventually fell to the recognition of its own inconsistency. How does one verify verifiability? Later, eminent philosophers such as Karl Popper, Hilary Putnam, Willard Van Orman Quine, and Thomas Kuhn pointed out that all observations have a theoretical element to them, they are what is called theory-laden. Time is what is measured on a clock, but it is also a quantity, t, appearing in theoretical models. While logical positivism is no longer in fashion, the essential point that we have no way of knowing about anything except by observation remains an accepted principle in the philosophy of science.

Getting back to atoms, are atoms real or just theoretical constructs? Boltzmann was not dogmatic about it. He recognized that “true reality” can never be determined and that science can only hope to apprehend it step-by-step in a series of approximations.28 Mach's insistence that atoms were inappropriate elements of a theory because they are not observed would be proven grossly wrong when atoms were convincingly observed. Today we have quarks that not only have never been observed, but they are also part of a theory that says they never will be observed. Indeed, if quarks are someday observed, the theory that introduced them in the first place will be falsified!

Unhappy in Vienna, where he felt unappreciated and was becoming increasingly emotionally unhinged, in 1900, Boltzmann moved to Leipzig where Ostwald magnanimously had found him a place. However, he accomplished nothing there and returned to Vienna in 1902. His lectures were well received, but he showed no interest in the new physics that was blossoming with the turn of the century: Röntgen rays, Becquerel rays, and Planck quanta.

Instead, Boltzmann took to lecturing in philosophy, taking over a course taught by Mach, who had retired after suffering a stroke. Boltzmann had difficulty grasping the subject. After attempting to read Hegel, he complained, “what an unclear, senseless torrent of words I was to find there.” In 1905 Boltzmann wrote to philosopher Franz Brentano (1838–1917), “Shouldn't the irresistible urge to philosophize be compared to the vomiting caused by migraines, in that something is trying to struggle out even though there is nothing inside?”29

In 1904, Boltzmann attacked Schopenhauer in a lecture he gave before the Vienna Philosophical Society that was originally to be titled, “Proof That Schopenhauer Is a Stupid, Ignorant Philosophaster, Scribbling Nonsense and Dispensing Hollow Verbiage That Fundamentally and Forever Rots People's Brains.” Actually, Schopenhauer had written these precise words to attack Hegel.³⁰ Boltzmann changed the title but still came down hard on Schopenhauer.

During these last years, Boltzmann traveled extensively, including two trips to America. In 1904, he attended a scientific meeting in conjunction with the St. Louis World's Fair. In 1905, he gave thirty lectures in broken English at Berkeley. (He could have lectured in German, which was familiar to scholars of the day.) At the time, Berkeley, of all places, was a dry town, and Boltzmann had to steal to a shop in Oakland regularly to get bottles of wine. Passing through dry states on the train back to New York, he had to bribe attendants to bring him wine.³¹

Back in Vienna, Boltzmann found it impossible to continue his lecturing and was increasingly depressed. He did not seem to be aware of the fact that in 1905 Einstein had provided the necessary theory that would ultimately lead to a convincing verification of the atomic picture, as will be described in the next section. In late summer of 1906, Boltzmann traveled with his family to the village of Duino on the Adriatic coast for a respite by the sea. There, on September 5, his fifteen-year-old daughter, Elsa, found him hanging in their hotel room. His funeral in Vienna a few days later was attended by only two physicists. The academic year had not yet begun.

EVIDENCE

Despite the great success of the atomic theory of matter in accounting for the observations made during the great experimental advances of nineteenth-century chemistry and physics, that century still provided no direct empirical support that atoms really existed. But that would finally come early in the twentieth century.

Einstein is remembered for his special and general theories of relativity. But in the same year that he produced special relativity, 1905, Einstein also published two other papers that helped establish once and for all that all material phenomena can be described in terms of elementary particles.

One of these publications proposed that light is particulate in nature. I will forego that discussion until the next chapter. Here, let us take a look at his least-remembered work, which presented a calculation showing how measurements of Brownian motion could be used to determine Avogadro's number with much greater confidence than existed for earlier estimates and, thus, set the scale of atoms.

Recall from chapter 1 that Lucretius wrote how the dust motes seen in a sunbeam dance about “by means of blows unseen.” Now, these dust motes are moved about by air currents as well as by random motion. Such motions are difficult to quantify. However, in 1827, Scottish botanist Robert Brown (1773–1858) was examining under a microscope grains of pollen suspended in water. He noted that they moved about randomly and any water-current effects were negligible. This is called Brownian motion. Earlier, in 1785, Dutch biologist Jan Ingenhousz (1730–1799) observed the same random motion for coal dust particles in alcohol.

As suggested by Lucretius, the Brownian particles, which are large enough to be seen with a microscope, are bombarded randomly by the unseen molecules of the fluid within which they are suspended. A nice animation of the effect is available on the Internet.32

Einstein argued that the more massive the bombarding atoms in the fluid, the greater would be the fluctuation in the pollen particle's motion. Thus, a measure of that fluctuation can be used to determine the mass of the atoms and thus Avogadro's number.³³

Shortly after Einstein's publication, French physicist Jean Baptiste Perrin carried out experiments on Brownian motion, using Einstein's calculation to determine Avogadro's number. Perrin applied other techniques as well and was very much involved in ultimately achieving a final consensus, among chemists as well as physicists, on the discrete nature of matter and the small size of atoms. Earlier, in 1895, he had shown that cathode rays were particles with negative electrical charge that were identified two years later by J. J. Thomson as “corpuscles.” Thomson estimated the mass of the corpuscle to be a thousand times lighter than an atom. In 1894, George Stoney named the corpuscles electrons. Today we still regard the electron as a point-like elementary particle.

By the 1920s, the nineteenth-century antiatomists had died off along with their antiatomism. Ostwald finally had been won over by the data and, in 1908, had stated his belief in atoms in a new introduction to his standard chemistry textbook, Outline of General Chemistry.

Mach continued to drag his feet, however, writing against atomism as late as 1915, losing the respect of people like Planck and Einstein who had previously held him in high regard. Einstein had (temporarily) adopted a positivist view in defining time as what one reads on a clock, which should have pleased Mach. Mach did not like relativity, however. It was too theoretical. He died in 1916 at the age of seventy-eight.³⁴