
What, then, is light according to the electromagnetic theory? It consists of alternate and opposite rapidly recurring transverse magnetic disturbances, accompanied with electric displacements, the direction of the electric displacement being at the right angles to the magnetic disturbance, and both at right angles to the direction of the ray.
—James Clerk Maxwell1
THE NATURE OF LIGHT
Most believing scientists today have no difficulty accepting the notion that matter is composed of particles. They just object to the notion that particles are all there is. Before addressing that issue, however, we need to spend a few chapters tracing the developments that led to our current comprehension of the nature of matter. By the time we are finished, we will see how little room there is left for anything else.
Until the early twentieth century, it was generally assumed that matter and light were two separate aspects of physical reality. Light always carried with it a hint of the occult or spiritual. Even today, people often think of it as “pure energy,” not appreciating the meaning of E = mc2, that mass and rest energy are equivalent. Light is just as much material as a rock.
To talk about light, we must begin with the sense of vision. The ancients held two opposing views on vision. In one, called extramission, associated with Euclid (ca. 300 BCE) and Claudius Ptolemy (ca. 168 CE), rays of light are emitted by the eye onto an object, where they are then reflected back, as in modern radar, providing information about the object. In the second view, called intromission, held by both Aristotle and the atomists, objects themselves emit light that was then detected by the eye. The Arabic astronomer Ibn al-Haytham (ca. 1040), also known as Alhacen, argued convincingly against extramission by pointing out that bright objects can injure the eye, which would not happen if the source of light were the eye itself. He also noted that we are able to see objects at great distances, such as stars in the heavens, so it is unlikely that light from our eyes reaches out throughout the universe.2
It was not until the sixteenth century, however, that serious physical models for the nature of light were developed. Pierre Gassendi proposed a particle theory of light that was published in the 1660s after his death. Newton followed in 1675 with his corpuscular theory of light. This conflicted with the picture of light as a wave phenomenon proposed by Robert Hooke in the 1660s and by Christiaan Huygens in 1678.
In the 1660s, Newton had done a series of experiments with prisms that demonstrated a previously unrecognized fact that white light can be broken down into the colors of a rainbow. However, he kept that knowledge secret until 1672, when he was cajoled into sending a lengthy letter to the Royal Society on what became known as the “theory of light and colours.”3
There he ran into conflict with the man who would become his bitterest enemy over the years, Robert Hooke. Hooke was a very talented instrumentalist and original thinker, but he was nowhere near Newton in intellectual capacity. Each had high opinions of his own superiority, and they clashed incessantly until Hooke's death.
Hooke was the curator of experiments for the Royal Society when Newton submitted his paper and so was assigned the task of analyzing it. He gave it only a cursory look and was unconvinced. He had his own theory of light and wasn't about to let Newton displace it. He wrote:
For all the experiments & observations I have hitherto made, nay and even those very experiments which he alleged, do seem to me to prove that light is nothing but a pulse or motion propagated through an homogeneous, uniform and transparent medium.4
That is, light is a wave and Newton had proposed in the letter that light is a particle.
At first Newton ignored Hooke's claims, but he could not ignore the reaction of the Dutch physicist and astronomer Christiaan Huygens (1629–1695). Newton had far greater respect for Huygens, as did most of the scientific community, than he did for Hooke. At first, Huygens had expressed admiration for Newton's theory. But then, in a series of letters to the Royal Society in 1672 and 1673, Huygens objected that Newton's theory of colors was no theory at all but a hypothesis.5
Author Michael White makes an interesting observation:
To the modern mind, it seems odd that this same attack should be made without any form of experimental back-up from either dissenter. Huygens, like Hooke, could not accept what was then a completely novel approach—that a hypothesis is tested by experiment and dismissed only if the experiment shows that it is wrong. By 1673, Huygens had not conducted a single experiment in an attempt to prove or disprove Newton's theory. Instead he based his response on a priori reasoning alone.6
The empirical method has a long history. It had been championed by Francis Bacon and implemented by Galileo. However, it was not until Newton that the remnants of Aristotelian thinking were finally buried and experiment was given precedence over theory.
All this led to further vitriolic attacks back and forth between Newton and Hooke. The famous Newtonian line, “If I have seen further it is by standing on ye shoulders of giants” appeared in a 1676 personal letter from Newton to Hooke.7 Instead of being a grand gesture of humility, as it is usually regarded, White interprets this as a vicious slap at Hooke, who was “so stooped and physically deformed that he had the appearance of a dwarf.”8
If you eliminate the personal animosity between Newton and Hooke, and the lack of a full appreciation by Huygens and others at the time of the distinction between theoretical hypotheses and experimental facts, the dispute comes down to one over rival theories on the nature of light. Hooke and Huygens, for good reasons, promoted the wave theory while Newton, also for good reasons, promoted the corpuscular theory. In 1672, Newton clarified his position in a paper read before the Royal Society, with Hooke in attendance. Newton admitted that he had argued for the corpuscular nature of light but said, “I do it without any absolute positiveness, as the word perhaps intimates, & make it at most but a very plausible consequence of the doctrine, and not a fundamental supposition.”9
So let us get back to the physics. The wave theory implied that light should exhibit a phenomenon observed for water and sound waves, namely, diffraction, the ability to turn corners. Newton objected to the wave theory of light, claiming it did not diffract. We can hear—but we can't see—around corners. Here the great physicist known for his experimental as well as theoretical brilliance failed to empirically test his belief. The diffraction of light is easily observed by holding a card with a small pinhole in it up to a lamp (don't use the sun). Instead of a sharp outline of the hole, you will see a diffuse spot of light. That's diffraction. We can see around corners—just not very far.
Hooke had done nothing to empirically test the wave theory. However, Huygens was eventually able to demonstrate how diffraction and other optical effects such as refraction and interference are wave phenomena. He proposed that each point on a wave front acts as the source of a spherical “wavelet.” These wavelets then combine to give the next wave front.
So, I would say that at the time of Newton and Huygens, the empirical evidence for the wave theory of light was already solid, while the corpuscular theory had no way of accounting for the observed properties of diffraction and interference. Still, by virtue of his immense authority, Newton's corpuscular theory of light prevailed until 1800 when Thomas Young (1773–1829) performed experiments on light interference that finally won over the scientific community.
By the nineteenth century, then, the wave nature of light was confirmed. This would seem to discredit the basic tenet of atomism, that everything is just particles and void. But the story was not yet over.
Light waves had to be vibrations of some sort of medium, just as sound waves are vibrations of materials such as air, water, and even solids. In the case of light, the medium of vibration was termed the aether and was viewed as pervading all of space. All that was needed now was some sort of empirical confirmation of the existence of the aether.
THE AETHER
Two opposing views of the physical world mark the contrast between atomism and antiatomism. Atomism envisages a universe that divides up into material parts separated by empty space—atoms and the void. Antiatomism accepts that the universe has parts, but these move around more holistically in a continuous background medium, a plenum, that is either the aether or something more spiritual.
The aether has no voids. It is smooth and continuous. In Greek mythology, aether was the air breathed by the gods. Aristotle considered it to be the fifth element, after air, fire, water, and earth. He called it the quintessence and proposed that it was responsible for the motion of celestial bodies. In short, Aristotle's aether is not just another part of the universe; it is the central, governing part that unites everything into one harmonious whole.
Until the twentieth century, the atomists were the only natural philosophers who did not take it for granted that bodies in the universe swim about in an all-encompassing, continuous aether. For example, Descartes held that the planets were maintained in their orbits by swirling vortices in the aether.
In the 1680s, Newton rejected Descartes's vortex gravity in favor of a more mysterious action-at-a-distance force that he visualized in terms of the alchemic notion of an “active spirit.” Alchemists did not distinguish matter from spirit and imagined God as guiding the process by which matter could be mutated from one form to another. Newton took gravity to be a similar action of the spirit of nature.10
So, quite ironically, Newton adopted the materialistic model of atoms and the void, doing away with the need for a continuous aether. But in order to explain gravity, he invoked the existence of another reality, one that was immaterial.
On the other hand, the wave theory of light was fully materialistic. It did not need any active spirit. But if light was an undulation, some medium had to be doing the undulating, and this was naturally taken to be the aether.
Newton had raised another objection to the aether model, pointing out that the planets would be slowed down and eventually brought to a halt by friction. So the ad hoc assumption had to be made that the aether, if it exists, must be frictionless.
In the nineteenth century, Michael Faraday (1791–1867) performed a host of intricate experiments demonstrating the properties of electricity and magnetism. These experiments led to important applications such as electric motors and generators and ultimately to a full understanding of these phenomena. One simple experiment of Faraday's is still widely used in elementary-school science demonstrations. Faraday sprinkled iron filings onto a sheet of paper held over variously shaped magnets, showing the “lines of force” that we associate with magnetic fields (see fig. 6.1). Faraday noted that gravity and electricity could be also visualized as acting by way of lines of force.

Faraday proposed that the action-at-a-distance force that seems to occur when a body interacts by way of gravity, electricity, or magnetism actually takes place through intervening matter. However, it is important to note that Faraday did not view this intervening matter as a necessarily continuous fluid, as the aether is usually interpreted to be. He wrote:
It appears to me possible, therefore, even probable, that magnetic action may be communicated by the action of intervening particles [emphasis added], in a manner having a relation to the way in which the inductive forces of static electricity are transferred to a distance (by transferring its action from one contiguous particle to the next).11
Faraday did associate the intervening matter with the aether (ether):
Such an action may be a function of the ether; for it is not at all unlikely that, if there be an ether, it should have other uses than simply the conveyance of radiations.12
However, keep in mind that rather than a continuous fluid with no voids between them, as the Aristotelians claimed, Faraday's aether is actually composed of discrete particles, like the pebbles of sand on a beach.
FIELDS
Faraday and other nineteenth-century physicists applied a mathematical concept called a field to physical phenomena such as gravity, electricity, and magnetism. In physics, a field is a quantity that has a value, or set of values, for each point in space. Time can also be included, but let's put that off and just think of a field at a given time. The simplest field is a scalar field that has only one value at each spatial point. Examples of scalar fields are the pressure and density of a fluid, each of which require just one number to define it at each point.
The Newtonian gravitational field along with the classical electric and magnetic fields are examples of vector fields that have both a magnitude and a direction at each point in space. Since it takes two numbers to define a direction in three-dimensional space, a vector field requires three numbers to specify. In Einstein's general theory of relativity, the gravitational field is actually a tensor that needs sixteen numbers (not all independent) to define. But we need not get into that at this time.
Let's start with the Newtonian gravitational field at a point in space a distance r from a particle of mass m. By Newton's law of gravity, the field will have a magnitude that is directly proportional to m and inversely proportional to the square of r. The direction of the field will be along the line from the spatial point to the mass.
Now, we can see how to map out the field around the sphere. We just put a test particle at various points and watch the direction in which the particle accelerates. We can then sketch “lines of force” following these paths, as shown in figure 6.2. Note that we never actually see the field. All we see is the test particle accelerating through space.
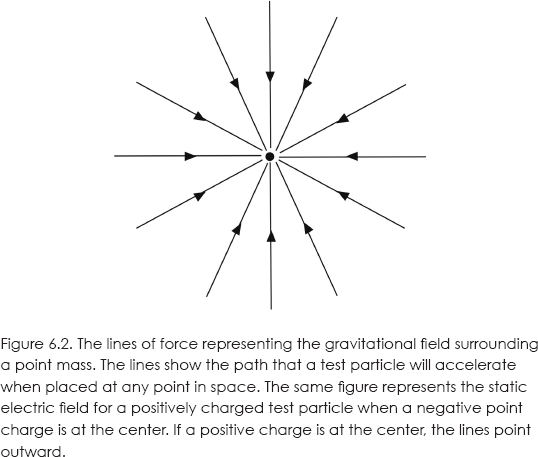
The same procedure can be used to map the electric field surrounding a point particle of electric charge q. Suppose q is negative. If we use a positively charged test particle, the field lines will again point from the test particle to q, as in figure 6.2. Here the magnitude of the field, given by Coulomb's law, is proportional to q and, as with the law of gravity, inversely proportional to the square of the distance r.
If the central charge is positive, the field lines will point outward. In either case, the field points in the direction in which a positive test particle accelerates.
Suppose instead of a single point charge we have two opposite charges. This is called a dipole. A single point charge is an electric monopole. We can use the same procedure of putting a test charge at various points. In this way, we map out the field shown in figure 6.3.

The magnetic field is more difficult to define. The source of a magnetic field is an electric current—a moving electric charge. The magnetism of materials such as iron results from moving charges inside the material. However, Faraday showed how to map out the magnetic field. Magnetic filings are little bar magnets with North and South poles. A compass needle is a bar magnet. So you map a magnetic field by placing a small compass at various points and seeing the direction in which the needle points, as we see in figure 6.4. Note that because opposite magnetic poles attract, a compass needle will actually point to the South Pole of another magnet. That is, what we call the North Magnetic Pole of Earth is technically (at least in physics) the South Magnetic Pole!
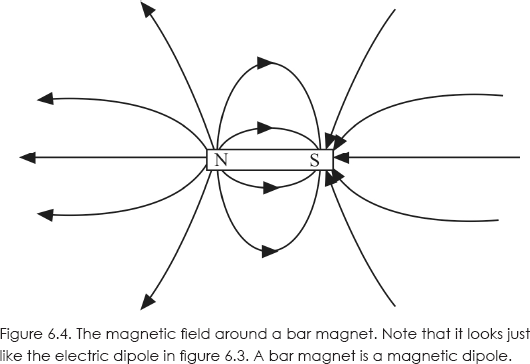
We see that the magnetic field of a bar magnet looks just like that of the electric dipole in figure 6.3. That is, a bar magnet is a magnetic dipole. Then what happened to the magnetic monopole? No magnetic monopoles have ever been observed. If you have an electric dipole, such as a hydrogen atom, then you can pull the two charges apart and get two electric monopoles. However, if you cut a bar magnet in half, you get two bar magnets.
Modern particle theories predicted the existence of magnetic monopoles in the early universe. However, searches for them in the present have turned out negative. In chapter 12, we will see how this absence is now plausibly explained by inflationary cosmology.
The fields we have discussed—pressure, density, gravitational, electric, and magnetic—are each continuous in the assumed mathematical formalism. They are also regarded as functions of three coordinates needed to define a point in space—x, y, and z in the familiar Cartesian coordinate system. These coordinates are also assumed to be continuous variables, even in the most advanced physics discussions. Later, quantum mechanics would challenge that assumption. But for now, let us note that even when space is continuous, the fields need not be.
Take the field defined by the density of a fluid such as the air in a room. We now know that air is composed of particulate bodies, molecules of nitrogen, oxygen, and other ingredients such as carbon dioxide (more now than there used to be). So when we speak of the density of air at a certain point, we are averaging over the molecules in a small region around that point. This works well on the macroscopic scale because even if we average over a square micron (one-millionth of a meter), the number of molecules in that region will be almost a billion.
Similarly, the vector fields describing gravity, electricity, and magnetism can be well approximated by continuous fields, at least in everyday experience and in nineteenth-century laboratories.
ELECTROMAGNETIC WAVES
In 1865, James Clerk Maxwell proposed a set of equations that enabled the calculation of electric and magnetic fields for any arrangement of charges and currents. Maxwell's equations had a solution in a region absent of charges and currents that corresponded mathematically to that of a wave. Furthermore, the electromagnetic wave traveled precisely at the speed of light in a vacuum, which was a number that was not inserted independently into the theory but came out as a result.
Light was thus interpreted as an electromagnetic wave. Since no limits were placed on the wavelength of such a wave, the existence of waves of both lower and higher wavelengths than the visible spectrum was implied. In 1887, German physicist Heinrich Hertz (1857–1894) produced radio transmissions in the laboratory that traveled at the speed of light. Interpreted as waves, they had a wavelength of 8 meters, compared to that of visible light, which ranges from 400 to 700 nanometers, where a nanometer is one-billionth (10–9) of a meter. Wavelengths in the electromagnetic spectrum range from one-hundredth of a nanometer and lower for gamma rays to a meter and above for radio waves. I have worked with telescopes that have detected gamma rays from space with apparent wavelengths on the order of one-billionth of a nanometer (10–18 meter). At the other end of the scale, observers at radio telescopes have detected radio signals that are interpreted as electromagnetic waves with wavelengths of many kilometers.
While the successful prediction of electromagnetic waves might be seen as the final confirmation of the existence of the aether, Maxwell claimed it as only a model. Unlike the theory of sound in which the mechanical vibration of a continuous medium is assumed as a starting point, no such assumption is made in Maxwell's theory. In fact, electromagnetic waves just fell out of the mathematics once he had placed the various independent principles of electricity and magnetism that had previously been discovered, such as Ampere's law, Gauss's law, and Faraday's law, into a single set of equations.
THE DEMISE OF THE AETHER
As I have already indicated, whether the aether exists is a major determining factor in the conflict between atomism and antiatomism. In one form or another, this issue has surfaced historically and, as we will see, still rises up on occasion even today.
For now, however, let us focus on the electromagnetic aether, the medium in which the electric and magnetic fields each are presumed to exist as some kind of tension analogous to that in the stretched skin of a drum. Electromagnetic waves, then, are viewed as analogous to the sound waves that would be set up when the drum is struck with a hammer.
If electromagnetic waves were analogous to sound waves, then the speed of light should vary depending on the relative motions of the source and observer through the aether. At the dawn of the twentieth century, two American physicists, Albert Michelson (1853–1931) and Edward Morley (1838–1923), attempted to detect the motion of Earth through the aether by comparing the speeds of light in two perpendicular beams. These speeds should have differed if light were a vibrating wave in the aether because the beams would be heading in different directions through the aether. Although Michelson and Morley were capable of measuring a speed difference of one-hundredth of that expected, they found no difference.
Now, it is important to note that while the Michelson and Morley result seemed to violate Galileo's principle of relativity, they in fact agreed with Maxwell's theory. Maxwell's equations do not say that the speed of light is c + v when a source is moving toward you with a speed v, and c – v when the source is moving away at that speed, as expected from our experience with sound waves (the Doppler effect). Maxwell's equations say that the speed of light in a vacuum is always c = 299,792,458 meters per second in any and all reference frames. (As we see below, this number is the speed of light by definition.) Michelson and Morley confirmed that this is indeed a fact. Evidently, electromagnetic waves travel in the atomist's void—a region completely empty of matter or substance of any kind.
But how can the speed of light be absolute? Doesn't the principle of relativity say that all velocities, and thus speeds, are relative? In 1905, Einstein had the flash of insight to ask what the consequences would be if both Galileo and Maxwell were correct; that is, the principle of relativity is valid, and the speed of light in a vacuum is absolute. The result was the special theory of relativity.
Recall the way I worded the principle of Galilean relativity. It does not say all velocities are relative. It says that you cannot distinguish between being at rest and being in motion at constant velocity. Special relativity maintains that principle, but bodies moving near or at the speed of light behave very differently from those of everyday experience. The equations that describe “relativistic” motion are significantly modified from those of “nonrelativistic” Newtonian mechanics. That is not so say the latter are wrong. The relativistic equations all reduce to the nonrelativistic ones in the limit of speeds very much less than the speed of light.
In any case, the electromagnetic aether failed to be confirmed empirically, and it was shown to be not only unnecessary for understanding the phenomena of light and other electromagnetic waves but also inconsistent with both data and theory. Nevertheless, despite the failure to find evidence for the aether, the electromagnetic wave theory successfully described most of the observed behavior of light prior to the twentieth century. However, there were a few exceptions that, as we will see in the next chapter, led to quantum mechanics and a drastic revision of Newtonian mechanics.
TIME AND SPACE IN SPECIAL RELATIVITY
Einstein resolved the apparent contradiction between Galileo's principle of relativity and Maxwell's equations for electromagnetism by assuming they both were correct. In particular, the speed of light in a vacuum, c, is the same in all reference frames. But then, something had to go, and that was our commonsense notions of space, time, and matter.
Let us consider a clock in which a light pulse is sent back and forth between two mirrors, as shown in figure 6.5 (a). Each time the pulse hits either mirror, we get one tick in the clock. Suppose the mirrors are 3 meters apart. Since c = 0.3 meter per nanosecond (1 nanosecond = one-billionth of a second), it then takes 10 nanoseconds to go between mirrors. Thus, each tick will occur 10 nanoseconds apart to an observer in a reference frame in which the clock is at rest. Let's take her reference frame to be that of Earth.
Now suppose that the clock is moving with a speed of 0.6 c with respect to the same observer on Earth. She will see the light pulse still moving at a speed c, but now it has to travel along a longer, diagonal path, and so takes longer to go between the mirrors. Applying the Pythagorean theorem to figure 6.5 (b), it can be shown that the observer will hear the ticks on the moving clock every 12.5 nanoseconds. In that time, the clock has moved (0.6 c)(12.5) = 7.5 nanoseconds.
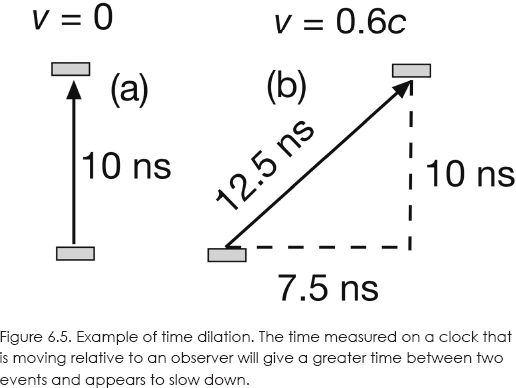
In other words, the time between two events separated in space depends on the reference frame of the observer. Time intervals are relative. In the above example, a clock that is moving with respect to an observer will measure a longer time between two events in that observer's reference frame. That is, it will appear to run slower. Its ticks will be farther apart than the clock at rest. This is called time dilation.
Since time intervals are relative, so must be space intervals. In the above example, the original observer on Earth measures the distance traveled by the clock in the time the pulse goes from one mirror to another to be its speed 0.6 c times 12.5 nanoseconds, which is 2.25 meters. However, to an observer in the clock's reference frame, the elapsed time is still 10 nanoseconds, since the clock is at rest in that reference frame. To him, Earth has traveled (0.6 c)(10) = 1.8 meters.
In other words, an observer in one reference frame will see distances measured in a reference frame moving with respect to it contract in the direction of motion. Another way to look at it is to let a meter stick be attached to the ground. To the observer in the reference frame of the clock, the meter stick is moving at 0.6 c. It will appear shortened to (1.8/2.25)(1) = 0.8 meter. This is called Fitzgerald-Lorentz contraction.
Now, these phenomena are often mistakenly described as “a moving clock slows down,” and “a moving object contracts,” as if a moving clock physically slows down, or a moving object really contracts. But remember, motion is relative. Einstein maintained Galilean relativity, which says that all reference frames moving at constant velocity with respect to one another are equivalent. If an earthling sees a clock in a spaceship slow down, an observer in the spaceship will see no change in her clock. In fact, she will see the earthling's clock slow down.
When Einstein first presented this result, people thought it was paradoxical. How could both clocks run slower? This is called the clock paradox or, also, the twin paradox. If an astronaut goes off on a trip, she will be younger when she returns than her twin left back on Earth.
Einstein pointed out that the two observers can't compare their clocks without one turning around and coming back, that is, accelerating. Then the two frames are no longer equivalent.
In figure 6.6, I show how the clock paradox is resolved quantitatively. We have three clocks, one on Earth and one each on two spaceships, A and B. The vertical axis shows time measured on the Earth clock in years. The horizontal axis shows distances measured on Earth in light-years. (One light-year is the distance traveled by light in a vacuum in one year.)
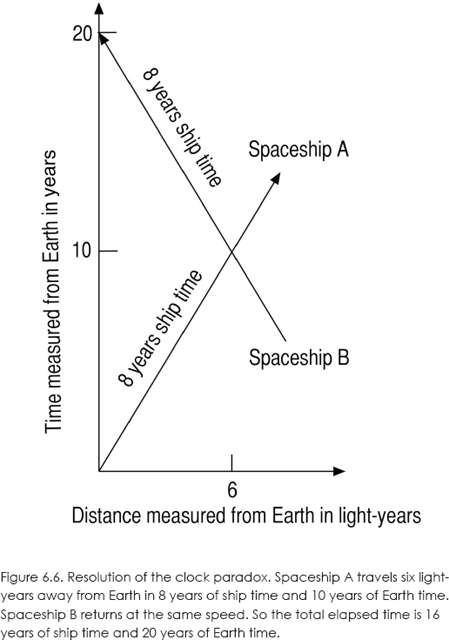
At time zero, Spaceship A moving at 0.6 c passes close to Earth. Its clock is synchronized with one on Earth. After 10 years, as measured on Earth, Spaceship A has traveled six light-years from Earth. However, the elapsed time measured on Spaceship A's clock is only 8 years.
At that instant, Spaceship B, heading toward Earth at the same speed of 0.6 c, passes close to Spaceship A and the clocks on the two ships are synchronized. Spaceship B reaches Earth 8 years later as measured on its clock, and so the total trip time for A's trip out and B's trip back is 16 years of ship time. However, 20 years have elapsed on Earth.
The difference is no more paradoxical than noting that a crooked path between two points has a different length than a straight path; except in time units, the straight path is the longest between two events.
DEFINING TIME AND SPACE
Notice that in all this discussion we never talk about what space and time “really” are. Most people will certainly assume they are aspects of reality, but we have only considered what is measured with clocks and meter sticks. That is, we have avoided getting into any metaphysical issues by just dealing with what we measure with our measuring devices. As we saw in chapter 2, Einstein said time is what you measure with a clock (although he may have changed his mind later). By international agreement, the basic unit of time is the second, which in 1967 was defined as 9,192,631,770 periods of the radiation corresponding to the transition between the two specific energy levels of the Cesium-133 atom.
Until 1983, the meter was defined separately from the second. By then, however, the special theory of relativity was so well established empirically that it was agreed to treat space and time on the same footing. So the meter was redefined as the distance between two points when the time it takes light to go between the points in a vacuum is 1/299,792,458 second. In other words, distance is no longer defined as what you measure with a meter stick. Like time, it is defined by a measurement on a clock.
Many people, including many scientists, still think the speed of light in a vacuum is something you must measure to obtain its value. Well, it is not. It is an arbitrary number that simply depends on what units you would like to use for length. In the metric system, the speed of light in a vacuum is c = 299,792,458 meters per second by definition. In the English system, c = 983,571,056 feet per second by definition.
Oh, you can go ahead and measure the speed of light in a vacuum if you want, with a meter stick and a clock. But you will have to get 299,792,458 meters per second because whatever device you use to measure distance will be calibrated to give 299,792,458 meters when whatever device you use to measure time measures exactly one second to the same precision.
If you are an astronomer, you might prefer to measure distance in light-years and then the speed of light in a vacuum is, by definition, one light-year per year. (Actually, many astronomers still use an antiquated unit called the parsec, which is 3.26 light-years.) Particle physicists also like to work in units where c = 1, which gets rid of a lot of useless c's in their equations.
By defining both distance and time in terms of measurements made with a clock, space and time were placed on the same footing. Time is now treated as another dimension added to the three dimensions of space. Rather than call it the fourth dimension, we count from zero so that time is the “zeroth” dimension. So we can think of the position of an event occurring at coordinates x, y, and z in three-dimensional space and at time t in the zeroth dimension of time, combined as a 4-vector (t, x, y, z).
MATTER AND ENERGY IN SPECIAL RELATIVITY
Einstein showed that the relativity of time and distance requires substantial changes in the way we describe matter and motion. I will not attempt to prove the equations that replace those from nonrelativistic physics (v << c), but will just give the results. The three quantities that define the properties of a material body and its motion are mass, energy, and momentum. Mass is the measure of a body's inertia, that is, its sluggishness or resistance to changes in its motion. The more massive a body is, the greater the force that must be applied to accelerate it to a higher speed or decelerate to a lower speed. When a body is moving, its internal clocks, such as atomic motions, will be observed to slow down. Thus, such a body will appear to be more sluggish and thus more massive. That is, a moving body will have a greater measured mass than one at rest, as measured in the reference frame in which it is moving.
Einstein associated the mass of a body at rest with a certain quantity called rest energy, that is, E0 = mc2, which popular writers always refer to as “Einstein's famous equation.”13 Now, we saw that c is just an arbitrary constant, so let us simply take c = 1. Then the mass of a body, m, is the same as its rest energy.
So a body at rest has an energy m. When it is moving, the body has an additional energy K we call the kinetic energy. Then the total energy of a free body, that is, one without any forces acting on it, is E = m + K.
The quantity of motion that was used by Newton in his laws of motion is the momentum p (just the magnitude is needed here). The three quantities of matter and motion are related by m2 = E2 – p2. That is, only two are independent variables. The mass m is invariant, that is, it is the same in all reference frames. E and p depend on frame of reference. (Recall discussion of frames of reference in chapter 3.) However, in any given frame, both are conserved in the absence of any external forces, as they are in Newtonian physics.
Let the 3-momentum of a particle be defined as (px, py, pz), where px is the component of the momentum projected on the x-axis, and so on. Just as in the previous section, where we defined the 4-vector position of an event in space-time, we can define the 4-momentum of a particle as (E, px, py, pz), where E is the particle's energy. That is, like time and space, energy and momentum are on the same footing. Matter is then defined as anything with a 4-momentum.
In the following chapters on atomic, nuclear, and particle physics, I will use units in which c = 1. In that case, mass, energy, and momentum all have the same units. The basic unit will be the electron volt (eV) and multiples of it (keV, MeV, GeV, TeV). This is a unit defined as the kinetic energy an electron gains when it falls through an electric potential of 1 volt. The energies involved in atomic physics and condensed matter physics and chemistry are typically in the eV and keV range. Nuclear energies are typically in the MeV range (1 MeV = 106 eV). Particle-physics energies are usually measured in GeV (1 GeV = 109 eV) or, more recently, TeV (1 TeV = 1012 eV). In these “energy units,” the mass of an electron is 0.511 MeV and the proton is 938 MeV.
INVARIANCE
When a quantity has the same value in all reference frames, it is said to be invariant. In this chapter, we have seen that the speed of light in a vacuum and the mass of a body are invariant. On the other hand, space and time intervals, energy, and momentum are not invariants.
In physics, we express our mathematical models in terms of measurable quantities, such as distance, time, energy, and momentum. If we want those models to be objective and universal, they should not change from reference frame to reference frame. That is, we would like our models and theories to be invariant.
Consider a simple example. In a given reference frame, the distance x a photon will travel in a vacuum in a time t will be x = ct. In another reference frame moving at a constant speed with respect to the first, the distance x′ a photon will travel in a vacuum in a time t′ will be x′ = ct′. Notice that the distance and times are different, which is why I put primes on their symbols. But since this is a photon in a vacuum, its speed is the same in each reference frame, that is, c with no prime. Thus, we can write x – ct = x′ – ct′ = 0. That is, the equation x – ct = 0 is an invariant model describing photon motion in all reference frames. The notion of invariance played a key role in the development of twentieth-century physics.
SYMMETRY
Let us do a flashback at this point and discuss the ever-increasing recognition that symmetry principles are the foundation of physics. Recall that symmetry and invariance are related concepts. When an object looks the same from all angles, we say it is rotationally invariant and possesses spherical symmetry. When it looks the same in a mirror, we say it is reflection invariant and possesses mirror symmetry.
Similar statements can be made about the mathematical models of physics. Consider a model that describes observations in terms of space and time. (Most do, but not all). The spatial positions of particles, for example, might be described by a set of Cartesian coordinates (x, y, z) at various times t. If the equations in the model do not change when you move the origin of the coordinate system from one place to another, then the model is space-translation invariant and possesses space-translation symmetry. If the equations in the model do not change when you rotate the axes of the coordinate system, then the model is space-rotation invariant and possesses space-rotation symmetry. If the equations in the model do not change when you change the time you start your clock, then the model is time-translation invariant and possesses time-translation symmetry.
Recall the principle of Galilean relativity. We can regard that as a symmetry principle. It implies that our physics models must be the same in all reference frames—invariant—moving at constant velocity with respect to one another.
When we move from Galileo to Newton we find that Newton's laws of motion and gravity possess all the symmetries mentioned so far, including mirror symmetry. The laws of thermodynamics, which, as we have seen, follow from Newtonian mechanics, also possess these symmetries. The same holds for the laws of electrodynamics, which also are invariant to a change in the sign of electric charge—what is called charge-conjugation symmetry.
When we get to the twentieth century, we have special relativity in which Galilean invariance is replaced by Lorentz invariance, a different equation but the principle is the same. Einstein introduced the term general covariance to describe the principle in which physical models are invariant to arbitrary coordinate transformations of the type we have been discussing. In general relativity, he extended that to include accelerated reference frames.
THE SOURCE OF CONSERVATION PRINCIPLES
One of the most import contributions to twentieth-century physics was made by a German mathematician named Emmy Noether, who is only now getting the full recognition that she deserves.14 In 1915, Noether proved the following theorem.15
Noether's Theorem:
For every continuous symmetry of the laws of physics, there must exist a conservation law.
For every conservation law, there must exist a continuous symmetry.
This is not only a profound physics result; it is a profound philosophical one. It means that the most important of the so-called laws of physics are not what is commonly believed they are, that is, that they are rules built into the structure of the natural world that govern the behavior of matter. Rather, each is an automatic ingredient of any physical theory that possesses the associated symmetry.
Here are the quantities that are conserved with each specific symmetry:
| Time-translation symmetry | conservation of energy |
| Space-translation symmetry | conservation of linear momentum |
| Space-rotation symmetry | conservation of angular momentum |
For example, if a physicist builds a mathematical model that possesses time-translation symmetry, then that model will necessarily obey conservation of energy.
Noether's theorem can be looked at another way. If a physical system does not conserve one of these quantities, then that system will not possess the corresponding symmetry. For example, a body dropped from the top of a tower gains linear momentum at a fixed rate; that is, linear momentum is not conserved. A series of video frames taken at various intervals along its path to the ground would not be identical. The first frame might show the body at rest. Each succeeding frame will show the body moving faster than the frame before.
So the conservation principles will not necessarily hold for every physical system. However, over the centuries, they have been observed to hold for isolated systems, that is, those that do not interact in some way with other systems. If we consider Earth and the body dropped from the tower, then in that system, momentum is conserved.
When we consider the universe as a whole, then all known conservation principles seem to hold. We conclude from this that our universe comprises an isolated system and possesses the associated symmetries. This means there is no special moment in time (the universe could have appeared at any time), no special place in space (the universe can be anyplace), and it is rotationally symmetric (the universe looks the same from all directions) so no special direction in space is singled out.
Thus, the validity of the three great conservation laws of physics is testimony to a universe that is isolated from anything on the outside and looks just like it should look if it came from nothing.