CHAPTER 5
Order Entry and Processing
PTCE Knowledge Domain: Order Entry and Processing
21.25% of Exam
Knowledge Areas:
▪ Procedures to compound nonsterile products (e.g., ointments, mixtures, liquids, emulsions, suppositories, enemas)
▪ Formulas, calculations, ratios, proportions, alligations, conversions, sig codes (e.g., b.i.d., t.i.d., Roman numerals), abbreviations, medical terminology, and symbols for days supply, quantity, dose, concentration, dilutions
▪ Equipment/supplies required for drug administration (e.g., package size, unit dose, diabetic supplies, spacers, oral and injectable syringes)
▪ Lot numbers, expiration dates, and National Drug Code (NDC) numbers
▪ Procedures for identifying and returning dispensable, nondispensable, and expired medications and supplies (e.g., credit return, return to stock, reverse distribution)
After reading Chapter 5 you will be able to:
▪ Use sig codes, pharmacy abbreviations, and medical terminology to process prescriptions
▪ Use ratio-proportion and dimensional analysis to solve dosage calculations
▪ Convert between metric, household, and temperature systems
▪ Explain how to calculate days’ supply and concentrations and dilutions
▪ Demonstrate the steps of nonsterile compounding, including alligations and supplies needed
▪ Describe expiration dates, lot numbers, and NDC numbers
▪ Differentiate between credit returns, return to stock, and reverse distribution
Pharmacy technicians across many settings are an integral part of the order entry process. This includes both prescriptions in a retail setting and medication orders in the institutional setting. Pharmacy technicians accept new prescriptions and refills from patients, collect and maintain patient data and profiles, and may initiate calls to providers for refill authorizations. This chapter reviews procedures for prescription processing, including dosage calculations, nonsterile compounding, supplies needed for dispensing and administration medications, and the process for returning unused or expired drugs.
Pharmacy Calculations
To process prescriptions and medication orders efficiently, pharmacy technicians must have a good understanding of pharmacy calculations, abbreviations, and sig codes. This includes starting with basic math and applying it to pharmacy calculations.
Sig Codes
Abbreviations used on prescriptions and medication orders are known as sig codes. These codes are used by physicians and pharmacies to communicate prescription information such as dosing frequency and time, route of administration, and dosage form. Sig codes are not intended for patients to understand. It is the duty of the pharmacy to translate the code onto a label that can be understood by the patient.
The following is a guide to sig codes and their meaning. You should spend some time reviewing and practicing these codes to prepare for certification and reading prescriptions.
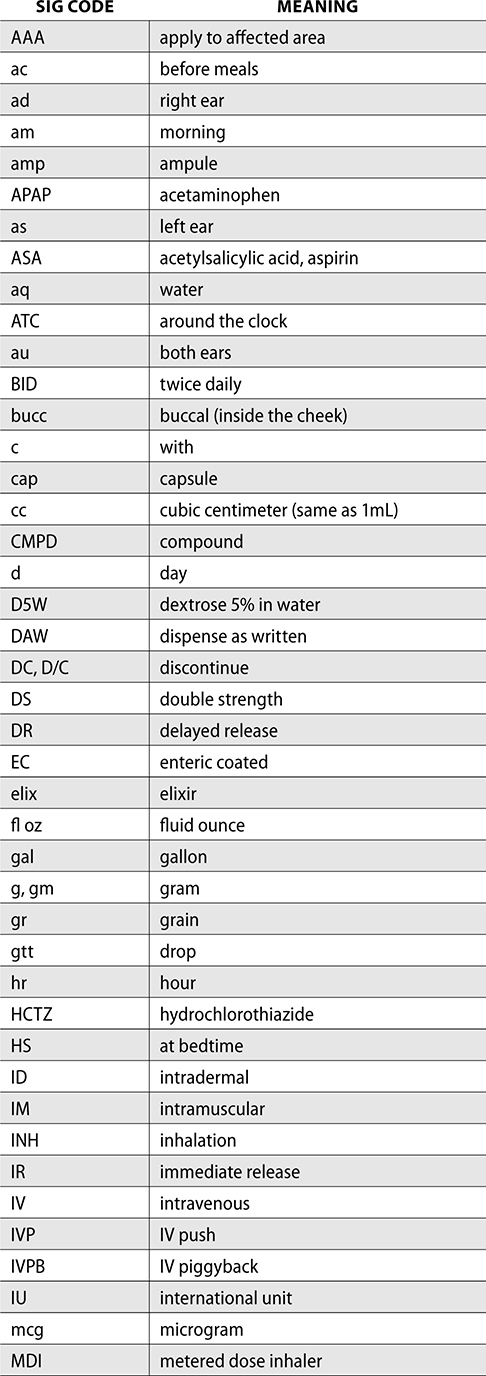
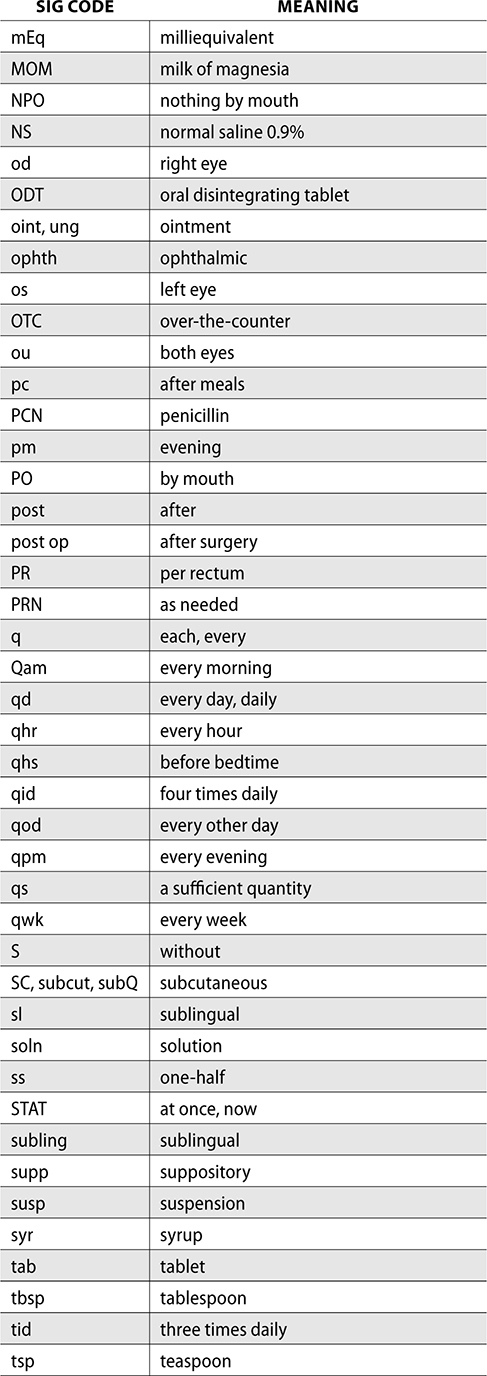
Many prescriptions are written with pharmacy sig codes for abbreviations and Roman numerals indicating quantity.
The following is a Roman numeral conversion up to 1,000.
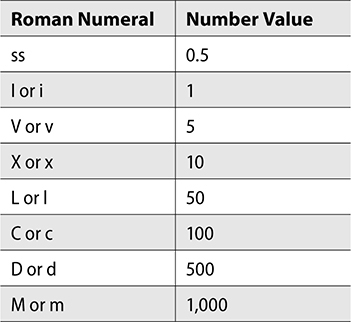
When reading Roman numerals, there are a few rules to remember to make sure you’re calculating the accurate value.
1. If the value of the Roman numeral decreases from left to right, the total is the sum of all the numerals. Example: XV = 10 + 5 = 15.
2. If a Roman numeral is repeated three times in a row, these three numbers are added. It cannot be repeated more than three times. Example: XXX = 30.
3. If a smaller Roman numeral is written to the left of a larger value, you should subtract the smaller value from the larger. Example: IV = 5 – 1 = 4.
Self-Test: Define the following:
1. II tab PO BID ×7d
2. III cap PO TID PRN
3. 5mL PO QID ×5d
Answers:
1. Take 2 tablets by mouth twice daily for 7 days.
II = 2
tab = tablet
PO = by mouth
BID = twice daily
×7d = for 7 days
2. Take 3 capsules by mouth three times daily as needed.
III = 3
cap = capsule
PO = by mouth
TID = three times daily
PRN = as needed
3. Take 5mL by mouth four times daily for 5 days.
PO = by mouth
QID = four times daily
×5d = for 5 days
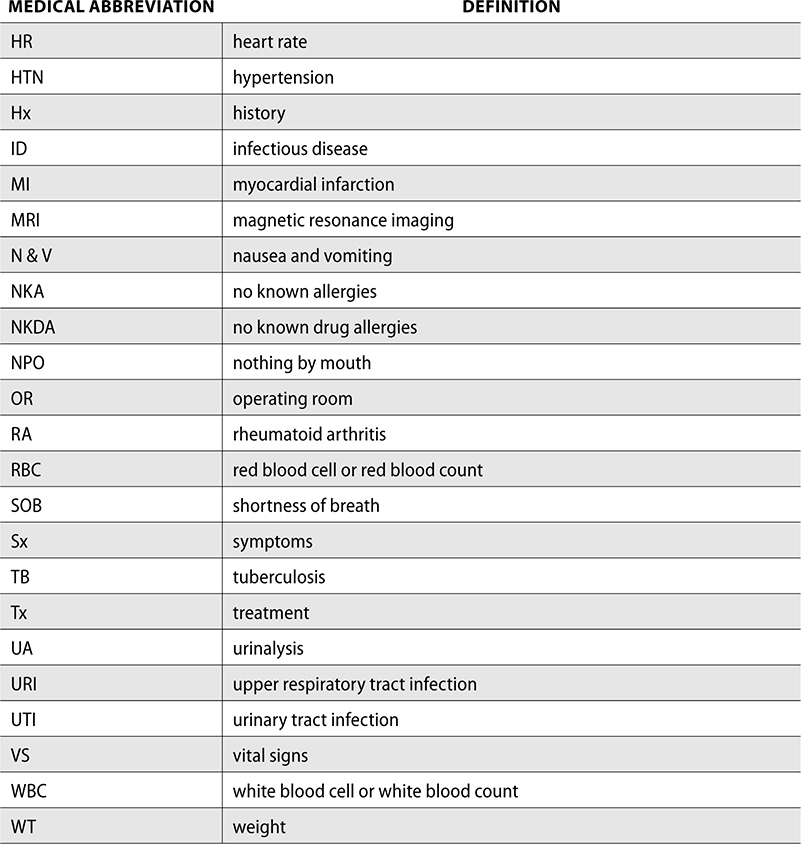
Medical Abbreviations
Medical abbreviations for diseases are also used frequently in pharmacy practice. The following is a list of medical conditions and the corresponding abbreviation. You should spend some time familiarizing yourself with these abbreviations as they may show up in patients’ charts or prescriptions when you are processing orders.
Medical Terminology
In addition to abbreviations, pharmacy technicians frequently encounter medical terms that are composed of a prefix, root word, and suffix. Having an understanding of these parts of a word can help you describe many illnesses, body processes, procedures, and even pharmacology.
Each of the following tables are frequently used prefixes, roots, and suffixes.
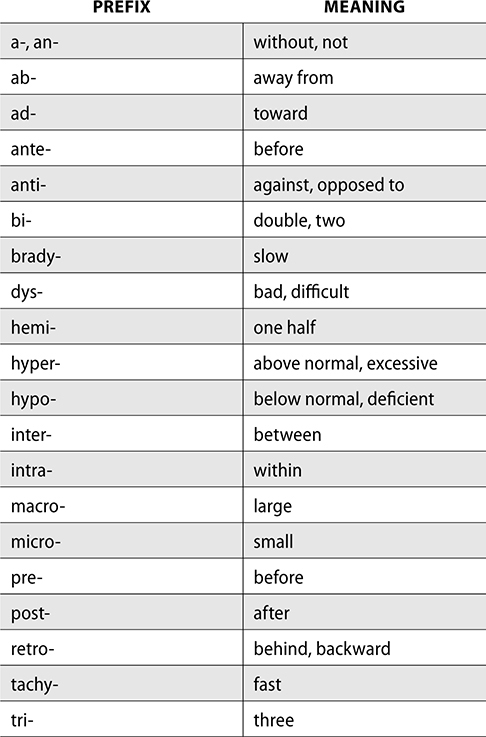
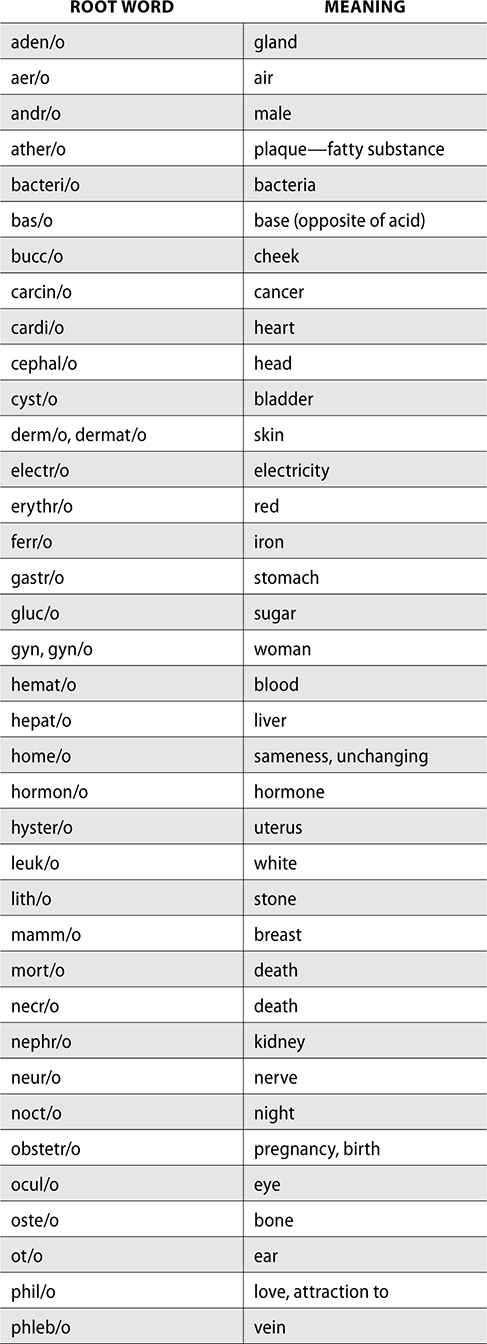
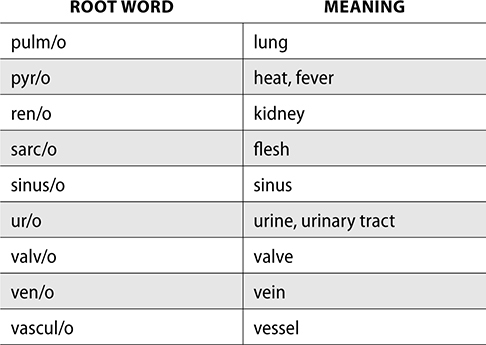
Medical terms can be used to build words or define them. For example, acetaminophen is an antipyrogenic medication. Define this word.
Anti—against
Pyr/o—fever, heat
Genic—to produce
So an antipyrogenic would be “against production of fever.”
Self-Test: Define or build words.
1. sinusitis
2. cardiopathy
3. nerve pain
Answers
1. inflammation of the sinus
sinus/o = sinus
-itis = inflammation
2. disease of the heart
cardi/o = heart
pathy = disease
3. neuroalgia
nerve = neur/o
pain—algia
Fractions, Decimals, and Percents
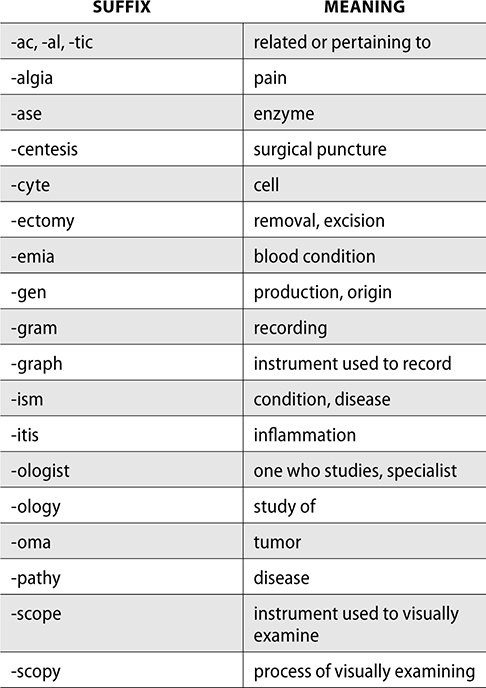
A fraction is a value that is not a whole number. The top of the fraction is the numerator, and the bottom is the denominator. If a patient is to take 1/4 of a tablet daily, 1 is the numerator and 4 is the denominator. Fractions can be converted into a decimal by dividing the numerator by the denominator.
Example: Convert 1/4 into a decimal.
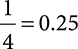
The dose could then be written as 1/4 tablet or 0.25 tablet.
A decimal is a fraction written with a denominator as a power of 10. For example 4/10 would be written as 0.4. Numbers written to the rig of the decimal point are below 1, whereas numbers on the left of the decimal point are greater than 1. So 0.4 is less than 1.4. As you move the decimal point to the right or the left one space, the value either decreases or increases by a factor of 10. This is indicated by the following chart.
To convert a decimal into a fraction, remove the decimal point from the number for the numerator, and for the denominator, count the number of places to the right of the decimal point. Decimals can be converted into fractions by the following steps:
Example: Convert 0.75 to a fraction.
1. Rewrite the decimal as the numerator over 1, with 1 being the denominator.
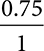
2. Multiply both the numerator and denominator by 10 for every digit after the decimal. For example, 0.75, there are 2 places after the decimal = 100.
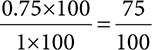
3. Reduce or simplify the fraction.
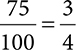
When completing pharmacy calculations, you often encounter decimals that need to be rounded appropriately for dosage calculations. Sometimes the tenth place is appropriate, but sometimes the hundredths or thousandths place is needed for accuracy. You should always consult the pharmacist if unsure which place to round. To round a decimal, look at the digit one space to the right on the desired place. If it is greater than 5, round the number up. If it is less than 5, the number remains the same.
Example: Round 8.426 to the hundredths place.
1. First, determine which is the hundredths place: 8.426
2. Look at the digit one space to the right of the hundredths. Is it greater than 5? 8.426
3. Because 6 is greater than 5, this number would be rounded up.
4. Round up the hundredths place for the answer: 8.43
Remember that you always want a leading zero, and never want a trailing zero!
Percents are also used frequently in pharmacy calculations. A percent is a part per 100. So 70% solution means there are 70 parts of active ingredient in 100 total parts. Percentages can be converted into and from fractions and decimals easily.
Example: 30% is the same as saying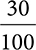 
as a fraction.
To convert into a decimal, you can either divide the percent by 100 or move the decimal point over two spaces to the left.
Dividing by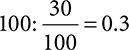 
To get a percent from a fraction or decimal, you can multiply the decimal by 100.
Example: If a patient needs to take 0.5 tablet, what percent of a tablet is this?
0.5 × 100 = 50%
If you are starting with a fraction, convert into a decimal first, and then follow the previous steps to convert into a percent.
Example: A patient is taking ½ tab. What percent of a tablet is this?
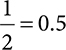
Now use the decimal to convert into a percent by multiplying by 100.
0.5 × 100 = 50%
Conversion between fractions, decimals and percentages is an important skill to have as a baseline before moving on to dosage calculations. Test yourself with a few practice conversions to make sure you’re ready for ratios and proportions.
Self-Test: Round to the nearest tenth place
1. Convert 1/3 into a decimal.
2. Convert 0.85 into a percentage.
3. Convert 68% into a fraction.
4. Convert 2/3 into a percentage.
5. Convert 0.25 into a fraction.
6. Convert 90% into a decimal.
Answers:
1. 0.3
2. 85%
3. 17/25
4. 66.7%
5. 1/4
6. 0.9
Ratios and Proportions
A ratio is a relationship between two quantities that can be used to solve dosage calculations in pharmacy practice. A ratio indicates how many times one number contains another. For example, if a medication is 20mg/mL, this means each mL contains 20mg. Mg/mL is a common ratio in both retail and inpatient pharmacies. Two equal ratios are known as a proportion, and this is helpful when determining an unknown quantity if three other values are known.
To solve a ratio-proportion calculation, write out the ratios with like units on the top and bottom. Then solve for the unknown.
Example: Using the previous example, calculate how many mL would be needed for a dose of 46mg if a medication is available as 20mg/1mL.
1. Start with setting up your two ratios, using x mL for the answer you’re solving for. Keep mL together on one level and mg together on the other.
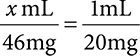
2. Once the proportion is set up, solve for x. Complete this through cross multiplying first.
(1)(46) = (x)(20)
3. Next, solve for x, by dividing both sides to get x by itself. In this equation, that would be 20.
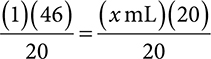
4. Multiply and divide to solve for x. Divide both sides by 20 to get x by itself.
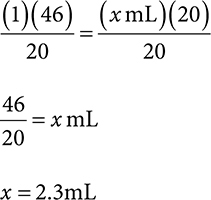
Remember, you can estimate what the answer should be close to, so you have an idea if your calculations are correct. In this case, if you know your dose is 46mg and the medication is available in 20mg/mL, you can guess that the answer should be a little bit more than 2mL since 20mg can go into 46 twice. So if you get an answer like 20mL or 0.2mL, that should give you a clue that your answer is off.
Dimensional Analysis
Another method of calculating unknown variables in an equation is through dimensional analysis. This process uses the cancelation method of like units to determine the answer. Setting up dimensional analysis equations are different from ratio-proportion in that you want to keep the same units on the top and bottom so they can be cancelled.
Example: Using the previous example, calculate how many mL would be needed for a dose of 46mg if a medication is available as 20mg/1mL.
1. Start with setting up your equation so that the like units are on the top and bottom so they can be cancelled. In this case, we know that 46mg is 1 dose and there are 20mg in 1mL. We would want the mg to be on the top and bottom.
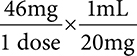
2. Next, cancel your like units, and determine what you have remaining. With the units remaining, our answer will be mL/dose, which is what we are looking for.
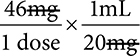
3. To solve, multiply the numbers across the top. Then multiply the numbers across the bottom.
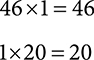
Take the product of the numerators divided by the product of the denominators, and this will give you your answer.
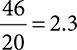
4. Be sure to include your units—in this case, we were solving for mL/dose, so the answer would be 2.3mL.
Self-Test: Round to the nearest tenths place
Use ratio-proportion or dimensional analysis to answer the following.
1. How many mg is in a dose of 7.5mL of a 250mg/5mL suspension?
2. What volume dose would be given for a patient who had a dose of 84mg of a 100mg/5mL solution?
3. A patient has a dose of 1,250mg. The medication is available as 500mg tablets. How many tablets are in each dose?
Answers:
1. 375mg
Ratio-proportion:
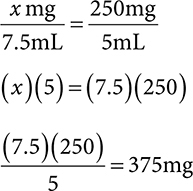
Dimensional analysis:
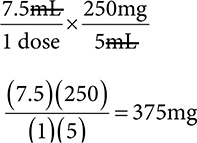
2. 4.2mL
Ratio-proportion:
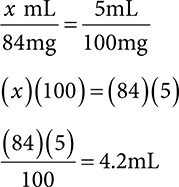
Dimensional analysis:
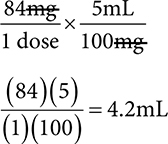
3. 2.5 tabs
Ratio-proportion:
Dimensional analysis:
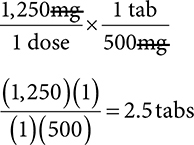
The Metric System
The metric system is a system of measurement used around the world and in hospitals, pharmacies, and healthcare systems. The metric system is based on a factor of 10, and conversion between units is an important part of dosage calculations.
For length, the base unit is a meter, but millimeter and kilometer are also common. Mass has a basic unit of gram, but in pharmacy practice, micrograms, milligrams, and kilograms are all used regularly. For volume, the liter is the base unit, but many pharmacy calculations and most liquid medications are dosed in milliliters.
The three most common prefixes you will use in pharmacy practice are micro-, milli-, and kilo-. These prefixes follow with their value and an example for each.
To convert between units in the metric system in pharmacy calculations, there are three methods you can use.
Move the Decimal Point
If you are converting from a smaller unit to a larger unit, move the decimal point to the left (the number gets smaller).
If you are converting from a larger unit to a smaller unit, move the decimal point to the right (the number gets bigger).
The following chart gives an idea of how many decimal points you would need to move. If converting between each unit, such as from micrograms to milligrams, you would move the decimal point three places. If you convert to the next unit, such as from micrograms to grams, you would move the decimal point six places. If you were to convert between micrograms and kilograms, you would move the decimal point nine places.
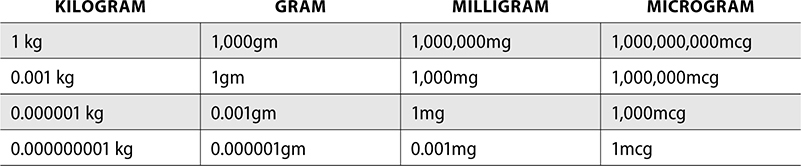
Example: Convert 458mg to g.
1. We are moving from mg to g, which is a smaller unit to a bigger unit, so the decimal point will go to the left and the number will get smaller.
2. Mg to g is 3 places.
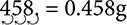
Multiply or Divide
This method has the same theory as moving the decimal point. If you are converting from a smaller unit to a larger unit, you will divide (the number gets smaller).
If you are converting from a larger unit to a smaller unit, you will multiply (the number gets larger).
The amount to divide or multiply depends on the value of the unit conversions. Similar to moving the decimal point 3 spaces, if you are converting from one unit to another next to each other on the previous chart, you will multiply or divide by 1,000 (such as microgram to milligram). If you skip a unit, such as converting from milligram to kilogram, you will divide by 1,000,000. Converting from microgram to kilogram would be dividing by 1,000,000,000.
Example: Convert 458mg to g.
1. Moving from mg to g means a smaller unit to a larger unit, so you will divide.
2. Mg and g are next to each other on the unit table, so you will divide by 1,000.
Ratio-Proportion
The ratio-proportion method uses the conversion factors listed in the previous chart. The x should always be opposite of the number you are converting from. This ratio should equal the conversion factor, such as 1 g = 1,000mg or 1mg = 1,000mcg.
Example: Convert 458mg to g.
1. Set up your ratio-proportion, keeping like units on the top and bottom.
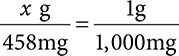
2. Cross multiply and divide.
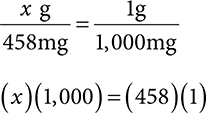
3. Solve for x.
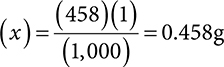
The same conversion can be done for volume, using liter and milliter. The conversions for volumes follow.
Example: A patient has an order for 2,500mL of fluid. How many L is this?
Converting from mL to L is converting from a smaller unit to a larger unit, so to solve, divide by 1,000, move the decimal point three places to the right, or set up using ratio-proportion.
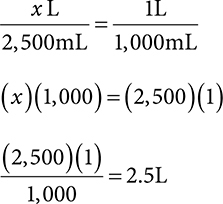
Self-Test: Complete the conversions
1. Convert 2.2g to kg.
2. Convert 500mL to L.
3. Convert 0.125mg to mcg.
Answers:
1. 0.0022kg
g to kg = smaller to bigger unit
Divide by 1,000.
Move the decimal point three places to the left.
Set up ratio-proportion:
2. 0.5L
mL to L = smaller to bigger unit
Divide by 1,000.
Move the decimal point three places to the left.
Set up ratio-proportion:
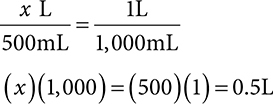
3. 125mcg
mg to mcg = bigger to smaller unit
Multiply by 1,000.
Move the decimal point three places to the right.
Set up ratio-proportion:
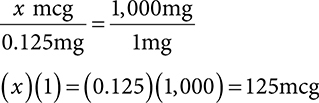
The Household System
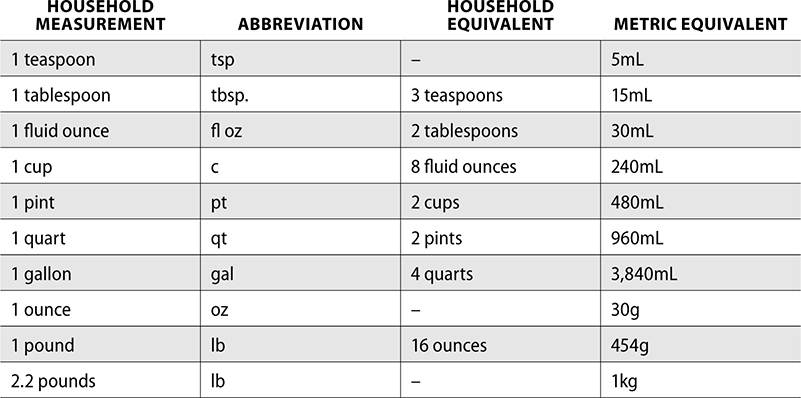
The household system of measurement is used in the United States and mainly in homes or kitchens. You may see prescriptions written for patients to take a teaspoon or tablespoon of a medication. This is an example of a household measurement. This system of measurement is less accurate than metric. Not everyone is going to measure one teaspoon in a measuring spoon or cup, and not all teaspoons are created equal. When completing the order entry process for prescriptions with household measurements, you should also include the metric equivalent for more precise dosing.
The household system measurements for volume and weight follow, along with their metric conversions.
For example, a common calculation pharmacy technicians complete is conversion of a patient weight from lb to kg. This can be completed through the ratio-proportion method or by simply dividing the total pounds by 2.2. The opposite is true if needing to calculate from kg to lb. You would then multiply by 2.2 to get your answer. Remember that the kg value will always be less than the lb value.
Example: A patient weighs 96 lb. Determine how much she weighs in kg. Round your answer to the tenths place.
Ratio-proportion
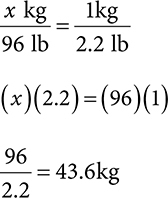
The other option to solve is to remember that when converting from lb to kg, dividing by 2.2 will give you the same solution.
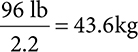
Converting from fl oz to mL is also a common conversion pharmacy technicians will complete regularly. Knowing that 1 fl oz = 30mL is helpful when using the ratio-proportion method to solve. Another way to solve is to remember that when converting from fl oz to mL, you multiply the number of fl oz by 30 to get your total mL. Conversely, when converting from mL to fl oz, you divide by 30 to get your total fl oz.
The following is a chart of fl oz to mL conversion.
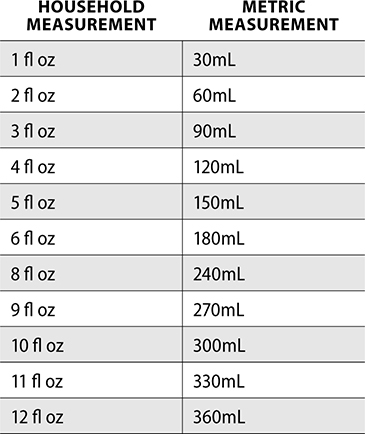
Example: A prescription is written for 3 fl oz. How many mL is this?
Ratio-proportion:
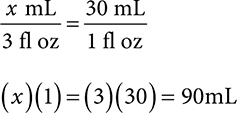
This can also be solved by remembering that converting from fl oz to mL means you should multiply your total fl oz by 30 to get your total mL.
(3 fl zo)(30) = 90mL
Self-Test: Complete the conversions
1. Convert 180mL to fl oz.
2. Convert 45mL to tablespoons.
3. Convert 24kg to lb.
Answers:
1. 6 fl oz
Ratio-proportion:
Converting from mL to fl oz = divide by 30
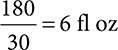
2. 3 Tbsp
Ratio-proportion:
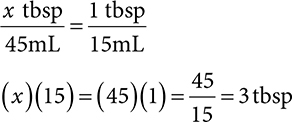
Converting from mL to tbsp: there are 15mL in 1 tbsp so you can simply divide by 15.
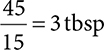
3. 55 lb
Ratio-proportion:
Converting from kg to lb = multiply by 2.2
(25)(2.2) = 55 lb
The Apothecary System
The apothecary system is a very old measurement system that has minimal use in pharmacy practice today. Though there are some medications that may still use the apothecary system as a form of measurement, it has overall been replaced with the metric system. Apothecary symbols are considered dangerous abbreviations and should not be used.
The following are a few apothecary measurements and the corresponding metric conversions.
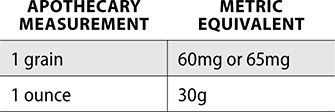
Aspirin, thyroid medication, and phenobarbital may still use grains as a form of measurement. Also, medication vials used in the pharmacy may be measured as drams—an apothecary unit of measurement for weight.
Temperature Conversions
Understanding temperature measurement systems is an important skill for pharmacy technicians. Part of the metric system is the Celsius scale. In the Celsius scale, water freezes at 0°C and boils at 100°C. The United States uses the Fahrenheit scale. In this scale, water freezes at 32°F and boils at 212°F. Converting between Fahrenheit and Celsius scales may be necessary for proper inventory management and storage. As a pharmacy technician, you may be responsible for logging daily temperatures of refrigerators, freezers, and room temperature for drug storage units. If a refrigerator or freezer contains a vaccine, the temperatures must be logged twice a day.
When converting between temperature measurement systems, use the following equations and plug in the known temperature to calculate the solution.
To convert from Celsius to Fahrenheit:
°F = (1.8 × °C) + 32
To convert from Fahrenheit to Celsius:
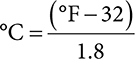
Example: Convert 76°F to Celsius. Round to the tenths place.
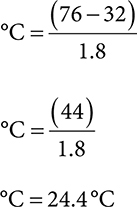
Pharmacy Dosage Calculations
When solving dosage calculations, keep in mind that a dose is a specified amount of drug that is taken at a certain time. You may need to calculate how many doses there are in a quantity of medication, how long a medication will last, or using known variables to solve for the unknown amount. Ratio-proportion and dimensional analysis are both used to solve dosage calculations.
Example: How many mL are in a 250mg dose of a medication available as 125mg/5mL?
You can use ratio-proportion or dimensional analysis to solve.
Ratio-proportion:
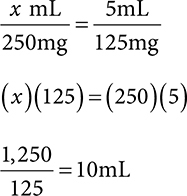
Dimensional analysis:
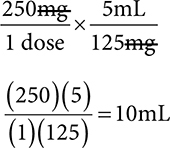
Dosage calculations often include weight-based dosing, in which you must determine the dose for a patient with a specified weight.
Example: A prescriber orders trastuzumab 4mg/kg to be infused over 90 minutes. The patient weighs 175 lb. What will the dose be?
1. The order is written for mg/kg and the patient’s weight is given in lb. First convert the lb to kg.
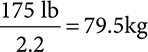
2. The patient is getting 4mg for every 1 kg. To solve for the dose, multiply the 4mg by the total patient kg. This can be set up as ratio-proportion as well.
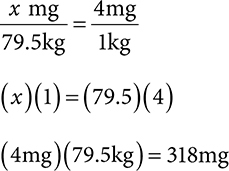
In addition to weight, some orders, such as chemotherapy or pediatric, may use body surface area (BSA) as a precise method of dosing. BSA is a dosing based on the patient’s height and weight and is measured in m2.
Example: A patient has an order for vincristine 2mg/m2. The patient’s BSA is 1.4 m2. Calculate the dose for this patient.
Use ratio-proportion and solve for x.
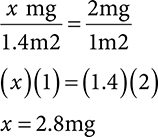
Milliequivalents (mEq) and units are other measurements used for specific medications. MEq may be used when calculating orders for potassium, especially if preparing to compound total parenteral nutrition (TPN).
Example: A patient is prescribed 100mEq total daily in four divided doses. How many mEq are in each dose?
To determine each dose, divide the total daily amount by the number of doses given each. You can also set up a ratio-proportion.
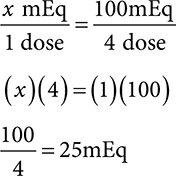
Units are used for dosing in medications such as heparin, penicillin, and insulin and for certain vitamins. Standard insulin vials contain 1,000units/10mL, though there are also 300units/3mL vials, insulin pens with varied dosing, and concentrated U-500 insulin, at 500units/mL.
Example: A patient is prescribed 36 total units of insulin per dose. How many mL from a 1,000unit/10mL vial will the patient inject for one dose?
Set up a ratio proportion.
Self-Test: Complete the dosage calculations
1. How many mL are needed for a 64mg dose of a 100mg/10mL solution?
2. How many 0.8g tablets are needed for a dose of 4,000mg?
3. How many grams are in 2,000mL of a 500mg/50mL solution?
Answers:
1. 6.4mL
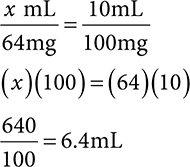
If you want to do a quick check that your answer makes sense, think about 64mg and that this is over half of 100mg. That means our answer needs to be greater than 5mL (half of 10mL).
2. 5 tablets
First we need to convert g to mg.
3. 20g
Days’ Supply and Quantity
Pharmacy technicians often complete calculations needed for a total days’ supply for prescriptions. This calculation is important for insurance billing if patients have a specified day limit on medications. If the total drug dispensed is incorrect for the days’ supply billed to the patient’s insurance, it could result in the patient not having sufficient supply for the time frame billed.
Example: A patient is prescribed Norco 1–2 tabs PO Q6–8h PRN pain dispense 40 tabs. Calculate the total days’ supply for this order.
1. Start by determining how many tablets the patient will take in 1 day. For range orders, such as 1–2 tablets and 6–8hr, assume the maximum amount a patient could take. In this example, 2 tablets every 6 hours is the most the patient should take.
2. After finding how many tablets the patient will take in 24 hours, divide the total tablets prescribed by the total needed for 24 hours.
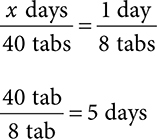
This prescription would be billed for 40 tablets = 5-day supply. It’s important to assume the patient will take the maximum amount for range orders. If this was calculated as 1 tablet every 6 hours, that would only be a total of 4 tablets per day, which would equal a 10-day supply for 40 tablets. If the patient needed a refill after 5 days, it could be flagged as too early to refill. Calculating days’ supply accurately is important not only for clinical safety but also for patient compliance and insurance processing.
Other days’ supply orders include calculating the quantity needed for a total days’ supply. For example, if a patient is taking 1 tab BID for 30 days, how many tablets are needed to fill this prescription?
To solve, calculate how many tablets are needed for 24 hours, then multiply by the total days’ prescribed. For this example, BID = 2 tablets taken daily. 30 days × 2 tabs daily = 60 total tabs.
Example: A patient is taking 2 tab PO QID for 14 days. How many tablets are needed to fill this order?
1. Calculate 24 hr supply. Assume QID = 4 times daily or Q6H.
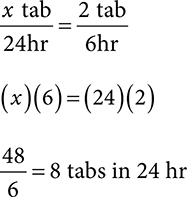
2. Next, multiply the 24hr quantity by the total days’ supply needed.
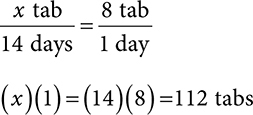
You may also encounter calculations in which the answer is not an even number. Always round down for days’ supply calculations. Even if your answer is 7.8 days, that is not 8 and by rounding up, a patient wouldn’t have enough for the total days.
Example: A patient takes Lantus 15 units subQ TID. How long will one vial of insulin last? Assume 1 vial = 1,000 units/10mL.
1. Calculate how much is taken in 24 hours. You can use ratio-proportion or multiply 15 units by 3 (TID = three times daily).
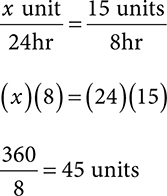
2. Use the total vial contents to determine how many mL is needed for 45 units per day dose.
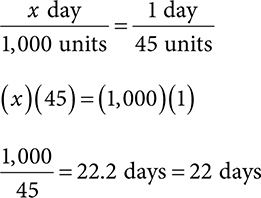
Self-Test: Calculating days’ supply
1. A prescriber orders prednisone 20mg 5 tabs QD × 5 days, then 4 tab QD × 3 days, then 2 tabs QD × 3 days, then 1 tab QD × 3 days. Calculate the total amount of prednisone tablets needed to fill this order.
2. A patient is prescribed 200mg of a 250mg/5mL suspension PO QID × 7 days. How many mL is needed to fill the whole prescription?
3. A patient uses 17 units of insulin TID. How many vials of 1,000 units/10mL does he need for a 30-day supply?
4. A patient has a prescription for Lantus SoloSTAR insulin pen. Each pen contains 450 units of insulin in 1.5mL. There are 3 pens per box. A patient takes 30 units BID and must prime the pen with 2 units at each injection. Calculate how many days the box of pens will last the patient.
Answers:
1. 46 tabs
Start by calculating the daily amount for each quantity. Remember that QD = daily.
5 tabs QD × 5 days = 25 tabs
4 tabs QD × 3 days = 12 tabs
2 tabs QD × 3 days = 6 tabs
1 tab QD × 3 days = 3 tabs
25 + 12 + 6 + 3 = 46 tabs
2. 112mL
First, determine how many mL are needed for 1 day.
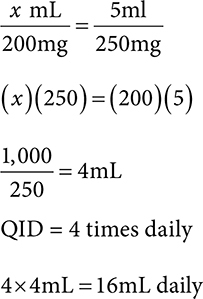
Next, multiply the total days needed by the daily amount.
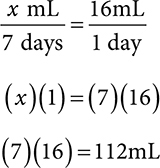
3. 2 vials
First, calculate the daily amount of insulin total.
TID = 3 times daily
(17)(3) = 51 units daily
Next, determine how many days 1 vial will last
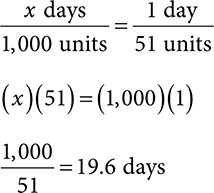
1 vial will last 19 days, so divide 30 (days in a month) by the total days per 1 vial to see how many vials are needed.
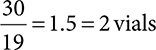
4. 23 days
First, calculate how many insulin units the patient needs daily.
BID = 2 times daily
(30)(2) = 60 units daily
(2 units to prime)(2)=4 units
(60) + (4) = 64 total units daily
Next, calculate the total of units in one box of pens.
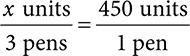
(450)(3) = 1,500 units in 1 box
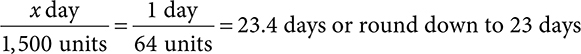
Percent Concentration
Percent concentrations are an expression of the ratio of active ingredient in total product. This is expressed as a solid in a liquid (w/v), solid in a solid (w/w), or liquid in a liquid (v/v). For example, a 5% solution of alcohol is 5mL alcohol in a 100mL solution.
See the following chart for a summary of each percent concentration.
Percent concentrations are used often to determine how much active ingredient is in a specified amount, in order to properly dose a medication.
Example: How much hydrocortisone is in a 2.5% tube of 45 grams?
This would be considered a w/w percent, as there is a solid (hydrocortisone) dissolved in 45g of cream base. To solve, set up a ratio-proportion. In this case, the unknown is how many grams hydrocortisone are in 45g. The ratio is 2.5g in every 100g (2.5%).
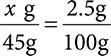
Then solve for x.
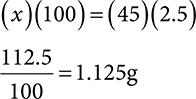
Again, you can check your answer by looking at the problem and checking that it makes sense. If there are 2.5g in every 100g, and we are trying to find how many grams are in 45g, look at the relationship between 45 and 100. 45 is just about half of 100. This means the answer should be just about half of 2.5.
The same type of problem can be completed with a w/v.
Example: How many grams of sodium chloride are in a 500mL bag of 0.9% solution?
Set up your ratio-proportion. Remember w/v = g/100mL.
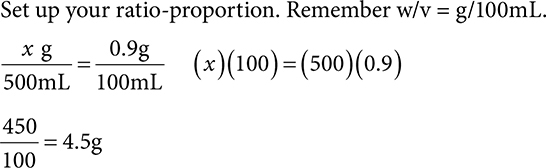
Last, in a volume/volume or v/v, you can calculate how many mL are in a solution.
Example: How many mL of IPA are in 15mL of a 60% solution?
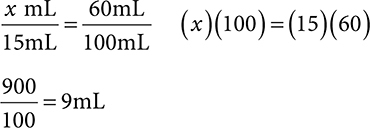
Self-Test: Percent concentration
1. How many g ingredient are in 15g of a 5% cream?
2. How many mg are in 200mL of a 10% solution?
3. How many mL are in 500mL of a 3% solution?
Answers:
1. 0.75g
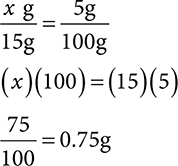
2. 20,000mg
This question is asking for mg, but remember w/v is in g/100mL. You must first find the grams, then convert to milligrams.
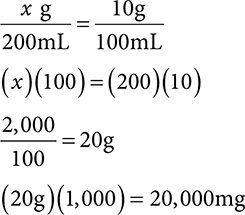
3. 15mL
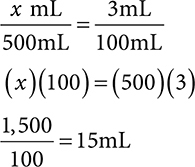
Dilutions
A dilution is the process of decreasing the concentration of a solution. This is usually done through the addition of more solvent, or base solution. In the pharmacy, you may see more concentrated solutions that are then diluted to a less-concentrated form or larger volume.
Calculating a dilution can be completed using the following equation.
Example: An order is written for 100mL of a 10% solution. You have a 15% solution in stock. How much stock solution and how much diluent is needed to compound this order?
First, determine the values for the variables in the equation.
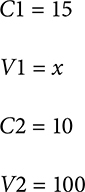
Solve for x.
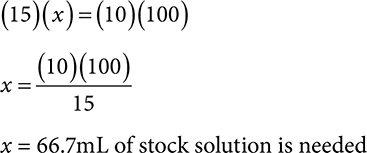
This question also asks for quantity of diluent needed with the stock solution. This can be found by taking the final volume and subtracting the stock volume needed.
100mL − 66.7mL = 33.3ml
33.3mL diluent is added to 66.7mL stock solution to get a final volume of 100mL.
Self-Test: Dilutions
1. An order is written for 250mL of a 20% solution. You have a 40% solution in stock. How much stock solution and how much diluent are needed to compound this order?
2. An order is written for 500mL of a 50% solution. You have a 75% solution in stock. How much stock solution and how much diluent are needed to compound this order?
Answers:
1. 125mL stock, 125mL diluent
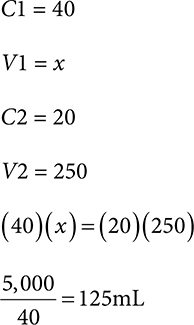
125mL of 40% solution is needed.
Now find the diluent by subtracting from the total desired volume.
250 − 125 = 125mL
2. 333.3mL stock, 166.7mL diluent
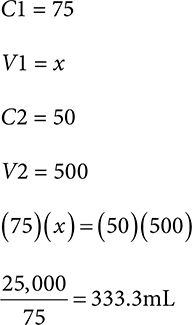
333.3mL of 75% solution is needed.
Now find the diluent by subtracting from the total desired volume.
500 − 333.3 = 166.7mL
Alligations
Alligations are another method of calculating dilutions. In this method, you have two stock concentrations and are calculating how much of each is needed to compound a final product. The final product will have a concentration between the two stock solutions used.
To solve an alligation, you set up a grid or tic-tac-toe board.
Next, place the higher concentration in the top left corner, the lower concentration in the bottom left, and the desired strength (what you are solving for) in the middle box.
After the table is set up, subtract the desired concentration from the higher concentration and put this value in the bottom right corner. Do the same for the lower concentration, and put this number in the upper right hand corner (ignore the negative value).
These values reflect the number of parts needed for the higher strength and lower strengths, respectively.
These differences total the number of parts needed for each concentration. The top right is equivalent to the total parts needed for the higher strength and the bottom left is equal to the total parts needed for the lower strength. Adding these parts together will equal the total parts needed.
Now a ratio-proportion can be set up to determine the total parts that will be needed for each concentration. There are some diluents, such as water or petrolatum, that have no concentration, and therefore 0 will be used as the concentration percentage in the grid.
Example: Prepare 300 grams of 2.5% hydrocortisone cream using 5% and 1% hydrocortisone base. Determine how many grams of each are required to compound this order.
1. Set up the alligation putting the higher concentration in the top left, lower concentration in the bottom left, and desired concentration in the middle. You do not need to include the units (%).
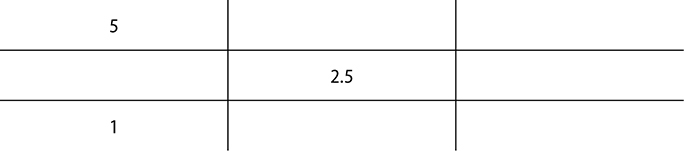
2. Next, subtract the difference to find the total parts needed and place this into the top right and bottom right squares.
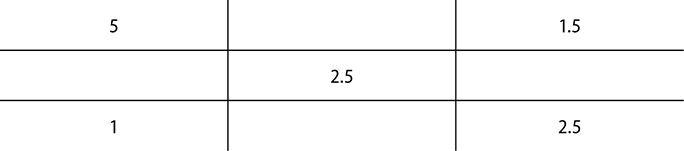
3. Looking at the differences of each diagonal subtraction, there are 1.5 parts of the 5% and 2.5 parts needed of the 1%. Now add together these parts to get the total parts needed.
1.5 + 2.5 = 4 total parts
4. Now you can set up a ratio-proportion to determine the quantity of each needed.
For the 5% hydrocortisone, we need 1.5 parts out of 4 total parts. We can compare this to the total amount to be compounded (300g).
5. The same process should be completed to determine how much 1% hydrocortisone is needed. For 1% hydrocortisone, 2.5 parts are needed out of 4 parts.
The answers would be 112.5g of hydrocortisone 5% and 187.5g of hydrocortisone 1%. To check your answer, be sure that the two totals from each concentration add up to the desired quantity. In this case 112.5 + 187.5 = 300.
Self-Test: Alligations
Round the answer to the nearest tenth place.
1. Prepare 100mL of 75% isopropyl alcohol using 90% and 20% IPA base. Determine how many mL of each are required to compound this order.
2. Prepare 45 g of 5% coal tar ointment using a 3% and 10% base. Determine how many grams are required to compound this order.
Answers:
1. 76.8mL of the 90% IPA and 21.4mL of the 20% IPA
First set up your alligation grid.
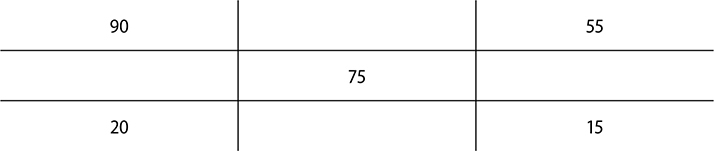
Add up your total parts: 55 + 15 = 70
Set up a ratio-proportion. Remember the parts per each concentration are directly to the right of each concentration.
For the 90% IPA:
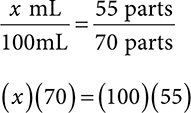
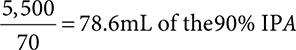
For the 20% IPA:
Check your answers by adding your two quantities together:
78.6 + 21.4 = 100mL
2. 12.9g of 10% and 32.1g of the 3%
First set up your alligation grid.
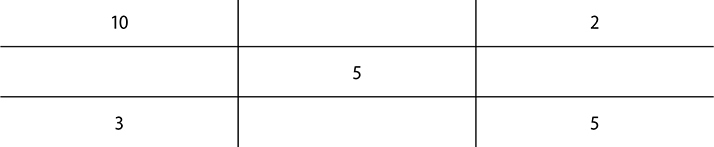
Add up your total parts: 2 + 5 = 7
Set up a ratio-proportion. Remember the parts per each concentration are directly to the right of each concentration.
For the 10% coal tar:
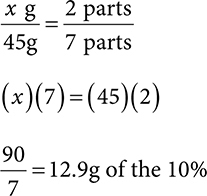
For the 3% coal tar:
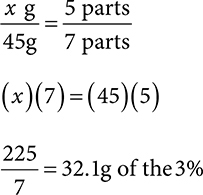
Check your answers by adding your two quantities together:
12.9 + 32.1 = 45g
Nonsterile Compounding Processes
Compounding is the process of mixing together two or more ingredients to create a medication specific to the needs of a patient. Compounded medications are those that are not available from a manufacturer and must be altered in some way for a patient order. Nonsterile compounding is often prescribed for patients to allow for a different dosing method or flavor, which in turn may help improve patient compliance. Compounding includes the addition of an active ingredient to an inert or inactive substance known as an excipient. The inactive substance could be a filler, flavor, binder, dye, or other component that does not alter the active ingredient, but assists the delivery of the medication.
Having the proper equipment is essential to following all standards and practices in nonsterile compounding. A clean area is required for compounding, and proper PPE must be worn. This may include just gloves, though it is recommended to don a hair cover, gown, and mask with a lab coat or clean scrubs. PPE is essential when compounding hazardous substances or aerosolizing particles.
When compounding nonsterile products, a balance is often used to weigh substances. Many states require pharmacies to have a Class A balance. This type of balance consists of a two-pan system, with the substance being weighed in one pan and the calibration weights in the other, measuring the weight of the substance. Weigh papers or weigh boats are used to keep the ingredients in place while weighing. After the weight of the paper or boat is found, it is zeroed from the scale so it will not be included in the final weight of the measured substance. An electronic or digital scale can also be used for measuring.
For liquids, measurement occurs in beakers and graduated or conical cylinders. A beaker (Figure 5.1) is a cylindrical container, usually glass, that has a flat bottom. It typically will have a spout to pour from and can also be used for mixing and heating liquids. A graduated cylinder (Figure 5.2) is a tall, narrow container which has straight sides. A conical cylinder (Figure 5.3) is similar to a graduated cylinder, except it is cone-shaped (wider at the bottom than the top). When you are measuring a liquid, it is important to read the measurement at the bottom of the curved fluid surface, which is known as the meniscus (Figure 5.4). This allows for a more accurate measurement, as reading the top of the meniscus would be an inaccurately high value and too much liquid would be used. Glass stirring rods can be used if any compound needs dissolved or to be mixed thoroughly.
Figure 5.1 Beaker
Figure 5.2 Graduated cylinders
Figure 5.3 Conical cylinders
Figure 5.4 Graduated cylinder showing the meniscus
If tablets or powders must be crushed or mixed, a mortar and pestle (Figure 5.5) may be used. A mortar is a bowl, and a pestle is a tool with a rounded end that is used for crushing and grinding. Trituration is the process of reducing a particle to a powder through grinding using a mortar and pestle.
Figure 5.5 Glass mortar and pestle
When compounding pastes, gels, creams, or ointments, a spatula (Figure 5.6) may be used for mixing ingredients. A spatula has a handle and a flat blade on the end that is typically made of stainless steel, rubber, or plastic. Spatulation is the process of using a spatula to mix substances together. An ointment slab may be used for mixing, which is a large glass or porcelain slab that offers a hard, nonabsorbable surface for combining ingredients.
Figure 5.6 Stainless Steel Spatula
Levigation is also a technique used to mix substances together, specifically grinding powder (similar to tritruation) but with a small amount of liquid. The liquid used is known as a levigating agent, and this helps make a smoother compound.
When mixing together powders that are of unequal size, geometric dilution is the process that can be used to ensure a well-mixed compound. In this process, the smallest amount of powder is added first and mixed with an equal amount of the powder in the larger quantity. That mixture is then mixed with an equal amount of the larger quantity and repeated until the entire mixture is completed.
Compounding Record Keeping
Once you have the supplies needed for your compound, it is important to review the master formula record (MFR) or “recipe” for your compound you are preparing. USP<795> requires the MFR be followed for all compounds. The MFR contains:
▪ Drug name, strength, and dosage form
▪ Amount of all component needed
▪ Complete instructions for preparation, including equipment, supplies, and compounding steps
▪ Description of final product
▪ Assigned beyond-use-date (BUD) and requirements for storage (reference also required)
▪ Calculations if applicable
▪ Labeling requirements, such as “shake well”
▪ Quality control procedures, such as visual inspection or expected result
The MFR is the process to be followed for each compound to ensure standardization of the formula. A compounding record is also required for each compound. This is different from the MFR in that it is unique for each specific compound completed. The MFR is the recipe used each time, while the compounding record is a log of the actual compound that is made. A compounding record must include:
▪ Name, strength, and dosage form of final compound
▪ Date and time of preparation
▪ Assigned internal identification number (such as prescription number)
▪ Individuals involved in the compounding process
▪ Lot numbers, expiration dates, and manufacturer of each component used
▪ Weight or measurement of each component
▪ Total quantity compounded
▪ Assigned BUD and required storage
▪ Calculations if any were required
▪ Physical description of final product
▪ Results of final control procedures
▪ Copy of the MFR
▪ Copy of the patient label
Beyond-use-dates (BUDs) are calculated based on guidance from USP<795>. The final BUD of a compounded product cannot exceed the expiration date of any of the individual components. So if there are three ingredients in a compound, and one of them expires in 4 days, the BUD will have to be 4 days.
The required storage conditions and BUDs for compounded products follow.
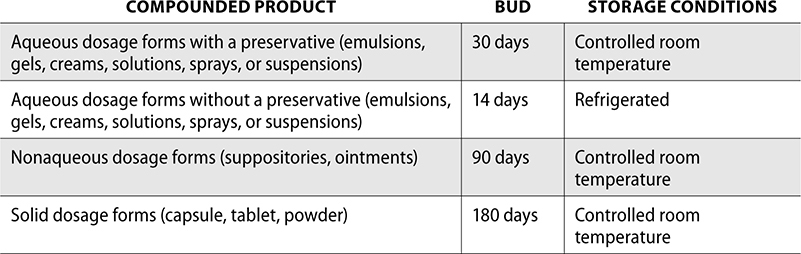
Now you know the tools and documentation needed for nonsterile compounding. Let’s discuss the different types of compounds you may encounter as a pharmacy technician.
Compounding Ointments
An ointment is a semisolid compound used topically on the skin. Ointments help protect the skin by providing a barrier against moisture and air. When compounding an ointment, the medication is added to a base. For example, hydrocortisone ointment is made by adding hydrocortisone to a semisolid base. Some examples of bases used in compounding ointments include:
▪ Petrolatum (Vaseline)
▪ Lanolin
▪ Paraffin
▪ Eucerin
▪ Polyethylene glycol (PEG)
Ointments are compounded through spatulation and geometric dilution to mix a semisolid base with the active ingredient. They may also require heat to melt the waxy base and dissolve all substances; once cooled, the compound will congeal into an ointment. After the ointment has been compounded, it is transferred into an ointment jar to be labeled and dispensed.
Compounding Mixtures and Emulsions
An emulsion is a mixture consisting of two liquids that do not normally mix together. There are two different types of emulsions—oil-in-water (o/w) and water-in-oil (w/o). Creams and lotions are emulsions and can be either o/w or w/o. If it is oil-in-water, it contains more water than oil and will leave a wet sensation on the skin. Water-in-oil has more oil content and leaves a greasier feel after being applied. Creams typically have a higher oil content than lotions, which makes them thicker. Lotions have a higher water content and are moisturizing. This allows lotions to be spread over large parts of the body, as thinner emulsions are easier to spread.
The active ingredient is first weighed, prior to compounding. If needed, a mortar and pestle can be used to crush it to a powder. A levigating agent can be added to wet the mixture. Following the formulation record closely is very important. The cream or lotion base can be added into the mixture. When compounding emulsions, it is important to make sure the emulsion is well-mixed to allow the active ingredient to be consistent in each dose. After compounding, the cream or lotion can be transferred to a container, similar to an ointment jar, and labeled to be dispensed.
Compounding Liquids
Oral liquid dosage forms can be compounded into elixirs, solutions, suspensions, or syrups. An elixir is a clear, sweet solution that contains alcohol. The amount of alcohol in elixirs varies depending on the compound—the concentration needed is the amount required to keep the drug in solution. Elixirs are used infrequently, and there are many patients who should avoid use of elixirs, including children, patients who take medications that may interact with alcohol, patients with a history of alcohol abuse, and patients who are pregnant.
Solutions are composed of a liquid with a completely dissolved active ingredient. A beaker and stirring rod may be used to help compound a solution with a liquid and powder. A solution may also be a dilution of a concentrate. This is compounded by adding a diluent to the concentrated liquid to reduce the concentration and increase the volume. Because a solution is completely dissolved, it does not require shaking after compounded.
Suspensions, on the other hand, must be shaken before administering each time to disperse the drug evenly. A suspension is a powder with a specified amount of diluent added. The powder never fully dissolves, and this is one of the disadvantages of suspensions, as there is potential for settling of the drug and nonuniformity throughout the bottle. Suspensions do allow for flavoring and the ability to mask unpleasant taste. When compounding a suspension, a compounding record and MFR is not required, as the instructions for mixing are supplied by the manufacturer.
Syrups are made of mostly sugar and water. They can be flavoring syrup, such as cherry syrup, or medicinal syrup, which has an active ingredient added, such as loratadine syrup. Syrups are sticky and become stickier with higher sugar content. They should be avoided in patients with diabetes.
Oral liquids are often compounded for flavoring to help with patient compliance. Pharmacy technicians may add flavoring agents to suspensions or solutions prior to dispensing. A specific formula is followed, depending on which flavor is used and which medication is being flavored. Flavoring does require a compounding record or modify the BUD of the suspension or solution.
Compounding Capsules
Capsules can be compounded for patients who may be unable to or have difficulty swallowing tablets. They can also be compounded for a patient if the prescribed dose is unavailable or if a patient has a sensitivity to one of the inactive ingredients in the manufactured product.
Capsules consist of a base known as a body, and a cap, known as the head. Sizes of capsules range from 5 being the smallest to 000 being the largest.
The following chart indicates the capsule size and the average mg amount contained.
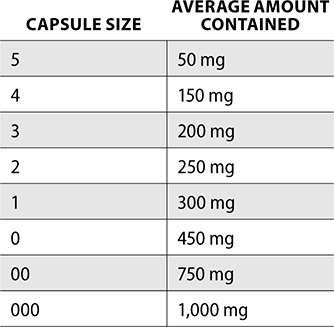
To compound capsules, a capsule-filling machine or the punch method can be used. A filling machine is a device that can fill many capsules at one time. The punch method is used for a smaller quantity. In this method, the height of the active ingredient powder is the same height as the capsule base. The pharmacy technician compounding can then punch the capsule into this powder, which will fill the entire base. This method does create some difficulty in ensuring an even distribution of ingredient in each capsule.
Compounding Suppositories
Suppositories are solid dosage forms that are inserted into the body and melt at body temperature or dissolve into the mucous membranes. They are compounded using a mold depending on the type of suppository (they can be administered into the rectum, vagina, or urethra).
There are a few different types of bases used for suppositories. Cocoa butter is solid at room temperature, but around body temperature, it melts into an oil and can release medication into the surrounding membranes. Suppositories made of cocoa butter should be refrigerated in warmer climates.
Another base use is polyethylene glycol (PEG), which does not melt at body temperature but dissolves and provides a more prolonged release. These suppositories also do not require refrigeration, as they do not dissolve at elevated temperatures.
When compounding suppositories, the active ingredient is added to the base and melted into a liquid to be mixed thoroughly. This solution is poured into the suppository mold and cooled until the suppositories harden. They are then packaged and dispensed to a patient with proper storage instructions depending on the base used for compounding.
Compounding Enemas
Enemas are solutions that are administered rectally to help initiate a bowel evacuation. Because they are not administered into the bloodstream, they are safe to compound in a clean, nonsterile environment.
To compound an enema, the active ingredient is measured and weighed. This may require crushing of tablets into a fine powder to dissolve into the solution. For example, if a prescriber requests an antibiotic enema of 1,000mg, and the pharmacy stocks 500mg tablets, two tablets must be triturated with a mortar and pestle. This powder is then mixed into the vehicle base solution of enema and titrated to the desired quantity. This is then poured into an enema bag for patient administration.
Equipment and Supplies for Drug Administration
As a pharmacy technician, you will be filling different types of orders for patients. With each order, you will choose the best package type and size to dispense the medication. For safety and to prevent accidental poisoning of children, all medications must be dispensed in a child-resistant container. This is a result of the Poison Prevention Packaging Act of 1970 (PPPA), which requires most OTC and prescription drugs be packaged in containers that cannot be opened by 80% of children under five, but can be opened by 90% of adults. Patients who have difficulty opening containers may request a non-child-resistant container and sign a waiver or acknowledgment in the pharmacy computer system so future prescriptions are filled without the safety cap. There are exceptions to the PPPA and drugs that are exempt from child-resistant packaging. Some of these include sublingual nitroglycerin, oral contraceptives, or powdered aspirin.
Package Size
Pharmacy technicians in a retail pharmacy count prescriptions and dispense into amber vials (Figure 5.7). Many medications are sensitive to light, and the amber bottle helps protect from light degradation. Amber prescription vials are measured in drams. They typically range in size from a 6-dram vial (smallest) to a 60-dram vial (largest).
Figure 5.7 Amber vials
After counting the prescription on a counting tray (Figure 5.8), use the spout to pour the medication into the vial (Figure 5.9). You should choose a vial that is a closest fit to the quantity dispensed, but careful to not overfill the bottle.
Figure 5.8 Capsules being counted on a counting tray
Figure 5.9 Using the spout to pour into the bottle of an appropriate size
When dispensing liquid medications, you use amber bottles that are measured in fluid ounces. Remember the conversion for fluid ounces to mL (1 fl oz = 30mL). The same is true for liquids as solid doses—select the bottle size closest to the prescription without overfilling the bottle. You may need to do some quick math when selecting the bottle size for your prescription. For example, if a prescription is written for 115mL, which size bottle would you select?
Look at the bottles in Figure 5.10. You can choose between a 2, 3, 4, or 6 fl oz bottle. If you choose a 3 fl oz bottle, that would be 90mL—not enough. If you choose a 6 fl oz bottle, that would be 180mL—which seems like some wasted space. A 4 fl oz bottle gives you 120mL, which is the perfect size. If you ever aren’t sure of the size of a bottle, you can look at the fl oz markings on the side. Figure 5.11 shows the fl oz markings on a 14 fl oz bottle in increments of 2 fl oz.
Figure 5.10 Amber bottles for liquids
Figure 5.11 Fluid oz markings for amber liquid bottle
Many pharmacies stock a variety of different-size bottles for liquid medications, while some stick with the four most commonly used sizes, as shown previously. A conversion chart for fluid ounces to mL for a quick reference follows.
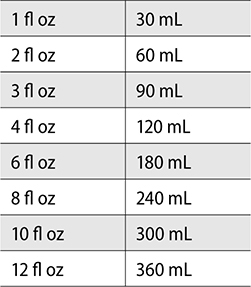
Unit Dose, Repackaging, and Unit-of-Use
A unit dose medication is a drug packaged for a single administration. They can be purchased from the manufacturer as a unit dose or repackaged on site from a bulk bottle into unit dose packages. Oral solid medications are the majority of unit dose products, such as tablets or capsules, though liquids can also be packaged in unit dose cups (Figure 5.12).
Figure 5.12 Unit dose capsules and tablets
Unit doses are dispensed most commonly in the institutional setting, because it allows reuse of a medication if the package has not been opened. Unit dose also allows the nurse or caregiver administering the medication the ability to dispense without manipulation, and scan to the bar code prior to dispensing. This is safer for the patient and more efficient for the nurse.
In a hospital, much of the drug inventory stored outside of the main pharmacy is within an automated dispensing machine or cabinet (ADM or ADC). Unit dose medications must be used to stock the ADMs, as bar code scanning is required prior to loading the machine. The doses in dispensing cabinets are not patient specific, so if a nurse pulls five different medications for a patient and then the patient is discharged and unable to take those medications, they can be returned back to the machine to be redispensed to another patient (if unopened). This helps decrease costs of inventory and prevents wasting the drug. The packaging of the drug protects both the identification as well as the integrity (prevents breakdown) of the medication.
The FDA does have requirements for the labeling of each unit dose medication. This includes:
▪ Drug name and quantity of active ingredient per unit (e.g., 300mg in 5mL or 30mg tablet)
▪ Expiration date
▪ Lot number
▪ Name of manufacturer
▪ Special storage requirements, such as refrigerate or protect from light
▪ Special dosing characteristics, such as sustained release or enteric coated
▪ Statement: Warning may be habit forming, for controlled substances
▪ Bar code
▪ NDC number (not required but is recommended)
Although unit dose medications are safer and more efficient for hospitals, they are not always cheaper to purchase. A hospital may find that buying a bulk bottle of medication and repacking is more cost effective than purchasing the unit dose directly from the manufacturer. Or a medication may not yet be available in unit dose packaging. Regardless of the reason, hospitals must dispense unit dose medications to patients and ensure the labeling and bar coding is appropriate for administration. Repackaging is a common practice that allows hospitals to dispense unit dose medications and maintain safety and efficiency.
The FDA defines repackaging as “taking a finished drug product from the container in which it was distributed by the manufacturer and placing into a different container without further manipulation.” In other words, a pharmacy technician removes the drug from a bulk bottle and packages into individual doses for distribution.
Labeling of repackaged medication is just as important as unit dose medications. Repackaged drugs act similarly to unit dose, though the BUD is typically shorter due to removal from original packaging. A pharmacy must keep a log of all repackaged medications. The log should include the information required on the label (a copy of the label will work), how much was repacked, and the signatures of the technician repacking and pharmacist verifying accuracy.
The label on a repackaged medication must include the following:
▪ “This drug was repackaged by [NAME OF FACILITY]”
▪ Address and phone number of facility repacking
▪ Drug name
▪ Lot number of drug being repackaged
▪ Dosage form and strength
▪ Date of drug repackaging
▪ BUD as the expiration date for the repackaged product
▪ Storage and handling instructions
▪ NDC of repackaged drug
▪ Manufacturer name and lot number
The BUD of the repackaged drug depends on the dosage form. These BUDs are for nonsterile repacking only, which follows USP<795> guidelines. For pharmacies completing sterile repacking, USP<797> standards must be followed.
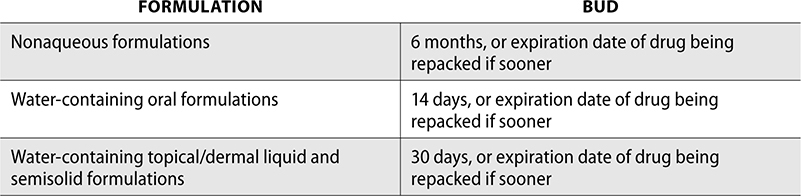
Unit-of-use packaging is packaging that allows for a medication to be dispensed directly to a patient without any manipulation except applying a label (Figure 5.13). Whereas unit dose delivers enough medication for one dose, or for 24 hours, unit-of-use is designed to deliver medication for the duration of therapy. For example, a blister pack of oral contraception for a 28-day supply is dispensed as a pack with a label applied. The tablets are not punched through the blister pack and put in a bottle for the patient. This is considered unit-of-use. Additional examples include 30-day starter packs or a steroid dose pack that is administered as a full course of treatment.
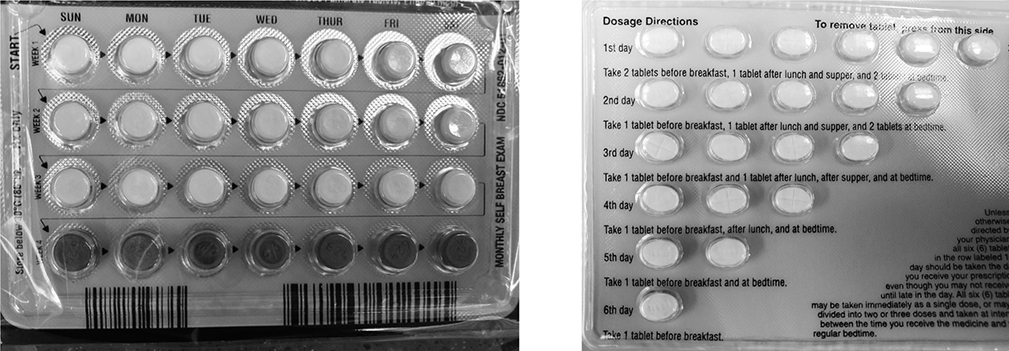
Figure 5.13 Unit-of-Use Medications
Oral and Injectable Syringes
Syringes are used for both oral administration and injection of medications. An injectable syringe should use a Luer lock so a needle can be screwed on the top, whereas an oral syringe has a flat or slip tip that a cap can slip on (Figure 5.14). Luer-lock syringes have a threading mechanism that allows a needle to screw on tight and prevent it from falling off.
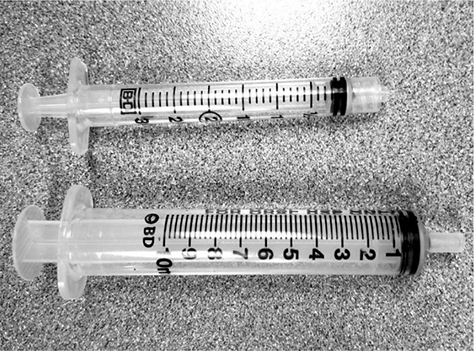
Figure 5.14 An injectable syringe with a Luer lock versus an oral syringe
Because of the similarity between oral and injectable syringes, the ISMP has developed safe practice recommendations to avoid inadvertent administration of an oral medication into an IV line. These may include using amber-colored oral syringes and implementing a quality assurance process when a patient has both an IV line and any kind of tube-feeding line. Oral syringes are labeled with “FOR ORAL USE ONLY” to help prevent errors (Figure 5.15).
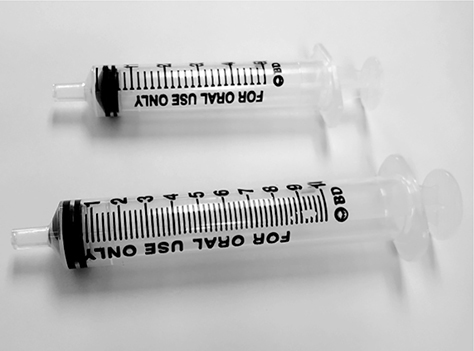
Figure 5.15 Oral syringe without Luer lock
Oral syringes are used for liquid medications, most commonly for pediatric patients. They are used without a needle, but are more precise than a dosing cup or household tool (such as a teaspoon or tablespoon). A syringe cap is attached to the tip of an oral syringe after drawing up the medication.
Injectable syringes are usually hypodermic and can hold anywhere from 3mL to 60mL. A needle is attached to a hypodermic syringe and can be used for sterile compounding or patient administration, such as IM or IV push. Selecting the smallest size syringe to fit the total volume is similar to selecting the smallest size vial to fit the tablets being counted. The closer to the total volume you can get without overfilling, the better. For example, you have a 3mL, 5mL, and 10mL syringe in stock and need to draw up 4.8mL. You would choose the 5mL syringe, as the 3mL would not be large enough, and the 10mL would be less accurate than the 5mL measurement.
Insulin syringes are also used for patients with diabetes when administering insulin. These syringes hold 1mL or less, and are measured in both mL and insulin units. Insulin syringes will indicate total units per mL. For example, a U-100 syringe contains 100 units/1mL.
Tuberculin syringes are also small syringes that are designed for 1mL intradermal administration of tuberculin purified protein derivative (PPD). This injection helps diagnosis tuberculosis in a patient. Tuberculin syringes often come prepackaged with the needle already attached.
Syringes are all made of the same components—a plunger and a barrel. The plunger is used to draw up the medication into the syringe. The barrel is a tube with the calibration lines used for measuring volume. The top of the plunger is black rubber within the syringe that is used to determine where to read the measurement. The top of the plunger is where the measurement should be read. (See Figure 5.16.)
Figure 5.16 Parts of the syringe
Needles
A needle is attached to a syringe for sterile compounding and for medication administration. Pharmacy technicians use various size needles depending on the type of solution or suspension that is being drawn up. Needles used for medication administration are typically smaller to help minimize pain with injection.
There are three main parts to a needle. The hub of the needle is the bottom portion, which secures or locks into the syringe. The shaft is the long stem of the needle, which ends in a sharp point. The point of the needle is known as the bevel. The lumen is the hollow bore of the bevel.
Figure 5.17 Parts of a needle
The size of the needle is determined by the gauge and length. The gauge of the needle ranges from 6G to 32G, with the most commonly used gauges between 15G and 32G. The size of the needle increases as the number of gauge decreases, so a 6G needle is the largest gauge and a 32G needle is the smallest. The size of gauge used depends on what procedure is being administered. Small gauge or large needles are used for viscous or thick liquids to help draw fluid into the syringe. Using this size for administration, however, would be painful, so larger gauge, or smaller, needles should be used.
The following chart shows the gauge of needle used for medication administration.
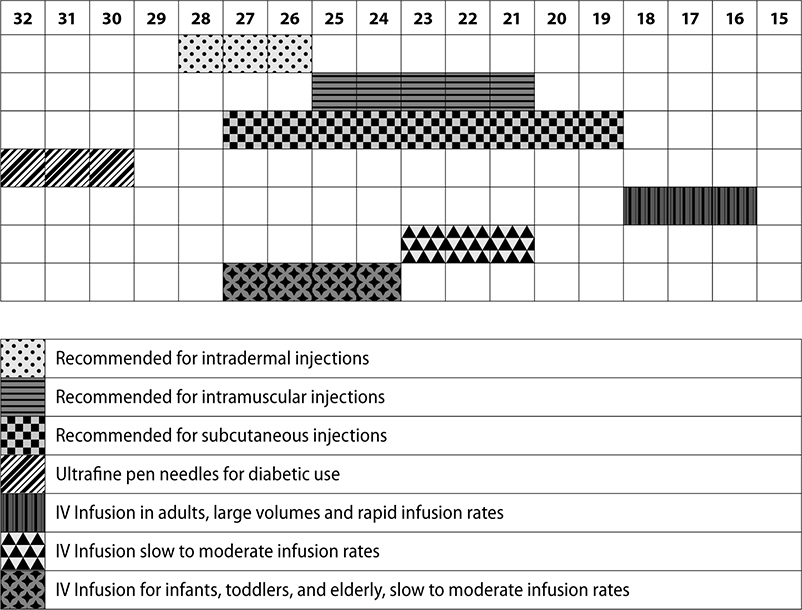
The length of the needle is also important when selecting a size. Needle lengths range from 3/8 inch to 3 1/2 inch. Smaller length needles would be used for injections closer to the surface of the skin, such as intradermal injections. For intramuscular injections, the needle must inject under the muscle and must therefore be longer. Needle length and gauge are indicated on the needle packaging. For example, the following needle is a 22 gauge 1 1/2 inch needle (Figure 5.18).
Figure 5.18 Needle with cap indicating size
Injections are also given at specific angles depending on the injection type. The following chart and graphic (Figure 5.19) showing the location and angle of each injection. This can be helpful when understanding what size needle should be used for administration of medication.
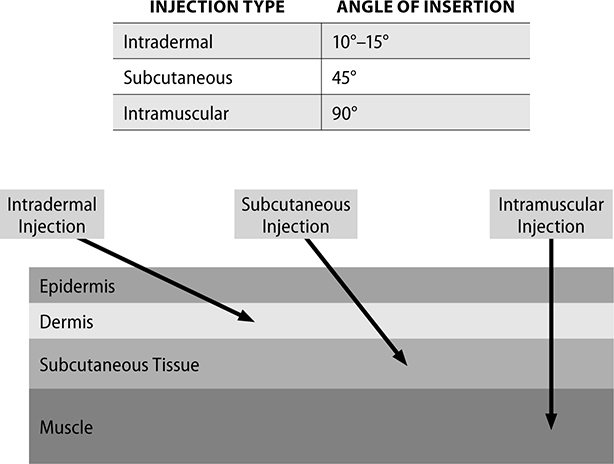
Figure 5.19 Location and angle of injections
Diabetic Supplies
Patients with diabetes often need help understanding what supplies they need, how to use them, and how they can get them at a reasonable price. Pharmacy technicians can play a vital role in diabetes management by procuring supplies, sourcing items for patients, and locating discounts or savings opportunities to patients without insurance coverage. Diabetic supplies for patients with Medicare fall under durable medical equipment, or DME. DME also includes items such as canes or crutches, wheelchairs, or other medical devices.
Patients with diabetes need to continuously monitor blood glucose levels. To do this at home, a glucometer is recommended. Glucometers are manufactured by many different vendors, and each has its own unique test strips. The test strip collects the blood from the patient and is inserted into the glucometer, which then reads the blood glucose levels. To draw blood, a patient may use a lancet, which is a device that quickly pricks the skin.
If patients are using insulin from a vial, they need insulin syringes and needles for administration. Newer forms of insulin are administered through an insulin pen, which is a prefilled cartridge that has a dial for measuring doses, instead of using a syringe and needle. Insulin pens use pen needles, which are smaller, often less painful, needles.
As a pharmacy technician, it is important you understand what each diabetic supply is used for and how to match test strips with glucometers. The following is a quick summary of the most often used supplies for diabetes.
Respiratory Supplies
DME is also used for respiratory ailments. This includes nebulizers and spacers. A nebulizer is a machine that uses a nebule (vial of solution) and turns it into a mist to be inhaled. For example, a nebule of albuterol is opened and poured into the nebulizer. The machine then takes the liquid and turns it into fine droplets that can be inhaled. A patient wears a mask so the mist can be breathed in directly.
Another way to get medication into the lungs is through a metered dose inhaler (MDI). Sometimes when the inhaler is puffed, the medication does not get completely into the lungs. A spacer attaches to the end of the MDI so the aerosolized medication stays within the chamber, and then the patient breathes into the other end of the spacer to absorb more of the drug. Spacers can be a variety of sizes, depending on the size of the patient.
Lot Numbers, Expiration Dates, and National Drug Code (NDC) Numbers
A lot number is a number assigned to a batch of medication. It allows the manufacturer to trace potential adverse incidents in a particular group of drugs. If a recall is necessary, lot numbers are used to identify the specific drugs impacted. Pharmacies then use that information to pull from inventory. Lot numbers can also be used for supply chain security. The lot number is printed on each bottle or unit dose and is often next to the expiration date.
The expiration date of a drug is the last date at which the product is known to remain stable and able to retain strength, quality, and purity when stored in its labeled conditions. Expiration dates are different from BUDs in that the expiration date is assigned by the manufacturer and printed on the product. A BUD is assigned by the pharmacy and calculated based on risk level, stability, and sterility.
Expiration dates may be in a month/day/year format, or just month/year format. If a manufacturer indicates a month and year only, you can assume it is the last day of this month—meaning if an expiration date is 5/25, this product would be good until 5/31/2025. As a pharmacy technician, one of your jobs is to pull outdated medications each month and to look for expired drugs, including nursing units, floor stock dispensing cabinets, crash carts, and pharmacy inventory.
Along with a lot number and expiration date, each drug has a national drug code (NDC) that has been required by the FDA since the Drug Listing Act of 1972. An NDC is made up of 10 or 11 digits, grouped into three different segments. The FDA maintains a searchable database of all NDCs, including OTC drugs. Although 10-digits are required, 11 digits are used for billing purposes, so if a manufacturer uses a 10-digit NDC, the pharmacy will add a 0 in a specific location to bill correctly.
The first series of numbers is known as the labeler code and represents the manufacturer, repackager, or distributor. The labeler code is 5 numbers, but if the 10-digit format is used, it may be 4. To make it a 5-digit code, the pharmacy would add a 0 before the first number. So if the labeler code was 9876, the pharmacy would add a 0 to the beginning and the 5-digit code would then be 09876.
The second set of numbers is the product code. This identifies the product, including the drug strength and dosage form. For example, if the same manufacturer makes diphenhydramine in capsules and liquid, the first set of numbers (labeler code) would be the same, but the second set would remain different, even though they are both diphenhydramine. The product code is 4 numbers, unless the manufacturer uses a 10-digit format, then it could be 3 digits. In this case, if the digits are 543, the pharmacy would add the 0 to the beginning and use 0543 as the product code.
The last set of numbers is the package code. This describes the packages size and type. The package code is 2 digits, though if a manufacturer uses a 10-digit NDC, it may be only 1. The pharmacy will put a 0 before the last digit in this case.
Figure 5.20 is an example of an NDC number in the 5-4-2 (11-digit) format.
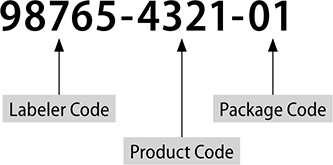
Figure 5.20 An NDC number in the 5-4-2 (11-digit) format
It may also be helpful to understand where to add a “0” when converting from a 10-digit NDC to an 11-digit NDC. The following are 10-digit formats and examples of each and where the 0 would be added to convert to 11-digits.
Procedures for Identifying and Returning Medications and Supplies
Pharmacy technicians have an important role in inventory management in the pharmacy. As a pharmacy technician, you will need to continuously monitor expired or soon-to-expire drugs for returns, returning to stock, or reviewing return with a reverse distributor.
Credit Returns
Managing excess inventory is important in controlling cost that is tied up in inventory. Excess inventory could be a result of errors in ordering, stocking for patient-specific medication who may have changed regimens, or overall change in prescribing. A credit return is a credit from the wholesaler to an invoice after sending back eligible drugs. Medications eligible for credit cannot have been opened or damaged or be close to expiration. Typically, drugs need to have at least 6 months out from the expiration to be returnable for credit.
Not all medications are eligible for credit from the wholesaler. Unless the medication arrived damaged or in error, the product must be able to be resold to be returned. Drugs that may not be returnable include frozen or refrigerated medications, some hazardous drugs, and special orders that a wholesaler may “drop ship” to a pharmacy. Prior approval is given from the wholesaler and paperwork to process the return. When the wholesaler has received the medications and approves the return, credit is issued back to the pharmacy account.
Return to Stock
Prescriptions that have not been picked up for a specific number of days in a pharmacy are able to be returned back to stock. Return to stock (RTS) drugs are put back into the pharmacy inventory and can be dispensed to another patient. It is important to note that prescriptions can only be returned to stock if they have not left the pharmacy. If a prescription leaves a pharmacy, it cannot be returned, as would be impossible to verify it was stored appropriately or not tampered with. Medications to be returned to stock must not be expired, and when they are returned to the shelf, they must remain in the original container in which they were filled. The label should not be removed, though the patient information should be blacked out if possible. Keeping the label on the bottle ensures the NDC and manufacturer can be matched to the inventory on the shelf. If the prescription was a unit-of-use or sealed manufacturer bottle, the label may be removed to be relabeled for another future patient. Contents of a RTS prescription must never be returned back into the manufacturer’s stock bottle, as the original stock bottle may be a different lot number or have a different expiration date.
Each pharmacy has a unique timeline for how long a prescription can be available before returning to stock. This is typically between 7 to 10 days. As a pharmacy technician, you will help with the RTS process by running daily reports of prescriptions due to be returned to stock and notifying patients. If the prescription is still not picked up, a pharmacy technician can process the RTS and put the bottle back on the shelf with the other inventory. Insurance companies may also dictate the RTS time frame. Part of the RTS process is reversing the claim if it was processed through insurance. If the prescription was not reversed, the pharmacy would still claim payment on the prescription without the patient picking up the medication. This would be a form of insurance fraud.
Reverse Distribution
Credit returns and RTS are for medications that are not expired. Outdated medications cannot be returned to a wholesaler, so a reverse distributor can be used instead. A reverse distributor processes expired or damaged drugs from a pharmacy and removes them to be returned back to the manufacturers for credit. Pharmacies in return can then receive back partial credit for expired medications, and also benefit from not having to dispose of the expired medications themselves.
Not all expired drugs are eligible for credit. Medications that are compounded are not eligible for return to a manufacturer. Partially filled liquid bottles may not be eligible. A reverse distributor can remove expired or damaged drug from a pharmacy, return to manufacturers where appropriate, then give the pharmacy back the credit. Reverse distributors typically take part of the credit as their payment for service.
Review Questions
The following questions help you review the chapter. Test your knowledge by working through the next 50 questions to test yourself and identify any areas you may need to review.
1. A prescription filled for a patient that has not been picked up in a specified number of days is able to be
A. sent with a reverse distributor for manufacturer credit
B. sent back to the wholesaler for a refund
C. returned to stock
D. given back to the manufacturer for a refund
2. A credit from the wholesaler may be given for
A. expired drugs
B. damaged drugs
C. all refrigerated drugs
D. unopened drugs not close to expiration
3. A medication is available as 125mg/5mL. How many mL is a 112mg dose?
A. 4.5mL
B. 5.2mL
C. 5.4mL
D. 6.2mL
4. The last set of numbers in an NDC describes
A. the drug
B. the package size
C. the manufacturer
D. the expiration date
5. A medication is prescribed to a patient at 3.5mg/kg. The patient weighs 92 lb. How many mg is one dose for this patient?
A. 122mg
B. 146.3mg
C. 163.5mg
D. 322mg
6. An expiration date on a drug stock bottle of 12/26 would expire on
A. December 26 of the current year
B. December 31 of 2026
C. December 1 of 2026
D. December 26 of 2026
7. How much active ingredient (in mg) is in 5mL of a 35% solution?
A. 1.75mg
B. 204mg
C. 1,750mg
D. 1,895mg
8. Which of the following is a machine that turns a liquid into fine droplets able to be inhaled?
A. spacer
B. nebulizer
C. MDI
D. nebule
9. How many mL of active ingredient are in 150mL of a 5% solution?
A. 1.5mL
B. 5.4mL
C. 6.2mL
D. 7.5mL
10. Which device is used to draw blood for a point of care test?
A. test strip
B. glucometer
C. lancet
D. DME
11. How many mg of hydrocortisone is in a 15g tube of 1% ointment?
A. 150mg
B. 1.5mg
C. 250mg
D. 375mg
12. Which gauge needle would be most likely selected to draw up thick or viscous liquid?
A. 32g
B. 29g
C. 27g
D. 21g
13. How many mL are needed to fill a 7-day supply of a 500mg/5mL medication given TID?
A. 22mL
B. 64mL
C. 105mL
D. 115mL
14. A patient has a prescription for 4 fl oz. How many mL is this?
A. 30mL
B. 60mL
C. 120mL
D. 180mL
15. When reading a measurement for a liquid, such as in a graduated cylinder, you should read
A. at the bottom of the meniscus
B. at the top of the meniscus
C. at the bottom of the bubble
D. even with the top of the water line
16. Which of the following would be used to crush or mix powders?
A. conical cylinder
B. mortar and pestle
C. beaker
D. spatula
17. How many mg will a 64kg patient take per dose, if the order is written for 2.5mg/kg/day in 3 divided doses?
A. 35.3mg
B. 42.9m
C. 53.3mg
D. 160mg
18. The process of grinding a particle to a powder is known as
A. spatulation
B. geometric dilution
C. trituration
D. reconstitution
19. A liquid dosage form that is compounded so the active ingredient is completely dissolved is a
A. cream
B. suspension
C. solution
D. gel
20. A drug packaged for a single administration is a(n)
A. BCMA
B. ADC
C. unit-of-use
D. unit dose
21. How many mg are in a 150mL of a 12% solution?
A. 12,000mg
B. 13,000mg
C. 16,000mg
D. 18,000mg
22. A patient has a prescription for the following:
Lantus insulin 1,000units/10mL vial
Inject 30 units in the morning and 20 units in the evening subcutaneously.
How many vials should be dispensed for a 30 day supply?
A. 1.5 vials
B. 2 vials
C. 2.5 vials
D. 3 vials
23. Define the following prescription:
1 tab PO Q4–6H PRN HA
A. 1 tablet dissolved under the tongue every 4 to 6 hours as needed for heartburn
B. 1 tablet by mouth every 4 hours as needed for hypertension
C. 1 tablet by mouth every 4 to 6 hours as needed for headache
D. 1 tablet in the cheek every 4 to 6 hours as needed for heart rate
24. How many mg are in a dose of 15mL of a 250mg/5mL suspension?
A. 250mg
B. 500mg
C. 750mg
D. 1,000mg
25. A 189 lb patient is prescribed 5mg/kg Q8H. How many mg does the patient take in one day?
A. 945mg
B. 1,298mg
C. 2,393mg
D. 2,835mg
26. A patient has an order for 0.025 L of a medication PO QID. How many mL will the patient take daily?
A. 0.1mL
B. 75mL
C. 100mL
D. 1,000mL
27. A patient is prescribed a medication 2.3mg/m2. The patient’s BSA is 1.8 m2. What is the dose for this patient?
A. 0.78mg
B. 1.28mg
C. 4.14mg
D. 5.9mg
28. An inactive or inert substance is known as a(n)
A. active ingredient
B. tritruation
C. meniscus
D. excipient
29. What is the process of mixing two substances together, sometimes on an ointment slab, using a spatula?
A. spatulation
B. trituration
C. geometric dilution
D. levigation
30. A hospitalized patient has an order for 16mEq of potassium injection 2mEq/mL in a 20mL vial. How many mL should be drawn up for one dose?
A. 1.25mL
B. 8mL
C. 10mL
D. 32mL
31. A technique used for mixing, in which a small amount of liquid is mixed with a powder, is known as
A. tritruation
B. levigation
C. geometric dilution
D. spatulation
32. Which of the following would require a mold when compounding?
A. enema
B. elixir
C. suppository
D. cream
33. An order is written for 50mL of a 10% solution. You have a 35% solution in stock. How much stock solution and how much diluent is needed to compound this order?
A. 40mL of stock, and 10mL of diluent
B. 49mL of stock and 1mL of diluent
C. 42.9mL of stock and 7.1mL of diluent
D. 38.4mL of stock and 11.6mL of diluent
34. A technician is preparing 30g of 2% hydrocortisone ointment using a 1% and 10% base. Determine how many grams of each base are required to compound this order.
A. 28g of 10% and 2g of 1%
B. 3.3g of 10% and 26.7g of 1%
C. 4.8g of 10% and 25.2g of 1%
D. 9.4g of 10% and 20.6g of 1%
35. A prescription for 160mL would best fit in which size bottle?
A. 3 fl oz
B. 4 fl oz
C. 5 fl oz
D. 6 fl oz
36. Which part of the syringe has the calibration lines to measure volume?
A. barrel
B. plunger
C. hub
D. bevel
37. A patient has an order for 100mg suspension to be taken every 6 hours. How many doses can the patient get from one 300mL bottle of 250mg/5mL?
A. 15 doses
B. 75 doses
C. 100 doses
D. 150 doses
38. A pharmacy must compound sodium bicarbonate into a syringe. How much active ingredient is needed to make 50mL of an 8.4% solution?
A. 4.2g
B. 0.4mg
C. 8.4mg
D. 0.08g
39. A device that measures blood glucose levels at home is known as a
A. spacer
B. nebulizer
C. lancet
D. glucometer
40. A pediatric patient is ordered 3.5mcg/kg PO BID. The child weighs 23 lb. What volume should be given per dose, if the medication is available as 125mcg/1mL?
A. 0.29mL
B. 3.675mL
C. 2.93mL
D. 36.75mL
41. A lot number is used for
A. expiration dating
B. recalls
C. fast mover information
D. LASA
42. An order for prednisone reads:
Prednisone 10mg. Take 3 tabs TID × 3 days, then 2 tabs TID × 3 days, then 1 tab BID × 5 days, then 1 tab QD × 3 days.
How many prednisone 10mg tablets are needed to fill this order?
A. 47 tabs
B. 52 tabs
C. 57 tabs
D. 58 tabs
43. The middle set of numbers in an NDC will tell the
A. manufacturer
B. drug
C. package size
D. wholesaler
44. How many clonidine patches are needed to fill a prescription for a patient applying 1 patch every 7 days for a 30-day supply?
A. 3 patches
B. 4 patches
C. 5 patches
D. 6 patches
45. A pharmacy technician is completing temperature checks and notes a temperature as 35.3°C. What temperature in °F is this?
A. 70.2°F
B. 79.6°F
C. 86.8°F
D. 95.4°F
46. A pharmacy technician is drawing up 34 units of insulin into an insulin syringe. If the vial holds 1,000units/10mL, how many mL will be drawn up into the syringe?
A. 0.1mL
B. 0.34mL
C. 3.4mL
D. 10mL
47. How many 25mg tablets are needed to compound 150mL of a 0.5mg/mL suspension?
A. 1 tab
B. 3 tabs
C. 7 tabs
D. 9 tabs
48. A pharmacy is compounding 200mL of a 10% dextrose solution. The pharmacy has 50% dextrose on hand and is mixing with sterile water. How much sterile water should be mixed with the dextrose to reach 10%?
A. 40mL
B. 74mL
C. 140mL
D. 160mL
49. How much volume of magnesium sulfate 50% would be needed for a dose of 32g?
A. 18mL
B. 36mL
C. 64mL
D. 97mL
50. A cephalexin suspension is available as 250mg/5mL. A patient is prescribed 7.5mL PO BID. How many mg will a patient take daily?
A. 375mg
B. 425mg
C. 585mg
D. 750mg
Answers
1. C
Prescriptions that have not been picked up for a specific number of days in a pharmacy can be returned back to stock.
2. D
A credit return is a credit from the wholesaler to an invoice after sending back eligible drugs. Medications eligible for credit cannot have been opened or damaged or be close to expiration. Typically, drugs need to be at least 6 months out from the expiration to be returnable for credit.
3. A
4.5mL.
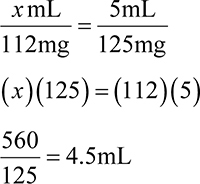
4. B
The last set of numbers is the package code. This describes the package’s size and type.
5. B
146.3mg.
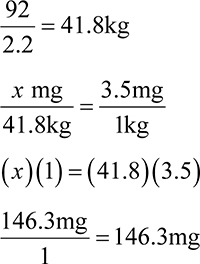
6. B
If a manufacturer indicates a month and year only, you can assume it is the last day of this month, so 12/26 would be 12/31/2026.
7. C
1,750mg.
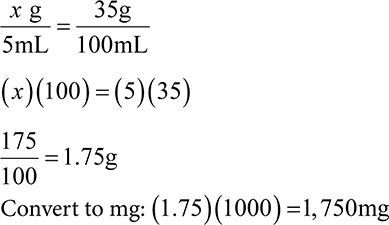
8. B
A nebulizer is a machine that uses a nebule (vial of solution) and turns it into a mist to be inhaled.
9. D
7.5mL.
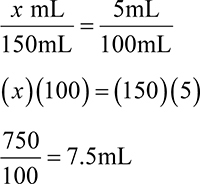
10. C
To draw blood, a patient may use a lancet, which is a device that quickly pricks the skin.
11. A
150mg.
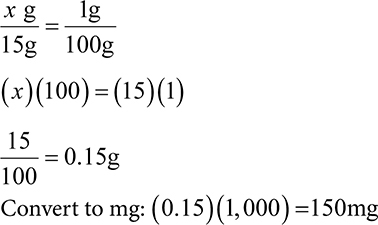
12. D
21g. The size of gauge used depends on what procedure is being administered. Smaller gauge or large needles are used for viscous or thick liquids to help draw fluid into the syringe.
13. C
105mL.
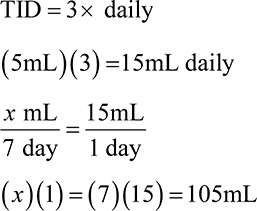
14. C
120mL.
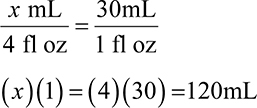
15. A
When you are measuring a liquid, it is important to read the measurement at the bottom of the curved fluid surface, which is known as the meniscus. This allows for a more accurate measurement, as reading the top of the meniscus would be an inaccurately high value and too much liquid would be used.
16. B
If tablets or powders must be crushed or mixed, a mortar and pestle may be used. A mortar is a bowl, and a pestle is a tool with a rounded end that is used for crushing and grinding.
17. C
53.3mg.
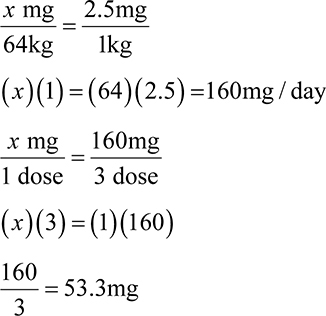
18. C
Trituration is the process of reducing a particle to a powder through grinding using a mortar and pestle.
19. C
Solutions are composed of a liquid with a completely dissolved active ingredient.
20. D
A unit dose medication is a drug packaged for a single administration.
21. D
18,000mg
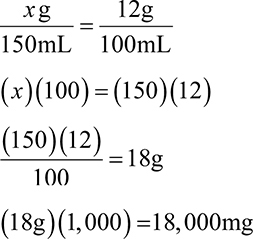
22. B
2 vials.
First, determine how many units the patient is using per day:
30+20 = 50 units.
Because the pharmacy cannot dispense a half of a vial, the patient will need 2 vials.
23. C
1 tablet by mouth every 4 to 6 hours as needed for headache.
tab = tablet
PO = by mouth
Q4–6h = every 4 to 6 hours
PRN = as needed for
HA = headache
24. C
750mg.
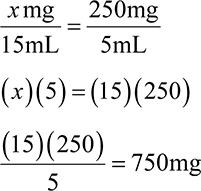
25. D
2,835mg.
26. C
100mL.
QID = 4 × daily
(0.025)(4) = 0.1L
(0.1)(1,000) = 100mL
27. C
4.14mg.
28. D
An inert or inactive substance is known as an excipient.
29. A
Spatulation is the process of using a spatula to mix substances together.
30. B
8 mL.
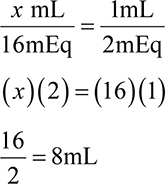
31. B
Levigation is a technique used to mix substances together, specifically grinding powder, but with a small amount of liquid.
32. C
Suppositories are solid dosage forms that inserted into the body and melt at body temperature or dissolve into the mucous membranes. They are compounded using a mold depending on the type of suppository.
33. C
42.9mL of stock and 7.1mL of diluent.
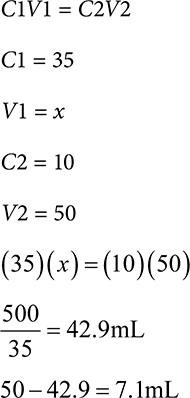
34. B
3.3g of 10% and 26.7g of 1%.
35. D
6 fl oz.
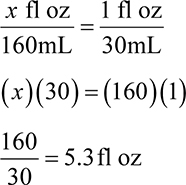
The best size would be 6 fl oz to accommodate all of the liquid.
36. A
The barrel is a tube with the calibration lines used for measuring volume.
37. D
150 doses.
38. A
4.2g.
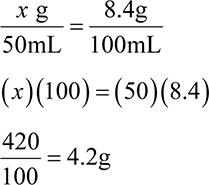
39. D
Patients with diabetes will need to continuously monitor blood glucose levels. To do this at home, a glucometer is recommended.
40. A
0.29mL.
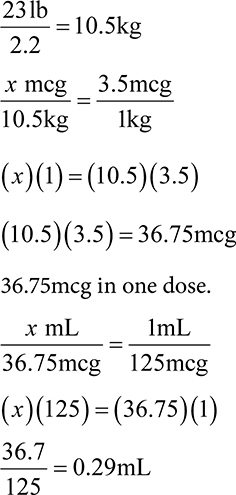
41. B
A lot number is a number assigned to a batch of medication. It allows the manufacturer to trace potential adverse incidents in a particular group of drugs. If a recall is necessary, lot numbers are used to identify the specific drugs impacted.
42. D
58 tabs
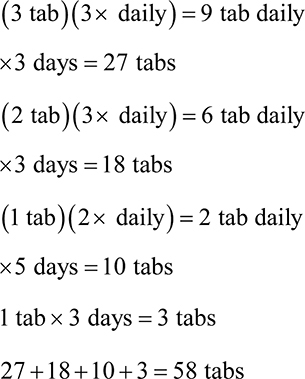
43. B
The second set of numbers is the product code. This identifies the product, including the drug strength and dosage form.
44. B
4 patches will last the patient over 30 days.
45. D
95.4°F.
°F = (1.8 × 35.3) + 32
63.36 + 32 = 95.4°F
46. B
0.34mL.
47. B
3 tabs.
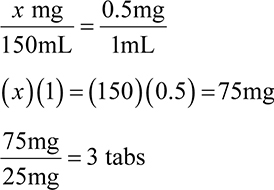
48. D
160mL.
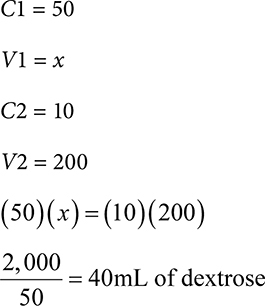
To determine how much diluent needed, subtract from total: 200mL − 40mL = 160mL diluent.
49. C
64mL.
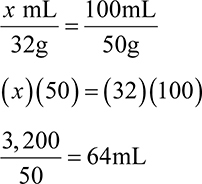
50. D
750mg.
