Another element that statisticians have to pay attention to is variability, which is a measure of the spread of a data set. Let’s say you are looking at the scores the students in a single grade have on a physical fitness test. It would be useful to have a way to look at how much variation there was in the scores to know if all the students had roughly the same success on the test or if there was a lot of variation in their results.
MEASURES OF VARIABILITY, OR DISPERSION
Two distributions may have averages that are exactly alike, yet there may be little or no variation in one and great variation in the other. For example, the arithmetic mean for the two distributions that follow is 4, yet in the second series the variation is zero:
Series I: 1234567
Series II: 4444444
This example shows the need for a measure that will tell whether the data cluster closely about the average or are scattered widely. Variability, like averages, is described by the statistician with a single number in order to make it easier to compare dispersions. Several measures of variability have been devised.
RANGE
The simplest measure of variability is the range—the difference between the highest and the lowest scores in the sample. In Table II the range is 7.6 grades—the distance from the highest grade level, 11.2, to the lowest, 3.6. The chief difficulty with the range as a measure of variability is that extreme scores are given too much significance.
INTERQUARTILE RANGE
When central tendency is measured by the median, percentiles may be used to indicate the spread. The interquartile range includes the middle 50 percent of the cases. It is found by determining the point below which 25 percent of the cases fall (the 25th percentile, or first quartile) and the point above which 25 percent fall (the 75th percentile, or third quartile). The difference between these two values measures the middle 50 percent of the scores or measures. In Table II the interquartile range is 2.1 (the difference between 8.4 and 6.3).
Statisticians more commonly use half this distance as their measure of variability. This is called the semi-interquartile range, or the quartile deviation. In this example it would be 1.05.
AVERAGE DEVIATION
The average, or mean, deviation is obtained by subtracting each score from the mean score and averaging the deviations—disregarding the fact that some are positive quantities and some are negative. The obtained value can be interpreted as a measure of how much the individual scores deviate, on the average, from the mean. The larger the average deviation, the greater the variability.
The best measure of variability is the standard deviation. Like the average deviation, it is based on the exact deviation of each case from the mean. The deviations, however, are squared before being added. Then the sum is divided by the number of cases and the square root is extracted. In the series of numbers 2, 4, 7, 7, 8, 9, 12, 15, 17, the mean is 9. The standard deviation is 4.6. This can be verified by performing the operation described above.
COMPARING TWO GROUPS OF SIMILAR DATA
The data presented so far consist of a single measurement for one group. Frequently it is desirable to compare two groups with regard to a single measure.
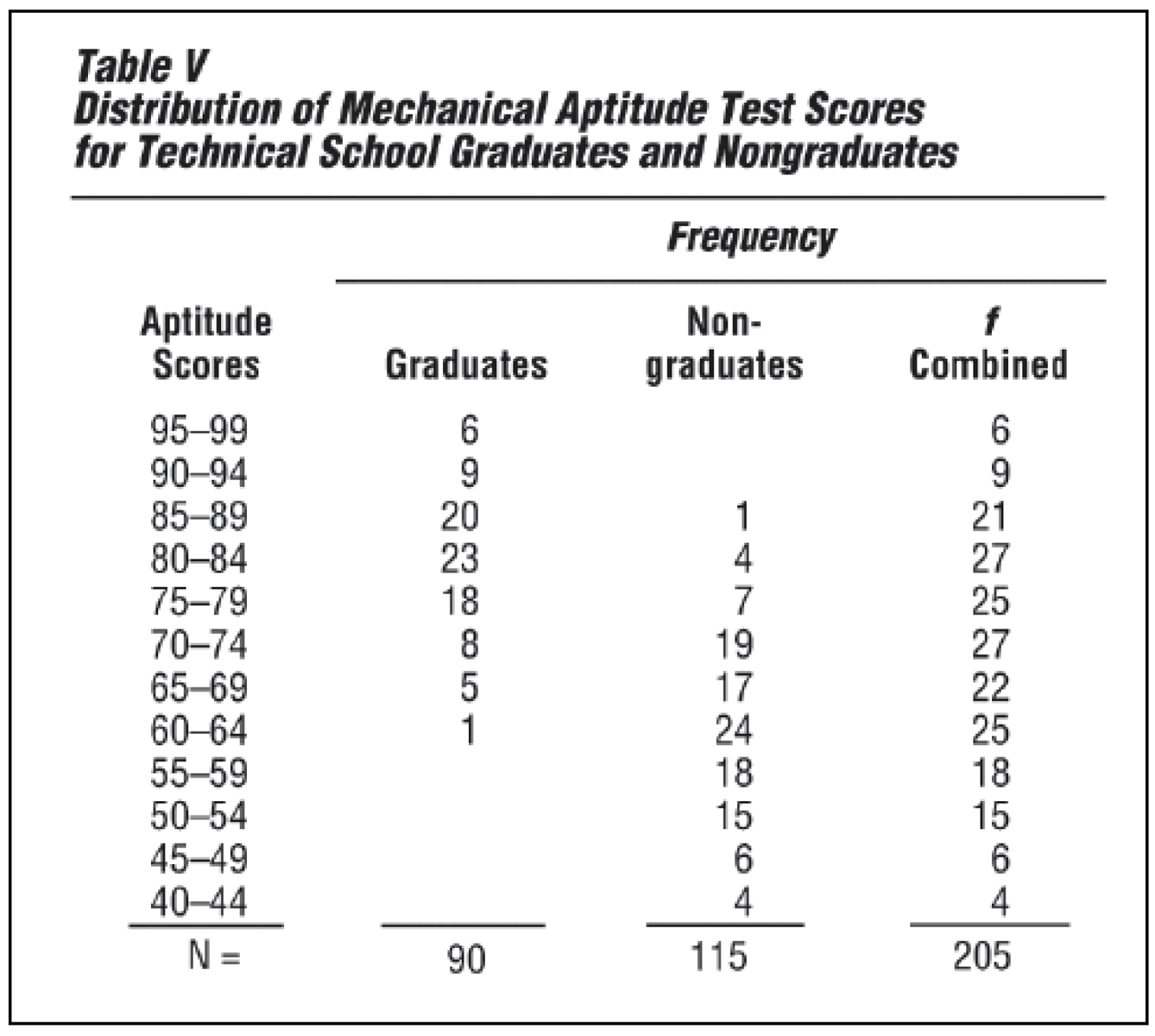
Suppose you are interested in selecting better students for a technical school with the aim of decreasing the proportion of students who fail or drop out before they finish the course. It is decided to give all entering students a mechanical aptitude test and then follow up later to see whether the test actually predicts anything about success in the school.
Table V shows the results that might have been obtained in such a study. The criterion of success is simply graduation. Before deciding to use the aptitude test for selection, however, the averages and variabilities of the two groups must be studied.
Encyclopædia Britannica, Inc.
Table VI shows very clearly that the students who graduated had a higher average score than those who did not. This is true whether one compares the modes, the medians, or the means. Note that 90 percent of graduates exceeded the mean for the total group, while only 15 percent of the nongraduates exceeded it. In addition, while there is considerable variation in each group, there is greater variability among the nongraduates than among the graduates. There is even greater variation in the combined group.
Encyclopædia Britannica, Inc.
Figure B shows two simple frequency polygons on the same chart.
Figure C shows the two distributions in terms of cumulated percentage frequencies. The distance between the two curves shows that the graduates scored distinctly higher than did the nongraduates all along the line. Any score equivalent (such as the median score, or 50th percentile) can be obtained by running up from the percentile scale to the curve and across to the score scale. Figure C actually constitutes a set of norms for this test, because any applicant’s score can be evaluated in terms of how the applicant compares with either group.
MEASURES OF RELATIONSHIP
When data are obtained for two or more traits on the same sample, it may be important to discover whether there is a relationship between the measures. For example, statisticians may try to answer questions such as: Is there a relationship between a person’s height and weight? Can one judge a person’s intelligence from any physical characteristic? Is personality related to job success? Is income related to how far a person went in school?
These questions are examples of correlation, or relationship, problems. In every case there has to be a pair of measurements for each person in the group before one can measure the correlation. For example, to determine the correlation between height and weight for high-school students, each student’s height and weight must be known. By tabulating each pair of measurements on a scattergram, or scatter diagram, a visual idea of the correlation is possible.
Figure D, a scatter diagram, shows the paired grade-level scores on a test of paragraph meaning and a test of word meaning for a group of sixth-grade pupils. The vertical axis (y) is laid out in terms of grade level for the paragraph-meaning test scores. The horizontal axis (x) is laid out in terms of grade level for the word-meaning test scores. Each tally mark represents both scores for one pupil. For example, one pupil scored 8 on word meaning and 5 on paragraph meaning. The two scores are represented by a single tally mark placed in the square that is directly above the 8 on the horizontal scale and across from the 5 on the vertical scale.
Table VII is a contingency table that shows the scores grouped by class intervals, with numerals in place of the tally marks. In both the scatter diagram and the contingency table, the scores tend to fall into a straight band that rises from left to right. It is evident that there is a decided trend toward higher scores on paragraph meaning to go with higher scores on word meaning. This is called positive correlation. Note, however, that the correlation is not perfect. For example, ten pupils who scored at the sixth-grade level for paragraph meaning scored at the seventh-grade level for word meaning, as indicated in Figure D.
Encyclopædia Britannica, Inc.
Sometimes there are negative correlations. This means that higher scores for one variable tend to be associated with lower scores for the other variable. Zero correlation indicates that there is no relationship between the two; knowing a person’s score or rank on one variable would not enable the prediction of the person’s score on the other variable.
CORRELATIONS AND CAUSES
High correlations—whether positive or negative—are extremely useful because they enable statisticians to make accurate predictions. Zero correlations—which will not predict anything—are also useful. They may show, for example, that one cannot judge a person’s intelligence from head size. In this case the correlation between head size and intelligence is close to zero. However, a high correlation between two traits does not necessarily mean that one trait caused the other trait.
The amount of evidence required to prove a cause-effect relationship between two traits is much greater than that needed to simply show a correlation. The size of the correlation coefficient as computed for the data shown in Figure D is 0.76. Since this correlation is not extremely high, a good statistician would bear this in mind and proceed with caution in predicting one variable from the other.
Statisticians use a number called the correlation coefficient to express numerically the degree of relationship. The correlation coefficient runs from -1.00 (perfect negative correlation) through 0 (no correlation) to +1.00 (perfect positive correlation).
THE MANIPULATION OF STATISTICS
One of the chief problems with statistics is the ability to make them say what one desires through the manipulation of numbers or graphics. Graphs are frequently used in newspapers and in the business world to create a quick and dramatic impression. Sometimes the graphs used are misleading. It is up to the reader to be alert for those graphs that are designed to create a false impression. For example, changing the scales in a graph or chart or omitting a portion of the items in the sample creates a false impression. Figure E shows two graphs comparing the student populations of three schools. The second graph exaggerates the population differences by showing only the top part of the scale.