8
Basics of Parallel Programming

Today, almost all computer systems, including embedded and mobile systems, are equipped with multicore microprocessors – not to mention graphics programming units (GPUs), which are equipped with thousands of cores. However, all the programs we have written and analyzed until now perform sequentially. That is, although we have multiple functions and calls between them, a microprocessor sequentially processes only instruction at a time. This does not seem like the most efficient way to use the available hardware resources. Before we go into detail, let's summarize the main topics we will learn about in this chapter:

  1. Basic concepts of parallel computations
  2. What concurrent multitasking and threads are
  3. The risk of using shared objects, and how to protect their access
  4. How to make standard algorithms like std::transform , std::sort , and std::transform_reduce operate in a parallel mode
  5. Programming asynchronous tasks with std::future
  6. Basic construction of the OpenMP library – e.g. how to launch and synchronize multiple tasks, and how to make for operate in parallel to significantly speed up matrix multiplication

8.1 Basic Concepts of Parallel Computations

Since an example is better than a hundred words, let's start by analyzing the behavior of a simple function Task_0 run simultaneously on two threads (later, we will show what a thread is and how to make code run on multiple threads). Let's also assume that Task_0 accesses a global variable x . The situation is outlined in Figure 8.1.

After launching the two threads, each running the same Task_0 , the output may look like the following

or it may look totally different. On five threads, the output may look like this:

Schematic illustration of an example of parallel execution of two tasks that access the same global object x. Since each instruction for each task can be executed at any time and simultaneously, the results of such free access are unpredictable and usually wrong.

Figure 8.1 An example of parallel execution of two tasks that access the same global object x . Since each instruction for each task can be executed at any time and simultaneously, the results of such free access are unpredictable and usually wrong. The way out of this problem is to make all lines that access common shared objects protected, to allow only one thread to execute at a time. Code that needs this type of protection is called a critical section, and the protection can be provided using synchronization objects such as a semaphore or a mutex.

More often than not, the results are incorrect and different from run to run. Such a situation is called a race condition or a hazard. In such a case, we would be lucky to diagnose the incorrect output, since this issue can turn on the red light indicating that something is wrong and needs to be fixed. However, in many cases, errors are stealthy and appear randomly, which makes debugging and verifying parallel code much more difficult.

We have to realize that each instance of Task_0 runs concurrently. This intersperses the execution of Task_0 's sequential instructions with the execution of analogous instructions, but in different instances (threads). So, for example, an instance run by thread 0 finishes executing line [3], after which thread 5 is faster and manages to execute lines [3–6] of its code. This changes the common object x . If thread 0 now gets its portion of time and executes line [6], the values of x and loc will be far from what is expected and usually random. Also, the expression on line [8], whose intention was to display the two values, is not atomic. That is, its execution can be partitioned between different threads that happen to execute this code at more or less the same time, which leads to haywire output.

There is nothing wrong with Task_0 itself. If run sequentially – for example, in a for loop – it produces correct results that can be easily verified. This simple experiment should alert us that entering the realm of parallel programming can be like entering quicksand. Of course, this is the case only if we are not careful. Knowledge and conscious software design are the best protection measures.

The broad domain of parallel programming is gaining in importance and popularity. Providing more than an introduction is outside the scope of this book, but we can recommend many resources (Pas et al. 2017; Fan 2015; Schmidt and Gonzalez-Dominguez 2017). The intention of this section is to show that with a few new techniques and carefully analyzed cases, writing simple parallel components in C++ is not that difficult. The gain is worth the effort – as we will see, one additional line of code or a single parameter in a function can instantly make our code perform a few times faster than its sequential counterpart. This is in the spirit of C++, which also means better performance.

Before we show these techniques, we will briefly explain the most important concepts related to the domain of parallel programming:

  1. Task, multitasking – A procedure, function, etc. to be executed. Multitasking usually refers to the concurrent realization of multiple tasks
  2. Thread, multithreading – A thread is a separate path of code execution. It can be seen as the code and computer resources necessary to perform a task. Multithreading means the ability to run multiple threads concurrently. Threads can be executed by a single core or multiple cores of a processor. A single core can also run one or more threads by means of the OS's thread-preemption mechanism: a thread can be preempted at any moment and put into the queue of waiting threads; it can be then resumed by the OS as the result of an event, a specific condition, elapsed time, etc
  3. Thread pool – A group of pre-created threads that wait to be assigned to tasks for a concurrent execution. Maintaining a pre-created pool of threads increases performance by avoiding time-costly creations and deallocations of threads, but at a cost of increased resource usage. Once created, the pool of threads is usually maintained until the last parallel region is executed in the program
  4. Team of threads – A group of threads for work sharing inside a parallel region. One of the threads is appointed the master and the others are worker threads, as shown in Figure 8.2. The process of spawning multiple threads is sometimes called a fork. When threads meet at a common point, this is called a join (i.e. they are synchronized)
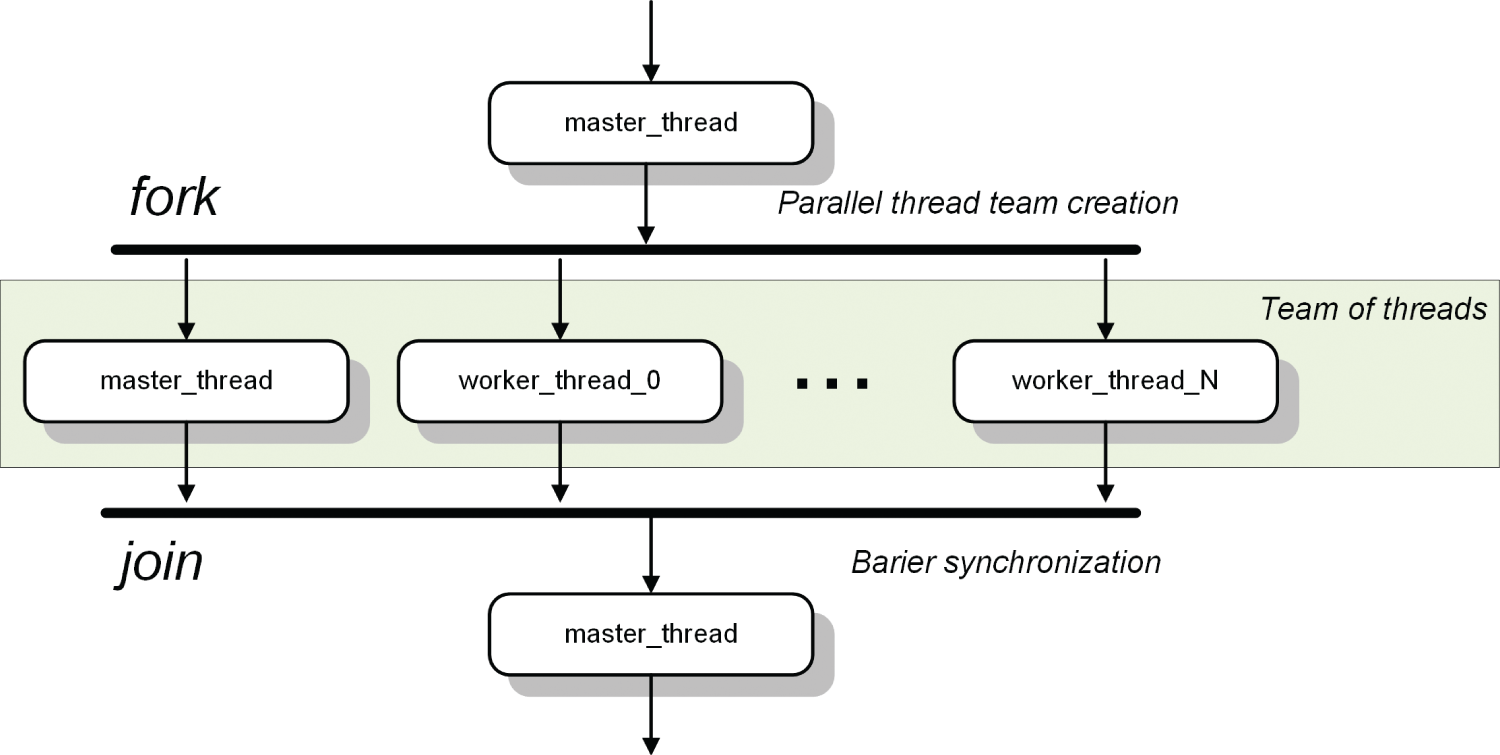
    Schematic illustration of the team of threads operating in parallel on an array of data. Each thread takes its assigned chunk of data. Processing is performed independently in an asynchronous fashion. After all the threads finish processing the entire data array, their common results can be gathered and processed further.

    Figure 8.2 UML activity diagram showing the launch of a team of threads.

  5. Concurrency – The simultaneous execution of multiple tasks/threads
  6. Shared objects (resources) – Resources (objects) that can be accessed concurrently by many threads. If a resource can be changed by any of the threads, then special protection techniques should be used to allow access by only one thread at a time, to prevent hazardous results
  7. Private objects (resources) – Resources (objects) that are entirely local to a task/thread and to which other threads do not have access (e.g. via a pointer, etc.); Private objects do not need to be protected for exclusive access since each thread has its own copies
  8. Critical section – Part of the code in a task/thread that accesses a shared object and should be protected to ensure exclusive access of only one thread at a time
  9. Mutual exclusion – A mechanism that allows only one thread to execute uninterrupted its critical section. This is achieved by applying an available thread synchronization object
  10. Deadlock – An error situation in which threads wait for each other to unlock common resources and cannot proceed
  11. Atomic instruction – An instruction that can be completed by a thread without interruption by other threads. Atomic instructions are used to perform safe access to shared resources
  12. Synchronization – The process of waiting for all threads to complete. Such a common point of completion is a barrier. Sometimes synchronization refers to the mechanism of providing exclusive access to resources. System mechanisms such as semaphores, locks, mutexes, signals, etc. are synchronization objects
  13. Thread safety – A safety policy for an object or class when operating in a multithreading environment. A class is said to be thread-safe if, when an object of that class is created that is local to that thread, it is safe to call any method from that object (this is not the case if e.g. a class contains data members declared static or that refer to global objects, etc.). An object is thread-safe if it can be safely accessed by many threads with no additional protection mechanism; this means, if necessary, synchronization mechanisms have been implemented in that object

As we saw in this section and the simple example, writing correct parallel code is much more difficult than simply multiplying instances of sequential code. As we may expect, one of the most important aspects is locating and properly protecting all accesses to common, i.e. shared, objects, especially if these are changed by the code. But in practice this can be extremely difficult due to code complexity, which hides common regions and objects. A hint from this lesson is to first take a closer look at all global and static objects. When porting a sequential algorithm into its parallel counterpart, it is also good practice to compare the results of both versions: for example, by writing proper unit tests, as discussed in Appendix A.7.

8.2 Adding Parallelism to the Standard Algorithms

In this section, we will show how to make the standard algorithms perform in a parallel fashion. As we will see, this is easily achieved by adding a single parameter. But we should not do this blindly – as always in an analysis of parallel algorithms, we should identify and protect shared resources to avoid uncontrolled access by more than one thread at a time. However, if there are no shared objects, then many calls to the standard libraries can be treated as separate tasks that can run in parallel. As we will see, adding std::execution::par as the first parameter will make this happen.

In the following sections, we will build parallel systems based on splitting an initial array of data into a number of chunks that will then be independently processed by separate threads, as shown in Figure 8.3. This methodology is called data parallelism and usually gives good results when processing massive data, such as mathematical arrays, image and video files, etc. We will rely on programming techniques that make this process as simple and error-free as possible.

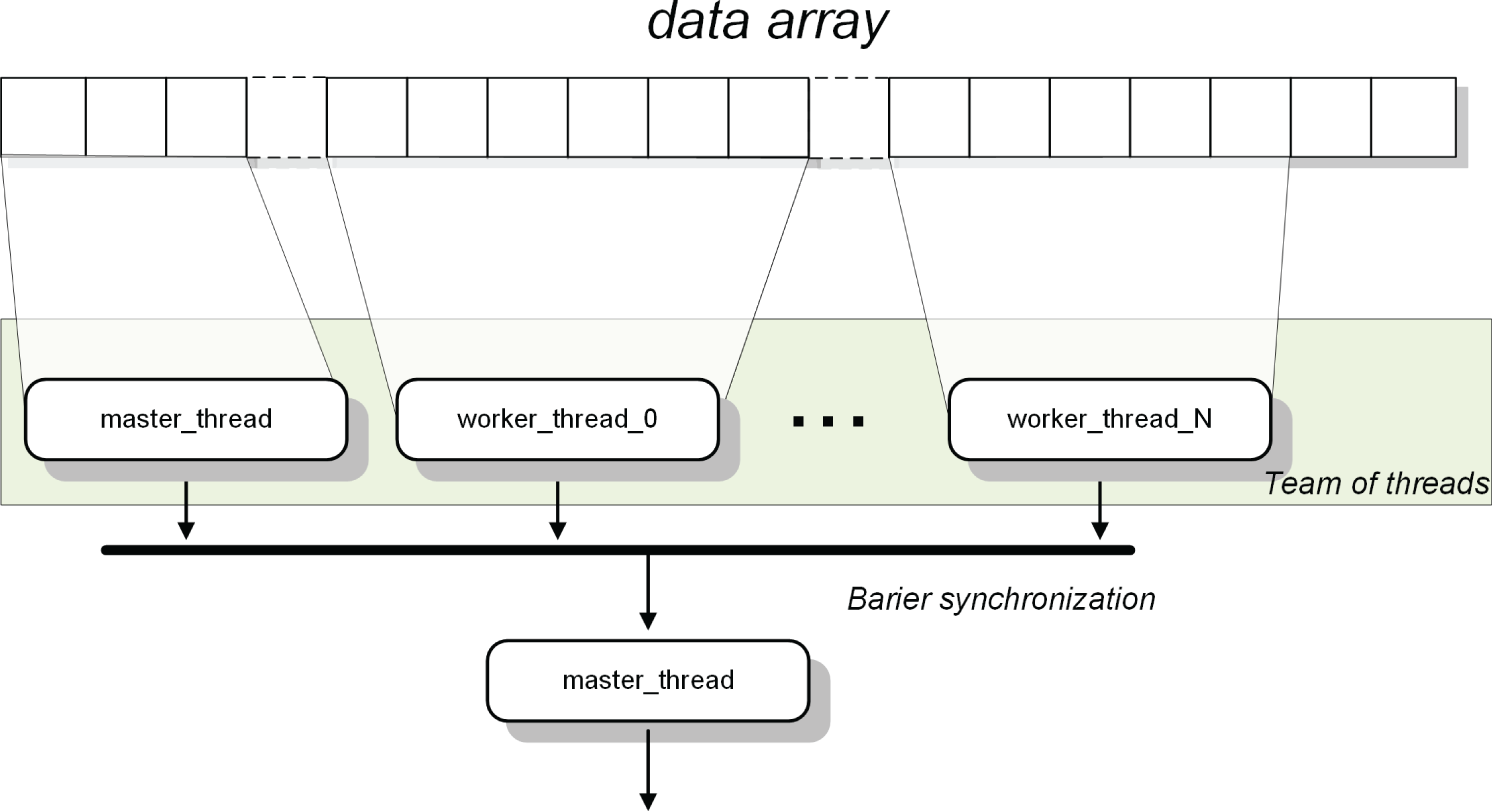
Schematic illustration of the team of threads operating in parallel on an array of data. Each thread takes its assigned chunk of data. Processing is performed independently in an asynchronous fashion. After all the threads finish processing the entire data array, their common results can be gathered and processed further.

Figure 8.3 Team of threads operating in parallel on an array of data. Each thread takes its assigned chunk of data. Processing is performed independently in an asynchronous fashion. After all the threads finish processing the entire data array, their common results can be gathered and processed further.

Listing 7.14 shows the InnerProducts namespace. It contains three serial algorithms for computing the inner product between vectors (Section 7.4.7). Let's recall their characteristic features:

  1. InnerProduct_StdAlg – Calls std::inner_product and returns its result
  2. InnerProduct_SortAlg – Creates a vector of individual products between the corresponding elements of the two vectors. These products are then sorted and finally added together. Thanks to sorting, we achieve much more accurate results as compared with the InnerProduct_StdAlg algorithm. However, sorting significantly increases computation time
  3. InnerProduct_KahanAlg – A version of the accurate Kahan summation algorithm of the products of the corresponding elements of the two vectors

In this section, we will present new versions of the first two functions: they will perform the same action but in a parallel fashion, potentially taking advantage of available multicore processor(s). A parallel version of the third function is presented in the next section.

The first two parallel functions are as follows:

  1. InnerProduct_TransformReduce:Par – Based on the std::transform _reduce algorithm, which, unlike std::inner_product , allows for parallel operation. Briefly, transform-reduce is a classical scheme of parallel processing in which a problem is split into a number of smaller problems (transformation) that are then solved, after which the partial results are gathered together (reduction)
  2. InnerProduct_SortAlg_Par – A version of the serial InnerProduct_SortAlg that calls the parallel implementation of the standard sorting algorithm std::sort

The definition of the InnerProduct_TransformReduce:Par function begins on line [11] in Listing 8.1. There is only one expression on line [13], although we have split it into multiple lines for better readability. What is important is the new std::transform _reduce function with the first parameter std::execution::par . In our example, it performs the same action as std::inner_product ; but, unlike std::inner_product , it is able to operate in parallel. Going into detail, on line [14] it takes three iterators that define the range of its operation. That is, two input vectors v and w are element by element multiplied, and these products are added together. This is exactly what transform-and-reduce means – the input elements are transformed in some way (here, they are multiplied) and then reduced to a scalar value, i.e. in our case they are summed. These reduce and transform actions are defined by the two lambda functions on lines [15, 16].

InnerProduct_SortAlg_Par , defined on line [20], is a parallel version of the serial InnerProduct_SortAlg defined in Listing 7.14. Let's compare the two versions. The first difference appears on line [22], as well as in the following std::transform . When entering the domain of parallel algorithms, back_inserter is the last thing we wish to use. Although it worked fine in the serial implementation, in the parallel world we cannot let many threads back-insert into vector z . But the way around this is simple: we only need to reserve enough space in z , as on line [22]. Thanks to this simple modification, std::transform can operate in parallel and independently with any chunk of data. More specifically, the main difference between the serial and parallel versions is on line [27]. The serial approach uses back_inserter . In this version, however, we simply provide an iterator to the beginning of z , since it has already been allocated enough space to accommodate all of the results. We don’t need to protect z for the exclusive access since each of its elements is accessed only by one thread, whichever it is. Then, on line [31], the parallel version of std::sort is invoked. The difference between calling the serial and parallel versions is the presence of the first argument std::execution::par .

Finally, the sorted elements need to be summed. In the serial version, we did this with the familiar std::accumulate ; but it has no parallel version. Instead, we use std::reduce , again called with the first parameter set to std::execution::par , as shown on line [35].

The only reason we go to all this trouble with converting algorithms to their parallel counterparts is performance. Obviously, the performance time of the serial and parallel versions is the best indicator of success. But in practice, we may be surprised, at least in some of the cases. In the next section, we will show how to perform such measurements and explain what they mean.

We have only scratched the surface of parallel execution of the standard algorithms. The best way to learn more is to read the previously cited resources and visit websites such as www.bfilipek.com/2018/11/parallel-alg-perf.html and https://en.cppreference.com/w/cpp/algorithm/execution_policy_tag_t.

8.3 Launching Asynchronous Tasks

Still in the domain of the task of efficiently computing the inner product between two vectors, Listing 8.2 shows the InnerProduct_KahanAlg_Par function. This is a parallel version of InnerProduct_KahanAlg from Chapter 7. But in this case, rather than simply adding the parallel command std::execution::par to the standard algorithms, we will go into the realm of C++ multitasking. As we pointed out earlier, task parallelism can be achieved by launching a team of threads that concurrently process the tasks. In this section, we will exploit this possibility.

The definition of InnerProduct_KahanAlg_Par begins on line [5]. First, lines [8–14] define the initial control objects. Since InnerProduct_KahanAlg_Par performs in parallel, each task is attached to its specific chunk of data, with k_num_of_chunks denoting the number of chunks. In practice, data does not split equally, so usually there is some data left. This is held by k_remainder . Each chunk of data is then summed independently. Therefore, each result goes to the par_sum container defined on line [16]. Also, a summing function is called independently for each chunk of data. Such tasks are easily defined with lambda functions (Section 3.14.6). In our case, this is fun_inter , shown on lines [18–19].

The most characteristic part begins on line [21] with the definition of a std::vector storing std::future < double > objects. This allows us to define tasks that, after being properly created, can be asynchronously executed. In the loop on lines [25–28], the objects returned by the call to std::async with the parameters std::launch::async , fun_inter , and its local parameters are pushed into the my_thread _pool container. But the tasks are only collected – they are not invoked yet. A similar thing happens on lines [31–34] if there is a remainder.

Line [24] is also interesting: its purpose is to define a variable i with the same type as the k_num_of_chunks object. So, how do we determine the type of an object given the name of or a reference to that object? Line [24] explains how. First we need to call the decltype operator, which returns the type of k_num_of_chunks , which is then stripped of any decorators such as a reference, a const, etc. using std::decay . Finally, we specify what we are interested in: std::decay<>::type .

Let's now return to parallel operations. We have prepared our tasks, which are now deposited in the my_thread _pool container. This way, tasks that are created are invoked in the loop on lines [37–38]. More specifically, the call to future<>::get on line [38] launches whatever resources are necessary to execute our tasks. Thanks to our design, these operate independently; hence we were able to use async .

Finally, all the tasks finish their jobs – i.e. are synchronized – before the Kahan _Sum function is called on line [40]. Obviously, its role is to sum up all the partial sums returned by the tasks to the par_sum repository on line [38].

The lambda function fun_inter , on line [18], is based on a serial version of InnerProduct_KahanAlg , outlined on line [42]. This is an overloaded version of InnerProduct_KahanAlg but with simple pointers defining the beginning of the two data vectors. As a result, the function easily operates with chunks of data that have been allocated in memory.

Next is the most interesting moment – verifying whether all these parallel methods were worth the effort. We ran the serial and parallel versions on a single machine and compared their execution times; the results obtained on our test system1 are shown in Table 8.1.

Table 8.1 Execution times for computing inner products between vectors with 20 000 000 elements each. Three groups of algorithms were tested: simple accumulation, sorting and accumulation, and using the Kahan algorithm. In each case, the timings of the sequential and parallel implementations were compared.

Algorithm InnerProd vs. TransRed Sort_Ser vs. Sort_Par Kahan_Ser vs. Kahan_Par
Serial [s] 29 2173 129
Parallel [s] 12 475 11
Speed increase 2.4 4.6 11.7

The most impressive speed increase can be observed for the pair of Kahan-based algorithms. The parallel version outperforms its serial counterpart by more than an order of magnitude! Also, for the algorithms that employ prior element sorting, the speed increases more than four times. This shows that parallel programming is worth the effort. However, in more complex algorithms, an in-depth analysis should be performed in order to spot parts of the code that consume the most processor time. This analysis should be based on measurements and not on guessing. The profiler delivers reliable data to start with, as described in Appendix A.6.3.

8.4 Parallelization with the OpenMP Library

Running parallel versions of some of the algorithms from the SL is simple. But since operations are limited to specific tasks, this mechanism only solves some of the problems involved in implementing parallel systems. We can also design our own threads or run tasks using the ample C++ parallel library (Stroustrup 2013). Doing so has the immediate advantage of building an upper-level interface for the lower-level OS multithreading mechanisms. A correctly designed parallel implementation of the C++ parallel library will work on most modern systems; however, this level of programming requires substantial knowledge, experience, and effort to obtain good results.

The OpenMP library project, which brings us to a slightly higher level of parallel systems programming began in the 1990s. It is aimed at two languages: Fortran and C/C++. It has strong support from the steering committee, and at the time of writing, version 5.0 has been released (www.openmp.org). The most important features of OpenMP are:

  1. Higher-level programming focusing on tasks that automatically create a team of threads and support synchronization mechanisms
  2. Operation in a hybrid hardware environment (parallel code can be run on both CPU and GPU)
  3. Seamless integration with existing C++ code using the preprocessor #pragma (Appendix A.1). OpenMP code is added in the form of OpenMP directives with clauses. There are also some OpenMP-specific functions

An in-depth presentation of the most important features of OpenMP could consume a book by itself. In this section, we show only a few basic examples. However, they are very characteristic of the common uses of OpenMP, so we can try other parallel algorithms based on them. There are many good sources of information about OpenMP, including the OpenMP web page (OpenMP 2020). A very accessible introduction is Guide into OpenMP by Joel Yliluoma (https://bisqwit.iki.fi/story/howto/openmp). Also, we recommend the recent books by Pas et al. (2017) and Schmidt and Gonzalez-Dominguez (2017). Let's start with a simple example that will demonstrate the basic features of OpenMP.

8.4.1 Launching a Team of Threads and Providing Exclusive Access Protection

The first thing to do when using OpenMP is to add #include <omp.h> in the source file, as shown on line [4] in Listing 8.3. The definition of the OpenMP_Test function starts on line [8]. Line [13] creates the outStream object. This is a string stream to which all output produced by our parallel branches of code will be sent. But we can easily spot that this is a classic example of a shared object. Hence, access to it must be protected to avoid hazards, as will be shown. On line [16], the OpenMP function omp_get_num_threads is called. It simply returns the number of threads in the team currently executing the parallel region from which it is called. There is also a counterpart omp_set_num_threads function, which lets us set a number of desired threads.

Line [23] contains the first characteristic #pragma construction with an OpenMP directive: omp parallel says to create and launch a team of threads and to process the following block of code (lines [24–42]) concurrently in each of these threads. shared( outStream ) explicitly marks the outStream object as being shared. However, this does not protect it yet from an uncontrolled access by the threads.

The variable thisThreadNo created on line [27] is an example of a private object. That is, each thread contains a local copy. In each, thisThreadNo is initialized with the current thread number obtained from a call to the OpenMP function omp_get_thread_num . So, if there are 12 threads, the numbers are 0–11. Another local object kNumOfThreads on line [30] receives the total number of threads executing the parallel region by calling the previously described omp_get_num_threads function (these names can be confusing).

Now we wish to print information about the number of the thread that executes this portion of code, as well as the total number of threads involved. The operation is as simple as using the familiar std::cout or outStream in our case. However, recall that outStream is a shared object and needs to be treated specially: only one thread can perform operations on it at a time, while the others wait. To accomplish such mutual exclusion, on line [36] and again using #pragma , we create the omp critical ( critical_0 ) construction. It tells OpenMP to add a synchronization barrier. As can be easily verified, if critical was omitted, the output would be rather messy.2 Then we can be sure that the operation on lines [38–39] is performed entirely by a single thread until it finishes.

Line [42] ends the parallel block, and we are back in the sequentially executed part of the code. So, with no additional commands, on lines [49–50] we can print out the number of threads executing on behalf of this block. Likewise, line [53] prints all the information from the outStream object, which was stored there by the threads. Also note that in OpenMP, all thread implementations and manipulations are performed behind the scenes. Therefore it is a very convenient library.

The output of this code can be as follows:

Notice that a total of 12 threads are created in the team and that the critical section is accessed in a random order. But before and after the parallel region, only one thread is active.

An example of an explicit call to the omp_set_num_threads is shown on line [58]. If this is omitted, the number of threads in the team will be set to a default value (usually this is the number of cores in the microprocessor).

Also notice that including the omp.h header is not sufficient to use OpenMP in our projects. We also need to explicitly turn on the OpenMP compiler option. For example, in Microsoft Visual C++, we open the project's property pages and under C/C++, Language, set Open MP Support to Yes (/openmp). In the gcc and clang compilers, we set the –fopenmp flag in the command line.

8.4.2 Loop Parallelization and Reduction Operations

The next example shows what is probably the most common operation with OpenMP: parallelizing the for loop. The function Compute_Pi shown on line [3] in Listing 8.4 computes the value of the constant π in a parallel way. This is done in accordance with the method outlined by Eq. (7.52), which computes the integral in Eq. (7.55).

In Listing 8.4, we can see two objects. The first, defined on line [5], is a constant dx . The second, on line [8], is a simple variable sum of type double . Both are shared, but only sum will be changed, since tithis is the total sum of all of the elements that are added in the loop. Therefore, it needs to be synchronized. But since this operation is very common, OpenMP has a special reduction clause that allows for easy, safe updates of the shared variable.

Let's now analyze line [11]. Its first part, omp parallel for , is an OpenMP directive that joins the action of creating a team of threads with concurrent execution of the loop (in OpenMP, only for can be parallelized this way). That is, dividing the data into chunks and distributing computations to threads, as illustrated in Figure 8.3, are entirely up to OpenMP. If the #pragma line is removed, we are left with a perfectly functional sequential version of the code. As mentioned previously, the shared variable sum is used to collect the sum of the series computed by all the threads. Therefore, after each thread finishes its job, the partial result needs to be added to sum . All of these actions are performed safely by providing the reduction ( + : sum ) clause at the end of line [11].

The for loop on lines [12–18] is processed in parts by a team of threads. Note that the iterator i on line [12] is a local object and does not need to be treated in any special way. The same is true for c_i on line [14]. Also, the update of sum on line [17] does not require special protection since OpenMP knows its purpose as a result of the previous reduction clause and inserts a proper protection mechanism for us. Finally, the result is computed by the master thread on line [21], after the parallel section.

The only thing left is to launch Compute_Pi with various numbers N of elements in the series, as well as to measure the execution time. The OpenMP _Pi_Test function, defined on line [23], performs these actions.

First, line [26] creates a list of N values to test. Then, on line [28], a sequential loop starts, which on line [32] launches Compute_Pi , each time with a different value of N . To measure the execution time, the OpenMP omp_get_wtime function is called two times to capture the start and finish timestamps.

The results, printed on lines [35–36], were as follows on our test system:

On the other hand, running the code with the #pragma commented out – that is, in a sequential fashion – gave the following output.

The computed values of π are identical for the same N. Naturally, this is good news. But even if we have coded correctly to avoid hazards with unprotected shared variables, there can be differences in numerical values. Why does this happen? Because operations on floating-point values are burdened by phenomena such as rounding errors. In effect, this means addition is not associative in general, as discussed in Section 7.4. Hence, the differences in the order of summation between the sequential and parallel implementations can result in slightly different values.

Interesting conclusions can also be drawn from collating the execution times for corresponding values of N, as shown in Table 8.2. Notice that in all the cases except the last, the sequential version of the code is faster than the parallel version. This may be surprising at first glance. But the explanation is apparent as soon as we recall that creating and calling threads consumes time and memory. Thus it is not efficient to launch threads for tasks with a small amount of data. This also explains why, for significant values of N, the parallel implementation is over six times faster. OpenMP has a special if clause that turns on the parallel mechanism only after a given condition is met. Hence, if line [11] is changed to the following

the previous code will execute as desired.

Table 8.2 Timings for sequential and parallel versions of the series summation algorithm with respect to the number N of summed elements.

N 100 1000 10 000 100 000 000
Serial [s] 6e-07 4.6e-06 4.52e-05 0.51
Parallel [s] 0.027 7.9e-06 6–05 0.079
Speed increase 2.2e-5 0.58 0.75 6.5

8.4.3 Massive Data Parallelization

Our final example shows a parallel implementation of multiplying EMatrix objects. The EMatrix class was defined in Listing 4.7.

The definition of operator * begins on line [2] in Listing 8.5. The code follows the MultMatrix function presented in Listing 3.23; the only change is the addition of lines [15–18]. They contain the OpenMP directive with clauses to make the outermost for operate in a parallel fashion. We will explain their meaning and then test the performance of this function.

Actually, lines [15–18] are only visible as split into multiple lines: because of the line ending with the backslash symbol \ , its following (but invisible) newline character is simply ignored by the preprocessor. In this context, \ operates as a line continuation character, effectively reducing lines [15–18] to one line, which is necessary to be correctly interpreted as an OpenMP directive. We emphasize that to be a line continuation, \ must be the last character in a line. We have already seen \ in another context, i.e. in two-character escape sequences, such as \n , \t , and \\ . Hence, \ means two different things depending on the context.

The first omp parallel for on line [15], seen earlier in Compute_Pi , instructs OpenMP to prepare a team of threads that will run portions of for concurrently. The division of work is performed by the OpenMP library, but we will be able to give it some clues.

The second line shared() on line [16] declares all of the arguments to be shared objects. We know that these need to be treated in a special way to avoid hazards. However, since they are only read here, we do not need to include any synchronization objects like the critical , etc.

default( none ) on line [17] tells the compiler to list all of the objects used in the parallel section. Although all objects by default are treated as shared, their proper classification as shared or private is very important to avoid race conditions.

Finally, in line [18], schedule( static ) defines the required work-assignment scheme for the threads. This line does not end with a slash, since it closes the entire omp parallel for directive. In the static scheme, each thread obtains roughly the same amount of work, which is optimal for a balanced workload. There are also other schemes, such as dynamic (OpenMP 2020).

The OpenMP directive with clauses pertains only to the first for loop on line [20]. The other two, i.e. on lines [21, 22], are local to each thread. Moreover, in each thread, these for loops operate sequentially, although nested threads are also possible in OpenMP.

Finally, note that all the other objects, such as ar , bc , and ac , are local: each thread will create its own copies of these objects. Therefore, they need not be protected from access by other threads. But as always, we need to be sure they are properly initialized.

If threads need to make a local copy of an object that is defined before #pragma omp , the object should be declared with the private clause. But this way, objects declared private are not initialized by default. To ensure proper initialization, we must either place the initialization (assignment) in the code or use the firstprivate clause.

The OpenMP_MultMatrix_Test function, defined on line [27], serves to prepare random matrix objects and run matrix multiplication to measure its performance time. Again, time measurement is accomplished with the omp_get_time function.

The results measured on our test machine are shown in Figure 8.4. Because only one line has the OpenMP directive (and with no other changes to the code), execution was six times faster.

Bar chart depicts comparing the performance times for multiplying matrices of different sizes in a sequential implementation and a parallel implementation with OpenMP. For large matrices, speed increases by more than six times.

Figure 8.4 Comparing the performance times for multiplying matrices of different sizes in a sequential implementation (blue) and a parallel implementation with OpenMP (red). For large matrices, speed increases by more than six times.

But again, we have only scratched the surface. There have been great achievements in the acceleration of computations. CPU/GPU hybrid systems are especially remarkable and led to the foundation of deep learning and AI. Returning to the problem of matrix multiplication, EMatrix is not an optimal representation. Also, more advanced multiplication algorithms are available to take advantage of cache memory (Section 2.1). For example, faster execution speed can be achieved by first transposing the second of the multiplied matrices and then using the multiplication algorithms with the second matrix transposed. As a result, if matrix elements are arranged by rows in memory, cache accesses are more optimal. Table 8.3 summarizes the most common OpenMP constructs, clauses, and functions.

Table 8.3 Common OpenMP constructs, clauses, and functions with examples.

OpenMP directive Description Examples
#pragma omp parallel for [clause[[,] clause]… ] Fork for loop iterations to parallel threads. In this example, a minimum value and its index are found in a vector. omp parallel starts a team of thread; firstprivate declares loc_val and loc_offset to be private for each thread and, at first, initialized exactly as in their definitions; and shared declares the objects to be co-used by all threads. omp for nowait says to execute the following for loop in parallel and not wait for other sub-loops, but to immediately proceed to omp critical . This is a guard for the critical section and can be entered by only one thread at a time. 
std::tuple< int, int > FindMin( const std::vector< int > & v )
{
     const auto data_num = v.size();
     if( data_num == 0 )
          return std::make_tuple( -1, -1 );     const auto * src_data_ptr = & v[ 0 ];     auto sh_val = * src_data_ptr;
     auto sh_offset { 0 };     // Take an upper limit to find the lowest value
     auto loc_val { std::numeric_limits< int >::max() };          
     auto loc_offset { -1 };     // Use firstprivate to convey the initial values of loc_val and loc_offset.
     // Shared objects are 
     #pragma omp parallel default( none ) \
               firstprivate( loc_val, loc_offset ) \
               shared( sh_val, sh_offset, src_data_ptr, data_num )
     {
          // Each thread will take its payload and determine 
          // its lowest local pixel (reduction for min)
          #pragma omp for nowait
          for( auto i = 0; i < data_num; ++ i )
          {
               auto elem { src_data_ptr[ i ] };
               if( elem < loc_val )
               {
                    loc_val = elem;
                    loc_offset = i;
               }
          }     // no barrier here due to the nowait clause          // Enter a critical section here
          #pragma omp critical 
          if( loc_val < sh_val )
          {
               sh_val = loc_val;                         // Save lowest value in this thread
               sh_offset = loc_offset;          // and its position
          }     }     // a barrier here     return std::make_tuple( sh_val, sh_offset );
}
#pragma omp parallel Starts independent units of work.
#pragma omp single Ensures that exactly a single thread executes a block of code.
#pragma omp critical Construction for mutual exclusion: at any instant only one thread can perform the block encompassed by critical .
#pragma omp parallel sections Creates a team of threads, and starts independent sections. Sections execute in parallel to each other.
#pragma omp section Starts independent units of work in a section.
private( list ) Declares a variable as private. Each thread contains its own uninitialized copy (for initialization, use firstprivate ).
firstprivate( list ) Initializes a private variable with the value of the variable with the same name before entering the thread.
lastprivate( list ) Makes the last value of a private variable available after termination of a thread.
reduction( operator : list ) Orders parallel execution of the associative and commutative operations (such as + , * , etc.) with the aggregation of partial results at the thread barrier.
ordered Forces a sequential order of execution within a parallel loop.
schedule( kind [,chunk size]) Controls the distribution of loop iterations over the threads. The scheduling modes are static, dynamic, and guided.
shared(list) Declares objects that will be shared among the threads. Each object can be freely accessed by each of the threads at any moment. Hence, objects that are written to have to be protected, e.g. with omp critical .
nowait Threads don't wait for synchronization at the barrier at the end of the parallel loop construction.
default( none | shared ) Tells how the compiler should treat local variables. If none , then each variable needs to be explicitly declared as shared or private. If shared , then all variables are treated as shared.
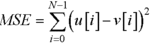num_threads( N ) Sets the number of threads to be used in a parallel block. MSE computes the mean squared error from the vectors u and v : images.
omp parallel for is used to start parallel execution of a team of threads, reduction( + : sum ) introduces a shared variable sum to be safely updated by the threads (so no synchronization is necessary), schedule( static ) imposes an even burden on the threads, and if launches parallel execution only if N > 10 000. 
// Computes the mean squared error (MSE) between two real vectors
double MSE( const std::vector< double > & u, const std::vector< double > & v )
{
     const auto data_num = std::min( u.size(), v.size() );     if( data_num == 0 )
          return -1.0;     // Simple error checking     const auto * u_data = & u[ 0 ];
     const auto * v_data = & v[ 0 ];     auto sum { 0.0 };          // Shared due to the reduction clause     #pragma omp parallel for default( none ) \
               shared( u_data, v_data, data_num ) \
               reduction( + : sum ) \
               schedule( static ) \
               if( data_num > 10000 )     for( auto i = 0; i < data_num; ++ i )
     {
          auto diff = u_data[ i ] - v_data[ i ];
          sum += diff * diff;
     }     // Here we have a common barrier     return sum / static_cast< double >( data_num );
}
omp_get_num_threads() An OpenMP function that returns the number of threads in the current team.
omp_set_num_threads( N ) Sets the number of threads to N.
omp_get_thread_num() Returns a thread number (its ID) within the parallel region.
omp_get_nested() Check whether nested parallelism is enabled.
omp_set_nested( 0/1 ) Enables or disables nested parallelism
omp_get_wtime() Returns an absolute wall clock time in seconds. In this example, a parallel pipeline is organized in sections. Threads in each section operate in parallel. 
void ParSections( void )
{
     const auto N { 100000 };
     // ... init data     omp_set_nested( 1 );          // Allow for nested parallelism     // Sections allow for a pipeline organization.
     // Create a team of threads.
     // If sufficient threads, the sections execute simultaneously.
     #pragma omp parallel sections
     {
          // Executes simultaneously with the next secton
          #pragma omp section
          {
               // If sufficient threads, there will be nested parallelism
               #pragma omp parallel shared( N ) num_threads( 2 )
               for( auto i = 0; i < N; ++ i )
               {
                    // ... compute something
               }
          
          }
     
          // Executes simultaneously with the previous secton
          #pragma omp section
          {
               #pragma omp parallel shared( N ) num_threads( 4 )
               for( auto i = 0; i < N; ++ i )
               {
                    // ... compute something
               }          }
     
     }}

The omp_set_nested function allows nested parallelism. The num_threads function sets a number of threads to be allocated for the closest parallel section. If a sufficient number of threads are available, then the for loop within section will execute the nested threads.

8.5 Summary

Questions and Exercises

  1. Refactor the matrix addition code shown in Listing 4.10 to allow for parallel operation. Hint: follow the code in Listing 8.5.
  2. As shown in Listing 8.5, matrix multiplication requires three loops. In theory, they can be organized in 3! = 6 permutations. Extend the code from Listing 8.5, and measure the performance of different loop structures.
  3. Consider the following matrix identity
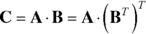
    equation

    where BT means transposition of matrix B. What would be a computational benefit of implementing matrix multiplication in the following two steps?

    1. Matrix transposition B → BT
    2. Multiplication of a matrix with the transposed-matrix: ABT

    Implement matrix multiplication in accordance with these two steps, and measure its performance. Compare with the code in Listing 8.5. Hint: analyze the operation of the microprocessor cache memory (Section 2.1).

  4. Implement a parallel version of the definite integration for any integrable function. Consult exercise 23 in Section 7.6. Measure its performance.
  5. Write test functions for the code snippets shown in Table 8.3, and measure their performance.
  6. Data variance provides a measure of how values from a data sample differ from their mean (data deviation measure). One of the methods to compute the variance is based on the following relations:
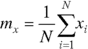
    equation

    where

    equation

    denotes the mean value of a vector x, and N stands for the number of elements in the vector.

    1. Implement a serial version of this two-pass algorithm.3
    2. Write a test function that will (i) create a vector with randomly generated values from a given distribution and (ii) compute their variance.
    3. Implement a parallel version of the two-pass algorithm. Compare the return values and execution times of the serial and parallel versions.
    4. Apply the compensated summation algorithms discussed in Section 7.4.7. Compare the results.
  7. C++20 comes with an interesting feature – coroutines. These are functions that can suspend execution and store the current state, to be resumed later with the state restored. This allows for a number of interesting mechanisms such as asynchronous tasks, non-blocking I/O handling, value generators, etc. A function becomes a coroutine if it contains any of the following constructions: co_await , co_yield , or co_return . For example, the following next_int_gen coroutine returns the consecutive integer value on each

    call:

    co_yield suspends execution of the next_int_gen function, stores the state of val object in the generator< int > , and returns the current value of val through the generator< int > object.

    1. Read more about coroutines (https://en.cppreference.com/w/cpp/language/coroutines), and write a test function to experiment with next_int_gen.
    2. Try to implement a new version of the range class from Section 6.5, using coroutines.
  1. Implement a parallel version of the MSE defined in Table 8.3 using the std::transform_reduce . Compare performance of your implementation with the OpenMP based version.
  2. Using the std::transform_reduce and the std::filesystem::recursive_directory_iterator implement a serial code to recursively traverse a given directory and to sum up sizes of all regular files (see Section 6.2.7). Then design a parallel solution. However, since the above iterator cannot be directly used in a parallel version of the transform_reduce , implement a producer-consumer scheme.

Notes

  1. 1  Tests performed on a computer with a six-core processor: Intel Xeon E-2186 M @ 2.90GHz.
  2. 2  This can also happen by mistakenly omitting the keyword omp.
  3. 3  More variance algorithms can be found at https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance.