CHAPTER 18

RANGE OF SWAPS

Due to the true simplicity of the basic swap (i.e., an exchange of assets), the application of the concept is applied to many needs. Some are very straightforward, some are more complex, but the basic theme remains. Actually, the swap concept is applied to three major categories: currency, cash flows, and commodities.

• ACCRETING SWAP •

The opposite version of an amortizing swap discussed later is called an accreting swap. In this type of swap the notional amount that the swap is based on is increasing over the life of the swap and therefore the swap payments going back and forth in the case of the fixed payment leg and the floating payment leg increase accordingly. An accreting swap’s notional value increases over time. The users are those whose assets are increasing over time also, such as building or development companies. In a swap that could span years, the creditworthiness of the counterparty becomes even more important than in a conventional swap because the exposure and risk is increasing as the notional value is increasing. Other names for this type of swap are accumulation swap, appreciating swap, and step-up swap.

• AMORTIZING •

An amortizing swap is one that has a fixed rate of interest on one leg and a floating rate of interest on the other. Both of the legs are based on a notional amount of principal that is amortized over time, therefore as the amount of outstanding principal decreases, so does the amount of the interest payments. A mortgage is this type of product; rather than maturing, it is just amortized to zero. Each interest payment in an amortized swap is less than the one preceding it because the notional value is decreasing, and therefore the swap payments decrease accordingly. The payments are based on the amount of principal or notional value that is enforced at that particular period of time. There are several asset-backed securities that use this type of swap. The amortizing schedule can be a set dollar amount each period, a delayed amortizing swap (kicking in after X years), or modeled after mortgage payments. Mortgaged-backed securities and collateralized mortgage obligations (CMOs) are examples of this type of product.

• ASSET •

An asset swap is the “swapping” of two cash flows emanating from two assets. The major difference between an asset swap and a credit is that in an asset swap a tangible asset is the referenced object. Credit swaps use interest rates or the rates of credit interest. The payments are based on a notional value of a fixed dollar amount. As with other derivatives, the notional value is never exchanged. The payments are prescheduled and do not have to occur at the same time. For example: one leg could be a quarterly payer, the other could be a semiannual payer. In a similar manner one leg could be fixed, and the other could be floating. The rate and payment schedule are completely negotiable. This type of swap has many uses. An institution with a large long-term bond portfolio can hedge its short-term needs by entering into a swap. An investor who has seen a bond investment deteriorate can swap out into a more flexible position.

Here’s an example:

The owner of a bond wanting to convert the bond’s fixed interest payments for a floating rate enters into a fixed-for-floating swap. As the bond is tangible, having a real issuer, interest rate, maturity date, and price, the asset swap spread. This is the amount over floating rate (LIBOR) that the bond owner receives. To find the asset swap spread, first determine the yield to maturity. This yield is used as the bond or income-paying debt asset will not be sold during the swap on period. Next determine the appropriate floating rate from the yield curve of the floating rate source. After that, subtract the appropriate floating rate from the asset’s yield. The larger the number in the answer, the riskier the bond is, and the lower the number the safer the instrument.

Many of the types of swaps mentioned in this section are applicable by substituting the cash flow from an income-paying asset instead of the cash flows based on LIBOR or U.S. Treasury rates.

• BASIS •

The next type of swap is a basis swap. Here’s how it works: 100 basis points equals 1 percentage point. Therefore a basis swap would be based on two floating-rate instruments, with each leg of the swap backed by, or affected by, one of these floating interest rates, such as the Treasury bill rate and the LIBOR rate. These could also be of the same underlying rate but cover a different period of time, such as the three-month versus six-month bill rates.

The concept of a basis swap can also be applied to a cross-currency situation. Payments would be based on the two streams of money market floating rates represented by these two different currencies. What is exchanged is not the rates themselves, but the basis/difference between the two rates. While the U.S. Treasury bill rate and the LIBOR rate are most often recited, other domestic rates used include the federal funds rate, prime rate, cost of funds index (COFI) rate, and the certificate of deposit (CD) rate.

• CALLABLE/PUTABLE •

A swap may have a call or put feature built into the terms of the agreement. In the case of a callable swap, the party who holds the fixed leg, the payer of the fixed amount, has the right at their “option” to terminate the swap on or before the scheduled maturity date. The party of the other leg, the floating-rate payer, is compensated for this option either by a premium paid at the start of the swap or an increase in the fixed rate received. As this is a fixed-income instrument and also an interest-rate instrument, the person paying the fixed rate would “call” the swap and terminate it only if he or she believed interest rates were going to fall. The person paying the fixed rate might also terminate it if the interest rates have fallen and might now enter into a similar agreement for far less cost.

Since there’s a callable swap, there must be a putable swap. The putable swap allows the party paying the floating rate to terminate the swap. For this privilege the floating-rate payer would reduce the fixed rate received by making an up-front fee payment to the fixed-rate payer. One use of a putable swap would be for an issuer of fixed-rate callable bonds. Should interest rates drop, the bonds could be called in and it will simultaneously exercise the right to terminate the swap. By doing so, the fixed-rate bond payer has converted it into a floating-rate instrument, and as interest rates fall they can get out of the situation by calling the bonds in and then terminating the floating-rate leg of the swap. If agreed to in the initial contract, or later in the swap’s life, a swap can be extended if the parties agree to the extension and the new terms that will follow when the original swap expires.

• CAPPED •

In this type of swap, one or both of the legs is a floating-rate swap. If one of the legs is a fixed rate, that rate is determined at the beginning of the swap and consistent throughout the duration. The floating rate is unknown from period to period, therefore, should interest rates rise, the floating rate will also increase. The side that is paying the floating rate has to be concerned as to how high interest rates could go; remember that the other side of that swap is either a fixed rate with a steady income stream or a floating-rate that may not be affected as much as the rate that the floating rate payer is paying. To protect themselves, the fixed-rate side will cap that rate, putting a maximum amount that the floating-rate side or sides will pay during the duration of the swap. Once that cap is reached, that’s the maximum rate that will be paid for the duration of the swap unless interest rates fall again, at which time the floating rates will be adjusted downward. In return for the cap, the floating-rate payer either pays an up-front fee for compensation purposes or lowers the rate of the fixed-income side they are receiving.

Since there is a cap that sets the maximum that the floating-rate payer would have to pay in interest, there must also be a floor. The floor sets the minimum amount that the floating-rate payer would have to pay. Should interest rates drop so that the floating rate goes below the floor, the payer of the floating rate is responsible for that floor amount. It is also possible to have a cap and a floor, which set the maximum that the floating-rate payer will pay and the minimum that the floating-rate payer will pay. For each of these features the participants of the swap will negotiate a lower fixed-income payment base.

• CIRCUS •

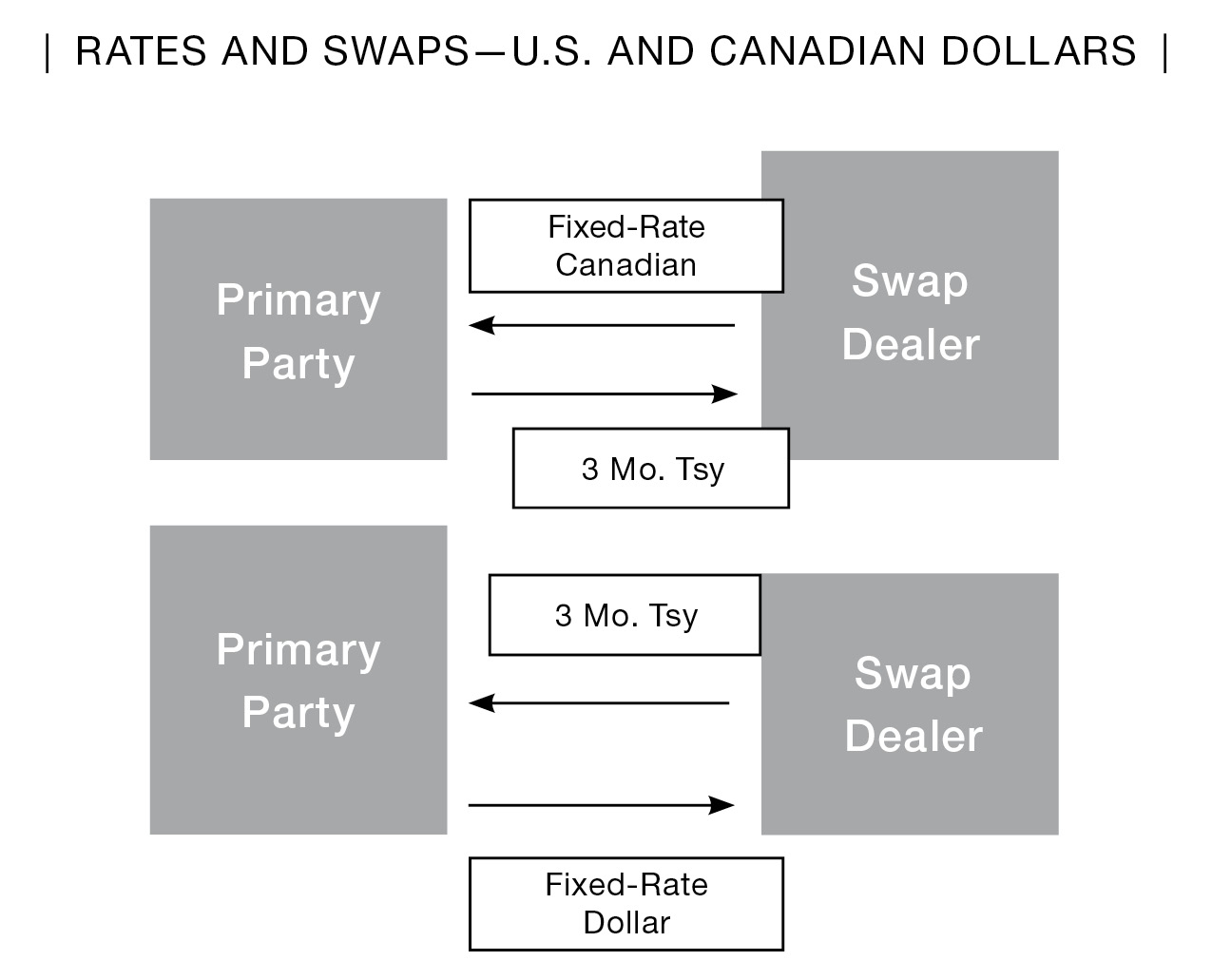
A circus swap is one that has one currency and a fixed rate on one side and a different currency and floating rate on the other side. It may also have two different currencies that can also have fixed-for-fixed or floating-for-floating. The term “circus” stands for “combined interest rate and currency swap.”

For example, a Canadian firm has swapped a 5¾ percent fixed-rate U.S. dollar obligation for a U.S. Treasury three-month rate plus 1½ percent. The company then turns around and swaps a U.S. Treasury three-month rate plus 1½ percent for a fixed-rate 5¹/₈ percent Canadian dollar obligation.

• COMMODITY •

Mainly used in the oil sector, the commodity swap is based on one leg having a fixed price and the other leg floating. In the following example both the farmer and the processor have floating rates, versus the swap broker that has the fixed rate.

A contract of 100,000 widgets has been trading between $0.95 and $1.05 per widget for several months. The widget farmer and the widget processor want to level monthly variance in pricing. A swap is set up by which the widget farmer will receive $0.99 per widget, and the processor will pay $1.01. The $0.02 difference is paid to the swap broker for setting up the agreement.

MONTH 1

Widget contracts settle at $1.05.

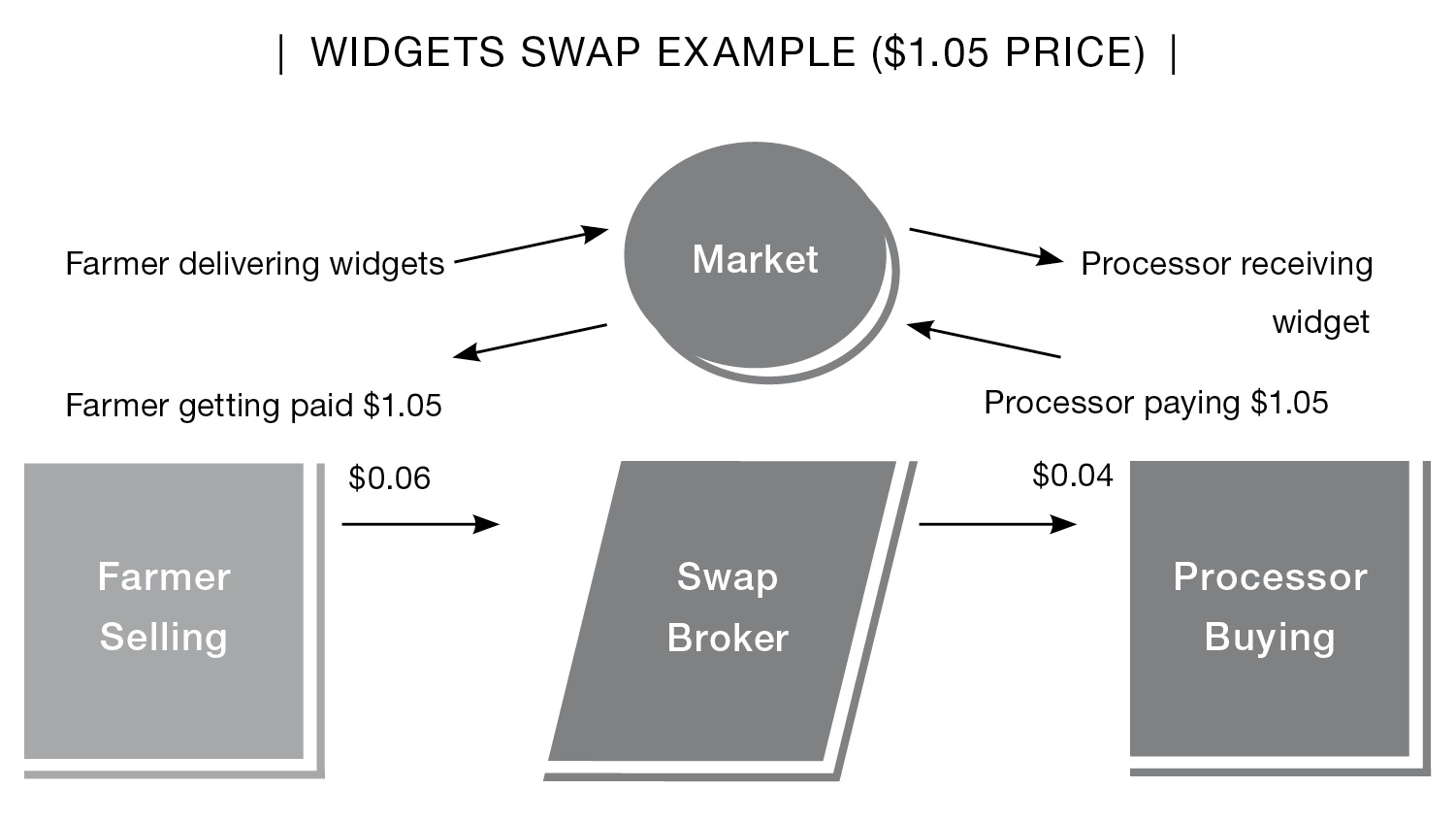
Farmer delivers widget contracts into the market and receives $1.05 per widget. From the proceeds the farmer pays the swap broker $0.06 = net $0.99.

Processor receives the widgets from the market and pays $1.05. The swap broker pays the processor $0.04 = Net $1.01.

MONTH 2

Widget contracts settle at $0.95.

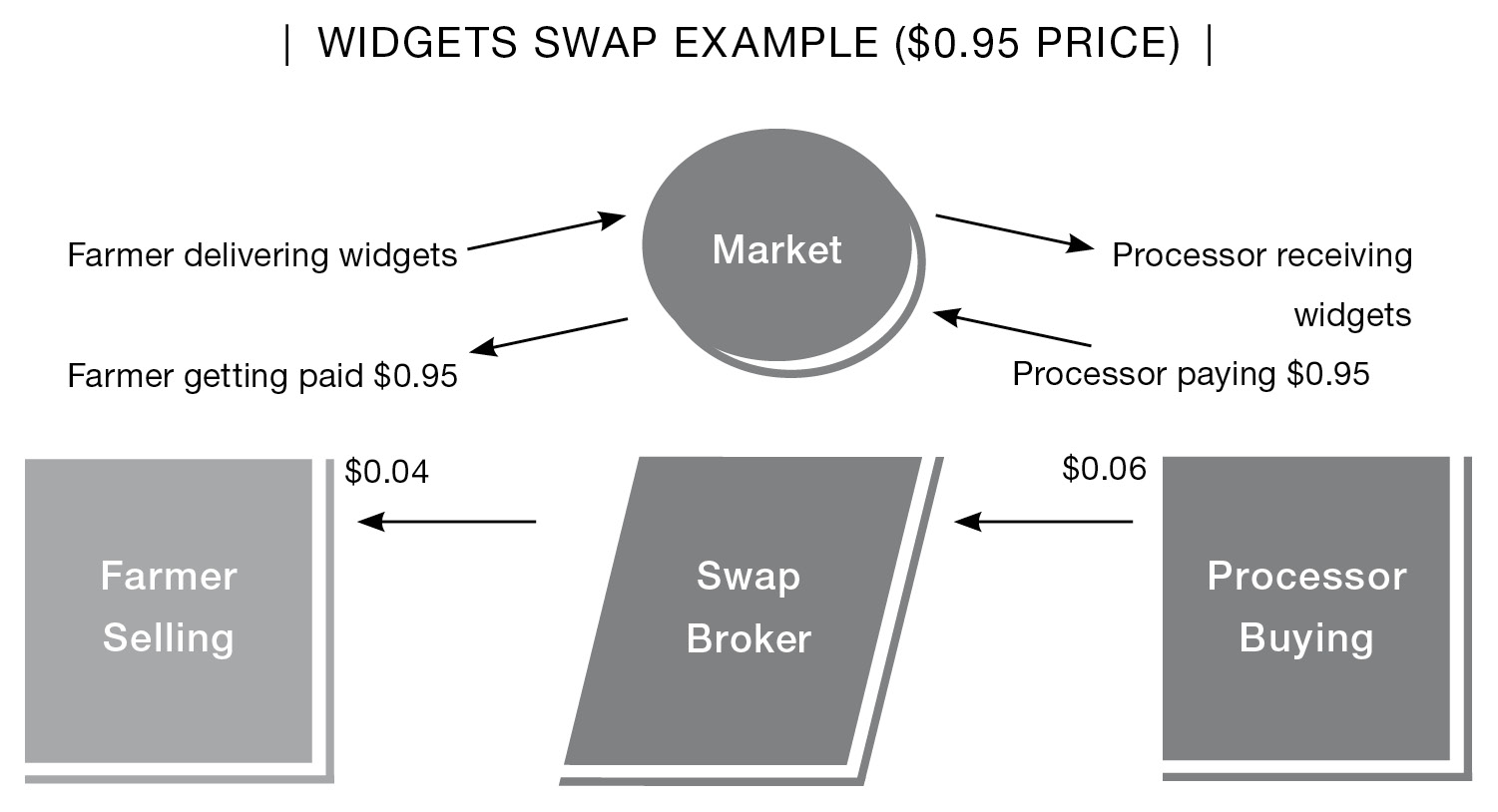
Farmer delivers widget contracts into the market and receives $0.95 per widget. The swap broker pays the farmer $0.04 for a net of $0.99.

Processor buys the widget from the market, paying $0.95 per widget, and then pays $0.06 to the swap broker for a net cost of $1.01.

• CONSTANT MATURITY •

A constant maturity swap (CMS) is one where the interest rate on one leg can be periodically reset by referencing a market swap rate other than LIBOR. The other leg is tied to LIBOR, however. It is a variation on the regular interest rate swap. Both legs are floating rate, with one being the referenced rate. Due to the use of two floating rates, the constant maturity swap can be single- or multicurrency. Usually the reset rate is shorter-term than the referenced rate. The referenced rate is a fixed maturity market rate. By being able to reset the rate, the investor can adjust the spread between the two rates to his or her advantage.

• INFLATION •

Inflation swaps are long-term swaps consisting of one leg tied to the rate of inflation and the other tied to a periodic interest payment or a zero-coupon bond discounted at a predetermined rate. That rate determines the value of the bond at the beginning of the swap. At the end of the swap’s tenor the two legs are compared and the greater side keeps the difference. Inflation swaps are also called real rate swaps or inflation-indexed swaps. Those swaps that involve a zero coupon usually settle the monetary difference at the end of the swap. Those that have one leg tied to an interest-bearing instrument settle periodically and can reset rates at that time.

• INTEREST RATE •

In order to delve deeper into interest rate swaps, we first must understand their purpose. While we refer to the interest rate, it is the resulting cash flow it produces that is important. The two critical aspects here are principal versus rate. Interest rates in the market are constantly changing. Not only are the rates rising and falling, the spread between long-term and short-term rates is also changing. Products that are interest rate sensitive react to these changes. The more sensitive to interest rate changes an issue is, the more it will react to them. Those instruments that are expected to pay the same rate of interest from initiation until maturity (a fixed rate) will see their market price change so as to adjust their yield to reflect the new benchmark rate. Those instruments that have a floating rate will see their price remain stagnant but their interest rate change to reflect the current condition.

Fixed for Floating

We will start with a basic fixed-for-floating rate swap, which has a life span of five years. The referenced instrument has a notional value (in this case the principal amount) of $10 million. The LIBOR rate is 4 percent.

Let’s assume the debt is a promissory note with a fixed 5 percent annual interest payment. The owner of the note, Mr. Michael Rafone, would prefer a floating-rate note to better offset other investments in his portfolio. Mike is more interested in preservation of capital than he is in income. He contacts his broker at Stone, Forrest and Rivers (SF&R), which is also a swap dealer, and arranges a swap of 5% fixed vs. LIBOR + 1%, with a contra side of LIBOR + 1% vs. 4.90% fixed for five years on $10,000,000. Mike is a swap payer. Therefore every year Mike will:

Pay $500,000, the fixed interest payment, and receive LIBOR + 1%, while the contra party will pay LIBOR + 1% and receive $490,000.

To Stone, Forrest and Rivers, the LIBOR payments cancel each other out and Stone, Forrest and Rivers is left with an annual profit of $10,000 ($500,000 received − $490,000 paid out = $10,000). Stone, Forrest and Rivers would stand to make $50,000 for the five years if all parties held their positions for the full tenor of the contract. Let’s take a look at the situation from a different angle now.

What would happen if SF&R could only offset the position for four years? Unless a favorable offsetting position materializes, SF&R would receive $500,000 from Mike Rafone and have to pay LIBOR + 1%, which could result in a greater profit (if LIBOR is lower than it was at LIBOR + 1% setting) or a loss (if LIBOR is higher than it was at LIBOR + 1% setting), all other things being equal. If the LIBOR “leg” was to rise to 5%, SFR would receive $500,000 from Mike but would have to pay $590,000 (LIBOR at 5% = $490,000 + 1% = $100,000 for a total of $590,000). Therefore, unless SF&R wanted the risk, it would hedge the open side with some other derivative product such as an index derivative that tracks the LIBOR.

Fixed for Fixed

Fixed rate for fixed rate is primarily used when the payment dates need to be better aligned or in currency transactions. In the United States, corporate bonds pay interest every six months. As explained in the bond section of this book, the payment dates are January–July, February–August, March–September, April–October, May–November, and June–December. In other countries, bonds may pay interest only annually. This schedule only exacerbates the misalignment problem.

While those who rely on interest income try to acquire bonds whose interest payments meet their needs, there is the ongoing value rating dilemma known as the bond market. When acquiring new bond assets, either as an addition to a portfolio or as a replacement for called or matured bonds, the desired payment period may not be available. What’s more likely, though, is that it might not be the best investment choice. Therefore the portfolio manager will make the correct bond choice, and in doing so, unbalance the interest payments. Depending on when the payments are needed and the amount involved, this disconnect could cause an obligatory payment shortfall. To mitigate the risk, the portfolio manager may enter into a fixed-for-fixed swap on terms that are beneficial to the counterparty, who may need to realign its payment schedule or who is just willing, for a fee or some other compensation, to accommodate the portfolio manager.

Fixed for Fixed, with Currency Exchange

Another, and perhaps the more dominant type of fixed-for-fixed swap, involves currency and interest rates.

Stone, Forrest and Rivers has an American client trying to fund the building of a German residential complex. The client must transact business in euros. The current funding rate in the United States for that type of dollar loan would cost the client 4 percent. In Germany that same type of loan would cost 6 percent. Stone, Forrest and Rivers also has a German client who is trying to expand business in the United States. It would cost 7 percent for the German company to borrow U.S. dollars for the expansion project. In Germany, the same type of loan in euros would cost the company 5 percent. SF&R enters into a swap agreement with both parties, by which the German client borrows euros at 5 percent and the U.S. client borrows dollars at 4 percent and SF&R sees that the swap is executed. The effect is that the German client has borrowed dollars at 4 percent and the U.S. client has borrowed euros at 5 percent.

	U.S. DOLLARS	EUROS
U.S. Client	4%	6%
German Client	7%	5%

The swap occurs:

	U.S. DOLLARS	EUROS
U.S. Client		5%
German Client	4%

The German company will pay the interest in U.S. dollars and repay the loan in U.S. dollars. The U.S. client pays both interest and principal in euros.

The German client has saved 3 percent per million, while the U.S. client has saved 1 percent per million.

As with most of the examples presented, these are simple because their purpose is explanatory. In the above example, the terms of the swap, the duration, payment periods, and amortization, etc., would all have been negotiated and listed in the swap agreement.

Floating for Floating

Another name for a floating-for-floating rate swap is a “basis swap.” Unlike the swaps where one leg or both legs are set to some fixed rate (the current twenty-year Treasury bond rate, for instance), here the legs are tied to two different money rates (for instance, one might be tied to the three-month U.S. Treasury bill and the other might be tied to the three-month LIBOR rate). The object of the basis swap is to try to take advantage of aberrations in the basis spreads between the two rates. The spread could widen if the more expensive one increased and/or the less expensive one lost value. The spread could decrease if the reverse happened.

Let’s assume the three-month LIBOR rate is 0.46685 and the six-month LIBOR rate is 0.73640. The current spread between the two is 0.26955. If two parties took loans, with Cindy Ash paying six-month LIBOR to the other party, and Carol Ling paying three-month LIBOR plus 27 basis points, which party would be in a better position if the three-month LIBOR remained the same but the spread decreased to 25 basis points? In order for this to happen, the six-month LIBOR would have to have fallen to 0.71685. Cindy Ash is better off in this scenario because the three-month is costing more: 0.46685 + 0.27 = 0.73685.

A floating-for-floating rate swap may be based on different reset dates. Some events occur periodically, but on a regular basis—such as annually, semiannually, quarterly, or monthly. The first three occurrences create a potential liability to a company. Mismatching of any of the payment schedules could cause a firm embarrassment and/or penalties if payment cannot be made on time. The annual receivable versus annual payable situation is, perhaps, the schedule with the greatest risk, as it could include an accumulation of what would be shorter-term payments, and/or incur the greatest credit risk. In the case of a long payment period, it can even be worse if the receivable is paid well in advance of when it is needed. In that scenario, when the offsetting payable is due, the firm might find itself short of funds. In today’s world, effective cash management increases the ability and possibility of profit. In the global business environment, it is imperative that the correct sum of money, in the correct currency, arrive at the correct location exactly when it is needed.

Scheduling Payment

As mentioned above, the semiannual payment schemes are J & J (January and July), F & A, M & S, A & O, M & N, and J & D. The quarterly cycle is J,A,J,O (January, April, July, and October); F,M,A,N (February, May, August, November); and M,J,S,D (March, June, September, December). Many of the payments, expiration dates, and maturity dates in most business transactions follow one or more of these conventions. In America, most bonds pay interest twice a year, some debt pays quarterly, GNMA pass-through instruments pay down interest and principal monthly, and U.S. Treasury bills are issued on a three-month, six-month, and one-year tenor. They are discounted instruments that pay interest at maturity. In swaps agreements where payments are to be made during the tenor of the swap, these conventions are employed.

• ROLLER-COASTER •

In the standard multipayment swap, the dates of payment are preset and the amount of money due at each payment is fixed. This type of swap, which is the dominant form, is not always in the best interest of the users. As the terms of the swap are negotiable, the parties may be better off using a variable payment schedule. Companies whose businesses are of a cyclical nature would be much better served by a swap where the payments follow the company’s cash flow. During periods when the business is at the height of its annual or seasonal period, the payments should be at the highest point. During periods when there is a lull in the business, the payments should be at a much lower point. The type of swap where payments change from period to period is called a roller-coaster swap. A business such as a sporting goods company specializing in outdoor sporting equipment would be better served if the payments were larger in the summer than in the winter when business is in a lull. Of course the structure of this type of swap would be dependent on the business itself and the geographic area it serves. Businesses involved with seasonal decorations would also benefit from this type of swap.

• TOTAL RATE OF RETURN (TROR) •

The total rate of return (TROR) swap is a contract between two parties in which one party transfers market risk and credit risk to another for a flow of income and a guarantee of principal for a predetermined period of time.

This type of swap obtains its name from the fact that the swap seller is buying insurance that will protect the principal of the investment at a point in time, as well as receiving a cash flow based on a predetermined floating rate. In return for this, the swap seller will forfeit any appreciation in the reference asset’s value and any interest payments made by the referenced asset. The swap buyer is going to receive any appreciation in value of the referenced asset plus all interest payments made to the asset, but pay out any depreciation in the referenced asset’s value as well as paying out a floating rate of interest. In other words, the swap seller owns the referenced asset without market risk. The swap buyer synthetically owns the referenced asset, as he or she will benefit from any appreciation in value and incur loss from any depreciation.

Here’s an example:

Loster Financial owns 5,000 Regal Corporation bonds (nominal value $5,000,000) that pay 5 percent interest annually. The bonds are currently trading at “96” ($0.96 on the dollar). The present value is $4,800,000 and the semiannual interest payment is $125,000 ($5,000,000 × 5%/2). Loster Financial enters into a TROR with Mercury Bank. In return for Regal Bonds’ interest payments, Mercury Bank will pay Loster Financial LIBOR plus x basis points. Should the bonds increase in value, Loster Financial will pay Mercury Bank the amount over the referenced value. If, on the other hand, the bonds lose market value, Mercury Bank will pay Loster Financial the amount under the referenced value.

In this total return swap the paying party of the TROR swap will be paying periodic interest payments that the bond pays in return for a negotiated steady income based on some other rate, such as LIBOR plus basis points. At the end of the swap’s tenor, with each interest payment having been received, the value of underlying referenced issue at the time of the swap transaction is still intact. The swap does not have to expire at the same time that the bond matures. Therefore, in the above example, if the TROR was for three full years, the TROR payee would pay the TROR receiver the interest payments received from the bonds plus any appreciation in the value of the bond. In return, the receiver pays the payer a floating rate based on LIBOR plus basis points, as well as any depreciation in the value of the underlying bond.

Let’s compare the two parties:

TROR Seller	TROR Buyer
Owns the referenced asset	Synthetically owns referenced asset
Buys the insurance	Sells the insurance
Has lower cost of finance	Does not tie up capital
Pays out referenced asset’s interest payments	Receives referenced asset’s interest payments
Receives floating-rate interest	Pays floating-rate interest
Receives any depreciation in referenced value	Pays any depreciation in referenced value
Pays any appreciation in referenced value	Receives any depreciation in referenced value
Transfers market risk	Accepts market risk
Has interest-rate risk	Has interest-rate risk

The duration of the TROR is negotiated and not preset in the marketplace. The typical transaction contains the following: details of the referenced asset, its interest rate, its nominal value, its agreed-to price or value, a start date, an end date, the duration, the interest payment dates, the floating rate (with basis points), floating-rate payment dates, settlement date, and method of payment.

Referring back to the example above, let’s start with Loster Financial. It owns the bonds, having acquired $5 million worth of bonds. Whether it paid for the acquisition in full or on margin is not for discussion at this time as it brings in tangential topics. However, as owner of the bonds, Loster Financial is expecting to receive periodic interest payments. These payments, from Regal’s paying agent, should be in Loster’s control on the payment due date. What if they aren’t? Depending on the cause, Loster Financial may be held in default of the contract. Mercury Bank would begin legal remedies up to and including claiming the bonds themselves. In other words, payment from Loster Financial to Mercury Bank is not contingent on Regal Corporation’s paying Loster Financial. There are exceptions, such as a force majeure, which may negate the ability of Loster Financial to make payment.

• YIELD CURVE •

Since there is a need for swaps based on short-term rates, we don’t have to look too far to find a need for swaps on long-term rates also. The yield curve swap is one that involves a bond or other long-term instrument, and a very similar instrument with a different duration. The swap involves the difference between two interest rates that these bonds or debt instruments are carrying. So in the case of a corporation issuing a fifteen-year bond and a twenty-year bond, all other things being equal except for the duration of the two bonds, the twenty-year bond should carry a higher interest rate than the fifteen-year bond. However, the prices for those bonds in the market are determined by the Treasury benchmark yield curve and the relationship of this company’s bonds to it. As the yield curve changes due to the supply and demand for funding at various periods of longevity, the difference between the prices of the two bonds will change also, which creates a basis price difference. The swaps could be based on those differences.

• ZERO-COUPON •

One form of swap that is much different from all the rest we’ve looked at is one with a floating rate against a zero-coupon bond or a fixed rate against a zero-coupon bond. In both cases, the fixed-rate and the floating-rate sides, the swap will receive periodic payments; the zero-coupon bond will not. At the end of the instrument’s life or at the end of the swap, the zero-coupon bond will pay off. For those not familiar with the zero-coupon bond, it is a deep-discounted instrument that pays its principal at the end of its life; therefore, while the zero-bond owner is paying annual income tax on the interest it is theoretically earning, but not paying out, the owner will receive full payment at the end of the bond’s life. If the zero-coupon bond has a longer tenor than the swap, the bond will be valued at the present value of its cash flow based on the negotiated interest rate up to the end of the swap.

• THE PRINCIPAL AMOUNT AND THE NOTIONAL AMOUNT •

Throughout this book, we are using two terms that seem to be the same, but they are not. The “principal amount” is one term and the “notional amount” is the other term. While in some cases they are the same, in many cases they do not refer to the same product. The principal amount is the amount that is going to be changed or the amount that something is computed from, such as on a standard bond. The accruing of interest is a percentage of the face amount known as the principal amount. If you were to buy or sell that bond, the amount of money that would be exchanged would be based on the price multiplied by the principal amount. A $1,000 bond selling at 60 would cost $600. The interest on that bond would be computed based on the $1,000 amount. The notional value is one that has value but is not pertinent to the computations.