If you’ve been waiting impatiently for a neat package of curricula, in-class exercises, and homework problems, all ready to photocopy, with instructions on what to do in all the contingencies that come up when working with others, you’re about to be disappointed. Mathematics is freedom, and part of the exhilaration of doing it is that you just don’t know what will happen next. You’ve set up a destination in your own mind, you have a general map of some routes to it, but between setting out and getting there are all the adventures that mind and the world make for each other—not to mention the differently angled wishes and wills of your fellow voyagers. You may lose the way or find a new one; you may end up somewhere else; you may stumble and slide or run effortlessly along the shortest path. What we have for you is a representative skeletal outline of one course and, from the journal of some others, notes that tell you more about the actual doing than an outline could: assorted vignettes, anecdotes, reflections, and bits of advice. In prospect, the engineering of any great undertaking can’t help but be piecemeal: that’s what it means to be synthetic. It is only in retrospect that the falls are seen as fall-lines, and the architecture as a priori.
What is the landscape over which this adventuring roams? Ask a mathematician what math is and you’ll likely be answered with a version that has his part of it in or near the middle. This is reasonable, since being of infinite extent, its center is everywhere. But someone who loves math and isn’t a professional, eager to start a Math Circle, needs some sort of diagram that will help to show the hang of things. This is a fraught undertaking, since any such map is bound to suffer more distortions than Mercator’s, given its maker’s point of view. Still, here is a glimpse—more a sketch on the back of an envelope than a pocket guide, because it leaves out so many close connections among distant fields.
Math studies structure. Since structure shows itself through shape and number, the two great branches of math are geometry and arithmetic/algebra (the kinds of and relations among numbers, that is, enriched by the fiction of an “unknown number”).
As the notion of “unknown number” evolves to that of “variable,” analysis—which asks about the structure of change—rises from these two main branches, with such branches of its own as calculus of one, then of several variables, and complex analysis (calculus on the complex plane). Meanwhile thought also moves downward toward foundations: mathematical logic, set theory, category theory (the interplay between branches of math), the history of mathematics, philosophical underpinnings.
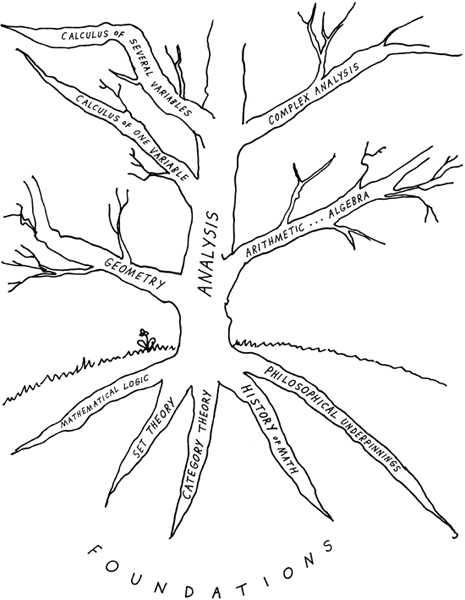
Math studies structure—but of what? In the end, of everything; but immediately, of what follows from a limited cast of characters (certain kinds of numbers or of shapes) acting under the constraints—axioms—that describe their nature. How must they combine? And just as character is fate in human drama, so the design of each structural microcosm follows from and is revealed by the interplay of their makeups.
Sometimes one of these microcosms models well an aspect of the world about us so that we can then apply insights from the model, the better to understand and predict how things happen: applied math.
Like anything organic, math sends out new growth from its intersections—number theory, for example, angling off from arithmetic to look at the structure of whole numbers and the primes that generate them. There will be numerous unexpected cross-products between any of these sprouts—one as an adjective modifying another as a noun—which will become beautiful flowerings of their own. None is trivial, each grows, as does all of mathematics, in response to our desire and pursuit of the whole.
Many different courses have appeared in The Math Circle since it began in 1994. Some topics suited all ages, when adjusted to the right level of sophistication. These included:
Cantorian set theory
Group theory
Knots
Map coloring
Number theory (always focusing on a specific issue, from congruences and continued fractions, to which numbers are the sums of two squares, and quadratic reciprocity)
Probability
Sequences and series
Straight edge and compass constructions
The Pythagorean Theorem
Tiling
Are there numbers between numbers?
Arithmetic machines
Clock arithmetic
Eulerian and Hamiltonian circuits
Figurate numbers
Fractions and decimals
Functions and their graphs
Interesting numbers
Kinds of numbers
Prime numbers
The Euclidean Algorithm
The mathematics of origami
What is area?
Angle trisection—or not
Calculus via maxima, minima, optima
Complex numbers
Construction of polyhedra, and the Euler Characteristic
Convex figures
Equidecomposability
Game theory
Graph theory
Information theory
Interesting points in triangles
Logarithms
Mathematical games
Mathematical modeling
Numbers and nimbers
Pascal’s Triangle and fractals
Projective geometry
Propositional calculus
Random walks
Solution of polynomials by radicals
Styles of proving
The Divine Proportion
The Fibonacci sequence
The Intermediate Value Theorem
Visual proofs
What is ii?
Algebraic geometry
Classification of surfaces
Computational complexity theory
Fractals
Group theory, topology, and physics
Hyperbolic geometry
Mathematical logic and Gödel’s Theorem
Measure theory
Proofs from The Book
Quantum mechanics
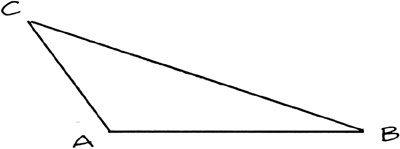
Here is a triangle ABC (best drawn large, and as obtuse): what you see is what you get.
A casual, seemingly unrelated question: are there any points exactly midway between the two fixed points, P and Q?
If the midpoint is offered: is it unique? Lead them to the perpendicular bisector of line-segment PQ (if offered as a line-segment, lead to a line; if anyone points out that there is a whole plane of bisectors, note it and return to the plane of the triangle).
So we have a perpendicular bisector m of AB. And of AC? Yes, call it n.
Do they intersect?
We’ve reached a bristle-point—the discussion can, fruitfully, go off in many possible directions: if (as we mentioned earlier) you draw m and n as parallel or asymptotic to one another, intuition will be outraged, and interesting discussions—which may (fruitfully) displace the initial aims—will begin, such as: how trust ink or chalk representations? Aren’t we talking about ideal lines and points, which our drawings only suggest? How, why, trust the visual at all? Relation of math to the world, or: launching into a proof that these two perpendicular bisectors must meet.
This is an important and ambitious project, which will give the students their first taste of some Euclidean axioms and of deductive proof (with issues here too of elegance and economy, and of intuition leading the way). Let axioms arise on a “need to have” basis: only those definitions and axioms should surface that are needed in order to prove intersection of these two lines (so the concept of “parallel,” for example, will come up). Always let the students struggle to find suitable definitions and axioms; take the latter as desperate measures, to stop endless regression. Note: take SAS as an axiom, and when ASA is needed, take it as an axiom too (saying that we might have been able to deduce it from what we have), unless it seems right to digress into the proof of it. It is very rewarding to have confirmed, after much work, that m and n indeed intersect—and begins to adjust the relation between intuition and proof.
With m ∩ n = O, ask about r, the perpendicular bisector of BC. Draw it as intersecting m and n in different points P and Q, pause, and let conjecture and intuition have their say.
Their discovery of the circumcenter via transitivity alone (since O is on m, it is equidistant from A and B; since it also lies on n, from A and C—hence by transitivity, it is equidistant from B and C) is elating—it may also misleadingly suggest that all proofs will be this short or simple.
Having started with an obtuse triangle leaves O vividly outside it. Where will it be in an acute, in a right, triangle? Bristle-point: shall we look at its trajectory, or think about continuity?
Are there other such points of concurrence? Are there other interesting triples of lines to concur? Angle bisectors tend to come up next, and it is pleasant if they do: for their concurrency is moderately intuitive, and a proof advances the grasp of Euclidean geometry, but not uncomfortably.
Medians are unlikely to be thought of: it would be well to suggest them here. Bristle-point: proofs of their concurrency abound, with different flavors (some leaning on physics and centroids, some descending from generalizations such as Ceva’s; some are ponderous, as in Euclid, some daring and dapper, as from projective geometry—the rest of the course, or a course in itself, could be devoted to this variety and its implications).
Now altitudes and the orthocenter. This seems the least intuitive concurrency, and reaching for proofs the most strenuous. It comes as a salutary shock—the shock of elegance—as we mentioned in chapter 8, to prove their concurrency via seeing them as the perpendicular bisectors of the triangle similar to, twice the size of and enclosing (inverted) the given triangle.
Bristle-point: what about concurrences of analogous lines or planes in tetrahedra?
The second stage of the course: we now have circumcenter O, incenter P, centroid G, and orthocenter H. Is there a structure hidden here? Yes: the Euler Line, on which lie O, G, and H. While this collinearity may be seen, its proof is unlikely to be devised. Following Euler’s, however—with as many of the steps as possible found, or justified, by the students—will raise their level of mathematical sophistication.
Third stage: more, and deeper, hidden structure: the nine-point or Feuerbach Circle (whose center lies on the Euler Line!). Again, they will more likely be assisting at than inventing a proof, so encourage doubts, criticism, variations, that their savoring may be that of apprentice rather than spectator.
More and more points show up on the nine-point circle (such as points of tangency with each of ΔABC’s three exocircles, and with its in-circle—and in fact an infinity of others); more and more invariant points associated with a triangle may now arise (the Symmedian Point, Brocard Points …), and other lines (the Soddy and Gergonne Lines), and other triangles: Brocard Triangles, the Euler-Soddy-Gergonne Right Triangle. Endless directions in which to go from here: into higher dimensions or on to n-gons, and the significance of collinearity and concurrency could equally well lead to projective geometry and duality. What began as no more than a triangle ends with invisible structure becoming palpable to the eye—but more significantly, to the mind.
Note: knowing how rich the harvest can be, it is important to restrain oneself and let the pace of the course be andante: better that the students end up having discovered for themselves no more than the circumcenter, than to leave them drowsy with other men’s flowers.
Here are some notes we’ve handed out to new colleagues, a week or so before they begin to lead a class.
1. “I heard myself saying ‘Wait a minute, let me show you how to do this.’” The moment you become aware of its effects, you’ll have broken the habit we have all developed of turning our students into spectators. The most fundamental message of The Math Circle is that you learn math by inventing or discovering it yourself.
2. A frustrated student gives up. “I’ll bet you know the answer!” You probably do, or know pretty well how to get it, but that’s of no importance. The fiction that you were all working on this together—that the problem, not accidents of knowledge, mattered—has been broken and needs to be restored. A good reply is the honest one: that the answer is still not known to the group, and that they’d no more want to be told it than a sprinter would like someone else to do his training or run his race for him; that does nothing at all for his muscles or his self-esteem. The Math Circle’s motto comes from the eighteenth-century physicist G. C. Lichtenberg: “What you have been obliged to discover by yourself leaves a path in your mind which you can use again when the need arises.” It doesn’t matter who—or indeed if anyone—knows how to do this: it’s our turn now. It is only the temporary fatigue brought on by frustration that makes you want to be told the story instead of writing it yourself. Regroup, refocus, return to the details of the problem at hand and ask: What exactly stands in our way?
3. Up the airy mountain. The conversation has become more and more general, the fecund details of the problem blurred away. This is inevitable, given the abstract impulse native to math, and can lead wonderfully on—at the right time. Make a public record (handouts, blackboard) of these paths leading away, so that the air is cleared, no one feels cheated of his insight nor distracted by the other vistas opened up, and then come back to the problem at hand, your imaginations refreshed by these opened windows.
4. Down the rabbit hole. The conversation has turned in ever tighter spirals into details of details, until all sight of what you’ve been doing it for is lost. Judge what the right moment is to surface again, survey how far you’ve come and where you’re going. A systematic sketch of gains and losses, asking now for strategy and tactics, renews the enterprise—but don’t make it too tidy, lest a mechanical ideal displace the imaginative.
5. Careening away in the wrong direction. Someone comes up excitedly with a conjecture, which is just dead wrong. Fine: let it play out. “That’s interesting; what does it imply?” Or with equal excitement: “Let’s try it on an example,” or “Fascinating! What makes you think so?” Many a time real insights come from errors; in any case, it sharpens the critical faculties of all to probe at a conjecture, right or wrong. Keep the risky character of this enterprise alive; it makes the whole undertaking more exciting, and when a sound path is eventually hit on, the experience is all the more stunning. Out on the frontier one tends to make wrong guesses more often than right ones. If one wrong turn follows another until the initial issue is lost in the fog, nudge the conversation back in a fruitful direction—but nudge as unobtrusively as you can (coming up with a suggestive example for them to work on is always helpful).
6. “What’s the point of doing this anyway?” The course or the class began with an abstract question (Can you tile a rectangle with incongruent squares? What is ii?) and everyone plunged enthusiastically in, caught up in the spirit of the hunt. But once the group is bogged down, with self-confidence on the ebb, it is natural to turn on the source of annoyance and try to dismiss it. Suit what you say to your temper and theirs, but points worth making are that anything leads to everything; that math’s history is one of research as an end in itself always turning out later to bear significantly on understanding and controlling the world around us; that as an art the point is in the beauty of the revelations; that it is, after all, frustration which has undermined our efforts and made us question their value. Time for a pause and a step back in order to leap forward.
7. “What time is it?” This question stands for disengagement, which can become contagious. If the students are very young, the moment has come to drop whatever you’re doing (no matter how interesting it has become to you) and play a game (function machines) or tell jokes or anecdotes that will have some later value. If the question comes from a student in an older class, feel free to say that there’s no compulsion to stay: The Math Circle is supposed to be fun, and if you’re not finding it so, we’ll think none the worse of you for leaving. But the implication of the question must be addressed on the spot. And check your watch: class may have ended ten minutes ago, and your questioner has just noticed the crowd at the door.
8. “I know, I know!” Eagerness and lack of self-awareness may excite people of perfectly good will to want to answer every question, even the rhetorical ones. “I’m eager to hear your idea, but it’s Alice’s turn now.” Keep the shares in the conversation evenly divided; arrange auctioneer’s signals with the shy. Even if an enthusiast bursts into tears (as five-year-olds have been known to do) at not being called on, go on blithely to others and return to him, when he seems under better control, with a new question.
9. A student runs up, takes the chalk from your hand and begins to write out a conjecture, an approach, a proof, a diagram, a counterexample, on the board. This is what you’ve waited for, when they begin to take over. It won’t be smooth sailing, but better a rough voyage with them at the helm than a smooth one steered by you, which they sleep through in their cabins. Encourage others to come up to the board too (standing helpfully near the shy and away from the bold); if it is always the same student who rushes up, explain in an age-appropriate way about taking turns.
10. A voice from the back of the room. If you decide that well-behaved parents may audit a class with their children, tell them ahead of time that auditing means just that. You may nevertheless find a parent, or a visitor, breaking into a discussion with “That isn’t true!” Parents are less good than their children at understanding your role as Sherpa or dumb friend. “I have a proof” is another familiar baritone aria. Smile and congratulate the latter, smile and raise an eyebrow to the former, tell both after class that the students have right of way.
11. Children as hand puppets. “My daughter wanted to say …” “My son really means …” Well-intentioned parents sitting beside their offspring can not only stifle their initiative and confuse them about what they thought, but rock everyone back on his heels. A good policy is to ask parents, who stay after all with their offspring’s permission, to sit at the back. If they natter away noisily with one another, don’t hesitate (looking at the ceiling, perhaps) to ask them for the same attention their young are giving. If a child’s shyness really makes it seem right for the parent to be alongside, ask at the first of these hand-puppet moments for the child’s opinion. Some of the less perceptive parents need to have the idea spelled out for them after class. Some really want success and recognition more than learning—that’s worth a telephone call before the child is pushed into deception or despair.
12. The breakthrough. Suddenly the light dawns—for all, or some, or someone. Celebration is in order, but not excessive praise. The focus has to stay on the issue at hand, the insight pinned down, explored, made clear by its discoverers to all, its consequences turned to. Too much praise not only loses sight of the math but is condescending, and it revives the competitive spirit we so much want to divert into the energy of inquiry. It is inevitable, too, that praise of one is heard as diminishment of another. Mark the moment and move on: for small victories, “Good. Now—.” For large ones: “We’ve done it! Now—” and on to consequences or further conjectures.
13. The Pied Piper. You want to be followed—but only so far. Your energy, enthusiasm, optimism, and goodwill are crucial at the beginning; they give a class its buoyancy and make everyone rightly feel part of an important enterprise. Gradually, however, you want them to take over: you become their secretary at the blackboard, or referee, or companion climber, or their slow friend for whom everything must be spelled out. Your radiance remains, but in the background. You want them to leave correctly thinking: “We”—not “I” or “He”—“figured it out!”
14. No idea. A student comes up with a conjecture or a suggestion or a line of thought that leaves you simply without a clue. Follow it out with the class; feel not the least twinge of embarrassment in admitting you don’t know whether this is a sound idea or not; say you’ll work on it and hope they will too. If you get nowhere with it at home, try a friend, a colleague, or the Internet. At the next class, report on your efforts and find out about theirs (you’re all now fully engaged in the real work of doing math). If they came up with nothing, ask a question that will set them on the new track you’ve found.
15. “Well, that’s because I’m a genius and you’re not!” Especially in new groups there are likely to be those who have to prove their credentials at the expense of others—and nothing can kill a class deader. For while it is crucial to our approach that classes be small, so that every voice can be heard and responded to, a drawback is that one person can easily be its centroid, setting the mood of the whole: saying “cool” will excite enthusiasm; being cool, destroy it—destroy the willingness to risk. You have to address put-downs as soon as you hear the least whisper of them. An upbeat, serious remark to the class as a whole sometimes works best: “We’re working together here, in good spirit, and math is too profound for our little egos to get in the way.” A word afterwards with the self-aggrandizers may be in order; it isn’t rare for them to change when they realize that this isn’t the culture of the present society. If nothing works, it is vital to ask these disturbers of congenial conversation to leave. If you charge for attendance, refund their money in full.
16. Clever Hans. Children are masters at reading subliminal signals: your hand moving toward the board as their ideas approach what you have in mind; the half smile, the half frown, that betrays what you think of their efforts. Most teaching is acting. Try for uniform enthusiasm or neutrality (as suits you), remembering always that you want them to do the discovering—and of math, not of your secret knowledge or opinion. If you’re going to play favorites, play it with everyone.
17. “Do this thing to that thing …” Lack of experience, lack of vocabulary, sheer excitement, will make students blur their insights and explanations. Judge when to ask for more rigor: not so soon as to kill initiative nor so late that all of you have become hopelessly confused. “So this thing …” “You mean this median?” “Yes, well …” “OK, give it a name.” “This median m …”—and you’re on your way.
18. The shuttle. Not just your students but all mathematicians shuttle endlessly between intuition and rigor. This becomes part of the balancing act that is a Math Circle class: you want excitement and meaning—so often missing from schoolroom presentations—but you want technique and precision too. You need to decide when one becomes excessive and lead the conversation toward the other. “All right, I get it” is a good signal that an approach is rigorous enough (you don’t want to legalize it to a standstill, and can always come back to snap up unconsidered trifles). Saying “I’m confused—this is getting too blurry for me” works well when intuition runs headlong away.
19. Was the class, was the course, a success? Often the best guide to that is whether you enjoyed it. But cast a mental eye back over what happened to see if anyone had been left out of the fun. Did you get to where you had wanted to go—or to somewhere else equally valuable? Above all, did the students singly and together catch a sight of the matchless beauty of math?
The outline of “Interesting Points in Triangles” tells you what you need to know about the mechanics of a course, and the notes for new teachers above add substance. But they don’t touch on what actually happens, and how the mechanical becomes organic in the presence of personalities. Lest you think that our classes are symposia of Platonic beings rather than quirky people, here are extracts from a journal tracking the difficulties that arose in three different sections of a fall course on polygon construction. Sections A and B were ten-year-olds, section C was eleven to twelve.
A class of ten, including five pals from the same school, all clearly used to having their own way. They ignored the other kids rather pointedly. So now we have a social issue to deal with as well as a mathematical. Handed out compasses (note: they were cheap ones, and that’s a false economy—too stiff or too flexible to be useful, with a clip which allowed the pencil to slat about), and gave them a whole hour to fool around with making patterns. Neat-fingered girls, C and S, produced Gothic arches, quilt patterns, yin-yang designs. J decided to do them freehand, because his technique (hold the compass still, rotate the paper) wasn’t too effective. Boys with poor small muscle control gave up quickly—perhaps they will be the force that moves us to abstraction. N gave up, H and Z went to the board and used string and chalk. Question: is it worth having a practical component? Yes. The Platonic idea is, of course, in the head, but it’s important that the hand get a glimpse of what making actually is.
Is it spoiledness, TV jump cuts, overscheduled lives or what, that makes modern youth so ready to give up? J decided it wasn’t worth trying to bisect a line segment before the problem had even been posed. I raised the question of the sum of a regular polygon’s interior angles—triangle, square, then went on to hexagon, because I thought it easier to calculate in the remaining time. Class instantly leapt into pattern-searching: 3 × 60°, 4 × 90° => 6 × 120° “because they go up by 30”—but then somebody noticed the 5 was missing, and a shouting war broke out between adherents of 120° and 150°. N cut a hexagon into 6 equilateral triangles, so won the war for 120°, but their question is always “what’s the right answer,” not “how do you know that’s the right answer”—and “it looks equilateral/parallel/equal” is totally satisfactory for them.
The Gang of Five was overexcited. Sugar may not be a cause, but bringing candy to class and not sharing it equally certainly is. I ban eating in class with a vivid fable of cockroaches among the overhead steam pipes. A’s mother, while people are settling in, fears he has not told me about the multiplication pattern he has discovered: 6 × 6 = 36; subtract 1 and 35 = 7 × 5; subtract 3 and get 32 = 8 × 4, subtract 5 and get 27 = 9 × 3. She wants admiration for her boy—he looks embarrassed, but clearly wants admiration too (especially because the Gang pretends he isn’t there). Question: stop the topic we’re working on and let A show this for social good (but will it do the trick)? Get the whole class working on trying to figure out how it works (if x is a square number, call it n—then (x+1)(x–1) = x2 – 1 = n – 1; (x+2)(x–2) = x2 – 4 = (x2 – 1) – 3 = (n – 1) – 3 …)? While distracted by simultaneously hearing this saga and trying to decide what to do, the class has arrived and gotten out of hand. Z announces that he remembers nothing of the previous classes, no one has brought in a compass (my solution to their complaints about the crummy ones I’d provided was suggesting they bring their own). Figure I’d better save A’s hypothesis for later and get the show on the road. Dropped my voice a fifth and said that if we were going to get to the polygon stuff we’d have to use our time better—and it worked. There was real concentration on how to create a square. C got a right angle by bisecting a line segment. A had an interesting idea of drawing a circle and constructing tangents to box it in—except he couldn’t find a unique point. Then N made a right angle, swung an arc from the angle to hit the two sides to get adjacent equal sides, and then found the fourth vertex by swinging arcs of that length from his two new vertices.
A day saved from chaos—until the end of class when N had to throw his shoe to knock down the paper airplane that had got caught among the steam pipes and it almost landed on A. …
Three new kids arrived in the class, so a chance for people to demonstrate to them all the things we could construct. A new octagon construction suggested—“make a cross of five squares and connect the points”—looked very good, but J pointed out that the hypotenuse of a right triangle has to be longer than its sides, so it wasn’t a regular octagon. A great event—a revelation to the “it looks like it so it is” brigade, who for the rest of the class demanded proof; but usually by asking J or me to provide it. J is attentive, dogged, and imaginative—a real spark to the class and a great help in showing that the topic is not the sole property of the teacher.
Good discussion arose about pentagons—first appearance of conditional thinking: if we had a 36°–72°–72° triangle, giving us a length of x, would that mean that having x we could create a 36°–72°–72° triangle?
Lots of schools apparently use April Fool’s Day as a Saturnalia, so there was a constant undertone of giggle, and we never had more than half the class involved in any discussion—so as people rotated into consciousness there had to be a lot of recapitulation, which bored a previous conversationalist into dropping out. One scary moment: A was very disturbed by our finding out that 
wasn’t rational. He kept saying, “Tell me what it is!” and got red in the face and close to tears at its refusal to turn into a fraction.
“This is the best class we’ve ever had,” say N and H. Why? We were actually making a pentagon—which they found very hard, but they knew what they wanted to do, stuck to it, and ended up with perfect, if grimy, pentagons. We’ve really established why 
is crucial, where it comes from, how to construct it—and they were confident that if they just tried they would get a pentagon. J got a nonagon—twice! Other factors: Z and M weren’t there, and since they are often not there, they usually haven’t a clue and so distract their neighbors.
I started by drawing a really crude triangle on the board. “What can you say about this?” Chorus: “It’s a triangle.” (In tone of duh—how old do you think we are?) G: “It’s a pretty pathetic triangle.” So we set up a spectrum from pathetic to perfect (Platonic) and constructed. Lots of good comments—that it was impossible to write “perfect” perfectly on the board; that one must have the Platonic triangle in one’s mind to know that the pathetic triangle was pathetic. Oddly, this group is much more manually dexterous with the compasses, even L, whose mother thought she’d never seen one.
O and Knowledge: he knows that the sum of the angles in a triangle is 180°, he’s known it for years. He sees no need to prove it, because it’s a fact. “Do you want to prove that this hat is green?”
People are attached to their methods—there is the “copy a length by carrying it with a compass” school, and the “take another radius of the circle with the given length as radius” school. “You’re just measuring.” “Well, your line segment is attached to the original one.”
There are now thirteen people in this section, but it works pretty well, because they are all willing to talk.
Great class. We were closing in on —. “618,” says G, at regular intervals—and I’d say that everyone except P (and R, who was absent) was involved all through. We hit the rational/irrational issue and faced it head-on. L, of course, knew the decimal form for 1/7, and then we divided 7 into 1 (which was quite an event: several people had never seen a division algorithm—you either “just know” from times tables or use a calculator) and saw that it repeats on a six-period and saw why it must repeat (“cool!”); so nonrepeaters can’t be rationals—but maybe repeats and we just don’t know it. Decided to risk trying the proof by contradiction and we did it in full, to total satisfaction. “Weird kind of fraction!” repeated around the room. Even O was willing to say that “” was more useful notation than a decimal approximation—but G points out that “real scientists” use decimals, not fractions.
Another great class. Fascinating to find that last week’s comfort with irrationals did not stretch to—or maybe prohibited—dealing with –1. “How can you subtract a Number from … an irrational?” Numbers should only do arithmetic with other Numbers. Well, what things are Numbers? Everyone agreed that positive integers were, but some doubt about negatives, because people had heard that minus times minus was plus and couldn’t see why. Fractions unpleasant, but OK. Irrationals are exciting and can describe lengths, but not clear that they are Numbers. Clear that we’ve got a very Pythagorean group here.
I raised the historical issue of doubt about 1 being a number (a nose, 2 eyes)—how long it took before 1 was admitted to citizenship, since numbers were thought of as collections of units, so the unit itself wasn’t a number. Then of the difficulties with fractions—if 1 is the unbreakable (atomic) unit, 1/3 is a calculation, not a number. Or, as reflected in “numerator” and “denominator”, third is a name even when 1 is a number. This is also a very verbal group, and their generous hearts allowed them to welcome . “As long,” says L, “as it behaves like other numbers.” “It behaves better than zero,” says G.
Idle conversation about the meaning of Greek “atom,” and the shock of an atom not being atomic, bore fruit later when G said a 7-gon was inconstructible—because he’d asked a scientist—ah, and what if you’d asked him about atoms? We slowly approach the idea that opinion is not identical to truth.
Lively, and full of unexpected stuff. Even the least mechanically adept produced recognizable 15-gons. To keep G from announcing one more time that he was finished, set him to turning his 15-gon into a 30-gon, hoping he’d see the limit is a circle.
A: “The ideal triangle can’t lie in the clouds because you could reach it in an airplane.” R: “It would be so perfect it would evade you, always circling the globe opposite you.” There’s been a dramatic change in this class. Last term it was dominated by D’s constant put-down of every question. Now T and K are set free to talk about ideas, U to ask for help with constructions. All sorts of loosely linked topics came up: the metric system vs. “normal”: “God gave man a foot and an inch and a yard—” We were all amazed that it was ten minutes past the usual end of class.
Three new girls added to the eight prepubescent boys. They spent every second before class brushing their hair, and as much time as they dared reading magazines. Apparently one of them wanted to join the class but didn’t want to come by herself, and her friends wanted to make it very clear that they were present only physically. Amazingly, the little guys never noticed—only K raised an eyebrow—when B had a screaming fight with her embarrassed mother.
F knows that the sum of the angles in a polygon goes up by 180° as the number of sides goes up. How does he know? It’s in his math book, and it shows that it’s true for up to 12 sides. Well, that beats “My dad told me.” Next time, deal with “true as far as 12”—and the difference between science proof and math proof.
A great class. Began shakily, with W veering out of control (a long anecdote about future people in a story shooting garbage into outer space) but F was jolly, attentive, cooperative; which somewhat eases my guilt at telling him off for antisocial behavior that he was probably totally unconscious of. At the end of class T, really concentrating, calculated the product of 
and 
with speed, accuracy, and delight in the solution. Wonderful side trips into Newtonian vs. Einsteinian physics, non-Euclidean geometry, the minimal ideal for axioms—the nicest sort of conversation with little boy touches, like A conversing with B by telling me what he would say to B.
A day of total madness. E’s hexagon didn’t close up, which convinced him that he could go around and around like an ammonite building on slightly-less-than 60° slices and so construct any n-gon. People pointed out that spiraling wouldn’t create any closed figure, but he was sure that that problem was trivial. U waited until everybody was on to the next issue before saying he had no idea of what was going on—and did that three times. F assured me that even his relativity seminar was brainless today. His theory is that there is too much sunshine today for our northern brains to deal with.
V suddenly began to talk, and then, blushingly, Y. A silly, friendly conversation about having braces on your teeth. But they kept on talking when we started looking at the series of inscribed and circumscribed triangle, square, etc. My plan was to get to the idea of visually trapping a circle. F: “This looks like trigonometry!” “What’s trigonometry?” OK—so we took that tack—defining terms, fitting angles and ratios of sides into our previously Euclidean world. Everyone was curious and involved, asking questions, making guesses.
Why was this such a good class? I hadn’t prepared it, so there was no place I was impatient to get to, and no program for people either to follow or rebel against. We were all enthusiastic and disorganized, so they were freer about making suggestions and kept the discussion focused. Their contributions were genuinely intended to be helpful, not attempts to “do well.” It was a real experience of being mathematicians working on a problem, not teacher and students in a class.
* * *
Here are some notes from a fall course for seven- to nine-year-olds. If the question ever came up of what the topic was, the answer was simply: “Big Numbers”.
Only five at the first class—four of them extremely talkative, relaxed, and joking. It’s going to take a great deal of care in formulating questions to keep from descending into chaos. It was, for example, a mistake asking “What’s the biggest number you know,” expecting a trillion or a googolplex—and producing 45 seconds of 99999. … At the school W goes to they celebrate the hundredth day of school by having each child bring in 100 of something. W planned to take in his toy cars but lost track at 75. Another revelation: seven-year-olds talk with as much sophistication as eight-year-olds, but they have real trouble reading handwriting on the blackboard—implying I should print up handouts. But how can you print up in advance what hasn’t happened yet?
How does one cure a migraine? Spend an hour with six yammering children. The Role of Adrenaline in Teaching. We started today with how to write big numbers in small spaces by using exponents—on our way to Archimedes and his myriads of myriads. Fell into a developmental cleft: N and W hadn’t a clue. O and J got it instantly. It was right on target for E and S: they like structure applied to enormous size. They were both troubled by the idea of a finite universe (my image was of a crystal sphere slowly being filled with sand, like the bottom of an hourglass). S: “But where would you be?” E: “How can they say how many particles in the universe? How can they measure?” W has the solution: hire a scientist to count the grains.
T claimed that 3(x + 2) was the same as 3x + 6, but C said they weren’t. T said yes they were, it worked every time. A: “You haven’t tried it for every number!” I put in my oar: “Remember when we figured out an easy way to do 5 × 107 as 5 × 100 + 5 × 7?”
S: “But that wouldn’t work for small numbers!”
Working on Kaprekar’s constant.18 Amazing concentration with which they went through seven successive steps to arrive at the cycle. N, S, and W now sit together in a triangle, one in the front row, two in the second, as far away as possible from J and O, who sit at the other end of the front row. E sits alone in the third row, but on the J and O side. This allows me to teach three separate sections—each knows when its eye is being caught for a sophistication-appropriate question. The seven-year-olds had never seen borrowing, so we did it in detail: theory, practice, chant. Nine-year-olds are good subtractors, and E’s speed kept O from complaining of boredom. N (randomly as usual) announced that 
was 100—his calculator said so. We disproved that quickly, then tried to find what was. 
, then narrowing—quite reasonably, to 
—and again impressive determination. J: “Try 33 1/3!”—which required totally new techniques. We got to 
and left it for the future.
S happily calculated 220, but could see no sense in 22k, because k was a letter, not a number—this despite his former happiness with letting x take on a range of values when playing function machines. So I said Fermat’s “formula” was just another function machine, but he preferred to use k for his inputs. S was then happy, but I wasn’t, sensing an abyss just glided over. Wrote “variable” on the board, and asked if anyone knew what that word meant. O: “It means different kinds of food. We’re doing an experiment at school and the variable is what they eat.” Children and language learning: they are programmed to pick up and use new words they have a rough sense of by context, but their using them by and large correctly is no demonstration of their knowing their actual meaning. A real issue in math, where there is a great deal of “naming of parts,” easily confused with learning concepts.
We forget what a miasma of myths our certainties emerge from: error and hearsay maintained through endless generations of eight-year-olds. We had turned to function machines when concentration lapsed, and C’s secret rule was “times 2.” S put in –1 and all hell broke loose. C calculated to himself, then announced: “You don’t realize how bad this is, because you get two different answers. If you say –1 × 2 you get –2, but if you say 2 × –1, you get +2, because when the minus is on the right, it reverses, because you’re going backward.”
“No,” said T, “it’s no problem at all, because 2 × –1 is –1 + –1, and that’s 0.”
“It isn’t the sign that reverses,” said A, “it’s what you do to the numbers. When the minus is on the right, times turns into divide, and 1 over 2 is 1/2.”
A mad run through what is now comfortably seen as Fermat’s function machine. We’d got to 225, i.e., 232 + 1, and doubled our way to 4,294,967,296 +1, decided we’d have to check all primes less than 65,536—and then found it wasn’t a prime. O was outraged at Fermat’s stupidity. J, the tinkerer, tried to persuade her that it was a very good guess, and that you have to make guesses and test them and expect that some of them will be wrong—but O was having none of it. What made her really mad was that she had put a lot of work into something that Fermat already knew was wrong: he shouldn’t be wasting her time like that—she has enough to do learning true stuff. Nervously moved on to Mersenne primes, hoping she’d allow their provisional nature. As people calculated them I wrote up, by chance in columns,
21 – 1 = 1
22 – 1 = 3
23 – 1 = 7
E saw a pattern: “You just double and add one for the next output.” Amazement and joy—no more need to raise 2 to outrageous powers. But why does it work? Well, 2(2n –1) +1 = 2n+1 – 1, but how extract that abstraction from an eight-year-old, whose interest is in does it work, not why.
O and J out of town, so could focus on the math level of the young, and since N was there, the seesaw was very tipped in the seven-year-old direction. We got (reanimating, with difficulty, the calculation of 2m × 2n, a tool the older kids specialize in) powers of two worked out through 220, and they would have gone on for the rest of the hour, had I not suggested relaxing by switching to powers of 10. I always forget how determined the young are to write out all the zeros (big numbers, like dinosaurs, as dangerous and powerful friends). 1020 was, I claimed, such an easy way to write a number whose name is never used and which is never written out—and they were hard at work writing a “complete” list of the powers of ten, their expansions, and their names. A different idea of control of the world through notation. Moral: in teaching ideas about math I’m very careful not to impose my understanding on their experimentation—but when it comes to wallowing in computation I tend to forget to repress my views.
Everything worked and all our simmering ideas came to a boil, so to celebrate we ended with an orgy of function machines. In high spirits, W put a canoe, two people, and a paddle into C’s machine, and C (who takes everything seriously) said he needed to multiply human times human and didn’t know what he’d get. “Human2,” said J. “Yes—but what is that?” No one had anything to say, until E offered: “Human divided by human would be 1, because anything divided by itself is 1.”
“Of course!” said C—then: “No! I wanted to multiply!”
I said, “I think it’s a complicated question. I just saw a book that said $2/2 = $1, but $2/$2 = 1.” Everyone said, “Of course.”
I went on: “But I don’t understand what $2/$2 means.”
“Nobody knows what it means,” said A, “but everyone knows the answer is still 1.”
I should have asked them whether $2 × $2 was four square dollars.
* * *
From a journal about two spring semester courses dealing with solving equations.
Thirteen-year-olds (and two parents) were in Section A, fourteen- and fifteen-year-olds in B.
The issue came up of whether infinity is completed or potential. N: “You just make one when you need one.” Counterview: they exist in the mind of God (eternal, omniscient, and won’t get filled up). N’s father, P: “So all infinities are equal?” G (another father and Math Circle veteran): “That’s another course.”
J: “Are they called rational because they make sense?” I tried to explain ratios using “If you need two cups of water for one cup of rice … ” but this is an all-male class, had never cooked, and couldn’t think of any other instance in which you might think in ratios.
What if you had 1/2 over 12/7? “That wouldn’t be a rational, because it’s not integer over integer.” K: “It would be if you multiplied top and bottom by 2 and then by 7.” This raised the whole question of time: Does that expression become rational, or was it rational all the time but just “invisible”?
We fell into the trap of calculation. People wanted to get “one more” decimal place in trapping a < 
< b—“I’m nearly finished.” It takes a person who dislikes arithmetic to say: “The method is clear and working it out is tedious.” The nonrepeating issue came up: how would one ever know? “How many places would you have to calculate to be sure it didn’t repeat?” K: “As many as there are counting numbers and we know we won’t get there.” J: “So we’ll never know.” We part in a combination of gloom and awe.
J comes in saying that what we have to do with is to prove that it is a fraction, and not try to catch it between decimals. N, groaning: “The task would be unending.” I wrote 
on the board and said “All we have to do is find a and b”—and slid in the idea that the real a/b should be in lowest terms to keep us from getting an infinite collection of the same thing.
Instant demand that we “square both sides” and then that we “multiply by b2.” Why? “It’s much easier to see things when the equations are simple.” But nobody saw anything: we stared at 2b2 = a2, people tried putting in values for a and b, unsuccessfully. (Interesting point: nobody tried substitution for a/b, because they were convinced from last time that that was a mug’s game—but once we had it in a different setting, that conviction faltered.)
P: “Stop! The Pythagorean Theorem proves it’s impossible!” His idea was that in the right triangle 1, 1, , a and b both equal 1, and since 2 ≠ 1, 2b2 couldn’t possibly = a2. I drew it on the blackboard and let it stand. N: “They’re different variables, Dad.” Impasse.
Me: “What if I floated the words ‘even’ and ‘odd’?” Universal belief that the square of an odd is odd, of an even is even. “How do you know that?” “It’s a fact.” “What if someone didn’t know that?” “He’d be stupid.” I seized the opportunity for a disquisition on the difference between ignorance and stupidity, but it will recur—thirteen-year-olds equate intelligence and knowledge, so logically must equate stupidity and ignorance. The usual problem of correlation and causation.
“Could you prove an odd squared is an odd?” Everybody starts calling out odd numbers and their odd squares—but N says “Stop! We’d have to do N of them!” Great! Quickly they decide 2n + 1 is odd, and “the square of that is 4n + 1, and that’s odd too.” Too close to the end of class to take up that whole issue, but not a good idea to let it pass. Me: “OK, if n=3, then 2n +1 = 7; what do we get for its square?” “13.” Horrified Chorus: “But that’s wrong!” Chorus of those who were annoyed that examples don’t prove: “You can just give an example!” Then the bell rang.
No meeting last week, but somehow the class has gelled. Everyone talked, not just the veterans. Started with the old problem of squaring 2n + 1, as paralleled by squaring 7 = 2(3) +1; A and M became responsible for arithmetic. Although K is convinced that it is a fact that (a + b)2 = a2 + b2, he admits that it doesn’t seem to be coming out right today. He’s going to check on it.
The proof that no fraction equals rolled up so quickly that I thought I’d better recap—no need. High energy and general participation has led to understanding.
But then, having successfully lined out (x – 3)2 = 4 as x2 – 6x + 9 = 4, and moved on to x2 – 6x + 5 = 0—when I asked if, coming into the room and seeing that expression on the blackboard you could turn it back into “a square = a number,” they were totally flummoxed, and went for x2 = 6x – 5 and even x(x – 6) = –5, which, said D, was impossible, because the product of two numbers couldn’t be negative. Sometimes you feel you are coaxing butterflies to march.
Moving from the raw material, what sorts of numbers there are, to putting them to work in functions, we got into translating the geometric idea “two points determine a line” into an algebraic statement about (a,b) and (c,d) => y = mx + k.
Thanks to giving directions, we got the map idea that a point is determined by how far up it is and how far over, and thanks to people’s having been to New York, got a grid with streets across and avenues up and down, and even distances as either on foot (“add up all the ups and all the overs”) or crow flies (Pythagoras)—but everything crashed at the transition from numbered points to abstract coordinates. We got a good definition of an unknown constant: “I have a birthday, you don’t know it, but it’s fixed—and you know that.” So we could get a line determined by two fixed points, but couldn’t get a way of describing any point on the line. Did get that “a line has to continue in the same way,” or “at the same angle.” Impasse—indicated by people repeating what they’d said before. Math as politics.
I decided to break the wrangle by talking about railroads and asking why they couldn’t climb up steep slopes. Rapidly produced “If they wanted to get over the Rockies they’d have to build a trestle starting at the Mississippi,” and the idea not of angle but of rise/run. Everybody had a steepness story, either of climbing or of skiing—general conversation, building the concept of slope into a physical context. And then K said: “If you go downhill do you call it negative slope?” and we segued right into abstraction. Another day when people wouldn’t leave, even for juice and cookies—they wanted to figure out: if you have two lines, can they only be parallel or intersecting at one point? What about two lines lying entirely on top of one another? Do they become one line?
Great breakthrough! K insisted we solve a quadratic by formula—“the real way”—and not waste our time completing the square. He stated it and began plugging in, and D (the guy who began the year with “I know, because somebody told me”) insisted that K explain: “Where does it come from? How does it work? What justifies it?” So we solved 5x2 – 24x + 27 across the four blackboards in parallel: (a) by factoring, (b) by completing the square—then we solved ax2 + bx + c = 0 by completing the square to produce the formula, and then (c) everyone agreed to allow K to use the formula—and the class ended on a note of universal satisfaction. Nicely, people have different favorite methods; the formula hasn’t conquered the homemade.
Conversation on the pains and delights of symbolism, inspired by Bhramagupta’s paragraph-long quadratic formula: how one yearns to tell him ours, vs. how annoyed one is at seeing some symbol one doesn’t understand. “My sister’s calculus book is full of long wiggles.” One of the Russian girls: “It’s like having things that are easier to say in Russian and things that are easier to say in English.” Impressive that they already see that math is expressed in symbols, rather than being symbols.
I had on the board “x – b/a = 0”, and then wrote x = –b. W: “How did you get –b?” Me: “Because I’m an idiot.” Delighted laughter—at the implied safety of asking a question, implied acceptability of making mistakes, at the ridiculousness of a typo being equated with idiocy—a moment worth twenty repetitions of “collegial, not competitive.” But joking isn’t universally valuable: in the other class D and L, who have no sense of irony, would just say, “Teacher admits to being an idiot.” A difficult balancing act.
A good example of the values of symbolism: S “couldn’t understand” completing the square of x2 – 64x because R had said “1024” so quickly; but x2 – 2ax got through. How frequently slow arithmetic produces a sense of incompetence, and hence readiness to skip the whole thing. Does that mean there should be more emphasis on mental arithmetic in the younger grades, or more abstraction? Rote certainly leads to boredom—and uses up a lot of valuable time—but abstraction may not be compatible with brain maturation.
The question arose of why the History of Math concentrates on different places at different times. Was nothing happening in other places? Did the Greeks just stop after geometry? Where is math now? What did Islamic math have that nobody else had at the time? Answer: both algebra and the idea of proof. The interesting phenomenon of a slightly different topic bringing new people into the discussion—and once people have started talking, they tend to continue. A good argument for widely read teachers.
Discussion of whether math is truth or is culturally determined (arose in the context of clay tablet Plimpton 322). E is convinced that it is all created in the mind of man, and only technologically determined insofar as tasks suggest realms of invention. There is no external truth. B says 3 – 2 = 1 is a universal truth. E and M argue about imaginary numbers—E that they are no more imaginary than any other numbers, M that the mathematical properties of the other numbers are intuitive. T says that minus times minus is plus is just as artificially designed, so negative integers are just as imaginary as imaginaries. T had a lot of trouble making herself heard over P, E, and V. That’s a real problem for girls in math: having to shout and hit, which they learn to stop doing by age ten (it doesn’t happen as much in other subjects, because boys are less interested—or argumentative—in discussing literature or history).
Working on finding middle terms of Hippocrates’ cube doubling, leading to Appollonius’ conic section solution. Good questions about the value of stating hypotheses even if you couldn’t prove them (leading to a digression about Fermat and Wiles). Then I asked: “If you see ‘ratio,’ where do you go to look?”—expecting similar triangles—and A said “trig functions,” and then W asked whether they were really functions: how, for example, does a calculator answer when you ask for sine 32°? (The great usefulness of giving children calculators lies in all the applications they don’t know how to use, which really exercise their imaginations—they play around and try to make sense of what comes up). My taste is geometric, so instead of curves I drew triangles—getting 45°, 30°, 60°—and at 
coming out of the calculator as .7071, B raised the Greek objection to approximation.
Back to conic sections with cone and slicing planes, good arguments about parabola vs. hyperbola, limiting cases (circle just one of a set of ellipses), everybody popping confidently with contributions.
N: “I’m not particularly religious, but those numbers today could persuade you.”
Moving toward the idea of a cubic formula—a machine into which one could plug data—and to the graphic representation of cubics, with al Tusi’s idea of the local max of a cubic being based on the max of a quadratic at x = –b/2a. The class split instantly into algebraists vs. geometers, with each convinced that reality lay in only one of the two formulations.
Moving through the permutations of symbols to produce the cubic formula: an amazing universal balk at change of variable. Everyone agrees that it would be useful to replace x with y – b/3, but it seems immoral (I’m glad I didn’t follow the convention that replaces x with x – 3: that would have turned them off math forever!). Very important in planning a course, a class, to predict the places where people will hit the “do bats eat cats” barrier, where words (or symbols) have stopped conveying meaning and just turn into sounds. Especially because some students are so good at memorizing nonsense syllables that you might not notice that they don’t know what they’re saying. Another argument for conversation.
* * *
I hope this journal gives some sense of the exhilaration of teaching in The Math Circle style. It requires preparation so thorough that it’s completely internalized, being able to turn on a dime, sharing the excitement of the chase, thinking on several levels and from different standpoints. Where did we ever get the idea that teaching should be predictable and uneventful, with challenge and excitement saved for weekends and vacations? While colleagues are counting the time (“Only thirty-two more years!”) to retirement, after decades at the chalkface, I still enter a classroom with the same anticipation I felt on my first day of teaching.
The Math Circle will spring up, as it has in our neck of the woods, when the demand of enough dissatisfied parents finds a supply of interested teachers. But this leaves too much to chance, and the luck of finding energetic enthusiasts, for it to spread very widely. We can think of several other ways for it to take hold.
Loose networks, like those of home-schoolers, might form more or less spontaneously, drawing on people whose different agendas coincided perhaps in no more than the desire to have math developed collegially, and in depth. As you saw from the Competition section in chapter 8, there are already associations of competitive math circles, with meets and prizes. These would be unlikely to morph into our approach, but families and teachers who are engaged in them, because they are the only option at present, might welcome the chance to join a more collegial group. A problem with spontaneous groups, however, is their dependence on individuals: doctrinal differences might well swamp them, and another Movement would have run its course.
A tighter network, as of after-school Math Clubs meeting on school grounds, would be a second possibility. Were these funded and overseen by some central organization, like an existing mathematical body, some sort of cohesion might follow. Drawbacks include all those of centralized bureaucracies, to which the freedom of mathematics would be especially vulnerable. In addition, by being in the after-school slot, competing for students’ time with sports and activities, their reach would likely be limited to the few already enthusiastic about math. Better still would be an informal federation of Math Circles (sharing topics, successes, and failures via the Internet—and perhaps visits in person), each run in its own way, with courses chosen by and suited to those in it (math pure or applied, leading to or from the sciences). For the sake of that freedom so central to mathematics, keep administration and hierarchy to a minimum. Each ship, then, on its own bottom—but all flying the flags that signal collegiality rather than competition, serious content, and discovery rather than instruction.
The best way, certainly, would be for The Math Circle’s approach to replace that in regular school classes—and this will surely happen one day. The question is how to move that day closer to this. The steps are straightforward. For generations, school math curricula, from twelfth grade down to first, have been largely determined by college entrance requirements; and here The Math Circle style of teaching works far better than the present curricula, with their petrified remnants of business math and practical math—poorly combined with math for fun and math worksheets to free the teacher for other tasks.
We’ve seen our students consistently master what’s thought to be very advanced material, because they wrestle and think their way through it, propelled by the fun of the chase. A course begins slowly, as people mull the problem over, but then speeds up with the excitement of discovery, and no time is wasted on review because it is their intellectual property. Nothing is memorized, because it is understood: in math, the need to memorize testifies to not understanding. A model to keep in mind is the old shop class: you don’t have to memorize whether a saw, pliers, or a hammer is most conveniently used for driving in a nail. The level aimed for isn’t cabinet-making, but it isn’t wood-butchery either: solid carpentry lets you advance.
As always, we come down to the problem of developing teachers able to run such courses. Math has traditionally been the least favorite subject of elementary school teachers; few have studied more math than what they had in high school, and even fewer have a real interest in it. In order to teach a flexible and inventive math course, they would have to master a lot more math, not just a new methodology. The job would have to be made attractive, both in pay and esteem from colleagues and the community—and these political and social issues rest ultimately on the perceived need for a mathematically literate population (a need that grows as automata take over less skilled jobs). Given the body of people eager to teach, how prepare them? By using The Math Circle approach in teachers’ colleges. We’ve now narrowed the problem down to the much smaller population of those able to teach the teachers.
Perhaps—as in countries where literacy was spread by insisting that whoever could read should teach two more—those who will teach the teachers will come from the ranks of Math Circle teachers and students. Three of our graduates have already taught courses, and our colleague Jim Tanton now runs just such a training program for future teachers. Perhaps this book will inspire others, in who knows how many different ways: mathematics is freedom.
Whenever we’ve given a demonstration class, conversation afterward in the teachers’ lounge followed the same pattern: surprise at the number of students who got involved (“Sally never says a word”), amazement at the sophistication their students could handle (“They can’t reliably add 7 and 3—and here they were figuring out the sum of the first hundred integers in no time!”), envy of the fun we were having—and then, always: “But of course I couldn’t do anything like that; we can barely get through the syllabus as it is.”
The Math Circle has, indeed, the luxury of an after-school program’s freedom from responsibility, but we too have taught in K–12 schools and universities, and know that you are never free from the syllabus, the exam, the necessity of preparing for the next course (we never are, but always to be, blessed with boundless exploration). Is it really impossible to harness the energy of The Math Circle to the cart of meeting requirements?
Not at all. The greatest innovation takes the least time. Instead of stating a rule and then assigning “exercises” which use it, start with the problem and work as a group to discover the rule: not “A = bh/2, what is A if b = 3 and h = 5?” but “Here’s a triangle; how could we find its area?”—so turning conscripts into colleagues. It may take ten minutes to come up with the answer, but no one will ever “forget the formula” when they can re-create it as they need it. That works as well for AP Calculus as for fourth-grade Shapes and Their Properties—a technique one devised oneself won’t revert to symbol-pushing after a week. Curiosity, and pride in workmanship, will have been awakened.
With this approach, the term begins with your class running behind the syllabus, but it catches up about midyear—and has lots of spare time in the weeks usually devoted to review before the exam. But what if you have to pass a checkpoint on time every week, as in a course with many sections and common tests? Then you can divide the class period into meat-and-potatoes and dessert: first a quick and active discussion of the day’s topic, still letting the students discover, but directing the search a bit more—and then as a reward, a completely free discussion of some ongoing unrequired topic (the Web is a good source). The promised reward focuses attention, and you have Math Circle minutes, if not hours.
Another great time-saver is intellectual honesty: “Why do we have to learn this technique?” is a fair question, and should be answered to the best of one’s ability—how its use helps, how they could have developed it themselves—and then the revolt, which was unspoken—“They’re just making us memorize nonsense”—subsides, and the next topic will be greeted with an open mind.
There is one more serious problem that classroom teachers face and that no approach can entirely solve: classes of over twenty-five inevitably decline into lectures, with a few active students and a large passive back of the room. What we are learning about working memory shows that for many people, being told something registers far less well than doing it oneself, so lecturing is about the least effective form of teaching. If economics dictates that large classes are more important than effective classes, call on the goodwill of local college math departments and their students, on parents, on fellow teachers with a free period, or on some of your students—and split the class at least part of the time into small, problem-solving groups.
And what can parents do? Agitate for smaller classes—and when you’re not engaging with the local school board, encourage your child’s interest in math. You don’t have to know much yourself to puzzle together over whether there are more counting numbers than even numbers, or how to find the balance-point of a triangle, or what the odds are of getting a royal flush: such conversations often draw the generations together. Steal a few minutes on the Web to find good questions, and even if they come with answers, try letting your child figure it out, with the fewest nudges: a fine exercise in patience and good humor. It’s also fun to play Fermi Estimates (named for their inventor, the Nobel laureate, Enrico Fermi): how could you make an enlightened guess at the number of piano tuners in the greater Cleveland area? How many slates are there on the roofs of your town? How many stars can we see? How many hairs on the average head or words on a newspaper page? How long would it take to drive from here to Maracaibo? These games sharpen the number sense and once again, using the Web, help explore the world.
Let’s think—students, parents, and teachers alike—more broadly and boldly. Why confine this approach through imagination and thoughtfulness to mathematics alone? Why shouldn’t history, literature, languages, and the sciences be subjects of collegial inquiry from the start—savoring their phenomena and making them accessible through reason rather than memory, engrossing ourselves in their substance rather than diminishing it to multiple-choice scores?
Thanks to a grant from the Joseph and Claire Flom Foundation in 2008, and now the Flom Family Foundation, we’ve been able to hold a Math Circle Teacher Training Institute at Notre Dame each July. Members come from across America and around the world, spending an intense week learning and practicing our approach, on a population of students ranging in age from five to eighteen, provided from nearby Mishawaka and South Bend by our colleague, Amanda Serenevy. The intention is for them to open Math Circles when they return home, or incorporate our approach into their teaching.
Mornings we hold classes with them as students, the conversation moving between the mathematical topic and how it would appear in a Math Circle setting with kids. Later in the morning these discussions come to focus on teaching issues: How much should the leader try to nudge the conversation in a preferred direction? How can one work with the shy student at one extreme, the aggressive at the other? What topics best bring out inventiveness, imagination, insight? How to establish and keep the tone of the enterprise in the high humor of the greatest dramas? Then in the afternoons members lead groups of students (of the age they prefer to work with), followed by helpful observations from others. In the evenings discussions focus on mathematical topics they wish to explore—in the course of which the Math Circle’s collegial style broadens and deepens: freedom from fear of being wrong; freedom to ask, explore, conjecture.
Does it work? Members have since begun their own Math Circles in many American cities and abroad, and imported our approach into public school classrooms and home-schooling living rooms. Here are some answers, over the institute’s first five years, from questionnaires at the week’s end:
This was one of the best math institutes I have been to—it challenged me to go far beyond my knowledge of math. It helped me to go into the “deep end” of learning math. The instructors were so dynamic and extremely knowledgeable. They pushed me farther than I ever thought I could go. I have a much more passionate love for math because of this workshop. I liked being able to work on the hands-on projects and it was very beneficial to share the institute information with the students. This workshop helped me become a much better teacher and I can’t wait to implement what I have learned in the classroom. From this workshop I have learned that math is such a risk but it is only when you risk that you grow. Thank you for having such an incredible workshop!
There are numerous reasons that this has been a refreshing experience. The most influential factor has been the people. This institute has not only attracted a multinational group of participants, but a multi-professional group as well. The presence of non-teachers at what could be considered a professional development opportunity for teachers speaks well for the idea, and provides a unique source of inspiration for teachers. During the week, a vibrant and diverse cohort has formed simply for the love of math. There has also been an intrinsic motivation for the cohort to establish a way to persist (a Wiki is born!)
This institute has been the best math teacher training I have had since starting to teach in 1982. The leaders provided and shared so much of their knowledge in an inspiring and energetic way. Their passion for math is contagious!
My favorite part of the week was doing math. I learned so much about how my students learn and work on math by learning and working on math myself. The morning sessions (and the wonderful infinity evenings) gave me a treasure trove of excellent math problems that I could use with students and it was really helpful to have struggled with it myself and to see where the math goes. I had a really wonderful time flourishing in this beautiful space you have created where you can take risks, play, and be excited about math. More than anything, this reminded me that I love math and why I love math, which is such a refreshing feeling! Thank you! And thank you for inspiring me to do the same with my students.
I love love loved solving math work together in a group. It was one of the most joyful experiences of my life (yes, I mean that literally). Once I felt comfortable with my peers: to work together, to bounce ideas, to work alone, come back together, to be wrong, to be given time, to question each other, to explain, to follow our own ideas.
We have an inborn urge to know, to make, and to enjoy the world around us, that neither fatigue nor fear can long suppress. It shows up as wonder that turns to awe; as a knack for engineering; and as what we’ve called the architectural instinct. These all, as they draw us on, reveal a labyrinth of shape and number that we move through. Daedalus made his wings out of feathers and wax; we make ours out of observation and reflection—and so rise out of the labyrinth, and see the whole world spread below us.