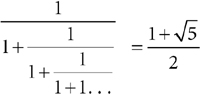
Sam Lichtenstein was a student in The Math Circle every semester from the age of ten. When he was seventeen and a high school junior, he struck us as a potentially wonderful leader—and so indeed he turned out to be. Here are some thoughts of his, written in December 2004, his second year of working with us.
* * *
In elementary school, my friends and I would compete to see who could do our quizzes on multiplication and division the fastest. In retrospect, this might have been a bit of a burden on my teachers—how were they to teach math when some of the students were quite literally racing ahead? Subsequently, my teachers arrived at a solution: give me and the other mathy kids puzzles, puzzles, and more puzzles. The best, and most prominent, of these puzzles were “logic grids.” An example of the type of question these asked would be to match up a group of kids with their hat color—say, figure out who among Billy, Yasmine, and Greg has a blue hat, who has a yellow one, and who has a green one. The only tools we were given would be a series of statements, such as “No kid has a hat whose color begins with the same letter as their name.” And with these statements, we were to figure out everything, using logic.
The reason they were called “logic grids” was that there was a set strategy for such puzzles: write a table with the kids’ names on one axis and the colors on the other axis. Then in the appropriate box of the grid, place an X when a situation (e.g., Billy’s hat being blue) is logically inconsistent with the given statements. Using a process of elimination, the solutions were generally straightforward. Now that I think about it, it seems likely that some of the more difficult puzzles required the use of some rather sophisticated, yet still intuitively obvious, concepts, such as the Pigeonhole Principle. But at the time, it all fell under the heading of “logic,” and it was a good way to spend a day of school. Unfortunately, after the hundredth or so puzzle, they started to seem repetitive.
But then I discovered The Math Circle.
I don’t know how my parents found out about it, but they did, and I started going. I must have had a great time, because I put up with conflicts with soccer practice, Hebrew school, etc., in order to attend class at Harvard on Wednesday evenings. And in fact, I know I had a great time, because I remember some of the fantastic things we were learning. Cantorian set theory stands out, of course; so do ruler-and-compass constructions and complex numbers. All of it appealed to me and got me excited about math—which was, it turned out, so much more than logic grids and multiplication tables. It was Infinity, it was Games like constructing things with a ruler and compass, it was Fantasy like “imaginary” numbers! In short, it was cool. So I kept going, and I’ve never stopped.
Meanwhile, I was learning some okay stuff in math at school, but nothing really exciting until sixth grade when a particularly good teacher gave me extra algebra to do, setting me on a path to take more advanced classes in middle school and high school. Basically, I got lucky. The difference between a good teacher and a bad one was what defined my public school math career. Looking back on it, it was a near thing! And this is why programs like The Math Circle are potentially so valuable: they have the power to transform math education from a gamble into a delight.
Bob and Ellen Kaplan and Jim Tanton got me hooked at the Wednesday classes. The style was pretty much perfect for me; as I saw fit I could participate or observe, believe or question, conjecture, theorize, or experiment on my own. Most important, I was tackling problems and ideas that were fascinating and expertly presented. At some point, I switched up to Sundays, and the classes got cooler—if that’s even possible. Knot theory from Bob in addition to Jim’s regular topological tidbits, Babylonian mathematics from Ellen (the sophistication of which I am really only coming to appreciate now!), a proof of Gauss’s Fundamental Theorem of Algebra using winding numbers that was, if not totally understandable, at least accessible to a middle schooler. It was awesome, and that’s why I keep going.
Then, in 2004, Bob and Ellen invited me to teach a class for the younger students. I almost literally jumped at the opportunity—I was going back to the Wednesday night classes I had loved so much back in elementary school. Boy, was I in for a surprise!
I had done a summer program (PROMYS) at Boston University in 2003, and among the topics covered were Simple Continued Fractions. I liked the fact that the continued fraction
is the Golden Mean you see in Fibonacci numbers, rectangles, pentagons, phyllotaxis, and various other miraculous mathematical phenomena. So I planned my class starting with this fact, and it turned out my students liked it too! (Ah, success!)
As the semester progressed, our investigation of simple continued fractions took us far afield. This was partly due to my own inexperience as a teacher: SCFs are (in my opinion) a pretty difficult number theory topic, and I neglected to take into account the tools of number theory. These are of two sorts. The most important are observation, experimentation, and curiosity. This was fine; the kids had all these things in spades. But the second most important tool is algebra, and this was something the kids were a little less comfortable with.
I tried to think back to my own experiences as a Wednesday nighter. Obviously, I couldn’t have known algebra then. But we covered topics that can only really be considered algebraic (for example, the algebraic properties of Cantor’s transfinite ordinals, which lack commutativity). How did Bob and Ellen and Jim swing that? It seemed that they must have been tricky about it, sneaking the abstractions and generalizations up on the students, after we were so comfortable with the concrete examples and knew the rules of their behavior so intimately, that the abstraction—whether or not we comprehended the algebraic symbols—was merely an expression of our gut feelings.
Well, this is easier said than done, and the Kaplans are a tough act to follow. (After all, they had been doing this a tad longer than I had.) But I did my best, and we made some pretty decent progress on SCFs, although we fell short of my admittedly overambitious goal of proving the theorem of Lagrange: that any quadratic surd has an eventually periodic continued fraction. No matter, the kids were moving on. Someone mentioned the classic puzzle of connecting three houses to three utilities without crossing the pipes. And thanking the gods for dropping a topic on me just when it seemed I was empty-handed, halfway through the course, I began introducing the students to graph theory.
After some work, we solved the Utilities puzzle, and solved it completely. (I’ll leave it as an Exercise to the Reader, because it is an excellent puzzle.) But where to go from there? I knew and the students knew that Math Circle is not about presenting a subject—such as graph theory—in a condensed format, but rather about playing with the subject, fooling around. So that’s what we did; we played games: first games with graphs, and then soon all kinds of games. Before I knew it, we were investigating Conway’s Nim-games (games of full information, which is to say, no element of chance) and their associated strategies. And thus the class grew into its own. We were really into the swing of things, when, sadly, the semester ended.
I took a deep breath. That was way harder than I thought it would be! (I’ll always look at Bob and Ellen and Jim and the others with a little more awe now, knowing that they taught several Math Circle classes each week, and were also teachers—and prophets of The Math Circle—in “real life.” Sheer madness!) But I knew I had to do it again.
This semester I’ve been teaching about modular arithmetic, repeating decimals, and cryptography. With a little more experience, I’ve been a little more comfortable. But I’ve also made a big breakthrough in my teaching recently. When I first started, I planned my lessons extensively—everything from topics I wanted to cover to order and manner of presentation to activities to keep the kids engaged. Recently, though, I’ve started taking risks, reading up on a topic, exploring a few interesting pathways, and going into the week’s class “blind.” And strangely enough, often these have been the best classes. The key is lack of planning, having fun, and just fooling around along with the kids.
I think this secret I’ve stumbled upon is the Secret of the Kaplans, the secret that all the best Math Circle teachers have known—Jim and the rest. And the explanation is that Math Circle is all about fluidity, the kind of fluidity of ideas that only kids are really capable of. So teaching is not about “lowering” the level of the material to meet the kids, but rather about looking at it from the same angle they are.
I must have known this secret deep down when I was a Wednesday nighter myself, but forgotten it. Why might this be so? After all, I’ve been attending Sunday classes all through high school. Perhaps such forgetfulness is a symptom of “mathematical maturity”: as we learn algebra more thoroughly, codify the rules of the game, and climb the ladder to its “ultimate achievement” (calculus class: from a standard high school perspective, the End of Math), we become set in our thinking. In school, these things we’re manipulating (variables, operations, integrals, derivatives) become game pieces, perhaps something like Mancala stones, which we move from place to place in certain ways. At the next level, we abstract the stones and treat their behavior as stemming from their geological properties—we examine algebraic structures like groups and fields; we make rigorous such intuitive notions as limits and infinity.
Teaching Math Circle, I’ve been relearning how to just look at the stones, play with them, marvel at them. And boy, am I glad!