Spring
1.
As I progressed, my eye progressed, and more than solving algebra problems by grasping their design, I became more clever at reading questions. To do better, though, I had to become vigilant. For someone who thought that there were shortcuts and faster passageways to learning, this was unwelcome. I had never understood that learning needs to be done patiently. One can be impatient to learn or for learning in general, but that is a matter of temperament. I am having to learn how to learn. In school they expect you to learn, but they don’t teach you how to learn, at least they didn’t in my childhood.
I am accustomed to remembering what I hear and being able to draw on it. Learning algebra requires a secondary use of information, though, a sorting and referencing, a repetition of experience, so that it actually is experience. With algebra I’m not simply collecting information, I am having to classify and comprehend it. We do this naturally as children in classrooms, partly because the distant future seems as if it will never arrive, but it is a different matter to be older and feel that one’s capital of time is remorselessly diminishing. Such a consideration adds a complicating haste and impatience.
DIVIDING THE FRACTION 7/2 by 2, I confused the properties of exponents, and thought that the product is 7, since 7 × 2 = 14 and 14/2 = 7, when in fact the answer is 7/4, since dividing a fraction by 2 is the same as multiplying by 1/2, but I got the answer wrong and got angry at math and called Amie, and she wouldn’t talk to me until I calmed down. She wasn’t always calm, either. Once I heard Benson, her husband, in the background say, “Why are you yelling at him?”
When I had worn Amie’s patience too thin, I would call Deane Yang, my friend who is a mathematics professor at NYU. “The way you remember procedures is you remember why,” he said.
“Because?”
“Because people learn math as a collection of procedures,” he said. “When things get difficult, they’re lost, and math becomes religion class. The teacher says what’s right and wrong, and for all you know math came out of the sky, and some prophet told you how to do it, and it’s just blind belief then. The goal is to take on questions that appear to be complicated, and to recognize that a complicated question can be broken down into simpler questions, some of which can be answered independently of each other.”
Among the algebra shortcuts I have been taking is writing out only the portion of an equation that I am working on, while keeping the rest in my head, which is an efficient way to lose control of plus and minus signs. (x + 7) – (y – 4), for example, is an expression. (An equation has an equal sign: (x + 7) – (y – 4) = 21.) As for plus and minus signs, the minus between the two entries means that the y is actually –y and –4 is 4, since the minus sign is the equivalent of a –1 in front of the parentheses and –1 × y = –y and –1 × –4 = 4, since a negative number times a negative number is a positive number. In the midst of the calculations, the signs change, and when the formulas are longer, and there are more steps, I tend to get lost.
“With math you have to be very, very disciplined,” Deane said. “Normally with algebra, you’re trying to make something complicated simpler, but often, temporarily, you have to make it more complicated. The only way to be properly disciplined is to remember exactly what you’re allowed to do, and what you’re not allowed to do. You have to write everything down, line by line. Math is very painstaking.”
These remarks had an almost Zen-like forcefulness for me. They were both abstract and practical, they spoke to my distress, and for a while things got better.
2.
To respond to Gregory Chaitin, the case that there is a reality different from the apparent one can be presented in an orderly way, beginning with the assertion that the reality we perceive is not objective reality, it only appears so. Hummingbirds and certain other animals see more colors than we see. To them the world looks more as it is. There are other hidden things behind all the things that we can see, even if all we allow is scale. Our bodies as a pattern of atoms or Saturn shown at its actual size are images that are only conceptually possible.
In We, a novel published in 1921 by the Russian writer Yevgeny Zamyatin, a practical case for a separate realm is made. “We have never seen any curve or solid corresponding to my square root of minus one,” Zamyatin writes. “The horrifying part of the situation is that there exist such curves or solids. Unseen by us they do exist, they must, inevitably; for in mathematics, as on a screen, strange, sharp shadows appear before us. One must remember that mathematics, like death, never makes mistakes. If we are unable to see those irrational curves or solids, it means only that they inevitably possess a whole immense world somewhere beneath the surface of our life.”
To believe in ideas is to believe in the possibility of a transcendent realm. Perhaps in a practical transcendent, where ideas reside, where the material of dreams comes from, something less like Plato’s non-spatiotemporal realm than Jung’s collective unconscious, which is patterned on Plato’s example but exemplifies humanist principles and not strictly metaphysical ones. Ideas do not seem to be part of physical reality, unless one believes that they exist only as transactions within our brains, which, of course, is possible, too.
Mathematicians who aren’t comfortable with Platonism are nevertheless comfortable with there being an exalted feeling to doing mathematics. Awe and wonder are the feelings Amie says she has doing math. Uniqueness and passion are what the Harvard professor Barry Mazur says he experiences. So where are they located imaginally when they have these feelings? Is the explanation simply self-enlarging; are they simply smarter than others who haven’t thought of such things, or maybe can’t think of such things; is that all there is to it? Or is it, by means of endeavor and talent and aptitude, a matter of being enfolded within, having access to, a territory not always close at hand and not easy to reach?
With the ancients, admittance to this territory depended on a sponsor, a muse. It required preparations, grace, and a plea’s being made. There is still a superstitious feeling among creative people about being admitted to and allowed to remain in a realm that appears to be separate from ordinary life.
“It’s still possible, you close your eyes, you forget about all your problems, and you try with your intuition to reach the Platonic world of ideas,” Chaitin told Robert Lawrence Kuhn in Kuhn’s broadcast series Closer to Truth.
Of course, these notions are speculations. The mathematician Michael Harris defines “speculative philosophy” as “taking phenomena as symptomatic of something that remains concealed,” a remark I admire for its concision.
PLATONISM: THE FIRST philosophical position a mathematician encounters is whether mathematics is created or discovered. It is practically unavoidable. If I think that mathematics is discovered, then it has a perfection, an orderliness, and a permanence that a human mind cannot achieve on its own. If I think mathematics is created, then it is necessarily imperfect, opportunistically ordered, and parts of it are impermanent, since it reflects human misconceptions and shortcomings, which require revision, and perfection is an abstraction anyway.
Mathematicians don’t tend to endorse Platonism, if they do, because they have read Plato. Platonism in mathematics is not something that Plato thought about, except obliquely. It is a modern more than an ancient concern. Plato’s name was attached to mystical assertions about mathematics in 1934 by the Swiss mathematician Paul Bernays at a talk in Geneva. Bernays noted that both Euclid and the German mathematician David Hilbert discussed mathematical objects as “cut off from all links with the reflecting subject,” by which he meant human beings. “Since this tendency asserted itself especially in the philosophy of Plato, allow me to call it ‘Platonism,’” Bernays said, invoking the non-spatiotemporal realm, the forms of which were replicated in lesser versions by the Demiurge whom Plato believed had fabricated the world.
Among Western theologians of the Middle Ages, mathematics was generally regarded as one of the things that God created, either from the chaos of the void, which resembled the non-spatiotemporal realm, or, as Christians began to think in the second century CE under the influence of Philo, from nothing, ex nihilo. Or they thought of mathematics sometimes as a tool that God made available so that his works might be understood if only partially. Alain Connes says that Blaise Pascal, whom Connes describes as “the most famous mathematical mystic,” thought of the infinitely small and the infinitely large as mysteries that nature had posed so that they might be admired, even while they could not be understood.
In Timaeus Plato writes that God lit the heavens so that the animals, of which humans were the highest form, “might participate in number, learning arithmetic from the revolutions” of the stars and the planets. So that these could be observed in their entirety, he created day and night. The sky provided a means of transit from the mathematics of visible things to the mathematics of invisible things.
A Platonist believes that the native territory of numbers and mathematics is somewhere else than in physical reality. This elsewhere is abstract, indifferent to us, was here before us, and will be after. It is neither eternal nor everlasting, since those are temporal distinctions and the non-spatiotemporal realm is atemporal; it simply is. (Jung’s collective unconscious is spatiotemporal, requiring the presence of human beings as something like channelers or vessels.) This adjacent reality is not connected in any clear way to the physical world, but it is somehow accessible to human thinking.
THE EXPLANATIONS FOR how mathematics is apprehended and how mathematicians might be in touch with a non-spatiotemporal realm include mathematics being viewed as something like a dream—a serial vision or a narrative, that is—apparently fashioned within the Unconscious, which makes of the Unconscious a kind of worldly conduit to the non-spatiotemporal realm. Mathematics then is an activity that the Unconscious performs and delivers to waking life, which is how Poincaré and Hadamard saw it. This exchange is one-sided in that the Unconscious can produce mathematics but a mathematician cannot commission work; he or she can only inquire into whether the Unconscious has any results to offer. Pleading and attentiveness are the only means of engaging it.
The influential German mathematician and logician Kurt Gödel was a Platonist. In the paper “On Gödel’s ‘Platonism,’” Pierre Cassou-Noguès quotes passages from Gödel’s papers saying that “something in us different from our ego” provides results, and that the question in mathematics is “to find out what we have perhaps unconsciously created.” Gödel writes that mathematical ideas “form an objective reality of their own, which we cannot create or change, but only perceive and describe.” And, “Mathematics describes a non-sensual reality, which exists independently both of the acts and of the dispositions of the human mind and is only perceived, and probably perceived very incompletely, by the human mind.” According to Cassou-Noguès, among Gödel’s papers there is a note from 1946 in which “Gödel mentions the possibility that we see mathematical truths in God’s mind.” This might make a superior mathematician a type of clairvoyant.
“I believe that mathematical reality lies outside us, that our function is to discover or observe it, and that the theorems which we prove, and which we describe grandiloquently as our ‘creations,’ are simply our notes of our observations,” Hardy writes in A Mathematician’s Apology.
It seems likely that wherever mathematical reality resides, it does not appear to be entirely within us, and that we do not bring it into being simply by thinking of it, since if that were the case, different people might think of different mathematics, which might happen if there were no general agreement of the need for proof, and there wouldn’t be, since there would not likely be any general agreements at all. There would be only opinions and convictions about what is correct mathematics. Like a faith then, mathematics could split into sects. Also, it would seem that if math were created instead of discovered then the rules could change by consent, as in a game, which they can’t. (Deciding that 1 is not prime isn’t changing a rule, it is coming to an agreement about a case; deciding that 3 + 3 = 7 would be changing a rule.)
IF THE THINGS that we take in with our senses are not everything that there is to reality, then where, if anywhere, is the rest of it? A neurological explanation might say that the missing parts are in our minds, in consciousness, somehow. It doesn’t ask much of our reasoning to believe, as Carl Jung did, that human beings are born with a primitive cultural knowledge, a heritage of symbols and archetypes, and that some part of this inventory is productive of pure mathematics or at least sympathetic to producing it.
According to Plato, we are fitted from birth to recognize mathematical truths, specifically geometrical ones. The capacity is part of some collective human reservoir. In Meno, he has Socrates, by means of questioning, lead an uneducated boy to discover truths about the areas of squares that Socrates draws in the sand. Since it appears plain that the boy could not have learned these truths, Socrates concludes that he must be recollecting something he knew from before he was born. This demonstrates that there is such a thing as true knowledge, knowledge of the eternal, and that the “soul has been forever in a state of knowledge,” Socrates says.
Some parts of mathematical knowledge do seem inherent and intuitive. Mathematicians like to point out the complicated mathematics involved in crossing a crowded street, which we solve without being aware that we are solving it. This seems to suggest either that we know certain mathematical truths without having learned them or that we learn them without knowing we are learning them.
3.
Once I encountered Platonism, I was a goner. Mathematics mostly rebuffed me, since I could perform it usually only badly, but thinking about mathematics I could do, because anyone can. The question of whether mathematics is created or discovered appeals to me deeply. I get a little avid when I talk about it, and I am brought up short each time I realize that someone I’m speaking to isn’t as keen about it as I am.
It turns out there are degrees of Platonism, if you can stand it. An Absolute Platonism regards mathematics as perfect and timeless and independent of human beings. A Strict Platonism believes that a complete version of mathematics exists, has been being revealed for thousands of years, and may be inexhaustible. A slightly less emphatic version asserts that mathematics is a description of an adjacent world, a type of inventory or a census. The mathematician who said that mathematics is “a proto-text whose existence is only postulated” was expressing a Platonic point of view.
About 65 percent of mathematicians are Platonists, at least that is the figure I find most often. The bulk of them tend to endorse a type of passive Platonism that allows that mathematics has aspects that human minds cannot account for, its capaciousness, for one thing, as well as objects that are inherently too large and complex for human minds to encompass.
For the mathematician and physicist Roger Penrose, to say that a mathematical statement is Platonic is to assert that it is true objectively—true, that is, whether anyone believes it or not. The assessment becomes a declaration of authenticity. Instead of believing that mathematics resides in a non-spatiotemporal realm, Penrose thinks of mathematics as encompassing a realm of its own. He gives the example of a Mandelbrot set. A Mandelbrot set is produced by mapping points involving complex numbers. A complex number is a number that can be written as a + bi, in which a and b are real numbers and i = √ – 1, a number designed to have the property i2 = –1. Since no real number fulfills this equation, any number that includes i is called an imaginary number. When drawn, Mandelbrot sets are made of star shapes and waves and spikes and spirals and clusters of other geometric forms that repeat ceaselessly in finer and finer detail; some of the versions I have watched in videos look a little like perpetual and ever-diminishing depictions of the Hokusai woodblock The Great Wave off Konagawa. Mandelbrot sets do not exist “within our minds, for no one can fully comprehend the set’s endless variety and unlimited complication,” Penrose writes. Instead they can reside only “within the Platonic world of mathematical forms.” This also shades toward a mystical interpretation.
The German mathematician and logician Gottlob Frege also saw mathematics as having a truthfulness of an ideal kind, meaning that a mathematical statement is true “whether anyone takes it to be true. It needs no bearer. It is not true for the first time when it is discovered.”
Mathematics in this case is like a river, which exists before it is given a name.
PARTLY IT’S OBVIOUS that mathematics exists without us, and partly it isn’t obvious. Obvious because if we vanish and leave no trace, painting and sculpture as we practice them might be lost, writing might be lost, music might be lost, but mathematics will exist whether we do it or not. Numbers won’t arrange themselves differently or work in different ways or have different properties, because they haven’t been used for a while or are being used by different creatures. Two objects added to another object will be three objects. The numbers 2 and 3 will still have the qualities of being prime, although those qualities might be latent until a new species identifies them. A replacement species might give numbers a different name, but the numbers themselves, with their attributes, are inviolable. According to Warren S. McCulloch in his 1960 lecture “What Is a Number, That a Man May Know It, and a Man, That He May Know a Number?,” around 500 CE St. Augustine wrote, “7 and 3 are 10; 7 and 3 have always been 10; 7 and 3 at no time and in no way have ever been anything but 10; 7 and 3 will always be 10. I said that these indestructible truths of arithmetic are common to all who reason.” Augustine regarded each of his remarks as an eternal verity, “true regardless of the time and place of its utterance,” McCulloch writes. “Each he calls an idea in the Mind of God, which we can understand but can never comprehend.”
Not obvious has factions, too. There is a belief that numbers represent actual objects and another that they represent mental ones. Plato thought that numbers were abstract objects, and Aristotle thought that they were abstractions from actual objects. In Platonism and Anti-Platonism in Mathematics, Mark Balaguer says that the thinking in favor of actual objects would say that when 2 objects and 1 object are added, we have 3 objects, no matter what objects they are or whether or not they are identified. As for mental objects, 2 objects added to another is a remark about what 1, 2, and 3 stand for and says nothing about any objects involved.
The main arguments opposed to Platonism are Formalism, Constructivism, and Intuitionism. Formalism is the brainiest. It says that mathematics is simply a pastime, a game played by rules and properties that have meaning only within the game. In Formalism, 4, say, is used to play mathematics the way a pawn is used to play chess. Axioms, theorems, numbers, proofs, symbols, and equations, the whole paraphernalia of mathematics, are immaterial in the sense that they have no existence except as they appear on the page. They are gestures signifying intent and pursuit, and while seeming to be the most literal of statements and intensely specific they are also totally conceptual. Equations are symbols arranged serially. Formalism seems akin to the neurological notion that dreams are images that are too insignificant to find their way into waking thought and are being shed during sleep. According to this reasoning, to suggest that the images have deeper meaning is to misunderstand them fundamentally. It makes fabulists of figures such as Freud and Jung.
Formalism appeared during the late nineteenth and early twentieth centuries as a means of making mathematics more rigorous by revising its principles so as to rid them of intuitive assumptions, intuition being then regarded as a weakening force in mathematics. Formalism is identified with the mathematician David Hilbert. It has a surrealist quality. In relation to Euclid, Hilbert says, “One must be able to say at all times—instead of points, straight lines, and planes—tables, chairs, and beer mugs.” It seems fanciful and strange, the notion of a satirist dismissing the imagination as a source of insight and instruction, but it is also an attempt to clarify mathematics and to make it more infallible, more unshakable than it already is. Whatever else Formalism accomplishes, though, it doesn’t give mathematics a closer correspondence to reality, since to a Formalist there is no correspondence to begin with.
Formalism excludes all but the surface of things. Creative thought can perhaps be carried out according to rules, especially rules that helpfully limit an apparent infinity of choices, but the game wouldn’t seem able to advance without intuitions about how to use the rules in new ways. A divorce from the realm of psychic associations may not even be possible, though, considering all that the psyche appears to harbor and give rise to.
4.
An amateur dissenter from Formalism might wonder timidly if it doesn’t allow even the origins of Formalism to be Platonic, since the non-spatiotemporal realm includes concepts and ideas in their perfect form. Formalism says only that humans take part in mathematics by agreeing to certain arrangements. Endorsing Formalism would seem equivalent to saying that any thought is essentially a succinct neurological event, a synapse turning on and then off. A thought shared among a number of people says nothing about the character or truthfulness of the thought, it says only that different human brains can have similar thoughts or conduct similar operations. Formalism appears to see human beings and their thoughts as being at the center of existence, whereas Platonism sees them as existing at some remove.
Formalism and Platonism are also twinned, but retroactively. Or perhaps, like many themes in mathematics, they are parallel. A Formalist would say that numbers exist to play the game, and that the rules reflect their attributes. The numbers 2 and 3 and 5 and 7 are prime because the quality of being prime is among the rules, but this doesn’t really respond to the possibility of primeness being an attribute independent of the game, or that the game is played with entities that existed before anyone thought to use them in a game.
INTUITIONISM ALSO BELIEVES that mathematics is the mind’s creation, and that it doesn’t describe anything realistic. A more emphatic version of Intuitionism is Constructivism, which believes that the mind constructs mathematics according to intuitive dispositions such as the inclination to assess the world in terms of numbers. The basic principles of arithmetic emerge from a human capacity for counting and for handling simple arithmetic procedures. The mathematics that we have, in other words, is the mathematics that we have brought about and can do. To a Constructivist, a mathematical formula is a tool or a prop, and the mind is something like a theater in which mathematics performs.
The belief that there are no such things as abstract objects, and that therefore mathematical statements, which rely on abstract objects, are not true, is called Fictionalism. They aren’t false, either, so much as fanciful. According to an argument I find in the Stanford Encyclopedia of Philosophy under Formalism, to say that 3 has the quality of being prime is like saying that among the tooth fairy’s qualities is generosity.
THE SIMPLEST, OLDEST, and most obdurate argument dogging Platonism is the epistemological argument. It says that if mathematical objects are abstract, then they exist outside of space-time, and human beings, who live in space-time, could not know about them. Since human beings know about them, they can’t be abstract, so Platonism is false.
I might offer that there is more than one explanation of how a person could be connected to a non-spatiotemporal realm, all of them conjectural, of course. There is Plato’s belief in Meno that our souls know about abstract objects such as the forms and that learning mathematics is a matter of remembering what we know. Furthermore, one can infer from things that Socrates says in Books VI and VII of Republic that Plato believes that a part of the soul itself is non-spatiotemporal or has the potential to be. I am partial to St. Augustine in On the Free Choice of the Will, who writes, “The double of any number is found to be exactly as far from that number as it is from the beginning of the series,” which for the purposes of simplicity might be thought of as zero. “How do we find this changeless, firm and unbroken rule persisting throughout the numerical series? How can any phantasy or phantasm yield such certain truth about numbers which are innumerable? We must know this by the inner light, of which bodily sense knows nothing.”
Mathematics, in its independence and timelessness, becomes also a type of self-intoxication, and self-justifying, a creator’s romance with his or her creation, qualities that more than one culture have attributed to God.
5.
A citizen Platonist responds (briefly) to further dissent before turning out the lights: In The World of Mathematics, James Newman says that the discovery of non-Euclidean geometry, in the early nineteenth century, meant the end of metaphysical speculations about the origins of mathematics, since non-Euclidean geometry involves figures such as spheres and other objects with properties that are different from those of triangles and squares and circles on a flat plane and also includes figures that can be extended to spaces of three and more dimensions, that such a field is a creation of the human mind. Wouldn’t it also be true, however, to say that, as with the principles of geometry, those of non-Euclidean geometry were latent and waiting to be discovered? As with Euclidean geometry, mathematicians didn’t invent the forms of non-Euclidean geometry, they observed and described them. The forms being identified by means of intellectual effort does not address their origins, since, like all processes of thought, mathematics is the result of intellectual effort.
For Timothy Gowers, in Mathematics: A Very Short Introduction, the case of i appears to refute Platonism: i requires that a person think abstractly, Gowers says, because either i or –i could be chosen to equal √ – 1, since i’s only trait is that i2 = –1. Therefore, any true statement about i is also true of –i. “It is difficult, once one has grasped this, to have any respect for the view that i might denote an independently existing Platonic object,” Gowers writes.
By definition, though, the Platonic realm includes objects with split identities. As with counting numbers, the human mind contributed the terminology, but not the concept. Also by definition, anything that exists in the spatiotemporal realm exists in the non-spatiotemporal realm, including concepts such as justice and freedom and numbers with peculiar attributes.
ENDORSING PLATONISM MEANS allowing the possibility of the world’s being more capacious than we can conceive. Evolution might be progressing on a grand scale, too. All that we are meant to know or might be capable of knowing could be unfolding over a longer span than a human life or even generations of lives can enclose. We might not yet be equipped to think all that there is to be thought.
When I read, under “Profession of Faith,” in Simone Weil’s “Draft for a Statement of Human Obligation,” that “there is a reality located outside the world, that is to say, outside time and space, outside man’s mental universe, outside the entire domain that human faculties can reach,” something inside me that, having no better word for it, I will call my spirit responds.
6.
Mathematics, which settles all questions it is capable of settling, and has plenty of pronouncements about real and imaginary worlds, offers very little about where it comes from. Mathematics is like the enthralling dinner companion you speak to intimately all evening then realize as you rise from the table that all the revelations were your own.
With mathematics it is impossible to avoid metaphysical questions. It begins, after all, with an unanswerable question: Where do numbers come from? This is one reason mathematics is bound up with spiritual explanations. To think about the origin of numbers is to allow a metaphysical answer or at least not be able to exclude it. It doesn’t insist on it, but it accepts the possibility. I don’t know if there is another subject that allows this that isn’t already philosophy. We know when the universe began and how. We know how life came to be and how it refines itself through evolution. We don’t know where numbers come from or why they have the properties they do, unless you believe that they are a system invented by humans based on the ways in which we apprehend the world, a creation of our thinking and therefore our neurology. In that case numbers and mathematics form a mechanical system that we expand according to rules we make up. While this is an assertion that I don’t find persuasive, I cannot dismiss it, either.
I did not expect to be drawn into thinking about these kinds of things. I didn’t even want to be. I thought I was merely setting out to do teenage math. It has made me have to consider in detail what I believe, which is taxing and never-ending, since, as with all of us, what I believe progresses, or at least changes, so long as I read and talk with others. To believe in anything is also to risk having the belief overthrown, which is not always pleasurable. It’s a form of exposure.
The outcome of thinking, of self-consciousness, suggests that it is always possible to be on the way to becoming some other version of oneself. Does that mean that we are always discovering aspects of ourselves that we didn’t know about or that we are instead creating new ones? Do we have potential selves? Are there an infinite number of them? Last self known + 1? Do we not arrive at the end of ourselves for the same reason we can’t arrive at the end of numbers: we run out of time? Plato describes time as the “moving image of eternity.” It is one of those occasions when an ancient mind seems startlingly modern.
7.
Around eleven weeks in, it occurred to me, later than it might have, that it would have helped me as an adolescent to know the theoretical basis of the work I was being asked to do, and that I was leaving arithmetic, which was mechanical, for algebra, which was conceptual. “I call x a number to be named later,” Deane Yang told me. “Like you’re trading baseball players, but at the moment, you don’t know what number it is. So algebra is same rules as arithmetic, but you’re dragging along a number to be determined later. You can’t make it disappear like the 2 + 1 you can make disappear and become 3. x + 1 won’t disappear. That’s the conceptual idea of algebra.”
It was, I see now, the secret knowledge that the others had been let in on, although by whom and how I don’t know. Or maybe it had been explained, and I hadn’t paid close enough attention.
It was also borne in on me that something that works can’t be proved not to work, and I would have to accept that the shortcoming was almost entirely my own. I hadn’t been cheated. I hadn’t been wronged. I was wrong. The fault was in my reactionary thinking. This was not fun to own up to, but it allowed me to loosen the grip of the embittered adolescent.
IDEAS DO NOT organize themselves for me easily; they change position and occasionally switch places. I sometimes think that I am intellectually dyslexic. I admire straightforward, logical thinking, but I can’t do it, so I don’t like doing puzzles. Seeing puzzles as an opportunity for defeat is one reason I grew frustrated at being balked by algebra problems. Equations in adolescent algebra are simple sentences, equivalent to the sentences in books for young adult readers. To be unable to read a simple sentence correctly made me feel flat-out dense. What Deane had been telling me, obliquely, was that I was reading them too closely. They weren’t each an occasion to be reasoned out, they were invitations to evoke principles I was expected to recognize and enact. They were generalizations. It was strange to become aware in early old age that a temperamental circumstance, my tendency to look too closely at things and be too subjective, also operated in me as a boy and kept me from seeing what the teacher and the textbooks had plainly intended that I see. I had felt only the sense of knowledge withheld, of secretiveness, of being excluded from the circle of initiates, and the adolescent imperative to conceal that I was lost.
FROM A JOURNAL, week twelve:
I am fatigued by the number of rules, procedures, and formulas. I feel as if I am training for a profession that I plainly won’t be good at. Not grasping the degree to which generalizations are allowed only makes it harder to advance. I can think of no equivalent except the obvious one that Deane points out, grammar, but there is something natural about learning spoken grammar—the ear listens and tends to adapt, without all that much study, as if we already knew some of what to do. There is no mathematical equivalent I can think of. We don’t go through childhood converting the flights of birds into vectors and parabolas, or parsing the passing of traffic, or the number of people we encounter and the intervals in which we encounter them compared to the hours that pass. Beyond counting and arithmetic, there is no natural way of learning mathematics. It’s true that we perform a number of complex mathematical calculations effortlessly—we figure out how to catch a ball, we estimate whether waiting on a line is sensible—but they aren’t occasions we address by consciously considering their mathematics.
It is staggering to make so many simple mistakes. In no other part of my life am I so inept, so far as I know. Simple competence eludes me.
I assumed in my second encounter that eventually I would get everything right, but that isn’t the way it happened. I never achieved mastery in algebra or even, really, much proficiency. I was maybe a B–, C+ student. I had meant to enjoy prevailing. I imagined meeting algebra again as being like the encounter one has at a twentieth reunion with the high school quarterback who now does odd jobs and breaks out his wallet to show you the clippings of his best games.
I had hoped to solve problems by knowing the right methods and carrying them out infallibly. Sometimes I chose the right method and carried it out fallibly, so that the answer might be –4 and I had 4. Sometimes I began with the wrong method and ended with a term that was absurdly remote from the answer. Then I would go backward through the steps and was especially vexed if I got to where I had started without finding the wrong turn I had taken. What I had intended to enact was a ruthless and complacent accuracy, like what my bright classmates had shown. When the teacher placed the tests on our desks and said, “Begin,” they picked up their pencils and lowered their heads and took off like trains intent on reaching their destinations on schedule or maybe even early. Copying their work, I found it difficult sometimes even to keep up with them.
After three months of algebra, I was feeling unsteady. I had expected to be pleased at having unraveled starter math’s intricacies and using them the way I might be using new French to read Le Monde or Spanish to watch telenovelas. I had thought a world would be opening to admit me, and I guess it was, but only tepidly and in evening light, or as if I were stuck looking at the view from the back of the crowd. What was supposed to make me happy was making me unhappy. Cunning is what it seems to me that student math often requires, not thought. Thought is expansive. Cunning is opportunistic and narrow and strategic.
Despite my resolutions, I persisted in feeling that equations were rigged. When I examined them, I was looking not for how to solve them so much as where the ambush was. This was not an efficient state of mind. Receptivity was called for, not skepticism. When I was feeling that way, mathematics struck me as a species of fancy grifter.
I LIKE, THOUGH, that I am learning an ancient practice, that I am reading from “the book of dark or mysterious things.” I sometimes feel a kindred quality to this in church, on the few times I am ever there, a sense that the procedures were established by antiquated figures and have been invoked the world over by uncountable numbers of people on uncountable occasions since. Mathematics, though, is older than church. One might reply, perhaps, that ideas of divinity are even older, but while they are entertained in the mind, they don’t seem to be thoughts. They are responses, intuitions, and impressions, and somehow static and different from the dynamic quality of thinking, which revises itself constantly or it isn’t thinking. Both the occult and the mathematical, though, have a degree of superstition in their upbringings, divinity through the contributions of spirit-thinkers and mathematics through Pythagoras.
I find myself annoyed at having to accept an illogical standard, the square root of 4, for example, being both 2 and –2. In Notes from the Underground, Dostoyevsky writes that mathematical certainty is an insufferable fact. “I admit that twice two makes four is an excellent thing,” he writes, “but if we are to give everything its due, twice two makes five is sometimes a very charming thing too.”
WEEK FOURTEEN: JUDGING from the biographical notes at the back of textbooks, a considerable number of math teachers prefer to be called educators. They also believe that learning algebra is a regular minefield of unexpected pleasures. I think it would have been pleasant for me not to have felt left behind. Being not educated was decidedly not fun. Finding even a beginner’s way through the thicket of symbols and procedures might have given me a satisfaction and confidence I felt the lack of acutely. I see now that learning math wasn’t entirely beyond my capabilities, but I didn’t then, when it mattered more.
To defend myself as a boy against the assault that failing at math was causing, I had to feel that math was irrational and inconsistent. Or perhaps that a secret knowledge had been denied me. Or to think that I had no ability for the task. Now, equipped to untangle some of the enigmas, I see, as Amie has told me, that math is logical, and I feel indignant that this, and not something mysterious and enlarging, is what was withheld from me.
Amie’s husband, Benson Farb, is also a mathematician, and once when I told her my feelings about math’s contradictions, she said, “I can’t tell you how many times Benson and I have said to each other over the years, ‘I found a contradiction in math.’”
“There really are such things?”
“No, it’s what you say when you don’t get the answer you expect.”
Mathematics might be the only creative pursuit in which inevitability figures. Other artists might be defeated by a task beyond their capabilities, but they do not live with knowing that sooner or later, if their work is consequential, someone will do what they haven’t been able to do. Mathematicians work within a discipline in which, so long as their suppositions are correct, there is always a precise and irrefutable answer, even if they can’t find it.
8.
I was interested to know what I could of how a pure mathematician thought and what it was like to inhabit an imaginary world. Amie suggested I speak to Yitang Zhang, a solitary part-time calculus teacher at the University of New Hampshire who had received several prizes, including a MacArthur award, for solving a problem that had been open for more than a hundred and fifty years. His proof was deeply complex, she said, but its outlines were not so difficult.
The problem that Zhang chose, in 2010, is from number theory and is usually called “bounded gaps.” It concerns prime numbers and whether there is a boundary within which, on an infinite number of occasions, two consecutive prime numbers can be found, especially out in the region where the numbers are so large that it would take a book to print a single one of them. Daniel Goldston, a professor at San Jose State University; János Pintz, a fellow at the Alfréd Rényi Institute of Mathematics, in Budapest; and Cem Yıldırım, of Boğaziçi University, in Istanbul, working together in 2005, had come close to establishing whether there might be a boundary, and what it might be. Goldston didn’t think he’d see the answer in his lifetime. “I thought it was impossible,” he told me.
Zhang, who also calls himself Tom, had published only one paper, to quiet acclaim, in 2001. In 2010, he was fifty-five. “No mathematician should ever allow himself to forget that mathematics, more than any other art or science, is a young man’s game,” Hardy wrote in A Mathematician’s Apology. He also wrote, “I do not know of an instance of a major mathematical advance initiated by a man past fifty.” Zhang had received a PhD in algebraic geometry from Purdue in 1991. His adviser, T. T. Moh, with whom he parted unhappily, wrote a description on his website of Zhang as a graduate student: “When I looked into his eyes, I found a disturbing soul, a burning bush, an explorer who wanted to reach the North Pole.” Zhang left Purdue without Moh’s support and, having published no papers, was unable to find an academic job. He lived, sometimes with friends, in Lexington, Kentucky, where he had occasional work, and in New York City, where he also had friends and occasional work. In Kentucky, he became involved with a group interested in Chinese democracy. Its slogan was “Freedom, Democracy, Rule of Law, and Pluralism.” A member of the group, a chemist in a lab, opened a Subway franchise as a means of raising money. “Since Tom was a genius at numbers,” a member of the group told me, “he was invited to help him.” Zhang kept the books. “Sometimes, if it was busy at the store, I helped with the cash register,” Zhang told me when I went to see him in New Hampshire. “Even I knew how to make the sandwiches, but I didn’t do it so much.” When Zhang wasn’t working, he would go to the library at the University of Kentucky and read journals in algebraic geometry and number theory. “For years, I didn’t really keep up my dream in mathematics,” he said.
“You must have been unhappy.”
He shrugged. “My life is not always easy,” he said.
With a friend’s help, Zhang eventually got his position in New Hampshire, in 1999. Having chosen bound gaps in 2010, he was uncertain of how to find a way into the problem. “I am thinking, Where is the door?” Zhang said. “In the history of this problem, many mathematicians believed that there should be a door, but they couldn’t find it. I tried several doors. Then I start to worry a little that there is no door.”
“Were you ever frustrated?”
“I was tired,” he said. “But many times I just feel peaceful. I like to walk and think. This is my way. My wife would see me and say, ‘What are you doing?’ I said, ‘I’m working, I’m thinking.’ She didn’t understand. She said, ‘What do you mean?’” The problem was so complicated, he said, that “I had no way to tell her.”
Deane Yang told me that a mathematician at the beginning of a difficult problem is “trying to maneuver his way into a maze. When you try to prove a theorem, you can almost be totally lost to knowing exactly where you want to go. Often, when you find your way, it happens in a moment, then you live to do it again.”
ZHANG IS DEEPLY reticent, and his manner is formal and elaborately polite. Once when we were walking, he said, “May I use these?” He meant a pair of clip-on shades, which he held toward me as if I might want to examine them first. His enthusiasm for answering questions about himself and his work is slight. About half an hour after I had met him for the first time, he said, “I have a question.” We had been talking about his childhood. He said, “How many more questions you going to have?” He depends heavily on three responses: “Maybe,” “Not so much,” and “Maybe not so much.” From diffidence, he often says “we” instead of “I,” as in, “We may not think this approach is so important.” Occasionally, preparing to speak, he hums. After he published his result, he was invited to spend six months at the Institute for Advanced Study, in Princeton. The filmmaker George Csicsery has made a documentary about Zhang, called Counting from Infinity. In it, Peter Sarnak, a member of the Institute for Advanced Study, says that one day he ran into Zhang and said hello, and Zhang said hello, then Zhang said that it was the first word he’d spoken to anyone in ten days. Sarnak thought that was excessive even for a mathematician, and he invited Zhang to have lunch once a week.
Matthew Emerton, a colleague of Amie and Benson at the University of Chicago, also met Zhang at Princeton. “I wouldn’t say he was a standard person,” Emerton told me. “He wasn’t gregarious. I got the impression of him being reasonably internal. He had received another prize, so the people around him were talking about that. Probably most mathematicians are very low-key about getting a prize, because you’re not in it for the prize, but he seemed particularly low-key. It didn’t seem to affect him at all.” Deane attended three lectures that Zhang gave at Columbia in 2013. “You expect a guy like that to want to show off or explain how smart he is,” he said. “He gave beautiful lectures, where he wasn’t trying to show off at all.” The first talk that Zhang gave on his result was at Harvard, before the result was published. A professor there, Shing-Tung Yau, had heard about Zhang’s paper, and invited him. About fifty people showed up. One of them, a Harvard math professor, thought Zhang’s talk was “pretty incomprehensible.” He added, “The problem is that this stuff is hard to talk about, because everything hinges on some delicate technical understandings.” Another Harvard professor, Barry Mazur, told me that he was “moved by his intensity and how brave and independent he seemed to be.”
In New Hampshire, Zhang worked in an office on the third floor of the math and computer science building. His office had a desk, a computer, two chairs, a whiteboard, and some bookshelves. Through a window he looked into the branches of an oak tree. The books on his shelves had titles such as An Introduction to Hilbert Space and Elliptic Curves, Modular Forms, and Fermat’s Last Theorem. There were also books on modern history and on Napoleon, who fascinates him, and copies of Shakespeare, which he reads in Chinese, because it’s easier than Elizabethan English.
Eric Grinberg, a former chairman of the math department at the University of Massachusetts Boston, was a colleague of Zhang’s in New Hampshire from 2003 to 2010. “Tom was very modest, very unassuming, never asked for anything,” Grinberg told me. “We knew he was working on something important. He uses paper and a pencil, but the only copy was on his computer, and about once a month I would go in and ask, ‘Do you mind if I make a backup?’ Of course, it’s all in his head anyway. He’s above average in that.”
Zhang’s memory is abnormally retentive. A friend of his named Jacob Chi told me, “I take him to a party sometimes. He doesn’t talk, he’s absorbing everybody. I say, ‘There’s a human decency; you must talk to people, please.’ He says, ‘I enjoy your conversation.’ Six months later, he can say who sat where and who started a conversation, and he can repeat what they said.”
“I may think socializing is a way to waste time,” Zhang says. “Also, maybe I’m a little shy.”
A few years ago, Zhang sold his car, because he didn’t really use it. He rented an apartment about four miles from campus and rode to and from his office with students on a school shuttle. He sits on the bus and thinks. Seven days a week, he arrives at his office around eight or nine and stays until six or seven. The longest he has taken off from thinking is two weeks. Sometimes he wakes in the morning thinking of a math problem he had been considering when he fell asleep. Outside his office is a long corridor that he likes to walk up and down. Otherwise, he walks outside.
Zhang met his wife at a Chinese restaurant on Long Island, where she was a waitress. Her name is Yaling, but she calls herself Helen. A friend who knew them both took Zhang to the restaurant and pointed her out. “He asked, ‘What do you think of this girl?’” Zhang said. Meanwhile, she was considering him. To court her, Zhang went to New York every weekend for several months. The following summer, she came to New Hampshire. She didn’t like the winters, though, and moved to California, where she works at a beauty salon. She and Zhang have a house in San Jose, and he now lives in California and teaches at UC Santa Barbara.
Until Zhang was promoted to professor, as a consequence of his proof, his appointment had been tenuous. “I was chair of the math department, and I had to go to him from time to time and remind him this was not a permanent position,” Eric Grinberg said. “We were grateful to him, but it’s not guaranteed. He always said that he very much appreciated the time he had spent in New Hampshire.”
ZHANG DEVOTED HIMSELF to bounded gaps for a couple of years without finding a door. “We couldn’t see any hope,” he said. Then, on July 3, 2012, in the middle of the afternoon, “within five or ten minutes, the way is open.”
Zhang was in Pueblo, Colorado, visiting Jacob Chi, who is a music professor at Colorado State University Pueblo. A few months earlier, Chi had reminded Zhang that he had promised one day to teach his son, Julius, calculus, and since Julius was about to be a senior in high school Chi had called and asked, “Do you keep your promise?” Zhang spent a month at the Chis’. Each morning, he and Julius worked for about an hour. “He didn’t have a set curriculum,” Julius told me. “It all just flowed from his memory. He mentioned once that he didn’t have any numbers in his phone book. He memorized them all.”
Zhang had planned a break from work in Colorado, and hadn’t brought any notes with him. On July 3, he was walking around the Chis’ backyard. “We live in the mountains, and the deer come out, and he was smoking a cigarette and watching for the deer,” Chi said. “No deer came,” Zhang said. “Just walking and thinking, this is my way.” For about half an hour, he walked around at a loss.
More or less suddenly, “I see numbers, equations, and something even—it’s hard to say what it is,” Zhang said. “Something very special. Maybe numbers, maybe equations—a mystery, maybe a vision. I knew that, even though there were many details to fill in, we should have a proof. Then I went back to the house.”
Zhang didn’t say anything to Chi about his breakthrough. That evening, Chi was conducting a dress rehearsal for a Fourth of July concert in Pueblo, and Zhang went with him. “After the concert, he couldn’t stop humming ‘The Stars and Stripes Forever,’” Chi said. “All he would say was, ‘What a great song.’”
9.
I asked Zhang, “Are you very smart?” and he said, “Maybe, a little.” He was born in Shanghai in 1955. His mother was a secretary in a government office, and his father was a college professor whose field was electrical engineering. As a small boy, he began “trying to know everything in mathematics,” he said. “I became very thirsty for math.” His parents moved to Beijing for work, and Zhang remained in Shanghai with his grandmother. The revolution had closed the schools. He spent most of his time reading math books that he ordered from a bookstore for less than a dollar. He was fond of a series whose title he translates as “A Hundred Thousand Questions Why.” There were volumes for physics, chemistry, biology, and math. When he didn’t understand something, he said, “I tried to solve the problem myself, because no one could help me.”
Zhang moved to Beijing when he was thirteen, and when he was fifteen he was sent with his mother to the countryside, to a farm, where they grew vegetables. His father was sent to a farm in another part of the country. If Zhang was seen reading books on the farm, he was told to stop. “People did not think that math was important to the class struggle,” he said. After a few years, he returned to Beijing, where he got a job in a factory making locks. He began studying to take the entrance exam for Peking University, China’s most respected school: “I spent several months to learn all the high school physics and chemistry, and several to learn history. It was a little hurried.” He was admitted when he was twenty-three. “The first year, we studied calculus and linear algebra—it was very exciting,” Zhang said. “In the last year, I selected number theory as my specialty.” Zhang’s professor insisted, though, that he change his major to algebraic geometry, his own field. “I studied it, but I didn’t really like it,” Zhang said. “That time in China, still the idea was like this: the individual has to follow the interest of the whole group, the country. He thought algebraic geometry was more important than number theory. He forced me. He was the university president, so he had the authority.”
During the summer of 1984, T. T. Moh visited Peking University from Purdue and invited Zhang and several other students, recommended to him by Chinese professors, to do graduate work in his department. One of Moh’s specialties is the Jacobian conjecture, and Zhang was eager to work on it. The Jacobian conjecture, a problem in algebraic geometry that was introduced in 1939 and is still unsolved, stipulates certain simple conditions that, if satisfied, enable someone to solve a series of complicated equations. It is acknowledged as being beyond the capacities of a graduate student and approachable by only the most accomplished algebraic geometers. A mathematician described it to me as a “disaster problem,” for the trouble it has caused. For his thesis, Zhang submitted a weak form of the conjecture, meaning that he attempted to prove something implied by the conjecture, rather than to prove the conjecture itself.
After Zhang received his doctorate, he told Moh that he was returning to number theory. “I was not the happiest,” Moh wrote me. “However, I was for the student’s right to change fields, so I kept my smile and said bye to him. For the past 22 years, I knew nothing about him.”
After graduating, most of the Chinese students went into either computer science or finance. One of them, Perry Tang, who had known Zhang in China, took a job at Intel. In 1999, he called Zhang. “I thought it was unfair for him not to have a professional job,” Tang told me. He and Zhang had a classmate at Peking University who had become a professor of math at the University of New Hampshire, and when the friend said that he was looking for someone to teach calculus Tang recommended Zhang. “He decided to try him at a temporary position,” Tang said.
10.
Zhang finished “Bounded Gaps Between Primes” in late 2012; then he spent a few months methodically checking each step, which he said was “very boring.” On April 17, 2013, without telling anyone, he sent the paper to Annals of Mathematics, widely regarded as the profession’s most prestigious journal. In the Annals archives are unpublished papers claiming to have solved practically every math problem that anyone has ever thought of, and others that don’t really exist. Some are from people who “know a lot of math, then they go insane,” a mathematician told me. Such people often claim that everyone else who has attacked the problem is wrong. Or they announce that they have solved several problems at once, or “they say they have solved a famous problem along with some unified field theory in physics,” the mathematician said. Journals such as Annals are skeptical of work from someone they have never heard of.
In 2013, Annals received nine hundred and fifteen papers and accepted thirty-seven. The wait between acceptance and publication is typically around a year. When a paper arrives, “it is read quickly, for worthiness,” Nicholas Katz, the Princeton professor who is the journal’s editor, told me, and then there is a deep reading that can take months. “The paper I can’t evaluate off the top of my head, my role is to know whom to ask,” Katz said. “In this case, the person wrote back pretty quickly to say, ‘If this is correct, it’s really fantastic. But you should be careful. This guy posted a paper once, and it was wrong. He never published it, but he didn’t take it down, either.’” The reader meant a paper that Zhang posted on the website arXiv.org, where mathematicians often post results before submitting them to a journal, in order to have them seen quickly. Zhang posted a paper in 2007 that fell short of a proof. It concerned another famous problem, the Landau-Siegel zeros conjecture, and he left it up because he hopes to correct it.
Katz sent “Bounded Gaps Between Primes” to a pair of readers, who are called referees. One of them was Henryk Iwaniec, a professor at Rutgers, whose work was among that which Zhang had drawn on. “I glanced for a few minutes,” Iwaniec told me. “My first impression was: so many claims have become wrong. And I thought, I have other work to do. Maybe I’ll postpone it. Remember that he was an unknown guy. Then I got a phone call from a friend, and it happened he was also reading the paper. We were going to be together for a week at the Institute for Advanced Study, and the intention was to do other work, but we were interrupted with this paper to read.”
Iwaniec and his friend, John Friedlander, a professor at the University of Toronto, read with increasing attention. “In these cases, you don’t read A to Z,” Iwaniec said. “You look first at where is the idea. There had been nothing written on the subject since 2005. The problem was too difficult to solve. As we read more and more, the chance that the work was correct was becoming really great. Maybe two days later, we started looking for completeness, for connections. A few days passed, we’re checking line by line. The job is no longer to say the work is fine. We are looking to see if the paper is truly correct.”
After a few weeks, Iwaniec and Friedlander wrote to Katz, “We have completed our study of the paper ‘Bounded Gaps Between Primes’ by Yitang Zhang.” They went on, “The main results are of the first rank. The author has succeeded to prove a landmark theorem in the distribution of prime numbers.” And, “Although we studied the arguments very thoroughly, we found it very difficult to spot even the smallest slip.… We are very happy to strongly recommend acceptance of the paper for publication in the Annals.”
When Zhang heard from Annals, he called his wife in San Jose. “I say, ‘Pay attention to the media and newspapers,’” he said. “‘You may see my name,’ and she said, ‘Are you drunk?’”
11.
“Bounded Gaps Between Primes” is a backdoor attack on the twin-prime conjecture, which was proposed in the nineteenth century and says that, no matter how far you travel on the number line, even as the gap widens between primes, you will always encounter a pair of primes that are separated by two, such as 5 and 7. The twin-prime conjecture is still unsolved. Zhang established that there is a distance within which, on an infinite number of occasions, there will always be two primes.
“You have to imagine this coming from nothing,” Eric Grinberg said. “We simply didn’t know. It is like thinking that the universe is infinite, unbounded, and finding it has an end somewhere.” Picture it as a ruler that might be applied to the number line. Zhang chose a ruler of a length of seventy million, because a number that large made it easier to prove his conjecture. (If he had been able to prove the twin-prime conjecture, the number for the ruler would have been two.) This ruler can be moved along the line of numbers and enclose two primes an infinite number of times. Something that holds for infinitely many numbers does not necessarily hold for all. For example, an infinite number of numbers are even, but an infinite number of numbers are not even, because they are odd. Similarly, this ruler can also be moved along the line of numbers an infinite number of times and not enclose two primes.
From Zhang’s result, a deduction can be made, which is that there is a number smaller than seventy million which precisely defines a gap separating an infinite number of pairs of primes. You deduce this, Amie told me, by means of the pigeonhole principle. You have an infinite number of pigeons, which are pairs of primes, and you have seventy million holes. There is a hole for primes separated by two, by three, and so on. Each pigeon goes in a hole. Eventually, one hole will have an infinite number of pigeons. It isn’t possible to know which one. There may even be many, there may be seventy million, but at least one hole will have an infinite number of pigeons.
Having discovered that there is a gap, Zhang wasn’t interested in finding the smallest number defining the gap. This was work that he regarded as a mere technical problem, a type of manual labor—“ambulance chasing” is what a prominent mathematician called it. Nevertheless, within a week of Zhang’s announcement mathematicians around the world began competing to find the lowest number. One of the observers of their activity was Terence Tao, who had the idea for a cooperative project in which mathematicians would work to lower the number rather than “fighting to snatch the lead,” he told me.
The project, called Polymath8, started in March of 2013 and continued for about a year. Incrementally, relying also on work by a young British mathematician named James Maynard, the participants reduced the bound to 246. “There are several problems with going lower,” Tao said. “More and more computer power is required—someone had a high-powered computer running for two weeks to get that calculation. There were also theoretical problems. With current methods, we can never get better than six, because of something called the parity problem, which no one knows how to get past.” The parity problem says that primes with certain behaviors can’t be detected with current methods. “We never strongly believed we would get to two and prove the twin-prime conjecture, but it was a fun journey,” Tao said.
12.
“Is there a talent a mathematician should have?”
“Concentration,” Zhang said. We were walking across the campus in a light rain. “Also, you should never give up in your personality,” he continued. “Maybe something in front of you is very complicated, it’s lengthy, but you should be able to pick up the major points by your intuition.”
When we reached Zhang’s office, I asked how he had found the door into the problem. On a white-board, he wrote, “Goldston-Pintz-Yıldırım” and “Bombieri-Friedlander-Iwaniec.” He said, “The first paper is on bound gaps, and the second is on the distribution of primes in arithmetic progressions. I compare these two together, plus my own innovations, based on the years of reading in the library.”
When I asked Peter Sarnak how Zhang had arrived at his result, he said, “What he did was look way out of reach. Maybe forty years ago the problem appeared hopeless, but in 2005 Goldston-Pintz-Yıldırım put it at the doorstep. Everybody thought, Now we’re very close, but by 2011 no one was making any progress. Bombieri, Friedlander, and Iwaniec had the other important work, but it looked like you couldn’t combine their ideas with Goldston. Their work was just not flexible enough to jive—it insisted on some side conditions. Then Zhang comes along. A lot of people use theorems like a computer. They think, If it is correct, then good, I’ll use it. You couldn’t use the Bombieri-Friedlander-Iwaniec, though, because it wasn’t flexible enough. You have to take my word, because even to a serious mathematician this would be difficult to explain. Zhang understood the techniques deeply enough so as to be able to modify Bombieri-Friedlander-Iwaniec and cross this bridge. This is the most significant thing about what he has done mathematically. He’s made the Bombieri-Friedlander-Iwaniec technique about the distribution of prime numbers a tool for any kind of study of primes. A development that began in the eighteen-hundreds continued through him.”
“Our conditions needed to be relaxed,” Iwaniec told me. “We tried, but we couldn’t remove them. We didn’t try long, because after failing you just start thinking there is some kind of natural barrier, so we gave up.”
I asked if he was surprised by Zhang’s result. “What Zhang did was sensational,” he said. “His work is a masterpiece. When you talk of number theory, a lot of the beauty is the machinery. Zhang somehow completely understood the situation, even though he was working alone. That’s how he surprised. He just amazingly pushed further some of the arguments in these papers.”
Zhang used a very complicated form of a simple device for finding primes called a sieve, invented by Eratosthenes, a contemporary of Archimedes. To use a simple sieve to find the primes less than a thousand, say, you write down all the numbers, then cross out the multiples of two, which can’t be prime, since they are even. Then you cross out the multiples of three, then five, and so on. You have to go only as far as the multiples of thirty-one. Zhang used a different sieve from the one that others had used. The previous sieve excluded numbers once they grew too far apart. With it, Goldston, Pintz, and Yıldırım had proved that there were always two primes separated by something less than the average distance between primes that large. What they couldn’t identify was a precise gap. Zhang succeeded partly by making the sieve less selective.
13.
I asked Zhang if he was working on something new. “Maybe two or three problems I would like to solve,” he said. “Bounded gaps is successful, but still I have something else.”
“Will it be as important?”
“Yes.”
According to other mathematicians, Zhang is working on his incomplete result for the Landau-Siegel zeros conjecture. “If he succeeds, it would be much more dramatic,” Peter Sarnak said. “We don’t know how close he is, but he’s proved that he’s a genius. There’s no question about that. He’s also proved that he can speak with something over many years. Based on that, his chances are not zero. They’re positive.”
“Many people have tried that problem,” Iwaniec said. “He’s a private guy. Nothing is rushed. If it takes him another ten years, that’s fine with him. Unless you tackle a problem that’s already solved, which is boring, or one whose solution is clear from the beginning, mostly you are stuck. But Zhang is willing to be stuck much longer.”
Zhang’s preference for undertaking only ambitious problems is rare. The pursuit of tenure requires an academic to publish frequently, which often means refining one’s work within a field, a task that Zhang has no inclination for. He does not appear to be competitive with other mathematicians, or resentful about having been simply a teacher for years while everyone else was a professor. No one who knows him thinks that he is suited to a tenure-track position. “I think what he did was brilliant,” Deane told me. “If you become a good calculus teacher, a school can become very dependent on you. You’re cheap and reliable, and there’s no reason to fire you. After you’ve done that a couple of years, you can do it on autopilot; you have a lot of free time to think, so long as you’re willing to live modestly. There are people who try to work nontenure jobs, of course, but usually they’re nuts and have very dysfunctional personalities and lives, and are unpleasant to deal with, because they feel disrespected. Clearly, Zhang never felt that.”
One day, I arrived at Zhang’s office as he was making tea. There was a piece of paper on his desk with equations on it and a pen on top of the paper. Zhang had an envelope in one hand. “I had a letter from an old friend,” he said. “We have been separated for many years, and now he found me.”
He took a pair of scissors from a drawer and cut open the envelope so slowly that he seemed to be performing a ritual. The letter was written in Chinese characters. He sat on the edge of his chair and read slowly. He put the letter down and took from the envelope a photograph of a man and a woman and a child on a sofa with a curtain in the background. He returned to reading the letter, and then he put it back in the envelope and in the drawer and closed the drawer. “His new address is in Queens,” he said. Then he picked up his tea and blew on it and faced me, looking at me over the top of the cup like someone peering over a wall.
I asked about Hardy’s observations regarding age—Hardy also wrote, “A mathematician may still be competent enough at sixty, but it is useless to expect him to have original ideas.”
“This may not apply to me,” Zhang said. He put his tea on the desk and looked out the window. “Still I am confident of myself,” he said. “Still I have some other visions.”
14.
My adult life has been framed by the attempt to find words to convey my experience to another person. One of the difficulties is writing a sentence that means what I intend it to mean. If you think of the number of ways in which an actor might recite a line, then you recognize the ways in which a sentence can be interpreted. Numbers are precise in a way that words can’t be, but numbers cannot explain my feelings for my wife or my son or how rain feels or what it is like to stand beside the ocean in a storm.
It isn’t that numbers are incapable of describing the world of feelings, it is more as if they have the capacity to represent a parallel experience, the way psychedelic drugs or alcohol makes a person aware of a parallel reality. (“The sway of alcohol over mankind is unquestionably due to its power to stimulate the mystical faculties of human nature,” William James writes in The Varieties of Religious Experience, published in 1902.) With numbers, though, the reality exists and represents an analogous means of taking the measure of the world. Rain is no longer a sensation or an accessory to one’s mood but a measurement of how much rain fell or how quickly or with what force. Quantitative implies time, another means of measuring sensation: when this amount of rain falls, I feel this way. The precision conveys meaning. I can find patterns in my surroundings the same way that I can find patterns among my impressions. The impressions run alongside the precise ones and sometimes they intersect, as in the case, say, of considering why the universe is structured in this or that way.
The finding of a formula for predicting the arrival of primes, if there is one, might not teach us anything that we don’t already know. But what if it did? What if other things became apparent in the world’s design because we understood this antique enigma? What else are primes linked to? Is it workmanlike knowledge or pure art? Or something else, I don’t know what. Would it imply a divinity? And in what sense a divinity?
15.
Week fifteen: When the steps aren’t obvious, I find it difficult to keep in mind all of an equation’s terms. Knowing when to apply which steps has become a torment, since some equations that seem to involve dedicated procedures also don’t seem to always. I feel a kinship with an autistic boy I read about who said, “I understand that people cry when they’re sad, but I’m told that people also cry when they’re happy. How am I supposed to know the difference?”
More than once and maybe more than twice, I have felt like an immigrant in a country whose language I don’t entirely comprehend, unassimilated, sitting at the dinner table with my children who are fluent, saying things that are funny to them and not funny to me. I feel only the restrictions on my ability to speak. Marooned among math problems, I feel that I have a language, but a defective one.
To begin a day learning math, I have to prepare my mind, so as not to let my resistances overtake me. I know that I have to find the, apparently for me, elusive consistencies, the places where things behave as I expect them to, and where I am just employing methods to complete a task, where my textbook is a manual and not an inscrutable document.
16.
Now this: beauty has been largely dismissed in the humanities, since historical standards no longer persuade, but it still figures in mathematics. Mathematicians use the word beauty without irony or hesitation and differently from the way it is used in aesthetics. For mathematicians beauty is more a quality than an appraisal. Bertrand Russell writes, “Mathematics, rightly viewed, possesses not only truth, but supreme beauty—a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection.”
The German mathematician Hermann Weyl writes, “Mathematics has the inhuman quality of starlight, brilliant and sharp, but cold.” Shing-Tung Yau, the professor at Harvard who invited Zhang to speak, told me that beauty was one of the most important elements of mathematics. “Otherwise it would be very boring and then you would not be able to stand it,” he said.
Beauty does not depend on a correspondence with taste; it tends to make its claim in the interval before the mind focuses itself, and it is more easily felt than decided on. For mathematicians notions of mathematical beauty accord with a belief that the laws of the natural world, which mathematics frequently articulates, and the relations of whatever objects or circumstances mathematics is describing have a harmony, whether in the way that water moves or the orbits of the planets or the operations of shapes too complicated to see. Beauty in mathematical explanations is often a reflection of something glimpsed of a structure that seems to fit the world, although there is no explanation for why it should. Something, furthermore, that has been present but undetected and perhaps even unsuspected, the theory of relativity, for example. It illuminates a territory where the seen and unseen meet. This is a Pythagorean notion, never given up.
The philosopher Michael B. Foster, who taught at Oxford and died in 1959, believed that Christianity brought modern science into being, since it made the natural world worth examining for evidence of God’s plan. During the Renaissance, mathematics began to be regarded as able to provide confirmation of God’s gestures and thoughts by making hidden structures apparent. By the seventeenth century there is a near ecstatic blend of mathematics and the divine. This is exemplified by Descartes, who believed that God was a mathematician, and later, Newton, who said that space was the sensorium of God, meaning, I think—the remark has had a number of interpretations and is thought by some philosophers to be nonsense—that it was the territory in which God existed and operated and was itself a divine embodiment. This seems similar to me to Kepler’s notion of the sphere as a godly metaphor. Newton also said, “Every newly found truth, every experiment or theorem, is a new mirror of the beauty of God,” which is a quasi-Platonic remark.
Neuroscientists in Great Britain discovered that the same part of the brain that responds to art and music was activated in the brains of mathematicians when they looked at mathematics they thought beautiful. This finding was published, in the journal Frontiers in Human Neuroscience, in the article “The Experience of Mathematical Beauty and Its Neural Correlates.” The mathematicians were asked to rate equations as ugly, neutral, or beautiful. Best of all they liked Leonhard Euler’s identity eiπ + 1 = 0, “which links five fundamental mathematical constants with three basic arithmetic operations, each occurring once.” Sir Michael Atiyah, a mathematician and one of the study’s authors, told an interviewer, “It involves π; the mathematical constant e;… i, the imaginary unit; 1; and 0—it combines all the most important things in mathematics in one formula.” Atiyah regarded it as the mathematical equivalent of “To be, or not to be.” While the equation made use of only five symbols, it encapsulated “beautifully deep ideas,” Atiyah said, “and brevity is an important part of beauty.”
The equation that the mathematicians rated often as ugly and liked least was Srinivasa Ramanujan’s infinite series for 1/π,
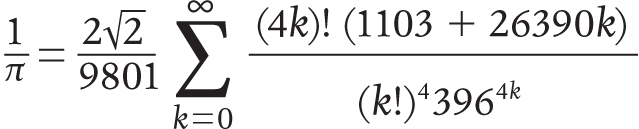
which I find strangely beautiful, in an elaborate, architectural sort of way. I like it also because the right-hand side of the equation seems like the inflated image that the left-hand side privately has of itself.
According to Hardy, a mathematical assertion is serious when it embodies significant ideas. What appears to be essential are “a certain generality and a certain depth.” Generality means that an idea should be “constituent in many mathematical constructs,” meaning useful in many ways and contexts. It also ought to be capable of being expanded to fit larger situations, and it should exemplify a class of theorems. Moreover, it should connect ideas that hadn’t been connected. Theorems that are too specific, that don’t illuminate larger ideas, various other mathematical peculiarities such as 8,712 and 9,801 being the only numbers smaller than 10,000 that are also “the only four figure numbers which are integral multiples of their ‘reversals’: 8712 = 4 × 2178 and 9801 = 9 × 1089” are only “odd facts, very suitable for puzzle columns and likely to amuse amateurs, but there is nothing in them which appeals much to a mathematician.” Their proofs are “a little tiresome,” and can’t be generalized or made into what Hardy calls a “high-class theorem.” A too-general theorem, however, is insipid. Mathematical ideas for Hardy are alive the way people are and “become dim unless they have plenty of individuality.”
Generality is partly a matter of the ability to provide order. Mathematicians find pleasure in establishing order where there had not been order before, what Jean-Pierre Changeux describes as extracting “structure and invariance from the midst of disarray and turmoil.” Often they achieve this by finding relations between or among unrelated fields. Poincaré said in 1908 that “the mathematical facts worthy of being studied” are “those which reveal to us unsuspected kinship between other facts, long known, but wrongly believed to be strangers to one another.” Deane Yang told me that “mathematicians want for there to be two different universes, then you find a door between them, and all of a sudden they’re one universe. Then you want to explore all the ways to get from one to the other.”
Bertrand Russell liked thinking about deep mathematics because what was not human broadened one’s sense of what was human. “The discovery that our minds are capable of dealing with material not created by them, above all, the realisation that beauty belongs to the outer world as to the inner,” he writes, “are the chief means of overcoming the terrible sense of impotence, of weakness, of exile amid hostile powers.”
The older I get the more I find this observation sustaining.
17.
The classroom, also week fifteen: Deane said I needed to understand logic, because math is unforgiving of logical errors. Math often left things out, to avoid being “too verbose.” To avoid going forward blindly, I had to know what was missing. (This is different from math textbook writers leaving things out. Mathematicians leaving out unnecessary things are being concise. Textbook writers leaving out necessary things are being coy.)
“To have the exact intended meaning, every mathematical statement and equation has to be a complete, grammatically correct sentence,” he said. “Focusing on mathematical grammar will force you to understand the meaning of what you are being asked to solve. You’ll have to work more slowly for a while, but you’ll be able to go faster once you know what you’re doing.”
By using correct grammar I took him to mean that I had to follow carefully the progress of each stage of an equation and not just quickly perform half of the equation, usually the easier half—a phrase, that is—then hastily transfer my solution into a following step without allowing completely for how the solution affected the meaning of the equation. If I felt lost at confronting a variable, I could insert a number in its place. “Professional mathematicians do this all the time, but it’s rarely taught to students,” he said. As it happened, I had already stumbled across this tactic, as a DIY means of demystifying equations. A lot of things I did in algebra I did in the spirit of exposing its irrationality, that is, destructively. I had a bad attitude. I was a type of math punk. Out of frustration, I sometimes inserted numbers in the place of variables, thinking, Show me how this is wrong, too, I dare you, and understood nothing when it wasn’t.
It is important to learn algebra, Deane said, but more useful is learning the procedures that support it. I might begin by learning how to calculate the distance between two points by constructing a right triangle and using the Pythagorean theorem, and from there move to the equations defining the radius and diameter of a circle and satisfy myself as to why they work. When I reach a place where I don’t understand what I’m doing, I should put the work aside to learn what else I needed. If I came to his classroom, he would give me problems and insist that I solve them sequentially, with no leaving one step for another until I had persuaded him that I knew why I could leave. I was aware that this was a kind and generous offer and sensible, too, but I didn’t want to go to math camp. Furthermore, I didn’t want to struggle in front of a witness and demonstrate that I might not be very bright, so for a while I avoided him.
Deane and Amie each have their biases. Amie wonders why I would bother learning word problems. Deane wonders why, while studying algebra, I would bother learning the quadratic formula, which is  and useful for finding solutions to quadratic equations. Partly I learned it because it was a shiny object that drew my attention. Also, because while it looks complicated, it isn’t difficult to use. It is simply a matter of knowing values for a, b, and c. Squaring b and subtracting 4 times the product of ac and taking its square root then subtracting b and dividing it by 2 times a is something I could have done even before I started math again. Using it made me feel in a playacting way that I was doing complicated operations with numbers. Moreover, it was one of the few things I recognized already from its name, so it flattered me to have possession of it. Mainly, though, I thought it figured importantly in calculus, but he said it doesn’t.
and useful for finding solutions to quadratic equations. Partly I learned it because it was a shiny object that drew my attention. Also, because while it looks complicated, it isn’t difficult to use. It is simply a matter of knowing values for a, b, and c. Squaring b and subtracting 4 times the product of ac and taking its square root then subtracting b and dividing it by 2 times a is something I could have done even before I started math again. Using it made me feel in a playacting way that I was doing complicated operations with numbers. Moreover, it was one of the few things I recognized already from its name, so it flattered me to have possession of it. Mainly, though, I thought it figured importantly in calculus, but he said it doesn’t.
So far as I can tell, there are two ways that math is taught. The more common method insists on the inviolability of the material—it has its own rationale, which you must apprehend and submit to. The less common approach is that of trying to understand why a student finds learning math hard. As a boy I saw in mathematics only deceptions and tricks, so I searched for inconsistencies and grew resentful, bound to happen. If math was consistent, how come I couldn’t learn it? I was anyway subject always to the first method, which, in the service of efficiency, is willing to shed you if you falter. Only so much time can be spent before a class grows restless, and the caravan folds its tents and moves on.
18.
I finished algebra plagued by the feeling that I had to get every problem right. I had felt lost as a boy in geometry and in Algebra II, but that was because I never found a foothold, and I had never expected to. With algebra, I had started hopefully and been throttled. What I had wished for on my second engagement was to see algebra as rational and cohesive, and therefore benign, so that I could dispose of the mystery it had left me with. If I were able to do that, I would have made use of ways of thinking that challenged me to expand my, shall I call it, my intellect? My capacity for regarding problems whose solutions require the management of symbols, something I had never been good at. I had always been fond of Hemingway’s saying that in The Old Man and the Sea, the man was a man, and the fish was a fish. I might have gone the rest of my way through life believing that objects are only what they appear to be, if Amie hadn’t told me of Maxwell’s remark, which left me wondering what there was of the world to know that I didn’t know, and what might be close enough at hand to be apprehended and made use of, even if awkwardly at first.
The enlargement of one’s intellectual reach isn’t the kind of circumstance a person can identify empirically. One can only sense it about oneself. I felt I was beginning to change, to a degree, perhaps only in a cursory way, but I also felt, superstitiously, that to acknowledge it might be prideful, which might lead to its being revoked by whatever agency it is that lurks inside superstitious moral attitudes. The Sunday school teacher who tells you that God sees everything and unsettles you about whether you are safe from notice as you lie in bed in the dark trying not to have thoughts you were told you shouldn’t have. Anyway, I finished algebra, I came to the end of the textbook. It had taken five months, not six weeks. I had learned things, though, I had some new skills, even if rudimentary ones. I could do things I hadn’t been able to do, and I was pleased. The accomplishment was not substantial, but it was my own, and I had worked for it. I raised a private glass to myself and said, “Well done,” in the middle of an afternoon.
19.
All the mathematicians I knew told me that I would like geometry. Algebra was necessary and tolerable, but geometry had pleasures, they said. They practically insisted on it. I wonder if this attitude is partly sentimental. Algebra’s origins are opaque. No one can place it precisely in history, and al-Jabr is a remote and not easily imagined figure, and on top of that an Arab, so all the prejudices of Western culture in favor of itself come down on his head, whereas geometry has the grand old man, Euclid, the Santa Claus of axioms. Geometry lends itself to a narrative. Algebra’s past seems as diffuse as algebra is abstract.
Geometry also has a definitive text representing a contribution to culture that few men or women have ever made so concisely, perhaps no one else has. People writing about Euclid’s Elements often like to point out that it is the second-best-selling book in the Western world, after the Bible. I would like to point out that it is strangely private and interior. Only a severely gifted mind, I think, could have addressed simple structures with such fanatic specificity.
Plato said, “Geometry is knowledge of what always is. It draws the soul towards truth, and produces philosophical thought.” Euclid lived a generation after Plato and heard more arguments and geometrical truths than Plato had, and he wrote them down. In Elements, he is a compiler of historical and contemporary work. His book is a compendium of immortal remarks concerning the natural world, but it is generally agreed that only some of the remarks, and maybe almost none of them, are his own. His original work on mathematics he published in Optics and Phaenomena.
In Elements each entry leads to the next. It is regarded as a manual for how to think logically, and, so far as anyone knows, it is the first one that Western culture produced. Its methods of reasoning are adaptable to any field that is subject to procedural thinking. Abraham Lincoln, while a lawyer in Illinois, spent a year reading Euclid in order to teach himself to reason cogently. From Euclid someone can learn to construct an unassailable assertion. According to Stanislas Dehaene, Euclid makes explicit “the difference between if and if and only if.”
Euclid was describing the attributes of forms when the world was new or at least hadn’t had so many eyeballs on it. His was the period when the Greeks were naming the sky, and it must have seemed as if all creation were laid out for them to catalog and describe, and that there was an essential and beautiful order to the world. “Euclid alone has looked on Beauty bare,” Edna St. Vincent Millay writes.
A STRIKING THING about geometry is that it begins with the acceptance of a point, and only one straight line that passes through two points, but whereas a line is real, a point is imaginary. A point is a location, and there are more of them in the universe than a number can be written to enumerate, but no one can find a point, because it has no width, height, or volume, and therefore no area. (“A point is that which has no part,” Euclid says.) It’s an idea accepted as a thing and is the simplest example I can think of to make one aware of how mathematics is both real and not real. Mathematics is rigorous largely because of Euclid and his insistence of proof, yet Euclidean geometry begins with a conceptual object being taken for an actual one. This seems to me a fantastically strange circumstance, not to say another example of math’s inconsistencies, but everyone else seems okay with it.
Euclid begins by assuming five propositions that appear indisputable. He calls them postulates. They are perhaps sufficiently well known that I needn’t list them, but even so, here they are, according to Thomas Heath’s translation, published in 1909 and regarded as definitive:
Let the following be postulated:
- To draw a straight line from any point to any point.
- To produce a finite straight line continuously in a straight line.
- To describe a circle with any centre and distance.
- That all right angles are equal to one another.
- That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
Postulate one means that a straight line can be drawn between any two points. Technically, this is a line segment; a line continues infinitely in two directions. Postulate two means that a line segment can become a line by being extended. Postulate three means that from a straight line segment a circle can be drawn with the segment as its radius; one end point is the center of the circle. Postulate four is probably plain enough, all right angles are ninety degrees. Postulate five says that two lines, if a third line is drawn across them, will intersect eventually on the side on which the angles created by the third line are each less than ninety degrees. This is called the parallel postulate, since if the angles are ninety degrees, the lines are parallel.
The first four assertions unfold from one another, but the fifth does not and is unprovable. The belief that it might be proved was given up in the nineteenth century when non-Euclidean geometries were discovered. With these figures, the parallel postulate does not hold. On a sphere, for example, lines can be drawn that have a common perpendicular, as parallel lines do in the Euclidean sense, but they also intersect. Also, on a sphere, the shortest distance between two points is not always a straight line, which is why long airplane trips follow arcs.
Mathematicians have treated geometric forms, especially the circle, as species of natural history, as objects, that is, with attributes and inflexible behaviors. By Olympiodorus, a philosopher of the sixth century, the circle was regarded as a metaphor for the soul, “because it seeks itself, and is itself sought, finds itself and is itself found.” When Ms. Scharfenstein, my teacher in second grade, said that it is impossible to draw a perfect circle, I don’t think she knew that she was invoking Plato. I was at the age where such a remark seemed a challenge, and for a while I tried. With a protractor I found in a drawer in my father’s workshop I drew circles that looked perfect and gave me an obscure sense of completion, of enclosing a space but also of the enclosure’s being somehow endless, since a completed circle has no end point and therefore an everlasting continuity. It is the simplest object I can think of that is also beautiful. It is easy to see why it fascinated ancient thinkers so thoroughly, being both enclosure and boundary, finite within itself and infinite beyond its border. Celtic fishermen used sometimes to recite an invocation that included the lines “God be my unfolding / God be my circle.”
20.
About infinity: Geometry implicitly addresses infinity, since a line has no end. The simplest description of infinity is a > b, although it is only an allusion. So far as I can discover, the concept of infinity first appears among the Jainists, a schismatic Hindu sect, in the sixth century BCE. The Jains believed that calculating with large numbers expanded a person’s awareness. They had methods for estimating the time that a soul would need to complete its journey, and they had five descriptions of infinity: infinite in one and two directions, infinite size, infinite everywhere, and infinite perpetually, which read like a prayer.
The Greeks acknowledged two types of infinities, complete and incomplete, which are also called actual and potential. A complete infinity is a collection such as the set of whole numbers. An incomplete infinity is a series such as one that begins 1, 2, 3,… The first is specified by a concept in which all the terms are identified. The second accepts infinity as a term that is something like a direction toward which a collection heads. The first is bounded; the second is not. No matter where you are in either sequence, the end is never in sight.
Aristotle accepted only incomplete infinities. Among the Scholastics, whose ideas were taken from Aristotle’s and were widely taught in Europe between the twelfth and eighteenth centuries, a completed infinity involved the “annihilation of number.” Whereas with any whole number a + b = c, a + infinity = infinity, meaning a disappeared. The Greeks saw infinity as a boundary that could never be reached. The Scholastics saw a complete infinity as challenging God’s omnipotence, since only God was infinite. Augustine believed not only that God was infinite, but that He was also absolute, meaning that He contained infinity. Thinking about infinity led one toward Him. In Leaders of the Reformation, published in London in 1860, John Tulloch quotes Martin Luther, sounding piqued in a dispute at a conference in 1529, saying, “I will have nothing to do with your mathematics! God is above mathematics!”
The early Greeks, those of, say, the fifth century BCE, imagined infinity as boundless. Aristotle, in the fourth century BCE, believed that something’s being without bound was a specious idea, since, by definition, there could not be a body without boundaries. Infinity could exist only potentially, and it couldn’t be demonstrated.
A companion theological belief is that the capacity to appreciate infinity was given to human beings by God. Being finite, we wouldn’t have been able to conceive of infinity on our own. God gave us the means so that we could better appreciate His works. For Augustine, this proved God’s existence.
Pure mathematics is a form of contemplation different from prayer or meditation, but for Jean-Pierre Changeux, the rigor and stringency of mathematics bring the human mind into contact with notions of God. A secular version of this is the belief that mathematics is the method for thinking explicitly about infinity, for making it apprehensible. Hermann Weyl says that “the goal of mathematics is the symbolic comprehension of the infinite with human, that is finite, means.” This makes the most precise of sciences a way of approaching the most unknowable part of our existence.
To understand how past human beings had simplified ideas of infinity, it helps to remember that consciousness is an evolving project. Translations modernize texts, so we read ancient writing and think that it was done by people who appear to talk like we do, although sometimes more formally, and forget that they were often spirit thinkers who knew practically zero about how the world actually ran. Nearly every explanation they had for what they saw and experienced was mystical to the point of being irrational. Gods speaking through charms and chance, through entrails and the patterns of birds in flight, and lest one remark that such people were pagans and that Christianity corrected such thinking and made the world modern I would remind us—and it is no observation of my own—that the metaphor governing Christian Communion is a type of blood sacrifice.
We cannot know how earlier people felt intimations of a divine presence, because things are simply too different now. We have accounts from those figures in the desert that are vehement and awestruck. They had visions and visitations and experiences that aren’t easy to fit into ordinary life, at least not our version of ordinary life. Words go only so far to acquaint us with a fierce and compelling experience had by someone so different from ourselves. And who knows what it was to live in that kind of darkness, which was so deep and enfolding as to have almost a texture. With no terrestrial light except firelight to compete with them, the stars must have looked as if they were hung just out of reach and to be as bright as neon. I wonder if the stars didn’t seem to be as if hovering, observing, impersonal and imperial, the eyes of gods. The Greeks saw them as sufficiently animated as to find arrangements among them and to give these patterns names and qualities and purposes. Hysteria as a clinical circumstance more or less disappeared with candlelight’s being replaced by gas and electric light, and who knows how many ancient authorities would these days be given a diagnosis and a prescription.
When I look at the night sky, I tend to think of it as the ancients did, as a place. The notion that the sky goes on forever is a modern one.
21.
Infinity occasionally contradicts intuition. There are as many fractions as there are whole numbers, for example, but there are also an infinite number of fractions between any two whole numbers. Between any two fractions, no matter how tightly bound, there is sufficient room to place an infinite number of other fractions.
An infinite collection of numbers exists, but there is also an infinite collection of numbers that haven’t been imagined yet. As for geometry, in Two New Sciences Galileo noted the discordance in considering two line segments of unequal length. Each segment consists of an infinite number of points, but the longer segment would seem to have more points. He concluded that less, greater, and equal didn’t apply to infinite things, and that there might also be a greater circumstance than infinity.
Something is infinite when it includes collections that have as many terms as it does, Bertrand Russell writes. Something is also infinite when you can take things from it without making it smaller. Such observations, while concisely Western, also seem Zen-like.
Since the nineteenth century, dividing by zero has been regarded as undefined, contradictory, and illogical. Dividing 10 by smaller numbers, say 5 or 2, provides a clean answer. Dividing 10 by 7 or 3 is more complicated. Nevertheless, the larger dividing number provides the smaller answer. The inverse is also true; the smaller dividing number returns a bigger answer: 10 divided by 1/4 is 40. The answer to 10, or any other number’s, being divided by zero would appear to be infinity.
An infinity that can be placed into a correspondence with the natural numbers is called countable, because each member of the infinite set can be assigned a counting number. The set of even numbers is countable, and so is the set of prime numbers.
All three sets are the same size. An example of an uncountable infinity is the set of all the numbers there are—negative and positive, fractions, decimals such as pi that never end, and so on. These are called the real numbers. The most populous real numbers are the irrational numbers, which are numbers such as pi that can be written as a decimal but not as a fraction. There are so many irrational numbers that by the laws of probability if you pick a random number on the number line the odds that you picked an irrational number are 100%.
A list of real numbers will always be incomplete, because there is always a number that is not on the list. This is easily demonstrated: changing the digit corresponding to each number’s place on the list produces an absent number. In other words, if your list begins .1234 … and continues .1235,.…1236,… and so on, you change the 1 in the first number to another number, you change the 2 in the second number, the 3 in the third, until, having changed all the endless digits of all the endless numbers, you will have a number that hasn’t been included on your original list, verifying that the list of real numbers is too large to correspond to the list of whole numbers.
Pairing whole numbers and fractions toward the end of the nineteenth century, the German mathematician Georg Cantor, the founder of set theory, showed that there were as many whole numbers as fractions, even though there are an infinite number of fractions between two whole numbers. He also showed that there are more real numbers than fractions. Trying to pair off fractions with real numbers would always overlook a number, such as pi, that has an endless sequence of digits that don’t repeat.
The Greeks thought of infinity concretely. Euclid wrote of prime numbers not that there are an infinite number of them but that they exceed “any assigned multitude of prime numbers.” Until Cantor identified specific infinities, likely before 1878, no one had thought that there was more than one or such a thing as a higher infinity. Philosophers regarded infinity as either endlessly extensive or endlessly diminutive. Religious-minded people believed that being infinite was a characteristic of the divine, and mathematicians saw infinity as a boundary in calculus.
Before Cantor it had seemed self-evident that if you have a collection of things and you add things to it, the collection grows larger, and that taking things from it makes it smaller. Cantor realized that for each infinity, though, there would be a larger one, that there are a multitude of infinities, and that infinities ought to be able to be added to one another.
Infinity for Cantor consisted of collections, a many that could be thought of as a one, he said. Numbers that define the size of sets are called cardinal numbers. The cardinal number for a set of five objects is five. The cardinal number for a set of infinite objects is a transfinite cardinal, which is a conceptual object. The set of even numbers and the set of whole numbers, being the same size, have the same cardinality.
Set theory was also capable of constructing numbers and therefore infinities. Zero is the empty set. One is the set whose only member is the empty set. Two is the set containing the empty set and the set that contains the empty set. Three contains the empty set, the set containing the empty set, in the set made up of the empty set and the set containing the empty set.
Cantor was a Lutheran and, like Newton and Kepler, he believed that his work exemplified thoughts in the mind of God. Sometimes he heard a voice telling him that his conclusions were correct, no matter what anyone else said. In 1884, when he was thirty-nine, he was hospitalized for manic depression. Of his illness and confinement, he wrote in a letter that it had “in no way broken me, but in fact made me stronger inwardly, happier and more expectantly joyful.” He also said that it had allowed him to think and work without being disturbed. For periods afterward, though, he withdrew from mathematics, and for a while he taught philosophy. He also became engaged by the belief that Francis Bacon had written Shakespeare’s plays, a field now called Baconian theory.
It interests me that someone who struggled with stability created, with set theory, a field that might be regarded as permanently stable.
22.
Beginner algebra insists that a student be comfortable with symbols. Geometry, on the other hand, is visual. You can draw a triangle with a right angle and illustrate the Pythagorean theorem to a child. Temple Grandin, who says that she thinks in pictures, has written, “My area of weakness is in algebra, because there is no way to visualize it.”
Kid algebra, I felt, required that I think. Starter geometry asked that I reason. The difference, as I see it, is that thinking is open-ended. Given the terms of an algebra problem, I had to decide which among them would help identify the variable the problem was considering. Each step in geometry requires that I make a judgment based on logical premises, whereas in algebra each step after the first step involves a single reply to the step before it. In simple algebra one thinks at the start of a problem, then enacts a procedure; in geometry one reasons to the end.
More than algebra, geometry engaged whatever intellectual resources I have. Algebra felt cloistered. Geometry seemed expansive. Observing the saw-toothed profile of the city skyline or the pattern of winter tree limbs like lines on a grid made me feel that I lived among it. This was obscurely cheering. I began to think that things actually are, in their essence, numbers, or that numbers are at least capable of describing identities precisely. Algebra has a mystic quality, while geometry at first appears prosaic, even though all mathematics, all pure mathematics anyway, eventually engages the mystical. When I’m hitting on all cylinders, though, algebra seems procedural in a way that geometry doesn’t seem to be.
PERHAPS BECAUSE GEOMETRY relied on words used plainly, a standard established in Elements, it seemed coherent in a way that algebra is not. I did not feel adrift in geometry among barely apprehensible and concealed possibilities, as I did in algebra. In Euclidean geometry one intends to prove an assertion and begins with the simplest thing one can prove or assume from other proofs. In algebra, having chosen a tactic, one pursues it to the end, where the answer is correct or not. In geometry there is a self-consciousness in that one takes a step then contemplates the next one. There is not always a single correct answer. The Pythagorean theorem has more than 317 proofs. Leonardo da Vinci had one, James Garfield had one when he was a congressman from Ohio, before he was president, and Einstein had one when he was twelve.
I PLANNED TO learn geometry from Euclid, which is how I imagined that the pros did it. Also, I wanted to do it like Abraham Lincoln had. I saw geometry as a return from an exile amid the trials of algebra in order to spend a sojourn among the Greeks and pure thought. I imagined people asking what I was up to and answering, “At the moment? Reading Euclid,” then basking in their admiration. For a while I carried Elements on the subway, like a badge.
Elements, it turns out, is very challenging. It almost hurt to read it. The propositions I could mostly understand, but the proofs were taxing. Proposition 2 is “From a given point to draw a straight line equal to a given straight line,” which seems simple, draw a line equal to the length of another, but one arrives at the following drawing, after approximately twenty steps.
Grasping a proof involved a state of attention so laborious to enact that I grew impatient. I would give up and try again later and get nowhere one more time. It was the first occasion when I experienced mental work so demanding that sometimes I would feel that I had to lie down, but I wasn’t actually tired. Except for Finnegans Wake, which I have never finished, nothing I had read was so difficult. It made me feel like a dunce. If I lived in ancient Greece, I would like to think that I would seek out Socrates or Plato or Aristotle, but I might cross the street to avoid Euclid. Don’t ask a question unless you really want to know the answer, is how I might feel about him.
Amie told me that Elements hadn’t been part of the reading for any class she’d taken in college or in graduate school and that she hadn’t ever read it, and this made me feel free to seek other means of instruction.
23.
I found a geometry text and set to work, and a few weeks in I took a break and went to the Museum of Modern Art, where I stopped in front of Broadway Boogie Woogie, which was painted in 1943 by Piet Mondrian. The painting is sufficiently familiar that I probably don’t need to say that it is a collection of grid-like yellow and red and blue and black rectangles and squares on a white ground, arranged up and down and across, like a crossword puzzle. The musician Jason Moran has said that it looks to him like a jazz score, and he has played it. From my novice engagement with geometry, the painting looked different to me from how it had before, more nervous, more brilliant as an observation, and more precise, as if a schematic depiction of movement in the city and in its way Pythagorean. A conceptual companion to Giacometti’s love of watching people cross open spaces in the city, while noting the paths they chose and the patterns they formed as they moved among one another.
It would seem to serve no purpose to notice this, except that such an activity is a kind of theorizing about the world, a means of connecting one moment to another. And why is it necessary anyway that every thought have a purpose? Thoughts that appear to be peripheral lead sometimes toward thoughts that aren’t. They recall and suggest other thoughts and form ideas that become, partly by aggregation, consequential. Everything that happens is happening on the way to something else. This is a truism, of course, but geometry made it apparent to me.
EVERY NOW AND then something in geometry seems familiar, a definition or the stages of a proof, and I realize, I was here before. I remember then the other boys in my class, and my teacher, whose name was Dawes Potter. He was tall and in middle age, with an oval face and black hair in a crew cut, and he always wore a bow tie, which gave him an old-fashioned appearance. He looked like a character in a comic strip. In my mind’s eye, I can see him observing me, and as an older man I know that the expression he is fixing on me is part confusion and part exasperation from not knowing what to do with a boy who appeared otherwise to be intelligent, but sat sullen and silent in class and much of the time simply stared out the window. How obtuse he wouldn’t even have known, since my answers on paper were often the answers of the boy I was sitting next to, a kind of academic ventriloquism.
24.
Set theory, divinity, and contradiction: for any set, there is always a larger set—the set to which another element has been added. Eventually one arrives at the set that contains all other sets, “the single, completely individual unity in which everything is included,” Cantor wrote to a friend in 1908. The set that contained all of its subsets, however, would be larger than the set of everything, but anything cannot be larger than everything.
Cantor believed in his work “because I have followed its roots, so to speak, to the first infallible cause of all created things,” and he resolved the paradox theologically. He wrote the mathematician Grace Chisholm Young that what surpasses all was “the single, completely individual unity in which everything is included, which includes the Absolute, incomprehensible to the human understanding. This is the Actus Purissimus, which by many is called God.”
Since God is unknowable and absolute it made sense to Cantor that any finite system would collapse into paradox as one came near to the divine. Furthermore, in the region of absolute infinity it also made sense that the terms of the spatiotemporal realm would no longer hold. As Rilke writes in Worpswede, his monograph on landscape painting, “We shall often have to call a halt before the unknown.”
A philosopher or theologian might have accepted Cantor, because there are always paradoxes and unresolved problems in dealing with deeply difficult questions, but mathematicians did not. Cantor was sketchy, and mathematics wasn’t. “You were getting reasoning that seemed very simple,” Gregory Chaitin told Lawrence Kuhn about Cantor, “and then you were saying 1 equals 0.”
For some Christian theologians, though, God could be the only infinite. Cantor’s inquiries as to the extent of an infinity were pointless, since they could have no answer.
BERTRAND RUSSELL FOUND a second paradox in set theory. In Introduction to Mathematical Philosophy, he suggests forming a class (or set) of all classes that are not members of themselves. “This is a class: is it a member of itself or not? If it is, it is one of those classes that are not members of themselves, i.e., it is not a member of itself. If it is not, it is not one of those classes that are not members of themselves, i.e. it is a member of itself. Thus of the two hypotheses—that it is, and that it is not, a member of itself—each implies its contradictory.”
The discordance was addressed in the early twentieth century by the Zermelo-Fraenkel axioms of arithmetic, which are named for Ernst Zermelo and Abraham Fraenkel. The axioms provide a formal system that stipulates how sets are formed, and they do not allow a set of everything to be made.
25.
Very few ancient ideas regarding physical reality have any permanence, but the idea that numbers are the means for comprehending the design of the natural world persists. Pythagoras is supposed to have said, “Number is the measure of all things.” Also, “Number rules the universe,” and “Number is the within of all things.” The adaptability of numbers allowed them to become a symbolic language that describes physical structures and movements. In more than one place I have read that absent numbers, physics is mute.
Mark Balaguer, a philosopher of mathematics, makes a distinction between high school math, which is a skill, and the math that lies beyond it, which is a theoretical practice, being “a theory about the world in the way that physics and biology are.” In physics and biology, precise things are known about real objects, whereas in mathematics things are known infallibly about unreal objects. Both a scientist and a mathematician explore a territory, a habitat. The home ground of a species whose existence is conjectured tends to be circumscribed; the more capacious the habitat, the more likely the object is to have been found already. The territory, however, is real. A mathematician can bring a mathematical object into being only by thinking about it, and its home ground is abstract and infinite. In the essay “Mathematical Creation,” published in 1910, Henri Poincaré writes that mathematics is “the activity in which the human mind seems to take least from the outside world.”
MATHEMATICS IS SOMETIMES described as the study of structures, with the primary structure being 1, 2, 3,… Observations about this structure allowed the proposal of more elaborate structures. There is no explanation for why conclusions reached by an imaginary pursuit should describe processes and objects in the physical world, but occasionally they do. “An enigma presents itself which in all ages has agitated inquiring minds,” Einstein said in Berlin in 1921 in an address to the Prussian Academy of Sciences. He asked how mathematics, “which is independent of experience, is so admirably appropriate to the objects of reality?”
Some of the patterns that numbers embody—the way they describe distance or temperature, for example—are simple and self-imposed, but mathematics sometimes also describes structures that suggest further structures. For a physicist the most desirable mathematics describes an observation and predicts others that then are found. “One seeks the most general ideas of operation which will bring together in simple, logical and unified form the largest possible circle of formal relationships,” Einstein writes. This happened with Newton’s law of gravitation, which described why objects fall to the ground and then was discovered also to describe the attractions among heavenly bodies and their orbits and also the tides.
The physicist Paul Dirac said, in 1939, “Pure mathematics and physics are becoming ever more closely connected, though their methods remain different. One may describe the situation by saying that the mathematician plays a game in which he himself invents the rules while the physicist plays a game in which the rules are provided by Nature, but as time goes on it becomes increasingly evident that the rules which the mathematician finds interesting are the same as those which Nature has chosen.”
Like Pythagoras, Galileo saw mathematics as a text or a key to the physical world. “Philosophy is written in this grand book, the universe, which stands continually open to our gaze,” he writes. “But the book cannot be understood unless one first learns to comprehend the language and read the characters in which it is written. It is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures without which it is humanly impossible to understand a single word of it; without these one is wandering in a dark labyrinth.” Such thinking makes mathematics seem to be, whatever else it is, a sacred code.
Many scientists believe as Pythagoras does that numbers are embodied in the natural world. That mathematics could make predictions about nature without performing experiments has no explanation, but “must be ascribed to some mathematical quality in Nature,” Dirac says, “a quality which the casual observer of Nature would not suspect, but which nevertheless plays an important role in Nature’s scheme.”
In 1960 the physicist Eugene Wigner published an essay, “The Unreasonable Effectiveness of Mathematics in the Natural Sciences,” which includes the observation that “the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious.” Wigner wasn’t surprised that mathematics described orbits, since he accepted that mathematics characterized the physical world. Wigner was surprised when a piece of pure mathematics, presumed to be totally abstract, was discovered to have a useful application, a circumstance that had no explanation.
The world gives an appearance of conforming to certain mathematical structures, and this idea is hard to shed entirely. The physicist Paul Davies told Lawrence Kuhn that the universe seems to be “a package of marvels. It’s ingenious, it’s ordered, it’s mathematical.” If there is no mathematical structure in nature, why does mathematics seem to find one? Davies has said that there might be a “primal accord between mathematics and the universe. The more that is discovered, the more this relation seems to be enforced.”
C. N. Yang, a theoretical physicist, said, “What could be more mysterious, what could be more awe-inspiring, than to find that the structure of the physical world is intimately tied to the deep mathematical concepts, concepts which were developed out of considerations rooted only in logic and the beauty of form?” These of course are Platonic-shaded remarks.
In back of such a thought also is the appeal of symmetry. Symmetry and proportion have figured in Western culture at least since Plato, but they also appear in the art and architecture of cultures that never heard of Plato. Symmetry seems innately sympathetic to some quality of being human. In Metaphysics Aristotle says, “The main species of beauty are orderly arrangement, proportion, and definiteness; and these are especially manifested by the mathematical sciences.” Mathematics evinces beauty and goodness, he says, “in the highest degree.” Such thinking might regard Newton as having uncovered, not imposed, a unification and to believe that further ones are to be found. Since mathematics is the language of physics it would suggest that any universal theory of physics would also be a mathematical one.
26.
Three responses to the applicability of mathematics to the physical world are common; the first two are compatible. One is that Pythagoras and Plato and Kepler and Galileo and Einstein and Dirac are correct in assuming that mathematicians and physicists find mathematical formulas underlying the world’s design because the world is, inexplicably, built according to mathematical principles. The second is that mathematics is the most precise language we have for describing physical structures and so it is sensible that it would describe the physical world better than anything else does and now and then with a precision that is uncanny.
The third possibility is discordant with the others. It is that human beings contribute an arrangement to nature that isn’t actually there. They do it without seeing that they do it. In “Cognitive Science and the Connection Between Physics and Mathematics,” Anshu Gupta Mujumdar and Tejinder Singh write that mathematics results from prehistoric perceptions of “object, size, shape, pattern and change” from which have been built, by means of metaphor, “numbers, point, line,” and the entire concrete and conceptual tackle box of mathematics. In physics, these concepts lead to ideas about force and movement and notions such as “field and symmetry.” Since physics is built on the same ancient principles that brought mathematics into being, Mujumdar and Singh write, “this demystifies the extraordinary success of mathematics in physics. It could not have been otherwise.” The correspondence between physics and mathematics is the result of the mind’s being disposed to respond to regularity. Such a connection is “not mysterious. Rather, it is inevitable.”
As with all categorical but (so far) unprovable claims, what can one reply except, “Possibly.” And to remind oneself that the patterns that humans contribute to nature are nevertheless there.
Stanislas Dehaene also believes that mathematics has evolved to fit the structure of the physical world. “The evolution of mathematics is a fact,” he writes. “Science historians have recorded its slow rise, through trial and error, to greater efficiency. It may not be necessary, then, to postulate that the universe was designed to conform to mathematical laws. Isn’t it rather our mathematical laws, and the organizing principles of our brain before them, that were selected according to how closely they fit the structure of the universe? The miracle of the effectiveness of mathematics, dear to Eugene Wigner, could then be accounted for by selective evolution.”
Neurology aside, is it possible that mathematics is more inclined to refinement than evolution? Evolution depends on accident, whereas mathematics depends on thinking to invoke it, and only in the sense of its being a creative and contemplative act does it include accident. Evolution is opportunistic. An adaptation succeeds because it works better than previous versions, whereas a piece of mathematics prevails because it is true. Epiphanies and coincidences, such as Newton’s with the apple, are not the same as accidents of thought. Also, unlike as in evolution, earlier versions of mathematics are not discarded, they remain useful. Their primacy may lapse, but they don’t become extinct. Except in the fossil record, you cannot find all the iterations of a species, but all the iterations of a piece of mathematics are extant. They don’t get eliminated, they crowd up; in the guise of fields and specialties, they form neighborhoods.
There is not a trail of discredited and discarded mathematics or an archive of them, either, because mathematics is proved. Older mathematics might reflect a period’s intellectual shortcomings, and sometimes it is wrong, but it doesn’t tend to be wrong, it isn’t usually wrong. There is no natural selection in mathematics, either. More powerful methods may ask earlier ones to step aside, but earlier ones occasionally return with uses not seen earlier. Sometimes areas of study with unsolved problems are eclipsed or are overlooked and return. Or, with applied mathematics, are solved by scientists in other fields. Or are put aside for being too difficult, or simply fall out of fashion. When I look for examples of this, I find things I don’t entirely understand, such as a case given by Branko Grünbaum in his Lectures on Lost Mathematics, from 1975. Grünbaum says that there are problems “rooted in phenomena that are of interest to architects, engineers, some modern sculptors, and geometers: The rigidity or mobility of variously hinged systems of polygons, rods (= segments), cables, etc. Cauchy’s theorem on the rigidity of polyhedra that have as faces rigid polygons hinged along common edges is probably the deepest known result.” Cauchy’s theorem is from the nineteenth century.
When I asked Amie for an example of a piece of mathematics that has fallen into disuse but is still useful, she wrote that she had asked her friends and one had said, “Cayley-Salmon theorem on the flecnode polynomial. This is a polynomial whose vanishing on a 2 dimensional surface in C3 guarantees that the surface is ruled. (The theorem is that the surface is ruled if there is a line tangent to it to 3rd order at each point.)” Cayley’s theorem on the flecnode polynomial appears in a book Cayley published in 1865. A librarian at the University of Chicago told Benson Farb, Amie’s husband, that she regularly retrieves books and papers from earlier than the 1840s for mathematicians. Earlier mathematics typically forms part of a foundation.
Dehaene has other sensible objections to Wigner, though. Mathematicians have produced a gigantic amount of mathematics, he says, and only a small portion of it works in physics. A reply might be that pure mathematicians do not do mathematics in order to be useful to physicists, although if they did perhaps more mathematics might apply. Dehaene also observes that Kepler was not strictly correct in describing the orbits of the planets as ellipses. “The earth would perhaps follow an exact elliptic trajectory if it were alone in the solar system, if it was a perfect sphere, if it did not exchange energy with the sun, and so on,” Dehaene writes. “In practice, however, all planets follow chaotic trajectories that merely resemble ellipses and are impossible to calculate precisely beyond a limit of several thousand years.” This is completely true.
We (maybe just me) are still left with an (apparent) conundrum: If numbers and mathematical objects are mental constructions arising from the adaptation of the human brain to the regularities of the universe, then why are there primes, whose natures and behaviors have nothing to do with us? Also, it is still possible that, rather than an adaptation, the applicability of mathematics involves the observation of something that might be true and seems to hold throughout creation. We don’t know for sure either way.
The mind sees what it is capable of seeing, Dehaene says, and scientists tend to overlook that “the brain is not a logical, universal, and optimal machine.” It reasons poorly, he says, and does not do well with long chains of calculation (Amen). Also, it is subject to bias. Onto the physical world it projects structure “where only evolution and randomness are at work. Is the universe really ‘written in mathematical language,’ as Galileo contended? I am inclined to think instead that this is the only language with which we can try to read it.”
On the other hand, Roger Penrose, a Nobel laureate, says, “It is undoubtedly the case that the more deeply we probe Nature’s secrets, the more profoundly we are driven into Plato’s world of mathematical ideals as we seek our understanding.”
There is no settling the argument about Platonism or the relevance of numbers as describers of the natural world, not empirically anyway. There is only taking a side or being disinterested. The concept of a divine entity may be as far as mathematicians can go in their assertions before something powerful, enigmatic, and obdurate resists them, and they turn back, as if enacting Cantor’s belief that as one approaches the far ranges of infinity the claims and assumptions of the spatiotemporal world break down. Dante’s description of the Rose of Paradise is exquisite, but past it he isn’t able to see clearly.
27.
I still don’t totally know why starter math was so hard for me. I have wondered whether there are capacities native to all of us, the proportions of which determine what becomes congenial to our thinking. Did I lack ones favorable to mathematics? I have wondered whether there is a difference between procedural thinking and associative thinking. Certainly some people are capable of both and some, such as myself, can manage only degrees of one or the other. I think that the resistance I feel to studying math, which is nearly visceral, is a resistance to being made to think in a way that contradicts my nature or the way I am made or whatever you want to call it, a problem with authority, with being compelled to do something that allows no deviation. In the nature versus nurture argument I believe mainly in nature. We do not all begin at the same neurological starting line. Talent, I am persuaded, is a consequence of the way that our brains are built, and it is individual, either native or not. The circumstances into which we fall are surely important, and whom we fall among, but I’m not sure that we can exceed temperamentally or psychically or perhaps even intellectually what we have it in us to become any more than, to repeat a familiar observation, a young man or woman by means of determination and without the given attributes of size and strength can make it to the professional ranks of basketball. The brain can compensate for gross sensorial deficits such as the loss of one’s hearing or eyesight, it is to some degree plastic, but not sufficiently to address the neurological peculiarities involved with, say, autism. This may be the consequence of the brain’s being less able to detect the subtler difficulties as deficits, although it is also not my experience as the father of an autistic child that all autistic people regard their capabilities as deficient, even though they are frequently told that they are.
So far as I can tell, what I also appear to be averse to is solving problems that require holding several procedures in mind at once, the sort of thinking where one gets three or more steps removed from the start, as happens with equations. Circumstances where I have to identify a variable, say, conceive of a formula or a function that handles it, and complete the calculations while bearing in mind the rules imposed by the formula or function. Such procedures become something like automatic for many people, so that such people are not always aware even that they are thinking, but I have never found such blithe competency simple to enact. Perhaps I spend too much effort engaged with the procedures and not enough on thinking broadly. Here, though, is where the capacity for associative thinking figures. If I am reading a difficult piece of writing, I don’t try to understand it by noting the steps in the writer’s reasoning or design, although this is a very good method. I allow myself, and this happens without my conscious engagement, to welcome associations, many of which are dismissed until the ones that are left fall into place, assuming I am not defeated.
In neophyte math the problems are practical and literal but the solutions involve the apprehension of concepts. Going through them I feel like a plodder, one of the ungifted, the unblessed, blighted and meanwhile often aware that in the presence of difficult matters my mind might surrender. At times this can make me feel doubtful to the point of uneasiness about who I think I am and what my abilities are.
Some, often very intelligent, people design themselves around an aggressive embrace of their limitations, and often they are very successful. It makes their lives simpler than the confrontation with their deeper identities would entail. I see this division, for example, between people who believe that the world separates itself into types, and those who believe that each human life is singular. I fall adamantly into the second class, but I am aware that people in the first class arrive at judgments more quickly and tend to have more of them, although the judgments risk being shallow and ordinary.
Such people evaluate their observations according to a system. Would math be simpler for me if I had a systematic way of thinking? If I considered only categories and not individual cases? It’s difficult to answer, of course, but I think, Probably. I feel at a loss when learning things that have an inherent order, and I feel unhappy at lacking the capacity. I have to focus on my ability to read the world differently, but, until the higher stages, which I will never reach, math doesn’t reward individuality. Plus, as a result of this trait, I waste a lot of time.
It has made me wonder, was my inability a missing talent or the consequence of having inhibited myself years ago, when math first became hopeless. There is no way for me to know, of course. I can’t be, cognitively, two people at once, although, like anyone, I can be two and perhaps more people at once emotionally or psychically. I am trying to untangle this, since I am suggesting that emotional responses might be involved, an inhibition brought about by a surrender to being overwhelmed. Some, maybe many, of the behaviors we adopt in childhood are designed to protect us from harm, but they aren’t always useful later in life. They don’t always age well.
There is a further circumstance that my renewed engagement with mathematics insists I consider, also not attractive, which is that I might simply be lazy. Maybe I have avoided things that are hard to learn and to think about. Self-candor later in life has two sides. One side is the pleasure of correcting a fault, and the other is the reckoning of all the difficulty and harm that the fault has brought about, the gestures and episodes of defeat and chagrin included in the wagonload of small miseries that one is yoked to. The archive of mature experience more and more displays the capacity to be conflicted, or perhaps it is only that it grows richer. In the midst of celebrating, we are also mourning, which is an echo of the line from the Book of Common Prayer “In the midst of life we are in death,” another observation that deepens for me with the years.
ONE CAN MEMORIZE, or one can aspire to understand. It’s not always clear to the aspirant when one prevails over the other, or where the boundary between them is, either. An actor speaking lines doesn’t need to know why the writer wrote them. The knowledge might enlarge his or her performance, but it isn’t required, I don’t think. No one knows anything about the figures in Greek drama or what Shakespeare thought beyond what the plays and the poems suggest. Sometimes one has a cast of mind into which ideas land in their entirety, with their design revealed like a tool that arrives with its use understood intuitively. I don’t think it is uncommon in mathematics for a young person to feel a reverberation with the forms that he or she is learning to use. Karen Olsson describes such a feeling, and I know that Amie has had it, too. Probably such a capacity makes learning math simpler, but it doesn’t appear to be essential.
On this encounter I wanted to understand everything I could about the math I was learning; I even thought I would be able to, because I was older and the math I was studying was for kids, but this, I was forcefully made aware, was prideful. Simply too many elements are involved. The thought is too wide-ranging, which is not surprising, considering that even adolescent math is more than what Euclid knew. It was also borne in on me, something I might have realized earlier, that if I had the capacity to understand math now, I might not have had so much trouble in the first place.
Sometimes I wondered if maybe I had been taught poorly. Or by being inept and by means of embarrassment had I just fallen through the cracks? I’m not sure. I remember the child that I was, I can close my eyes and see him and hear him speak and watch him, but I am no longer that same being. He is independent of me. He exists in his own time.
28.
Mathematics draws on the human desire to simplify. To divine that what appears to be disorderly can be sorted and classified. One can see this impulse at work in procedures and taxonomies. The urge to classify seems as ancient as the beings who drew animals on the walls of caves. Whatever profound spirit thinking they were engaged in, they also were organizing categories, drawing herds, grouping like with like.
From a journal: Mathematics doesn’t solicit my opinion. Math doesn’t ask “Are you comfortable?” It is not congenial that way. Mathematics is cold, but there is a kind of liberation in its aloofness. It is an inverted liberation, though, a whose-service-is-perfect-freedom sort, since it comes about only by means of a submission to its terms.
What have I found difficult lately? I am baffled by the absurd idea that in an expression such as 2 × 105 m3 × 1.1 kg/m3 I can shed the cubic meters, since they cancel each other, but cubic meters are things and not numbers. I understand that I can cancel numbers, which are abstract, but a meter is a noun and material. How is their equivalence possible?
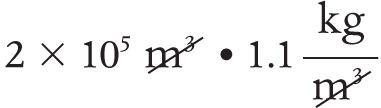
If I write, 2 × 105 turtles3 × 1.1 kg/turtles3, can I get rid of the turtles? As it turns out, yes, Amie says. “The turtles would be a unit in the problem you’re solving,” she writes. “Maybe each turtle eats 1.1 kg of turtle food and you’d like to figure out how much turtle food, in kilos, to order for 200,000 turtles, which is 2 × 105 turtles. Your final answer is in kilograms. The turtle units get canceled.”
Another moment when mathematics seems to depend on a loopy, self-serving, and clandestine logic. I read of a mathematician’s saying that sometimes solutions appear from unlikely places and procedures as by a kind of witchcraft, and I thought, Exactly.
29.
“Geometry is a completely idealistic world,” Deane said, invoking Plato. “It’s about things that don’t really exist—the perfect circle, the perfect square. Things that are roughly a square or roughly a circle, they exist. Math exists only in your head, not anywhere else.”
Plato said, “The knowledge of which geometry aims is the knowledge of the eternal.” The remark, “He is unworthy of the name of man who is ignorant of the fact that the diagonal of a square is incommensurable with its side,” is frequently attributed to him on the internet and said to have been written over the entrance to his academy, but if he said it, I can’t find where, nor could the scholars I consulted.
30.
As everyone had said, geometry turned out to be more congenial than algebra had been. I wouldn’t say it was welcoming, but I wasn’t roughed up, either. I didn’t come out of the encounter bruised and disheveled.
With geometry I had fewer days where I was exasperated. Algebra seemed to like to smack me around, because it could. What algebra I had possession of, though, I could use in analytical geometry, which was discovered by Descartes in the seventeenth century and involves graphing lines and curves using algebraic equations. As a result, I wasn’t beginning geometry as the same rube I had been when I opened Algebra for Dummies.
There continued to be periods, though, when I was serially defeated. I agree that defeat is not to be feared, but too much defeat is. A defeat surplus is. Defeat as a condition is withering. The company of failure can seem as permanent as a tattoo. I was not cheered by failing so often. I did not think, How great it will be when all this falls into place. I worried that it would never fall into place. That there was no place for it to fall into even. In math I am failing against a pitiless standard. There is no ambiguity, whereas failure in the eyes of others, as a writer, say, is a matter of other people’s judgment, of taste and bias and opinion, all of which are culturally conditioned and can be questioned. There are very few absolute standards to life, however much a person might sometimes wish that there were.
When people tell you how to deal with failure, they usually mean in the singular. They mean, You failed, here’s what you do. They don’t mean, You keep failing, even though you are trying. Nothing is working for you. Maybe give up, find something else. Perhaps they tell you that things can change. Most of us would avoid someone who seemed tagged with constant defeat. What came next for me, though, day upon day, was more of what I’d been failing at. I didn’t have simply to get through something. Apparently I had to be smarter than I actually was.
Perseverance furthers, though, and I was determined not to give up. Anyway, I could choose to view the daily failing cumulatively, as a single failure amounting to a judgment: I guess I’m not good at math.
To be unable to fulfill an intellectual task is frustrating, though. It is like being found to be weak, which no one likes, either. I turned away from math as an adolescent because it dented my hopes of becoming a capable person. It is vexing to find that it still has the capacity to undermine me.
Of course, math is actually taxing in a demonstrable way. In The Number Sense Stanislas Dehaene mentions that brain scans show that subtracting 3 repeatedly involves “intense bilateral activation of parietal and frontal lobes. If an operation as elementary as subtraction already mobilizes our neuronal network to such an extent, one can imagine the concentration and the level of expertise needed to demonstrate a novel and truly difficult mathematical conjecture! It is not so surprising, then, that error and imprecision so often mar mathematical constructions.”
I found this cheering. Everyone needs to make his or her own mistakes, and one of mine might have been to study math. We have things to tell each other in the form of advice and instruction, but very little of it is ironclad or will mean the same to one person as another. Experience is individual. And making a mistake is maybe not the same thing as failing.
Even so, failing is daunting. Research by Judith Rodin at Yale suggests that mastering a task later in life makes a person more confident and that this confidence can be used to attempt other, presumably more demanding, tasks. I couldn’t find any research on the subject of failure later in life. It’s a territory one would rather avoid.
AT TIMES WITH geometry the annoyance I had felt with algebra returned. Sometimes I’d get angry, and then I did stupid things repetitively. It would begin by my noting that a solution, say for finding the proportions between line segments on a graph, had varied perversely from what (I believed) I had been led to think was the correct way to find them. I would get a problem wrong and attempt another, insisting on the same approach, as if I could force the problem to surrender, as if I could break its spirit.
On such days, I rebuked Amie for perpetuating the lie that math was rational. Clearly when you interrogated it, contradictions fell out of it all over the place. I never got anywhere with this argument, though. Math in her mind was blameless.
31.
The shapes in geometry are straightforward and simple, but Euclid examines them and their attributes in such a way that they aren’t simple anymore. The ubiquity of lines, circles, squares, and rectangles in the natural world makes you feel as if you were seeing something fundamental about its design. One can imagine the Greeks’ astonishment at the world’s seeming to reflect their suppositions. Or at believing that they had discovered something essential lurking just below its surface, seeing in the flight of a bird a parabola and regarding it as a confirmation.
A deep engagement with pure mathematics is like prayer, in that one is attempting to speak to an unknown power, across a divide, and awaiting an answer.
32.
Applied mathematics, a case: Poker played poorly is purely a gambler’s game. Losers tend to think that they didn’t get the cards, and not that they were beaten by someone who played better than they did. They return to the table and wait for big hands and lose more. Accomplished players strive to diminish the effects of luck. From their opponents’ bets and behaviors, they work like detectives to determine their cards. They play opportune hands deceptively, and feckless ones, too, and shed unpromising ones before the cards cause them too much harm. They know that some hands that seem auspicious are not, and that others are stronger than they appear.
Games for which a flawless strategy is known are said to be solved. Tic-tac-toe is solved; blackjack is solved; checkers is solved. Chess is not solved, and poker is not, either. Solutions theoretically exist; they are simply too intricate, so far, to be comprehended. Among mathematicians, chess is regarded as a game of perfect information, because nothing is hidden. If its ideal strategy were discovered, there would no longer be any reason to play it—no move could be made for which the response was not already known. Poker is a game of imperfect information, since so much is concealed. Solving it would not overcome the disadvantage of being unable to know why your opponent is acting as he or she is. Such concepts derive from an abstruse field of applied mathematics called game theory, which was formulated, in the 1940s, to address difficult economic problems.
Game theory was conceptualized by John von Neumann, who was one of the mathematicians involved in the Manhattan Project, and who collaborated with Einstein. In 1944, von Neumann, with Oskar Morgenstern, published Theory of Games and Economic Behavior. Until then, people typically entered markets with a strategy, but such preparation could help them only if they knew what other people would do. Von Neumann saw that the tidal rhythms of transactions and uncertainties involved in markets were embodied in the narratives of parlor games, and especially in poker, where each player also has a strategy to claim the largest share of the money changing hands. Since the strategies of most games were subject, if simplified, to fairly concise mathematical calculations, the workings of markets could be also.
Theory of Games and Economic Behavior is riddled with charts, equations, and diagrams. Without an understanding of higher math, it is impenetrable. In an essay reprinted in the book’s sixtieth-anniversary edition, John McDonald, quoting John Maynard Keynes, writes, “‘Businessmen play a mixed game of skill and chance, the average results of which to the players are not known by those who take a hand.’ Von Neumann’s theory is designed to narrow this gamble … It tries to make the imponderable ponderable.”
To diagram certain game theory problems, von Neumann used hands of poker as examples. Fifty years later, Chris Ferguson, a UCLA undergraduate, thought to apply game theory concepts to grand-master poker. Relying on them, he became, in 2000, the first person to win more than a million dollars in a poker tournament.
FERGUSON IS TALL and lanky, with very long brown hair and a brown goatee; his admirers call him Jesus. When he plays cards, he wears a black cowboy hat that he was given by a friend. The brim protrudes over his forehead like an overhang, sometimes throwing his eyes, behind dark glasses, into shadow. At the poker table, he has all the animation of a state trooper handing out a speeding ticket. When he’s especially engaged, he sits almost cataleptically still, with his hands clasped in front of his chin. His right hand is balled into a fist, and his left hand rests open on top of it. To bet, he lowers his right arm like a lever, then returns to his original pose. The gesture is exactly the same whether the bet is a bluff or a boast.
One year at the World Series of Poker, in Las Vegas, Ferguson played poker ten hours a day for thirty-five days in a row. He had a room in the Rio Hotel, where the tournament was held, and when he was finished playing, usually around three or four in the morning, he went upstairs and slept until noon, then came back to the lobby and sat down at a table. A few times, he finished at seven in the morning. Eventually, he found himself unable to fall asleep any earlier than that.
I went to his room one night so that he could show me some fancy forms of shuffling—cheat forms, shuffles that allow dealers to deal specific cards. Leaning on one elbow, he used the bed for a table and showed me a double shuffle, a shuffle that appears to be genuine but isn’t a shuffle at all—all the cards remain where they were. “I learned it for protection, in the nineties,” he said, “to see if people were doing it to me. A really good magician is going to beat a good spotter. A good dealer is supposed to deal in a way that you know he can’t be cheating.”
Ferguson was born in Los Angeles in 1963. His mother, Beatriz, was a mathematician and his father, Tom, taught game theory at UCLA. Tom Ferguson brought home specialized board games and card games and taught them to Chris and his older brother, Marc, who is a computer programmer. “Whenever there was a rainy day, we would get to stay inside and play Risk,” Tom Ferguson told me. His younger son “learned to think about playing and strategies and what other people know about what you know. It’s not important in chess, but it’s important in poker. It’s a rather deep game, when you get involved.”
Ferguson doesn’t recall when his father taught him poker—he feels as if he’s known it all his life—but he remembers that when he was in the fourth grade he lost thirty-five cents in a game, and it bothered him. In high school, he played on the weekend with friends. At seventeen, accompanied by some of them, he began making trips to Las Vegas. He and his friends would pool gas money, sleep in cheap hotels, and eat at the buffets. He liked Vegas because the people in the casinos called him Sir, and “you could lean back in your chair and no one would yell at you, unlike school.” His friends went for fun, but Ferguson went to establish whether he played poker well. “I saw Vegas as a challenge,” he told me. “Play ten hours a day, pay for my room and my food, and get home with more money than I started with. I think of that as my transition into manhood—when I was able to prove to myself that if I had no support from my family, and no job, as long as I could get to Vegas, and have a hundred dollars in my pocket, I could survive.”
From a fifty-two-card deck, 2,598,960 five-card hands are possible. The basis for most poker strategy is a ruthless notion: What can I discern about my opponents’ habits that I can attack? Such an approach is called “maximally exploitive.” It is the way nearly all professionals proceed, relying on logic and intuition. While Ferguson was still a student, he decided also to employ a method called “optimal strategy,” which derives from a game theory question posed by Claude Chevalley, in 1945, in View: “Each player being ignorant of the strategies followed by his opponents, which strategy will he follow in order to get the maximum possible advantage for himself?”
The optimal strategy “doesn’t mean ‘How do I win the most?’” Ferguson says. It means, when up against an expert opponent, “How do I lose the least?” Part of it is mathematically determining whether one’s cards are favorable, but a player using optimal strategy also builds into his play bets that sometimes appear improbable and make it mathematically difficult for the opponent to know what to do. With optimal strategy, “if we’re playing heads up, you might get lucky and beat me, but you’ll never outplay me,” Ferguson said.
Ferguson made trips to Las Vegas during his five years as an undergraduate and his thirteen years as a graduate student in computer science. On the entry forms of poker tournaments, for many years, he listed his occupation as “student.” His thesis adviser was Leonard Kleinrock, whose lab sent what was considered the first message over the internet, in 1969. Kleinrock told me that Ferguson was “one of the more brilliant and creative young men that I’ve known in my career at UCLA.” During the late eighties, Ferguson was working as a programmer for a more advanced doctoral candidate when the student got a result he couldn’t interpret. “Chris, this lowly programmer, writing code, explained what was causing the result,” Kleinrock said. “It was a very deep theoretical idea, and his manner was very low-key, no bravado, just pure intelligence, and, when I saw that, I thought, I want to follow through with this guy.”
Kleinrock said that Ferguson “would spend hours bouncing ideas around. All kinds of esoteric mathematical and computer subjects—genetic algorithms, search algorithms, and so on—reams of ideas, then he’d come back the next day pursuing some of them, having thrown the others away.” He went on, “Or he would show me how he was progressing on cutting the deck down to any number of cards—sixteenth card or thirty-fourth card—and the perfect riffle of them. I was not the type of supervisor to demand a schedule—we were both enjoying the academic and scientific ideas. He was, by far, the student who took the longest to graduate, though.” Ferguson finished his doctorate in 1999, when he was thirty-six, by which time he had spent half his life at UCLA. “He was never the go-go-go academic achiever that wanted to race up there and set the world on fire,” Kleinrock said. “Plus, the year after he graduated he became the world champion and won all that money.”
33.
Poker allows two ways to win: own the best hand, or make the best hand go away, sometimes by bluffing. The imperative to bluff, it turns out, is inherent. “I can take a purely mathematical model of poker and hunt for a purely mathematical solution,” Harold Kuhn, a professor at Princeton who knew von Neumann, told me, “and a phenomenon will appear which has always seemed to be psychological but isn’t—it’s mathematical—which is that you will bluff, and your opponent will drop out. The necessity for bluffing is built into the mathematics of the model.”
Any hand has multiple strategies, Ferguson said. “If I’m facing someone I’ve never played before and have no idea of his weakness, and I play an optimal strategy, I know I will not make a mistake that will give him any money,” he said. “If you don’t know the optimal strategy, you don’t know your weaknesses or his; you don’t know when he’s taking advantage of you and you can take advantage of him. As people deviate from optimal strategy—as they bluff or fold or call too often or not enough—it’s actually pretty clear. If you’re able to see how they deviate, you can see how to take advantage of them.”
A player using optimal strategy assumes that his opponents know he is doing so—in other words, that his strategy has been found out. He can announce, for example, that a third of his bets will be bluffs, and then construct the game in such a way that his opponent still can’t tell whether it is better to fold or call. If two players have each put fifty dollars into the pot, and the optimal-strategy player bets a hundred dollars and his opponent folds, the opponent loses fifty dollars. If he calls, one-third of the time he will win, because the optimal-strategy player is bluffing, and two-thirds of the time he will lose, because the optimal-strategy player is betting a hand that is strong enough to win. The opponent now has no means of knowing when it is better to call than to fold. This is described as making the opponent “indifferent.” He might as well flip a coin. “Now it’s a mind game,” Ferguson said.
“What are the guys who don’t play optimal strategy doing?” I asked.
“I’m not sure what they’re thinking,” Ferguson said. “They’re flying by the seat of their pants. I learned poker by sitting at home and thinking how to play hands—if I play my hands this way, what can my opponent do to take advantage of me, and if he can, what do I need to do so that he can’t anymore? I want to be the least exploitable player. Other people learn through experience, and if they’re good they’re going to come up with a strategy that’s pretty similar to what I do. It turns out that there’s just a right way to play. I learned by applying game theory. They learned through what I consider a more arduous process, playing countless hands. Am I smarter because I use game theory? I don’t think so. It’s hard to learn poker, because you can play a hand horribly and win, and also play perfectly—almost—and lose. How’s the guy who doesn’t know the game well going to know the difference?”
Some players think that approaching poker through mathematics causes someone like Ferguson to lose sight of all the peripheral elements of the game, such as “tells,” unconsciously revealing behaviors that intuitive players regard as rich in information. Ferguson doesn’t dismiss these aspects of the game—he both looks for tells and tries not to display them—but he believes that game theory protects him from making intuitive judgments that might fail, or from being distracted by information that’s not necessarily germane. Exploitive players “model their opponents, and then they come up with a strategy that will beat that opponent—‘He raised here, he must have that hand’ or ‘He plays that way, I’m going to play this way’—and they stop there,” Ferguson said. “I don’t stop there. I say, ‘If I play this way, how can he play to counteract what I’m doing—how might he adjust?’ The beauty of it is that it doesn’t depend on your opponent. Once I figure out what the optimal strategy is, I know it. A year from now, it will be the same. It doesn’t matter who I’m playing against. The research is everlasting.”
Another player who uses game theory and mathematics as heavily as Ferguson does is Andy Bloch, who has two degrees in electrical engineering from MIT and a law degree from Harvard. “Most other people are trying to outplay you—bluff you out of pots, trying to get a read on you,” Bloch told me. “If you’re playing against someone like that, you can manipulate them into making bad calls and folds. Chris is one of the most difficult people to get an edge on, if you can get an edge at all. Against other players, I’m going to try, but with Chris I don’t even really try. He’s too difficult to read. Players unfamiliar with game theory, the intuitive players, are going to have a really hard time reading and understanding him, because some of the plays he makes are going to confuse them. They’ll see a bluff and think he bluffs too much, because the bluff doesn’t make sense.”
34.
At the tail end of the World Series of Poker that year, the Bellagio held a tournament, and Ferguson entered, although he was exhausted—he had played in thirty-three of fifty-five events of the series, and had won around seven hundred thousand dollars. The buy-in at the Bellagio was fifteen thousand dollars, cash only. Ferguson paid with three five-thousand-dollar chips that a friend had given him to satisfy a debt. He sat with eight other players at a table in a high-ceilinged room with huge windows at one end, off the casino proper. In all, there were four hundred and forty-six players at forty-five tables. There was a low, sibilant rustle in the room, the sound of chips being agitated in hundreds of hands. On the walls were television screens showing a golf tournament and an action movie, with the sound turned off.
Ferguson calls himself a tournament specialist, meaning that he doesn’t play for table stakes—what are known as live games. In live games, players can always buy more chips when they lose. Ferguson regards this as tedious. In a tournament, when you’ve lost your chips, you’re done. A tournament player has to accumulate chips to withstand challenges, which become more consequential as the match progresses. Players are often allowed to enter tournament games a few hours after play has started, which is what he likes to do. “I lose the advantage of knowing the table,” he says, meaning the other players, but, because he has rested, his decisions are better.
Thousands of men and women are believed to play poker for a living. The entry fees at big tournaments can be so high that chairs are sometimes filled by people representing syndicates—groups of players who have pooled their money and sent one player to represent them. If there are winnings, they split them.
Ferguson kept getting cards he didn’t want. He turned their edges over slightly to read them, then tossed them back and folded his arms across his chest and looked impassively at the movie. Now and then he leaned back on the legs of his chair. He was roused briefly by a man in a white T-shirt and black shorts, with shiny black hair, who walked mostly sideways among the tables and chairs toward the door. “I’m a friggin’ idiot,” the man said. “That’s what I am. Stone-cold idiot.”
I stood near Ferguson’s table. Julio Rodriguez, who writes for CardPlayer.com, was filing updates on the game. I asked Rodriguez how unusual Ferguson was in being so fluent in math. “A lot of players know the math,” he said. “There’s no way around it, really, but the majority of them go on instinct, or feel, or a read on a player. It seems like a lot of them are just born with a sense of games. If you talk to a lot of these guys outside, they’re never not playing a game. They’re reading you. That’s why they’re so engaging. They know what people want; it’s very easy for them to please you. They also know how to deceive.”
I asked why he thought Ferguson appeared to be playing so cautiously. This early in the tournament, he said, “everyone’s mostly sitting on their hands, waiting for someone to make a mistake. Chris is very stoic. He’ll wait as long as he has to. He’s watching the other players.”
“They’re watching him, too?”
Rodriguez pursed his lips and shook his head slightly, as if to say the effort would be pointless. “He’s like a robot,” he said. “You get nothing.”
As it happened, the afternoon went poorly for Ferguson. Almost two hours in, he had lost nearly half his chips. His expression remained flat. He lifted his hat a few times and scratched his head. Three times in a row he was raised out of a pot. Much of the time, his cards had been good enough to get him into the hand but not sufficient to allow him to stay. He called a ten-thousand-dollar bet and lost. Finally, he shoved all his chips toward the center of the table, showed his cards, and was out. He shook hands with the other players and wished them well, reminding me of something his father had said: “One of the nice things about Chris growing up and playing games is he didn’t mind losing. Most kids I play with are scared of losing. He knows that losing, you learn something.” I asked Chris if losing bothered him, and he said it only really upset him if he lost as the result of a mistake. Anyway, he said, thinking you would win all the time at poker was unrealistic.
FERGUSON AND I went to dinner at a Mexican restaurant at the Palms. The restaurant didn’t have a table ready. The hostess gave us a beeper, so that we could wander around the casino. Ferguson was tired and wanted to sit down. The first chair we found was in front of a row of video poker machines. I put a dollar in the machine.
“This is something I never do,” Ferguson said. The machine offered several games. “The only one I know the optimal strategy for is Jacks or Better.”
“Play that,” I said.
“They don’t have it,” he said. He chose one called Super Double Double, the closest he could find to Jacks or Better, and five cards appeared on the screen. He played quickly, hitting a button to hold or to draw cards.
A pair of tens arrived. “This is a really bad hand,” he said, and drew three more cards, none of which improved it. He talked as he played. “I’m trying to figure out whether to hold ace-queen, to the two fours, because the payout is different,” he said. And, “Here’s what I’m thinking: pair of queens and the sevens. I’m throwing away the sevens—I don’t think there’s any question about it.” And, “What’s the payoff to me if I just held the kings? There’s a chance I get another king about one-eighth of the time. There’s a chance I get four kings; I’m guessing that’s an additional eighth unit toward the payout—I’m up to three-eighths. I need to get up to a half.”
The red light on our beeper began flashing. Two nines appeared. Ferguson discarded the three other cards, and in the draw he got two more nines. At the cashier’s cage, I collected fourteen dollars and applied it to the dinner.
35.
Mathematics being the same everywhere means that one does not have to study Arabic math or Chinese math or Canadian math. Math isn’t balkanized. If you are of the correct temperament or talent or intellect, mathematics in its higher ranges is about the intellectual reach of humanity and the contents of your own thinking.
Sometimes I didn’t understand what I was doing, but I could do it anyway. This was the case with radians, which, like degrees, are a means of measuring angles. A 360-degree angle is a 2pi radian angle. Figuring the ratios of circles according to their radians, I felt as I did the work, flawlessly as it turned out for a change, that I understood nothing of the concepts I was enacting. The task, I suppose, is not that difficult, but I almost never understood how I had reached the answer, except to say that the formulas had provided it.
Occasionally I would come to something that I remembered partially from childhood, such as tangents and their relationship to a circle, and I would have a sinking feeling, recalling how difficult the subject had been, but also wondering if I would understand it now and would I understand why I hadn’t been able to learn it before. Having approached it more deliberately this time, I expected to do better. This wasn’t always the case. At times, when problems got difficult, and I failed one after another, I felt as if I’d been left at a senior center and given a textbook of problems to pass my day, because the attendants had been told I enjoyed math. Something had happened to my powers of reasoning, though, and I couldn’t solve the problems anymore.
I end up talking back to books. That’s impossible, that’s stupid. You’re wrong. You made a mistake, idiot book.
IN Mathematics: A Very Short Introduction, by Timothy Gowers, I encounter the notion that to succeed at math “one should learn to think abstractly, because by doing so many philosophical difficulties simply disappear.” I hadn’t considered that besides the practical difficulties I was having, I was also having philosophical ones. Learning to become less rigid in my thinking with math was like submitting to the charm of the books I argued with. I did my best to submit to math’s charm, but I didn’t always think it was charming. Doing math sometimes felt like playing with a dog that bites.
THE COMPLICATED STRUCTURES of mathematics can be explained the way any other work of art can be explained, except that understanding mathematics requires more learning than most of us possess. I can understand the outline of what Amie does, sort of, but if I turn the pages of, say, “The Cohomological Equation for Partially Hyperbolic Diffeomorphisms,” which is among her more cited papers, I cannot grasp any of its assertions. At best, I recognize a few symbols. Another of her papers is called “Stably Ergodic Approximation: Two Examples.” I consistently misread this as “Sadly Ergodic Approximation,” which sounds like the title of a piece of music by Frank Zappa.
Someone to whom a theorem has been explained, depending on its complexity, might feel like someone who has learned to play a complicated piece of music and now understands its design. He or she might appreciate the way certain passages are formed, the logic applied, the rules of harmony engaged or acted against. This is a satisfaction of art, of being made aware of deeper relationships than the ones that are plain on a first encounter. You have completed a task. You can play that piece of music now. You can try to play other pieces based on its logic and the technique you acquired in learning it. You have broadened yourself, your abilities, perhaps your capacity for wonder, expanded your life list. You have seen something of the design that the world suggests. Ever elusive. Ever hovering at the edges of sight, of apprehension. Such awareness is consoling. It finds for us a place in the world. A standpoint from which another horizon is always in view.