Mathematician Ralph Abraham once said of non-ordinary states of consciousness: “Any models that we can build, verbal, visual, or mathematical, are feeble compared to the experience itself. On the other hand, this experience is within all, […] so the tiniest resonance from the feeblest model may suffice to excite, as poetry excites emotion, spirit. The essence of communication is to have a compact representation of an experience that’s infinitely complex. […] Representations restricted to verbal mode alone might be too feeble to excite by resonance, the similar state.”1 It is inspired by these words that I now set out to achieve an ambitious goal: that of finding and conveying a simple, coherent, and holistic representation of personal experiences that have been formidably complex and nuanced. And this representation must not be grounded on language, as the discussions of the previous chapters have been, but must instead add a new and synthesizing perspective to our story.
The tool we will use is mathematics. But fear not: there will be no equations or complex notations whatsoever. All I will use to elicit your intuition are pretty pictures, which happen to be mathematically generated. Nonetheless, if you are really uncomfortable with any kind of formal thinking at all, you may skip this chapter, for it adds no new information to what has already been discussed. It is simply an attempt to consolidate and further illustrate previously introduced ideas. On the other hand, for those of you whose minds resonate with formal logic, the discussion that follows provides an integrative perspective, in the framework of which many ideas will come together. It will also allow us to study, by means of computer simulations of a toy dreamed-up reality, some of the implications of the ideas discussed in the preceding chapters. For those eager to dive into all the mathematical details, I provide further information in the appendix.
At this point, an important disclaimer should be made. It may be tempting to interpret the upcoming pages as an attempt by me to model reality according to an outlandish and unsubstantiated set of premises. No, I am not that naïvely ambitious. My intent is solely to construct a metaphor of my own interpretation of the subjective experiences I underwent, in the hope of communicating that interpretation with clarity and of deriving some of its implications. The difference between these two things is crucial: while a model of reality starts from objective observations of facts, seeking to articulate these observations in a framework of cause and effect, the metaphor I seek starts from my own intuitions. What you will find in the pages that follow is an exfoliation of ideas, not a model of facts. After all, this is not a book with a thesis. Moreover, as any metaphor, the one described in the coming paragraphs is not perfect: while most of its elements accurately correspond to my intuitions, others do not and may even contradict aspects of those intuitions.
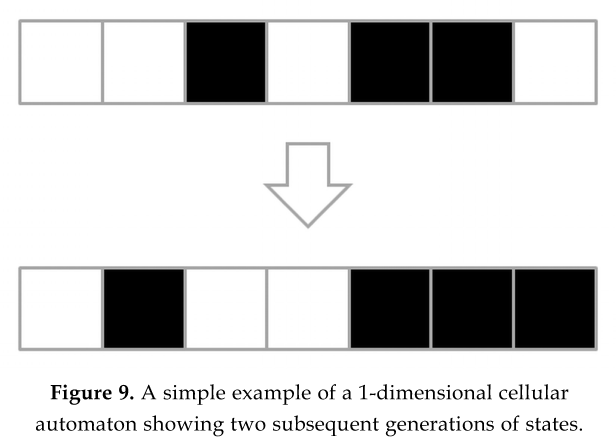
Before we get started, we need to lay some simple foundations and terminology so you will be able to interpret the upcoming pictures. The first term we need to get acquainted with is “cellular automaton,” a mathematical construct well studied over the past several decades.2 Though the name “cellular automaton” may sound intimidating, there is actually nothing complicated about the idea. In fact, Figure 9 is an example of a simple cellular automaton. For now, look only at the upper row of squares in the figure. Each square is called a “cell.” The cellular automaton is the set of all seven cells shown in Figure 9. Each cell may be either black or white. We say that a cell can have one of two different “states” at any moment in time: black or white. Many authors prefer the more dramatic terminology “alive” or “dead” for the two possible states of a cell. That is fine too.

Each cell has two neighboring cells: one to the left and the other to the right. Together, the cell and its neighbors form a “neighborhood.” Clearly, each cell has its own neighborhood and the neighborhoods of different cells partially overlap. We assume that the topology of the cellular automaton is a ring. This way, the left neighbor of the leftmost cell is the rightmost cell. Similarly, the right neighbor of the rightmost cell is the leftmost cell. In other words, the row of cells “wraps around” forming a closed ring, though that is not shown in Figure 9. There, instead, the ring is shown “cut” and “stretched open” for ease of depiction. Because the cellular automaton contains a single row of cells – that is, a single dimension (left-right) – we say that it is a 1-dimensional automaton.
Now, the key point is this: the state of each cell in the cellular automaton changes over time, depending on its own current state and the current states of its neighbors. In other words, the next state of each cell depends on the current configuration of states in the cell’s own neighborhood. It is this that renders cellular automata useful tools for studying dynamical systems. In fact, it has been suggested by scientists that the universe itself may operate like a cellular automaton of cosmic proportions.3 On a more practical scale, cellular automata have been successfully used for modeling a variety of physical systems.4 Clearly, thus, cellular automata are good vehicles for a metaphor of reality, which is what we are attempting to construct.
The set of all cell states in the automaton at a given moment in time is called a “generation.” The way the state of the cells changes from one generation to the next, over time, is determined by a so-called “state transition rule.” The state transition rule must specify the next state of a cell depending on the current configuration of states in the cell’s neighborhood. Here is a simple example of a state transition rule: the next state of each cell becomes black (alive) if the current state of exactly one of the cell’s respective two neighbors is black; in all other cases, it becomes white (dead). In Figure 9, the lower row of cells shows the new generation of the cellular automaton when exactly this state transition rule is applied to the generation represented in the upper row. Have a look and check it for yourself, so you get some intuition about how cellular automata work. Do not forget: what you see is actually a ring cut open, so all cells have two neighbors.
This may all be sounding very abstract to you at this point. But bear with me a little longer, for the purpose and usefulness of all this is going to become clear shortly. The path we will be pursuing is, first, to port the intuitions of subjective exploration onto the framework of cellular automata. Then we will simulate the evolution of these automata on a computer, thereby generating the promised pretty pictures, to see what it tells us about the implications of those intuitions.
As mentioned earlier, the cellular automaton in Figure 9 has a single dimension (left-right). However, we could add an extra dimension by stacking the representations of subsequent generations on top of each other. For instance, in Figure 9, by stacking the rows corresponding to each of the two consecutive generations on top of one another, we add the dimension of time to the automaton (past-future). We will come back to this point later on. For now, let us look at the possibility of adding an extra dimension of space to the automaton, as opposed to a dimension of time.
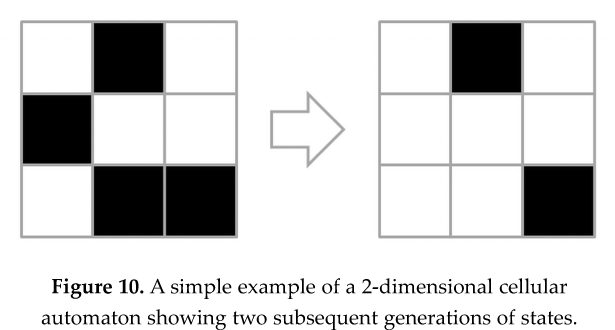
Figure 10 illustrates a 2-dimensional automaton where, in addition to the left-right dimension, a top-down dimension is added. So now, instead of a row, the cellular automaton entails a three by three array of cells, each cell being either dead (white) or alive (black). The same, simple state transition rule discussed above is applied to produce the next generation of the automaton: from the generation on the left to the generation on the right of Figure 10, a cell becomes or stays alive if, and only if, exactly one of its neighbors is alive. Notice that each cell has now four neighbors: to the left, right, up, and down. Diagonally adjacent cells, in this case, do not count as neighbors. Notice also that, again, we assume that the cellular automaton “wraps around” in both directions. In other words, the upper neighbor of a cell in the top row is the cell occupying the same column but in the bottom row. Similarly, the left neighbor of a cell in the first (leftmost) column is the cell occupying the same row but in the last (rightmost) column. Technically, the topology of such automaton is said to be “toroidal;” that is, doughnut-shaped. The representation in Figure 10 basically corresponds to the doughnut being “cut open” and “unwrapped” to form a flat square.
As the states of the automaton change from one generation to the next, new configurations of black and white cells in the 2-dimensional array are produced. Each of these generations thus corresponds to a frame in a kind of black & white movie, each cell corresponding to a pixel in the respective movie frames. By displaying the frames in rapid succession, one can actually see an animation of the evolution of the cellular automaton’s states. Artists have used this possibility to amazing effect, simulating not only physical phenomena but the appearance of life itself.5 The result is that we are now dealing with a total of three dimensions – two in space and one in time – namely: left-right, top-down, and past-future. However, since a book page has only two dimensions, it becomes now impossible to display all these successive generations in a single picture. Instead, we will need to show them side by side, as separate frames.
Our ordinary experience is that we live in a 4-dimensional world with three dimensions of space (left-right, up-down, back-forth) and one of time (past-future). When I suggested that the Source unfolded in a hyper-dimensional realm, the implication was that such realm would need to span more than the four dimensions mentioned, which is impossible to represent graphically. Therefore, inspired by Prof. Abraham, we will use a dramatic simplification: we will attempt to represent the unfolding of the Source in only two dimensions, so the representation can be printed on a page of this book. To do that, we will use a 2-dimensional cellular automaton, like that illustrated in Figure 10, but with a more sophisticated state transition rule.
In the 2-dimensional cellular automaton under consideration, each cell has four neighbors. Therefore, each neighborhood comprises five cells: the center cell and the four cells orthogonally adjacent to it (technically, this is called a “von Neumann neighborhood of range 1”). Since each of these five cells can assume one of two possible states (alive or dead), there are 25 = 32 different possible state configurations in a neighborhood. Therefore, the state transition rule must determine, for each of these thirty-two possibilities, whether the center cell goes dead (white) or alive (black) in the subsequent generation.
Let us now start building the metaphor itself. Each of these thirty-two possibilities corresponds to a pattern both in space (that is, the current configuration of black and white cells in the neighborhood) and in time (the implied color of the neighborhood’s center cell in the next generation). A key intuition about the unfolding of the Source was its radial symmetry; that is, the idea that the unfolding Pattern would not change when subjected to a rotation. For instance, a square is symmetric to rotations of 90 degrees, in that if you rotate a square by 90 degrees you get the same square again. Let us thus require the same kind of symmetry of our 32 possible neighborhood patterns: let us require that the state transition rule be such that all 90-degree rotations of a given neighborhood pattern lead to the same next state for the neighborhood’s center cell. With this requirement, we just need to specify the state transition rule for the twelve neighborhood patterns shown in Figure 11. All other possible neighborhood patterns can be derived by 90-degree rotations of the ones shown. Therefore, since the state transition rule must specify the next state of the center cell for each of these twelve patterns, we have 212 = 4,096 possible state transition rules.

In the days immediately following the third experiment, for some reason unclear to me, I felt compelled to experiment with some of these 4,096 different possibilities and investigate the evolution of the corresponding cellular automata. I did not know what I was looking for until I stumbled upon one particular state transition rule. Never mind this mild unlikelihood. The particular rule I stumbled upon is illustrated in Figure 11 by means of the cell pointed to by the arrow below each of the twelve patterns shown. The color of that cell represents the next state of the center cell given the corresponding neighborhood pattern. This way, the state transition rule shown in Figure 11 may read as follows (from the left-upper corner to the lower-right corner): if the center cell is dead and all its four neighbors are dead, the center cell remains dead; if the center cell is alive and all its four neighbors are dead, the center cell remains alive; if the center cell is dead but a single one of its four neighbors is alive, then the center cell goes alive; … if the center cell is alive and all its four neighbors are also alive, the center cell remains alive. Notice that each and every cell in the cellular automaton is the center cell of its respective neighborhood – different neighborhoods partially overlapping – so the state transition rule fully specifies how the state of each cell evolves over time.
Okay, if you have followed it up until this point, it is downhill from here. What I now did was to define a cellular automaton in the form of a square array wherein the number of rows and columns was a power of two plus one cells (for instance, 28 + 1 = 257 cells). As I found out later, the effect described below works only in case the array is defined this way; another mild unlike-lihood. I initially set all cells in the array as dead (white), except the one cell at the very center of the array, which I initially set as alive (black). Thereafter, I recursively applied the state transition rule illustrated in Figure 11. What then happened was amazing.
In Figure 12, a few frames of the evolution of the resulting cellular automaton are shown. Each frame corresponds to a generation of the automaton, from the 32nd to the 512th generation, at intervals of thirty-two generations. As it can be seen in the figure, the single live cell at the center of the array begins to unfold fractally into an amazing, composite, triangular-themed Pattern. The static frames in Figure 12 do not capture the amazing dynamics one sees when watching an animation of the cellular automaton in action. As this composite, unfolding Pattern reaches the boundaries of the array, it folds back onto itself. The edges of the unfolding Pattern proceed towards the center of the array without interfering with the outgoing segments of itself, as if moving in a hyper-dimensional plane that is actually not part of the cellular automaton algorithm at all. The effect is extraordinary and profoundly counterintuitive from a mathematical perspective.
As the evolution of the automaton continues, the now incoming and outgoing segments of the unfolding Pattern conflate into new and surprising fractal rearrangements. New form is created everywhere in the array, with surprising harmony and coherence. Though the basic triangular theme persists throughout, triangular arrangements with different configurations blossom out of other triangular arrangements at various points of the array, in a seemingly continuous rebirthing of new shapes out of prior shapes. Eventually, as we can see when comparing the 8th and 16th frames shown in Figure 12, the evolution of the automaton returns to a previous configuration and then starts repeating itself in a cycle. This way, the automaton never stops. It continues on in an open-ended rebirthing of fractal form; a perpetual, continuous, and recursive morphogenesis that requires nothing from the outside. As far as the automaton is concerned, there might just as well be no outside. It is entirely self-sufficient in its potential for creation. Indeed, all of what is seen in Figure 12 is simply the result of the recursive application of the basic rules shown in Figure 11 to a single live cell at the center of a 2-dimensional array. Nothing more. No intervention is required once the system is set in motion. However, although the fractal never stops unfolding, novelty is limited: no truly new forms can be produced beyond the point when the cycle starts repeating itself.

This is the metaphor I sought for the Source. The neighborhood patterns of Figure 11 are a metaphor for the elemental thought patterns underlying reality. The single live cell at the center of the array is a metaphor for the elusive home of the Source and its initial creative impetus. By recursively applying the elemental thought patterns to Itself, the Source unfolds into an endless, hyper-dimensional creation of a higher-level, composite thought Pattern wherein the dynamics of the entire creation are completely encoded in the original, elemental thought patterns themselves. In the composite, unfolding thought Pattern represented in Figure 12, the original forms of the elemental thought patterns of Figure 11 are dispersed. For any mathematically naïve observer watching the evolution of the unfolding Pattern in Figure 12, it would be nearly impossible to infer that the elemental thought patterns of Figure 11 were actually the underlying reality of everything he or she was observing; that there was nothing more to what is seen in Figure 12 than the recursive application, or the unfolding, of the space-time patterns of Figure 11.
The fractal nature of the unfolding Pattern can be more clearly seen in Figure 13, which is a higher resolution version of the fourth frame shown in Figure 12. At multiple levels, the arrangements of triangles repeat themselves self-similarly. This way, a version of the entire unfolding Pattern can be seen in smaller parts of itself. Different segments of the unfolding Pattern can be seen repeated again and again, at different magnifications and orientations, without ever breaking the harmonious symmetry of the whole. It may be worthwhile that you spend some time observing Figure 13 to clearly see what I mean here. That figure alone is fertile ground for many discoveries, if you know how to look. Intuitively, it may feel like a wonder that all the complexity and sophistication seen in Figure 13 are but a composite reflection, or an amalgamation in space and time, of the simple patterns shown in Figure 11. Notice also that, just like the elemental thought patterns in Figure 11, the entire unfolding Pattern shown in Figure 13 remains exactly the same if rotated by 90 degrees. This is like a fractal resonance of characteristics of the elemental thought patterns on their own compound manifestation, but at a higher level of complexity.

The coherence of the unfolding Pattern depends on the strict application of the state transition rule represented in Figure 11 to all cells of the cellular automaton array. Any disruption in this process breaks its coherence and eventually leads to a total breakdown of the unfolding Pattern. Indeed, in Figure 14 the same cellular automaton evolution of Figure 12 is displayed, but this time a single cell (out of 66,049) at the center of the left-upper quadrant of the array has been fixed at a dead state, regardless of the application of the state transition rule. In other words, a single cell is stuck in “white,” while the other 66,048 operate normally. The result of this minimal disruption is seen starting from the 5th frame shown in Figure 14. Notice that, eventually, that small disruption causes the entire unfolding Pattern to collapse into chaos and entropy. Instead of forever repeating itself in a regular, predictable, fractal manner, the unfolding Pattern dissolves into unpredictable, non-repeating noise.
But my intuition was that the Source continuously unfolds in perfect regularity. It never breaks down into irregular, chaotic behavior. Therefore, given that chaos – that is, unpredictable irregularities – seems to be a prerequisite for novelty, there must be another way in our present metaphor to represent how novelty is continuously created.

And indeed there is. The way to do it can be derived from the following observation: chaos, disorder, and entropy can be attested to be facts only of manifested reality. The intuition of the underlying reality of nature, according at least to my own experiences, does not encompass chaos. Much to the contrary: the realm of the Source seems to be the ultimate embodiment of perfect order and structure. So it is not in the plane of the Source, represented in Figures 12 and 13, that we should look for chaos. Instead, it is in another plane – that of manifested reality – that we should expect to find it. And then, somehow, the perfect order of the Source must transmute into a fertile ground for novelty when projected at that plane of manifestation.
How do we bring a plane of manifested reality into our cellular automaton metaphor? The first thing to consider is that, from the experiences of subjective exploration, it appears that the world of consensus reality is a lower-dimensional world than the plane of the Source. So this should be reflected in our metaphor. Given that our representation of the plane of the Source has used two dimensions of space, we are left with only one alternative: to represent the plane of manifested reality with a single dimension of space. That brings us back to a 1-dimensional cellular automaton structure like that illustrated in Figure 9.
However, the state transition rule of this 1-dimensional automaton should be better thought out now. A key intuition from subjective exploration has been that consensus reality is a kind of amalgamation, or constrained synchronization, of the images projected by different consciousnesses onto a shared fabric of space-time. We can capture this idea in the state transition rule of the 1-dimensional automaton in a relatively simple way: we can have each cell obey its own, private state transition rule. In other words, each cell now seeks to determine how its own state should change over time, in a idiosyncratic manner. As a metaphor for the freewill of each cell, we can randomly initialize their corresponding state transition rules. Each cell, with its own, private, randomly initialized state transition rule then becomes a metaphor for an independent, individual consciousness capable of freewill. What we now have to add to the scheme is the idea that manifested reality is somehow synchronized across different consciousnesses.
To represent that, we can do the following: let us imagine that the individual state transition rule of a cell not only influences how its own state changes, but also how the states of its two neighbors change. In other words, let us imagine that the freewill of a cell is projected out onto what happens to its neighbors, according to the worldview – that is, the state transition rule – of that cell. For instance, if a cell “looks around” and finds its two neighbors to be black while the cell itself is white, its free-willed worldview may dictate that it should turn black in the next generation. But it then also tries to project its own worldview onto its neighbors, by “expecting” that both neighboring cells will also turn black when they are white and their respective neighbors are black. Its neighbors will be doing the same thing: each will be trying to determine its own future state according to its respective, free-willed worldview – that is, its private state transition rule – and projecting that worldview onto its neighbors. So which worldview wins for which cell? The intuition from subject exploration is that this synchronization of different worldviews is the mechanism by means of which a common, shared reality emerges.
While we need to keep our metaphor simple, we do not want to oversimplify it to the point where it becomes trivial. So let us do as follows. There are three different causal influences in determining the next state of each cell: the worldview of the cell itself and those of its two neighbors. Let us say that the worldview of a cell has twice the weight of those of its neighbors in determining the cell’s own next state. This is a metaphor for the fact that force fields in our universe are stronger over shorter distances. So we basically have three “voters:” one of them (the cell itself) casting two identical “votes” and the other two (the cell’s neighbors) each casting a single vote. Since the next state of the cell can only be black or white, each vote can be either for black or for white. A majority-rule is the obvious way to decide which state actually manifests from the projected worldviews of the three cells involved. For instance, if three or four of the votes are for “black,” the cell becomes black in the next generation; analogously for “white.” However, in case of a tie – that is, when both neighbors vote for one state while the cell itself votes for the opposite state, resulting in a two-two vote – the next state is then determined by a “cross-dimensional influence” from the Source, as will be described below. This determination of an element of manifested reality from outside the system, when no favored direction is consciously chosen from within the system, can be seen as a metaphor for the quantum chance underlying nature.
We are almost there. Only two extra elements are now missing from our metaphor of manifested reality. Bear with me a little longer.
When we say that a cell only looks at itself and its two neighbors to form its image of what should happen next in its immediate surroundings, this works as a metaphor for the fact that our own perception of reality is limited to our immediate vicinity. After all, we can only see, hear, or otherwise perceive that which is near to us. Our five senses are local by their very nature. However, when we limit the “range of perception” of a cell solely to itself and its two neighbors, all of which have randomized state transition rules, the result is absolute disorder. Each cell tries to project its own random worldview around itself. Its neighbors do the same thing. Although the majority view wins, all contributors to that view act randomly, so the end result is also pure randomness.
That is not quite how our own consensus reality seems to work. Although we do live in a world of entropy and disorder, that world also has elements of order and structure: crystals and living organisms, for example. In fact, it seems that it is precisely those regular and structured elements that seem to give meaning to the dance of manifested existence, for pure randomness is meaningless. To capture this in our metaphor, we need to link up the 1-dimensional plane of manifested reality to the 2-dimensional plane of the unfolding Pattern. In other words, we need to extend the range of perception of each cell – each cell being a metaphor for a free-willed conscious entity – to a projection of the Source. In our metaphor, it must be the unfolding regularity of the Source that injects order and structure into what would otherwise be an entirely meaningless plane of manifestation. Similarly, it must be the potential disorder of the plane of manifestation – originating from the free-willed and independent worldviews of its cells – that introduces novelty in the hierarchy of all planes.
To operationalize these concepts, let us look at Figure 15. Two planes are shown: that of manifested reality on top and, below, a plane containing a 1-dimensional projection of the unfolding Pattern illustrated in Figure 12. There are many different ways we could define such a projection, but the simplest is to simply take a single row or column from the unfolding Pattern. That is indeed what I did, and I arbitrarily chose a row half way between the center of the array and its boundary. Since the evolution of the unfolding Pattern seems to flow cyclically across all rows and columns anyway, an arbitrary choice here is reasonable. Both planes illustrated in Figure 15 comprise a single row of cells. The other rows of cells drawn in the background, with dashed lines, represent the previous generations of states of these cells as such states evolved over time, according to the arrow of time shown.
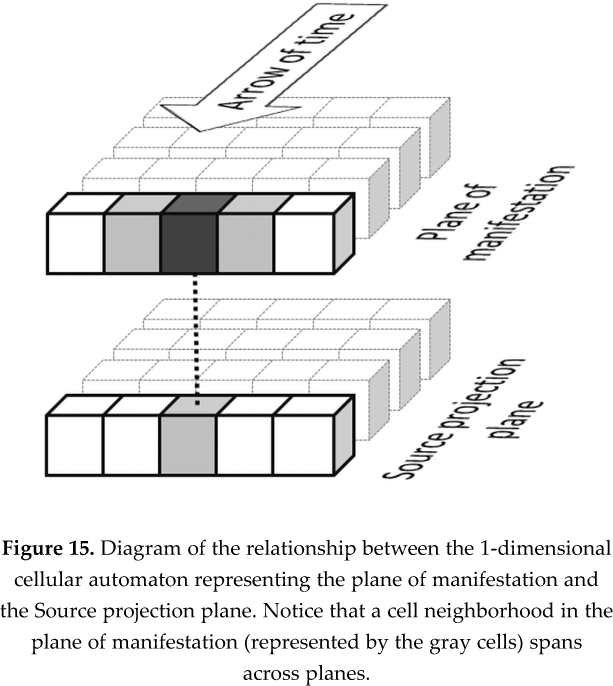
In the plane of manifestation shown in Figure 15, a cell is represented in dark grey. This cell is just a reference cell: the entire discussion that follows applies equally to all other cells in that plane. In lighter grey, the reference cell’s two neighbors are shown. But now the corresponding cell in the underlying Source projection plane – it too represented in lighter gray – is also made part of the reference cell’s neighborhood. In other words, the range of perception of the free-willed conscious entity represented by the reference cell now extends beyond its immediate vicinity in the plane of manifestation and into the underlying Source projection plane. In our metaphor, this perception by the reference cell of a corresponding cell in the Source projection plane could be seen as a kind of cross-dimensional, perhaps subconscious, extra-sensorial perception – or intuition. In addition, and as briefly mentioned earlier, we also do the following: not only will each neighborhood cross-dimensionally encompass a cell from the Source projection plane; in case of a tied vote, the next state of this cell will also determine the reference cell’s next state. In our metaphor, this would correspond to a structured, patterned control of the “row of the quantum dice” when the conscious entities in the plane of manifestation are unable to make an unambiguous choice about which reality should manifest.
Let us now elaborate on the last element we need in our metaphor, before we run the resulting simulations and interpret the images produced. This last, missing element is learning. As we have seen, each cell in the plane of manifestation of Figure 15 operates in the following way: first, it looks at its own current state, the current states of its two neighboring cells, and the current state of the corresponding cell in the Source projection plane; then, on the basis of these observations and of its own, initially random worldview – that is, its state transition rule – it determines what its next state should be and projects that determination not only at itself, but also at its two neighbors. Since each neighbor will be doing the same thing, the next state of each cell is determined by the “majority vote” across the three different expectations of reality being projected onto the position of that cell, the cell’s own expectation having twice the weight of those of its neighbors. If the vote is tied, the cell’s next state is then determined entirely by the Source projection plane. What we will now do is the following: once the winning cell states emerge out of this “voting” system, each cell observes what actually happened to itself and its neighbors in the plane of manifestation. In other words, each cell compares the expectations it projected onto its surroundings to the reality that actually manifested. It may then find that what actually happened is not what it had expected to happen. And here is the crucial point: upon this realization, we program the cell to learn from what actually manifested. In other words, each cell adapts its own state transition rule to make it consistent with the cell states actually taken on by itself and its neighbors after the “voting.” This way, the initially random state transition rules change over time, conforming to the local reality observed by the respective cells. With this learning, each cell will adjust its own expectations, cognition models, or worldviews – all equivalent words in the context of our metaphor – in accordance with their supposedly objective observations of manifested reality.
Now we are done. All that is left is to actually run the simulations, look at the results, and interpret their implications in the framework of our metaphor.
Figure 16 is divided vertically into three columns. The leftmost column is a top-view of the state evolution of the “plane of manifestation,” as explained in Figure 15. The middle column is a top-view of the state evolution of the “Source projection plane,” also explained in Figure 15. Finally, the rightmost column shows, through different shades of grey, the differences between the worldviews – that is, state transition rules – of the different cells in the “plane of manifestation.” Each worldview is represented by a different shade of grey. In all three cases, the arrow of time points down; that is, each row of the plane of manifestation and the Source projection plane shows the corresponding cell states at a given moment in time. Analogously, each row of the rightmost column codes, with a shade of grey, the state transition rule of each cell of the plane of manifestation at a given moment in time. The idea of the rightmost column is to show how the relative differences between the state transition rules of different cells evolve over time. In other words, the idea is to show how, through learning in a shared reality, the initially random state transition rules slowly converge to a common, shared worldview – as represented by the decreasing number of different shades of grey as time goes by.

Let us look at Figure 16 in more detail. We start the simulation at the top. Initially, in the plane of manifestation, a single cell is alive (black) at the center of the corresponding cellular automaton row. All cells are initialized with random state transition rules. Interestingly, as time goes by, black-filled triangular patterns begin to evolve in the fabric of manifested space-time. These triangular patterns are an echo of the triangular fractals that concurrently evolve in the Source projection plane. Indeed, although the middle column of Figure 16 is merely a 1-dimensional projection of the unfolding Pattern shown in Figure 12, its fractal characteristics are preserved in that projection.
Notice that, although the triangular patterns evolving in the Source projection plane are regular, orderly, and repetitive, their triangular echoes in the plane of manifestation occur at seemingly random locations in both space and time. They also have seemingly random sizes. Finally, and perhaps most importantly, they are not repetitive. There is unpredictability and novelty in the plane of manifestation. On the other hand, there also clearly is structure in the plane of manifestation. It is not purely random and chaotic. This shows that the influence of the Source projection plane in the state evolution of the plane of manifestation is decisive: it introduces structure and meaning where there would have been none. Notice also that, from the point of view of individual cells in the plane of manifestation, the influence exerted in it by the fractal structures of the Source projection plane seems to be non-local. Indeed, the large triangular patterns evolving in the Source projection plane instantaneously affect cells in the plane of manifestation that are far from one another in space. From the point of view of an observer restricted to the plane of manifestation, the correlations entailed would seem to contradict local realism. Notice also that this nonlocal influence crossing the boundaries of planes is fractal in nature: the same influences may take place at multiple scales of the plane of manifestation, from the microscopic to the macroscopic. The microscopic metaphor would correspond to small fractal triangles in the Source projection plane influencing adjacent cells in the plane of manifestation. The macroscopic metaphor, on the other hand, would correspond to large fractal triangles in the Source projection plane instantaneously influencing cells far from one another in the plane of manifestation. In both cases, the cross-dimensional influence would take on the same pattern: a triangle. As above, so below. The effects of the correlations entailed by the patterns in the Source projection plane would be felt in the plane of manifestation as a kind of Jungian synchronicity6 – that is, as unexplained “coincidences” – transcending causality.
Notice, in the rightmost column of Figure 16, that initially many different state transition rules – that is, worldviews – are concurrently operating in the plane of manifestation. This is represented by the many shades of grey initially present. Very quickly, however, starting at a point around the middle of the array where there is maximum entropy – that is, variability – of states in the plane of manifestation, the cells start learning. The higher the entropy of states in the plane of manifestation – that is, the more oscillation between black and white states there is – the more different situations the cells experience, thereby adjusting their respective state transition rules accordingly. As that happens, the cells quickly converge to common, shared worldviews. As it can easily be seen in Figure 16, after only a few generations only two different worldviews survive, as represented by the two remaining shades of grey.
Cells immersed in their own worldview – that is, cells surrounded by other cells that have the exact same state transition rule – find complete consistency between their own expectations and what actually manifests. Therefore, they stop learning and their worldview stays stable. In the rightmost column of Figure 16, two clearly defined regions can be seen, each with its own, dominating worldview. Only at the boundaries between these regions can learning take place. It is the dialectic tension between conflicting worldviews that leads to the adaptation of cognitive models. Of the two dominating world-views seen, the one represented by the darker shade of grey clearly wins ground over the other as time goes by. The consequence of this in the plane of manifestation is clearly visible: triangles with more strongly defined edges emerge in the regions where the stronger worldview gains ground.
Perhaps this metaphor can give us some insight into the dynamics of our modern world. In Figure 16, two worldviews survive because communication between adepts of different worldviews can only happen locally. Imagine how quickly these different worldviews would converge to a single, uniform one, if communication could take place remotely, over long distances and bypassing entire regions of space, like what has been possible in our society with technologies like radio, television, and the Internet. In almost no time would the entire world cognize reality in exactly the same way, expecting the exact same things, and the reality manifested in their surroundings would consistently reinforce these expectations. Instead of the clear differences in the plane of manifestation seen in Figure 16, all manifestation would be consistent with one and the same set of state transition rules.
As a matter of fact, a state transition rule is analogous to the laws of physics. One state transition rule corresponds to one coherent and internally consistent “physics,” so to say. If the physics of our universe could be boiled down to a single equation – that is, one “theory of everything” – then that one equation would correspond to a state transition rule in our metaphor. Indeed, when physicists attempt to model our physics with cellular automata, this is the correspondence they use. Therefore, Figure 16 tells us that, because of learning in a shared playing field of experience, what had initially been multiple and contradictory physics, operating concurrently at different points of the plane of manifestation, quickly converges to only two different physics. “Magic” in such a world can only happen at the boundaries of the regions dominated by each respective physics. After all, the phenomena occurring at these boundaries may contradict the cognitive models and expectations of the cells on either side of the boundary.
As time goes by, due to the continuing sharing of experiences and learning, one of the remaining worldviews progressively gains ground over the other, until it alone survives. This is illustrated in Figure 17, which shows the same array evolution of Figure 16 but at a later period of time. Here, the simulation clearly illustrates the power of shared experiences in driving an entire culture to give credit to a single worldview, even though reality itself is equally amenable to the idiosyncrasies of an arbitrary variety of worldviews. Once this convergence to a single physics is complete, magic disappears from the world of manifestation. All cognitive models and expectations – that is, all state transition rules – are harmonized, consistent with one another and with the reality that actually manifests. At this point, the world of our metaphor becomes a world without mysteries; a world that, although entirely created and projected onto the fabric of space-time by the imaginations of its own inhabitants, behaves exactly as if manifested reality were objective and independent of the individuals’ participation in its making. Theirs becomes a world of science over dreams; of analysis over creativity. Their reality becomes, quite literally, consensus reality.

But that is not all. Remember that the different physics – that is, the different state transition rules – represented in the rightmost column of figures 16 and 17 encompass both what happens in the plane of manifestation and in the Source projection plane. The respective cell neighborhoods span both planes, as shown in Figure 15. The inhabitants of such world, sub-consciously as it may be, are still connected and attuned to the subtle cross-dimensional influences of the Source, as represented by the vertical dotted line in Figure 15. Theirs is still a world of intuition and sensitivity. The very recognition that a single and supreme “theory of everything” governs their world is dependent upon the acknowledgement of these cross-dimensional influences. Without such acknowledgement, their scientists would not be able to see the consistency of the behavior of nature, for essential variables would be missing. There would be an appearance of contradiction where harmony actually is pervasive. Indeed, if their expectations of reality were based purely on what they perceive in the plane of manifestation, manifested reality would actually contradict their now over-constrained cognitive models.
What would happen if the inhabitants of such a world at some point decided to ignore and even deny the cross-dimensional, fractal influences of the Source projection plane in their reality? How would they then see their world? What expectations would they project onto the fabric of space-time and what manifested reality would then emerge? One wonders if the simulations of our metaphor could enrich our thoughts on these questions. So let us try it out.
I adapted the simulation so that, at a certain point in the evolution of the plane of manifestation, its cells simply stop looking at their counterparts in the Source projection plane. In other words, I modified the neighborhood shown in Figure 15 by removing from it the light-grey cell in the Source projection plane. This way, each cell of the plane of manifestation now only acknowledges, looks at, or otherwise perceives its two neighbors in the plane of manifestation itself. In our metaphor, this represents a materialistic denial of higher planes of reality and their influence in our lives; a “materialistic paradigm,” if you will. However, some influence from the Source remains: when the “vote” for determining a next cell state in the plane of manifestation is tied, it is still the corresponding cell state of the Source projection plane that makes the determination. So there is still influence from the Source exerted in the plane of manifestation. It operates as a kind of fractal bias – or tendency – in the underlying “quantum chance,” which percolates up to manifestation when no unambiguous conscious choice is made. In the metaphor, the conscious entities represented by the cells of the plane of manifestation – ignoring, as they now do, the Source – would acknowledge this influence merely as the expression of quantum randomness, remaining unaware, due to the lack of a sufficient number of data samples, that it actually embodies a subtle but structured pattern in space-time.
Figure 18 illustrates the results of the corresponding simulations. Approximately half way from the top, the cells in the plane of manifestation stop taking into account the cross-dimensional inputs from the Source. Surprisingly, the triangular theme survives this transition and remains in the plane of manifestation, albeit with a twist: what had been black-filled triangles up until that point turns into white-filled triangles. In a way, it is as though the very polarity of the plane of manifestation suddenly inverted. Triangles that before were filled with live cells are now filled with dead cells. Yet the balanced combination between structure and chaos survives the transition to this “materialistic paradigm” of cognition and beliefs. The resulting world remains one of novelty and meaning.

The explanation for this is as follows: although the cells of the plane of manifestation are no longer directly aware of the Source projection plane, they still learn – by adapting their respective state transition rules – from the states that actually manifest in their respective neighborhoods. Every time there is a tie in the conscious choice of a next cell state, that next cell state is then determined, as described earlier, by what happens in the Source projection plane. When the state so determined by the Source eventually manifests, the cells in the plane of manifestation learn that too. This way, their state transition rules end up learning and incorporating, indirectly and by bits and pieces, some of the fractal dynamics unfolding in the Source projection plane. In our metaphor, the conscious entities represented by the cells of the plane of manifestation are entirely unaware that their cognitive models are being indirectly influenced from another realm. They simply learn from what they see and then construct mental models that reflect their experiences. Eventually, through the sharing of experiences, they all converge to the exact same state transition rule. From this point on, there is never a tie in the conscious choice of a next cell state, for all cells are now projecting the same, consistent understanding of reality onto the fabric of space-time.
The rightmost column of Figure 18 now has a slightly different interpretation than in Figures 16 and 17. Instead of showing the spread of different state transition rules, it now illustrates the spread of apparent state transition rules, as construed from the point of view of an observer who ignores the existence of the Source projection plane. The apparent state transition rules are the rules implied by the observed state transitions when only the cells in the plane of manifestation are considered. In other words, they represent a pragmatic, empirical attempt to explain all state transitions as if such transitions were caused solely by what happens in the plane of manifestation. That is not how the automaton actually works before the switch to the materialistic paradigm, but simply how an observer confined to the plane of manifestation would have tentatively interpreted it to work. Such an observer would ignore the causal influence of the Source, seeking to empirically calibrate a model of state transitions on the basis of observations of the plane of manifestation alone.
Before the transition to the materialistic paradigm, one can see how dramatically such an explanatory approach would have failed to capture what is going on: multiple shades of grey are observed on the upper half of the rightmost column of Figure 18, indicating that many different and contradictory explanations of nature – or “theories of everything” – would be concurrently required. This variety of models would be necessary because certain causal elements of, or variables relevant to, what is going on are simply ignored. Therefore, the variability they entail must be captured in the structure of the explanation itself, leading to multiple and contradictory theories. Unsurprisingly, the variety of these “theories of everything” seems to increase along the main fractal contours of the unfolding Source projection pattern. In a world attuned to the Source, scientists would certainly not fail to realize that the materialistic paradigm would be an inappropriate explanation of manifested phenomena.
However, from the moment the transition to the materialistic paradigm takes place, things change very quickly. The apparent state transition rules now become equivalent to the actual state transition rules, since the cells of the plane of manifestation no longer take the Source projection plane into account in their respective neighborhoods. Notice that a single shade of grey takes over in the lower half of the rightmost column of Figure 18. This means that the cells very quickly adapt to the fact that the Source projection plane can no longer be perceived, coming up with an alternative worldview consistent with their now reduced cognitive abilities. There emerges a single “apparent” state transition rule representing one “theory of everything.” Although we have seen such convergence to a single physics happen before (see Figure 17), it is not obvious that it should happen again here. Indeed, this time the possible “theories of everything” have been arbitrarily constrained to the plane of manifestation, so their explanatory power is reduced. Yet, the materialistic assumption alone – that is, the assumption that all experiences must be explainable purely by what happens in the plane of manifestation – allows a single, arbitrarily constrained “theory of everything” to still coherently explain all manifested phenomena and take over the entire culture. The simulation dramatically illustrates the self-fulfilling power of the materialistic assumption: merely by expecting manifested reality to be explainable by what can be seen in a now reduced perceptual field, the cells project a new version of manifested reality onto the fabric of space-time that indeed can be explained this way. The simulation illustrates how learning in the context of shared experiences can easily lead to a manifested reality that behaves exactly as if it were objective and purely material, although such reality remains intrinsically subjective and hyper-dimensional. Materialistic scientists in such a world would be able to claim, with overwhelming empirical confirmation, that their purely materialistic models are sufficient to explain the manifested phenomena of nature in a causally-closed manner. Materialistic science would triumph in this world, even though its success would be a mere artifact of people’s free-willed choice to ignore subtle cross-dimensional inputs. The world these people live in, as an acquiescent mirror of their mental models and expectations, dutifully complies with the self-imposed limitations of their cognition.
Naturally, the idea that the entire population of the plane of manifestation would loose their intuitive connection with the Source is unreasonable. Unanimity is not an often observed phenomenon in our own world. Moreover, our simulations assume that cells in the plane of manifestation learn continuously and, other than the prejudice of ignoring the Source projection plane, without further biases. We know that is not how things normally work. Therefore, we could say that a more likely scenario, in the context of the metaphor, would be one where anomalies would remain: not all worldviews would be identical; not all manifestations would be consistent with the majority worldview. There would be cultural fringes in this more realistic metaphor. Some would claim to witness magic, psychic phenomena, fairies, UFOs, and the otherwise unexplainable. However, as our simulations suggest, these instances would likely be infrequent and ambiguous enough that they would not threaten the majority worldview.
Our metaphor, thus, has many-fold correspondences with the intuitions of subjective exploration, and even extends those intuitions beyond what we discussed in earlier chapters. It illustrates how a simple set of symmetric, elemental thought patterns in space-time (Figure 11) can produce, through recursion, an infinite unfolding of a composite, perfectly regular, fractal thought Pattern (Figures 12 and 13). It also shows that, if manifested reality is a lower-dimensional realm overlaid on a projection of the Source (Figure 15), then it is the cross-dimensional influence of the underlying Source that injects order and structure into the highly entropic and chaotic realm of manifestation. Indeed, it is through the subtle combination of disorder – generated by different conscious entities independently projecting their own free-willed expectations onto the fabric of manifested space-time – and order – injected cross-dimensionally into the realm of manifestation from the Source – that a structured but novelty-producing field of shared experience emerges (Figure 16). Moreover, through learning in the context of these shared experiences, those conscious entities tend to cluster and converge to common, shared worldviews, leading to the creation of a reality consistent with the assumption of objectivity (Figure 17). Finally, the metaphor informs us that a free-willed choice to deny and ignore the causal role of the Source inverts the polarity of manifested reality but does not destroy the delicate balance between entropy and structure. In this polarity-inverted version of manifested reality, a purely materialistic worldview correctly describes the phenomenology of manifested reality in a causally-closed manner (Figure 18), except perhaps for a few and far between anomalies.