I had not thought of making the very pretty use you make of Miss Leavitt’s discovery about the relation between period and absolute brightness.
—Henry Norris Russell, in a letter to Ejnar Hertzsprung
Hold a finger a couple inches from your nose and alternately blink from left eye to right. The finger rapidly changes position, and the farther you move it from your face the smaller the displacement becomes. The window frame on the wall shifts even less and the telephone pole down the block hardly at all. The separation between the eyes— astronomers and surveyors call it the baseline—is too small. We can sense the depth of the world close by, but the farther we look the flatter it appears. The distant mountains might as well be cut from cardboard.
Wired by nature to register this effect (remember it’s called parallax), the brain carries out a kind of neurological trigonometry. The two eyes and the object before them form a triangle, and you unconsciously compute the distance from base to apex. Without even thinking about it, you triangulate.
Get up now and walk from one side of the window frame to the other, a few feet away. The size of your baseline has increased, and now the telephone pole seems to shift against the building standing behind it. The effect is the same as having a very wide head, an eye at each side of the window looking out from two different angles. Measure the separation between the two observation points—the base of the imaginary triangle and the angles formed by each window and the pole. You can do this with a surveyor’s transit (think of it as a kind of protractor). With just this information and some high school trigonometry, you can calculate the altitude of the triangle—the distance to the telephone pole. The calculation itself needn’t concern us. Just know that the very nature of triangles ensures that they can be completely defined with only three scraps of information— two angles and one side or one angle and two sides. All the other dimensions follow from that.
With a wider baseline—an eye on each side of the block— you could measure how far the building is. With a long enough stretch, even the mountains on the horizon will seem to move.
The history of astronomical measurement preceding Henrietta Leavitt’s discovery can be compressed into a story of how people learned to use larger and larger triangles to point farther into the sky.
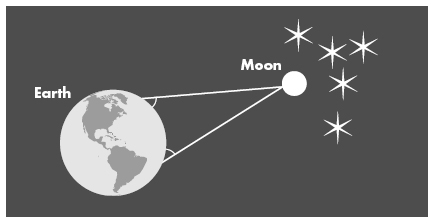
SEND TWO OBSERVERS to different places on the Earth’s surface and, if the separation is great enough, each will see the moon at a slightly different position against the backdrop of stars. Have them measure both angles simultaneously (they would need to synchronize their watches) and, if you know the length of the baseline, you can triangulate.
In a variation, the Greek astronomer Hipparchus in the second century B.C. used a solar eclipse as his timepiece. While the sun was blotted out completely at Hellespont, the strait in northwestern Turkey near the ancient city of Troy, the eclipse was only four-fifths full in Alexandria. If you could freeze time and hop back and forth between these two vantage points, the moon would seem to shift by an amount equal to one-fifth the size of the solar disk—the Earth blinking its eyes. The sun occupies about half a degree of the arcing bowl of sky, making the parallax of the moon one-tenth of a degree.

Lunar Parallax
Had Hipparchus known the distance between Troy and Alexandria—the size of the baseline—he would have had his answer. Instead, using a more complex arrangement of triangles, he was able to calculate that the distance of the moon must be about thirty times greater than the diameter of the Earth. He got the ratio right. The planet has since been measured at about 8,000 miles across. Using that number, Hipparchus’s method would put the moon 240,000 miles away. Two thousand years later, people learned to make the measurement by bouncing radar signals off the moon and measuring the delay of the echo. High-tech or low-tech, the figure comes out about the same.
Skipping past the Dark Ages, dominated by Ptolemy’s brilliantly wrong cosmology, with all the heavens looping around our planet like an amusement park ride, the next great leap didn’t come until the sixteenth century. Copernicus restored the sun to the center of the solar system, then Kepler refined the model, flattening the planets’ circular orbits into ellipses and showing how they must be arranged.
One of his laws is of particular interest to any would-be measurer of the universe: The farther a planet is from the sun, the longer it takes to complete its journey. From the length of the Martian year, one could deduce that the planet lies about one and a half times farther from the sun than Earth does. The same calculation could be done for Mercury, Venus, Jupiter, Saturn.…Once you had all the ratios, you could use parallax to determine just one of the distances. The others would automatically follow.
The task was easier said than done. Measuring the tiny displacement of the moon, viewed from two spots on the Earth, had been difficult enough. For even the closest planets, the parallax was so small that the slightest mistake in gauging an angle or the length of a baseline caused the calculation to fail.
That didn’t keep astronomers from trying. Coordinating their efforts with pendulum clocks, observers stationed in Paris and on the island of Cayenne in South America showed in 1672 that the position of Mars shifted by a mere 25 seconds of arc. Adopting the useful fiction that the heavens consist of a hemispherical dome arcing overhead, astronomers divide the sweep from horizon to horizon into 180 degrees, half a circle. Each degree is divided into 60 units called minutes, which can each be further subdivided into 60 seconds. Twenty-five arc-seconds is 1/144 of a single degree, an exceedingly small piece of sky.
The Martian distance computed from this delicate operation came close to the mark, but the accuracy was accidental. There was so much uncertainty in the measurements that errors canceled out errors, dumb luck stumbling onto a pretty good answer. Before more reliable methods became possible, another hundred years would go by.
2
Twice a century, just a few years apart, Venus, the closest planet, passes between the Earth and the sun. The result is like an eclipse, except that Venus is so distant that it appears only as a tiny dot. No one would notice the event who wasn’t deliberately watching. If observers in separate locations time how long it takes the planet to cross the solar disk, they can compare their different readings and triangulate. The result is Venus’s distance and, plugging the number into Kepler’s equations, the distances of every planet from the sun.
Edmond Halley, the great British astronomer, had missed his chance to observe this rare phenomenon, called the transit of Venus. He lived inconveniently between the pair of events of 1631 and 1639 and the recurrence predicted for 1761 and 1769. He satisfied himself by issuing a challenge, calling on the next generation of astronomers to disperse themselves around the world and measure the Venusian parallax.
They took him up on the dare, setting out for Siberia, Hudson Bay, Baja California, India, the Cape of Good Hope, Tahiti. Some of the expeditions failed, and some of the data was suspect because of the difficulty of determining precisely when fuzzy-edged Venus, a planet swathed in chemical clouds, actually passed into the circle of the sun. But with eyes placed all over the planet (there were 150 observations), astronomers compiled enough good information to measure all the way to Venus. Then, carrying the calculation a step further, they concluded, via Kepler, that the distance to the sun was 91 million miles, just 2 million shy of the number schoolchildren learn today.
It was a hard act to follow. With one star down and a whole galaxy to go, the craft of triangulation was already becoming stretched to the limit. Even with an imaginary triangle whose base extended across the full width of the Earth, the parallax of the nearest planets was just barely measurable. How could anyone hope to gauge the distance of stars?
Astronomers had made some rough estimates. If you pretend that all stars produce the same amount of light—that they are equal in intrinsic brightness—you can judge how much dimmer Sirius appears from Earth compared with our home star, the sun. Then with the inverse square law (something twice as far away shines a fourth as bright) you can estimate the distance. These rough calculations served to show that even the brightest stars must be hundreds of thousands of times farther than the sun, way beyond the reach of earthly parallax. Travel from one antipode to the other and you would not detect the slightest shift.
It seemed that measuring stellar distances would require leaving the planet, observing the position of a star from Earth and then from a point millions of miles away.…Or you could stay on Earth and let it carry you between the far extremes of its orbit. This was the next advance. The radius of this great ellipse—the distance from Earth to sun—was now known with some precision. So just double the amount: every six months earthlings are looking at the sky from positions separated by 186 million miles. Draw a triangle with this as the baseline and you can measure the parallax of nearby stars.
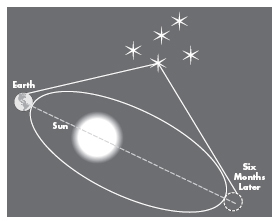
Parallax using the diameter of Earth’s orbit as a baseline
Galileo had suggested how such an experiment might be done. The sky is filled with double stars, some of which are presumably optical illusions: nowhere near each other in space, they just happen to line up because of the angle at which we see them. If one is actually much closer to us than the other, parallax will make them appear to come together and then move apart as we orbit the sun. (Think of two telephone poles, one behind the other, converging and then diverging as you drive by.)
It wasn’t until the late 1700s that instruments were good enough to make the measurements. The astronomer William Herschel built a 20-foot-long telescope with a mirror 19 inches across. When that wasn’t strong enough for him, he built a 40- foot scope with a 4-foot mirror—so large that it weighed a ton. Working with his sister, Caroline, he discovered Uranus and some 2,000 star clusters and nebulae (which, he ventured, were not small, nearby gas clouds but galaxies so distant that the individual stars blurred together). He also found hundreds of the double stars Galileo had suggested might be used for measuring distance.
In the end the project failed. A statistical survey showed that it was actually very rare for two stars to line up and mimic a double. Most doubles really were doubles, adjacent stars orbiting each other—too close together to exhibit any parallax.
It was with the next generation of astronomers that stellar triangulation came of age. Herschel’s son John (the one we heard earlier rhapsodizing about the Magellanic Clouds) established an observatory at the Cape of Good Hope, near the southern tip of Africa. There astronomers determined that every six months the star Alpha Centauri changed in position by less than a second of arc—1/10,000 of a single degree, a frustratingly tiny amount but enough to do some trigonometry. Calculating the height of this extremely skinny triangle led to the conclusion that the star was 25 trillion miles away—so far that its light took more than four years to get here. And this was just the next sun over, the closest star.
Two other neighbors were also measured around this time, Vega and a star called 61 Cygni. A little later came Sirius and Procyon. All were a few light-years away in a universe now believed to be billions of light-years wide. By the early 1900s, when Henrietta Swan Leavitt arrived at Observatory Hill, nearly a hundred more stars had been triangulated. But most stars by far showed no parallax at all, even across so enormous a baseline. They were inconceivably and, it seemed, immeasurably far away.
3
Had just one of Miss Leavitt’s blinking stars been within triangulating distance of home, astronomers could have leapt past the parallax barrier and begun measuring deep into space. Remember that two of her Cepheid variables pulsing at the same rate are, according to the relationship she discovered, of the same inherent brightness. If one appears to shine only a hundredth as brightly as the other, you know (because of the inverse square law) that it is ten times farther away. If you could use parallax to establish the distance of just one nearby Cepheid, you could infer the distance to the rest. By comparing Cepheid variables of various rhythms and intensities, you could leapfrog across the universe.
Nature, however, was not so obliging. The nearest known Cepheid, the North Star, was too far to show any shift in position, even when viewed from opposite ends of Earth’s orbit. It is, by modern reckoning, some 400 light-years away. Parallax would get you only a fraction that far. The Cepheids used to devise Leavitt’s law were many times farther still.
The best an astronomer could do was to say that a certain Cepheid was, as determined by its rhythm, one-tenth the distance of those in the Small Magellanic Cloud, while another was, perhaps, three times farther away. The universe could be portioned out in units called SMCs. But that begged the question: How far—in miles or light-years—was the Small Magellanic Cloud?
Before Miss Leavitt’s stars could be turned into true yardsticks, some way had to be found to extend parallax far enough to reach a nearby Cepheid. That meant making observations across an even longer baseline than the full width of spaceship Earth’s orbit around the sun. What was needed was a larger, faster craft. Unlikely as it seemed, one was at hand: the starship we call the sun.
According to folklore, when Galileo was called before the Inquisition and forced to recant his Copernican views, he muttered under his breath, “And yet it moves.” The reference, of course, is to our planet. He might have been as surprised as his tormentors to learn that the sun moves as well, on a slow drift through the Milky Way, carrying its planets alongside.
The movement is barely perceptible. In the late 1700s the elder Herschel, William, discovered that stars in the direction of the constellation Hercules move according to a peculiar pattern: over the years, they appear to be fanning out from a distant point, as snowflakes seem to do when viewed in the headlights of a car speeding through the night. In the opposite direction, back toward the constellation Columba, the stars converge, like snowflakes seen from the rear window. Our solar system, he concluded, was leaving Columba and heading toward Hercules. Astronomers have since clocked the speed of this journey through the galaxy at about 12 miles per second, or more than 30 million miles a year. The parallax from the voyage causes the constellations to become stretched and squeezed over time. The ancient Greeks were looking at a slightly different sky.
For a measurer of the universe, riding along with the sun, closer stars will move faster than farther ones, while the most remote stars will not seem to move at all. Carefully note the position of a Cepheid, then measure it again years later, when the sun has dragged Earth and its astronomers to a new location in space. Calculate the length of this enormous baseline, and then triangulate. With the distance of one Cepheid established, you can calibrate Leavitt’s yardstick and then measure the rest.
The first to attempt this was a Danish astronomer named Ejnar Hertzsprung. He used the motion of the sun to triangulate the distance to some Cepheids in the Milky Way. Then, correlating pulse rate with inherent brightness, he extrapolated outward, reporting in a journal called Astronomische Nachrichten that the distance of the Small Magellanic Cloud was about 3,000 light-years.
This was enormous by the astronomical standards of the time. In fact it was a misprint. Maybe a journal copy editor had recoiled at the real number, inadvertently dropping a zero. According to Hertzsprung’s calculations, the nebula was ten times farther, 30,000 light-years away.
Around the same time the American astronomer Henry Norris Russell used a different method to come up with an even more astonishing distance of 80,000 light-years. “I had not thought of making the very pretty use you make of Miss Leavitt’s discovery about the relation between period and absolute brightness,” he later wrote to Hertzsprung. “There is of course a certain element of uncertainty about this, but I think it is a legitimate hypothesis.”
The Cepheid yardstick still needed refinement, but astronomers finally had hope of leaping past the nearest stars, roughing out the shape and size of the galaxy … and what, if anything, lay beyond.
4
Henrietta Leavitt didn’t get to pursue the matter herself. Pickering kept her tied down with other projects. He wasn’t one to encourage theorizing, believing, as his colleague Solon Bailey put it, “that the best service he could render to astronomy was the accumulation of facts.” Beginning in August 1912, the year her discovery about the Cepheids was published, she documented her day-to-day routine, in language meaningful only to an astronomer, in a black-and-red leather-bound notebook:
October 8. Letter from Hertzsprung, dated Mount Wilson, Oct. 3, 1912. Subject, Method of transforming photographic to visual magnitudes by means of effective wavelengths. He finds that a change in the color index, using Dr. Mürch’s photographic magnitudes and Harvard photometric magnitudes, of one magnitude, corresponds to a change in effective wavelength (λf) of 200 Angstrom units.…
October 19. Tried superimposing Plates H 361, exp. 10m, limiting magn. 15.6 and H 385, isochromatic, limiting magnitude 14.9. The red stars appeared of nearly the same brightness on the two plates, white stars being brighter on H 361. The colors were assigned very easily.
October 22. Finished revision of 32 sequences north of +75 degrees, and comparison with marked chart. Gave plates to Miss O’Reilly for identification.
And so it went for the next four years, except for gaps, sometimes many months long, hints of recurring illness. In spring 1913 she was absent for three months recovering from stomach surgery. Only once in all those pages, on January 13, 1914, does she let some excitement show: “Completed discussion of Prov. Photovisual Magn. of N.P. Seq., this completing H.A. 71, 3. !!! after many years.”
Translation: She had finished, or so she believed, the measurements for her North Polar Sequence, ninety-six stars whose magnitude she had determined with such authority and care that they could be used as a standard for the rest of the sky. There were still revisions to be done. The work was finally published, three years later, in the Annals of the Astronomical Observatory of Harvard College, volume 71, number 3—all 184 pages of it. Perhaps she and her mother indulged in a split of champagne.
Dry as dust to the uninitiated, her report was a work of magnificence, combining data from 299 photographic plates taken by thirteen different telescopes. Every magnitude had to be meticulously checked and cross-checked, with a constant awareness of the difference between mere data and true phenomena. No matter how carefully measured, each number represented not the brightness of a star but rather the intensity of its image on a photographic plate. In a perfect world these two values would be the same. In reality, every telescope and every type of photographic plate had its own peculiarities—responding more readily to some colors than to others. Images near the center of the plate were rendered more accurately than those to the side.
Page after page, she described how she corrected for the various biases and uncertainties. There was a chain of reasoning behind every number. Each star was a project in itself.
When she reached the end of the study, she knew it wasn’t perfect. “It is desirable that the standard scale should be investigated by different observers, using independent methods,” she allowed. “Discrepancies will inevitably appear in the results.” But, as politely as possible, she warned future critics to proceed with caution.
“Too much weight may easily be assigned to results obtained from a single investigation, even if great precautions have been used.” Which is why, she gently reminded, her measurements “depend on many different methods, instruments, and observers.”
She concluded, “In view of these facts, it seems only reasonable that considerable time should be allowed to pass, and a large amount of varied material collected, before adopting definitive corrections to the scale here presented. For stars between the tenth and sixteenth magnitudes, such corrections are likely to be minute. For brighter and fainter stars, sensible changes may be made ultimately, but the scale is probably a close approximation to the true one.”
It was work to take pride in. Ph.D.s have been awarded for less.