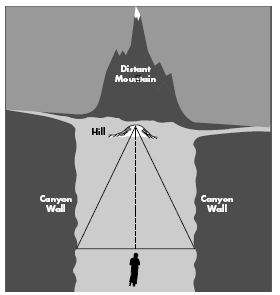
The village was hidden at the bottom of a deep chasm with sides so steep and slick that no one had ever climbed them. All that could be seen overhead was a narrow band of sky.
Looking down the canyon, one could spot a hill in the distance. How distant no one knew, for it was separated from the village by an impassable expanse. Beyond the hill, and even more inaccessible, was a faraway mountain, the edge of the knowable world.
The villagers had noticed that when they walked the width of their canyon, from one wall to the other, the top of the hill appeared to shift ever so slightly against the backdrop of the mountain, moving from one side of the peak to the other. No one believed the hill really moved, but they enjoyed the illusion.
One day a particularly observant citizen noticed an interesting subtlety. When he wandered up the canyon a ways, and then traversed its width from wall to wall, the hilltop still appeared to move, but much more slowly. And if he walked even farther and repeated the experiment, the movement was smaller still. Venture far enough, he discovered, and there was no perceptible shift at all.
He made an entry in his notebook: The amount the hill moves depends on its distance from the observer. He had discovered the phenomenon called parallax.
Returning to the village, where the hill was closest and the effect was most pronounced, he measured the separation between the canyon walls and began to sketch out a picture:
The width of the canyon and the line of sight from each canyon wall to the center of the hilltop formed an imaginary triangle. Using a surveying instrument, he could measure the two angles at the triangle’s base. Then, using what he had learned in school about the rules of trigonometry, he calculated the height of the triangle—the distance from the center of the baseline to the apex, from the village straight across the impassable badlands to the hilltop. By this measure, it was ten canyon widths away. It was still impossible to walk there, but it was comforting to know the distance. The world seemed a little tamer.

Triangulating a Mountain
In coming years, the villagers began to build stone lookout towers, climbing high enough to observe that beyond the hill was another one. Using the same measuring technique, they showed that the second hill was fifteen canyon widths away. Behind it was a third hill at twenty-five canyon widths. But beyond that the method failed. The hills were so far that they couldn’t be made to shift at all. The villagers’ canyon was not wide enough, their triangles were too small.
Most tantalizing of all was the dark immovable mountain on the horizon. It seemed to lie at infinity, a distance so great as to be immeasurable. A few villagers imagined launching an expedition, traversing the dangerous badlands between the village and the first hill and then forging beyond that, walking day after day until they had reached the mountain. But none was so foolish or so brave. The more imaginative citizens could envision what it might be like to rise up out of the canyon, where they would be free to move so far left and right that the mountain itself would shift against some even more distant backdrop. Then they could determine how long the journey would be. But that was just fantasy.
In theory, there was another way of indirectly determining the mountain’s distance: things looked smaller the farther away they were. Something twice as distant would appear half as high. If this rule applied outside the immediate area of the village—and why would it not?—there would be a means of measuring to the mountain.
One very clear day, an observer standing on the highest tower decided to try this technique. She had noticed long ago that there was vegetation on the nearest hilltop—appearing in the distance like miniature versions of the local flora, the spiny green bushes that covered the canyon floor. On this day she noticed that if she squinted her eyes, she could also make out, just barely, the tiniest fringe of green along the mountaintop, comforting evidence that this far-off land might not be unlike her own.
It took only a few moments for her to appreciate the larger implication. Working carefully, she measured the apparent height of the shrunken shrubs on the nearest hill. The even tinier fringe of green on the mountain appeared to be some ten times smaller. And so, it seemed, the mountain itself must be ten times farther than the hilltop—a full one hundred canyon widths away.
That was far but not infinite. Walking there might take a week or two—if someone could find a way to cross the impassable divide. Encouraged by her discovery, a party of volunteers set out for the mountain. From the highest towers the citizens watched as the explorers eventually found a way across the badlands, to the first hilltop and on past the second and the third, until in a few days they were out of sight.
After a week had passed, the villagers went back to the towers to watch for the expedition’s return. Two weeks later they looked again. Months went by, then a year before they stopped waiting.
Finally one day, a single member of the party staggered back home. The vegetation on the mountaintop, he reported, was very different from anything in the canyon. Towering trees rose ten times higher than any plant he had ever seen. He had climbed to the top of one of these behemoths and thought he could barely make out the tiny twinkling lights back home. He knew by then that while the logic of the measurement had been sound, the villagers had been misled by the limits of their imagination. Since the strange trees were ten times higher than the familiar bushes, the mountain was another ten times farther than had been reckoned, a full one thousand canyon widths away.…
2
In Robert Heinlein’s novel Time for the Stars, a charitable organization called the Long Range Foundation recruits pairs of identical twins for a mission to colonize space. The Earth, buckling under an exploding population, has already spilled over to all the planets of the solar system. Now it must look farther, to planets orbiting stars so distant that news of their discovery, traveling at light-speed, would take years to reach home.
That is where the twins come in. Scientists, according to the story, have discovered that many twins are telepathic, and that the signals they mentally exchange are not weighed down by the restrictions imposed on electromagnetic waves. The communication is instantaneous—faster than light—no matter how far apart the twins may be. With one twin on a spaceship and the other on Earth, they can converse instantly across light-years.
I read this story, now out of print, in junior high school and had forgotten all but the bare bones of the plot, which revolves around the relativistic effects of traveling near light-speed. Time slows down so Tom, the twin on the starship, ages only a fraction as quickly as Pat, his counterpart back home. He is an old man when Tom returns and marries Pat’s granddaughter, with whom he has been flirting telepathically.
What stuck in my mind all those years was not the rather obvious Einsteinian plot contrivances but a brilliant scene toward the end of the book: Tom is looking at the sky from a hospitable planet orbiting Tau Ceti, a star system eleven light-years from Earth. The constellations he sees are recognizable but slightly distorted from how they appear back home. He can make out the Big Dipper, “looking a little more battered than it does from Earth,” and he finds Orion, the great hunter, though his dog, Sirius, is stretched out of whack. The understated climax comes when Tom discovers, from where he now stands, that the constellation Boötes has acquired a new star, yellow-white and of about the second magnitude. It takes him a moment to realize that he is looking back at the sun.
I don’t know why that scene threw me for a loop. Maybe it should have been obvious even for an eighth grader how arbitrary the constellations are, not just the names taken from classical mythology (does anyone really think Ursa Major looks like a giant bear?) but the actual shapes. They are an accident of how the stars happen to line up from one among an infinity of possible points of view. Though Orion’s dog appears to follow faithfully at his heels, the constellation’s principal star, Sirius, 8.6 light-years from Earth, is nowhere near the hunter’s belt, whose stars are approximately 1,500 light-years away.
For that matter Orion’s belt is nowhere near his shoulders and the shoulders nowhere near his knees. Even the belt is an accident of perspective. From other parts of space these three stars would form a triangle or their order would be reversed. Viewed from just the proper angle, all three of them would merge into a single light, an illusory triple star. Travel to the center of the space the three stars enclose and each would appear in a far-flung corner of the sky.
3
For anyone raised on science fiction or the enthusiastic promises of the Kennedy era, the space program has turned out to be a dud. Who would have guessed that several decades later, after a few trips to the moon (about 250,000 miles or fifty round trips between Los Angeles and New York), our species would abandon human space exploration altogether, our leaders contenting themselves with the ridiculous space shuttle, which ventures about as far from Earth as Baltimore is from New York? The feeble broadcasts of the unmanned space probes—the oldest recently passed beyond the edge of the solar system—stir the imagination. But for the most part people have been content to sit at home and wait for the cosmic news to arrive in the form of light from other stars.
We are celestial couch potatoes. Yet what we lack in exploratory will we make up for in other ways. We don’t travel with our bodies. We travel with our minds.
Having never left home, the astronomers can say with some confidence that our own galaxy, the Milky Way, is more than 100,000 light-years from end to end and that Andromeda, the galaxy across the street, is 2 million light-years away. These and several other galaxies form our “Local Group.” The neighborhood. Just across town are other conglomerations of galaxies like the Sculptor group and the Maffei group, nearly 10 million light-years in distance. A little farther are the Virgo and Fornax clusters, lying some 50 million light-years from the Milky Way. Even if these were miles, the numbers would be staggering. A single light-year is almost 6 trillion miles.
We still haven’t left our hometown “supercluster,” a galaxy of galaxies a full 200 million light-years across. Beyond it lie more superclusters, stretching to the edge of the visible universe, 10 billion or so light-years from home.
Faced with so grandiose a vision, it is a little surprising to learn that as recently as the 1920s many astronomers thought the Milky Way was the universe. Whether there was anything beyond it was a matter of scholarly debate. What are now taken to be vast galaxies similar to our own were dismissed as small nearby gas clouds, insignificant smudges of light.
We were like the villagers in the canyon. Then we discovered a new way to measure.