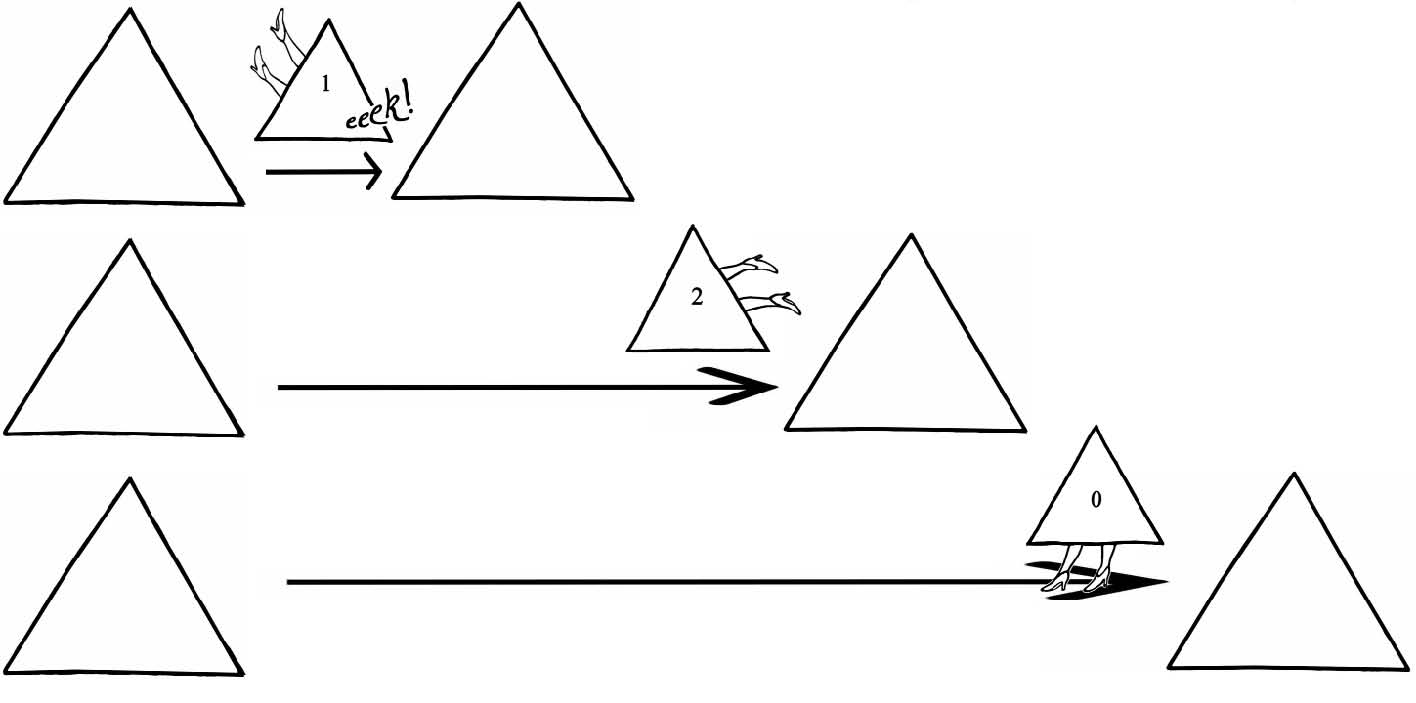
Saucy Miss Triangle!
The Outrage so far: An equal-sided triangle is symmetrical. It looks unchanged when you manhandle it through a third of a turn, two-thirds of a turn, or turn it all the way round.
Similar base operations can be performed on a square:

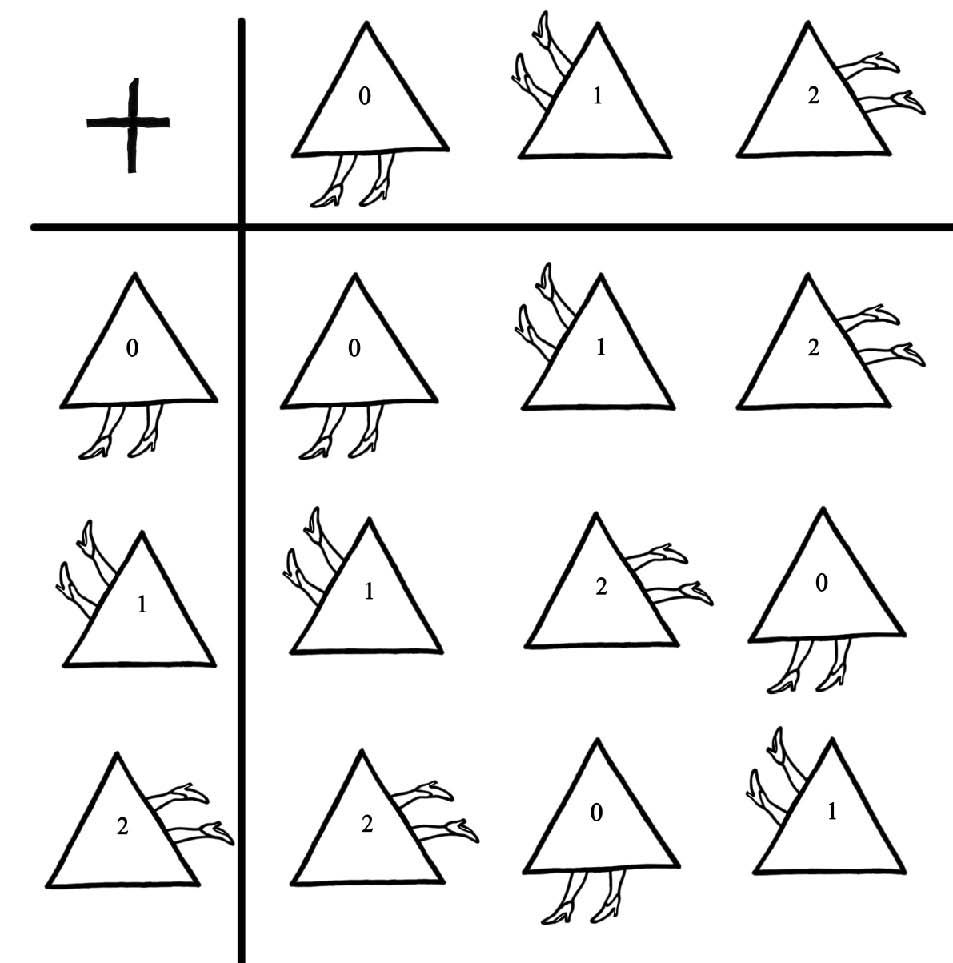
If you have the energy to perform two or more of these misdeeds at once, you can keep track of the overall effect with the help of a grid that looks like a sudoku table:
There’s another symmetry operation – nothing to do with rotations – that allows us to have our way with Triangle, and still leave it to all appearances untouched. We can flip it back to front:
Inwardly, Triangle may adjust its spectacles and primly pat its skirt, but outwardly it looks unperturbed. We record the act in our diaries by a new symbol:
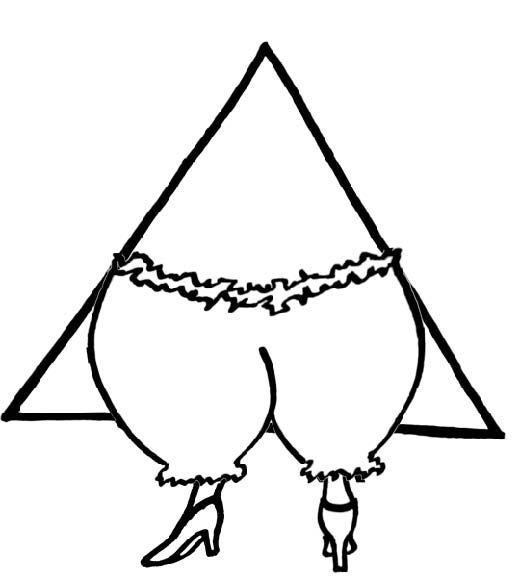
Remember: this is not the triangle itself. This is what we have done to it:
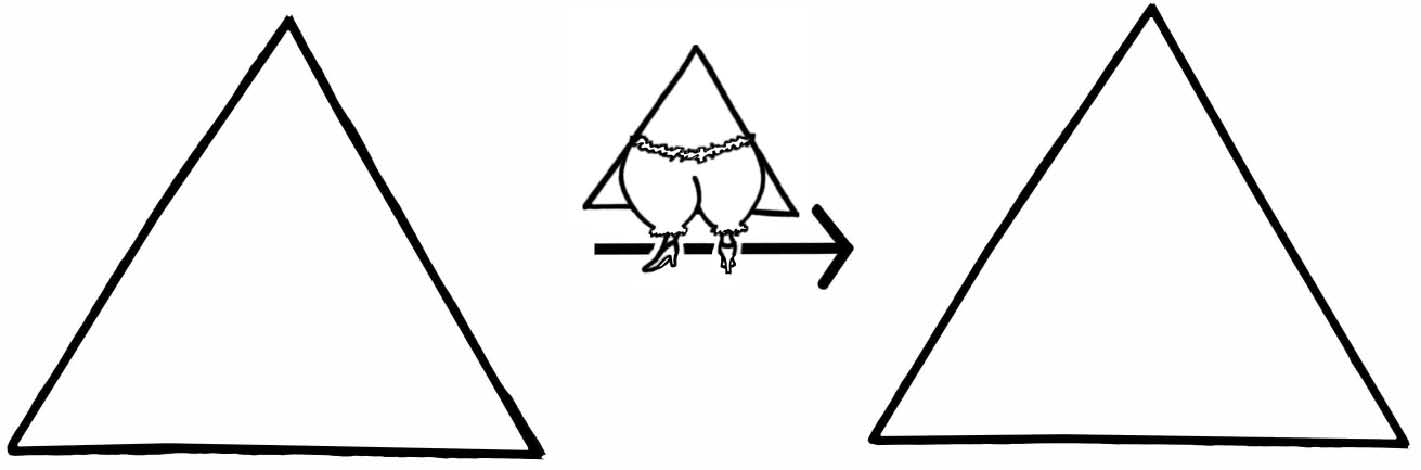
The embloomered shape represents the act of turning an equal-sided triangle over:
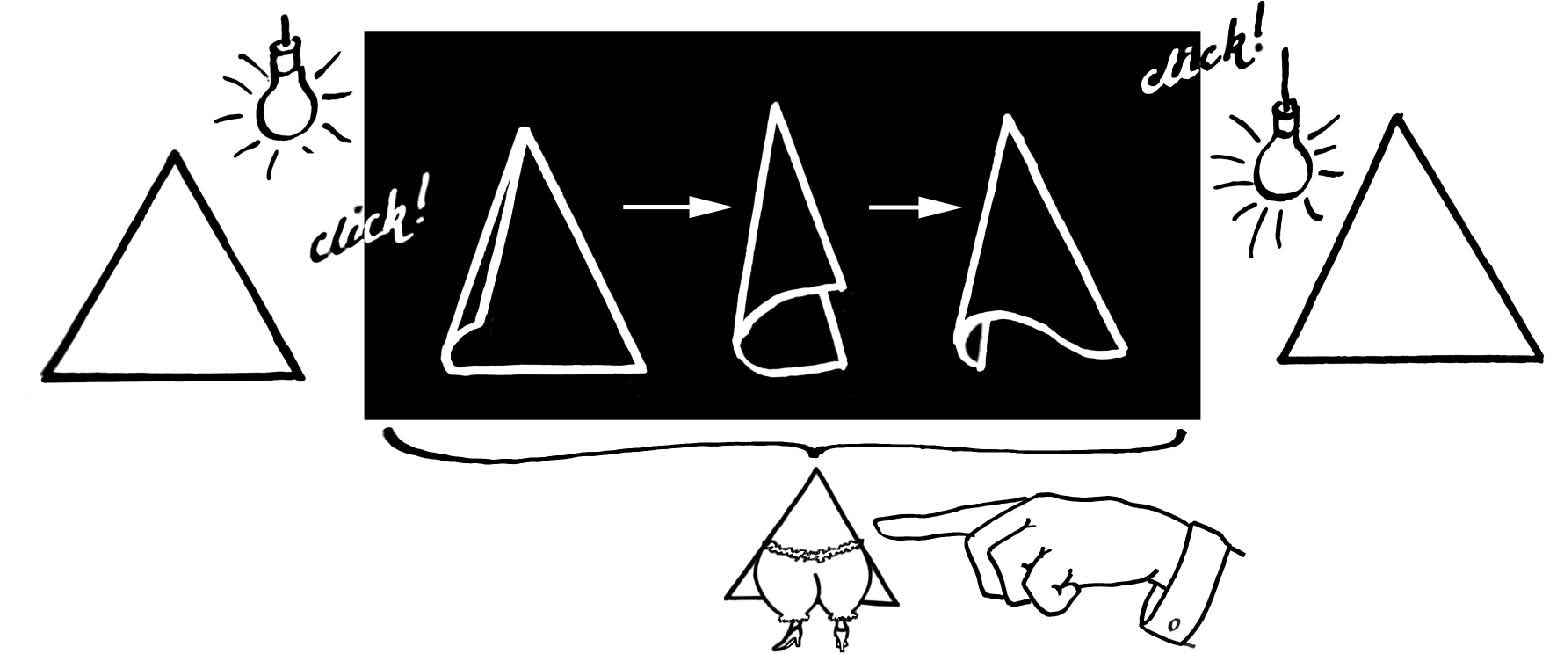
Irregular triangles, naturally, are not so circumspect. Flip one of these mis-shapes over and it shows very definite signs of adjustment. Anyone watching immediately spots what you’re up to. There’s none of Triangle’s finishing-school ability to keep the secret under wraps:

If we add all the ways we can flip an equal-sided triangle –

– to the three ways we can rotate the triangle, and construct a Group Table to keep track of how all these symmetry operations interact, we get the following lumbering object:

Next, a page for ladies:
We can do a similar flipping operation with Square:
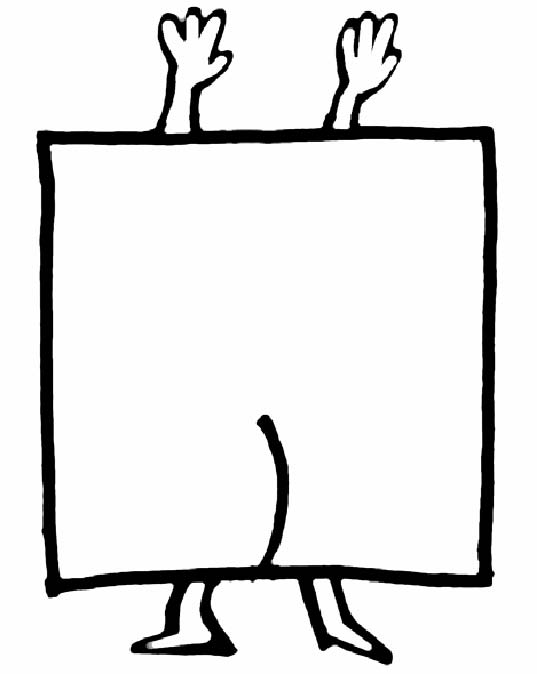
Turn off the light, flip Square over, turn the light on again, and Square looks delightfully unchanged.

Now we’re almost there. The critical, central idea – Subgroups – discovered by a French schoolboy in the nineteenth century. From this child’s revolutionary insight spring most of the complexities of Group Theory and a first glimpse of the Monster.