Symmetry is like a disease. Or, perhaps more accurately, it is a disease. At least in my case; I seem to have a bad case of it.
Joe Rosen, Symmetry Discovered: Concepts and Applications in Nature and Science (1975)
Mathematicians are subtle with language, but they have made a mess of the word ‘symmetry’. What ordinary people mean by ‘symmetry’ is kindergarten shapes (such as Square, Triangle, etc.) and snowflakes.
At the centre of what mathematicians mean by the word ‘symmetry’ is the word ‘always’.
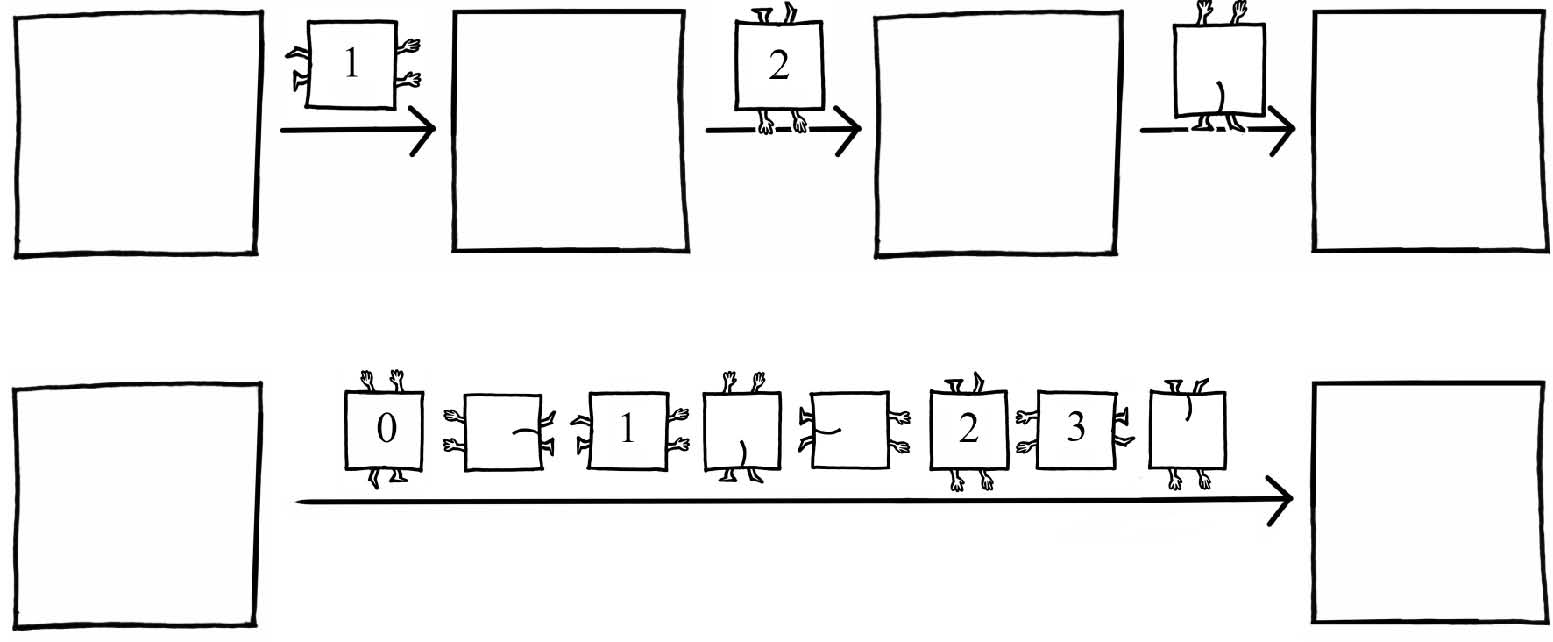
A square always looks the same when you rotate it through a quarter turn, or half a turn, or three-quarters of a turn, or turn it backside up; or do any combination of two, five, ten, or 743 of these things. It is symmetrical with respect to these operations.
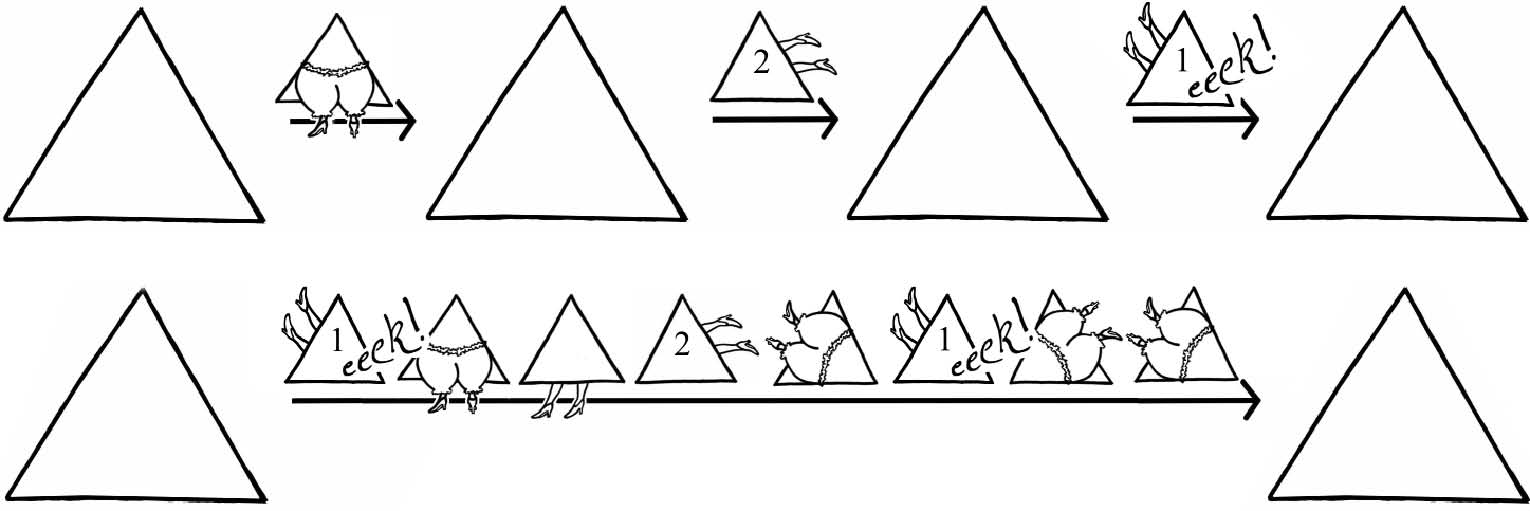
Triangle always looks the same when you manhandle it through a third of a turn, two-thirds of a turn, flip it bloomer-side and rotate it as many times as you like, or keep yourself churchlike and Sunday-mannered and pass it by altogether. It is symmetrical with respect to it all.
If you can phrase an idea – any idea, on any subject – to include the word ‘always’, then you’re within whistling distance of what mathematicians call ‘symmetry’.
• Simon always fills his bath too full
• I always get cross and kick shut the Excavation door when Simon cooks packet rice with Chinaman in it.
• E always equals mc2.
• The Monster always looks the same (although no one yet knows what that look is like) when you perform on it one of the 808,017,424,794,512,875,886,459,904,96 1, 710,757,005,754,368,000,000,000 symmetry operations in its Group Table.
• When drunk, Jim, our next-door neighbour, always leaps on his motorbike at 2 a.m. and starts revving the engine.
Each of these cases makes an appeal to symmetry. Symmetry is the invariability of some object, circumstance or relationship to a specified set of changes. Put Simon in the bath in our house or on a planet in Alpha Centauri; in the middle of a nuclear war; when he was five, seventy-five or upside down – it makes no difference. As far as the water in the bath is concerned, it’ll always dribble over the edge, seep under the skirting, ooze along the basement wall and cause toilets and stair treads to collapse. It’s a knack Simon has.
In the starched language of squares and triangles, ‘rotate’ Simon-in-a-bath among any of these different situations, and the result always looks the same:

However many times, in whatever order, we perform these operations, it will still be splish-splash Norton in the bath:

The anthropologist Claude Lévi-Strauss noted that certain types of marriage among Australian tribes are always considered incestuous and therefore forbidden. But he couldn’t figure out the underlying structure behind these taboos, so he went around New York (where he was living at the time) banging on the doors of mathematicians. The first was dismissive: ‘Mathematics has four operations, and marriage is not one of them.’ But the second was the young and brilliant André Weil, brother of the philosopher Simone. ‘When in doubt,’ cried Mr Weil, ‘look for the group!’ and he bustled Lévi-Strauss off the street into his study. Within a few days, Weil had solved the problem. Not only had he used the theory of symmetry to explain why certain marriages were taboo among Australian Aboriginals, but he’d also discovered that, by mathematics alone, it was possible to investigate a tribe today and determine if at some time in the past it had been in fact two different tribes, which had since met and settled together. There would be an imperfection in the ‘symmetry’ of the incest taboos – the ‘alwaysness’ of their rules – that would give the game away. You didn’t need to know the history of the tribe, or have any further anthropological knowledge than an understanding of the current restrictions on sex: all you needed was to pick up a glint of asymmetry, the murmur of a ‘sometimes’. With mathematics, you could see 1,000 years into the past.
I’ve charged about my study for hours trying to understand how going to bed with your sister is a mathematical statement, and failed, but it is.
(‘I don’t understand it either,’ grumbles Simon. ‘In fact, I’m not sure I believe in it.’)
The word ‘taboo’ suggests always forbidden, so symmetry must be involved somehow. ‘Rotate’ any one of the banned couplings in front of Australian tribal elders and there will always be uproar.
This is why symmetry is important: it’s everywhere. Symmetry does not mean just pre-school cut-out shapes like triangles and squares, it speaks for anything – from quantum fluctuations inside your eyelash, to the songs of the Beluga whale, to the despotic delusions of madmen in North Korea – that involves in some respect, however far-fetched, ‘immunity from change’. It is the study of imperturbability. If, under certain conditions, a situation always appears the same despite the fact that things are actually being done to it, then that’s symmetry.
This tells us something about Simon’s Monster. It is not a raging thing. Its power lies in its unchangingness. It is a monster of calm.
And here’s a fifteenth way to say it: a symmetry operation is an act that leaves a thing ‘unfazed’. Mess and boring bus journeys, for example, leave Simon unfazed. Mess and buses are a part of Simon’s symmetry.
‘I don’t think that’s an analogy at all,’ interrupts Simon, looking up, tongue clamped between teeth.
‘Loosely, “being unfazed” is an analogy to being symmetrical,’ I pursue.
‘No, not loosely. The two ideas have nothing to do with each other. A symmetry operation in mathematics is something that operates on something else. It needs to do something to be interesting, as in a rotation operating on a square. If that rotation makes the square appear different than it did before, it is not a symmetry operation; if the same, it is.’
‘Exactly. Operate on you with mess, and your character and mood don’t change.’
‘What do you mean, “operate” with mess? Operate how? I don’t understand that at all. The character of a human has nothing to do with operations. It’s just to do with what a human is. It’s nonsense to say they’re analogous. I don’t even know what that would mean, to talk about the mathematical character of humans. I really don’t want to talk about this any more.’
Mess, buses and nitpicking are part of Simon’s symmetry.