Hurry! Hurry! Back to the classroom! Time for more misdeeds with Triangle and Square!
To recap: Square and Triangle are symmetrical. You can do all manner of things to them – rotate them, flip them over, in any combination you fancy – and they’ll always look just the same after your wickedness as before:
In short, Group Theory is the study of the moves that always leave an equilateral triangle and a square (or other symmetrical object) looking the same. To show how these different moves combine (e.g. one turn of a square, followed by one more, equals two turns in total), we use a sudoku-type grid called a Group Table … Oi! You, yawning at the back! Pay attention!
How does a subject that’s for children – cutting squares and triangles out of dayglo paper, representing them being bullied
and shoved about by symbols such as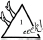 
and 
– lead to an intellectual discipline so intricate and metaphysically profound that it can absorb a genius like Simon for the majority of his adult life? These Group Tables for the turns and twists of Square and Triangle seem too bland for discussion. Their straightforwardness as secretarial devices makes them appear beyond analysis, stagnant with simplicity. How could there possibly be anything extra to say about them?
But there is.
The mathematics libraries of the world are crammed to the ventilation ducts with books that depend on an easy idea, gently hidden idea inside the Group Table for the rotations of Square but missing from the Table for Triangle.
It’s called a ‘Subgroup’.
Square’s Group Table of turns has one, and Triangle’s doesn’t.
(There’s a slight fuss about what Simon calls ‘trivial’ Subgroups, which all groups possess, but we’ll ignore this complaint here.)
A Subgroup is simply a Group within a Group, a smaller symmetry hidden inside the larger one. The Group Table for the turns of Triangle doesn’t contain any Subgroups. That’s why it’s considered an ‘atom’ of symmetry. It can’t be broken down into smaller symmetries.
A square’s Group Table of rotations does contain a Subgroup. It can be further broken down in symmetry terms so, therefore, it is not an ‘atom’ of symmetry, but a flibbertigibbet.
Subgroups are one of the keys to turning Groups from a distraction for children into a mathematical smash-and-grab raid for Simon Nortons.
In Chapter 25, we’ll see how to spot the hidden Subgroup in the Group Table of Square.
A last paragraph, for advanced readers: the ‘atoms’ of symmetry are to Group Theory what the prime numbers are to whole numbers – the building blocks of the entire system. Just as any whole, positive number can be constructed by multiplying together prime numbers, any finite Group can be made up by combining together these ‘atoms’ of symmetry. For example, the number 15 is composed by multiplying together the two primes 3 and 5. Similarly, the rotations of a pentadecagon (a fifteen-sided regular shape) can be constructed by combining the rotations of a triangle and the rotations of a pentagon.