
I used to worry at school that there was I enjoying numbers when everyone else was made to do boring things, like swimming or the American Civil War. Why didn’t the teacher tell them about the cyclic permutations of 142857?
Simon
‘No, don’t lie on the floor, please, Alex – do you mind if I call you Alex?’
It was the hypnotherapist speaking. Andrew Cunningham: a slight, soft-spoken man, the star of dozens of TV shows for curing stagefright, fear of dogs and heights, and for cramming the tremulous with braggadocio. For the Channel 4 programme Faking It, he transformed a City solicitor into a foul-mouthed, shaven-haired Garage MC.
I was going to be hypnotised. Hypnosis, I’d decided, would help me investigate the curlicues of Simon’s mind.
1 Harley Street is the last chance a hypnotist has to work in this prestigious part of London. It is the high-end numbers of Harley Street that belong to the lucrative professions like sucking out fat with a vacuum cleaner and burning women’s faces with acid. Fail to fit into some cubbyhole at Number 1, and you drop off into Cavendish Square; a little further south, and before you know it your business is camping alongside Clairvoyant Claire under Vauxhall Bridge.
I’d met Andrew in the entrance hall of this office block, beside a brass plaque stretched thin with company names suggesting empty one-room offices and unmanned telephones: Mindworks, Mindspa Clinics, Management Psychology Ltd, The London Therapy Centre. We had to go up and down so many corridors and back staircases to get to Andrew’s consulting room, that possibly it was no longer in London at all.
‘The first thing to know about hypnotism is that it doesn’t exist,’ Andrew said with satisfaction. ‘Here we are, third door on the left.’ After the urn of potpourri.
My idea was that if you could identify what motivated a monomaniacal genius like Simon to do mathematics all day long, then ask a hypnotist to make you feel that motivation too, you won’t be suddenly good at maths, but you might begin to study it in the correct pioneering spirit and force yourself to be better.
The noise of traffic outside disturbed his curtains.
‘Hypnotism can’t add something you haven’t already got,’ Andrew insisted. He’s had success helping people to flush their fags down the toilet because ‘Anyone can give up. The potential is already there. You’re not making them do something they can’t.’ Hypnosis ‘removes blocks to what is natural’. It’s similar to extreme day-dreaming. ‘If you talk to people who’ve been hypnotised, they won’t say, “He clicked his fingers and I was under, then I woke up and I don’t know what happened.” They’ll say, “I was aware, I just felt like pretending I was an artichoke.”’ You can mesmerise people to eat lemons believing they’re peaches, or to see green when they’re staring at purple, and people really do see green. Clinical psychologists have done experiments. The part of the brain that sees green registers. Everyone’s got the ability to be fooled.
Hypnotism is about ‘rapport: get the subject to feel responsive, then make suggestions that are easily taken up’.
‘Such as, “Congratulations, you’re a maths genius”?’
‘Exactly, except in mathematics, you’ll think you’re a genius, but what comes out will be rubbish. Now, how precisely do you imagine that this is going to be useful?’
A good question – but I was prepared.
Mathematics, I’ve realised from Simon, is a branch of painting. You can go to fine-art classes, take a first-class degree, study the masters from caveman to Rolf Harris, practise musculature and composition until your thumbs split … and still be bad at painting: your faces, technically perfect, are dead. Your gestures, flawless from the anatomical point of view, chopped out of cardboard. Your compositions, correct according to every authority since the Greeks and the Golden Section, without suggestion. You have no feel for vigour, unexpectedness, life. You are brilliantly trained, and the best stroke you could make would be to dump your brush in the vegetable grinder. Ditto, mathematics: unless you have natural talent, everything you do will be insipid, mechanical and lack adventure. A hypnotist cannot suddenly create natural talent, but he can give one an obsession. If I could wake up in this peculiar Queen Anne armchair in half an hour’s time, slavering to spot geometrical and numerical patterns, then I might also lie awake at night rabid with desire to characterise and make sense of these patterns. And that, I enthused to Andrew, grasping the air in my arms as though I were making off with an enormous coconut – the fruit of my delicious idea – is the essence of mathematical inspiration.
Andrew gave me a puzzled look, leaned to one side and made a mark on a pad of paper.
Mathematicians are aware if they’re creative or not, I hurried on. When they discover that they are not, it shudders their soul. I have friends with PhDs in number theory who wince with embarrassment whenever someone calls them ‘a mathematician’, because they know they are not worthy. They are to the authentic artist of mathematics what a weekend watercolourist is to Cézanne. At Trinity College in Cambridge, there was a man who scored a double first in his undergraduate degree, took his PhD in the flash of an eye, and still gave up in despair and became a tuba player. Since the age of twelve he’d doubted himself: under the sheets with a torch in his bedroom, he had not been able to pass a well-known childhood test of genius, i.e. to prove that the solution to any equation of the form
ax2 + bx + c = 0
must be, for reasons known otherwise only to God and magicians,
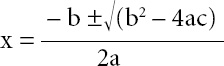
This man therefore believed – I lowered my arms at last, exhausted already by the algebra – that he could not ever be imaginative enough to call himself a proper mathematician.
Andrew tapped his fingers, beetled his brow – and made another mark on his pad of paper.
I’d read about how hypnotherapists work. Like biographers and mathematicians, they have to find the kinks in the surface of your problem before they can burrow into it. They pick on any catchy and summarising phrases you tell them during the twenty-minute warm-up period, then repeat these over and over again in the sleepy bit to help drive you ‘under’.
‘Simplicity,’ I summarised. ‘What drives Simon is a search for simplicities. I asked him for a question to test whether somebody has mathematical talent. He proposed, “Why is 11 x 11 equal to 121, and 111x111 = 12321 and 1111x1111 = 1234321?” Why, in other words, is that pretty rise and fall of the digits preserved?
‘“It’s not a question of why,” I’d snapped, “they just do it.”’
But it is a question of why – and ‘why’ is a question of discovering what is the simplest way to think about – visualise – sequences of 1s so that when you multiply them together you can see that obviously they must produce this charming answer with the bulge in the middle. I don’t know the reason. I can’t do it. 11 is just 11 to me, a pair of dumpy number 1s. I’d need to get out my pen and paper and devise ornate, well-trained formulas to parse 11 or 111 or 1111 into columns of units – tens, hundreds, etc. – then ram them together in a multiplicative frenzy that would leave x’s and y’s groaning all over the page. That would be my answer. But Simon does the opposite: he thonks down his pen; he sits back; he folds his hands behind his head; he makes one of his ghastly attempts at a whistling noise. The one thing all good mathematicians hate is honest labour. Instead of calculation, his mathematics requires an ability to see things in a different light, like those optical-illusion games in which you have to blur your eyes to turn a splatter of dots into a three-dimensional picture of an advancing stegosaurus.
‘Right, Alexander! Feet flat on the floor. Relax and close your eyes. Ten … maths is about finding simplicities … patterns …’ Andrew begins in a church-crypt murmur. ‘… nine … don’t divide up rows of ones and ram them together …’
That’s when the trouble starts: I can’t close my eyes. They flicker like beetle wings. Every inch of me starts to itch; every object on the street bellows. That isn’t a van honking, it’s a barricade of French juggernauts. That’s not a scratch in my ear, it’s a weevil boring towards my eye. Instead of feeling sleepy, I’ve jumped in the opposite direction: I’m less hypnotised than ever.
‘… eight … simplicities are everywhere and simple and you want to find them,’ counts Andrew.
A jackhammer starts up. Ants are making a nest in my nose. Most of us experience mild hypnotic states every day. Tests have shown that people blink less when they’re shopping – they’ve entered a state of mild hypnosis.
‘… seven … simplicity is joyful …’
But not for me. Andrew could go on counting down until he squeezed out the other side of zero and climbed to minus 1,000. I’ve never realised until now how infuriating the world is. Traffic noises fly through the window and bounce about the room like fifteen grasshoppers. Balloons filled with babies’ voices burst against the glass.
‘… six … patterns such as “two to the power of twenty-three spells sissors” … five …’
I try imagining the street full of integral signs climbing drainpipes, number sevens strap-hanging in buses, prams carrying Platonic solids – anything to get me into the world of maths and escape this hyper-wakefulness.
‘… four … next time you see a car number-plate you will want to factorise it … three …’
Hypnotisability has nothing to do with intelligence. Roughly 10 per cent of people are good hypnosis subjects. The Nobel Prize-winner Richard Feynman describes a hypnotist sitting him down and saying, ‘You can’t open your eyes,’ and Feynman couldn’t:
I said to myself, ‘I bet I could open my eyes, but I don’t want to disturb the situation: Let’s see how much further it goes.’
It was interesting: you’re pretty sure you could open your eyes. But, of course, you’re not opening your eyes, so in a sense you can’t do it.
Richard Feynman, Surely You’re Joking, Mr Feynman! (1985)
‘… two … your eyes are very heavy, so heavy … one … so very heavy, it is impossible now for you to open them …’ Andrew concludes in a soporific clincher.
I open my eyes, giggling with embarrassment for both of us.
One useful approach with therapeutic hypnosis is to find a structure, already present in the client’s mind, then doll it up with fresh encouragement and new suggestions.
Not long ago, a ten-year-old stepped into Andrew’s office – extraordinarily, he had exactly the same grouse as mine.
‘I want to do sums better.’
It’s not such a peculiar thing to ask for.
‘What are you good at already?’ Andrew asked. ‘And why?’
‘Stories. Words come to me through a door.’
‘What colour is the door?’
‘Red. With a big gold handle.’
So Andrew put him in a trance, took him back to the door, and started asking mathematical questions: ‘What’s two times two?’ A four sauntered out.
‘It was blue,’ remembers Andrew.
‘Three times three?’
Nine made an entrance, dressed in green.
‘Two times four?’
Eight stepped forth. Pink.
‘And this was not a weird child,’ said Andrew. ‘Just an ordinary young boy.’ Numerals had been hiding on the other side of the door all along. Hypnosis simply made them less bashful.
‘I, um, ah,’ I said, slapping my palms together to give me courage when I got back from hypnosis, ‘have been studying Cayley’s mathematics myself a little, as it happens.’
‘Hnnn,’ grunted Simon.
We were walking in Cambridge along the Backs – the section of the river that runs behind the ancient colleges – and turned off it up the path leading past the Library, on to the outcast newer colleges and University cricket pitch.
‘I gather that though Cayley published papers of great length, many are now considered somewhat arcane,’ I said.
‘Aaaagh,’ from Simon.
‘It’s his shorter notes that are thought to have captured the deepest insights. A vindication of his belief that the best work of a mathematician, like that of a biographer or artist, was often that done in five minutes.’
‘As I say, I don’t know that he did say that.’
‘I know you don’t know. That’s why I’m telling you. He did.’
‘If you say so.’
‘I do say so.’
‘Hnnnn.’
‘For example,’ I kept going, ‘the idea in Group Theory that is named after him: Cayley’s Theorem. That was one of those flash-of-insight triumphs.’
‘What’s Cayley’s Theorem?’
‘What’s Cayley’s …! Simon, you haven’t lost your marbles to that extent! Cayley’s Theorem: a fundamental theorem of Group Theory.’
‘Never heard of it.’
‘Well, let’s see, how does it go?’ I gathered in a pedagogic breath. ‘Yes, I think that would do it …’ I added in a tone of subtle calculation. In fact, I had spent several hours memorising it that morning from Schaum’s Outlines (‘The perfect aid for better grades!’) ‘Let S be a semigroup with Identity …’
For those of you not familiar with this language, note my use of the term ‘Identity’. Since hypnosis, I have had insight into Identity. Identity is much more important to Groups than it is to humans. Humans can have multiple identities, fractured identities, confused identities; identities which they’ve accidentally put in the dustbin and someone has stolen; identities that have wandered off to Thailand and for which the owner has to take six months’ sick leave to rush after and find. With Groups the situation is simple: a Group must have a very clearly defined object called an Identity Operation, or it is not a Group. Any Group Identity Operation claiming to be complex, split or misunderstood, is simply a liar. It should be instantly locked up.
For Groups an Identity Operation is one that does precisely bugger-all. It’s a scandal even to dignify it with such an energetic word as ‘Operation’.
The Identity Operation.
An Identity Operation leaves an object in exactly the same state as before. That’s how lazy it is. With Square, you can do various things that will leave a square looking the same as before; but you know, secretly, that these things have involved furtive twists and flips and turns. There’s only one operation that actually represents doing nothing to a square:
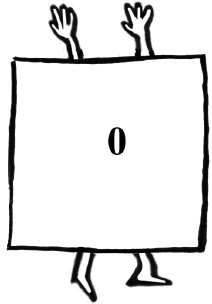
That’s the Identity Operation. With Triangle, the comparable Identity action is:
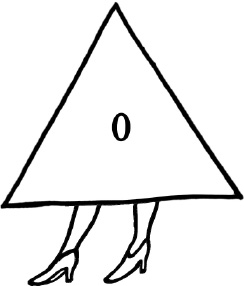
The Identity is everywhere in mathematics. With ordinary addition of numbers, what do you have to add to leave the number exactly as it is? Zero:
7 + 0 = 7
‘Adding zero’ is the Identity Operation for addition. For subtraction, just as for addition, 0 is the Identity:
7 – 0 = 0
7 minus 0 changes nothing; 7 is still 7.
This doesn’t make zero the Identity in all calculations. In multiplication, zero kills everything off:
7 x 0 = 0
It’s the number of annihilation in this case, not Identity. Everything zero touches in multiplication, it lays to desolation:
3 x 0 = 0
43,857 x 0 = 0
85,417,023,207 x 0 = 0
So, if zero isn’t the Identity Operation for multiplication, what is? What number can multiply with every other number without ever changing any of them, even slightly? The number one:
7 x 1 = 7
7 x 1 changes nothing: 7 is still 7.
Context in Identity Operations is everything, just as it is in life. Just across the park Simon and I were walking through is Charles Darwin’s old house. As a young man, all Darwin had wanted to do was race dogs, catch rats and get drunk. But, as with mathematics, so with humans: circumstances make all the difference. When Darwin gave up the sauce and pushed off to the Galapagos Islands on the Beagle, lo! that wastrel became the volcanic intellect of the age.
Any number can be an Identity if you make the circumstances right. Take twelve. It can’t oust zero as the Identity number for ordinary addition. It’s much too energetic:
7 + 12 = 19
In subtraction, twelve soon results in negativity and gloom:
7 – 12 = –5
With division, twelve is too pernickety:
7 ÷ 12 = 0.5833 …
For multiplication, it loses self-control. It sends numbers racing into the distance:
7 x 12 = 84
But every day, without thinking, billions of people around the world use a different sort of arithmetic in which twelve is the Identity: with clocks. Add twelve to any number on a twelve-hour clockface and the difference is bugger-all:
3 + 12 = 3
7.45 + 12 = 7.45
5.30 + 12 = 5.30
Now, to get back to my explanation of Cayley’s Theorem to Simon, as we walked out of the park and along the Backs towards the Mathematics Faculty.
‘Let S be a semigroup with Identity …’ I repeated manfully.
It doesn’t matter what a ‘semigroup’ is: I’m using it here just because it sounds good.
‘Let S be a semigroup with Identity, then by Cayley’s Theorem there is a monomorphism of S into MS, where MS is the semigroup of all mappings of the set S into itself.’
We reached a street corner, stepped out to cross, and Simon paused, apparently confused. The passing cars did not honk. They swerved gently to avoid us. Donnish behaviour is well understood at this road junction in Cambridge. Then he sighed, shook his head to release the furrows from his brow, and we hurried over the tarmac to Selwyn College, kicking at the fallen cherry blossom.
‘That’s so elementary,’ he said, ‘I didn’t even know it was a theorem.’