What do you mean, my genius vanished? That’s the first I heard of it.
Simon
The office where they worked was called ‘Atlantis’.
Magnolia paint frothed damply on the brick wall; the middle of the room was punctured by a pillar; the window frames were made of metal and shook in the wind. Atlantis was housed on the second floor (or was it the third? Simon’s uncertain) in a converted book warehouse. From the southwest corner of this building you could just see down to the river and punts, and, in a slice of park, girls stretching themselves along the grass, looking firmly away from mathematics.
Conway, Curtis, Parker, Wilson and Simon: Atlantis threatened at any moment to sink under the weight of paper these five mathematicians generated. Articles, books, abstracts, treatises, napkins, paper tablecloths, backs of envelopes, torn-off corners of cardboard boxes, reams of sprocket-holed computer print-outs – they soused the floor, suffocated the three office tables, bubbled up the window, drenched the door. Every day, more paper poured in – postcards from India, summaries from Novosibirsk, cuttings and marginalia from Honolulu, MIT, UCL, NYU, Beijing, St Petersburg, a carbon-copy manuscript from the University of Birmingham (always good for mathematics), pensées from São Paulo, scribbled notes of phone calls to Rome.
Conway, Curtis, Parker, Wilson and Simon were producing an almanac of Groups without normal Subgroups. Conway had had the idea in 1970: to gather together all known information about the different atoms of symmetry – a book of foundational wisdom. An atlas of symmetry.
It would take him, he thought, until 1973.
Conway would have to confirm every piece of known information, fill in thousands of gaps in the record, and dismiss all idiocies that had crept in when he hadn’t been in charge.
1974, at the outside.
In the end the project covered a fraction of the original idea, involved hundreds of mathematicians sending in contributions from around the world, and took fifteen years.
Conway, Curtis, Parker, Wilson and Simon were so different in character that nothing except mathematics could have kept them sitting together in that dreary, oppressive room.
Richard Borcherds, winner of the most prestigious award in mathematics, the Fields Medal, remembers standing in the faculty tearoom one day, discussing with another mathematician an ornate calculation he’d been working on for several days. At one point, Simon knocked past and overheard the conversation. Before he was out of earshot, he’d solved the problem and called back the answer over his shoulder.
Among a select group of mathematicians, Simon Phillips Norton’s status as a solver of long calculations of filigree delicacy is mythological. This is not the same as the conjuring tricks you read about in the papers, in which a schoolboy splurts out the answer to 987,654,678 x 770,645,321 in two seconds, or recites [H9266] to 30,000 places before you can tie your shoelaces. Those are unimportant, mechanical skills. Simon’s genius also isn’t the wild, Picasso-like brilliance of the world’s greatest mathematicians, who bolt together ideas that no one had previously imagined could be united. His ability is a precise, rigidly circumscribed, top-hat-and-cravat sort of genius. It’s a Nicholas Hilliard, exquisite miniaturist talent, lying a long way from the paint-by-numbers clunking of the [H9266]-chanters, but still at an angle to the chaos of frontier mathematics. It’s as though Simon shares his mind with a god who has a passion for making lace.
Solutions frequently appear to Simon without thought or questions about correctness. They appear – insofar as he can explain it at all – in the same way that hunger or lust or revulsion might appear to the rest of us.
Curtis, Wilson and Parker are all good mathematicians, but not in the same league.
Conway was Simon’s equal – and almost his opposite. They have contradictory temperaments. Conway is ebullient, teasing, garrulous, full of joyful and moving anecdotes, effortlessly eloquent, with a fine poetic sensibility (it was he who came up with the name Monster), and as arrogant, and eager with women, as a peacock.
Larissa Queen, a mathematician from Volgograd who became Conway’s second wife, remembers Simon for his modesty, good looks …
‘Good looks!’
‘Very good-looking. Several of the wives commented on it.’ … and total lack of sexuality. He always had ‘this enigmatic expression which I described as “I know, but can you guess?”’
I just smiled back, and that was it! I quickly realised that just because he smiles it doesn’t mean that we are going to have a conversation. There was a certain gentleness about him which I could describe only as intellectual kindness. He didn’t make you feel stupid, and he didn’t ever make you aware that you are wrong. He would just, kind of, you know, not do anything.
And another thing I remember! Whenever somebody entered the room he’d say, ‘Here comes my mother!’ It didn’t matter whether it was a man or woman, and it was the Maths Department, so it was usually a man. You would hear several times a day: ‘Here comes my mother.’
‘Simon, OK already!’ people would say. ‘I’ve had enough, could you please shut up!’ Oh, he said it loud enough for a group of ten people around him to hear … You could be as odd as you wanted to be in that Maths Department, and some people sometimes matched Simon’s oddness, but he was the most consistently, reliably odd. He maintained his permission to be odd.
And some people were not odd, and that was OK too.
Larissa often used to play Simon at the Child’s Game, a form of backgammon Simon had introduced. ‘More difficult, but with simpler rules,’
and very bright people, very good strategists could never beat him. He told me that he used to play it with his mother. I really got hooked, and practised and practised. I was determined to beat him, because for years he had this reputation in the Maths Faculty that nobody could beat him. At last I did beat him. And, you know, he reacted with joy. After that, he often suggested we play. And every time I beat him and he lost, he reacted with joy.
‘I tried Nola’s hymen!’
Another favourite faculty game played in the Common Room was making up anagrams, especially for Cambridge mathematicians. Nola’s defloration was an anagram of ‘Miles Anthony Reid’, now a Professor at Warwick.
‘Oil thy rim, Neasden!’ Parker shouted.
‘Slime ride, if you miss off the “Anthony”,’ exclaimed Conway.
Simon was by far the best in the department at this sort of thing. His answers were immediate, relevant, and you didn’t have to glance around to see if there were any children in the room before he said them. Miles Anthony Reid was a geometer; he had recently been to Russia.
‘Earthly dimension!’ brayed Simon, shaking his glass of lemon squash, because he refused to drink tea or coffee. ‘Lenin made history,’ he added a second later.
Another of Simon’s anagram triumphs, which Conway still remembers with amazement, was for ‘phoneboxes’, which Simon solved ‘as if with no thought’ before you can reach the answer given in this footnote.1
Simon’s attitude to mathematical problems was the same as it was to board games – what delighted him was the clever defeat of a puzzle. He was never interested in who got the credit for it:
He had the same smile when he came up with some brilliant solution. People would be working on a problem and he would just say a number, some long number. And people would continue talking, and maybe two or three hours later they would realise that this number explained the phenomenon they’d been puzzling over. Sometimes it would be hours later. They suddenly would realise what Simon meant – this number which is very brilliant and requires several very deep steps to arrive at – a whole sequence of extremely complicated thinking that other people who are the best mathematicians in the world and paid a lot of struggle and several hours to arrive at – and Simon just said it. And that would be it! He would never say ‘I told you so,’ or ‘Aha!’ He would have this joy of recognition; he would be silently pleased. And if without reason they didn’t remember what he’d said, he might repeat it. And add an additional clue. And the clue could be something else really deep – or it could be just, ‘Here comes my mother!’
Conway hates to lose. When I visited him at his house in Princeton he pointed out a photograph of himself on the bookcase, freshly fled from Cambridge and Group Theory, in his new office in America. It was taken a quarter of a century ago. Balanced at the top of a computer screen in the picture is a number, 15.92.
It’s his fastest time – in seconds – for calculating the days of the week for ten random dates. ‘I’m the best in the world at it,’ he pronounced. ‘There was a period when I was briefly ill, when I became second-best in the world and somebody overtook me. But that was only for about six months. Then I got better and was the fastest again! What’s your date of birth, Alex? Do you mind if I call you Alex? Ah, Tuesday.’
It was difficult to keep him on the subject of Simon.
‘Simon? I dunno, the life of an ageing prodigy is not easy. Inevitably, you compare yourself with what you were. I mean, we all suffer from it. We slowly substitute, you know, our knowledge and memory for our native wit. I mean, I was very bright, I wasn’t as natively bright as Simon … or … maybe I was! Er, you see, OK, so let me go off about myself again …’
Conway is crippled by alimony payments.
Mathematically also, Simon and Conway are poles apart. Simon is meticulous, never makes mistakes; he focuses on one particular problem to the point of burying himself in a rut over it; he’s a supreme manipulator of equations. Conway makes frequent schoolboyish blunders, such as putting in a minus where he should have had a plus – a small oversight, known as a ‘sign error’, but it instantly flings an answer from one side of the universe to the other, out of quiet correctness into blazing absurdity. This does not make him a bad mathematician; he spots the outrage soon enough.

Richard Parker (the ‘Parker’ of Conway, Curtis, Parker, Wilson and Simon) remembers one day in the Common Room watching Conway come back from the refreshment counter carrying a full mug of coffee. Slowly, Conway turned the mug upside down and spilled the contents onto the floor. Then he turned the mug the right way up, completed the walk to the table and sat down.
‘Conway!’ Richard cried. ‘What are you doing? What just happened?’
‘I made a sign error,’ admitted Conway. ‘Instead of keeping the mug up, I accidentally put in a minus sign and turned it upside down.’
Parker is a third sort of theorist. There is no one type of mathematician. They are as varied as lettuces. Conway, colourful, broad-ranging, flighty but also profound – radicchio; Simon, narrow, unforgettable, perfect in a thin field – endive; Parker, unfocused, watery, not at the same level as the first two, but now and again precisely right – iceberg.
I miss Parker terribly [says Conway]. He’s an ideas man. He would come in in the morning and say, ‘I think I can cure what’s wrong with last night’s maths argument – perhaps it’s like this …’ And I’d say, ‘Richard, that’s really stupid,’ and prove that it was just nonsense. Then he’d go away and say, ‘OK, how about this?’ So I’d say, ‘Give me ten minutes and I’ll come up with a counter-example.’ But he was never daunted. And every 100th time … Once, he’d taken three cases in which something corresponded to something else and said that maybe there’s a one-to-one correspondence between these things, and I said, ‘Richard, you’re so stupid.’ To base a conjecture on three cases was ridiculous. So we took a fourth case, and a fifth … I was getting a plane to New Jersey the next morning, and Neil Sloane [an eminent mathematician] met me at the airport because we had some project that we were going to work on. I said, ‘Drop all that, this idea of Richard Parker’s is absolutely fantastic.’ I lived off that paper for the next five years.
Parker was like that. One in a hundred of his ideas was OK, and there were ten a day at least!
This type of mathematician – enthusiastic, spotting shadows everywhere, occasionally putting better calculators or theoreticians on the right scent – has been vital to the history of Group Theory, and in particular the Monster.
Simon is different [says Conway]. He has this tremendous understanding, and he cannot rest if there’s some possible falsehood or contradiction lying around. Even if it’s somebody on a train saying something trivial. He’s like a dog gnawing at a bone. He has to find out what the truth is. I mean, I sort of know whether something I’m doing is deep and subtle and valuable mathematics or whether it’s just a frivolity, but I refuse to be intimidated by it now. I’m prepared to do whatever I like. But Simon to some extent doesn’t know. He really regards all things as equal.
Conway’s mathematical strength is in his flamboyant irreverence. He discovered:
1. The Game of Life. A game in which simple patterns made on a chequered board ‘evolve’ according to three extremely simple rules and (in certain variants) explain the coordinated movements of flocks of starlings, expose the organising principles of termites building up woodchips, and reveal the rationale behind the behaviour of human crowds.
2. An entirely new type of number called ‘Surreal Numbers’. He discovered them while sitting at a table in a café in Cambridge, playing Go. The way Go progresses as a game was, he realised, a code for a previously unknown counting system.
3. The Conway Groups in the twenty-fourth dimension (though Simon’s been unable to explain to me why Conway was looking for symmetries up there).
As a young man he wanted to ‘make some absolutely outstanding contribution and be “Conway, who’s the best mathematician in the world”’.
Well, I don’t necessarily mean the best, actually, just a certain standard … which is easiest to describe by saying ‘the best’.
Other mathematicians in the Cambridge faculty would come in at 11.30, spot Conway, Parker, Larissa Queen and Simon playing backgammon in the Common Room, and scowl. When these po-faced types staggered out of their offices again at 3 p.m. for a cup of tea, the four wastrels would still be playing.
There would always be a crowd of people standing round the board ‘kibitzing’, which meant offering advice [says Larissa]. Simon was a very, very active ‘kibitzer’, and the first time you play backgammon with seven or eight ‘kibitzers’ it’s impossible, your brain goes into a stupor and you can’t play because you hear eight different suggestions. The next stage comes when you can ignore them, and in the ultimate stage you can hear everybody. But it takes a long time to arrive there, lots of practice. You have to abandon your work for a while and concentrate on the backgammon. There was a certain vocabulary, a shorthand, you know. They would say, ‘Come screaming out,’ meaning to get out of your home table. In particular, there comes a time when no matter what you throw, the outcome is determined, and then people would say, ‘The dice are no longer,’ meaning the dice are no longer needed. And if Simon said, ‘The dice are no longer,’ people took it very seriously and stopped. They’d say, ‘Oh well, fine, start a new game,’ because on the few occasions when somebody computed, Simon was never wrong.
After his second marriage broke up, Conway tried to kill himself, and spent a week in hospital worrying about how he was going to face his students. Everyone in the faculty knew about the attempt. He knew they were all thinking about it. They knew that he knew that they knew; and so he wondered to himself, ‘What would Conway do? What would be a typically Conway-ish way to deal with this embarrassing moment?’
It would never cross Simon’s mind to think like this – to care so much about what his audience thought, or to talk about himself in the third person, as though he existed both as a human body and, like numbers themselves, a Platonic Ideal.
Conway solved the problem with combative brilliance. He borrowed a T-shirt from a friend who’d climbed a notorious granite outcrop in California, and appeared at the lectern wearing it – the logo read ‘Suicide Rock’.
Conway once invented a pair of spectacles to see in four dimensions:
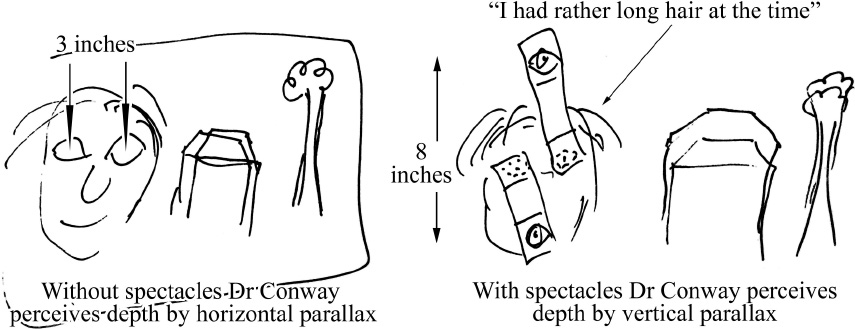
Drawing by John Conway.
He used a flying helmet to hold the spectacles in place, and spent a few hours stumbling round the mulberry tree in Sidney Sussex Fellows’ Garden. His brain adjusted, he walked around Cambridge with perfect ease, the first man in history to see hyperspheres, portholes to distant universes and observe the spirit world.
‘No, no, Alexander. Obviously my glasses were not going to let you see an extra dimension on top of the three we can already see. That would be ridiculous. Simon told me you were not a mathematician,’ concluded Conway worriedly, ‘but you do know that we can see only in three dimensions, don’t you?’
In the Atlantis office, Conway, Curtis, Parker, Wilson and Simon kept work on the atoms of symmetry that was finished or in immediate progress in a sweaty folder which sat on a chair, growing plump, bloated, disgustingly distended; finally, obese. Occasionally, it burst.
If any of the five men had a new idea about how to solve a problem, the chair plus the folder of flab was given a forceful kick, and rattled across to him to sort it out.
Whenever it seemed the room would certainly explode with all the gathered information about symmetry, one of the men – usually Parker, sometimes Conway, never Simon – would sit down at the office’s orange electric typewriter and type out the latest confirmed results on pages that were coloured – with deliberate nicety – Atlantic blue.
The most troublesome Groups were draped over the tables of the Common Room outside the door. Chairs and low tables ran down the middle of this dank, rectangular space, and ended in a ‘refreshments’ counter that was kept locked except at elevenses and mid-afternoon: 2p for a biscuit; sugar from a bowl; self-serve tea and coffee 5p a mug (mug not provided).
Anybody interested could come in, grab a cup or mug from the dirty crockery by the corner sink, splosh out a hot drink, perch over one of these sheets of cross-hatched paper bearing the latest state of knowledge about the symmetries of the universe, and add their tuppenceworth. Spotted a mistake in the top-right-hand-corner entries of J4? Don’t think the Harada-Norton Group is quite up to scratch in the 133rd dimension? Pop in your solution, let’s see … in this unscribbled-on scrap of margin here. See if Simon approves your suggestion when he gets back tomorrow from his bus trips to Bean (Kent) and Leek (Staffordshire).
This Common Room was the focal point of Cambridge mathematical life and, like a hospital, was open twenty-four hours a day. Even at 4 a.m. it was obscurely busy: slippered noises of people pacing back and forth in the surrounding offices; bursts of typewriter clatter; the hum of electrical fittings; a kettle boiling; the clack of dice and backgammon counters; a cry!; an office chair flung back; equations refusing to cooperate; shouts, swearing, feet pounding down concrete steps to street level.

Left to right: obese folder, Conway, Atlas.
The squeak, swing, squeak of the front door and a small returning rush of fresh air.
Simon’s time of Great Silence from the biographer’s point of view was his time of great noise in the hyperdimensional universe of mathematics.
Simon worked on half a dozen other projects during this period – not just the Atlas: surreal numbers, the Game of Life, Y monograms, the biMonster. He ‘masterminded’ the existence proof of the Harada-Norton Group.
But it is his work on the Atlas that keeps his name alive. After fifteen years of constipation –
(‘I think pregnancy is a better metaphor,’ mumbles Simon.)
– Simon’s most famous joint-mathematical publication at Cambridge, the Atlas of Finite Groups, was excreted.
(‘Born,’ hurries in Simon. ‘In 1985,’ he adds.)
The mathematical equivalent of a global malaria-eradication programme (the counterpart to malaria being ‘intellectual despair about Symmetry Groups’), the full title of the publication is the Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups. ‘Groups’ because the book is investigating symmetries, similar to  and
and  ; ‘Subgroups’ because that’s always the way forward in this subject; ‘Finite’ because the associated Group Tables of these symmetries have a countable number of entries; ‘Atlas’ because it attempts to cover all the types of foundational finite symmetry known to exist, and in a certain sense the tables can be regarded as a type of map; and ‘Simple’ because a) these Groups are all atoms of symmetry and b) because the contributors are lying through their teeth.
; ‘Subgroups’ because that’s always the way forward in this subject; ‘Finite’ because the associated Group Tables of these symmetries have a countable number of entries; ‘Atlas’ because it attempts to cover all the types of foundational finite symmetry known to exist, and in a certain sense the tables can be regarded as a type of map; and ‘Simple’ because a) these Groups are all atoms of symmetry and b) because the contributors are lying through their teeth.
The book is imbecilic with complexity – and littered with errors. Even with five of the best mathematicians in the university (two of them, Conway and Simon, among the best in the world) working for a decade and a half, there was too much information to master. Much of Simon’s work since this date has been to do with correcting the mistakes and filling out the gaps of understanding that still remain in the Atlas. The introduction to the Atlas, written by Conway, includes the following salaam to his brilliance:
Simon Norton constructed the tables for a large number of extensions, including some particularly complicated ones. He has throughout acted as ‘troubleshooter’ – any difficult problem was automatically referred to him in the confident expectation that it would speedily be solved.

Simon (after a haircut), Rob Wilson (another of the editors) and Conway at an Atlas reunion meeting in the King’s Street Run pub, Cambridge. The event was organised by Siobhan Roberts, Conway’s biographer. ‘There are so many biographers here,’ grumbled Conway, ‘we can hardly move.’
As the case of Triangle and three-pieces-of garbage-kicked around-Simon’s-Excavation showed, symmetries can be categorised into types. Those two symmetries (which appeared at first to have nothing to do with each other) turned out to be identical. The job of the Atlas of Finite Groups was to catalogue all the fundamental types of symmetry. That’s why they’re called the Simple Groups. They are the atoms of the subject. There can be other symmetries apart from these, but they will always be composed of one or more of the basic forms found in the Atlas, in the same way that a molecule is always composed of atoms from the periodic table. The Simple Groups catalogued in the Atlas are the elements, atoms or building blocks of Finite Group Theory. Every Finite Group can be broken down to a collection of one of these fundamentals, just as any molecule can be broken down into a combination of the elements in the periodic table, or any building can be fragmented into doors, windows, bricks, electrical wires, bent pipes and plaster dust. The Atlas is therefore the periodic table or builders’ catalogue for Group Theory.
This classification of Groups into their simplest components was a project of Victorian grandeur: a taxonomy (to use a third metaphor) of all the insects of Finite Symmetry – every mahogany drawer in the entomology halls of mathematics flung open, every tiny beetle sent in from a vicar’s garden plucked up and investigated to the last follicle.
The largest atom in the Atlas – the biggest brick, the most gargantuan and armour-plated insect – is the Monster. It is the largest Finite Group in the universe. There is nothing beyond it, except silence.
As soon as possible after the manuscript was published, Conway emigrated to a professorship in America, desperate never to look at a Group again.
The mathematician Benedict Gross has said that if his house was on fire, the one thing he’d battle back through the roaring flames and crashing timbers to rescue, leaping across cavernous molten stairwells, dodging the exploding gas boiler – would be the Atlas.
‘Which is quite unnecessary,’ points out Conway, ‘because you can get it online.’
Simon’s copy of this immortal book – torn to halfway down the ring binding, three blobs of biryani and Fern’s® brinjal pickle staining the top-right-hand corner – has moved from the place where we first met it, in Chapter 4. Simon consults the Atlas frequently. Now, it rests on top of the twizzle-legged table, under a love letter to his mother and a new paperback murder mystery called Zombies of the Gene Pool.
And abruptly we are here: the critical moment, the biographical climax of Simon’s story.
It’s so important to get this right – to get the pacing correct, to understand its immediacy, its horror.
I’ll use the present tense. It’s a moment of resonance for everyone, not just geniuses.
We’re back in the Atlantis office – or perhaps it was the Common Room. I’ll make an autocratic biographer’s decision, and call it the office. It is winter. The metal-framed windows ache with cold. Three people critical to the history of Group Theory are in the room, occasionally kicking a chair at each other between the towers of paper: Conway, Parker and Simon. They are discussing J4, the fourth Janko Group, page 188 of the Atlas.
Simon is sitting by the window. He blows his nose into a hand towel. He has a powerful interest in the Group J4. He’s been chasing it down in 112 dimensions, and has almost caught it.
Conway – we’ll put him at the desk with the orange typewriter, one hand delicately positioning the page, the other stabbing at the keys. With a Group Table that’s 86,775,571,046,077,562,880 columns wide, even the shorthand versions of the fourth Janko Group flop across two pages and require supreme secretarial skills.
‘Simon,’ says Conway, turning round, ‘if 2(1+12).3.(M22.2) is an involution centraliser of J4, what is …?’
Today, no one can remember what the question was – something ‘comparatively trivial’, recollects Parker.
Simon answered Conway instantly, of course.
Conway, satisfied, returned to his typing … then he stopped and gasped – Parker uses that word, ‘gasped’ – and turned back to Simon. The unbelievable had happened.
‘No, you’ve got that wrong. You must have made a mistake.’ Simon spotted the error too, and blushed.
‘That,’ said Conway, ‘is the beginning of the end.’
And it was.
1. Xenophobes.