Deterministic caching

Deterministic functions are the easiest and safest use case for caching. Deterministic functions always return the same value if given exactly the same input, so you can generally store their results indefinitely. The only limitation to this approach is storage capacity. The simplest way to cache results is to put them into process memory, as this is usually the fastest place to retrieve data from. Such a technique is often called memoization.

Memoization is very useful when optimizing recursive functions that may need to evaluate the same input multiple times. (We already discussed recursive implementations for the Fibonacci sequence in Chapter 9, Python Extensions in Other Languages.) Earlier on in this book, we tried to improve the performance of our program with C and Cython. Now, we will try to achieve the same goal by simpler means—through caching. Before we do that, let's first recall the code for the fibonacci() function, as follows:

def fibonacci(n): 
    """ Return nth Fibonacci sequence number computed recursively 
    """ 
    if n < 2: 
        return 1 
    else: 
        return fibonacci(n - 1) + fibonacci(n - 2)

As we can see, fibonacci() is a recursive function that calls itself twice if the input value is more than two. This makes it highly inefficient. The runtime complexity is O(2n) and its execution creates a very deep and vast call tree. For a large input value, this function will take a long time to execute, and there is a high chance that it will exceed the maximum recursion limit of the Python interpreter.

If you take a closer look at the following diagram, which presents an example call tree, you will see that it evaluates many of the intermediate results multiple times. A lot of time and resources can be saved if we reuse some of these values:

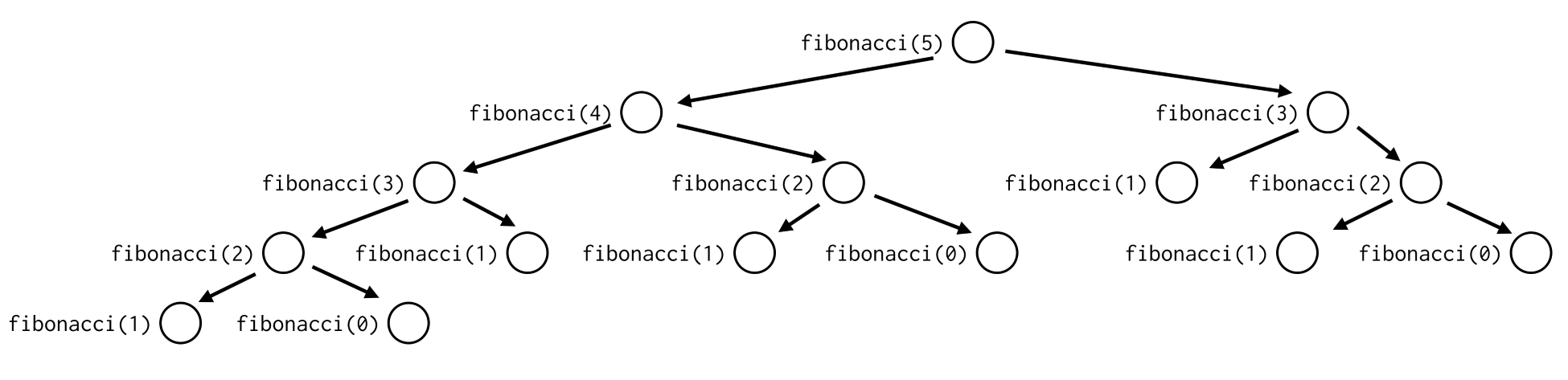
Figure 3: A call tree for the fibonacci(5) execution

An example of a simple memoization attempt would be to store the results of previous runs in a dictionary and to retrieve them if they are available. Both the recursive calls in the fibonacci() function are contained in a single line of code, as follows:

return fibonacci(n - 1) + fibonacci(n - 2)

We know that Python evaluates instructions from left to right. This means that, in this situation, the call to the function with a higher argument value will be executed before the call to the function with a lower argument value. Thanks to this, we can provide memoizaton by constructing a very simple decorator, as follows:

def memoize(function): 
    """ Memoize the call to single-argument function 
    """ 
    call_cache = {} 
 
    def memoized(argument): 
        try: 
            return call_cache[argument] 
        except KeyError: 
            return call_cache.setdefault(
                argument, function(argument)
            ) 
 
    return memoized 
 
 
@memoize 
def fibonacci(n): 
    """ Return nth Fibonacci sequence number computed recursively 
    """ 
    if n < 2: 
        return 1 
    else: 
        return fibonacci(n - 1) + fibonacci(n - 2)

We used the dictionary on the closure of the memoize() decorator as a simple storage solution from cached values. Saving and retrieving values in the preceding data structure has an average O(1) complexity, so this greatly reduces the overall complexity of the memoized function. Every unique function call will be evaluated only once. The call tree of such an updated function is presented in the following diagram. Even without mathematical proof, we can visually deduce that we have reduced the complexity of the fibonacci() function from the very expensive O(2n) to the linear O(n):

Figure 4:  A call tree for the fibonacci(5) execution with memoization

The implementation of our memoize() decorator is, of course, not perfect. It worked well for the preceding example, but it isn't a reusable piece of software. If you need to memoize functions with multiple arguments, or want to control the size of your cache, you will need something more generic. Luckily, the Python standard library provides a very simple and reusable utility that can be used in most cases when caching the results of deterministic functions in-memory is required. This utility is the lru_cache(maxsize, typed) decorator from the functools module. The name comes from the LRU algorithm, which stands for last recently used. The following additional parameters allow for finer control of the memoization behavior:

The usage of lru_cache in our Fibonacci sequence example would be as follows:

@lru_cache(None) 
def fibonacci(n): 
    """ Return nth Fibonacci sequence number computed recursively 
    """ 
    if n < 2: 
        return 1 
    else: 
        return fibonacci(n - 1) + fibonacci(n - 2)

In the next section, we will take a look at non-deterministic caching.