Figure 3.1 The normal distribution.
Humans and machines make errors of two kinds. “Systematic errors” are repeated errors that have a similar effect each time; we can often understand the causes of these errors and can predict and thus mitigate their impact. For example, suppose when I take my temperature I have a tendency to remove the thermometer from my mouth a little too soon: in that case, the temperature I think I am measuring will always be a little low. But if I discover that it is always a little low, I can work out a way to fix the problem—remind myself to keep the thermometer in my mouth for a bit longer, say. “Random errors” are more difficult to deal with. We cannot predict them, although we can estimate their typical size and the way they are “distributed”—as will be explained below.
We now want to apply this idea of error to track estimators such as Hawk-Eye. The problem the public faces is that track estimators are often presented as though they simply show what happened, without any error at all. But all machines make errors, just as all humans make errors. Engineers and scientists find no shame in this. Among scientists and engineers, it would be thought strange if a measurement were presented without an estimate of the error associated with it. This is just the scientific equivalent of you taking your temperature and seeing that it is 98° but knowing that the real temperature could be anywhere between 97° and 99°, because your thermometer is not that accurate and it is never quite clear if you have put it in the right place for the right time, and so on. Scientists and engineers have much more careful ways of dealing with these kinds of things.
What we need to do is make our own estimates of the kind of errors we think track estimators make, because not enough information about these errors is available to the public. It is true that some remarks about error can be found on Hawk-Eye’s website, even though in a sport like tennis the results are presented in real time as though they were perfect; but we are going to try to explain this question of error a little more in the way that scientists and engineers think about it, and then take another look at the way the track estimators should be showing their results.
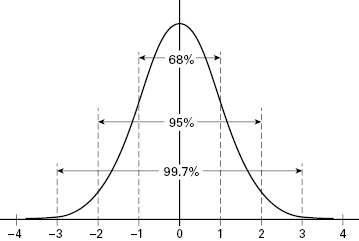
We’ll start with the idea of an “error distribution.” The idea is simple—if you take your temperature a large number of times you will hardly ever make a very large error, like getting the temperature wrong by two degrees, but you will make lots of small errors—a tenth of a degree here, a half a degree there. The idea of an error distribution is that small errors happen much more often than large errors, and you can show this on a diagram. If we create a diagram that has the number of errors represented by height on the vertical axis and the size of the error represented by distance from the true value on the horizontal axis, we will get what is called a bell-shaped curve—the shape of a bell if you cut it in half. Lots of kinds of measurements have bell-shaped error distributions; the most common shape for the bell is what is called a “normal curve” or “normal distribution.” A normal distribution is shown in figure 3.1.

Figure 3.1 The normal distribution.
You can imagine this curve represents you measuring your temperature thousands of times. You would get it right a lot of the time—the peak in the middle of the curve—and you would get it wildly wrong only very rarely, sometimes much too high—the tail at the right-hand side—and sometimes much too low—the tail at the left-hand side. The rest of the time your results would be in between the extremes, with many measurements close to the center and fewer and fewer as you move out and the level of error increases. The other lines in figure 3.1 show that in a normal curve 95 percent of all the measurements will be in a range bounded by two vertical lines set at a certain distance from the center. This distance is “two standard deviations,” and the other lines and numbers show how many of your measurements would be within one standard deviation, three standard deviations, and so on. But we do not need to worry about standard deviations; we need only to grasp three ideas:
Errors arise out of a whole raft of different causes. In the case of temperature, I might have just drunk a hot cup of tea so the temperature would read too high; I might have eaten ice cream, making it too low; I might have breathed a lot, cooling the thermometer while it was in my mouth; I might be too hot because I just ran five miles; I might have put the thermometer above my tongue or below my tongue or under my armpit; and so on. And, of course, lots of things might contribute to the final reading that we cannot even guess about. That is the way in which the bell shape can arise—big errors emerge (rarely) when lots of things combine, and small errors occur (more often) when only one factor is present. What we need to do is work out all the possible sources of the track estimators’ errors and, also, how they might add up.
As we started to explain in chapter 2, Hawk-Eye, when used to adjudicate calls in cricket and tennis, is a video-processing system that uses a number of cameras and a computer to store and process the data. The original patent application indicates that six cameras are used but also says that only two of these are needed for the system to work; the others provide redundancy (e.g., if one camera is blocked by a player). These cameras track the flight of the ball, and the computer then uses their feeds to reconstruct the trajectory of the ball by analyzing the pixels in each frame of each relevant camera. The field of play is also modeled within the system, as are some of the rules relating to the game. By combining the trajectory of the ball with the model of the pitch and the database of rules, the path of the ball can be reconstructed against the background of the main features of the playing area as a virtual reality, and a decision can be given (e.g., should the batter be given out in the case of cricket or, in the case of tennis, did the ball land inside or outside the line). The reconstruction can be shown to television viewers.
The cameras will have a limited frame rate, and the position of the ball between frames has to be reconstructed by the software. In the patent application, this process is not described in detail, but it is clear that the analysis is statistical, with predicted and measured paths being compared in order to generate the final trajectory.
In our analysis, we follow Hawk-Eye’s practice in describing how it works: its website presents the device as calculating a trajectory from a series of images of the ball captured in separate television frames.1 We are unconcerned with the exact statistical algorithm used in the reconstruction of the path of the ball. We take it that, as in all science and engineering, whatever the algorithm, the accuracy of the final result has an upper limit set by the accuracy and amount of the data. The crucial data concerning the path of the ball, then, consist of a series of “data points.” In the first instance, information is generated from camera frames containing certain pixels that are taken to signify the ball and other pixels that are taken to signify the line, wicket, or whatever is needed to locate the ball-pixels in the space of the playing area. When we refer to a “data point,” we mean a three-dimensional reconstruction of the position of the ball that involves information from two or more cameras. The idea of a data point serves the analysis adequately whether or not such data points are ever actually constructed as the Hawk-Eye processor runs. When we refer to “frame rate,” we are talking about individual cameras. It might be that the “effective frame rate” of Hawk-Eye is higher than that of a single camera because it combines frames from more than one camera to establish the trajectory of the ball in any one dimension. We simply do not know. Therefore, we assume that the “effective frame rate” is whatever frame rate we find mentioned in our sources. Any rough calculations we make are based on these seemingly plausible assumptions, but they are open to correction.
It would improve this analysis to have the answers to certain questions, which we will lay out in numbered form as we go through this chapter and the next. The first two questions bear on frame rate:
In our language, then, each effective frame provides a single data point; reconstructions will be more accurate with higher frame rates, as this minimizes the distance between data points. In addition, having more data points should allow more complex curves to be detected . Thus, two data points could provide information that can be used to infer the straight-line direction and velocity of the ball (subject to errors). For curved trajectories, more data points would be needed; and for trajectories where the rate of curvature changes, still more data points would be needed. It follows that, given a certain frame rate, the faster and curvier and more rapidly changing the flight of the ball, the more likely the reconstruction of its path will be subject to error.
In some circumstances, Hawk-Eye projects a hypothetical trajectory beyond its last data point. One such case is the “leg before wicket” (lbw) decision in cricket in which the continued trajectory of the ball beyond the last data point is projected forward and then represented on a virtual reality display that shows the television viewer what “would” have happened had the ball not hit the batter. We start with the lbw situation because the technicalities (if not the game) are relatively easy to understand, and it was the lbw decision that gave rise to our initial puzzlement about the claimed accuracy of track estimators. But before we proceed, let us explain our methods and why we have all these unanswered questions scattered throughout the chapter.
This chapter and the next two are about track estimators. Here we concentrate on Hawk-Eye as it was the first in use. Hawk-Eye was first introduced as an aid to judging the lbw rule in cricket, and this is why cricket is so central to this book. Track estimators are also well known for the use in tennis, and here we will compare the use in the two sports. Hawk-Eye, because it has been used for several years, has a well-developed website and has been the subject a range of media coverage and a few published articles. In what follows, nearly all the material we use in the analysis is drawn from such sources and so can be readily checked. Aside from some initial inquiries, we were unable to obtain significant information directly from Hawk-Eye Innovations, or from the makers of Hot Spot or the BBC in respect of the Match of the Day reconstructions of offside (see below). We did get considerable help from the makers of Tennis Electronic Lines and Auto-Ref, which are other technological devices applied to match officiating. We discovered toward the end of the analysis that a number of our questions and proposals had already been put by contributors to newspaper websites, but we cannot find any detailed response to the newspaper queries either, suggesting that our experience of meeting a near blank wall in the face of technical inquiries is not unrepresentative. (More details of what we were and were not able to find out about the Hawk-Eye system can be found in appendixes 2 and 3.)
The main professional work of the first two authors of this book is the analysis of science and technology. We have always found academic science readily accessible, and we have found academics ready to answer even our most intrusive technical questions. Thus Collins has spent around forty-five years studying the science of the detection of gravitational waves, writing four books about it, and has almost never experienced any problems of access to material. The secrecy we encountered when we set out to investigate track estimators is quite untypical of two lifetimes of experience working at the boundaries of science and technology. We consider that the secretiveness of the sports-measurement enterprises is dangerous and not in the public’s interest; the defense we have most often encountered when we have asked for details of the statistics of tests carried out is “You can’t have them because of commercial propriety.” This can only invoke deep suspicion.
Suspicion is not science, however, and to gain as much information as we could, we used the major search engines and databases systematically to search popular websites and the academic literature. Specifically, three people spent a total of about fifteen hours searching Google and Google Scholar (we looked at the first twenty pages that were returned) plus Web of Science (there were only three, irrelevant, hits) for articles relating to Hawk-Eye (spelled in various ways).2 Of the information we uncovered, we found the most useful on newspaper websites, a discussion site called “Cricinfo,” and Hawk-Eye Innovations’ own website. We also examined the original patent application, which is available online from the European Patent Office (reference number WO 01/41884). We also discovered an article in Scientific American (Fischetti 2007) and a published analysis of line calls in tennis (Mather 2008).
We found only one article about Hawk-Eye in an engineering journal but it was very hard to access, in both senses of the term. We discuss this paper more fully in appendix 3. We do not know how that paper, which reports on the development of a device under contract with Hawk-Eye Innovations, bears on the technology that is currently used, but, in any case, no substantive difference would be made to the analysis if it included more reference to this paper unless it is true, as the paper implies, that Hawk-Eye takes its television feeds from existing TV network cameras; this would indicate lower camera frame rates and a greater potential for error than we discuss in this chapter. In any case, we are sure the technology has moved on.
Reliance on data in the public domain means that our information about how Hawk-Eye works is not complete. If we had the kind of access that we have to the academic scientists and technologists with whom we normally work, we would have expected to gain answers to a number of questions; but now those questions are distributed throughout these chapters and, unfortunately, have not been answered. As we work through the analysis, we show where the answers to these questions would be useful. As it has turned out, then, we have mostly had to rely on “back-of-the-envelope” calculations based on what we can glean from the public domain, but, as will be seen, quite a lot can be learned using only this approach.
Turning back to the substance of our analysis, we now have to explain a bit more about cricket. To start with, bowling in cricket is quite different from pitching in baseball, for many reasons. For one, the bowler nearly always aims to hit the ground with the ball before it bounces up into the domain of the batter. Therefore, a crucial feature of bowling is the way the ball bounces off the pitch. Slow bowlers will aim to impart a lot of spin to the ball so that it jags sideways when it hits the ground, and faster bowlers will cause the ball to swing through the air both before and after it hits the pitch and also jag sideways off the pitch as a result of interaction between the pitch and the raised seam of the ball.
Another crucial difference between cricket and baseball is that in cricket there are no “balls” or “strikes.” There are illegitimate balls, as when the bowler oversteps the mark or bowls the ball beyond the batter’s reach, but these are rare exceptions rather than a regular part of play. Most important, in cricket matches there is no limit on the number of balls a batter may face; as far as the batter is concerned, the game lasts for as long as he or she can avoid being out. In longer forms of the game, batters have gone on for days; and even in the more frenetic short forms, the batter is always balancing the need to score runs quickly with the need not to be out. But there is nothing in the rules to make the batter end his “innings” if he does not score any runs.
As we have seen, if a ball from a bowler hits the wicket, the batter is out. The batter wears pads to protect each leg. Each pad is an armored sheath running from ankle to just above the knee. Allowing the ball to hit the pads is an integral part of the game; the batter would never be out if he or she simply stood in front of the wicket, blocking the path of the ball, kept the bat out of the way, and allowed the ball to hit the body or the pads every time. The notoriously complicated lbw rule stands in the way of this possibility. It says that the batter is out in certain restricted circumstances if the pads alone stop a ball that would otherwise have hit the wicket—this counts as out in virtue of leg before wicket or lbw.
We now need to go deeper into the heart of cricket’s darkness to explain the restricted circumstances that apply to the lbw rule and upon which the use of track estimators in cricket turns. Cricket, as the old hands say, is a sideways game. The bowler will deliver the ball from a sideways position like a javelin thrower and the batter will stand sideways to receive it (see figure 2.2 for a diagram of the field of play in cricket). A right-handed batter’s left leg will face up the pitch toward the bowler, with the right leg nearer to the wicket. A left-handed batter will be the other way round. Though batters are not exactly sideways, this roughly defines their orientation, and this orientation is important because it defines the sides of the pitch in relationship to the stance of the batter. The side of the pitch closest to the batter’s hands and bat is called the “offside,” whereas the side closest to his or her legs—the side on which he or she is standing—is called the “leg side” or “onside.” The “late cut,” which was discussed in the last chapter, is a deflection toward the offside, whereas the “leg glance” is a similar deflection toward the leg side. To understand the lbw restrictions one must imagine a rectangular strip, nine inches wide, painted on the wicket and stretching between both wickets (or drawn on the “pitch,” if “wicket” is too confusing). First, a batter cannot be out in virtue of lbw, even if the ball was going on to hit the wicket, if the ball pitches on the leg side of that strip, unless he or she was not trying to hit the ball with the bat (playing a stroke). Second, a batter cannot be out by lbw, even if the ball was going on to hit the wicket, unless the ball strikes the batter’s pad “between wicket and wicket”—that is, in the area above that imagined rectangular strip. Bear in mind that the ball can jag sideways off the pitch and the bowler can bowl from quite a wide position so that a ball that is going on to hit the wicket could hit the batters’ pads well outside the space above our imagine painted rectangle. Once more this applies only if the batter was “playing a stroke”; if just standing there with bat raised or hidden behind the pads, then the batter can be out “leg before wicket” even if struck outside of the wicket-to-wicket area above the strip. There is room for a lot of interpretation about whether a batter was playing a stroke—after all, it is all about the batter’s intention.
So, those are the restrictions. If those restrictions are satisfied, or if, in the umpire’s judgment, the batter was not playing a stroke, the batter is out if the ball hits the pad without hitting the bat first and was then going on to hit the wicket. For all nontelevised cricket, an umpire, who stands at the point from which the bowler bowls the ball, is the sole judge of whether the ball (a) falls within the restrictions and (b) would have gone on to hit the wicket. Nowadays, in top games, a track estimator can be called in to help the umpire’s decision. The track estimator will create a reconstructed image of the playing area with a virtual rectangle drawn between wicket and wicket and then reconstruct the track of the ball and project it onto the playing area. The reconstructed graphic shows where the ball is estimated to have pitched and, in particular, whether it pitched on the leg side outside of the virtual rectangle—ruling out lbw so long as the umpire judges that the batter was playing a stroke. (It can pitch outside the off side of the virtual rectangle so long as it hits the pads above the virtual rectangle and the batter was playing a stroke.) The track estimator also reconstructs the point at which the ball struck the batter’s pad and determines whether that point was above the virtual rectangle—that is, between wicket and wicket. Still more contentiously, the track estimator reconstructs the path that the ball would have taken had it not hit the batter’s pads, indicating whether it would have gone on to hit the wicket or not. Discussion of the accuracy of this kind of reconstruction, the kinds of error to which it is subject, and the way such errors are handled in cricket and tennis makes up this chapter and the next.
Figure 3.2 is a two-dimensional schematic version of the lbw situation from the side. The ball, traveling from left to right, bounces (“pitches”) and then hits the batter’s pad-protected leg. The dotted portion of the trajectory is what has to be judged or estimated. Television viewers see a three-dimensional virtual reality representation of the projected path of the ball against a virtual cricket field, and they can see where it pitched in relationship to the virtual rectangle drawn between wicket and wicket, where it struck the pad, and whether it was going on to hit or miss the wicket. For a number of years after the introduction of Hawk-Eye, cricket commentators would simply remark on what Hawk-Eye showed on the screen, giving the impression, perhaps inadvertently, that the virtual reality represented exactly what would actually have happened had the pad not been struck. This is where our analysis of Hawk-Eye begins.
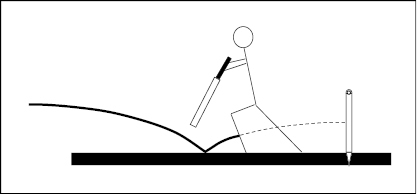
Figure 3.2 A two-dimensional schematic of a potential lbw situation.


Figure 3.4 Track estimator showing estimated path of ball from behind the wicket.
The trajectory of the ball after it hits the ground can vary enormously. The bounce depends on the speed, hardness, and texture of the ball—which changes during the game—the state of the ground at the exact point of the pitch, the spin on the ball, and the position of the seam. The “swing”—the aerodynamically induced curve in the flight of the ball, which can be in any plane—depends on the ball’s speed, its spin, its state, its orientation, the orientation of the seam, and the state of the atmosphere. As a result, what happens to the ball after it bounces is not predictable from its prebounce trajectory, so that the technology has to estimate the postbounce trajectory from postbounce behavior of the ball, for which it can gather data only between the bounce and impact on the pad. Paul Hawkins, then the director of Hawk-Eye Innovations, in response to a criticism from Dennis Lillee, the Australian fast bowler, explained the matter as follows:
“Hawk-Eye simply observes and then calculates the actual trajectory of the ball. Whether the cause of this trajectory was due to atmospheric conditions, the wicket, or the ball hitting the seam is irrelevant from a Hawk-Eye perspective. Hawk-Eye just tracks what happened—it does not try to predict nor to answer why it happened.”
So, if the ball rears up unexpectedly after hitting the seam or a crack on the pitch, Hawk-Eye will track the trajectory off the pitch to predict the future course of the ball. Similarly, the tracking system will come into play if the ball shoots along the ground after hitting a dry spot on the pitch. (Rajesh 2003)3
Our concern in analyzing what Hawk-Eye can do is to understand more fully what it means to “track” and “predict” the path of the ball. The accuracy of predictions is limited by, among other things, the quality of the data. To repeat what was established earlier in this chapter, no measurement is ever exact.
A decision is not a measurement. A decision is binary, like the “guilty/not guilty” decision of a jury; in cricket, the batter is either out or not out. The process of what we will call “digitization” is used to turn what are (always) inexact observations into discrete decisions. In most sports, the referees or umpires do the digitization, relying on their ontological authority; and what we are discussing here could be described as technical aids to this sort of digitization. The bails in cricket, for example, are one such aid to digitization. As discussed above, it can sometimes be difficult to tell whether the ball has touched the wicket and the falling of a bail converts this uncertainty into one of two discrete possibilities that, in most cases, have merely to be “read off” by the umpire.
In the case of lbw decisions, of course, the bails can’t help, because the flight of the ball has been stopped before it gets to the wicket. Instead, the umpire has to judge whether the bails would have been dislodged had the ball continued on its trajectory and passed “through” the batter instead of being stopped by the pads. So, can a track estimator effectively replace the bails in the decision-making process?
This kind of technological digitization cannot correspond exactly with that of the bails in all cases, because in some circumstances it will be impossible to predict with certainty whether the ball really would break the wicket if it had not hit the batter’s pad. To take the extreme circumstance where the ball just touches the wicket, whether the bails would fall would depend on how firmly they are sitting in their grooves, how rigidly the stumps are held in the ground (the tapered part at the base of each stump is hammered into the turf to hold them upright), or whether the bails and stumps are wet or dry. Again, the ball is not exactly spherical so whether it would cause a bail to fall can depend on its orientation as it passes the wicket. We assume that predicting all these things is beyond the capacity of both Hawk-Eye and human umpires; all we are doing in this paragraph is reestablishing the principle of the imperfection of all such measurements. It might help to have an answer to this question, however:
What we would like to know is what Hawk-Eye’s and other track estimators’ measurement errors look like. We would like to see a graph of the type that we have exemplified with human body-temperature measurement. We would like to know if the “bell” is narrow or wide and the size of the standard deviation. But we have not found any detailed indications of the dispersions of Hawk-Eye’s errors in the public domain. The nearest we could find are the following quotations from Paul Hawkins when interviewed by S. Rajesh on the Cricinfo website:
Hawk-Eye has shown that balls pitched on roughly the same area on the wicket have passed the stumps at widely varying heights. And in tests conducted, thousands of deliveries were bowled from a bowling machine and filmed by Hawk-Eye. The camera feeds were cut about two metres from the stumps, approximately the point where the batsman would normally intercept the ball. When the ball hit the wicket, Hawk-Eye was able to determine, to within about 5 mm, the point of impact. …
“Hawk-Eye requires between 1 to 2 feet of travel after the ball has pitched to be able to accurately track the ball out of the bounce (this is significantly less than an umpire requires). In instances when this does not happen, a Hawk-Eye replay is not offered to TV. (Rajesh 2003)
Watching a fair bit of cricket on TV, however, Collins has never encountered a case where Hawk-Eye did not provide a graphic when the bounce-to-pad distance was short; and so, another question we would like to ask is how often have such nonpresentations occurred? We would also like to know if a graphic has ever been offered even though the distance was very short and, in those cases, how the graphic was generated.
Hawkins explained in 2006:
In most cases Hawk-Eye’s output is accurate to within five millimetres in predicting the path of the ball. The accuracy levels are highest when the ball has travelled a fair distance after pitching, but even when the point of contact is very close to the pitch of the ball, the accuracy levels are still within 20 mm. (Rajesh 2006)4
Note that twenty millimeters is four-fifths of an inch, which is quite a long way when it comes to breaking or not breaking a wicket.
We don’t know if the developers of Hawk-Eye have attempted to estimate the dispersion of their errors in a way that is more exact than is indicated in the above quotations, but we have not found any such report. This gives rise to Question 5:
As the quotations intimate, the size of the error will be affected by the length of the bounce-to-pad trajectory, but it will also depend on other factors. The bounce-to-pad trajectory is not of fixed length; the position of the bounce is variable and deliberately varied by the bowler, and the batter can move forward or backward to try to reach a position from which he or she can most comfortably defend the wicket or strike the ball forcibly (hence opening up the possibility of stumping). The length of the projected pad-to-wicket trajectory depends, then, on the pitch of the ball and where the batter is standing when struck. The accuracy of Hawk-Eye’s estimates is likely to depend directly on the distance between the bounce and the moment of impact on the pad—the longer the better, because then more data points can be gathered so as to give a better estimate of the projected path of the ball, especially where that path is not a straight line. There will be an inverse dependence on the distance between the impact on the pad and the wicket—the shorter the better, because the longer the distance the more damaging an error would be in the estimate of the path. To help with this problem we would like answers to Questions 4 and 5 (above) and also to Question 6:
In the case of the human umpire making an lbw decision, it is acknowledged that the accuracy of the judgment is affected by how close the batter is to the wicket when the pads are struck by the ball. If the batter whose pads are struck is well forward—a long way from the wicket—then, traditionally, an “out” decision is rare. In this way, human judges deliberately introduce a systematic error into their judgments that favors the batter—the so-called “benefit of the doubt” rule. The importance of this rule will become clear later.
As we have said, none of the information that we have found in the public domain gives any indication of the overall dispersion of Hawk-Eye’s errors; the only indication of how the error increases with a short bounce-to-pad trajectory that we can find is given in the quotation above. We can find no systematic information about how the size of the error relates to the position at which the ball bounced, the speed of the ball, the length of pad-to-wicket trajectory, the length of bounce-to-pad trajectory, the degree of spin, the degree of swing, the nature of the pitch surface, and the nature of the atmosphere. Although the patent application does acknowledge that the distance of the camera to the ball is important (e.g., frame sizes are set to make the ball appear as large as possible) and that the position of the sun matters (e.g., it is important to distinguish the ball from its shadow), it does not tell us how variations in these or other parameters affect the accuracy with which the position of the ball can be tracked.
Unfortunately, the importance of accounting for these errors is greatest when the decision is most difficult. When the projected point of impact is well away from the edge of the wicket, there is unlikely to be any real doubt about the “correct” decision, and so Hawk-Eye’s errors are probably considered “hardly worth reporting.” In both cricket and tennis, Hawk-Eye’s and other track estimators’ digitized decisions are likely to be better than human judgment when the ball is not close to the critical zone; humans make big mistakes more frequently than machines make big mistakes.
But where the judgment is much more difficult—for both human and machine—then the potential error becomes crucial. To move forward it is necessary, first, to acknowledge that there is a distribution of error in the measurement and, second, to describe the characteristics of this distribution—wide or narrow. At worst, these should be described for the general case, but it would be much better to provide separate analysis for each of the main conditions that can affect the accuracy of the prediction. For example, it would be nice to know the distribution of error associated with fast balls and slow balls, with different lengths and ratios of the various trajectories, and, perhaps, with different condition of the pitch, the atmosphere, and the ball. For example, to what extent do track estimators make bigger errors in conditions when the ball tends to swerve as it travels through air after hitting the wicket?
The frame rate of the cameras will affect the accuracy of the prediction. Though the technical article referred to above suggests that Hawk-Eye takes its feed from standard broadcast cameras (which would have a frame rate of around 30 per second—“fps”), we will assume that the frame rate is 120 fps, as reported in 2004 on the Cricinfo website (see Questions 1 and 2 above).5 In this case, if the ball is traveling at 80 mph (just under 120 feet per second), it would travel one foot between frames. This would make sense of Hawk-Eye’s claim to need between one and two feet to make a prediction. In the worst case scenario, a ball traveling at 120 feet per second with a frame rate of 120 fps would need a minimum of two feet to provide three data points, which should be enough to estimate some kinds of constant curved trajectory, though there will obviously be some error and uncertainty. Fortunately, this lack of sure knowledge of frame rate and method of calculation does not affect the general principle of the argument, but it would still be nice to have an answer to Question 7:
We do not know if data from the tests involving “thousands of deliveries” (see above) have been preserved. If they have, they might give an initial indication of the distribution of error as per Question 8.
But, of course, measuring the errors means being sure of where the ball actually went, and we don’t know how this was measured and how accurate those measurements were:
The beginnings of a more complete analysis could be made if, in a test like this, the cutoff point for the camera feed was systematically varied and the bounce point of the ball was systematically varied so that a more complete range of potential errors was analyzed. In a still better test, these parameters, and other parameters that affect the post-bounce behavior of the ball, would be recorded and measured so that the likely size of error could be reported for different circumstances. Some of this may be beyond the capacity of companies who make track estimators, but if it is then it should be clearly stated.
In an ideal world, our preference would be as follows. The margin of error should be estimated from empirical tests, either in the way suggested above or in some other way. Reports on the method of testing and its degree of completeness and its possible unreliability should be made readily available. Subsequently, using whatever knowledge of the distribution of measurement error was available, confidence levels would either be associated with Hawk-Eye and other track estimators’ reconstructions in real time or, if this were not possible, incorporated into the rules that govern how track estimators are used. The graphic shown to television viewers could be adjusted either to show something like an error bar, or error circle, around the projected position of the ball, or to indicate in some other way (such as numerical) the confidence level for the prediction that wicket would have been struck or not struck. Figure 3.5 (the putative errors are not drawn to scale) indicates some of the possibilities, though no doubt it could be improved upon.
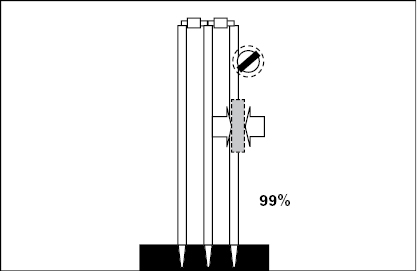
Figure 3.5 Some ways of indicating Hawk-Eye’s possible measurement errors (not to scale).
If such changes were implemented, commentators might remark, “The track estimator was 99.9 percent sure the ball was going to hit the wicket so the umpire was right,” or “The track estimator was only 90 percent sure the ball was going to hit the wicket—the umpire should not have given it out,” or some such. This way, not only would Hawk-Eye and other track estimators’ abilities be presented in a clearer and less easily misunderstood way, but the technology itself could fulfill a valuable role in educating the public about the way uncertainties are turned into decisions. What we are suggesting is not much more than is mentioned in the Hawk-Eye patent that we have found. There it is claimed that the HIT-MISS decision made by the apparatus is based on “whether the probability of the ball going on to hit the stumps is high e.g., above a given probability threshold” (8). We are asking for a more complete explanation of what the threshold is, what the probability is on any occasion, and for this information to be offered to the public. Nevertheless, we do think that the way track estimators are used in cricket is much more helpful than the way they are used in other sports (see chapter 5), particularly tennis, to which we’ll turn in the next chapter.