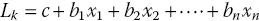21
Application of Multivariate Statistical Analysis/Chemometrics in Food Forensics
Introduction
The various measurements obtained from food samples or sources of foods (plants/animals, etc.) are desirable for analysts to acquire the target information about that food sample, for example food composition, presence of foreign substances in foods, taste properties, texture, aroma, color, origin, life‐span, changes that may occur to foods during processing, storage, authenticity, etc. All these food properties may be revealed by different types of instruments, which provide specific signals for various food properties. In certain circumstances, food properties may undergo alterations due to changes in certain food constituents and these changes can be monitored by specific techniques that will be indicative of the occurrence of physico‐chemical alterations in food composition caused by either endogenous or exogenous factors, which may include climatic conditions, agronomical practices, the ripening process, storage conditions and time, geographical origin, etc. When the composition of food is known, it makes it easier to establish whether there is an adulteration practice, or presence of irregularities in food processing procedures that may compromise quality or authenticity, etc.
However, food is a complex substance, both in terms of composition and its behavior under different biological/physico‐chemical conditions and this leads to complex signals during food analysis by different types of instruments. This signal complexity from food samples, which actually produces huge amounts of data from a variety of many signals, implies that a univariate statistical data treatment of the signals, which may involve a few signals to describe the trend or behavior of certain food constituents, is misleading to a large extent. This implies that the vast majority of other signals, which are not selected or considered for statistical univariate analysis, will be lost and valuable information that would have been deduced from them will not be harnessed. However, in order to properly identify and select the most important signals, as generated from the analytical instruments (i.e. signals that represent important variables in the food samples), one would require appropriate information concerning the properties of the food that has been analyzed. The issue will now be how to identify these crucial signals that are associated with important variables in food composition. The answer to this is to employ multivariate statistical analysis, also known as chemometric data analysis, an approach that can address adequately issues related to the identification and selection of important signals to explain the important variables in food samples, and also how to handle complex spectral patterns. Generally, multivariate methods of analysis make use of mathematical principles, statistics, informatics, and profound knowledge about the data (chemistry, electronics, and hardware) to extract the maximum useful information from a large number of data by reducing their dimensionality, with the aim of:
- classifying and/or discriminating among groups of food samples, on the basis of certain criterion such as geographical/botanical origin;
- mode of food processing;
- relationship between composition and physico‐chemical properties; and
- calibration for the prediction models for identification of unknown samples and/or control food processes.
Multivariate chemometrics techniques are capable of converting signals in a value, a process parameter or an instrument diagnostic. Multivariate chemometric techniques can be tuned to work for targeted/comprehensive/metabolic profiling by identifying and quantifying constituents in food samples and classifying them based on certain criteria, in order to identify biomarkers vital for identification in cases involving adulterations, provenance, etc. Normally the identification of food components is aided by standards/reference/model compounds. In addition to this, multivariate techniques can use metabolic fingerprinting, where metabolites are actually not being identified or quantified, but rather the signals due to food samples obtained from the instrument are subjected to statistical analysis to identify relevant spectral features or patterns that can differentiate samples that have been analyzed. In this way, it is possible to employ multivariate techniques for samples that generate highly complex data signals, which normally make it almost impossible to accurately integrate signals.
Procedures for Sample Selection Prior to Chemometrics Data Analysis
The requirements for having data analyzed by using multivariate chemometric statistical analysis include the sample size, which must involve large numbers of samples with representative properties sought in the study, in order to guarantee or ensure that there will be variability in the data collected. If this is not done properly, then there is the high possibility of collecting inappropriate samples or samples with undesirable properties and this will result in large errors in the statistical analyses and render the use of chemometrics valueless. It is therefore imperative to devise a proper sampling regime that contains precise, accurate, and complete information about the sample (e.g. sample identity, sample size, place and date, and method of sampling/coordinates, measurement data for the rheological properties data if done onsite … e.g. taste, color, etc.).
Sample Preparation Prior to Analysis Intended to Generate Data for Multivariate Analysis
It may be desirable to perform some sample pre‐treatment procedures such as extraction and purification. These procedures are specific to the types of food samples being analyzed, analytical procedures, the intended information required from the food samples and the type of instrumental technique being used for the analysis. After the analysis, the data signals generated (spectra, chromatograms, etc.) must be processed appropriately in terms of scales, retention times, peak areas, chemical shifts, etc. This step is generally known as the data pre‐processing step (Alam and Alam, 2005; Araníbar et al., 2006; Berrueta et al., 2007; Izquierdo‐Garcna et al., 2011; McKenzie et al., 2011; Vierec et al., 2008).
Targeted Metabolic Profiling Prior to Statistical Data Treatment
Targeted profiling of metabolites can be performed in steps, which include:
- the identification of all signals that belong to the analytes of interest, as generated from the instrument. These signals can be spectra, chromatograms, etc.;
- integrating these identified signals for analytes of interest;
- assigning the identity of the signals to the compounds they actually represent, using either stands/reference materials or a compound library database if it is incorporated in the software; and
- quantification of these compounds.
However, in almost all analytical data generated by analytical instruments, not all signals are associated with either of the targeted signals or important fragments that may be needed for statistical analysis and therefore such signals need to be eliminated, otherwise they will result in a weak predictive performance or poor discriminatory power. In other words, the analyst needs to do data reduction in terms of data dimensionality by performing data exploration to establish both the data quality as well as suitability, if they are to be subjected to statistical analysis (Berrueta et al., 2007).
The Analysis of Variance (ANOVA)
The analysis of variance (ANOVA) statistical technique is useful in splitting the overall total variability found in the data set. The splitting generates individual components that are important in explaining the contribution of individual/specific properties or variables to the overall total variability of the properties in the dataset. There are several statistical techniques that are known as ANOVA and these include one‐way ANOVA, two‐way ANOVA, and multivariate analysis of variance (MANOVA), which are useful in data analysis through experimental designs.
One‐way ANOVA as a statistical technique is employed when one wants to investigate the statistical significance (as evaluated by the Fisher test or F‐test) of the mean magnitudes of two or more sample groups that may be affected by one independent property/variable. Generally, the F‐test is used to test the null hypothesis and determine whether the samples are in the same class or not. In cases where the F‐test gives a high value for each of the variables, then the null hypothesis can be suggested to be wrong, implying that samples do not belong to the same group and therefore this particular property/variable can be suitable for use in the classification of samples.
Two‐way ANOVA, on the other hand, is useful to improve and strengthen the performance of one‐way ANOVA, by incorporating the effect of two differently independent variables/properties that may show on the response and also it incorporates the possible interaction factor between the two properties/variables.
In reality, far more large data is normally generated by analytical instruments, such that even two‐way ANOVA will be insufficient to classify or explain the diversity. In these cases, ANOVA needs to be extended to multivariate analysis of variance (MANOVA), a statistical technique in which a linear combination of several independent variables is utilized to discriminate samples within many classes/groups. MANOVA is far more attractive than either one‐way or even two‐way ANOVA, since it can provide the correlations that exist between variables and can reveal variability that cannot be shown by either one‐way or two‐way ANOVA.
Multivariate Statistical Analysis Techniques (Pattern‐recognition Methods) in Food Forensic Samples
Multivariate statistical analysis methods, also known as pattern‐recognition methods, make use of mathematical data pre‐treatments in order to accomplish the intended specific purposes in terms of the reduction of variables. These methods include principal component analysis, and other multivariate techniques, which are normally used for statistical qualitative analysis, and multivariate calibration for quantitative analysis of data. Generally multivariate statistical methods are known to be the most suitable for maximum extraction of the required analytical information contained in the analyte, as provided by the signal or data generated by analytical instruments and procedures on samples. There are several multivariate techniques that are normally employed in the extraction of information from data acquired from analytical procedures and/or instruments, but all of them are capable of quantitatively relating the measured analytical variables to their respective analyte properties and thereby qualitatively group samples with similar properties or characteristics into the same classes. These methods can therefore be useful in food provenance cases, food authenticity testing, food fingerprinting, etc., for different types of foods.
Multivariate/Chemometrics Techniques in Food Classification
Analytical instruments and methods normally produce lots of data with massive information, which as such requires steps that involve variable‐reduction procedures to reduce this massive information, to be able to deduce the trend that will play an important role in constructing the classification and calibration models, as well as the optimal number of correlated variables contained in the generated data.
Principal Component Analysis (PCA) as a Variable‐reduction Technique
Principal component analysis (PCA), a mathematically derived procedure capable of reducing variables by decomposing the data matrix composed of rows (samples) and columns (variables) into the product of a scores matrix, has been widely employed in variable‐reduction in many instances. In PCA, the scores represent the positions of the samples in the space of the principal components, while the loadings represent the contributions of the original variables to the principal components (PCs). Generally, principal components successive PCs (PC1, PC2 ….. PCn) are mutually orthogonal, with each successive PC containing fewer total variables of the initial data set as compared to the preceding ones. However, in normal practice, just a limited number of PCs are retained and those that may arise from noise are not retained and for this reason PCA reduces the dimensionality of the data, thereby making it possible to both visualize and classify as well as perform regression of the data being analyzed (Geladi, 2003).
Multivariate Qualitative Methods
In qualitative analysis, discrete values are to be assigned to analyte characteristics/properties that represent signals generated by the instrument, such that they are the ones used to identify the product or product’s state of quality, for example, the product is original, or the product is a blend, or the product is fresh, etc. Generally, multivariate classification methods are subdivided into two main groups, namely:
- Supervised pattern recognition methods: which are also known as discriminant analysis methods, are used only when the group to which the sample being analyzed belongs is known. The aim of the supervised pattern recognition in which the classification group to which the sample belongs is known, is to use a set of data with known classifications to teach the software to discriminate between classes and thereafter come up with working models and comprehensive libraries that can be used predict the classes to which unknown samples belong.
- Non‐supervised pattern recognition methods: these are used when the group to which the sample belongs is not necessarily known and therefore these methods are also known as exploratory methods. The intention of using the unsupervised pattern recognition is to gain knowledge regarding the data set through exploration of natural clustering of the samples and therefore understand the contribution of each variable to the clustering that has been worked out using unsupervised learning algorithms (Geladi, 2003).
Supervised Pattern Recognition (Discriminant Analysis) Methods
In supervised recognition (discriminant analysis) methods, the classification criteria can be based on either the data signal (as obtained from the analytical instrument) space or in a dimension‐reduced factor space. Generally, certain statistical techniques for data reduction, such as the principal component (PC) or partial least squares (PLS) analyses, may be employed to reduce data, even before subjecting the data to discriminant analysis to perform both size and co‐linearity reduction, and this step precedes the one that involves data‐signal treatment to mark the relation between the data signal and the class/group considered to be the one to which the sample belongs. The data signal treatment can be achieved using methods such as factorial discriminate analysis (FDA) (Karoui and Dufour, 2003); linear discriminant analysis (LDA); and k‐nearest neighbors (k‐NN) (Sikorska et al., 2005). These methods are useful in creating weighted linear combinations of the data, thus helping to minimize variance within classes and to maximize variance between classes, thereby ensuring that the distances between the data means/averages of the classes surpasses those within the classes. The distance between classes is vital, as it characterizes the partition that is obtained and at the end of the day this distance interval has to validate the method.
In terms of application of supervised pattern recognition methods in food forensic issues, these methods have been used in the analyses of a number of foodstuffs for different reasons and objectives such as profiling, fingerprinting, authentication, food quality control, data interpretation, etc. There are several techniques that are associated with supervised pattern recognition methods and these together with multivariate calibration and prediction models such as partial least squares (PLS), partial components regression (PCR), and multiple linear regression (MLR), are widely used as statistical methods in food analysis. They include PLS regression, classification and regression trees (CART), soft independent modeling of class analogies (SIMCA), discriminant analysis (DA), artificial neural networks (ANN), and k‐nearest neighbors (k‐NN) (Alam and Alam, 2005; Beebe et al., 1998; Berrueta et al., 2007; Izquierdo‐Garcna et al., 2011; McKenzie et al., 2011).
The attractive role these methods play is that they are capable of relating multiple data sets (data signals generated from the analytical instrument) to a characteristic property or several properties of samples and thereby assist in predicting the desired trend of information being investigated. The supervised pattern recognition methods and some of the multivariate calibration and prediction methods are discussed in the subsections below.
Partial Least Squares (PLS) Regression Multivariate Calibration and Prediction Method
This technique generalizes and makes use of features in other multivariate statistical methods, mainly principal component analysis, as well as multiple regression methods to predict and/or analyze a set of dependent factors (variables) from a set of independent factors (variables) or predictors.
This technique can be of valuable importance in the analysis of food samples presented for forensic analyses, because like all samples in the research fraternity that fall under science and engineering, they use massive controllable and/or easy‐to‐measure variables (factors) to either explain, regulate, or predict the behavior of other variables (responses) from samples presented as evidence in food forensic investigations. In some special cases, the method (PLS) can be used, even in cases where variables/factors are numerically few (implying that they are not significantly redundant or collinear), but if these variables do present a good relationship to the responses, then one can employ multiple linear regression (MLR) to process these same data into useful information that is able to predict responses. But generally, PLS is a statistical technique used to construct predictive models to describe the variability, trend, etc. in the data set when variables/factors are many and highly collinear (except in cases where one needs to gain an understanding of the underlying relationship between the variables). PLS is also not suitable if one needs to employ it as a screening tool for factors that might have a negligible effect on the responses.
Food forensic PLS has been applied in many cases to different food samples, for example in the quality assessment of fruit juices (Spraul et al., 2009) and beers (Nord et al., 2004), as well as in a case where it was required to establish correlations between the composition and sensory attributes of wine (Skogerson et al., 2009).
Linear Discriminant Analysis (LDA)
Linear discriminant analysis (LDA) is normally used to find a linear combination of features that characterize or separate two or more classes of samples. Unlike PCA, which despite its strengths and advantages, does not include label information of the data, LDA does utilize the label information in finding informative projections. In LDA, what is being done is actually the construction of linear discriminant functions (Li), also known as canonical roots. These linear discriminant functions are actually linear combinations of the (independent) variables (xn), commonly known as the input variables or predictors. Predictors with the highest discriminatory ability that are used in the LDA equation (Equation 21.1) can be selected by ANOVA:
where b1, b2, etc. are the discriminant coefficients and c is a constant.
Equation 21.1 implies that there are a total of k_1 discriminant functions for k number of classes of samples that are being investigated/analyzed. Therefore, what LDA does is to select the proper discriminant functions, which leads to the maximum separation among the given classes of samples. For example, the first discriminant function, i.e., L1 distinguishes the first group from groups 2, 3, 4,…, n groups and for the second discriminant function L2, it will therefore distinguish the second group from 3, 4,…, n groups, etc..
Despite these advantages, LDA analysis suffers from two major shortcomings, which include:
- cases where there are large differences in the number of samples in each class, which may result in directing the classification in the favor of the most populated class(es); and
- for LDA to give the best predictions, it requires the presence of a larger number of samples than the number of variables, otherwise LDA as the classification model will fail to predict new data, thus resulting into what is known as over‐fitting.
There are different variants of LDA that are also used in predicting patterns and they include the stepwise discriminant analysis (SDA) and the PLS‐DA.
Discriminant Analysis (DA)
Discriminant analysis (DA) is a pattern recognition statistical method based on a linear function constructed by observations whose group membership is already known and is used to predict the group membership of new samples/observations. To identify variables effectively, the stepwise discriminant analysis (SDA) model may be a better option, due to its capability to filter out variables with little contribution in the process to identify observations’ group membership.
Stepwise Discriminant Analysis (SDA)
Generally, stepwise discriminant analysis (SDA) approaches are attractive for:
- selection of useful subsets of variables; and
- evaluation of the order of importance of variables in the dataset. SDA can be done in two main ways:
- forward stepwise discriminant analysis (FSDA); and
- backward stepwise discriminant analysis (BSDA).
The FSDA method builds a classification‐prediction pattern in a stepwise manner, such that at every selection step all variables are reviewed and evaluated, in order to get the variable that mostly contributes to the discrimination between the classes of the samples being investigated and therefore this particular variable will be incorporated into the model and the same process will start again for the next discriminant function, until all discriminant functions have gone through the selection criteria.
In BSDA, all variables are included in the model and then at each selection step, the variable that least contributes to the prediction of class membership is removed and the subsequent selection step is performed in a similar fashion until the last one. This will finally create a model that is comprised of only variables with greater discriminatory power.
Partial Least Squares Discriminant Analysis (PLS‐DA)
Partial least squares discriminant analysis (PLS‐DA) combines PLS with DA to exploit the advantages of both statistical methods, so as to maximize or sharpen the separation amongst/between classes/groups of samples/observations under investigation. The maximum separation of groups of observations is achieved by rotating PCA components, in order to ensure that a maximum separation among classes is obtained, and to also enable a thorough understanding of the actual variables that highly influence the class separation. Generally, PLS‐DA is involved in a normal PLS regression system where the response variables are given a categorical numeral one (1) in the sense that this is replaced by the set of artificial/dummy variables (zero values) that describe the categories, but which express the class membership of the statistical units. In other words, in the PLS‐DA pattern recognition method, the PLS regression model can be worked out to enable the recognition of factors that relate the independent variables (the original matrix X) to an artificial (dummy) Y matrix, which is normally constructed with only zeros and ones, with as many columns as there are classes of the sample to be investigated. For example, if a vector matrix in PLS‐DA is presented in the matrix form [0, 0, 1, 0], it implies that of the four possible classes, the particular sample belongs to class 3.
Therefore, PLS‐DA does not allow for other response variables than the one for defining the groups of individuals. Due to this, all measured variables play the same role with respect to the class assignment. However, the PLS‐DA is a more attractive approach than the LDA discussed above, due to the fact that it is applicable in all cases, even where the number of samples is lower than the number of variables (Consonni et al., 2011).
k‐Nearest Neighbors Algorithm (k‐NN)
The k‐nearest neighbors algorithm (k‐NN) can provide a platform for use as a classification tool and/or regression (Rokach and Maimon, 2008) and the kind of output is mainly dependent on whether k‐NN is used for classification or regression. It can be useful in classifying an input by identifying the k data, i.e. the k “neighbors” in the known/training set that are closest to counting the number of “neighbors” that belong to each class of the target variable, classifying by the most common class to which its neighbor belongs. In other words, k‐NN classifies unknown samples based on their closeness/similarity with samples (the training/known data set or k‐subset) of known membership. In the process, it is required that one should look at a given unknown sample of the k nearest sample in the training data set and assign this sample to the class that appears most frequently in the k‐subset. For this to be accomplished, k‐NN requires:
- an integer k;
- a set of known samples (training set or k‐subset); and
- a metric to measure the nearness between samples, and one of the most commonly‐used distances between samples is the Euclidean distance metric/measure that calculates the distance between samples x and y, which have coordinates xi and yi over the n‐dimensional space (the index i ranges from 1 to n variables).
In both cases, whether used for classification or regression, k‐NN provides a useful tool in the assignment of weight to the contributions of the neighbors (as obtained from a set of observations/samples for which the class (for k‐NN classification) or the observation property value (for k‐NN regression) is known), such that the nearer neighbors will be expected to make more contribution on average than the ones that are further away (Quinlan, 1986; Stone, 1984). Moreover, k‐NN is attractive because it is analytically tractable due to its simple mathematics and implementation; it is free from statistical assumptions, for example the requirement for normal distribution of the variables; it is also nearly optimal for the large sample limit (n‐N); and it lends itself easily to parallel implementations. The main limitations of the k‐NN algorithm include the fact that it is sensitive to the local structure of the data. k‐NN is also known to have a large storage requirement; it cannot work well if large differences are present in the number of samples in each class; and also the use of the Euclidean distance makes k‐NN very sensitive to noisy features, which necessitates the modification of the Euclidean metric by a set of weights that stress the importance of a known sample as a neighbor to an unknown sample. This metric system ensures the nearest neighbor influences the classification more than the farthest ones.
Soft Independent Modeling of Class Analogies (SIMCA)
Soft independent modeling of class analogies (SIMCA) is a statistical software that makes use of a training (actual) set of samples with known identity. The actual (training) sample set is normally divided into separate sets, such that there is one for each class and then PCA is performed separately for each of the classes. In SIMCA, every region may contain samples either on a line, i.e. one principal component, or on a plane, i.e. two principal components, or on a 3‐D space, i.e. three principal components. It can also be extended to higher‐dimensional regions, i.e. “n” principal components. When SIMCA is performed on each class in the data set, it thus generates sufficient numbers of principal components that are retained and which play an important role in accounting for most of the variation within each class. This presence of a principal component model will be used to represent each class in the data set.
In each of the classes in a data set, the number of principal components retained are unique to that class and therefore care has to be taken to decide on the appropriate number of principal components that may need to be retained for each class, such that they are not too few to distort the signal or information content contained in the model about the class or too many to diminish the signal‐to‐noise. Generally a method known as cross‐validation, which also ensures that the model size can be determined directly from the data, can be employed to determine the number of principal components in the training set. Cross‐validation procedures for the determination of the number of the appropriate principal components number begins by omitting a certain portion of the data during the PCA by repeating the process, making use of PC1, PC2, PC3, etc. until every data element has been kept out (omitted) once and the omitted portion/segment of the data as well as the unknown samples are then predicted, matched, and compared to the training samples or actual values in the class models and assigned to classes according to their analogy with the training samples. From this process, the principal component model that yields the minimum prediction error for the omitted data is the one that will be retained and therefore cross‐validation will have served its purpose to find the number of principal components necessary to describe the signal in the data, while ensuring high signal‐to‐noise by excluding secondary or noise‐laden principal components in the class model.
Classification of the unknown sample (e.g. in samples presented as evidence in food provenance issues where the origin, authenticity, identity, etc. is being sought) can be achieved by comparing the residual variance of an unknown food sample to the average residual variance of those samples that make up the class. Having done that, it is possible to obtain a direct measure of the similarity of the unknown to the class. In other words, the sample being investigated can only be grouped as a member of a particular class if it is sufficiently similar to the other members of this class, otherwise it will be rejected and considered as an outlier.
Decision Trees: Classification and Regression Trees (CART)
Classification and regression trees (CART) are statistical tools that are useful for constructing prediction models from data sets. CART are actually tree models in which the target variable can take a finite set of values They make use of a decision tree as a predictive model, which maps out observations about the samples being analyzed to conclusions about the sample’s target value. In the CART tree model, leaves denote class labels, while branches denote conjunctions of features that lead to these class labels.
Decision trees as a statistical technique, useful in data mining, can be subdivided into two main types:
- Classification tree analysis: this is only applicable in cases where the predicted outcome is actually the class to which the data belongs.
- Regression tree analysis: this is applicable when the predicted outcome can be considered a real number (value), i.e. it is a class of decision trees in which the target variable takes continuous real numbers (values).
Generally, decision trees are meant for dependent variables that take a finite number of unordered values, with the prediction error measured in terms of misclassification cost and also for dependent variables that take continuous or ordered discrete values, with prediction error normally measured by the squared difference between the observed and predicted values. The classification and regression trees (CART) are used to generate a set of simple rules, which are suitable for predicting the origin of any new (unknown) sample being investigated. If the predicted outcome happens to be the class membership, then a classification tree is the one that will be constructed, but if a regression tree is created, then it implies that the predicted outcome is a real number, for example the value of a variable (Berrueta et al., 2007; Breiman et al., 1984).
Artificial Neural Network (ANN)
According to Marini (2009), the application of artificial neural network (ANN) in food analysis is scarce and less preferred as compared to other chemometric techniques, for example PCA, LDA, and PLS‐DA (Marini, 2009). ANN mimics the functioning of the neural network in the brain, such that just as the biological neurons systems in the central nervous system receive signals through synapses, so do the artificial networks receive input data that are then multiplied by weights that mimic the strength of the signals, and are then computed by a mathematical function, which determines the activation of the neurons (Berrueta et al., 2007; Marini, 2009). The operation of ANNs is as follows: as natural neurons receive signals through synapses, so the artificial networks receive input data that subsequently are multiplied by weights that mimic the strength of the signals, and then are computed by a mathematical function, which determines the activation of the neurons. Another mathematical function computes the output of the artificial neurons. In ANN, the higher the weight of an artificial neuron, the more influential is the input variable multiplied by it. By adjusting the weights and the variables that are used to feed the artificial neural network, specific outputs that explain the particular complex problem are obtained.
There are several variants of ANN that differ in terms of the input and/or output functions, the accepted values, and the learning algorithms, etc.
ANN is attractive in the statistical analysis of food samples presented as evidence in forensic cases, because it completes tasks that a linear program cannot and also its parallel nature guarantees continuous function, even when an element of the neural network fails and moreover learns and does not need reprogramming, and it can be implemented in applications without serious problems. The shortcomings associated with ANN include the fact that there is a need for training of the model, high processing time, and difficulty to interpret the original variables.
Non‐supervised Pattern Recognition Methods (Exploratory Methods)
Non‐supervised methods examine the natural classification or clustering of either samples or variables, or both, and are applicable in the first stages of the investigation in order to reveal the different property/characteristic levels, such as ripening levels of fruits within the subgroups in a data set and thereby the method served to cluster the products. Examples of cluster analysis techniques that can be employed include (i) hierarchical cluster analysis (HCA); and (ii) principal component analysis (PCA).
The Hierarchical Cluster Analysis (HCA)
The hierarchical cluster analysis (HCA) is normally used to assess the similarities between product samples according to their measured characteristic properties or variables whereby product samples are grouped into clusters based on their nearness in multi‐dimensional space. Normally, HCA results are depicted in the form of dendograms, such that either samples or variables that are similar or that show strong correlation with one another, fall in the same cluster of dendograms and also samples that are not similar or that show weak correlation are clustered in different groups in the dendograms (Poulli et al., 2005).
The HCA is further classified into two main subtypes, namely:
- agglomerating HCA: in which the process of clustering begins with each sample product forming a unique and specific cluster, then iteratively merges pairs of individually formed clusters that are closest to one another until one larger cluster is formed. HCA involves the calculation of the magnitude of distances among all samples that constitute different clusters that are joined to form one larger cluster, by using amalgamation rules such as Euclidian distance and also the single linkage.
- divisive HCA: which is the opposite of agglomerating HCA. Of these two HCA types, the agglomerating clustering is the one that is most widely used due to its simplicity and clustering power.
The Principal Component (PCA) Cluster Analysis
The principal component (PCA) cluster analysis is very useful in cases when one needs to find relationships between different parameters in either samples and variables and/or the detection of possible clusters within the samples and/or variables. This method involves the reduction of the dimensionality in terms of the number of variables of the data set, using as few axes or dimensions as possible. The new axes, which are known as the principal components (define the linear combinations of the original variables), are orthogonal to one another and serve to describe the variation within the data set.
PCA provides the analyst with a tool for initial investigations of large data sets to explore trends in terms of similarities and classifications, as well as the detection of outliers. Generally, in PCA, the first principal component presents the maximum magnitude of the variability in the data set, and each subsequent principal component accounts for the remaining variability. In the form of matrix notation, the data matrix X can be described as the product of a score matrix S and a loading matrix L, i.e. X = SLT, where LT = the transpose of the loading matrix. The S matrix contains the information about the magnitude of variance each principal component describes, while the loading matrix denotes the contribution of each variable to the construction of the principal components.
Multivariate Calibration for Quantitative Analysis
For quantitative analysis, multivariate regression methods are the ones widely used. Among the multivariate regression methods are:
- partial least‐squares regression (PLSR): which is capable of searching the directions of highest variability by comparing both signal of interest as generated by the analytical system and target characteristic property information with the new axes known as PLSR components or PLSR factors. In other words, PLSR represents the most relevant variations showing the best correlation with the target property values.
- principal component regression (PCR): which makes use of the principal components generated by the PCA to perform regression on the sample characteristic property that is to be predicted. Therefore, in this approach, the first principal component or factor in PCR denotes the widest variations in the sample signal generated by the analytical system (Geladi, 2003).
Validation Approaches for Chemometric Pattern Recognition Models
In chemometrics, there is a possibility of obtaining a close fit that may look like it is the convincingly desired one using more and more principal components in PCA experiments, but which may not present meaningful information. Under these conditions, a validation procedure becomes necessary in order to define and limit the number of principal components that will yield a sufficient number of components that are necessary to describe the trend and the data in general. Validation of the statistical pattern recognition chemometric models is also of significant importance for the purpose of the evaluation of the significant variables required to construct the model, as well as for the recognition and prediction ability of the model. Validation of chemometric pattern recognition models can be done by either employing:
- external validation: which is more applicable in cases where there are large number of samples;
- internal validation: also known as cross‐validation, k‐fold cross‐validation or the jack‐knife method, which is mostly applicable in cases where the number of samples is limited.
The external validation approach does not depend on the model building procedures that incorporate the actual data (training) set in cross‐validation as internal validation does.
Factors that Govern a Proper Choice of Statistical Technique in Food Forensic Samples
A number of factors may need to be considered in order to make an appropriate choice for the chemometric technique for food forensic samples and they may include the number of purposes of the analysis and chosen model, data structure, the variables required, the number of samples under investigation, as well as the metabolomic protocol that has been chosen for the samples (Berrueta et al., 2007).
For example, unsupervised pattern recognition methods, such as HCA and PCA, may be mostly suitable in cases where there is a need to investigate similarities and/or differences amongst food samples. The supervised pattern recognition models are mostly suitable in cases where there is a need to predict the class membership of future samples.
Conclusions
Multivariate techniques are highly useful as validation methods that are required to validate and prove the reliability of the methods and data generated with regard to the authenticity of the procedures and results. Every technique and method applied in food forensics needs to incorporate multivariate statistical methods, as well as data mining using these chemometric methods.
References
- Alam, T.M. and Alam, M.K. (2005) Chemometric analysis of NMR spectroscopy data: a review. Annual Reports on NMR Spectroscopy, 54: 41–80.
- Araníbar, N., Ott, K.‐H., Roongta, V. and Mueller, L. (2006) Metabolomic analysis using optimized NMR and statistical methods.Analytical Biochemistry, 355(1): 62–70.
- Beebe, K.R., Pell, R.J. and Seasholtz, M.B. (1998) Chemometrics: A Practical Guide. John Wiley & Sons Inc., New York.
- Berrueta, L.A., Alonso‐Salces, R.M. and Héberger, K. (2007) Supervised pattern recognition in food analysis. Journal of Chromatography A, 1158(1–2): 196–214.
- Breiman, L., Friedman, J.H., Olshen, R.A. and Stone, C.J. (1984) Classification and Regression Trees. Wadsworth & Brooks/Cole Advanced Books & Software, Monterey, CA.
- Consonni. R., Gagliani, R., Guantierg, V. and Simonato, B. (2011) Identification of metabolic content of selected Amarone wine. Food Chemistry, 129(2): 693–699.
- Geladi, P. (2003) Chemometrics in spectroscopy. Part I: Classical chemometrics. Spectrochimica Acta Part B, 58: 767–782.
- Izquierdo‐Garcia, J.L., Villa, P., Kyriazis, A., del Puerto‐Nevado, L., Pirez‐Rial, S. et al. (2011) Descriptive review of current NMR‐based metabolomic data analysis packages. Progress in Nuclear Magnetic Resonance Spectroscopy Journal, 59(3): 263–270.
- Karoui, R. and Dufour, E. (2003) Dynamic testing rheology and fluorescence spectroscopy investigations of surface to centre differences in ripened soft cheeses. International Dairy Journal, 13: 973–985.
- Marini, F. (2009) Artificial neural networks in foodstuff analyses: Trends and perspectives A review. Analytica Chimica Acta, 635(2): 121–131.
- McKenzie, J.S., Donarski, J.A., Wilson, J.C. and Charlton, J. (2011) Analysis of complex mixtures using high‐resolution nuclear magnetic resonance spectroscopy and chemometrics. Progress in Nuclear Magnetic Resonance Spectroscopy Journal, 59(4): 336–359.
- Nord, L.L., Vaag, P. and Duus, J.Ø. (2004) Quantification of organic and amino acids in beer by 1H NMR spectroscopy. Analytical Chemistry, 76(16): 4790–4798.
- Quinlan, J.R. (1986) Induction of decision trees. Machine Learning, 1: 81–106.
- Poulli, K.I., Mousdis, G.A. and Georgiou, C.A. (2005) Classification of edible and lampante virgin olive oil based on synchronous fluorescence and total luminescence spectroscopy. Analytica Chimica Acta, 542: 151–156
- Rokach, L. and Maimon, O. (2008) Data Mining With Decision Trees: Theory and applications. World Scientific Publishing Co. Inc., Singapore.
- Sikorska, E., Gorecki, T., Khmelinskii, I.V., Sikorski, M. and Kozio, J. (2005) Classification of edible oils using synchronous scanning fluorescence spectroscopy. Food Chemistry, 89: 217–225.
- Skogerson, K., Runnebaum, R., Wohlgemuth, G., De Ropp, J., Heymann, H. and Fiehn, O. (2009) Comparison of gas chromatography‐coupled time‐of‐flight mass spectrometry and 1H nuclear magnetic resonance spectroscopy metabolite identification in white wines from a sensory study investigating wine body. Journal of Agricultural and Food Chemistry, 57(15): 6899–6907.
- Spraul, M., Schuütz, B., Humpfer, E., Mörtter, M., Schäfer, H. et al. (2009) Mixture analysis by NMR as applied to fruit juice quality control. Magnetic Resonance in Chemistry, 47: S130–S137.
- Viereck, N., Nergaard, L., Bro, R. and Engelsen, S.B. (2008) Modern Magnetic Resonance (ed. G.A. Webb). Springer, Cambridge, UK, p. 1833.