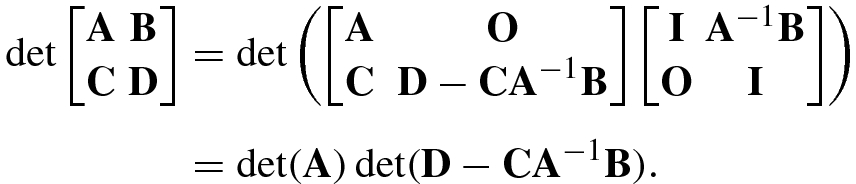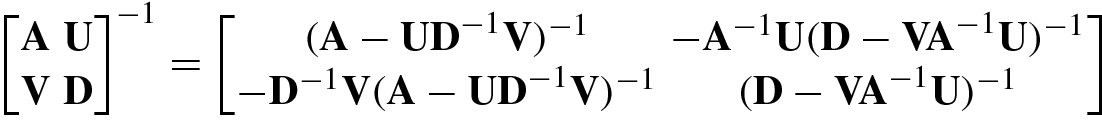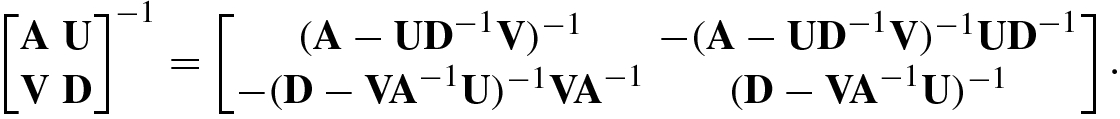© Springer Nature Singapore Pte Ltd. 2020
X.-D. ZhangA Matrix Algebra Approach to Artificial Intelligencehttps://doi.org/10.1007/978-981-15-2770-8_1

1. Basic Matrix Computation

Xian-Da Zhang1  
(1)
Department of Automation, Tsinghua University, Beijing, Beijing, China
 
 Deceased

In science and engineering, we often encounter the problem of solving a system of linear equations. Matrices provide the most basic and useful mathematical tool for describing and solving such systems. As the introduction to matrix algebra, this chapter presents the basic operations and performance of matrices, followed by a description of vectorization of matrix and matricization of vector.

1.1 Basic Concepts of Vectors and Matrices

First we introduce the basic concepts and notation for vectors and matrices.

1.1.1 Vectors and Matrices

A real system of linear equations
$$\displaystyle \begin{aligned} \left.\begin{aligned} a_{11} x_1^{\,} +\cdots +a_{1n} x_n &=b_1^{\,}\\ &\qquad \vdots\\ a_{m1} x_1^{\,} +\cdots +a_{mn} x_n &=b_m \end{aligned} \right\}{} \end{aligned} $$
(1.1.1)
can be simply rewritten using real vector and matrix symbols as a real matrix equation
$$\displaystyle \begin{aligned} \mathbf{Ax}=\mathbf{b},{} \end{aligned} $$
(1.1.2)
where
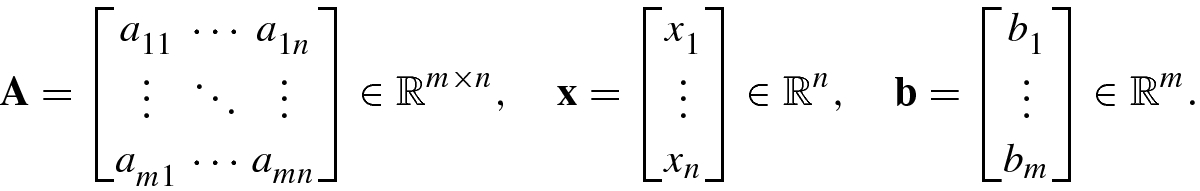
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ3_HTML.png
(1.1.3)
If a system of linear equations is complex valued, then $$\mathbf {A}\in \mathbb {C}^{m\times n},\mathbf {x}\in \mathbb {C}^n$$ , and $$\mathbf {b}\in \mathbb {C}^m$$ . Here, $$\mathbb {R}$$ (or $$\mathbb {C}$$ ) denotes the set of real (or complex) numbers, and $$\mathbb {R}^m$$ (or $$\mathbb {C}^m$$ ) represents the set of all real (or complex) m-dimensional column vectors, while $$\mathbb {R}^{m\times n}$$ (or $$\mathbb {C}^{m\times n}$$ ) is the set of all m × n real (or complex) matrices.

An m-dimensional row vector $$\mathbf {x}=[x_1^{\,} ,\ldots ,x_m ]$$ is represented as $$\mathbf {x}\in \mathbb {R}^{1\times m}$$ or $$\mathbf {x}\in \mathbb {C}^{1\times m}$$ . To save writing space, an m-dimensional column vector is usually written as the transposed form of a row vector, denoted $$\mathbf {x}=[x_1^{\,} , \ldots ,x_m ]^T$$ , where T denotes “transpose.”

There are three different types of vector in science and engineering [18]:

  • Physical vector: Its elements are physical quantities with magnitude and direction, such as a displacement vector, a velocity vector, an acceleration vector, and so forth.

  • Geometric vector: A directed line segment or arrow can visualize a physical vector. Such a representation is known as a geometric vector. For example, $$\mathbf {v}= \overrightarrow {AB}$$ represents the directed line segment with initial point A and terminal point B.

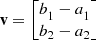  • Algebraic vector: A geometric vector needs to be represented in algebraic form in order to operate. For a geometric vector $$\mathbf {v}=\overrightarrow {AB}$$ on a plane, if its initial point is $$A=(a_1^{\,} ,a_2 )$$ and its terminal point is $$B=(b_1^{\,} , b_2)$$ , then the geometric vector $$\mathbf {v}=\overrightarrow {AB}$$ can be represented in an algebraic form ../images/492994_1_En_1_Chapter/492994_1_En_1_IEq18_HTML.gif. Such a geometric vector described in algebraic form is known as an algebraic vector.

The vectors encountered often in practical applications are physical vectors, while geometric vectors and algebraic vectors are, respectively, the visual representation and the algebraic form of physical vectors. Algebraic vectors provide a computational tool for physical vectors.

Depending on different types of element values, algebraic vectors can be divided into the following three types:

  • Constant vector: All entries take real constant numbers or complex constant numbers, e.g., a = [1, 5, 2]T.

  • Function vector: Its entries take function values, e.g., x = [x 1, …, x n]T.

  • Random vector: It uses random variables or signals as entries, e.g., $$\mathbf {x}(n)=[x_1^{\,} (n),\ldots ,x_m (n)]^T$$ where $$x_1^{\,} (n),\ldots ,x_m (n)$$ are m random variables or signals.

Figure 1.1 summarizes the classification of vectors.
../images/492994_1_En_1_Chapter/492994_1_En_1_Fig1_HTML.png
Fig. 1.1

Classification of vectors

A vector all of whose components are equal to zero is called a zero vector and is denoted as 0 = [0, …, 0]T.

An n × 1 vector $$\mathbf {x}=[x_1^{\,} ,\ldots ,x_n]^T$$ with only one nonzero entry x i = 1 constitutes a basis vector, denoted e i; e.g.,
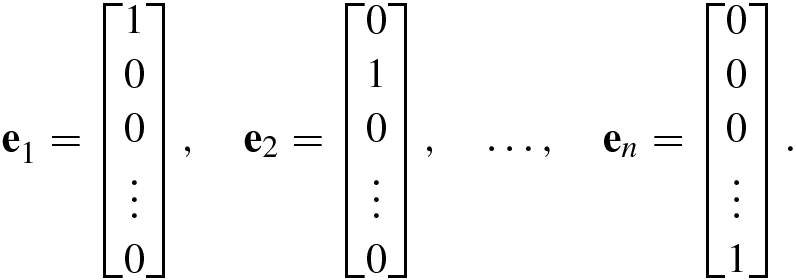
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ4_HTML.png
(1.1.4)

In modeling physical problems, the matrix A is usually the symbolic representation of a physical system (e.g., a linear system, a filter, or a learning machine).

An m × n matrix A is called a square matrix if m = n, a broad matrix for m < n, and a tall matrix for m > n.

The main diagonal of an n × n matrix A = [a ij] is the segment connecting the top left to the bottom right corner. The entries located on the main diagonal, a 11, a 22, …, a nn, are known as the (main) diagonal elements.

An n × n matrix A = [a ij] is called a diagonal matrix, identity matrix, and zero matrix if all entries off the main diagonal are zero, and some of all diagonal entries take nonzero values, all diagonal entries take 1 or 0, respectively; i.e.,
$$\displaystyle \begin{aligned} \mathbf{D}&amp;=\mathbf{Diag}(d_{11}^{\,} ,\ldots ,d_{nn}^{\,} ), \end{aligned} $$
(1.1.5)
$$\displaystyle \begin{aligned} \mathbf{I}&amp;=\mathbf{Diag}(1,\ldots ,1), \end{aligned} $$
(1.1.6)
$$\displaystyle \begin{aligned} \mathbf{O}&amp;=\mathbf{Diag}(0,\ldots ,0). \end{aligned} $$
(1.1.7)
Clearly, an n × n identity matrix I can be represented as $$\mathbf {I}= [{\mathbf {e}}_1^{\,} ,\ldots ,{\mathbf {e}}_n ]$$ using basis vectors.

In this book, we use often the following matrix symbols.

A(i, :) means the ith row of A.

A(:, j) means the jth column of A.

A(p : q, r : s) means the (q − p + 1) × (s − r + 1) submatrix consisting of the pth row to the qth row and the rth column to the sth column of A. For example,
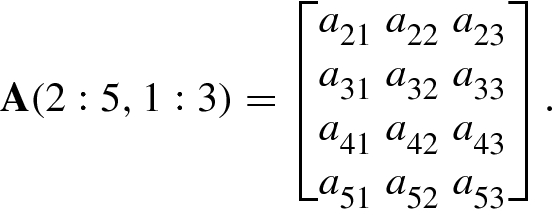
../images/492994_1_En_1_Chapter/492994_1_En_1_Equa_HTML.png
A matrix A is an m × n block matrix if it can be represented in the form
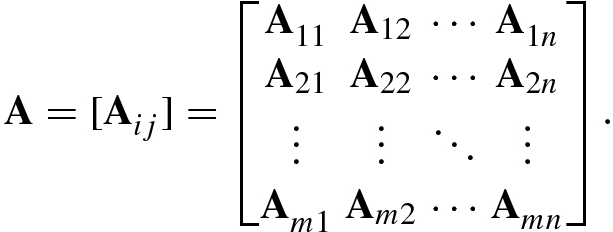
../images/492994_1_En_1_Chapter/492994_1_En_1_Equb_HTML.png

1.1.2 Basic Vector Calculus

The vector addition of $$\mathbf {u}=[u_1^{\,} ,\ldots ,u_n]^T$$ and $$\mathbf {v}=[v_1^{\,} ,\ldots ,v_n]^T$$ is defined as
$$\displaystyle \begin{aligned} \mathbf{u}+\mathbf{v}=[u_1^{\,} +v_1^{\,} ,\ldots ,u_n+v_n]^T. \end{aligned} $$
(1.1.8)
Vector addition obeys the commutation law and the associative law:

  • Commutative law: u + v = v + u.

  • Associative law: (u + v) ±w = u + (v ±w) = (u ±w) + v.

The vector multiplication of an n × 1 vector u by a scalar α is given by
$$\displaystyle \begin{aligned} \alpha\mathbf{u}=[\alpha u_1^{\,} ,\ldots ,\alpha u_n]^T. \end{aligned} $$
(1.1.9)
The basic property of vector multiplication by a scalar is that it obeys the distributive law:
$$\displaystyle \begin{aligned} \alpha (\mathbf{u}+\mathbf{v})=\alpha \mathbf{u}+\alpha \mathbf{v}. \end{aligned} $$
(1.1.10)
Given two real or complex n × 1 vectors $$\mathbf {u}=[u_1^{\,} ,\ldots ,u_n]^T$$ and $$\mathbf {v}=[v_1^{\,} ,\ldots ,v_n]^T$$ , their inner product (also called dot product or scalar product), denoted u ⋅v or 〈u, v〉, is defined as the real number
$$\displaystyle \begin{aligned} \mathbf{u}\cdot\mathbf{v}=\langle \mathbf{u},\mathbf{v}\rangle ={\mathbf{u}}^T\mathbf{v}=u_1^{\,} v_1^{\,} +\cdots +u_nv_n=\sum_{i=1}^n u_iv_i, \end{aligned} $$
(1.1.11)
or the complex number
$$\displaystyle \begin{aligned} \mathbf{u}\cdot\mathbf{v}=\langle \mathbf{u},\mathbf{v}\rangle ={\mathbf{u}}^H\mathbf{v}=u_1^* v_1^{\,} +\cdots +u_n^*v_n=\sum_{i=1}^n u_i^*v_i, \end{aligned} $$
(1.1.12)
where u H is the complex conjugate transpose (or Hermitian conjugate) of u.

Note that if u and v are two row vectors, then u ⋅v = uv T for real vectors and u ⋅v = uv H for complex vectors.

The outer product (or cross product) of an m × 1 real vector and an n × 1 real vector, denoted u ∘v, is defined as the m × n real matrix
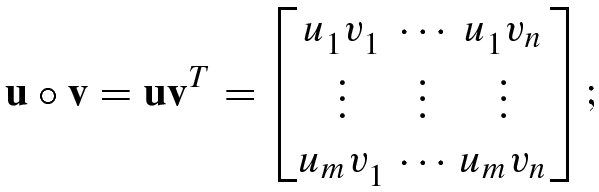
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ13_HTML.png
(1.1.13)
if u and v are complex, then their outer product is the m × n complex matrix given by
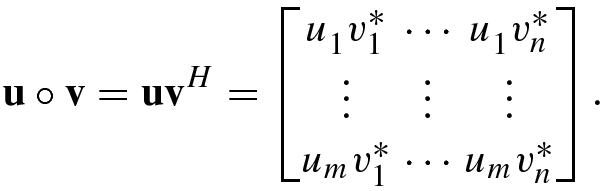
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ14_HTML.png
(1.1.14)

1.1.3 Basic Matrix Calculus

Definition 1.1 (Matrix Transpose)
If A = [a ij] is an m × n matrix, then the matrix transpose A T is an n × m matrix with the (i, j)th entry [A T]ij = a ji. The conjugate of A is represented as A ∗ and is an m × n matrix with (i, j)th entry $$[{\mathbf {A}}^*]_{ij} =a_{ij}^*$$ , while the conjugate or Hermitian transpose of A, denoted $${\mathbf {A}}^H\in \mathbb {C}^{n\times m}$$ , is defined as
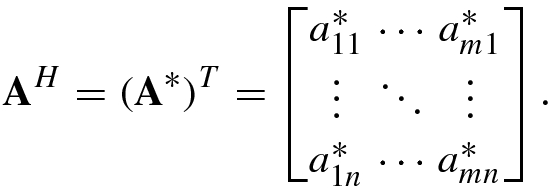
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ15_HTML.png
(1.1.15)
Definition 1.2 (Hermitian Matrix)

An n × n real (or complex) matrix satisfying A T = A (or A H = A) is called a symmetric matrix (or Hermitian matrix).

There are the following relationships between the transpose and conjugate transpose of a matrix:
$$\displaystyle \begin{aligned} {\mathbf{A}}^H=({\mathbf{A}}^* )^T=({\mathbf{A}}^T)^*. \end{aligned} $$
(1.1.16)
For an m × n block matrix A = [A ij], its conjugate transpose $${\mathbf {A}}^H=[{\mathbf {A}}_{ji}^H]$$ is an n × m block matrix:
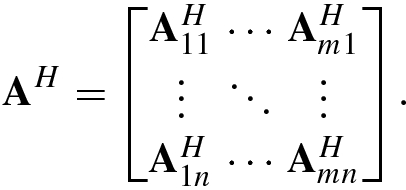
../images/492994_1_En_1_Chapter/492994_1_En_1_Equc_HTML.png

The simplest algebraic operations with matrices are the addition of two matrices and the multiplication of a matrix by a scalar.

Definition 1.3 (Matrix Addition)

Given two m × n matrices A = [a ij] and B = [b ij], matrix addition A + B is defined by [A + B]ij = a ij + b ij. Similarly, matrix subtraction A −B is defined as [A −B]ij = a ij − b ij.

By using this definition, it is easy to verify that the addition and subtraction of two matrices obey the following rules:

  • Commutative law: A + B = B + A.

  • Associative law: (A + B) ±C = A + (B ±C) = (A ±C) + B.

Definition 1.4 (Matrix Product)
The matrix product of an m × n matrix A = [a ij] and an r × s matrix B = [b ij], denoted AB, exists only when n = r and is an m × s matrix with entries
$$\displaystyle \begin{aligned}{}[\mathbf{AB}]_{ij} =\sum_{k=1}^n a_{ik} b_{kj},\quad i=1,\ldots ,m;~j=1,\ldots ,s. \end{aligned}$$

In particular, if B = αI, then [αA]ij = αa ij. If $$\mathbf {B}=\mathbf {x}=[x_1^{\,} ,\ldots ,x_n ]^T$$ , then $$[\mathbf {Ax}]_i =\sum _{j=1}^n a_{ij} x_j$$ for i = 1, …, m.

The matrix product obeys the following rules of operation:
  1. 1.

    Associative law of multiplication: If $$\mathbf {A}\in \mathbb {C}^{m\times n},\mathbf {B} \in \mathbb {C}^{n\times p}$$ , and $$\mathbf {C}\in \mathbb {C}^{p\times q}$$ , then A(BC) = (AB)C.

     
  2. 2.

    Left distributive law of multiplication: For two m × n matrices A and B, if C is an n × p matrix, then (A ±B)C = AC ±BC.

     
  3. 3.

    Right distributive law of multiplication: If A is an m × n matrix, while B and C are two n × p matrices, then A(B ±C) = AB ±AC.

     
  4. 4.

    If α is a scalar and A and B are two m × n matrices, then α(A + B) = αA + αB.

     

Note that the product of two matrices generally does not satisfy the commutative law, namely AB ≠ BA.

Another important operation on a square matrix is its inversion.

Put $$\mathbf {x}=[x_1^{\,} ,\ldots ,x_n ]^T$$ and $$\mathbf {y}=[y_1^{\,} , \ldots ,y_n ]^T$$ . The matrix-vector product Ax = y can be regarded as a linear transform of the vector x, where the n × n matrix A is called the linear transform matrix. Let A −1 denote the linear inverse transform of the vector y onto x. If A −1 exists, then one has
$$\displaystyle \begin{aligned} \mathbf{x}={\mathbf{A}}^{-1}\mathbf{y}. \end{aligned} $$
(1.1.17)
This can be viewed as the result of using A −1 to premultiply the original linear transform Ax = y, giving A −1Ax = A −1y = x, which means that the linear inverse transform matrix A −1 must satisfy A −1A = I. Similarly, we have
$$\displaystyle \begin{aligned} \mathbf{x}={\mathbf{A}}^{-1}\mathbf{y}\Rightarrow \mathbf{A}\mathbf{x}=\mathbf{AA}^{-1}\mathbf{y}\equiv \mathbf{y},\quad \forall\, \mathbf{y}\neq \mathbf{0}. \end{aligned}$$
This implies that A −1 must also satisfy AA −1 = I. Then, the inverse matrix can be defined below.
Definition 1.5 (Inverse Matrix)

Let A be an n × n matrix. The matrix A is said to be invertible if there is an n × n matrix A −1 such that AA −1 = A −1A = I, and A −1 is referred to as the inverse matrix of A.

The following are properties of the conjugate, transpose, conjugate transpose, and inverse matrices.
  1. 1.
    The matrix conjugate, transpose, and conjugate transpose satisfy the distributive law:
    $$\displaystyle \begin{aligned} (\mathbf{A}+\mathbf{B})^* ={\mathbf{A}}^* +{\mathbf{B}}^*,\quad (\mathbf{A}+\mathbf{B})^T ={\mathbf{A}}^T+{\mathbf{B}}^T,\quad (\mathbf{A}+ \mathbf{B})^H ={\mathbf{A}}^H+{\mathbf{B}}^H. \end{aligned}$$
     
  2. 2.
    The transpose, conjugate transpose, and inverse matrix of product of two matrices satisfy the following relationship:
    $$\displaystyle \begin{aligned} (\mathbf{AB})^T={\mathbf{B}}^T{\mathbf{A}}^T,\quad (\mathbf{AB})^H={\mathbf{B}}^H{\mathbf{A}}^H,\quad (\mathbf{AB})^{-1}={\mathbf{B}}^{-1}{\mathbf{A}}^{-1} \end{aligned}$$

    in which both A and B are assumed to be invertible.

     
  3. 3.
    Each of the symbols for the conjugate, transpose, and conjugate transpose can be exchanged with the symbol for the inverse:
    $$\displaystyle \begin{aligned} ({\mathbf{A}}^*)^{-1}=({\mathbf{A}}^{-1})^*={\mathbf{A}}^{-\ast},\ ({\mathbf{A}}^T)^{-1}=({\mathbf{A}}^{-1})^T={\mathbf{A}}^{-T},\ ({\mathbf{A}}^H)^{-1}=({\mathbf{A}}^{-1})^H ={\mathbf{A}}^{-H}. \end{aligned}$$
     
  4. 4.

    For any m × n matrix A, both the n × n matrix B = A HA and the m × m matrix C = AA H are Hermitian matrices.

     

An n × n matrix A is nonsingular if and only if the matrix equation Ax = 0 has only the zero solution x = 0. If Ax = 0 exists for any nonzero solution x ≠ 0, then the matrix A is singular.

For an n × n matrix $$\mathbf {A}=[{\mathbf {a}}_1^{\,} , \ldots ,{\mathbf {a}}_n ]$$ , the matrix equation Ax = 0 is equivalent to
$$\displaystyle \begin{aligned} {\mathbf{a}}_1^{\,} x_1^{\,} +\cdots +{\mathbf{a}}_n x_n =\mathbf{0}. \end{aligned} $$
(1.1.18)
If the matrix equation Ax = 0 has a zero solution vector only, then the column vectors of A are linearly independent, and thus the matrix A is said to be nonsingular.
To summarize the above discussions, the nonsingularity of an n × n matrix A can be determined in any of the following three ways:

  • its column vectors are linearly independent;

  • the matrix equation Ax = b exists a unique nonzero solution;

  • the matrix equation Ax = 0 has only a zero solution.

1.2 Sets and Linear Mapping

The set of all n-dimensional vectors with real (or complex) components is called a real (or complex) n-dimensional vector space, denoted $$\mathbb {R}^n$$ (or $$\mathbb {C}^n$$ ). In real-world artificial intelligence problems, we are usually given N n-dimensional real data vectors $$\{{\mathbf {x}}_1^{\,} ,\ldots ,{\mathbf {x}}_N^{\,}\}$$ that belong to a subset X other than the whole set $$\mathbb {R}^n$$ . Such a subset is known as a vector subspace in n-dimensional vector space $$\mathbb {R}^n$$ , denoted as $$\{ {\mathbf {x}}_1^{\,} ,\ldots ,{\mathbf {x}}_N^{\,}\}\in X\subset \mathbb {R}^n$$ . In this section, we present the sets, the vector subspaces, and the linear mapping of one vector subspace onto another.

1.2.1 Sets

As the name implies, a set is a collection of elements.

A set is usually denoted by S = {⋅}; inside the braces are the elements of the set S. If there are only a few elements in the set S, these elements are written out within the braces, e.g., S = {a, b, c}.

To describe the composition of a more complex set mathematically, the symbol “|” is used to mean “such that.” For example, S = {x|P(x) = 0} reads “the element x in set S such that P(x) = 0.” A set with only one element α is called a singleton, denoted {α}.

The following are several common notations for set operations:

  • ∀ denotes “for all ⋯”;

  • x ∈ A reads “x belongs to the set A”, i.e., x is an element or member of A;

  • x∉A means that x is not an element of the set A;

  • ∋ denotes “such that”;

  • ∃ denotes “there exists”;

  • $$\nexists $$ denotes “there does not exist”;

  • A ⇒ B reads “condition A results in B” or “A implies B.”

For example, the expression
$$\displaystyle \begin{aligned} \exists\ \theta \in V\ \ni \ \mathbf{x}+\theta =\mathbf{x}=\theta +\mathbf{x},\ \forall\,\mathbf{x}\in V \end{aligned}$$
denotes the trivial statement “there is a zero element θ in the set V  such that the addition x + θ = x = θ + x holds for all elements x in V .”

Let A and B be two sets; then the sets have the following basic relations.

The notation A ⊆ B reads “the set A is contained in the set B” or “A is a subset of B,” which implies that each element in A is an element in B, namely x ∈ A ⇒ x ∈ B.

If A ⊂ B, then A is called a proper subset of B. The notation B ⊃ A reads “B contains A” or “B is a superset of A.” The set with no elements is denoted by ∅ and is called the null set.

The notation A = B reads “the set A equals the set B,” which means that A ⊆ B and B ⊆ A, or x ∈ A ⇔x ∈ B (any element in A is an element in B, and vice versa). The negation of A = B is written as A ≠ B, implying that A does not belong to B, neither does B belong to A.

The union of A and B is denoted as A ∪ B. If X = A ∪ B, then X is called the union set of A and B. The union set is defined as follows:
$$\displaystyle \begin{aligned} X=A\cup B =\{ \mathbf{x}\in X|\, \mathbf{x}\in A\ \text{or}\ \mathbf{x}\in B\}. \end{aligned} $$
(1.2.1)
In other words, the elements of the union set A ∪ B consist of the elements of A and the elements of B.
The intersection of both sets A and B is represented by the notation A ∩ B and is defined as follows:
$$\displaystyle \begin{aligned} X=A\cap B =\{ \mathbf{x}\in X|\,\mathbf{x}\in A\ \text{and}\ \mathbf{x}\in B\}. \end{aligned} $$
(1.2.2)
The set X = A ∩ B is called the intersection set of A and B. Each element of the intersection set A ∩ B consists of elements common to both A and B. Especially, if A ∩ B = ∅ (null set), then the sets A and B are known as the disjoint sets.
The notation Z = A + B means the sum set of sets A and B and is defined as follows:
$$\displaystyle \begin{aligned} Z=A+B=\{ \mathbf{z}=\mathbf{x}+\mathbf{y} \in Z|\, \mathbf{x}\in A,~\mathbf{y}\in B\}, \end{aligned} $$
(1.2.3)
namely, an element z of the sum set Z = A + B consists of the sum of the element x in A and the element y in B.
The set-theoretic difference of the sets A and B, denoted “A − B,” is also termed the difference set and is defined as follows:
$$\displaystyle \begin{aligned} X=A-B=\{\mathbf{x}\in X|\,\mathbf{x}\in A,\ \text{but}~\mathbf{x}\notin B\}. \end{aligned} $$
(1.2.4)
That is to say, the difference set A − B is the set of elements of A that are not in B. The difference set A − B is also sometimes denoted by the notation X = A ∖ B. For example, $$\{\mathbb {C}^n\setminus \mathbf {0}\}$$ denotes the set of nonzero vectors in complex n-dimensional vector space.
The relative complement of A in X is defined as
$$\displaystyle \begin{aligned} A^{\mathrm{c}}=X-A=X\setminus A=\{\mathbf{x}\in X|\,\mathbf{x}\notin A\}. \end{aligned} $$
(1.2.5)
Example 1.1
For the sets
$$\displaystyle \begin{aligned} A=\{ 1,5,3\},\quad B=\{3,4,5\}, \end{aligned}$$
we have
$$\displaystyle \begin{aligned} A\cup B =\{ 1,5,3,4\},\quad A\cap B =\{5,3\},\quad A+B=\{4,9,8\}, \end{aligned}$$
$$\displaystyle \begin{aligned} A-B=A\setminus B=\{1\},\quad B-A=B\setminus A=\{4\}. \end{aligned}$$
If x ∈ X and y ∈ Y , then the set of all ordered pairs (x, y) is denoted by X × Y  and is termed the Cartesian product of the sets X and Y , and is defined as
$$\displaystyle \begin{aligned} X\times Y =\big\{ (\mathbf{x},\mathbf{y})\big |\mathbf{x}\in X,~\mathbf{y}\in Y\big\}. \end{aligned} $$
(1.2.6)
Similarly, $$X_1^{\,} \times \cdots \times X_n$$ denotes the Cartesian product of n sets $$X_1^{\,} ,\ldots ,X_n$$ , and its elements are the ordered n-ples $$({\mathbf {x}}_1^{\,} ,\ldots ,{\mathbf {x}}_n^{\,} )$$ :
$$\displaystyle \begin{aligned} X_1^{\,} \times\cdots \times X_n =\big\{({\mathbf{x}}_1^{\,} ,\ldots ,{\mathbf{x}}_n^{\,} )\big | {\mathbf{x}}_1^{\,} \in X_1^{\,} ,\ldots ,{\mathbf{x}}_n^{\,}\in X_n\big\}. \end{aligned} $$
(1.2.7)

1.2.2 Linear Mapping

Consider the transformation between vectors in two vector spaces. In mathematics, mapping is a synonym for mathematical function or for morphism.

A mapping T : V → W represents a rule for transforming the vectors in V  to corresponding vectors in W. The subspace V  is said to be the initial set or domain of the mapping T and W its final set or codomain.

When v is some vector in the vector space V , T(v) is referred to as the image of the vector v under the mapping T, or the value of the mapping T at the point v, whereas v is known as the original image of T(v).

If T(v) represents a collection of transformed outputs of all vectors v in V , i.e.,
$$\displaystyle \begin{aligned} T(V)=\{ T(\mathbf{v})\,|\, \mathbf{v}\in V\}, \end{aligned} $$
(1.2.8)
then T(V ) is said to be the range of the mapping T, denoted by
$$\displaystyle \begin{aligned} \mathrm{Im}(T)=T(V)=\{ T(\mathbf{v})\,|\, \mathbf{v}\in V\}. \end{aligned} $$
(1.2.9)
Definition 1.6 (Linear Mapping)
A mapping T is called a linear mapping or linear transformation in the vector space V  if it satisfies the linear relationship
$$\displaystyle \begin{aligned} T(c_1^{\,} {\mathbf{v}}_1^{\,} +c_2{\mathbf{v}}_2) =c_1^{\,} T({\mathbf{v}}_1^{\,} )+c_2 T({\mathbf{v}}_2){} \end{aligned} $$
(1.2.10)
for all $$\mathbf {v_1^{\,} },{\mathbf {v}}_2 \in V$$ and all scalars $$c_1^{\,} ,c_2$$ .
A linear mapping has the following basic properties: if T : V → W is a linear mapping, then
$$\displaystyle \begin{aligned} T(\mathbf{0})=\mathbf{0}\quad \text{and}\quad T(-\mathbf{x})=-T(\mathbf{x}). \end{aligned} $$
(1.2.11)

If f(X, Y) is a scalar function with real matrices $$\mathbf {X}\in \mathbb {R}^{n\times n}$$ and $$\mathbf {Y}\in \mathbb {R}^{n\times n}$$ as variables, then in linear mapping notation, the function can be denoted by the Cartesian product form $$f: \mathbb {R}^{n\times n}\times \mathbb {R}^{n\times n}\to \mathbb {R}$$ .

An interesting special application of linear mappings is the electronic amplifier $$\mathbf {A}\in \mathbb {C}^{n\times n}$$ with high fidelity (Hi-Fi). By Hi-Fi, it means that there is the following linear relationship between any input signal vector u and the corresponding output signal vector Au of the amplifier:
$$\displaystyle \begin{aligned} \mathbf{Au}=\lambda \mathbf{u}, \end{aligned} $$
(1.2.12)
where λ > 1 is the amplification factor or gain. The equation above is a typical characteristic equation of a matrix.
Definition 1.7 (One-to-One Mapping)

T : V → W is a one-to-one mapping if it is either injective mapping or surjective mapping, i.e., T(x) = T(y) implies x = y or distinct elements have distinct images.

A one-to-one mapping T : V → W has an inverse mapping T −1 : W → V . The inverse mapping T −1 restores what the mapping T has done. Hence, if T(v) = w, then T −1(w) = v, resulting in T −1(T(v)) = v, ∀ v ∈ V  and T(T −1(w)) = w, ∀ w ∈ W.

If $${\mathbf {u}}_1^{\,} ,\ldots ,{\mathbf {u}}_p$$ are the input vectors of a system T in engineering, then $$T({\mathbf {u}}_1^{\,} ),\ldots ,$$ T(u p) can be viewed as the output vectors of the system. The criterion for identifying whether a system is linear is: if the system input is the linear expression $$\mathbf {y}=c_1^{\,} {\mathbf {u}}_1^{\,} +\cdots +c_p{\mathbf {u}}_p$$ , then the system is said to be linear only if its output satisfies the linear expression $$T(\mathbf {y})=T(c_1^{\,} {\mathbf {u}}_1^{\,} +\cdots +c_p{\mathbf {u}}_p)=c_1^{\,} T({\mathbf {u}}_1^{\,} )+\cdots +c_p T({\mathbf {u}}_p)$$ . Otherwise, the system is nonlinear.

The following are intrinsic relationships between a linear space and a linear mapping.

Theorem 1.1 ([4, p. 29])
Let V  and W be two vector spaces, and let T : V → W be a linear mapping. Then the following relationships are true:

  • if M is a linear subspace in V , then T(M) is a linear subspace in W;

  • if N is a linear subspace in W, then the linear inverse transform T −1(N) is a linear subspace in V .

For a given linear transformation y = Ax, if our task is to obtain the output vector y from the input vector x given a transformation matrix A, then Ax = y is said to be a forward problem. Conversely, the problem of finding the input vector x from the output vector y is known as an inverse problem. Clearly, the essence of the forward problem is a matrix-vector calculation, while the essence of the inverse problem is to solve a matrix equation.

1.3 Norms

Many problems in artificial intelligence need to solve optimization problems in which vector and/or matrix norms are the cost function terms to be optimized.

1.3.1 Vector Norms

Definition 1.8 (Vector Norm)
Let V  be a real or complex vector space. Given a vector x ∈ V , the mapping function $$p(\mathbf {x}):V\to \mathbb {R}$$ is called the vector norm of x ∈ V , if for all vectors x, y ∈ V  and any scalar $$c\in \mathbb {K}$$ (here $$\mathbb {K}$$ denotes $$\mathbb {R}$$ or $$\mathbb {C}$$ ), the following three norm axioms hold:

  • Nonnegativity: p(x) ≥ 0 and p(x) = 0 ⇔x = 0.

  • Homogeneity: p(cx) = |c|⋅ p(x) is true for all complex constant c.

  • Triangle inequality: p(x + y) ≤ p(x) + p(y).

In a real or complex inner product space V , the vector norms have the following properties [4].
  1. 1.

    ∥0∥ = 0 and ∥x∥ > 0, ∀ x ≠ 0.

     
  2. 2.

    ∥cx∥ = |c| ∥x∥ holds for all vector x ∈ V  and any scalar $$c\in \mathbb {K}$$ .

     
  3. 3.
    Polarization identity: For real inner product spaces we have
    $$\displaystyle \begin{aligned} \langle \mathbf{x},\mathbf{y}\rangle =\frac 14\big (\|\mathbf{x}+\mathbf{y}\|{}^2-\|\mathbf{x}-\mathbf{y}\|{}^2\big ),\ \forall~\mathbf{x},\mathbf{y},{} \end{aligned} $$
    (1.3.1)
    and for complex inner product spaces we have
    $$\displaystyle \begin{aligned} \langle \mathbf{x},\mathbf{y}\rangle =\frac 14\big (\|\mathbf{x}+\mathbf{y}\|{}^2 -\|\mathbf{x}-\mathbf{y}\|{}^2 -\mathrm{j}\,\| \mathbf{x}+\mathrm{j}\,\mathbf{y}\|{}^2 + \mathrm{j}\|\mathbf{x}-\mathrm{j}\,\mathbf{y}\|{}^2\big ),\ \forall~\mathbf{x},\mathbf{y}. {} \end{aligned} $$
    (1.3.2)
     
  4. 4.
    Parallelogram law
    $$\displaystyle \begin{aligned} \|\mathbf{x}+\mathbf{y}\|{}^2 +\|\mathbf{x} -\mathbf{y}\|{}^2 =2\big (\|\mathbf{x} \|{}^2 +\|\mathbf{y}\|{}^2\big ),\ \forall~\mathbf{x},\mathbf{y}. \end{aligned} $$
    (1.3.3)
     
  5. 5.
    Triangle inequality
    $$\displaystyle \begin{aligned} \|\mathbf{x}+\mathbf{y}\| \leq \|\mathbf{x}\| +\|\mathbf{y}\|,\ \forall~\mathbf{x},\mathbf{y}\in V. \end{aligned} $$
    (1.3.4)
     
  6. 6.
    Cauchy–Schwartz inequality
    $$\displaystyle \begin{aligned} \left |\langle \mathbf{x},\mathbf{y}\rangle\right | \leq \|\mathbf{x}\|\cdot\|\mathbf{y}\|. \end{aligned} $$
    (1.3.5)

    The equality |〈x, y〉| = ∥x∥⋅∥y∥ holds if and only if y = c x, where c is some nonzero complex constant.

     
The following are several common norms of constant vectors.
  • ℓ 0-norm
    $$\displaystyle \begin{aligned} \|\mathbf{x}\|{}_0 \stackrel{\mathrm{def}}{=}\sum_{i=1}^m x_i^0,\quad \text{where ~}x_i^0=\bigg \{\begin{array}{ll} 1,&amp;~~\text{if }x_i\neq 0;\\&amp;{}\\ 0,&amp;~~\text{if }x_i=0.\end{array} \end{aligned}$$
    That is,
    $$\displaystyle \begin{aligned} \|\mathbf{x}\|{}_0=\text{number of nonzero entries of }\mathbf{x}. \end{aligned} $$
    (1.3.6)
  • $$\ell _1^{\,}$$ -norm
    $$\displaystyle \begin{aligned} \| \mathbf{x} \|{}_1^{\,} \stackrel{\mathrm{def}}{=} \sum_{i=1}^m |x_i | = |x_1^{\,} |+\cdots +|x_m^{\,} |, \end{aligned} $$
    (1.3.7)
    i.e., ∥x∥1 is the sum of absolute (or modulus) values of nonzero entries of x.
  • $$\ell _2^{\,}$$ -norm or the Euclidean norm
    $$\displaystyle \begin{aligned} \| \mathbf{x} \|{}_2^{\,} \stackrel{\mathrm{def}}{=}\|\mathbf{x}\|{}_E^{\,}=\sqrt{|x_1^{\,} |{}^2 +\cdots +|x_m^{\,}|{}^2}. \end{aligned} $$
    (1.3.8)
  • $$\ell _\infty ^{\,}$$ -norm
    $$\displaystyle \begin{aligned} \| \mathbf{x} \|{}_\infty \stackrel{\mathrm{def}}{=}\max \big\{|x_1^{\,} |,\ldots ,|x_m^{\,} |\big\}. \end{aligned} $$
    (1.3.9)
  • $$\ell _p^{\,}$$ -norm or Hölder norm [19]
    $$\displaystyle \begin{aligned} \| \mathbf{x} \|{}_p^{\,} \stackrel{\mathrm{def}}{=}\left ( \sum_{i=1}^m |x_i^{\,} |{}^p \right )^{1/p},\quad p\geq 1. {} \end{aligned} $$
    (1.3.10)

The ℓ 0-norm does not satisfy the homogeneity ∥cx∥0 = |c|⋅∥x∥0, and thus is a quasi-norm, while the ℓ p-norm is also a quasi-norm if 0 < p < 1 but a norm if p ≥ 1.

Clearly, when p = 1 or p = 2, the ℓ p-norm reduces to the ℓ 1-norm or the ℓ 2-norm, respectively.

In artificial intelligence, ℓ 0-norm is usually used as a measure of sparse vectors, i.e.,
$$\displaystyle \begin{aligned} \text{sparse vector }\mathbf{x}=\mathop{\text{arg min}}\limits_{\mathbf{x}}\|\mathbf{x}\|{}_0. \end{aligned} $$
(1.3.11)
However, the ℓ 0-norm is difficult to be optimized. Importantly, the ℓ 1-norm can be regarded as a relaxed form of the ℓ 0-norm, and is easy to be optimized:
$$\displaystyle \begin{aligned} \text{sparse vector }\mathbf{x}=\mathop{\text{arg min}}\limits_{\mathbf{x}}\|\mathbf{x}\|{}_1. \end{aligned} $$
(1.3.12)
Here are several important applications of the Euclidean norm.
  • Measuring the size or length of a vector:
    $$\displaystyle \begin{aligned} \mathrm{size}(\mathbf{x})=\|\mathbf{x}\|{}_2 =\sqrt{x_1^2+\cdots +x_m^2}, \end{aligned} $$
    (1.3.13)
    which is called the Euclidean length.
  • Defining the 𝜖-neighborhood of a vector x:
    $$\displaystyle \begin{aligned} N_\epsilon (\mathbf{x})=\big\{\mathbf{y}\big |\|\mathbf{y}-\mathbf{x}\|{}_2\leq\epsilon\big\}, \quad \epsilon &gt;0. \end{aligned} $$
    (1.3.14)
  • Measuring the distance between vectors x and y:
    $$\displaystyle \begin{aligned} d(\mathbf{x},\mathbf{y})=\|\mathbf{x}-\mathbf{y}\|{}_2=\sqrt{(x_1^{\,} -y_1^{\,} )^2+\cdots +(x_m^{\,} -y_m^{\,} )^2}. \end{aligned} $$
    (1.3.15)
    This is known as the Euclidean distance.
  • Defining the angle θ (0 ≤ θ ≤ 2π) between vectors x and y:
    $$\displaystyle \begin{aligned} \theta \stackrel{\mathrm{def}}{=}\arccos\left (\frac{\langle\mathbf{x},\mathbf{y}\rangle} {\sqrt{\langle \mathbf{x},\mathbf{x} \rangle}\sqrt{\langle \mathbf{y},\mathbf{y}\rangle}}\right )=\arccos\left (\frac {{\mathbf{x}}^H\mathbf{y}}{\|\mathbf{x}\|\| \mathbf{y} \|}\right ). \end{aligned} $$
    (1.3.16)

A vector with unit Euclidean length is known as a normalized (or standardized) vector. For any nonzero vector $$\mathbf {x}\in \mathbb {C}^m$$ , x∕〈x, x〉1∕2 is the normalized version of the vector and has the same direction as x.

The norm ∥x∥ is said to be a unitary invariant norm if ∥Ux∥ = ∥x∥ holds for all vectors $$\mathbf {x} \in \mathbb {C}^m$$ and all unitary matrices $$\mathbf {U}\in \mathbb {C}^{m\times m}$$ such that U HU = I.

Proposition 1.1 ([15])

The Euclidean norm ∥⋅∥2 is unitary invariant.

If the inner product 〈x, y〉 = x Hy = 0, then the angle between the vectors θ = π∕2, from which we have the following definition on orthogonality of two vectors.

Definition 1.9 (Orthogonal)

Two constant vectors x and y are said to be orthogonal, denoted by x ⊥ y, if their inner product 〈x, y〉 = x Hy = 0.

Definition 1.10 (Inner Product of Function Vectors)
Let x(t), y(t) be two function vectors in the complex vector space $$\mathbb {C}^n$$ , and let the definition field of the function variable t be [a, b] with a < b. Then the inner product of the function vectors x(t) and y(t) is defined as
$$\displaystyle \begin{aligned} \langle \mathbf{x}(t),\mathbf{y}(t)\rangle \stackrel{\mathrm{def}}{=}\int\nolimits_a^b {\mathbf{x}}^H(t)\mathbf{y}(t)\mathrm{d}t.{} \end{aligned} $$
(1.3.17)
The angle between function vectors is defined as follows:
$$\displaystyle \begin{aligned} \cos \theta\stackrel{\mathrm{def}}{=}\frac{\langle\mathbf{x}(t),\mathbf{y}(t)\rangle} {\sqrt{\langle \mathbf{x}(t), \mathbf{x}(t)\rangle}\sqrt{\langle \mathbf{y}(t),\mathbf{y}(t)\rangle}}=\frac {\displaystyle\int\nolimits_a^b {\mathbf{x}}^H(t)\mathbf{y}(t)\mathrm{d}t}{\| \mathbf{x}(t)\|\cdot\|\mathbf{y}(t)\|}, \end{aligned} $$
(1.3.18)
where ∥x(t)∥ is the norm of the function vector x(t) and is defined as follows:
$$\displaystyle \begin{aligned} \| \mathbf{x}(t)\| \stackrel{\mathrm{def}}{=}\left (\int\nolimits_a^b {\mathbf{x}}^H(t) \mathbf{x}(t)\mathrm{d}t\right )^{1/2}. \end{aligned} $$
(1.3.19)
Clearly, if the inner product of two function vectors is equal to zero, i.e.,
$$\displaystyle \begin{aligned} \int\nolimits_a^b {\mathbf{x}}^H(t)\mathbf{y}(t)\mathrm{d}t=0, \end{aligned}$$
then the angle θ = π∕2. Hence, two function vectors are said to be orthogonal in [a, b], denoted x(t) ⊥ y(t), if their inner product is equal to zero.

The following proposition shows that, for any two orthogonal vectors, the square of the norm of their sum is equal to the sum of the squares of the respective vector norms.

Proposition 1.2

If x ⊥ y, then ∥x + y∥2 = ∥x∥2 + ∥y∥2.

Proof
From the axioms of vector norms it is known that
$$\displaystyle \begin{aligned} \| \mathbf{x}+\mathbf{y}\|{}^2 =\langle\mathbf{x}+\mathbf{y}, \mathbf{x}+\mathbf{y}\rangle =\langle \mathbf{x},\mathbf{x}\rangle + \langle \mathbf{x},\mathbf{y}\rangle +\langle \mathbf{y},\mathbf{x} \rangle +\langle \mathbf{y},\mathbf{y}\rangle .{} \end{aligned} $$
(1.3.20)
Since x and y are orthogonal, we have 〈x, y〉 = E{x Ty} = 0. Moreover, from the axioms of inner products it is known that 〈y, x〉 = 〈x, y〉 = 0. Substituting this result into Eq. (1.3.20), we immediately get
$$\displaystyle \begin{aligned} \|\mathbf{x}+\mathbf{y}\|{}^2 =\langle \mathbf{x},\mathbf{x}\rangle +\langle \mathbf{y},\mathbf{y}\rangle =\| \mathbf{x}\|{}^2 +\| \mathbf{y}\|{}^2. \end{aligned}$$
This completes the proof of the proposition. $$\blacksquare $$

This proposition is also referred to as the Pythagorean theorem.

On the orthogonality of two vectors, we have the following conclusive remarks [40].

  • Mathematical definitions: Two vectors x and y are orthogonal if their inner product is equal to zero, i.e., 〈x, y〉 = 0.

  • Geometric interpretation: If two vectors are orthogonal, then their angle is π∕2, and the projection of one vector onto the other vector is equal to zero.

  • Physical significance: When two vectors are orthogonal, each vector contains no components of the other, that is, there exist no interactions or interference between these vectors.

1.3.2 Matrix Norms

The inner product and norms of vectors can be easily extended to the inner product and norms of matrices.

For two m × n complex matrices $$\mathbf {A}=[{\mathbf {a}}_1^{\,} ,\ldots ,{\mathbf {a}}_n ]$$ and $$\mathbf {B}=[{\mathbf {b}}_1^{\,} ,\ldots ,{\mathbf {b}}_n ]$$ , stack them, respectively, into the following mn × 1 vectors according to their columns: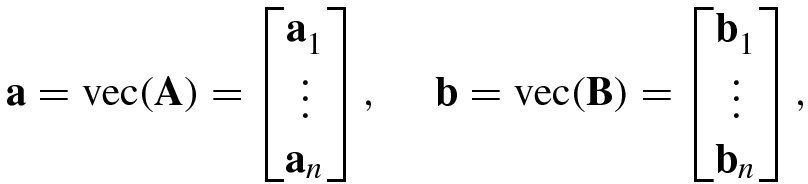
../images/492994_1_En_1_Chapter/492994_1_En_1_Equp_HTML.png
where the elongated vector vec(A) is the vectorization of the matrix A. We will discuss the vectorization of matrices in detail in Sect. 1.9.
The inner product of two m × n matrices A and B, denoted $$\langle \mathbf {A}, \mathbf {B}\rangle |\,\mathbb {C}^{m\times n}\times \mathbb {C}^{m\times n}\to \mathbb {C}$$ , is defined as the inner product of two elongated vectors:
$$\displaystyle \begin{aligned} \langle \mathbf{A},\mathbf{B}\rangle =\langle\mathrm{vec}(\mathbf{A}),\mathrm{vec}(\mathbf{B})\rangle =\sum_{i=1}^n{\mathbf{a}}_i^H {\mathbf{b}}_i =\sum_{i=1}^n\langle{\mathbf{a}}_i ,{\mathbf{b}}_i\rangle , \end{aligned} $$
(1.3.21)
or equivalently written as
$$\displaystyle \begin{aligned} \langle \mathbf{A},\mathbf{B}\rangle =(\mathrm{vec}\,\mathbf{A})^H\mathrm{vec}(\mathbf{B})=\mathrm{tr}({\mathbf{A}}^H\mathbf{B}), \end{aligned} $$
(1.3.22)
where tr(C) represents the trace function of a square matrix C, defined as the sum of its diagonal entries.
Let a = [a 11, …, a m1, a 12, …, a m2, …, a 1n, …, a mn]T = vec(A) be an mn × 1 elongated vector of the m × n matrix A. The ℓ p-norm of the matrix A uses the ℓ p-norm definition of the elongated vector a as follows:
$$\displaystyle \begin{aligned} \|\mathbf{A}\|{}_p \stackrel{\mathrm{def}}{=}\|\mathbf{a}\|{}_p=\|\mathrm{vec}(\mathbf{A})\|{}_p=\left (\sum_{i=1}^m\sum_{j=1}^n |a_{ij}|{}^p \right )^{1/p}. \end{aligned} $$
(1.3.23)
Since this kind of matrix norm is represented by the matrix entries, it is named the entrywise norm. The following are three typical entrywise matrix norms:
  1. 1.
    $$\ell _1^{\,}$$ -norm (p = 1)
    $$\displaystyle \begin{aligned} \|\mathbf{A}\|{}_1^{\,} \stackrel{\mathrm{def}}{=}\sum_{i=1}^m\sum_{j=1}^n |a_{ij} |. \end{aligned} $$
    (1.3.24)
     
  2. 2.
    Frobenius norm (p = 2)
    $$\displaystyle \begin{aligned} \|\mathbf{A}\|{}_F^{\,} \stackrel{\mathrm{def}}{=}\left (\sum_{i=1}^m\sum_{j=1}^n |a_{ij}|{}^2 \right )^{1/2} \end{aligned} $$
    (1.3.25)

    is the most common matrix norm. Clearly, the Frobenius norm is an extension of the Euclidean norm of the vector to the elongated vector a = [a 11, …, a m1, …, a 1n, …, a mn]T.

     
  3. 3.
    Max norm or ℓ ∞-norm (p = ∞)
    $$\displaystyle \begin{aligned} \|\mathbf{A}\|{}_\infty =\max_{i=1,\ldots ,m;\,j=1,\ldots ,n}\{|a_{ij}|\}. \end{aligned} $$
    (1.3.26)
     
Another commonly used matrix norm is the induced matrix norm, ∥A∥2, defined as
$$\displaystyle \begin{aligned} \|\mathbf{A}\|{}_2=\sqrt{\lambda_{\max}({\mathbf{A}}^H\mathbf{A})}=\sigma_{\max}(\mathbf{A}), \end{aligned} $$
(1.3.27)
where $$\lambda _{\max }({\mathbf {A}}^H\mathbf {A})$$ and $$\sigma _{\max }(\mathbf {A})$$ are the maximum eigenvalue of A HA and the maximum singular value of A, respectively.
Because $$\sum _{i=1}^m\sum _{j=1}^n |a_{ij}|{ }^2=\mathrm {tr}({\mathbf {A}}^H\mathbf {A})$$ , the Frobenius norm can be also written in the form of the trace function as follows:
$$\displaystyle \begin{aligned} \|\mathbf{A}\|{}_F^{\,} \stackrel{\mathrm{def}}{=}\langle\mathbf{A},\mathbf{A}\rangle^{1/2}=\sqrt{\mathrm{tr}({\mathbf{A}}^H\mathbf{A})}=\sqrt{\sigma_1^2+\ldots +\sigma_k^2}, \end{aligned} $$
(1.3.28)
where $$k=\mathrm {rank}(\mathbf {A})\leq \min \{m,n\}$$ is the rank of A. Clearly, we have
$$\displaystyle \begin{aligned} \|\mathbf{A}\|{}_2\leq \|\mathbf{A}\|{}_F. \end{aligned} $$
(1.3.29)
Given an m × n matrix A, its Frobenius norm weighted by a positive definite matrix Ω, denoted ∥A∥Ω, is defined by
$$\displaystyle \begin{aligned} \| \mathbf{A}\|{}_{\boldsymbol \Omega} =\sqrt{\mathrm{tr}({\mathbf{A}}^H{\boldsymbol \Omega}\mathbf{A})}.\end{aligned} $$
(1.3.30)
This norm is usually called the Mahalanobis norm.
The following are the relationships between the inner products and norms [15].
  • Cauchy–Schwartz inequlity
    $$\displaystyle \begin{aligned} \left |\langle \mathbf{A},\mathbf{B}\rangle\right |{}^2 \leq \| \mathbf{A}\|{}^2 \|\mathbf{B}\|{}^2.\end{aligned} $$
    (1.3.31)
    The equals sign holds if and only if A = c B, where c is a complex constant.
  • Pythagoras’ theorem
    $$\displaystyle \begin{aligned} \langle \mathbf{A},\mathbf{B}\rangle =0\quad \Rightarrow \quad \|\mathbf{A}+\mathbf{B} \|{}^2 =\|\mathbf{A}\|{}^2+\|\mathbf{B}\|{}^2.\end{aligned} $$
    (1.3.32)
  • Polarization identity
    $$\displaystyle \begin{aligned} \mathrm{Re}\left (\langle \mathbf{A},\mathbf{B}\rangle \right ) &amp;=\frac 14 \left (\|\mathbf{A}+\mathbf{B}\|{}^2 -\| \mathbf{A}-\mathbf{B}\|{}^2\right ), \end{aligned} $$
    (1.3.33)
    $$\displaystyle \begin{aligned} \mathrm{Re} \left (\langle\mathbf{A},\mathbf{B} \rangle \right ) &amp;=\frac 12 \left (\|\mathbf{A} +\mathbf{B}\|{}^2 -\|\mathbf{A}\|{}^2 -\|\mathbf{B}\|{}^2\right ),\end{aligned} $$
    (1.3.34)
    where $$\mathrm {Re}\left (\langle \mathbf {A},\mathbf {B}\rangle \right )$$ represents the real part of the inner product 〈A, B〉.

1.4 Random Vectors

In science and engineering applications, the measured data are usually random variables. A vector with random variables as its entries is called a random vector.

In this section, we discuss the statistics and properties of random vectors by focusing on Gaussian random vectors.

1.4.1 Statistical Interpretation of Random Vectors

In the statistical interpretation of random vectors, the first-order and second-order statistics of random vectors are the most important.

Definition 1.11 (Inner Product of Random Vectors)
Let both x(ξ) and y(ξ) be n × 1 random vectors of variable ξ. Then the inner product of random vectors x(ξ) and y(ξ) is defined as follows:
$$\displaystyle \begin{aligned} \langle \mathbf{x}(\xi ),\mathbf{y}(\xi )\rangle \stackrel{\mathrm{def}}{=}E\big\{ {\mathbf{x}}^H (\xi )\mathbf{y}(\xi )\big\}, \end{aligned} $$
(1.4.1)
where E is the expectation operator $$E\{\mathbf {x}(\xi )\}=[E\{x_1^{\,} (\xi )\},\ldots ,E\{x_n^{\,} (\xi )\}]^T$$ and the function variable ξ may be time t, circular frequency f, angular frequency ω or space parameter s, and so on.
The square of the norm of a random vector x(ξ) is defined as
$$\displaystyle \begin{aligned} \| \mathbf{x}(\xi )\|{}^2\stackrel{\mathrm{def}}{=}E\big\{{\mathbf{x}}^H(\xi )\mathbf{x}(\xi )\big\}. \end{aligned} $$
(1.4.2)
Given a random vector $$\mathbf {x}(\xi )=[x_1^{\,} (\xi ),\ldots ,x_m (\xi )]^T$$ , its mean vector μ x is defined as
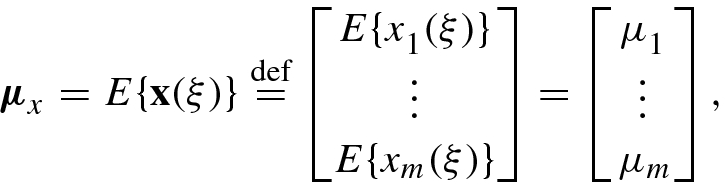
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ67_HTML.png
(1.4.3)
where E{x i(ξ)} = μ i represents the mean of the ith random variable x i(ξ).
The autocorrelation matrix of the random vector x(ξ) is defined by
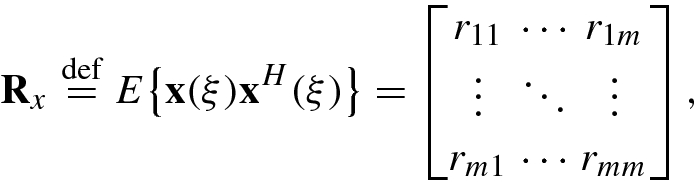
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ68_HTML.png
(1.4.4)
where r ii(i = 1, …, m) denotes the autocorrelation function of the random variable x i(ξ):
$$\displaystyle \begin{aligned} r_{ii} \stackrel{\mathrm{def}}{=}E\big\{ x_i (\xi )x_i^* (\xi )\big\}=E\big\{|x_i (\xi )|{}^2\big\} ,\quad i=1,\ldots ,m, \end{aligned} $$
(1.4.5)
whereas r ij represents the cross-correlation function of x i(ξ) and x j(ξ):
$$\displaystyle \begin{aligned} r_{ij} \stackrel{\mathrm{def}}{=}E\big\{ x_i (\xi )x_j^* (\xi )\big\} ,\quad i,j=1,\ldots ,m,~i\neq j. \end{aligned} $$
(1.4.6)
Clearly, the autocorrelation matrix is a complex conjugate symmetric (i.e., Hermitian).
The autocovariance matrix of the random vector x(ξ), denoted C x, is defined as
$$\displaystyle \begin{aligned} {\mathbf{C}}_x &amp;=\mathrm{cov}(\mathbf{x},\mathbf{x})\stackrel{\mathrm{def}}{=}E\big\{ (\mathbf{x}(\xi )-{\boldsymbol \mu}_x )(\mathbf{x}(\xi )-{\boldsymbol \mu}_x )^H\big\} \end{aligned} $$
(1.4.7)
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ72_HTML.png
(1.4.8)
where the diagonal entries
$$\displaystyle \begin{aligned} c_{ii} \stackrel{\mathrm{def}}{=}E\big\{ |x_i (\xi )-\mu_i |{}^2\big\}=\sigma_i^2,\quad i=1,\ldots ,m \end{aligned} $$
(1.4.9)
denote the variance $$\sigma _i^2$$ of the random variable x i(ξ), whereas the other entries
$$\displaystyle \begin{aligned} c_{ij} \stackrel{\mathrm{def}}{=}E\big\{ [x_i (\xi )-\mu_i ][x_j (\xi )-\mu_j ]^*\big\}=E\big\{ x_i (\xi )x_j^* (\xi ) \big\} -\mu_i \mu_j^* =c_{ji}^* \end{aligned} $$
(1.4.10)
express the covariance of the random variables x i(ξ) and x j(ξ). The autocovariance matrix is also Hermitian.
There is the following relationship between the autocorrelation and autocovariance matrices:
$$\displaystyle \begin{aligned} {\mathbf{C}}_x = {\mathbf{R}}_x-\boldsymbol{\mu}_x \boldsymbol{\mu}_x^H. \end{aligned} $$
(1.4.11)
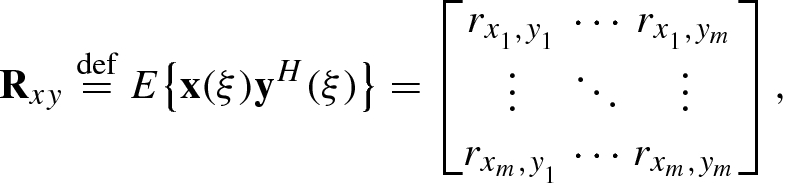
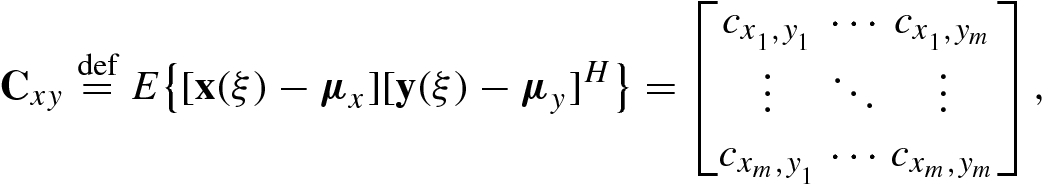
By generalizing the autocorrelation and autocovariance matrices, one obtains the cross-correlation matrix of the random vectors x(ξ) and y(ξ),
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ76_HTML.png
(1.4.12)
and the cross-covariance matrix
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ77_HTML.png
(1.4.13)
where $$r_{x_i ,y_j} \stackrel {\mathrm {def}}{=}E\big \{ x_i (\xi )y_j^* (\xi )\big \}$$ is the cross-correlation of the random vectors x i(ξ) and y j(ξ) and $$c_{x_i ,y_j} \stackrel {\mathrm {def}}{=}E\{ [x_i (\xi )-\mu _{x_i} ][y_j (\xi )-\mu _{y_j}]^*\}$$ is the cross-covariance of x i(ξ) and y j(ξ).
From Eqs. (1.4.12) and (1.4.13) it is easily known:
$$\displaystyle \begin{aligned} {\mathbf{C}}_{xy} ={\mathbf{R}}_{xy} -{\boldsymbol \mu}_x {\boldsymbol \mu}_y^H. \end{aligned} $$
(1.4.14)
In real-world applications, a data vector x = [x(0), x(1), …, x(N − 1)]T with nonzero mean μ x usually needs to undergo a zero-mean normalization:
$$\displaystyle \begin{aligned} \mathbf{x}\leftarrow \mathbf{x}=[x(0)-\mu_x ,x(1)-\mu_x ,\ldots ,x(N-1)-\mu_x ]^T, \end{aligned}$$
where $$\mu _x =\frac 1N\sum _{n=0}^{N-1}x(n)$$ .

After zero-mean normalization, the correlation matrices and covariance matrices are equal, i.e., R x = C x and R xy = C xy.

Some properties of these matrices are as follows.
  1. 1.

    The autocorrelation matrix is Hermitian, i.e., $${\mathbf {R}}_x^H={\mathbf {R}}_x$$ .

     
  2. 2.

    The autocorrelation matrix of the linear combination vector y = Ax + b satisfies R y = AR xA H.

     
  3. 3.

    The cross-correlation matrix is not Hermitian but satisfies $${\mathbf {R}}_{xy}^H={\mathbf {R}}_{yx}$$ .

     
  4. 4.

    $${\mathbf {R}}_{(x_1^{\,} +x_2^{\,} )y}={\mathbf {R}}_{x_1^{\,} y}+{\mathbf {R}}_{x_2^{\,} y}$$ .

     
  5. 5.

    If x and y have the same dimension, then R x+y = R x + R xy + R yx + R y.

     
  6. 6.

    R Ax,By = AR xyB H.

     
The degree of correlation of two random variables x(ξ) and y(ξ) can be measured by their correlation coefficient:
$$\displaystyle \begin{aligned} \rho_{xy}\stackrel{\mathrm{def}}{=}\frac {E\{(x(\xi )-\bar{x})(y(\xi )-\bar{y})^*\}}{\sqrt{E \{|x(\xi )-\bar{x}|{}^2 \}E\{|y(\xi )-\bar{y}|{}^2\}}}=\frac {c_{xy}}{\sigma_x \sigma_y}.{} \end{aligned} $$
(1.4.15)
Here $$c_{xy}=E\{(x(\xi )-\bar {x})(y(\xi )-\bar {y})^*\}$$ is the cross-covariance of the random variables x(ξ) and y(ξ), while $$\sigma _x^2$$ and $$\sigma _y^2$$ are, respectively, the variances of x(ξ) and y(ξ). Applying the Cauchy–Schwartz inequality to Eq. (1.4.15), we have
$$\displaystyle \begin{aligned} 0\leq |\rho_{xy} |\leq 1. \end{aligned} $$
(1.4.16)
The correlation coefficient ρ xy measures the degree of similarity of two random variables x(ξ) and y(ξ).

  • The closer ρ xy is to zero, the weaker the similarity of the random variables x(ξ) and y(ξ) is.

  • The closer ρ xy is to 1, the more similar x(ξ) and y(ξ) are.

  • The case ρ xy = 0 means that there are no correlated components between the random variables x(ξ) and y(ξ). Thus, if ρ xy = 0, the random variables x(ξ) and y(ξ) are said to be uncorrelated. Since this uncorrelation is defined in a statistical sense, it is usually said to be a statistical uncorrelation.

  • It is easy to verify that if x(ξ) = c y(ξ), where c is a complex number, then |ρ xy| = 1. Up to a fixed amplitude scaling factor |c| and a phase ϕ(c), the random variables x(ξ) and y(ξ) are the same, so that x(ξ) = c ⋅ y(ξ) = |c|ejϕ(c)y(ξ). Hence, if |ρ xy| = 1, then random variables x(ξ) and y(ξ) are said to be completely correlated or coherent.

Definition 1.12 (Uncorrelated)

Two random vectors 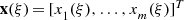../images/492994_1_En_1_Chapter/492994_1_En_1_IEq94_HTML.gif and $$\mathbf {y}(\xi ) = [y_1^{\,} (\xi ),$$ $$\ldots ,y_n^{\,} (\xi )]^T$$ are said to be statistically uncorrelated if their cross-covariance matrix C xy = O m×n or, equivalently, $$\rho _{x_i^{\,} ,y_j^{\,}}^{\,} =0,\forall \, i,j$$ .

In contrast with the case for a constant vector or function vector, an m × 1 random vector x(ξ) and an n × 1 random vector y(ξ) are said to be orthogonal if any entry of x(ξ) is orthogonal to each entry of y(ξ), namely
$$\displaystyle \begin{aligned} r_{x_i ,y_j} =E\{ x_i (\xi )y_j (\xi )\}=0,~\forall \,i=1,\ldots ,m,j=1,\ldots ,n; \end{aligned} $$
(1.4.17)
or R xy = E{x(ξ)y H(ξ)} = O m×n.
Definition 1.13 (Orthogonality of Random Vectors)
An m × 1 random vector x(ξ) and an n × 1 random vector y(ξ) are orthogonal each other, denoted by x(ξ) ⊥ y(ξ), if their cross-correlation matrix is equal to the m × n null matrix O, i.e.,
$$\displaystyle \begin{aligned} {\mathbf{R}}_{xy}=E\big\{ \mathbf{x} (\xi ){\mathbf{y}}^H (\xi )\big\} =\mathbf{O}. \end{aligned} $$
(1.4.18)

Note that for the zero-mean normalized m × 1 random vector x(ξ) and n × 1 normalized random vector y(ξ), their statistical uncorrelation and orthogonality are equivalent, as their cross-covariance and cross-correlation matrices are equal, i.e., C xy = R xy.

1.4.2 Gaussian Random Vectors

Definition 1.14 (Gaussian Random Vector)

If each entry x i(ξ), i = 1, …, m, is Gaussian random variable, then the random vector $$\mathbf {x}=[x_1^{\,} (\xi ),\ldots ,x_m (\xi )]^T$$ is called a Gaussian random vector.

Let $$\mathbf {x}\sim N(\bar {\mathbf {x}},{\boldsymbol \Gamma }_x )$$ denote a real Gaussian or normal random vector with the mean vector $$\bar {\mathbf {x}}=[\bar x_1^{\,} ,\ldots ,\bar x_m ]^T$$ and covariance matrix $${\boldsymbol \Gamma }_x =E\{(\mathbf {x}-\bar {\mathbf {x}} )(\mathbf {x}-\bar {\mathbf {x}})^T\}$$ . If each entry of the Gaussian random vector is independent identically distributed (iid), then its covariance matrix $${\boldsymbol \Gamma }_x =E\{(\mathbf {x}-\bar {\mathbf {x}})(\mathbf {x}-\bar {\mathbf {x}})^T\}=\mathbf {Diag} (\sigma _1^2 ,\ldots ,\sigma _m^2 )$$ , where $$\sigma _i^2 =E\{(x_i -\bar {x_i})^2\}$$ is the variance of the Gaussian random variable x i.

Under the condition that all entries are statistically independent of each other, the probability density function of a Gaussian random vector $$\mathbf {x}\sim N( \bar {\mathbf {x}},{\boldsymbol \Gamma }_x )$$ is the joint probability density function of its m random variables, i.e.,
$$\displaystyle \begin{aligned} f(\mathbf{x})&amp;=f(x_1^{\,} ,\ldots ,x_m )\\ &amp;=f(x_1^{\,} )\cdots f(x_m )\\ &amp;=\frac 1{\sqrt{2\pi\sigma_1^2 }}\exp \left (- \frac{(x_1^{\,} -\bar x_1^{\,} )^2}{2\sigma_1^2 }\right )\cdots \frac 1{\sqrt{2\pi\sigma_m^2}}\exp \left (-\frac {(x_m -\bar x_m )^2}{2\sigma_m^2}\right )\\ &amp;=\frac 1{(2\pi )^{m/2}\sigma_1^{\,} \cdots\sigma_m}\exp \left (- \frac{(x_1^{\,} -\bar x_1^{\,} )^2}{2\sigma_1^2 }-\cdots -\frac{(x_m -\bar x_m )^2}{2\sigma_m^2}\right ) \end{aligned} $$
or
$$\displaystyle \begin{aligned} f(\mathbf{x})=\frac 1{(2\pi )^{m/2}|{\boldsymbol \Gamma}_x |{}^{1/2}}\exp \left ( -\frac 12 (\mathbf{x} -\bar{\mathbf{x}})^T{\boldsymbol \Gamma}_x^{-1}(\mathbf{x}-\bar{\mathbf{x}})\right ).{} \end{aligned} $$
(1.4.19)
If the entries are not statistically independent of each other, then the probability density function of the Gaussian random vector $$\mathbf {x}\sim N( \bar {\mathbf {x}},{\boldsymbol \Gamma }_x )$$ is also given by Eq. (1.4.19), but the exponential term becomes [25, 29]
$$\displaystyle \begin{aligned} (\mathbf{x}-\bar{\mathbf{x}})^T{\boldsymbol \Gamma}_x^{-1}(\mathbf{x}-\bar{\mathbf{x}})=\sum_{i=1}^m\sum_{j=1}^m [{\boldsymbol \Gamma}_x^{-1}]_{i,j} (x_i -\mu_i ) (x_j -\mu_j ), \end{aligned} $$
(1.4.20)
where $$[{\boldsymbol \Gamma }_x^{-1}]_{ij}$$ represents the (i, j)th entry of the inverse matrix $${\boldsymbol \Gamma }_x^{-1}$$ and μ i = E{x i} is the mean of the random variable x i.
The characteristic function of a real Gaussian random vector is given by
$$\displaystyle \begin{aligned} \varPhi_{\mathbf{x}}(\omega_1^{\,} ,\ldots ,\omega_m)=\exp \left ( \mathrm{j}\, {\boldsymbol \omega}^T {\boldsymbol \mu}_x -\frac 12{\boldsymbol \omega}^T{\boldsymbol \Gamma}_x{\boldsymbol \omega} \right ), \end{aligned} $$
(1.4.21)
where $${\boldsymbol \omega }=[\omega _1^{\,} ,\ldots ,\omega _m]^T$$ .
If $$x_i\sim CN (\mu _i ,\sigma _i^2)$$ , then $$\mathbf {x}=[x_1^{\,} ,\ldots ,x_m ]^T$$ is called a complex Gaussian random vector, denoted x ∼ CN(μ x, Γ x), where $${\boldsymbol \mu }_x =[\mu _1^{\,} ,\ldots ,\mu _m ]^T$$ and Γ are, respectively, the mean vector and the covariance matrix of the random vector x. If x i = u i + jv i and the random vectors $$[u_1^{\,} ,v_1^{\,} ]^T,\ldots ,[u_m ,v_m ]^T$$ are statistically independent of each other, then the probability density function of a complex Gaussian random vector x is given by Poularikas [29, p. 35-5]
$$\displaystyle \begin{aligned} f(\mathbf{x})&amp;=f(x_1)\cdots f(x_m )\\ &amp;=\left(\pi^m\prod_{i=1}^m \sigma_i^2\right )^{-1}\exp \left (-\sum_{i=1}^m \frac 1{\sigma_i^2}|x_i -\mu_i |{}^2\right )\\ &amp;=\frac 1{\pi^m |{\boldsymbol \Gamma}_x |}\exp \Big (-(\mathbf{x}- {\boldsymbol \mu}_x )^H{\boldsymbol \Gamma}_x^{-1}(\mathbf{x}-{\boldsymbol \mu}_x )\Big ),{} \end{aligned} $$
(1.4.22)
where $${\boldsymbol \Gamma }_x =\mathbf {Diag}(\sigma _1^2 ,\ldots ,\sigma _m^2 )$$ . The characteristic function of the complex Gaussian random vector x is determined by
$$\displaystyle \begin{aligned} \varPhi_{\mathbf{x}}({\boldsymbol \omega})=\exp\left (\mathrm{j}\, \mathrm{Re}({\boldsymbol \omega}^H{\boldsymbol \mu}_x ) -\frac 14{\boldsymbol \omega}^H{\boldsymbol \Gamma}_x{\boldsymbol \omega}\right ). \end{aligned} $$
(1.4.23)
A Gaussian random vector x has the following important properties.

  • The probability density function of x is completely described by its mean vector and covariance matrix.

  • If two Gaussian random vectors x and y are statistically uncorrelated, then they are also statistically independent.

  • Given a Gaussian random vector x with mean vector μ x and covariance matrix Γ x, the random vector y obtained by the linear transformation y(ξ) = Ax(ξ) is also a Gaussian random vector, and its probability density function is given by
    $$\displaystyle \begin{aligned} f(\mathbf{y})=\frac 1{(2\pi )^{m/2}|{\boldsymbol \Gamma}_y |{}^{1/2}}\exp \left ( -\frac 12 ( \mathbf{y}-{\boldsymbol \mu}_y )^T {\boldsymbol \Gamma}_y^{-1}(\mathbf{y}-{\boldsymbol \mu}_y)\right ) \end{aligned} $$
    (1.4.24)
    for real Gaussian random vectors and
    $$\displaystyle \begin{aligned} f(\mathbf{y})=\frac 1{\pi^m |{\boldsymbol \Gamma}_y |}\exp \Big ( -(\mathbf{y}- {\boldsymbol \mu}_y )^H{\boldsymbol \Gamma}_y^{-1}( \mathbf{y}-{\boldsymbol \mu}_y )\Big ) \end{aligned} $$
    (1.4.25)
    for complex Gaussian random vectors.
The statistical expression of a real white Gaussian noise vector is given by
$$\displaystyle \begin{aligned} E\{ \mathbf{x}(t)\} =\mathbf{0}\quad \text{and}\quad E\big\{ \mathbf{x}(t){\mathbf{x}}^T(t)\big\}=\sigma^2\mathbf{I}. \end{aligned} $$
(1.4.26)
But, this expression is not available for a complex white Gaussian noise vector.
Consider a complex Gaussian random vector $$\mathbf {x}(t)=[x_1^{\,} (t),\ldots ,$$ x m(t)]T. If x i(t), i = 1, …, m, have zero mean and the same variance σ 2, then the real part x R,i(t) and the imaginary part x I,i(t) are two real white Gaussian noises that are statistically independent and have the same variance. This implies that
$$\displaystyle \begin{aligned} E\big\{ x_{\mathrm{R},i} (t)\big\} &amp;=0,\quad E\big\{ x_{\mathrm{I},i}^{\,} (t)\big\} =0,\\ E\big\{ x_{\mathrm{R},i}^2 (t)\big\}&amp;=E\big\{ x_{\mathrm{I},i}^2(t)\big\}=\frac 12\sigma^2,\\ E\big\{ x_{\mathrm{R},i}^{\,} (t)x_{\mathrm{I},i}^{\,} (t)\big\} &amp;=0,\\ E \big\{ x_i^{\,} (t)x_i^* (t)\big\} &amp;=E\big\{x_{\mathrm{R},i}^2 (t)\big\} +E\big \{ x_{\mathrm{I},i}^2 (t)\big\} = \sigma^2. \end{aligned} $$
From the above conditions we know that
$$\displaystyle \begin{aligned} E\big\{ x_i^2 (t)\big\} &amp;=E\big\{ (x_{\mathrm{R},i}^{\,} (t)+\mathrm{j}\,x_{\mathrm{I},i}^{\,} (t))^2\big\}\\ &amp;=E\big\{ x_{\mathrm{R},i}^2(t)\big\}-E\big\{x_{\mathrm{I},i}^2 (t)\big\}+\mathrm{j}\, 2 E\big\{x_{\mathrm{R},i}^{\,} (t) x_{\mathrm{I},i}^{\,} (t)\big\} \\ &amp;=\frac 12\sigma^2 -\frac 12\sigma^2 +0=0. \end{aligned} $$
Since $$x_1^{\,} (t),\ldots ,x_m (t)$$ are statistically uncorrelated, we have
$$\displaystyle \begin{aligned} E\big\{ x_i^{\,} (t)x_k^{\,} (t)\big\} =0,\quad \ E\big\{ x_i^{\,} (t)x_k^* (t)\big\} =0,\quad \ i\neq k. \end{aligned}$$
Therefore, the statistical expression of the complex white Gaussian noise vector x(t) is given by
$$\displaystyle \begin{aligned} E\big\{ \mathbf{x}(t)\big\} =\mathbf{0},\quad E\big\{\mathbf{x}(t){\mathbf{x}}^H(t)\big\}=\sigma^2\mathbf{I},\quad E\big\{ \mathbf{x}(t){\mathbf{x}}^T(t)\big\}=\mathbf{O}. \end{aligned} $$
(1.4.27)

1.5 Basic Performance of Matrices

For a multivariate representation with mn components, we need some scalars to describe the basic performance of an m × n matrix.

1.5.1 Quadratic Forms

The quadratic form of an n × n matrix A is defined as x HAx, where x may be any n × 1 nonzero vector. In order to ensure the uniqueness of the definition of quadratic form (x HAx)H = x HAx, the matrix A is required to be Hermitian or complex conjugate symmetric, i.e., A H = A. This assumption ensures also that any quadratic form function is real-valued. One of the basic advantages of a real-valued function is its suitability for comparison with a zero value.

If x HAx > 0, then the quadratic form of A is said to be a positive definite function, and the Hermitian matrix A is known as a positive definite matrix. Similarly, one can define the positive semi-definiteness, negative definiteness, and negative semi-definiteness of a Hermitian matrix, as shown in Table 1.1.
Table 1.1

Quadratic forms and positive definiteness of a Hermitian matrix A

Quadratic forms

Symbols

Positive definiteness

x HAx > 0

A ≻ 0

A is a positive definite matrix

x HAx ≥ 0

A ≽ 0

A is a positive semi-definite matrix

x HAx < 0

A ≺ 0

A is a negative definite matrix

x HAx ≤ 0

A ≼ 0

A is a negative semi-definite matrix

A Hermitian matrix A is said to be indefinite matrix if x HAx > 0 for some nonzero vectors x and x HAx < 0 for other nonzero vectors x.

1.5.2 Determinants

The determinant of an n × n matrix A, denoted $$\det (\mathbf {A})$$ or |A|, is defined as
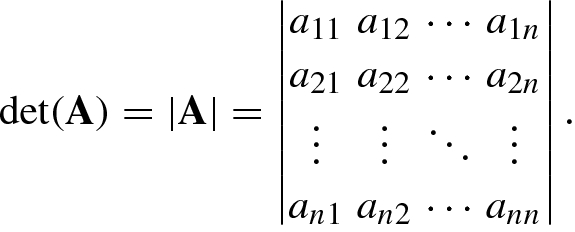
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ92_HTML.png
(1.5.1)
Let A ij be the (n − 1) × (n − 1) submatrix obtained by removing the ith row and the jth column from the n × n matrix A = [a ij]. The determinant $$A_{ij}=\det ({\mathbf {A}}_{ij})$$ of the remaining matrix A ij is known as the cofactor of the entry a ij. In particular, when j = i, A ii is known as the principal minor of A. The cofactor A ij is related to the determinant of the submatrix A ij as follows:
$$\displaystyle \begin{aligned} A_{ij} =(-1)^{i+j}\det ({\mathbf{A}}_{ij}). \end{aligned} $$
(1.5.2)
The determinant of an n × n matrix A can be computed by
$$\displaystyle \begin{aligned} \det (\mathbf{A})=a_{i1} A_{i1} +\cdots +a_{in} A_{in} =\sum_{j=1}^n a_{ij} (-1)^{i+j}\det ({\mathbf{A}}_{ij} ) \end{aligned} $$
(1.5.3)
or
$$\displaystyle \begin{aligned} \det (\mathbf{A})=a_{1j} A_{1j} +\cdots +a_{nj} A_{nj} = \sum_{i=1}^n a_{ij} (-1)^{i+j}\det ({\mathbf{A}}_{ij} ). \end{aligned} $$
(1.5.4)
Hence the determinant of A can be recursively calculated: an nth-order determinant can be computed from the (n − 1)th-order determinants, while each (n − 1)th-order determinant can be calculated from the (n − 2)th-order determinants, and so forth.
For a 3 × 3 matrix A, its determinant is recursively given by
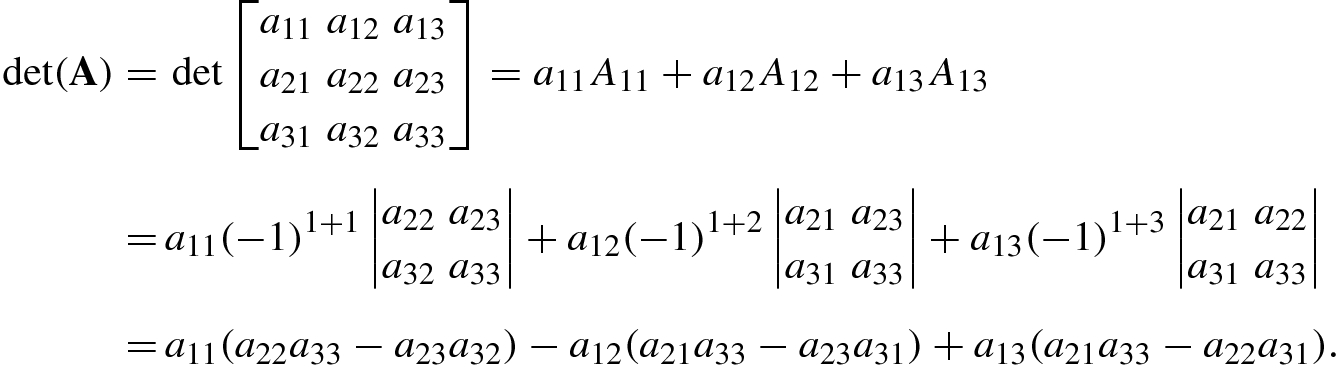
../images/492994_1_En_1_Chapter/492994_1_En_1_Equv_HTML.png
This is the diagonal method for a third-order determinant.

A matrix with nonzero determinant is known as a nonsingular matrix.

Determinant Equalities [20]
  1. 1.

    If two rows (or columns) of a matrix A are exchanged, then the value of $$\det (\mathbf {A})$$ remains unchanged, but the sign is changed.

     
  2. 2.

    If some row (or column) of a matrix A is a linear combination of other rows (or columns), then $$\det (\mathbf {A})=0$$ . In particular, if some row (or column) is proportional or equal to another row (or column), or there is a zero row (or column), then $$\det (\mathbf {A})=0$$ .

     
  3. 3.

    The determinant of an identity matrix is equal to 1, i.e., $$\det (\mathbf {I})=1$$ .

     
  4. 4.

    Any square matrix A and its transposed matrix A T have the same determinant, i.e., $$\det (\mathbf {A})=\det ({\mathbf {A}}^T)$$ ; however, $$\det ({\mathbf {A}}^H)=(\det ({\mathbf {A}}^T))^*$$ .

     
  5. 5.
    The determinant of a Hermitian matrix is real-valued, since
    $$\displaystyle \begin{aligned} \det (\mathbf{A})=\det ({\mathbf{A}}^H)=(\det (\mathbf{A}))^*. \end{aligned} $$
    (1.5.5)
     
  6. 6.
    The determinant of the product of two square matrices is equal to the product of their determinants, i.e.,
    $$\displaystyle \begin{aligned} \det (\mathbf{AB})=\det (\mathbf{A})\det (\mathbf{B}), \quad \mathbf{A},\mathbf{B}\in \mathbb{C}^{n\times n}. \end{aligned} $$
    (1.5.6)
     
  7. 7.

    For any constant c and any n × n matrix A, $$\det (c\cdot \mathbf {A})=c^n\cdot \det (\mathbf {A})$$ .

     
  8. 8.

    If A is nonsingular, then $$\det ({\mathbf {A}}^{-1}) =1/\det (\mathbf {A})$$ .

     
  9. 9.
    For matrices A m×m, B m×n, C n×m, D n×n, the determinant of the block matrix for nonsingular A is given by
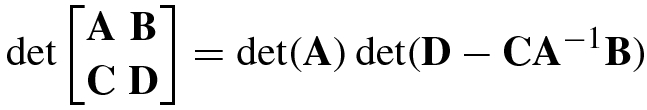    ../images/492994_1_En_1_Chapter/492994_1_En_1_Equ98_HTML.png
    (1.5.7)
    and for nonsingular D we have
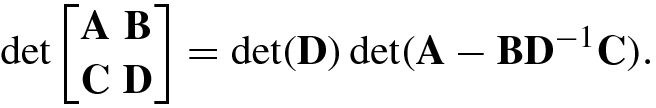    ../images/492994_1_En_1_Chapter/492994_1_En_1_Equ99_HTML.png
    (1.5.8)
     
  10. 10.
    The determinant of a triangular (upper or lower triangular) matrix A is equal to the product of its main diagonal entries:
    $$\displaystyle \begin{aligned} \det (\mathbf{A})=\prod_{i=1}^n a_{ii}. \end{aligned}$$

    The determinant of a diagonal matrix A = Diag(a 11, …, a nn) is also equal to the product of its diagonal entries.

     
Here we give a proof of Eq. (1.5.7):
../images/492994_1_En_1_Chapter/492994_1_En_1_Equx_HTML.png
We can prove Eq. (1.5.8) in a similar way.
The following are two determinant inequalities [20].

  • The determinant of a positive definite matrix A is larger than 0, i.e., $$\det (\mathbf {A})&gt;0$$ .

  • The determinant of a positive semi-definite matrix A is larger than or equal to 0, i.e., $$\det (\mathbf {A})\geq 0$$ .

1.5.3 Matrix Eigenvalues

For an n × n matrix A, if the linear algebraic equation
$$\displaystyle \begin{aligned} \mathbf{Au}=\lambda \mathbf{u}{} \end{aligned} $$
(1.5.9)
has a nonzero n × 1 solution vector u, then the scalar λ is called an eigenvalue of the matrix A, and u is its eigenvector corresponding to λ.
An equivalent form of the matrix equation (1.5.9) is
$$\displaystyle \begin{aligned} (\mathbf{A}-\lambda \mathbf{I})\mathbf{u}=\mathbf{0}.{} \end{aligned} $$
(1.5.10)
Only condition for this equation having nonzero solution vector u is that the determinant of the matrix A − λI is equal to zero, i.e.,
$$\displaystyle \begin{aligned} \det (\mathbf{A}-\lambda \mathbf{I})=0.{} \end{aligned} $$
(1.5.11)
This equation is known as the characteristic equation of the matrix A.
The characteristic equation (1.5.11) reflects the following two facts:

  • If (1.5.11) holds for λ = 0, then $$\det (\mathbf {A})=0$$ . This implies that as long as a matrix A has a zero eigenvalue, this matrix must be singular.

  • All the eigenvalues of a zero matrix are zero, and for any singular matrix there exists at least one zero eigenvalue. Clearly, if all n diagonal entries of an n × n singular matrix A contain a subtraction of the same scalar x ≠ 0 that is not an eigenvalue of A then the matrix A − xI must be nonsingular, since |A − xI|≠ 0.

Let eig(A) represent the eigenvalues of the matrix A. The basic properties of eigenvalues are listed below:
  1. 1.
    For A m×m and B m×m, eig(AB) = eig(BA) because
    $$\displaystyle \begin{aligned} \mathbf{ABu}=\lambda\mathbf{u}\Rightarrow (\mathbf{BA})\mathbf{Bu}=\lambda\mathbf{Bu}\Rightarrow \mathbf{BA}\mathbf{u}'=\lambda \mathbf{u}', \end{aligned}$$

    where u′ = Bu. However, if the eigenvector of AB corresponding to λ is u, then the eigenvector of BA corresponding to the same λ is u′ = Bu.

     
  2. 2.

    If rank(A) = r, then the matrix A has at most r different eigenvalues.

     
  3. 3.

    The eigenvalues of the inverse matrix satisfy eig(A −1) = 1∕eig(A).

     
  4. 4.
    Let I be the identity matrix; then
    $$\displaystyle \begin{aligned} \mathrm{eig}(\mathbf{I}+c\mathbf{A})&amp;=1+c\cdot \mathrm{eig}(\mathbf{A}), \end{aligned} $$
    (1.5.12)
    $$\displaystyle \begin{aligned} \mathrm{eig}(\mathbf{A}-c\mathbf{I})&amp;=\mathrm{eig}(\mathbf{A})-c. \end{aligned} $$
    (1.5.13)
     
Since u Hu > 0 for any nonzero vector u, from λ = u HAu∕(u Hu) it is directly known that positive definite and nonpositive definite matrices can be described by their eigenvalues as follows.

  • Positive definite matrix: Its all eigenvalues are positive real numbers.

  • Positive semi-definite matrix: Its all eigenvalues are nonnegative.

  • Negative definite matrix: Its all eigenvalues are negative.

  • Negative semi-definite matrix: Its all eigenvalues are nonpositive.

  • Indefinite matrix: It has both positive and negative eigenvalues.

If A is a positive definite or positive semi-definite matrix, then
$$\displaystyle \begin{aligned} \det (\mathbf{A})\leq \prod_i a_{ii}. \end{aligned} $$
(1.5.14)
This inequality is called the Hadamard inequality.
The characteristic equation (1.5.11) suggests two methods for improving the numerical stability and the accuracy of solutions of the matrix equation Ax = b, as described below [40].

  • Method for improving the numerical stability: Consider the matrix equation Ax = b, where A is usually positive definite or nonsingular. However, owing to noise or errors, A may sometimes be close to singular. We can alleviate this difficulty as follows. If λ is a small positive number, then − λ cannot be an eigenvalue of A. This implies that the characteristic equation |A − xI| = |A − (−λ)I| = |A + λI| = 0 cannot hold for any λ > 0, and thus the matrix A + λI must be nonsingular. Therefore, if we solve (A + λI)x = b instead of the original matrix equation Ax = b, and λ takes a very small positive value, then we can overcome the singularity of A to improve greatly the numerical stability of solving Ax = b. This method for solving (A + λI)x = b, with λ > 0, instead of Ax = b is the well-known Tikhonov regularization method for solving nearly singular matrix equations.

  • Method for improving the accuracy: For a matrix equation Ax = b, with the data matrix A nonsingular but containing additive interference or observation noise, if we choose a very small positive scalar λ to solve (A − λI)x = b instead of Ax = b, then the influence of the noise of the data matrix A on the solution vector x will be greatly decreased. This is the basis of the well-known total least squares (TLS) method.

1.5.4 Matrix Trace

Definition 1.15 (Trace)
The sum of the diagonal entries of an n × n matrix A is known as its trace, denoted tr(A):
$$\displaystyle \begin{aligned} \mathrm{tr}(\mathbf{A})=a_{11} +\cdots +a_{nn}=\sum_{i=1}^n a_{ii}. \end{aligned} $$
(1.5.15)

Clearly, for a random signal x = [x 1, …, x n]T, the trace of its autocorrelation matrix R x, $$\mathrm {trace}({\mathbf {R}}_x)=\sum _{i=1}^n E\{|x_i|{ }^2\}$$ , denotes the energy of the random signal.

The following are some properties of the matrix trace.

Trace Equality [20]
  1. 1.

    If both A and B are n × n matrices, then tr(A ±B) = tr(A) ±tr(B).

     
  2. 2.

    If A and B are n × n matrices and $$c_1^{\,} $$ and c 2 are constants, then $$\mathrm {tr}(c_1^{\,}\cdot \mathbf {A}\pm c_2\cdot \mathbf {B})=c_1^{\,}\cdot \mathrm {tr}(\mathbf {A})\pm c_2\cdot \mathrm {tr} (\mathbf {B})$$ . In particular, tr(cA) = c ⋅tr(A).

     
  3. 3.

    tr(A T) = tr(A), tr(A ∗) = (tr(A))∗ and tr(A H) = (tr(A))∗.

     
  4. 4.

    If $$\mathbf {A}\in \mathbb {C}^{m\times n},\mathbf {B}\in \mathbb {C}^{n\times m}$$ , then tr(AB) = tr(BA).

     
  5. 5.

    If A is an m × n matrix, then tr(A HA) = 0 implies that A is an m × n zero matrix.

     
  6. 6.

    x HAx = tr(Axx H) and y Hx = tr(xy H).

     
  7. 7.

    The trace of an n × n matrix is equal to the sum of its eigenvalues, namely $$\mathrm {tr} (\mathbf {A})=\lambda _1^{\,} +\cdots +\lambda _n^{\,}$$ .

     
  8. 8.
    The trace of a block matrix satisfies
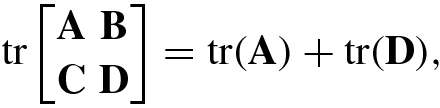
    ../images/492994_1_En_1_Chapter/492994_1_En_1_Equz_HTML.png

    where $$\mathbf {A}\in \mathbb {C}^{m\times m},\mathbf {B}\in \mathbb {C}^{m\times n},\mathbf {C} \in \mathbb {C}^{n\times m}$$ and $$\mathbf {D}\in \mathbb {C}^{n\times n}$$ .

     
  9. 9.
    For any positive integer k, we have
    $$\displaystyle \begin{aligned} \mathrm{tr}({\mathbf{A}}^k )=\sum_{i=1}^n \lambda_i^k. \end{aligned} $$
    (1.5.16)
     
By the trace equality tr(UV) = tr(VU), it is easy to see that
$$\displaystyle \begin{aligned} \mathrm{tr}({\mathbf{A}}^H\mathbf{A})=\mathrm{tr}(\mathbf{AA}^H)=\sum_{i=1}^n \sum_{j=1}^n a_{ij} a_{ij}^* =\sum_{i=1}^n\sum_{j=1}^n |a_{ij} |{}^2. \end{aligned} $$
(1.5.17)
Interestingly, if we substitute U = A, V = BC and U = AB, V = C into the trace equality tr(UV) = tr(VU), we obtain
$$\displaystyle \begin{aligned} \mathrm{tr}(\mathbf{ABC})=\mathrm{tr}(\mathbf{BCA})=\mathrm{tr}(\mathbf{CAB}). \end{aligned} $$
(1.5.18)
Similarly, if we let U = A, V = BCD or U = AB, V = CD or U = ABC, V = D, respectively, we obtain
$$\displaystyle \begin{aligned} \mathrm{tr}(\mathbf{ABCD})=\mathrm{tr}(\mathbf{BCDA})=\mathrm{tr}(\mathbf{CDAB})=\mathrm{tr}(\mathbf{DABC}). \end{aligned} $$
(1.5.19)
Moreover, if A and B are m × m matrices, and B is nonsingular, then
$$\displaystyle \begin{aligned} \mathrm{tr}(\mathbf{BAB}^{-1})=\mathrm{tr}({\mathbf{B}}^{-1} \mathbf{AB})=\mathrm{tr}(\mathbf{ABB}^{-1})=\mathrm{tr}(\mathbf{A}). \end{aligned} $$
(1.5.20)
The Frobenius norm of an m × n matrix A can be also defined using the traces of the m × m matrix A HA or that of the n × n matrix AA H, as follows [22, p. 10]:
$$\displaystyle \begin{aligned} \|\mathbf{A}\|{}_F =\sqrt{\mathrm{tr}({\mathbf{A}}^H\mathbf{A})}=\sqrt{\mathrm{tr}(\mathbf{AA}^H)}. \end{aligned} $$
(1.5.21)

1.5.5 Matrix Rank

Theorem 1.2 ([36])

Among a set of p-dimensional (row or column) vectors, there are at most p linearly independent (row or column) vectors.

Theorem 1.3 ([36])

For an m × n matrix A, the number of linearly independent rows and the number of linearly independent columns are the same.

From this theorem we have the following definition of the rank of a matrix.

Definition 1.16 (Rank)

The rank of an m × n matrix A is defined as the number of its linearly independent rows or columns.

It needs to be pointed out that the matrix rank gives only the number of linearly independent rows or columns, but it gives no information on the locations of these independent rows or columns.

According to the rank, we can classify the matrix as follows.

  • If $$\mathrm {rank}({\mathbf {A}}_{m\times n} )&lt;\min \{m,n\}$$ , then A is known as a rank-deficient matrix.

  • If rank(A m×n) = m (< n), then the matrix A is a full row rank matrix.

  • If rank(A m×n) = n (< m), then the matrix A is called a full column rank matrix.

  • If rank(A n×n) = n, then A is said to be a full-rank matrix (or nonsingular matrix).

The matrix equation A m×nx n×1 = b m×1 is said to be a consistent equation, if it has at least one exact solution. A matrix equation with no exact solution is said to be an inconsistent equation.

A matrix A with $$\mathrm {rank}(\mathbf {A})=r_A^{\,}$$ has $$r_A^{\,}$$ linearly independent column vectors. All linear combinations of the $$r_A^{\,}$$ linearly independent column vectors constitute a vector space, called the column space or the range or the manifold of A.

The column space Col(A) = Col(a 1, …, a n) or the range Range(A) = Range(a 1, …, a n) is $$r_A^{\,}$$ -dimensional. Hence the rank of a matrix can be defined by using the dimension of its column space or range, as described below.

Definition 1.17 (Dimension of Column Space)
The dimension of the column space Col(A) or the range Range(A) of an m × n matrix A is defined by the rank of the matrix, namely
$$\displaystyle \begin{aligned} r_{A}^{\,} =\mathrm{dim}(\mathrm{Col}(\mathbf{A}))=\mathrm{dim}(\mathrm{Range}(\mathbf{A})). \end{aligned} $$
(1.5.22)
The following statements about the rank of the matrix A are equivalent:

  • rank(A) = k;

  • there are k and not more than k columns (or rows) of A that combine a linearly independent set;

  • there is a k × k submatrix of A with nonzero determinant, but all the (k + 1) × (k + 1) submatrices of A have zero determinant;

  • the dimension of the column space Col(A) or the range Range(A) equals k;

  • k = n −dim[Null(A)], where Null(A) denotes the null space of the matrix A.

Theorem 1.4 ([36])
The rank of the product matrixABsatisfies the inequality
$$\displaystyle \begin{aligned} \mathrm{rank}( \mathbf{AB}) \leq \min \{\mathrm{rank}(\mathbf{A}),\mathrm{rank}( \mathbf{B})\}. \end{aligned} $$
(1.5.23)
Lemma 1.1

If premultiplying an m × n matrix A by an m × m nonsingular matrix P, or postmultiplying it by an n × n nonsingular matrix Q, then the rank of A is not changed, namely rank(PAQ) = rank(A).

Here are properties of the rank of a matrix.

  • The rank is a positive integer.

  • The rank is equal to or less than the number of columns or rows of the matrix.

  • Premultiplying any matrix A by a full column rank matrix or postmultiplying it by a full row rank matrix, then the rank of the matrix A remains unchanged.

Rank Equalities
  1. 1.

    If $$\mathbf {A}\in \mathbb {C}^{m\times n}$$ , then rank(A H) = rank(A T) = rank(A ∗) = rank(A).

     
  2. 2.

    If $$\mathbf {A}\in \mathbb {C}^{m\times n}$$ and c ≠ 0, then rank(cA) = rank(A).

     
  3. 3.
    If $$\mathbf {A}\in \mathbb {C}^{m\times m},\,\mathbf {B}\in \mathbb {C}^{m\times n}$$ , and $$\mathbf {C}\in \mathbb {C}^{n\times n}$$ are nonsingular, then
    $$\displaystyle \begin{aligned} \mathrm{rank}(\mathbf{AB})=\mathrm{rank}( \mathbf{B})=\mathrm{rank}(\mathbf{BC})=\mathrm{rank}(\mathbf{ABC}). \end{aligned}$$

    That is, after premultiplying and/or postmultiplying by a nonsingular matrix, the rank of B remains unchanged.

     
  4. 4.

    For $$\mathbf {A},\mathbf {B}\in \mathbb {C}^{m\times n}$$ , rank(A) = rank(B) if and only if there exist nonsingular  matrices $$\mathbf {X}\in \mathbb {C}^{m\times m}$$ and $$\mathbf {Y}\in \mathbb {C}^{n\times n}$$ such that B = XAY.

     
  5. 5.

    rank(AA H) = rank(A HA) = rank(A).

     
  6. 6.

    If $$\mathbf {A}\in \mathbb {C}^{m\times m}$$ , then $$\mathrm {rank}(\mathbf {A})=m\ \Leftrightarrow \ \det (\mathbf {A})\neq 0\ \Leftrightarrow \ \mathbf {A}$$ is nonsingular.

     

The commonly used rank inequalities is $$\mathrm {rank}(\mathbf {A})\leq \min \{m,n\}$$ for any m × n matrix A.

1.6 Inverse Matrices and Moore–Penrose Inverse Matrices

Matrix inversion is an important aspect of matrix calculus. In particular, the matrix inversion lemma is often used in science and engineering. In this section we discuss the inverse of a full-rank square matrix, the pseudo-inverse of a non-square matrix with full row (or full column) rank, and the inversion of a rank-deficient matrix.

1.6.1 Inverse Matrices

A nonsingular matrix A is said to be invertible, if its inverse A −1 exists so that A −1A = AA −1 = I.

On the nonsingularity or invertibility of an n × n matrix A, the following statements are equivalent [15].

  • A is nonsingular.

  • A −1 exists.

  • rank(A) = n.

  • All rows of A are linearly independent.

  • All columns of A are linearly independent.

  • $$\det (\mathbf {A}) \neq 0$$ .

  • The dimension of the range of A is n.

  • The dimension of the null space of A is equal to zero.

  • Ax = b is a consistent equation for every $$\mathbf {b}\in \mathbb {C}^n$$ .

  • Ax = b has a unique solution for every b.

  • Ax = 0 has only the trivial solution x = 0.

The inverse matrix A −1 has the following properties [2, 15].
  1. 1.

    A −1A = AA −1 = I.

     
  2. 2.

    A −1 is unique.

     
  3. 3.

    The determinant of the inverse matrix is equal to the reciprocal of the determinant of the original matrix, i.e., |A −1| = 1∕|A|.

     
  4. 4.

    The inverse matrix A −1 is nonsingular.

     
  5. 5.

    The inverse matrix of an inverse matrix is the original matrix, i.e., (A −1)−1 = A.

     
  6. 6.

    The inverse matrix of a Hermitian matrix A = A H satisfies (A H)−1 = (A −1)H = A −1. That is to say, the inverse matrix of any Hermitian matrix is a Hermitian matrix as well.

     
  7. 7.

    (A ∗)−1 = (A −1)∗.

     
  8. 8.

    If A and B are invertible, then (AB)−1 = B −1A −1.

     
  9. 9.
    If $$\mathbf {A}=\mathbf {Diag}(a_1^{\,} ,\ldots ,a_m )$$ is a diagonal matrix, then its inverse matrix
    $$\displaystyle \begin{aligned} {\mathbf{A}}^{-1}=\mathbf{Diag}(a_1^{-1} ,\ldots , a_m^{-1}). \end{aligned}$$
     
  10. 10.

    Let A be nonsingular. If A is an orthogonal matrix, then A −1 = A T, and if A is a unitary matrix, then A −1 = A H.

     
Lemma 1.2
Let A be an n × n invertible matrix, and x and y be two n × 1 vectors such that (A + xy H) is invertible; then
$$\displaystyle \begin{aligned} (\mathbf{A}+\mathbf{xy}^H)^{-1}={\mathbf{A}}^{-1}-\frac{{\mathbf{A}}^{-1}\mathbf{xy}^H{\mathbf{A}}^{-1}}{1+{\mathbf{y}}^H {\mathbf{A}}^{-1}\mathbf{x}}.{} \end{aligned} $$
(1.6.1)

Lemma 1.2 is called the matrix inversion lemma, and was presented by Sherman and Morrison [37] in 1950.

The matrix inversion lemma can be extended to an inversion formula for a sum of matrices:
$$\displaystyle \begin{aligned} (\mathbf{A}+\mathbf{UBV})^{-1}&amp;= {\mathbf{A}}^{-1}-{\mathbf{A}}^{-1}\mathbf{UB}(\mathbf{B}+\mathbf{BVA}^{-1} \mathbf{UB})^{-1}\mathbf{BVA}^{-1}\\ &amp;={\mathbf{A}}^{-1}-{\mathbf{A}}^{-1}\mathbf{U}(\mathbf{I}+\mathbf{BVA}^{-1}\mathbf{U})^{-1}\mathbf{BVA}^{-1}{} \end{aligned} $$
(1.6.2)
or
$$\displaystyle \begin{aligned} (\mathbf{A}-\mathbf{UV})^{-1}={\mathbf{A}}^{-1}+{\mathbf{A}}^{-1}\mathbf{U}(\mathbf{I}-\mathbf{VA}^{-1}\mathbf{U})^{-1}\mathbf{VA}^{-1}.{} \end{aligned} $$
(1.6.3)
The above formula is called Woodbury formula due to the work of Woodbury in 1950 [38].
Taking U = u, B = β, and V = v H, the Woodbury formula gives the result
$$\displaystyle \begin{aligned} (\mathbf{A}+\beta \mathbf{uv}^H)^{-1}={\mathbf{A}}^{-1}-\frac {\beta}{1+\beta {\mathbf{v}}^H{\mathbf{A}}^{-1}\mathbf{u}}{\mathbf{A}}^{-1} \mathbf{uv}^H {\mathbf{A}}^{-1}.{} \end{aligned} $$
(1.6.4)
In particular, if letting β = 1, then Eq. (1.6.4) reduces to formula (1.6.1), the matrix inversion lemma of Sherman and Morrison.
As a matter of fact, before Woodbury obtained the inversion formula (1.6.2), Duncan [8] in 1944 and Guttman [12] in 1946 had obtained the following inversion formula:
$$\displaystyle \begin{aligned} (\mathbf{A}-\mathbf{UD}^{-1}\mathbf{V} )^{-1}={\mathbf{A}}^{-1}+{\mathbf{A}}^{-1}\mathbf{U}(\mathbf{D}-\mathbf{VA}{}^{-1} \mathbf{U})^{-1} \mathbf{VA}^{-1}.{} \end{aligned} $$
(1.6.5)
This formula is usually called the Duncan–Guttman inversion formula [28].
In addition to the Woodbury formula, the inverse matrix of a sum of matrices also has the following forms [14]:
$$\displaystyle \begin{aligned} (\mathbf{A}+\mathbf{UBV})^{-1}&amp;={\mathbf{A}}^{-1}-{\mathbf{A}}^{-1}(\mathbf{I}+\mathbf{UBVA}^{-1})^{-1}\mathbf{UBVA}^{-1} \end{aligned} $$
(1.6.6)
$$\displaystyle \begin{aligned} &amp;={\mathbf{A}}^{-1}-{\mathbf{A}}^{-1} \mathbf{UB}(\mathbf{I}+\mathbf{VA}^{-1}\mathbf{UB})^{-1}\mathbf{VA}^{-1} \end{aligned} $$
(1.6.7)
$$\displaystyle \begin{aligned} &amp;={\mathbf{A}}^{-1}-{\mathbf{A}}^{-1}\mathbf{UBV}(\mathbf{I}+{\mathbf{A}}^{-1} \mathbf{UBV})^{-1} {\mathbf{A}}^{-1} \end{aligned} $$
(1.6.8)
$$\displaystyle \begin{aligned} &amp;= {\mathbf{A}}^{-1}-{\mathbf{A}}^{-1}\mathbf{UBVA}^{-1} (\mathbf{I}+\mathbf{UBVA}^{-1})^{-1}. \end{aligned} $$
(1.6.9)

The following are inversion formulas for block matrices.

When the matrix A is invertible, one has [1]:
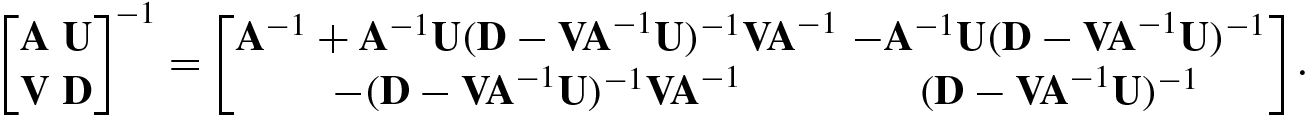
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ124_HTML.png
(1.6.10)
If the matrices A and D are invertible, then [16, 17]
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ125_HTML.png
(1.6.11)
or [8]
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ126_HTML.png
(1.6.12)
For a (m + 1) × (m + 1) nonsingular Hermitian matrix R m+1, it can always be written in a block form:
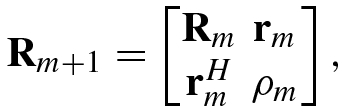
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ127_HTML.png
(1.6.13)
where ρ m is the (m + 1, m + 1)th entry of R m+1, and R m is an m × m Hermitian matrix. In order to compute $${\mathbf {R}}_{m+1}^{-1}$$ using $${\mathbf {R}}_m^{-1}$$ , let
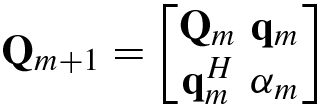
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ128_HTML.png
(1.6.14)
be the inverse matrix of R m+1. Then we have
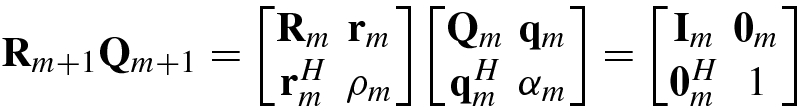
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ129_HTML.png
(1.6.15)
which gives the following four equations:
$$\displaystyle \begin{aligned} {\mathbf{R}}_m{\mathbf{Q}}_m +{\mathbf{r}}_m{\mathbf{q}}_m^H&amp;={\mathbf{I}}_m,{} \end{aligned} $$
(1.6.16)
$$\displaystyle \begin{aligned} {\mathbf{r}}_m^H{\mathbf{Q}}_m+\rho_m{\mathbf{q}}_m^H &amp;={\mathbf{0}}_m^H, \end{aligned} $$
(1.6.17)
$$\displaystyle \begin{aligned} {\mathbf{R}}_m{\mathbf{q}}_m+{\mathbf{r}}_m\alpha_m&amp;={\mathbf{0}}_m,{} \end{aligned} $$
(1.6.18)
$$\displaystyle \begin{aligned} {\mathbf{r}}_m^H{\mathbf{q}}_m+\rho_m\alpha_m &amp;=1.{} \end{aligned} $$
(1.6.19)
If R m is invertible, then from Eq. (1.6.18), it follows that
$$\displaystyle \begin{aligned} {\mathbf{q}}_m =-\alpha_m {\mathbf{R}}_m^{-1}{\mathbf{r}}_m. {} \end{aligned} $$
(1.6.20)
Substitute this result into Eq. (1.6.19) to yield
$$\displaystyle \begin{aligned} \alpha_m =\frac 1{\rho_m -{\mathbf{r}}_m^H {\mathbf{R}}_m^{-1} {\mathbf{r}}_m}.{} \end{aligned} $$
(1.6.21)
After substituting Eq. (1.6.21) into Eq. (1.6.20), we can obtain
$$\displaystyle \begin{aligned} {\mathbf{q}}_m =\frac{-{\mathbf{R}}_m^{-1}{\mathbf{r}}_m}{\rho_m -{\mathbf{r}}_b^H{\mathbf{R}}_m^{-1}{\mathbf{r}}_m}.{} \end{aligned} $$
(1.6.22)
Then, substitute Eq. (1.6.22) into Eq. (1.6.16):
$$\displaystyle \begin{aligned} {\mathbf{Q}}_m ={\mathbf{R}}_m^{-1}-{\mathbf{R}}_m^{-1}{\mathbf{r}}_m{\mathbf{q}}_m^H={\mathbf{R}}_m^{-1}+ \frac {{\mathbf{R}}_m^{-1} {\mathbf{r}}_m ({\mathbf{R}}_m^{-1} {\mathbf{r}}_m)^H}{\rho_m -{\mathbf{r}}_m^H{\mathbf{R}}_m^{-1}{\mathbf{r}}_m}.{} \end{aligned} $$
(1.6.23)
In order to simplify (1.6.21)–(1.6.23), put
$$\displaystyle \begin{aligned} {\mathbf{b}}_m &amp;\stackrel{\mathrm{def}}{=}[ b_0^{(m)},b_1^{(m)} ,\ldots ,b_{m-1}^{(m)}]^T=-{\mathbf{R}}_m^{-1} {\mathbf{r}}_m, \end{aligned} $$
(1.6.24)
$$\displaystyle \begin{aligned} \beta_m &amp;\stackrel{\mathrm{def}} {=}\rho_m -{\mathbf{r}}_m^H{\mathbf{R}}_m^{-1}{\mathbf{r}}_m =\rho_m + {\mathbf{r}}_m^H{\mathbf{b}}_m. \end{aligned} $$
(1.6.25)
Then (1.6.21)–(1.6.23) can be, respectively, simplified to
$$\displaystyle \begin{aligned} \alpha_m =\frac 1{\beta_m},\quad {\mathbf{q}}_m=\frac 1{\beta_m}{\mathbf{b}}_m,\quad {\mathbf{Q}}_m ={\mathbf{R}}_m^{-1} +\frac 1{\beta_m}{\mathbf{b}}_m{\mathbf{b}}_m^H. \end{aligned}$$
Substituting the these results into (1.6.15), it is immediately seen that
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ140_HTML.png
(1.6.26)
This formula for calculating the (m + 1) × (m + 1) inverse R m+1 from the m × m inverse R m is called the block inversion lemma for Hermitian matrices [24].

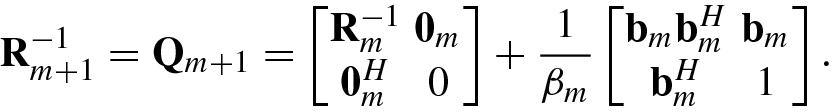
1.6.2 Left and Right Pseudo-Inverse Matrices

From a broader perspective, any n × m matrix G may be called the inverse of a given m × n matrix A, if the product of G and A is equal to the identity matrix I.

Definition 1.18 (Left Inverse, Right Inverse [36])

The matrix L satisfying LA = I but not AL = I is called the left inverse of the matrix A. Similarly, the matrix R satisfying AR = I but not RA = I is said to be the right inverse of A.

A matrix $$\mathbf {A}\in \mathbb {C}^{m\times n}$$ has a left inverse only when m ≥ n and a right inverse only when m ≤ n, respectively. It should be noted that the left or right inverse of a given matrix A is usually not unique. Let us consider the conditions for a unique solution of the left and right inverse matrices.

Let m > n and let the m × n matrix A have full column rank, i.e., rank(A) = n. In this case, the n × n matrix A HA is invertible. It is easy to verify that
$$\displaystyle \begin{aligned} \mathbf{L}=({\mathbf{A}}^H \mathbf{A})^{-1}{\mathbf{A}}^H {} \end{aligned} $$
(1.6.27)
satisfies LA = I but not AL = I. This type of left inverse matrix is uniquely determined, and is usually called the left pseudo-inverse matrix of A.
On the other hand, if m < n and A has the full row rank, i.e., rank(A) = m, then the m × m matrix AA H is invertible. Define
$$\displaystyle \begin{aligned} \mathbf{R}={\mathbf{A}}^H (\mathbf{AA}^H)^{-1}.{} \end{aligned} $$
(1.6.28)
It is easy to see that R satisfies AR = I but RA ≠ I. The matrix R is also uniquely determined and is usually called the right pseudo-inverse matrix of A.

The left pseudo-inverse matrix is closely related to the least squares solution of over-determined equations, while the right pseudo-inverse matrix is closely related to the least squares minimum norm solution of under-determined equations.

Consider the recursion $${\mathbf {F}}_m =[{\mathbf {F}}_{m-1}^{\,},{\mathbf {f}}_m^{\,}]$$ of an n × m matrix $${\mathbf {F}}_m^{\,}$$ . Then, the left pseudo-inverse $${\mathbf {F}}_m^{\mathrm {left}}=({\mathbf {F}}_m^H{\mathbf {F}}_m^{\,})^{-1}{\mathbf {F}}_m^H$$ can be recursively computed by Zhang [39]
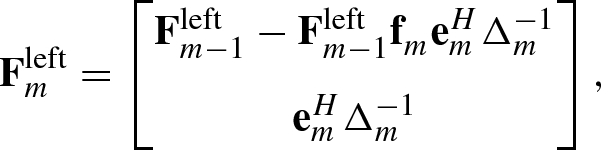
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ143_HTML.png
(1.6.29)
where $${\mathbf {e}}_m^{\,}=({\mathbf {I}}_n^{\,}-{\mathbf {F}}_{m-1}{\mathbf {F}}_{m-1}^{\mathrm {left}}){\mathbf {f}}_m^{\,}$$ and $$\Delta _m^{-1}=({\mathbf {f}}_m^H {\mathbf {e}}_m^{\,})^{-1}$$ ; the initial recursion value is $${\mathbf {F}}_1^{\mathrm {left}}={\mathbf {f}}_1^H/({\mathbf {f}}_1^H{\mathbf {f}}_1^{\,} )$$ . Similarly, the right pseudo-inverse matrix $${\mathbf {F}}_m^{\mathrm {right}}={\mathbf {F}}_m^H({\mathbf {F}}_m^{\,}{\mathbf {F}}_m^H )^{-1}$$ has the following recursive formula [39]:
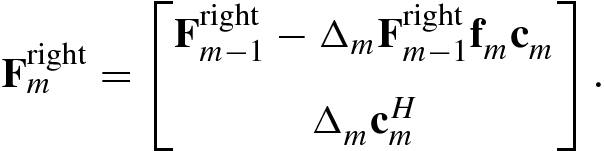
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ144_HTML.png
(1.6.30)
Here $${\mathbf {c}}_m^H ={\mathbf {f}}_m^H({\mathbf {I}}_n^{\,}-{\mathbf {F}}_{m-1}{\mathbf {F}}_{m-1}^\dagger )$$ and $$\Delta _m ={\mathbf {c}}_m^H f_m^{\,}$$ . The initial recursion value is $${\mathbf {F}}_1^{\mathrm {right}} ={\mathbf {f}}_1^H/({\mathbf {f}}_1^H{\mathbf {f}}_1^{\,} )$$ .

1.6.3 Moore–Penrose Inverse Matrices

Given an m × n rank-deficient matrix A, regardless of the size of m and n but with $$\mathrm {rank} (\mathbf {A})=k&lt;\min \{m,n\}$$ . The inverse of an m × n rank-deficient matrix is said to be its generalized inverse matrix, denoted as A †, that is an n × m matrix.

The generalized inverse of a rank-deficient matrix A should satisfy the following four conditions.
  1. 1.
    If A † is the generalized inverse of A, then Ax = y ⇒x = A †y. Substituting x = A †y into Ax = y, we have AA †y = y, and thus AA †Ax = Ax. Since this equation should hold for any given nonzero vector x, A † must satisfy the condition:
    $$\displaystyle \begin{aligned} \mathbf{AA}^\dagger\mathbf{A}=\mathbf{A}.{} \end{aligned} $$
    (1.6.31)
     
  2. 2.
    Given any y ≠ 0, the solution equation of the original matrix equation, x = A †y, can be written as x = A †Ax, yielding A †y = A †AA †y. Since A †y = A †AA †y should hold for any given nonzero vector y, the second condition
    $$\displaystyle \begin{aligned} {\mathbf{A}}^\dagger \mathbf{AA}^\dagger ={\mathbf{A}}^\dagger{} \end{aligned} $$
    (1.6.32)

    must be satisfied as well.

     
  3. 3.
    If an m × n matrix A is of full column rank or full row rank, we certainly hope that the generalized inverse matrix A † will include the left and right pseudo-inverse matrices as two special cases. Because the left and right pseudo-inverse matrix L = (A HA)−1A H and R = A H(AA H)−1 of the m × n full column rank matrix A satisfy, respectively, AL = A(A HA)−1A H = (AL)H and RA = A H(AA H)−1A = (RA)H, in order to guarantee that A † exists uniquely for any m × n matrix A, the following two conditions must be added:
    $$\displaystyle \begin{aligned} \mathbf{AA}^\dagger =(\mathbf{AA}^\dagger )^H,\quad {\mathbf{A}}^\dagger \mathbf{A}=({\mathbf{A}}^\dagger \mathbf{A})^H.{} \end{aligned} $$
    (1.6.33)
     
Definition 1.19 (Moore–Penrose Inverse [26])
Let A be any m × n matrix. An n × m matrix A † is said to be the Moore–Penrose inverse of A if A † meets the following four conditions (usually called the Moore–Penrose conditions):
  1. (a)

    AA †A = A;

     
  2. (b)

    A †AA † = A †;

     
  3. (c)

    AA † is an m × m Hermitian matrix, i.e., AA † = (AA †)H;

     
  4. (d)

    A †A is an n × n Hermitian matrix, i.e., A †A = (A †A)H.

     
Remarks

From the projection viewpoint, Moore [23] showed in 1935 that the generalized inverse matrix A † of an m × n matrix A must meet two conditions, but these conditions are not convenient for practical use. After two decades, Penrose [26] in 1955 presented the four conditions (a)–(d) stated above. In 1956, Rado [32] showed that the four conditions of Penrose are equivalent to the two conditions of Moore. Therefore the conditions (a)–(d) are called the Moore–Penrose conditions, and the generalized inverse matrix satisfying the Moore–Penrose conditions is referred to as the Moore–Penrose inverse of A.

It is easy to know that the inverse A −1, the left pseudo-inverse matrix (A HA)−1A H, and the right pseudo-inverse matrix A H(AA H)−1 are special examples of the Moore–Penrose inverse A †.

The Moore–Penrose inverse of any m × n matrix A can be uniquely determined by Boot [5]
$$\displaystyle \begin{aligned} {\mathbf{A}}^\dagger =({\mathbf{A}}^H\mathbf{A})^\dagger {\mathbf{A}}^H\qquad(\text{if}~m\geq n) \end{aligned} $$
(1.6.34)
or [10]
$$\displaystyle \begin{aligned} {\mathbf{A}}^\dagger ={\mathbf{A}}^H(\mathbf{AA}^H)^\dagger\qquad(\text{if}~m\leq n). \end{aligned} $$
(1.6.35)
From Definition 1.19 it is easily seen that A † = (A HA)†A H and A † = A H(AA H)† meet the four Moore–Penrose conditions.
For an m × n matrix A with rank r, where $$r\leq \min (m,n)$$ , there are the following three methods for computing the Moore–Penrose inverse matrix A †.
  1. 1.
    Equation-solving method [26]

    • Solve the matrix equations AA HX H = A and A HAY = A H to yield the solutions X H and Y, respectively.

    • Compute the generalized inverse matrix A † = XAY.

     
  2. 2.

    Full-rank decomposition method: If A = FG, where F m×r is of full column rank and G r×n is of full row rank, then A = FG is called the full-rank decomposition of the matrix A. By Searle [36], a matrix $$\mathbf {A} \in \mathbb {C}^{m\times n}$$ with rank(A) = r has the full-rank decomposition A = FG. Therefore, if A = FG is a full-rank decomposition of the m × n matrix A, then A † = G †F † = G H(GG H)−1(F HF)−1F H.

     
  3. 3.

    Recursive methods: Block the matrix A m×n into A k = [A k−1, a k], where A k−1 consists of the first k − 1 columns of A and a k is the kth column of A. Then, the Moore–Penrose inverse $${\mathbf {A}}_k^\dagger $$ of the block matrix A k can be recursively calculated from $${\mathbf {A}}_{k-1}^\dagger $$ . When k = n, we get the Moore–Penrose inverse matrix A †. Such a recursive algorithm was presented by Greville in 1960 [11].

     
From [20, 22, 30, 31] and [33], the Moore–Penrose inverses A † have the following properties.
  1. 1.

    For an m × n matrix A, its Moore–Penrose inverse A † is uniquely determined.

     
  2. 2.

    The Moore–Penrose inverse of the complex conjugate transpose matrix A H is given by (A H)† = (A †)H = A †H = A H†.

     
  3. 3.

    The generalized inverse of a Moore–Penrose inverse matrix is equal to the original matrix, namely (A †)† = A.

     
  4. 4.

    If c ≠ 0, then (cA)† = c −1A †.

     
  5. 5.

    If D = Diag(d 11, …, d nn), then $${\mathbf {D}}^\dagger =\mathbf {Diag}(d_{11}^\dagger ,\ldots , d_{nn}^\dagger )$$ , where $$d_{ii}^\dagger =d_{ii}^{-1}$$ (if d ii ≠ 0) or $$d_{ii}^\dagger =0$$ (if d ii = 0).

     
  6. 6.

    The Moore–Penrose inverse of an m × n zero matrix O m×n is an n × m zero matrix, i.e., $${\mathbf {O}}_{m\times n}^\dagger ={\mathbf {O}}_{n\times m}$$ .

     
  7. 7.

    If A H = A and A 2 = A, then A † = A.

     
  8. 8.
    If A = BC, B is of full column rank, and C is of full row rank, then
    $$\displaystyle \begin{aligned} {\mathbf{A}}^\dagger ={\mathbf{C}}^\dagger {\mathbf{B}}^\dagger ={\mathbf{C}}^H (\mathbf{CC}^H)^{-1} ({\mathbf{B}}^H\mathbf{B})^{-1} {\mathbf{B}}^H. \end{aligned}$$
     
  9. 9.

    (AA H)† = (A †)HA † and (AA H)†(AA H) = AA †.

     
  10. 10.

    If the matrices A i are mutually orthogonal, i.e., $${\mathbf {A}}_i^H{\mathbf {A}}_j =\mathbf {O},\, i\neq j$$ , then $$({\mathbf {A}}_1 +\cdots + {\mathbf {A}}_m )^\dagger ={\mathbf {A}}_1^\dagger +\cdots + {\mathbf {A}}_m^\dagger $$ .

     
  11. 11.

    Regarding the ranks of generalized inverse matrices, one has rank(A †) = rank(A) = rank(A H) = rank(A †A) = rank(AA †) = rank(AA †A) = rank(A †AA †).

     
  12. 12.

    The Moore–Penrose inverse of any matrix A m×n can be determined by A † = (A HA)†A H or A † = A H(AA H)†.

     

1.7 Direct Sum and Hadamard Product

This section discusses two special operations of matrices: the direct sum of two or more matrices and the Hadamard product of two matrices.

1.7.1 Direct Sum of Matrices

Definition 1.20 (Direct Sum [9])
The direct sum of an m × m matrix A and an n × n matrix B, denoted A ⊕B, is an (m + n) × (m + n) matrix and is defined as follows:
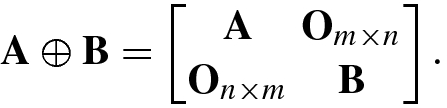
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ150_HTML.png
(1.7.1)
From the above definition, it is easily shown that the direct sum of matrices has the following properties [15, 27]:
  1. 1.

    If c is a constant, then c (A ⊕B) = cA ⊕ cB.

     
  2. 2.

    The direct sum does not satisfy exchangeability: A ⊕B ≠ B ⊕A unless A = B.

     
  3. 3.
    If A, B are two m × m matrices and C and D are two n × n matrices, then
    $$\displaystyle \begin{aligned} (\mathbf{A}\pm \mathbf{B})\oplus(\mathbf{C}\pm \mathbf{D})&amp;=(\mathbf{A}\oplus\mathbf{C})\pm (\mathbf{B}\oplus \mathbf{D}),\\ (\mathbf{A}\oplus\mathbf{C})(\mathbf{B} \oplus \mathbf{D})&amp;=\mathbf{AB}\oplus\mathbf{CD}. \end{aligned} $$
     
  4. 4.
    If A, B, C are m × m, n × n, p × p matrices, respectively, then
    $$\displaystyle \begin{aligned} \mathbf{A}\oplus (\mathbf{B}\oplus\mathbf{C})=(\mathbf{A}\oplus \mathbf{B})\oplus\mathbf{C}=\mathbf{A}\oplus\mathbf{B}\oplus\mathbf{C}. \end{aligned}$$
     
  5. 5.

    If A m×m and B n×n are, respectively, orthogonal matrices, then A ⊕B is an (m + n) × (m + n) orthogonal matrix.

     
  6. 6.
    The complex conjugate, transpose, complex conjugate transpose, and inverse matrices of the direct sum of two matrices are given by
    $$\displaystyle \begin{aligned} (\mathbf{A}\oplus \mathbf{B})^* &amp;={\mathbf{A}}^* \oplus {\mathbf{B}}^*,\quad (\mathbf{A}\oplus\mathbf{B})^T={\mathbf{A}}^T\oplus {\mathbf{B}}^T,\\ (\mathbf{A}\oplus \mathbf{B})^H&amp;={\mathbf{A}}^H \oplus {\mathbf{B}}^H,\quad (\mathbf{A}\oplus \mathbf{B})^{-1}={\mathbf{A}}^{-1}\oplus {\mathbf{B}}^{-1}~ (\text{if }\, {\mathbf{A}}^{-1}\,\text{and }{\mathbf{B}}^{-1}\,\text{exist}). \end{aligned} $$
     
  7. 7.
    The trace, rank, and determinant of the direct sum of N matrices are as follows:
    $$\displaystyle \begin{aligned} \mathrm{tr}\left (\bigoplus_{i=0}^{N-1} {\mathbf{A}}_i \right )\hskip -0.5mm \!=\!\hskip -0.5mm \sum_{i=0}^{N-1}\mathrm{tr}({\mathbf{A}}_i ),~~\mathrm{rank}\left (\bigoplus_{i=0}^{N-1}{\mathbf{A}}_i\right ) \hskip -0.5mm \!=\!\hskip -0.5mm \sum_{i=0}^{N-1}\mathrm{rank} ({\mathbf{A}}_i ),~~\left | \bigoplus_{i=0}^{N-1}{\mathbf{A}}_i \right |\hskip -0.5mm \!=\!\hskip -0.5mm \prod_{i=0}^{N-1}|{\mathbf{A}}_i|. \end{aligned}$$
     

1.7.2 Hadamard Product

Definition 1.21 (Hadamard Product)
The Hadamard product of two m × n matrices A = [a ij] and B = [b ij] is denoted A ⊙B and is also an m × n matrix, each entry of which is defined as the product of the corresponding entries of the two matrices:
$$\displaystyle \begin{aligned}{}[\mathbf{A}\odot \mathbf{B}]_{ij}=a_{ij} b_{ij}. \end{aligned} $$
(1.7.2)
That is, the Hadamard product is a mapping $$\mathbb {R}^{m\times n}\times \mathbb {R}^{m\times n} \to \mathbb {R}^{m\times n}$$ .
The Hadamard product is also known as the Schur product or the elementwise product. Similarly, the elementwise division of two m × n matrices A = [a ij] and B = [b ij], denoted A ⊘B, is defined as
$$\displaystyle \begin{aligned}{}[\mathbf{A}\oslash\mathbf{B}]_{ij}=a_{ij}/b_{ij}. \end{aligned} $$
(1.7.3)

The following theorem describes the positive definiteness of the Hadamard product and is usually known as the Hadamard product theorem [15].

Theorem 1.5

If two m × m matrices A and B are positive definite (positive semi-definite), then their Hadamard product A ⊙B is positive definite (positive semi-definite) as well.

Corollary 1.1 (Fejer Theorem [15])
An m × m matrix A = [a ij] is positive semi-definite if and only if
$$\displaystyle \begin{aligned} \sum_{i=1}^m\sum_{j=1}^m a_{ij} b_{ij} \geq 0 \end{aligned}$$

holds for all m × m positive semi-definite matrices B = [b ij].

The following theorems describe the relationship between the Hadamard product and the matrix trace.

Theorem 1.6 ([22, p. 46])
Let A, B, C be m × n matrices, 1 = [1, …, 1]T be an n × 1 summing vector and $$\mathbf {D}=\mathbf {Diag}(d_1^{\,} ,\ldots ,d_m )$$ , where $$d_i =\sum _{j=1}^n a_{ij}$$ ; then
$$\displaystyle \begin{aligned} \mathrm{tr}\left ({\mathbf{A}}^T(\mathbf{B}\odot \mathbf{C})\right )&amp;=\mathrm{tr}\left ( ({\mathbf{A}}^T \odot {\mathbf{B}}^T) \mathbf{C}\right ), {} \end{aligned} $$
(1.7.4)
$$\displaystyle \begin{aligned} {\mathbf{1}}^T{\mathbf{A}}^T(\mathbf{B}\odot \mathbf{C})\mathbf{1}&amp;=\mathrm{tr}({\mathbf{B}}^T \mathbf{DC}).{} \end{aligned} $$
(1.7.5)
Theorem 1.7 ([22, p. 46])
Let A, B be two n × n positive definite square matrices, and 1 = [1, …, 1]T be an n × 1 summing vector. Suppose that M is an n × n diagonal matrix, i.e., $$\mathbf {M}= \mathbf {Diag}( \mu _1^{\,} ,\ldots ,\mu _n )$$ , while m = M1 is an n × 1 vector. Then one has
$$\displaystyle \begin{aligned} \mathrm{tr}(\mathbf{AMB}^T\mathbf{M})&amp;={\mathbf{m}}^T(\mathbf{A}\odot\mathbf{B})\mathbf{m},{} \end{aligned} $$
(1.7.6)
$$\displaystyle \begin{aligned} \mathrm{tr}(\mathbf{AB}^T)&amp;={\mathbf{1}}^T(\mathbf{A}\odot \mathbf{B})\mathbf{1},{} \end{aligned} $$
(1.7.7)
$$\displaystyle \begin{aligned} \mathbf{MA}\odot {\mathbf{B}}^T\mathbf{M}&amp;=\mathbf{M}(\mathbf{A}\odot{\mathbf{B}}^T)\mathbf{M}.{} \end{aligned} $$
(1.7.8)
From the above definition, it is known that Hadamard products obey the exchange law, the associative law, and the distributive law of the addition:
$$\displaystyle \begin{aligned} \mathbf{A}\odot\mathbf{B}&amp;=\mathbf{B}\odot\mathbf{A}, \end{aligned} $$
(1.7.9)
$$\displaystyle \begin{aligned} \mathbf{A}\odot (\mathbf{B}\odot\mathbf{C})&amp;=(\mathbf{A}\odot\mathbf{B})\odot\mathbf{C}, \end{aligned} $$
(1.7.10)
$$\displaystyle \begin{aligned} \mathbf{A}\odot (\mathbf{B}\pm\mathbf{C})&amp;=\mathbf{A}\odot\mathbf{B}\pm\mathbf{A}\odot\mathbf{C}. \end{aligned} $$
(1.7.11)
The properties of Hadamard products are summarized below [22].
  1. 1.
    If A, B are m × n matrices, then
    $$\displaystyle \begin{aligned} (\mathbf{A}\odot \mathbf{B})^T={\mathbf{A}}^T\odot{\mathbf{B}}^T,\quad (\mathbf{A}\odot\mathbf{B})^H ={\mathbf{A}}^H\odot{\mathbf{B}}^H,\quad (\mathbf{A}\odot\mathbf{B})^* ={\mathbf{A}}^*\odot{\mathbf{B}}^*. \end{aligned}$$
     
  2. 2.

    The Hadamard product of a matrix A m×n and a zero matrix O m×n is given by A ⊙O m×n = O m×n ⊙A = O m×n.

     
  3. 3.

    If c is a constant, then c (A ⊙B) = (cA) ⊙B = A ⊙ (c B).

     
  4. 4.

    The Hadamard product of two positive definite (positive semi-definite) matrices A, B is positive definite (positive semi-definite) as well.

     
  5. 5.
    The Hadamard product of the matrix A m×m = [a ij] and the identity matrix I m is an m × m diagonal matrix, i.e.,
    $$\displaystyle \begin{aligned} \mathbf{A}\odot{\mathbf{I}}_m ={\mathbf{I}}_m\odot\mathbf{A}= \mathbf{Diag}(\mathbf{A})=\mathbf{Diag}(a_{11},\ldots ,a_{mm}). \end{aligned}$$
     
  6. 6.
    If A, B, D are three m × m matrices and D is a diagonal matrix, then
    $$\displaystyle \begin{aligned} (\mathbf{DA})\odot (\mathbf{BD})=\mathbf{D}(\mathbf{A}\odot\mathbf{B})\mathbf{D}. \end{aligned}$$
     
  7. 7.
    If A, C are two m × m matrices and B, D are two n × n Matrices, then
    $$\displaystyle \begin{aligned} (\mathbf{A}\oplus\mathbf{B})\odot (\mathbf{C}\oplus \mathbf{D})=(\mathbf{A}\odot \mathbf{C})\oplus (\mathbf{B}\odot\mathbf{D}). \end{aligned}$$
     
  8. 8.
    If A, B, C, D are all m × n matrices, then
    $$\displaystyle \begin{aligned} (\mathbf{A}+\mathbf{B})\odot (\mathbf{C}+\mathbf{D})= \mathbf{A}\odot\mathbf{C}+\mathbf{A} \odot\mathbf{D}+\mathbf{B}\odot \mathbf{C}+\mathbf{B}\odot\mathbf{D}. \end{aligned}$$
     
  9. 9.

    If A, B, C are m × n matrices, then $$\mathrm {tr}\left ({\mathbf {A}}^T(\mathbf {B}\odot \mathbf {C})\right )=\mathrm {tr}\left ((\mathbf { A}^T \odot {\mathbf {B}}^T)\mathbf {C}\right )$$ .

     

The Hadamard (i.e., elementwise) products of two matrices are widely used in machine learning, neural networks, and evolutionary computations.

1.8 Kronecker Products

The Hadamard product described in the previous section is a special product of two matrices. In this section, we discuss another special product of two matrices: the Kronecker products. The Kronecker product is also known as the direct product or tensor product [20].

1.8.1 Definitions of Kronecker Products

Kronecker products are divided into right and left Kronecker products.

Definition 1.22 (Right Kronecker Product [3])
Given an m × n matrix $$\mathbf {A}=[{\mathbf {a}}_1^{\,} , \ldots ,{\mathbf {a}}_n ]$$ and another p × q matrix B, their right Kronecker product A ⊗B is an mp × nq matrix defined by
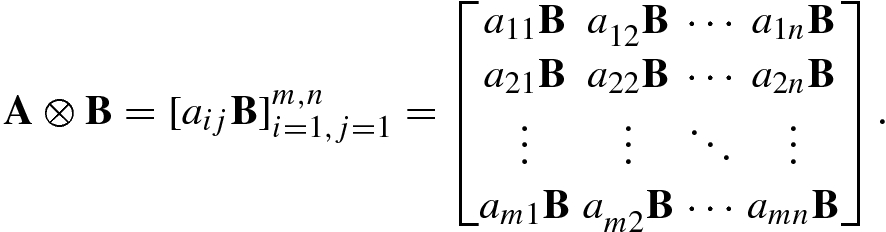
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ161_HTML.png
(1.8.1)
Definition 1.23 (Left Kronecker Product [9, 34])
For an m × n matrix A and a p × q matrix $$\mathbf {B}=[{\mathbf {b}}_1^{\,} ,\ldots ,{\mathbf {b}}_q ]$$ , their left Kronecker product A ⊗B is an mp × nq matrix defined by
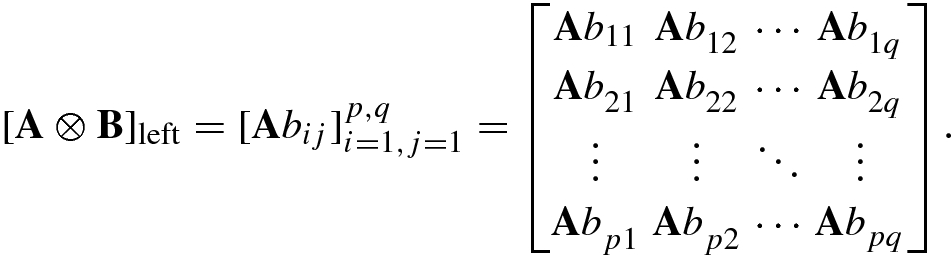
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ162_HTML.png
(1.8.2)

Clearly, the left or right Kronecker product is a mapping $$\mathbb {R}^{m\times n}\times \mathbb {R}^{p\times q}\to \mathbb {R}^{mp\times nq}$$ . It is easily seen that the left and right Kronecker products have the following relationship: [A ⊗B]left = B ⊗A. Since the right Kronecker product form is the one generally adopted, this book uses the right Kronecker product hereafter unless otherwise stated.

In particular, when n = 1 and q = 1, the Kronecker product of two matrices reduces to the Kronecker product of two column vectors $$\mathbf {a}\in \mathbb {R}^m$$ and $$\mathbf {b}\in \mathbb {R}^p$$ :
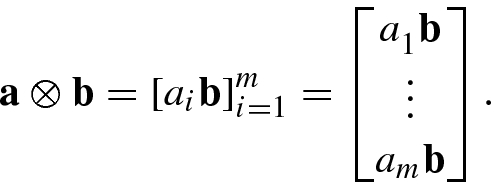
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ163_HTML.png
(1.8.3)
The result is an mp × 1 vector. Evidently, the outer product of two vectors x ∘y = xy T can be also represented using the Kronecker product as x ∘y = x ⊗y T.

1.8.2 Performance of Kronecker Products

Summarizing results from [3, 6] and other literature, Kronecker products have the following properties.
  1. 1.

    The Kronecker product of any matrix and a zero matrix is equal to the zero matrix, i.e., A ⊗O = O ⊗A = O.

     
  2. 2.

    If α and β are constants, then αA ⊗ βB = αβ(A ⊗B).

     
  3. 3.

    The Kronecker product of an m × m identity matrix and an n × n identity matrix is equal to an mn × mn identity matrix, i.e., I m ⊗I n = I mn.

     
  4. 4.
    For matrices A m×n, B n×k, C l×p, D p×q, we have
    $$\displaystyle \begin{aligned} (\mathbf{A}\mathbf{B})\otimes (\mathbf{CD})=(\mathbf{A}\otimes \mathbf{C})(\mathbf{B}\otimes \mathbf{D}). \end{aligned} $$
    (1.8.4)
     
  5. 5.
    For matrices A m×n, B p×q, C p×q, we have
    $$\displaystyle \begin{aligned} \mathbf{A}\otimes (\mathbf{B} \pm\mathbf{C}) &amp;=\mathbf{A} \otimes\mathbf{B}\pm\mathbf{A}\otimes\mathbf{C}, \end{aligned} $$
    (1.8.5)
    $$\displaystyle \begin{aligned} (\mathbf{B}\pm\mathbf{C})\otimes \mathbf{A}&amp;=\mathbf{B}\otimes \mathbf{A}\pm\mathbf{C}\otimes\mathbf{A}. \end{aligned} $$
    (1.8.6)
     
  6. 6.
    The inverse and generalized inverse matrix of Kronecker products satisfy
    $$\displaystyle \begin{aligned} (\mathbf{A}\otimes \mathbf{B})^{-1} ={\mathbf{A}}^{-1} \otimes {\mathbf{B}}^{-1},\quad \ (\mathbf{A}\otimes \mathbf{B} )^\dagger = {\mathbf{A}}^\dagger \otimes {\mathbf{B}}^\dagger. \end{aligned} $$
    (1.8.7)
     
  7. 7.
    The transpose and the complex conjugate transpose of Kronecker products are given by
    $$\displaystyle \begin{aligned} (\mathbf{A}\otimes \mathbf{B})^T={\mathbf{A}}^T \otimes{\mathbf{B}}^T,\quad \ (\mathbf{A}\otimes \mathbf{B})^H ={\mathbf{A}}^H \otimes{\mathbf{B}}^H. \end{aligned} $$
    (1.8.8)
     
  8. 8.
    The rank of the Kronecker product is
    $$\displaystyle \begin{aligned} \mathrm{rank}(\mathbf{A}\otimes \mathbf{B}) =\mathrm{rank}(\mathbf{A}) \mathrm{rank} (\mathbf{B}). \end{aligned} $$
    (1.8.9)
     
  9. 9.
    The determinant of the Kronecker product
    $$\displaystyle \begin{aligned} \det ({\mathbf{A}}_{n\times n}\otimes {\mathbf{B}}_{m\times m})=(\det \mathbf{A})^m (\det \mathbf{B})^n. \end{aligned} $$
    (1.8.10)
     
  10. 10.
    The trace of the Kronecker product is given by
    $$\displaystyle \begin{aligned} \mathrm{tr}(\mathbf{A}\otimes \mathbf{B})=\mathrm{tr}(\mathbf{A}) \mathrm{tr} (\mathbf{B}). \end{aligned} $$
    (1.8.11)
     
  11. 11.
    For matrices A m×n, B m×n, C p×q, D p×q, we have
    $$\displaystyle \begin{aligned} (\mathbf{A}+ \mathbf{B})\otimes (\mathbf{C}+\mathbf{D})=\mathbf{A}\otimes \mathbf{C} +\mathbf{A}\otimes\mathbf{D} +\mathbf{B}\otimes \mathbf{C} +\mathbf{B}\otimes \mathbf{D}.{} \end{aligned} $$
    (1.8.12)
     
  12. 12.
    For matrices A m×n, B p×q, C k×l, it is true that
    $$\displaystyle \begin{aligned} (\mathbf{A}\otimes \mathbf{B})\otimes\mathbf{C}=\mathbf{A}\otimes (\mathbf{B}\otimes \mathbf{C}). \end{aligned} $$
    (1.8.13)
     
  13. 13.

    For matrices A m×n, B p×q, we have $$\exp (\mathbf {A}\otimes \mathbf {B})= \exp (\mathbf {A})\otimes \exp (\mathbf {B})$$ .

     
  14. 14.
    Let $$\mathbf {A}\in \mathbb {C}^{m\times n}$$ and $$\mathbf {B}\in \mathbb {C}^{p\times q}$$ then [22, p. 47]
    $$\displaystyle \begin{aligned} {\mathbf{K}}_{pm}(\mathbf{A}\otimes \mathbf{B})&amp;=(\mathbf{B}\otimes \mathbf{A}){\mathbf{K}}_{qn}, \end{aligned} $$
    (1.8.14)
    $$\displaystyle \begin{aligned} {\mathbf{K}}_{pm}(\mathbf{A} \otimes \mathbf{B}){\mathbf{K}}_{nq}&amp;=\mathbf{B}\otimes \mathbf{A}, \end{aligned} $$
    (1.8.15)
    $$\displaystyle \begin{aligned} {\mathbf{K}}_{pm}(\mathbf{A}\otimes\mathbf{B})&amp;=\mathbf{B}\otimes \mathbf{A}, \end{aligned} $$
    (1.8.16)
    $$\displaystyle \begin{aligned} {\mathbf{K}}_{mp}(\mathbf{B}\otimes\mathbf{A})&amp;=\mathbf{A}\otimes \mathbf{B}, \end{aligned} $$
    (1.8.17)

    where K is a commutation matrix (see Sect. 1.9.1).

     

1.9 Vectorization and Matricization

Consider the operators that transform a matrix into a vector or vice versa.

1.9.1 Vectorization and Commutation Matrix

The function or operator that transforms a matrix into a vector is known as the vectorization of the matrix.

The column vectorization of a matrix $$\mathbf {A}\in \mathbb {R}^{m\times n}$$ , denoted vec(A), is a linear transformation that arranges the entries of A = [a ij] as an mn × 1 vector via column stacking:
$$\displaystyle \begin{aligned} \mathrm{vec}(\mathbf{A})=[a_{11},\ldots ,a_{m1},\ldots ,a_{1n},\ldots ,a_{mn}]^T. \end{aligned} $$
(1.9.1)
A matrix A can be also arranged as a row vector by row stacking:
$$\displaystyle \begin{aligned} \mathrm{rvec}(\mathbf{A})=[a_{11},\ldots ,a_{1n},\ldots ,a_{m1},\ldots , a_{mn}]. \end{aligned} $$
(1.9.2)
This is known as the row vectorization of the matrix.

For instance, given a matrix 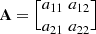../images/492994_1_En_1_Chapter/492994_1_En_1_IEq192_HTML.gif, then vec(A) = [a 11, a 21, a 12, a 22]T and rvec(A) = [a 11, a 12, a 21, a 22].

The column vectorization is usually called the vectorization simply.

Clearly, there exist the following relationships between the vectorization and the row vectorization of a matrix:
$$\displaystyle \begin{aligned} \mathrm{rvec}(\mathbf{A})=(\mathrm{vec}({\mathbf{A}}^T))^T,\quad \ \mathrm{vec}({\mathbf{A}}^T)=(\mathrm{rvec}\,\mathbf{A})^T. \end{aligned} $$
(1.9.3)
One obvious fact is that, for a given m × n matrix A, the two vectors vec(A) and vec(A T) contain the same entries but the orders of their entries are different. Interestingly, there is a unique mn × mn permutation matrix that can transform vec(A) into vec(A T). This permutation matrix is called the commutation matrix, denoted as K mn, and is defined by
$$\displaystyle \begin{aligned} {\mathbf{K}}_{mn} \mathrm{vec}(\mathbf{A})=\mathrm{vec}({\mathbf{A}}^T).{} \end{aligned} $$
(1.9.4)
Similarly, there is an nm × nm permutation matrix transforming vec(A T) into vec(A). Such a commutation matrix, denoted K nm, is defined by
$$\displaystyle \begin{aligned} {\mathbf{K}}_{nm} \mathrm{vec}({\mathbf{A}}^T)=\mathrm{vec}(\mathbf{A}).{} \end{aligned} $$
(1.9.5)

From (1.9.4) and (1.9.5) it can be seen that K nmK mnvec(A) = K nmvec(A T) = vec(A). Since this formula holds for any m × n matrix A, we have K nmK mn = I mn or $${\mathbf {K}}_{mn}^{-1}={\mathbf {K}}_{nm}$$ .

The mn × mn commutation matrix K mn has the following properties [21].
  1. 1.

    K mnvec(A) = vec(A T) and K nmvec(A T) = vec(A), where A is an m × n matrix.

     
  2. 2.

    $${\mathbf {K}}_{mn}^T{\mathbf {K}}_{mn}={\mathbf {K}}_{mn}{\mathbf {K}}_{mn}^T={\mathbf {I}}_{mn}$$ , or $${\mathbf {K}}_{mn}^{-1}={\mathbf {K}}_{nm}$$ .

     
  3. 3.

    $${\mathbf {K}}_{mn}^T={\mathbf {K}}_{nm}$$ .

     
  4. 4.
    K mn can be represented as a Kronecker product of the basic vectors:
    $$\displaystyle \begin{aligned} {\mathbf{K}}_{mn}=\sum_{j=1}^n ({\mathbf{e}}_j^T\otimes {\mathbf{I}}_m\otimes{\mathbf{e}}_j ). \end{aligned}$$
     
  5. 5.

    K 1n = K n1 = I n.

     
  6. 6.

    K nmK mnvec(A) = K nmvec(A T) = vec(A).

     
  7. 7.

    Eigenvalues of the commutation matrix K nn are 1 and − 1 and their multiplicities are, respectively, $$\frac 12n(n+1)$$ and $$\frac 12 n(n-1)$$ .

     
  8. 8.

    The rank of the commutation matrix is given by rank(K mn) = 1 + d(m − 1, n − 1), where d(m, n) is the greatest common divisor of m and n, d(n, 0) = d(0, n) = n.

     
  9. 9.

    K mn(A ⊗B)K pq = B ⊗A, and thus can be equivalently written as K mn(A ⊗B) = (B ⊗A)K qp, where A is an n × p matrix and B is an m × q matrix. In particular, K mn(A n×n ⊗B m×m) = (B ⊗A)K mn.

     
  10. 10.

    $$\mathrm {tr}({\mathbf {K}}_{mn}({\mathbf {A}}_{m\times n}\otimes {\mathbf {B}}_{m\times n}))=\mathrm {tr}({\mathbf {A}}^T\mathbf {B})=\left ( \mathrm {vec}({\mathbf {B}}^T)\right )^T{\mathbf {K}}_{mn}\mathrm {vec}(\mathbf {A})$$ .

     
An mn × mn commutation matrix can be constructed as follows. First let
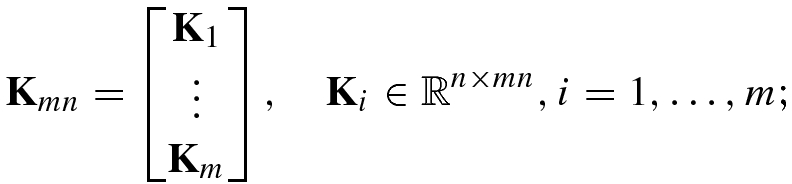
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ183_HTML.png
(1.9.6)
then the (i, j)th entry of the first submatrix K 1 is given by
$$\displaystyle \begin{aligned} K_1(i,j)=\left\{\begin{array}{ll} 1, &amp;~~j=(i-1)m +1,\,i=1,\ldots ,n,\\ 0,&amp;~~\text{otherwise}.\end{array} \right. \end{aligned} $$
(1.9.7)
Next, the ith submatrix K i (i = 2, …, m) is constructed from the (i − 1)th submatrix K i−1 as follows:
$$\displaystyle \begin{aligned} {\mathbf{K}}_i =[\mathbf{0},{\mathbf{K}}_{i-1}(1:mn-1)],\quad \ i=2,\ldots ,m, \end{aligned} $$
(1.9.8)
where K i−1(1 : mn − 1) denotes a submatrix consisting of the first (mn − 1) columns of the n × m submatrix K i−1.

1.9.2 Matricization of Vectors

Matricization refers to a mapping that transform a vector into a matrix. The operation for transforming an mn-dimensional column vector $$\mathbf {a}=[a_1^{\,} ,\ldots ,a_{mn}]^T$$ into an m × n matrix A is known as the matricization of column vector or unfolding of column vector, denoted unvecm,n(a), and is defined as
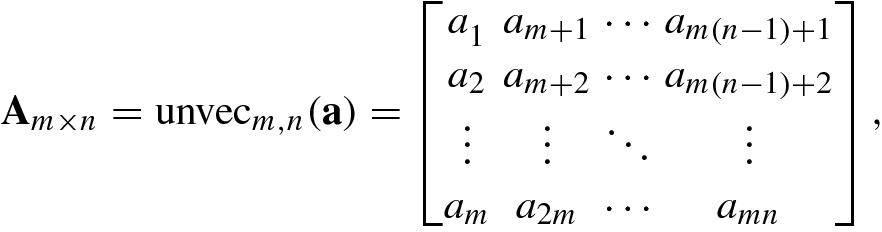
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ186_HTML.png
(1.9.9)
where
$$\displaystyle \begin{aligned} A_{ij} =a_{i+(j-1)m} ,\quad i=1,\ldots ,m,\,j=1,\ldots ,n. \end{aligned} $$
(1.9.10)
Similarly, the operation for transforming an 1 × mn row vector $$\mathbf {b}=[b_1^{\,} ,\ldots ,b_{mn}]$$ into an m × n matrix B is called the matricization of row vector or unfolding of row vector, denoted unrvecm,n(b), and is defined as
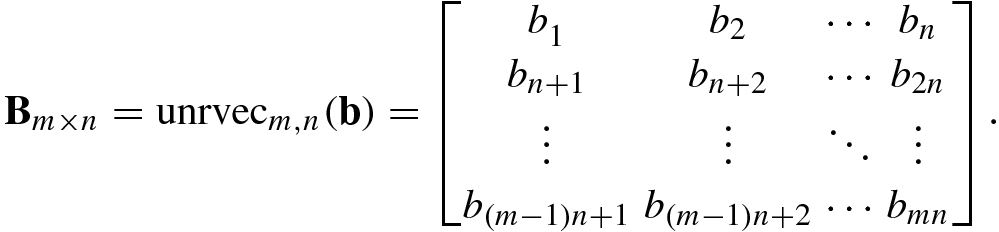
../images/492994_1_En_1_Chapter/492994_1_En_1_Equ188_HTML.png
(1.9.11)
This is equivalently represented in element form as
$$\displaystyle \begin{aligned} B_{ij} =b_{j+(i-1)n} ,\quad i=1,\ldots ,m,\,j=1,\ldots ,n.\end{aligned} $$
(1.9.12)
It can be seen from the above definitions that there are the following relationships between matricization (unvec) and column vectorization (vec) or row vectorization (rvec):
../images/492994_1_En_1_Chapter/492994_1_En_1_Equap_HTML.png
which can be written as
$$\displaystyle \begin{aligned} \mathrm{unvec}_{m,n}^{\,}(\mathbf{a})={\mathbf{A}}_{m\times n}\quad &amp;\Leftrightarrow\quad \mathrm{vec}({\mathbf{A}}_{m\times n}^{\,})= {\mathbf{a}}_{mn\times 1},{} \end{aligned} $$
(1.9.13)
$$\displaystyle \begin{aligned} \mathrm{unrvec}_{m,n}^{\,}(\mathbf{b})={\mathbf{B}}_{m\times n}^{\,}\quad &amp;\Leftrightarrow\quad \mathrm{rvec}({\mathbf{B}}_{m\times n}^{\,}) ={\mathbf{b}}_{1\times mn}. {}\end{aligned} $$
(1.9.14)
The vectorization operator has the following properties [7, 13, 22].
  1. 1.

    The vectorization of a transposed matrix is given by vec(A T) = K mnvec(A) for $$\mathbf {A}\in \mathbb {C}^{m\times n}$$ .

     
  2. 2.

    The vectorization of a matrix sum is given by vec(A + B) = vec(A) + vec(B).

     
  3. 3.
    The vectorization of a Kronecker product is given by Magnus and Neudecker [22, p. 184]:
    $$\displaystyle \begin{aligned} \mathrm{vec}(\mathbf{X}\otimes \mathbf{Y})=({\mathbf{I}}_m \otimes{\mathbf{K}}_{qp}\otimes{\mathbf{I}}_n)(\mathrm{vec}(\mathbf{X})\otimes\mathrm{vec}(\mathbf{Y})). \end{aligned} $$
    (1.9.15)
     
  4. 4.
    The trace of a matrix product is given by
    $$\displaystyle \begin{aligned} \mathrm{tr}({\mathbf{A}}^T\mathbf{B})&amp;=(\mathrm{vec}(\mathbf{A}))^T\,\mathrm{vec}(\mathbf{B}), \end{aligned} $$
    (1.9.16)
    $$\displaystyle \begin{aligned} \mathrm{tr}({\mathbf{A}}^H\mathbf{B})&amp;=(\mathrm{vec}(\mathbf{A}))^H\,\mathrm{vec}(\mathbf{B}), \end{aligned} $$
    (1.9.17)
    $$\displaystyle \begin{aligned} \mathrm{tr}(\mathbf{ABC})&amp;=(\mathrm{vec}(\mathbf{A}))^T({\mathbf{I}}_p^{\,} \otimes \mathbf{B})\,\mathrm{vec}(\mathbf{C}), \end{aligned} $$
    (1.9.18)
    while the trace of the product of four matrices is determined by Magnus and Neudecker [22, p. 31]:
    $$\displaystyle \begin{aligned} \mathrm{tr}(\mathbf{ABCD})=(\mathrm{vec}({\mathbf{D}}^T))^T({\mathbf{C}}^T\otimes\mathbf{A})\,\mathrm{vec}(\mathbf{B})=(\mathrm{vec}(\mathbf{D}))^T(\mathbf{A} \otimes {\mathbf{C}}^T)\,\mathrm{vec}({\mathbf{B}}^T). \end{aligned}$$
     
  5. 5.
    The Kronecker product of two vectors a and b can be represented as the vectorization of their outer product ba T as follows:
    $$\displaystyle \begin{aligned} \mathbf{a}\otimes \mathbf{b}=\mathrm{vec}(\mathbf{ba}^T) =\mathrm{vec}(\mathbf{b}\circ \mathbf{a}). \end{aligned} $$
    (1.9.19)
     
  6. 6.
    The vectorization of the Hadamard product is given by
    $$\displaystyle \begin{aligned} \mathrm{vec}(\mathbf{A}\odot \mathbf{B})=\mathrm{vec}(\mathbf{A})\odot \mathrm{vec}(\mathbf{B})=\mathbf{Diag}(\mathrm{vec}(\mathbf{A}))\,\mathrm{vec}(\mathbf{B}), \end{aligned} $$
    (1.9.20)

    where Diag(vec(A)) is a diagonal matrix whose entries are the vectorization function vec(A).

     
  7. 7.
    The relation of the vectorization of the matrix product A m×pB p×qC q×n to the Kronecker product is given by Schott [35, p. 263]:
    $$\displaystyle \begin{aligned} \mathrm{vec}(\mathbf{ABC})&amp;=({\mathbf{C}}^T\otimes\mathbf{A})\,\mathrm{vec}(\mathbf{B}),{} \end{aligned} $$
    (1.9.21)
    $$\displaystyle \begin{aligned} \mathrm{vec}(\mathbf{ABC})&amp;=({\mathbf{I}}_q\otimes\mathbf{AB})\,\mathrm{vec}(\mathbf{C})=({\mathbf{C}}^T{\mathbf{B}}^T \otimes{\mathbf{I}}_m )\,\mathrm{vec}(\mathbf{A}), \end{aligned} $$
    (1.9.22)
    $$\displaystyle \begin{aligned} \mathrm{vec}(\mathbf{AC})&amp;=({\mathbf{I}}_p\otimes \mathbf{A}) \,\mathrm{vec}(\mathbf{C})=({\mathbf{C}}^T\otimes {\mathbf{I}}_m )\,\mathrm{vec}(\mathbf{A}). \end{aligned} $$
    (1.9.23)
     
Example 1.2
Consider the solution of the matrix equation AXB = C, where $$\mathbf {A}\in \mathbb {R}^{m\times n}, \mathbf {X}\in \mathbb {R}^{n\times p}$$ , $$\mathbf {B}\in \mathbb {R}^{p\times q}$$ , and $$\mathbf {C}\in \mathbb {R}^{m\times q}$$ . By using the vectorization function property vec(AXB) = (B T ⊗A) vec(X), the vectorization vec(AXB) = vec(C) of the original matrix equation can be, in Kronecker product form, rewritten as [33]:
$$\displaystyle \begin{aligned} ({\mathbf{B}}^T\otimes \mathbf{A})\mathrm{vec}(\mathbf{X})=\mathrm{vec}(\mathbf{C}), \end{aligned}$$
and thus vec(X) = (B T ⊗A)†vec(C). Then by matricizing vec(X), we get the solution matrix X of the original matrix equation AXB = C.
Brief Summary of This Chapter

  • This chapter focuses on basic operations and performance of matrices, which constitute the foundation of matrix algebra.

  • Trace, rank, positive definiteness, Moore–Penrose inverse matrices, Kronecker product, Hadamard product (elementwise product), and vectorization of matrices are frequently used in artificial intelligence.