© Springer Nature Singapore Pte Ltd. 2020
X.-D. ZhangA Matrix Algebra Approach to Artificial Intelligencehttps://doi.org/10.1007/978-981-15-2770-8_4

4. Solution of Linear Systems

Xian-Da Zhang1  
(1)
Department of Automation, Tsinghua University, Beijing, Beijing, China
 
 Deceased

One of the most common problems in science and engineering is to solve the matrix equation Ax = b for finding x when the data matrix A and the data vector b are given.

Matrix equations can be divided into three types.
  1. 1.

    Well-determined equation: If m = n and rank(A) = n, i.e., the matrix A is nonsingular, then the matrix equation Ax = b is said to be well-determined.

     
  2. 2.

    Under-determined equation: The matrix equation Ax = b is under-determined if the number of linearly independent equations is less than the number of independent unknowns.

     
  3. 3.

    Over-determined equation: The matrix equation Ax = b is known as over-determined if the number of linearly independent equations is larger than the number of independent unknowns.

     

This chapter is devoted to describe singular value decomposition (SVD) together with Gauss elimination and conjugate gradient methods for solving well-determined matrix equations followed by Tikhonov regularization and total least squares for solving over-determined matrix equations, and the Lasso and LARS methods for solving under-determined matrix equations.

4.1 Gauss Elimination

First consider solution of well-determined equations. In well-determined equation, the number of independent equations and the number of independent unknowns are the same so that the solution of this system of equations is uniquely determined. The exact solution of a well-determined matrix equation Ax = b is given by x = A −1b. A well-determined equation is a consistent equation.

In this section, we deal with Gauss elimination method and conjugate gradient methods for solving an over-determined matrix equation Ax = b and finding the inverse of a singular matrix. This method performs only elementary row operations to the augmented matrix B = [A, b].

4.1.1 Elementary Row Operations

When solving an m × n system of linear equations, it is useful to reduce equations. The principle of reduction processes is to keep the solutions of the linear systems unchanged.

Definition 4.1 (Equivalent Systems)

Two linear systems of equations in n unknowns are said to be equivalent systems if they have the same sets of solutions.

To transform a given m × n matrix equation A m×nx n = b m into an equivalent system, a simple and efficient way is to apply a sequence of elementary operations on the given matrix equation.

Definition 4.2 (Elementary Row Operations)
The following three types of operation on the rows of a system of linear equations are called elementary row operations.

  • Type I: Interchange any two equations, say the pth and qth equations; this is denoted by R p ↔ R q.

  • Type II: Multiply the pth equation by a nonzero number α; this is denoted by αR p → R p.

  • Type III: Add β times the pth equation to the qth equation; this is denoted by βR p + R q → R q.

Clearly, any above type of elementary row operation does not change the solution of a system of linear equations, so after elementary row operations, the reduced system of linear equations and the original system of linear equations are equivalent.

Definition 4.3 (Leading Entry)

The leftmost nonzero entry of a nonzero row is called the leading entry of the row. If the leading entry is equal to 1 then it is said to be the leading-1 entry.

As a matter of fact, any elementary operation on an m × n system of equations Ax = b is equivalent to the same type of elementary operation on the augmented matrix B = [A, b], where the column vector b is written alongside A. Therefore, performing elementary row operations on a system of linear equations Ax = b can be in practice implemented by using the same elementary row operations on the augmented matrix B = [A, b].

The discussions above show that if, after a sequence of elementary row operations, the augmented matrix B m×(n+1) becomes another simpler matrix C m×(n+1) then two matrices are row equivalent for the same solution of linear system.

For the convenience of solving a system of linear equations, the final row equivalent matrix should be of echelon form.

Definition 4.4 (Echelon Matrix)
A matrix is said to be an echelon matrix if it has the following forms:

  • all rows with all entries zero are located at the bottom of the matrix;

  • the leading entry of each nonzero row appears always to the right of the leading entry of the nonzero row above;

  • all entries below the leading entry of the same column are equal to zero.

Definition 4.5 (Reduced Row-Echelon Form Matrix [22])

An echelon matrix B is said to be a reduced row-echelon form (RREF) matrix if the leading entry of each nonzero row is a leading-1 entry, and each leading-1 entry is the only nonzero entry in the column in which it is located.

Theorem 4.1

Any m × n matrix A is row equivalent to one and only one matrix in reduced row-echelon form.

Proof

See [27, Appendix A].

Definition 4.6 (Pivot Column [27, p. 15])

A pivot position of an m × n matrix A is the position of some leading entry of its echelon form. Each column containing a pivot position is called a pivot column of the matrix A.

4.1.2 Gauss Elimination for Solving Matrix Equations

Elementary row operations can be used to solve matrix equations and perform matrix inversion.

Consider how to solve an n × n matrix equation Ax = b, where the inverse matrix A −1 of the matrix A exists. We hope that the solution vector x = A −1b can be obtained by using elementary row operations.

First use the matrix A and the vector b to construct the n × (n + 1) augmented matrix B = [A, b]. Since the solution x = A −1b can be written as a new matrix equation Ix = A −1b, we get a new augmented matrix C = [I, A −1b] associated with the solution x = A −1b. Hence, we can write the solution process for the two matrix equations Ax = b and x = A −1b, respectively, as follows:
../images/492994_1_En_4_Chapter/492994_1_En_4_Equa_HTML.png
This implies that, after suitable elementary row operations on the augmented matrix [A, b], if the left-hand part of the new augmented matrix is an n × n identity matrix I, then the (n + 1)th column gives the solution x = A −1b of the original equation Ax = b directly. This method is called the Gauss or Gauss–Jordan elimination method.
Any m × n complex matrix equation Ax = b can be written as
$$\displaystyle \begin{aligned} ({\mathbf{A}}_{\mathrm{r}} +\mathrm{j}\,{\mathbf{A}}_{\mathrm{i}})({\mathbf{x}}_{\mathrm{r}} +\mathrm{j}\, {\mathbf{x}}_{\mathrm{i}} )={\mathbf{b}}_{\mathrm{r}} +\mathrm{j}\,{\mathbf{b}}_{\mathrm{i}}, \end{aligned} $$
(4.1.1)
where A r, x r, b r and A i, x i, b i are the real and imaginary parts of A, x, b, respectively. Expanding the above equation to yield
$$\displaystyle \begin{aligned} {\mathbf{A}}_{\mathrm{r}} {\mathbf{x}}_{\mathrm{r}} -{\mathbf{A}}_{\mathrm{i}}{\mathbf{x}}_{\mathrm{i}} &={\mathbf{b}}_{\mathrm{r}}, \end{aligned} $$
(4.1.2)
$$\displaystyle \begin{aligned} {\mathbf{A}}_{\mathrm{i}} {\mathbf{x}}_{\mathrm{r}} +{\mathbf{A}}_{\mathrm{r}}{\mathbf{x}}_{\mathrm{i}} &={\mathbf{b}}_{\mathrm{i}}. \end{aligned} $$
(4.1.3)
The above equations can be combined into
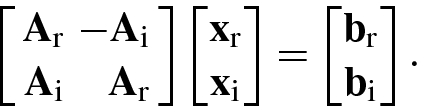
../images/492994_1_En_4_Chapter/492994_1_En_4_Equ4_HTML.png
(4.1.4)
Thus, m complex-valued equations with n complex unknowns become 2m real-valued equations with 2n real unknowns.
In particular, if m = n, then we have
../images/492994_1_En_4_Chapter/492994_1_En_4_Equb_HTML.png
This shows that if we write the n × (n + 1) complex augmented matrix [A, b] as a 2n × (2n + 1) real augmented matrix and perform elementary row operations to make its left-hand side become a 2n × 2n identity matrix, then the upper and lower halves of the (2n + 1)th column give, respectively, the real and imaginary parts of the complex solution vector x of the original complex matrix equation Ax = b.

4.1.3 Gauss Elimination for Matrix Inversion

Consider the inversion operation on an n × n nonsingular matrix A. This problem can be modeled as an n × n matrix equation AX = I whose solution X is the inverse matrix of A. It is easily seen that the augmented matrix of the matrix equation AX = I is [A, I], whereas the augmented matrix of the solution equation IX = A −1 is [I, A −1]. Hence, we have the following relations:
../images/492994_1_En_4_Chapter/492994_1_En_4_Equc_HTML.png
This result tells us that if we use elementary row operations on the n × 2n augmented matrix [A, I] so that its left-hand part becomes an n × n identity matrix then the right-hand part yields the inverse A −1 of the given n × n matrix A directly. This operation is called the Gauss elimination method for matrix inversion.
Example 4.1
Use the Gauss elimination method to find the inverse of the matrix
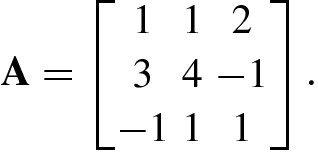
../images/492994_1_En_4_Chapter/492994_1_En_4_Equd_HTML.png
Perform elementary row operations on the augmented matrix of [A, I] to yield the following results:
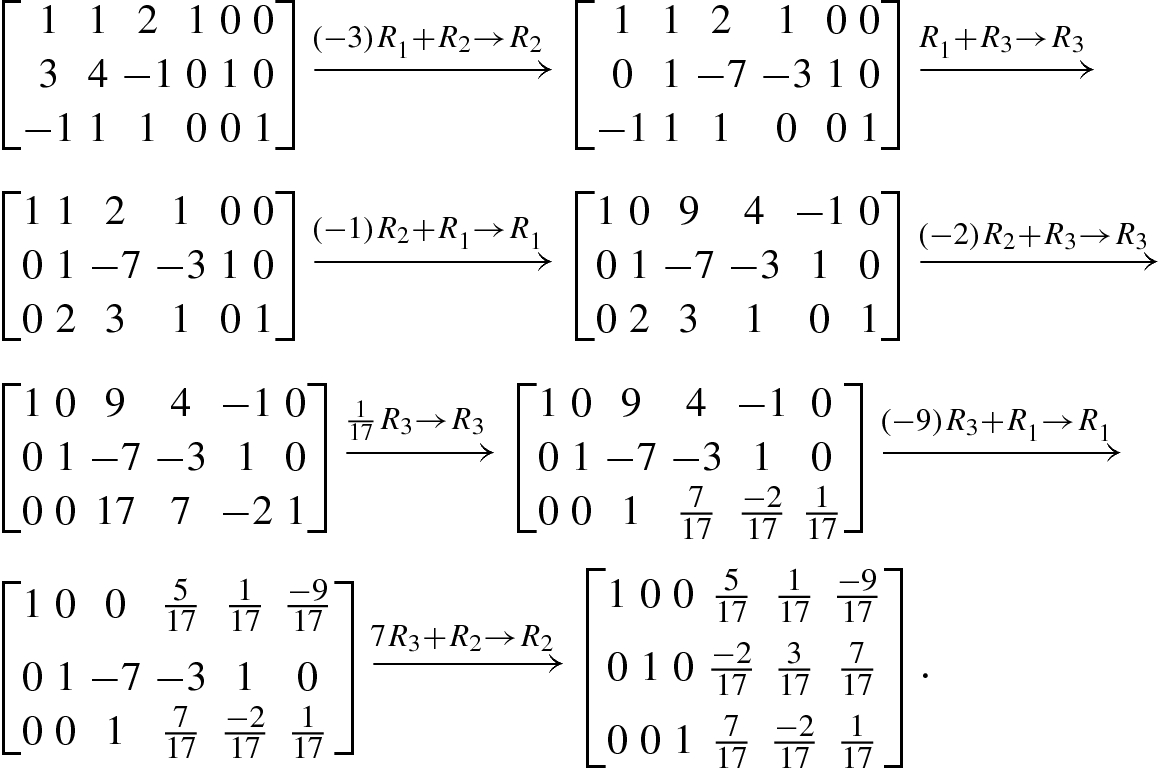
../images/492994_1_En_4_Chapter/492994_1_En_4_Eque_HTML.png
That is to say,
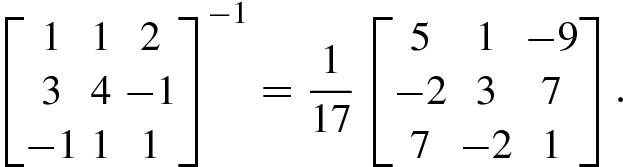
../images/492994_1_En_4_Chapter/492994_1_En_4_Equf_HTML.png
For the matrix equation
$$\displaystyle \begin{aligned} x_1^{\,} +x_2 +2x_3 &=6,\\ 3x_1^{\,} +4x_2 -x_3 &=5,\\ -x_1^{\,} +x_2 +x_3 &=2, \end{aligned} $$
its solution
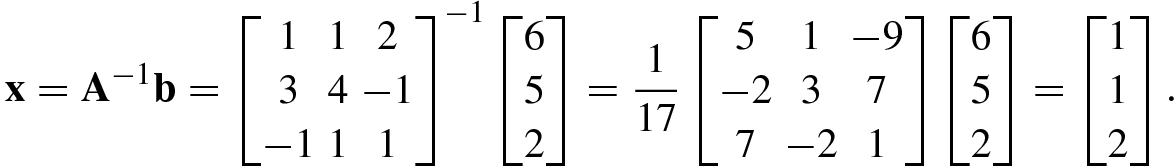
../images/492994_1_En_4_Chapter/492994_1_En_4_Equh_HTML.png
Now, we consider the inversion of an n × n nonsingular complex matrix A. Then, its inversion can be modeled as the complex matrix equation (A r + jA i)(X r + jX i) = I. This complex equation can be rewritten as
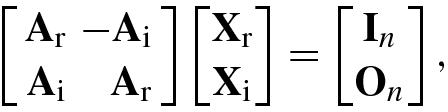
../images/492994_1_En_4_Chapter/492994_1_En_4_Equ5_HTML.png
(4.1.5)
from which we get the following relation:
../images/492994_1_En_4_Chapter/492994_1_En_4_Equi_HTML.png
That is to say, after making elementary row operations on the 2n × 3n augmented matrix to transform its left-hand side to a 2n × 2n identity matrix, then the upper and lower halves of the 2n × n matrix on the right give, respectively, the real and imaginary parts of the inverse matrix A −1 of the complex matrix A.

4.2 Conjugate Gradient Methods

Given a matrix equation Ax = b, where $$\mathbf {A}\in \mathbb {R}^{n\times n}$$ is a nonsingular matrix. This matrix equation can be equivalently written as
$$\displaystyle \begin{aligned} \mathbf{x}=(\mathbf{I}-\mathbf{A})\mathbf{x}+\mathbf{b}, \end{aligned} $$
(4.2.1)
which inspires the following iteration algorithm:
$$\displaystyle \begin{aligned} {\mathbf{x}}_{k+1}^{\,} =(\mathbf{I}-\mathbf{A}){\mathbf{x}}_k^{\,} +\mathbf{b}. \end{aligned} $$
(4.2.2)
This algorithm is known as the Richardson iteration and can be rewritten in the more general form
$$\displaystyle \begin{aligned} {\mathbf{x}}_{k+1}^{\,} =\mathbf{M}{\mathbf{x}}_k^{\,} +\mathbf{c},{} \end{aligned} $$
(4.2.3)
where M is an n × n matrix, called the iteration matrix.

An iteration in the form of Eq. (4.2.3) is termed as a stationary iterative method and is not as effective as a nonstationary iterative method.

Nonstationary iteration methods comprise a class of iteration methods in which $${\mathbf {x}}_{k+1}^{\,}$$ is related to the former iteration solutions $${\mathbf {x}}_k^{\,} ,{\mathbf {x}}_{k-1}^{\,} ,\ldots ,{\mathbf {x}}_0^{\,}$$ . The most typical nonstationary iteration method is the Krylov subspace method, described by
$$\displaystyle \begin{aligned} {\mathbf{x}}_{k+1}^{\,} ={\mathbf{x}}_0^{\,} +\mathcal{K}_k^{\,} , \end{aligned} $$
(4.2.4)
where
$$\displaystyle \begin{aligned} \mathcal{K}_k^{\,} =\mathrm{Span}({\mathbf{r}}_0^{\,} ,\mathbf{Ar}_0^{\,} ,\ldots ,{\mathbf{A}}^{k-1}{\mathbf{r}}_0^{\,} ) \end{aligned} $$
(4.2.5)
is called the kth iteration Krylov subspace; $${\mathbf {x}}_0^{\,}$$ is the initial iteration value and $${\mathbf {r}}_0^{\,}$$ denotes the initial residual vector.

Krylov subspace methods have various forms, of which the three most common are the conjugate gradient method, the biconjugate gradient method, and the preconditioned conjugate gradient method.

4.2.1 Conjugate Gradient Algorithm

The conjugate gradient method uses $${\mathbf {r}}_0^{\,} =\mathbf {Ax}_0^{\,} -\mathbf {b}$$ as the initial residual vector. The applicable object of the conjugate gradient method is limited to the symmetric positive definite equation, Ax = b, where A is an n × n symmetric positive definite matrix.

The nonzero vector combination $$\{{\mathbf {p}}_0^{\,} ,{\mathbf {p}}_1^{\,} ,\ldots ,{\mathbf {p}}_k^{\,}\}$$ is said to be A-orthogonal or A-conjugate if
$$\displaystyle \begin{aligned} {\mathbf{p}}_i^T\mathbf{Ap}_j^{\,} =0,\quad \forall\, i\neq j.{} \end{aligned} $$
(4.2.6)

This property is known as A-orthogonality or A-conjugacy. Obviously, if A = I, then the A-conjugacy reduces to general orthogonality.

All algorithms adopting the conjugate vector as the update direction are known as conjugate direction algorithms. If the conjugate vectors $${\mathbf {p}}_0^{\,} ,{\mathbf {p}}_1^{\,} ,\ldots ,{\mathbf {p}}_{n-1}^{\,}$$ are not predetermined, but are updated by the gradient descent method in the updating process, then we say that the minimization algorithm for the objective function f(x) is a conjugate gradient algorithm.

Algorithm 4.1 gives a conjugate gradient algorithm.

Algorithm 4.1 Conjugate gradient algorithm [16]
../images/492994_1_En_4_Chapter/492994_1_En_4_Figa_HTML.png
From Algorithm 4.1 it can be seen that in the iteration process of the conjugate gradient algorithm, the solution of the matrix equation Ax = b is given by
$$\displaystyle \begin{aligned} {\mathbf{x}}_k^{\,} =\sum_{i=1}^k \alpha_i^{\,}{\mathbf{p}}_i^{\,} =\sum_{i=1}^k\frac{\langle {\mathbf{r}}_{i-1}^{\,} ,{\mathbf{r}}_{i-1}\rangle} {\langle{\mathbf{p}}_i^{\,} ,\mathbf{Ap}_i^{\,}\rangle}{\mathbf{p}}_i^{\,} , \end{aligned} $$
(4.2.7)
that is, x k belongs to the kth Krylov subspace
$$\displaystyle \begin{aligned} {\mathbf{x}}_k^{\,}\in \mathrm{Span}\{{\mathbf{p}}_1^{\,} ,{\mathbf{p}}_2^{\,} ,\ldots ,{\mathbf{p}}_k^{\,}\}=\mathrm{Span}\{{\mathbf{r}}_0^{\,} ,\mathbf{ Ar}_0^{\,} ,\ldots ,{\mathbf{A}}^{k-1}{\mathbf{r}}_0^{\,}\} . \end{aligned}$$

The fixed-iteration method requires the updating of the iteration matrix M, but no matrix needs to be updated in Algorithm 4.1. Hence, the Krylov subspace method is also called the matrix-free method [24].

4.2.2 Biconjugate Gradient Algorithm

If the matrix A is not a real symmetric matrix, then we can use the biconjugate gradient method of Fletcher [13] for solving the matrix equation Ax = b. As the name implies, there are two search directions, p i and $$\bar {\mathbf {p}}_j$$ , that are A-conjugate in this method:
$$\displaystyle \begin{aligned} \bar{\mathbf{p}}{}_i^T\mathbf{Ap}_j^{\,} ={\mathbf{p}}_i^T\mathbf{A}\bar{\mathbf{p}}_j^{\,} &=0,\quad i\neq j;\\ \bar{\mathbf{r}}_i^T{\mathbf{r}}_j^{\,} ={\mathbf{r}}_i^T\bar{\mathbf{r}}_j&=0,\quad i\neq j;\\ \bar{\mathbf{r}}_i^T {\mathbf{p}}_j^{\,} ={\mathbf{r}}_i^T\bar{\mathbf{p}}_j&=0,\quad j<i. \end{aligned} $$
(4.2.8)
Here, ri and $$\bar {\mathbf {r}}_j$$ are the residual vectors associated with search directions p i and $$\bar {\mathbf {p}}_j$$ , respectively. Algorithm 4.2 shows a biconjugate gradient algorithm.
Algorithm 4.2 Biconjugate gradient algorithm [13]
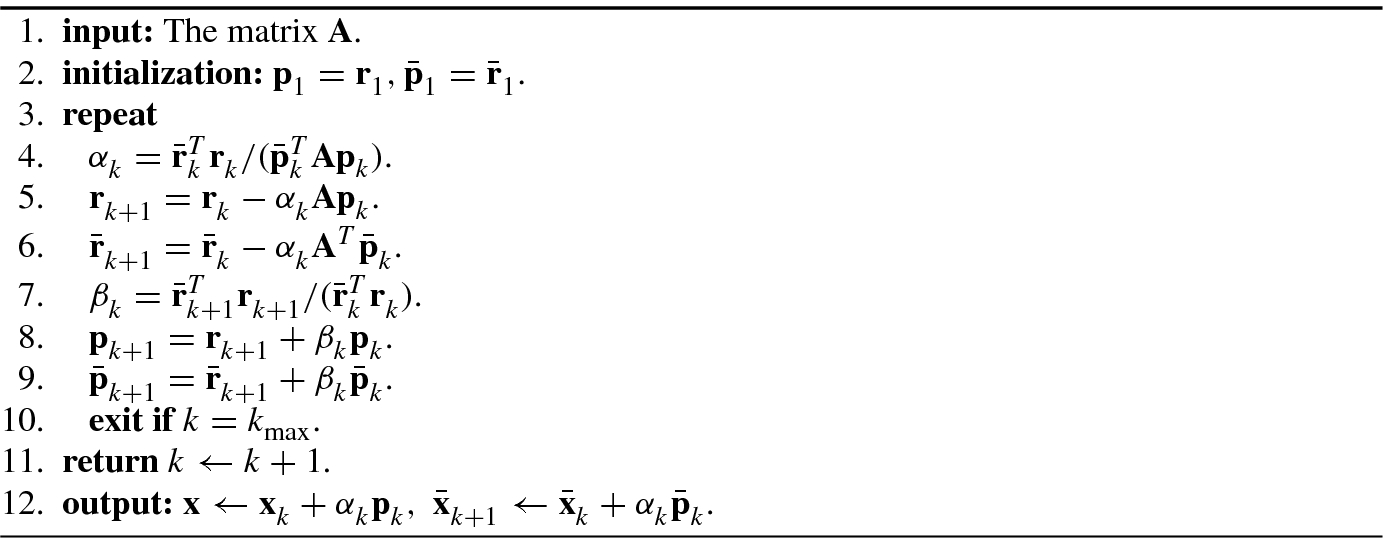
../images/492994_1_En_4_Chapter/492994_1_En_4_Figb_HTML.png

4.2.3 Preconditioned Conjugate Gradient Algorithm

Consider the symmetric indefinite saddle point problem
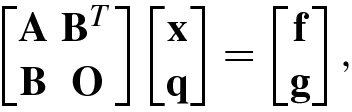
../images/492994_1_En_4_Chapter/492994_1_En_4_Equk_HTML.png
where A is an n × n real symmetric positive definite matrix, B is an m × n real matrix with full row rank m (≤ n), and O is an m × m zero matrix. Bramble and Pasciak [4] developed a preconditioned conjugate gradient iteration method for solving the above problem.

The basic idea of the preconditioned conjugate gradient iteration is as follows: through a clever choice of the scalar product form, the preconditioned saddle matrix becomes a symmetric positive definite matrix.

To simplify the discussion, we assume that the matrix equation with large condition number Ax = b needs to be converted into a new symmetric positive definite equation. To this end, let M be a symmetric positive definite matrix that can approximate the matrix A and for which it is easier to find the inverse matrix. Hence, the original matrix equation Ax = b is converted into M −1Ax = M −1b such that the new and original matrix equations have the same solution. However, in the new matrix equation M −1Ax = M −1b there is a hidden danger: M −1A is generally not either symmetric or positive definite even if both M and A are symmetric positive definite. Therefore, it is unreliable to use the matrix M −1 directly as the preprocessor of the matrix equation Ax = b.

Let S be the square root of a symmetric matrix M, i.e., M = SS T, where S is symmetric positive definite. Now, use S −1 instead of M −1 as the preprocessor to convert the original matrix equation Ax = b to S −1Ax = S −1b. If $$\mathbf {x}= {\mathbf {S}}^{-T}\hat {\mathbf {x}}$$ , then the preconditioned matrix equation is given by
$$\displaystyle \begin{aligned} {\mathbf{S}}^{-1}\mathbf{A}{\mathbf{S}}^{-T}\hat{\mathbf{x}}={\mathbf{S}}^{-1}\mathbf{b}. \end{aligned} $$
(4.2.9)

Compared with the matrix M −1A, which is not symmetric positive definite, S −1AS −T must be symmetric positive definite if A is symmetric positive definite. The symmetry of S −1AS −T is easily seen, its positive definiteness can be verified as follows: by checking the quadratic function it easily follows that y T(S −1AS −T)y = z TAz, where z = S −Ty. Because A is symmetric positive definite, we have z TAz > 0, ∀ z ≠ 0, and thus y T(S −1AS −T)y > 0, ∀ y ≠ 0. That is to say, S −1AS −T must be positive definite.

At this point, the conjugate gradient method can be applied to solve the matrix equation (4.2.9) in order to get $$\hat {\mathbf {x}}$$ , and then we can recover x via $$\mathbf {x}={\mathbf {S}}^{-T}\hat {\mathbf {x}}$$ .

Algorithm 4.3 shows a preconditioned conjugate gradient (PCG) algorithm with a preprocessor, developed in [37].

Algorithm 4.3 PCG algorithm with preprocessor [37]
../images/492994_1_En_4_Chapter/492994_1_En_4_Figc_HTML.png
The use of a preprocessor can be avoided, because there are correspondences between the variables of the matrix equations Ax = b and $${\mathbf {S}}^{-1}\mathbf {AS}^{-T}\hat {\mathbf {x}}={\mathbf {S}}^{-1}\mathbf {b}$$ , as follows [24]:
$$\displaystyle \begin{aligned} {\mathbf{x}}_k^{\,} ={\mathbf{S}}^{-1}\hat{\mathbf{x}}_k^{\,} ,\quad {\mathbf{r}}_k^{\,} =\mathbf{S}\hat{\mathbf{r}}_k^{\,} ,\quad {\mathbf{p}}_k^{\,} = {\mathbf{S}}^{-1}\hat{\mathbf{p}}_k^{\,} ,\quad {\mathbf{z}}_k^{\,} ={\mathbf{S}}^{-1}\hat{\mathbf{r}}_k^{\,} . \end{aligned}$$
On the basis of these correspondences, it is easy to develop a PCG algorithm without preprocessor [24], as shown in Algorithm 4.4.
Algorithm 4.4 PCG algorithm without preprocessor [24]
../images/492994_1_En_4_Chapter/492994_1_En_4_Figd_HTML.png

A wonderful introduction to the conjugate gradient method is presented in [37].

Regarding the complex matrix equation Ax = b, where $$\mathbf {A}\in \mathbb {C}^{n\times n},\mathbf {x}\in \mathbb {C}^n,\mathbf { b}\in \mathbb {C}^n$$ , we can write it as the following real matrix equation: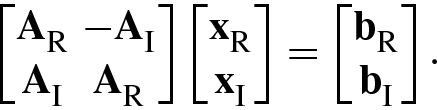
../images/492994_1_En_4_Chapter/492994_1_En_4_Equ15_HTML.png
(4.2.10)

Clearly, if A = A R + jA I is a Hermitian positive definite matrix, then Eq. (4.2.10) is a symmetric positive definite matrix equation. Hence, $$({\mathbf {x}}_{\mathrm {R}}^{\,} ,{\mathbf {x}}_{\mathrm {I}}^{\,} )$$ can be solved by adopting the conjugate gradient algorithm or the preconditioned conjugate gradient algorithm.

The main advantage of gradient methods is that the computation of each iteration is very simple; however, their convergence is generally slow.

4.3 Condition Number of Matrices

In many applications in science and engineering, it is often necessary to consider an important problem: there exist some uncertainties or errors in the actual observation data, and, furthermore, numerical calculation of the data is always accompanied by error. What is the impact of these errors? Is a particular algorithm numerically stable for data processing?

In order to answer these questions, the following two concepts are extremely important:

  • the numerical stability of various kinds of algorithms;

  • the condition number or perturbation analysis of the problem of interest.

Given some application problem f where d ∗∈ D is the data without noise or disturbance in a data group D. Let f(d ∗) ∈ F denote the solution of f, where F is a solution set. For observed data d ∈ D, we want to evaluate f(d). Owing to background noise and/or observation error, f(d) is usually different from f(d ∗). If f(d) is “close” to f(d ∗), then the problem f is said to be a “well-conditioned problem.” On the contrary, if f(d) is obviously different from f(d ∗) even when d is very close to d ∗, then we say that the problem f is an “ill-conditioned problem.” If there is no further information about the problem f, the term “approximation” cannot describe the situation accurately.

In perturbation theory, a method or algorithm for solving a problem f is said to be numerically stable if its sensitivity to a perturbation is not larger than the sensitivity inherent in the original problem. More precisely, f is stable if the approximate solution f(d) is close to the solution f(d ∗) without perturbation for all d ∈ D close to d ∗.

To mathematically describe numerical stability of a method or algorithm, we first consider the well-determined linear equation Ax = b, where the n × n coefficient matrix A has known entries and the n × 1 data vector b is also known, while the n × 1 vector x is an unknown parameter vector to be solved. Naturally, we are interested in the numerical stability of this solution: if the coefficient matrix A and/or the data vector b are perturbed, how will the solution vector x be changed? Does it maintain a certain stability? By studying the influence of perturbations of the coefficient matrix A and/or the data vector b, we can obtain a numerical value, called the condition number, describing an important characteristic of the coefficient matrix A.

For the convenience of analysis, we first assume that there is only a perturbation δb of the data vector b, while the matrix A is stable. In this case, the exact solution vector x will be perturbed to x + δx, namely
$$\displaystyle \begin{aligned} \mathbf{A}(\mathbf{x}+\delta\mathbf{x})=\mathbf{b}+ \delta\mathbf{b}. \end{aligned} $$
(4.3.1)
This implies that
$$\displaystyle \begin{aligned} \delta \mathbf{x}={\mathbf{A}}^{-1}\delta\mathbf{b},{} \end{aligned} $$
(4.3.2)
since Ax = b.
By the property of the matrix norm, Eq. (4.3.2) gives
$$\displaystyle \begin{aligned} \|\delta \mathbf{x}\|\leq \|{\mathbf{A}}^{-1}\|\cdot\|\delta \mathbf{b}\|.{} \end{aligned} $$
(4.3.3)
Similarly, from the linear equation Ax = b we get
$$\displaystyle \begin{aligned} \|\mathbf{b}\| \leq \| \mathbf{A}\|\cdot \|\mathbf{x}\|.{} \end{aligned} $$
(4.3.4)
From Eqs. (4.3.3) and (4.3.4) it is immediately clear that
$$\displaystyle \begin{aligned} \frac{\|\delta \mathbf{x}\|}{\|\mathbf{x}\|}\leq \left (\| \mathbf{A}\|\cdot\|{\mathbf{A}}^{-1}\| \right )\frac{\| \delta \mathbf{b}\|}{\|\mathbf{b}\|}.{} \end{aligned} $$
(4.3.5)
Next, consider the influence of simultaneous perturbations δx and δA. In this case, the linear equation becomes
$$\displaystyle \begin{aligned} (\mathbf{A}+\delta\mathbf{A})(\mathbf{x}+\delta\mathbf{x})=\mathbf{b}. \end{aligned}$$
From the above equation it can be derived that
$$\displaystyle \begin{aligned} \delta\mathbf{x} &=\big ((\mathbf{A}+\delta \mathbf{A})^{-1}-{\mathbf{A}}^{-1}\big )\mathbf{b} \\ &= \big [{\mathbf{A}}^{-1}\big ( \mathbf{A}-(\mathbf{A}+\delta\mathbf{A})\big )(\mathbf{A}+\delta\mathbf{A})^{-1}\big ]\mathbf{b}\\ &=-{\mathbf{A}}^{-1} \delta\mathbf{A}(\mathbf{A}+\delta \mathbf{A})^{-1}\mathbf{b} \\ &=-{\mathbf{A}}^{-1} \delta\mathbf{A}(\mathbf{x}+\delta\mathbf{x}). \end{aligned} $$
(4.3.6)
Then we have
$$\displaystyle \begin{aligned} \|\delta\mathbf{x}\| \leq \|{\mathbf{A}}^{-1}\|\cdot\| \delta \mathbf{A}\|\cdot\|\mathbf{x}+\delta\mathbf{x} \|, \end{aligned}$$
namely
$$\displaystyle \begin{aligned} \frac{\| \delta\mathbf{x}\|}{\|\mathbf{x}+\delta \mathbf{x}\|}\leq \big (\|\mathbf{A}\|\cdot\|{\mathbf{A}}^{-1}\|\big ) \frac{\|\delta\mathbf{A}\|}{\| \mathbf{A}\|}.{} \end{aligned} $$
(4.3.7)
Equations (4.3.5) and (4.3.7) show that the relative error of the solution vector x is proportional to the numerical value
$$\displaystyle \begin{aligned} \mathrm{cond}(\mathbf{A})=\| \mathbf{A}\|\cdot\|{\mathbf{A}}^{-1}\|,{} \end{aligned} $$
(4.3.8)
where cond(A) is called the condition number of the matrix A with respect to its inverse and is sometimes denoted κ(A).
Condition numbers have the following properties.

  • cond(A) = cond(A −1).

  • cond(cA) = cond(A).

  • cond(A) ≥ 1.

  • cond(AB) ≤cond(A)cond(B).

Here, we give the proofs of cond(A) ≥ 1 and cond(AB) ≤cond(A)cond(B):
$$\displaystyle \begin{aligned} \mathrm{cond}(\mathbf{A})&=\|\mathbf{A}\|\cdot\|{\mathbf{A}}^{-1}\|\geq \|\mathbf{A}{\mathbf{A}}^{-1}\|=\|\mathbf{I}\|=1; \\ \mathrm{cond}(\mathbf{AB})&\!=\!\|\mathbf{AB}\|\cdot\|(\mathbf{AB})^{-1}\|\!\leq\! \|\mathbf{A}\|\cdot\|\mathbf{B}\|\cdot (\|{\mathbf{B}}^{-1}\|\cdot\|{\mathbf{A}}^{-1}\|)\!=\! \mathrm{cond}(\mathbf{A})\mathrm{cond}(\mathbf{B}). \end{aligned} $$

An orthogonal matrix A is perfectly conditioned in the sense that cond(A) = 1.

The following are four common condition numbers.
  • ℓ 1 condition number, denoted as cond1(A), is defined as
    $$\displaystyle \begin{aligned} \mathrm{cond}_1(\mathbf{A})=\|\mathbf{A}\|{}_1^{\,}\|{\mathbf{A}}^{-1}\|{}_1^{\,} . \end{aligned} $$
    (4.3.9)
  • ℓ 2 condition number, denoted as cond2(A), is defined as
    $$\displaystyle \begin{aligned} \mathrm{cond}_2 (\mathbf{A})=\|\mathbf{A}\|{}_2^{\,}\|{\mathbf{A}}^{-1}\|{}_2^{\,} =\sqrt{\frac{\lambda_{\max}({\mathbf{A}}^H\mathbf{ A})}{\lambda_{\min}({\mathbf{A}}^H\mathbf{A})}}= \frac{\sigma_{\max}(\mathbf{A})}{\sigma_{\min}(\mathbf{A})}, \end{aligned} $$
    (4.3.10)
    where $$\lambda _{\max }({\mathbf {A}}^H\mathbf {A})$$ and $$\lambda _{\min }({\mathbf {A}}^H\mathbf {A})$$ are the maximum and minimum eigenvalues of A HA, respectively; and $$\sigma _{\max }(\mathbf {A})$$ and $$\sigma _{\min }(\mathbf {A})$$ are the maximum and minimum singular values of A, respectively.
  • ℓ ∞condition number, denoted as cond∞(A), is defined as
    $$\displaystyle \begin{aligned} \mathrm{cond}_\infty (\mathbf{A})=\|\mathbf{A}\|{}_\infty\cdot\|{\mathbf{A}}^{-1}\|{}_\infty . \end{aligned} $$
    (4.3.11)
  • Frobenius norm condition number, denoted as condF(A), is defined as
    $$\displaystyle \begin{aligned} \mathrm{cond}_F(\mathbf{A})=\|\mathbf{A}\|{}_F\cdot\|{\mathbf{A}}^{-1}\|{}_F=\sqrt{\sum_i\sigma_i^2\sum_j \sigma_j^{-2}}. \end{aligned} $$
    (4.3.12)
Consider an over-determined linear equation Ax = b, where A is an m × n matrix with m > n. An over-determined equation has a unique linear least squares (LS) solution given by
$$\displaystyle \begin{aligned} {\mathbf{A}}^H\mathbf{Ax}= {\mathbf{A}}^H\mathbf{b},{} \end{aligned} $$
(4.3.13)
i.e., $${\mathbf {x}}_{\mathrm {LS}}^{\,} =({\mathbf {A}}^H\mathbf {A})^{-1}{\mathbf {A}}^H\mathbf {b}$$ .

It should be noticed that when using the LS method to solve the matrix equation Ax = b, a matrix A with a larger condition number may result into a worse solution due to cond2(A HA) = (cond2(A))2.

As a comparison, we consider using the QR factorization A = QR (where Q is orthogonal and R is upper triangular) to solve an over-determined equation Ax = b then
$$\displaystyle \begin{aligned} \mathrm{cond}(\mathbf{Q})=1,\quad \mathrm{cond}(\mathbf{A})=\mathrm{cond}({\mathbf{Q}}^H\mathbf{A})=\mathrm{cond}(\mathbf{R}),{} \end{aligned} $$
(4.3.14)
since Q HQ = I. In this case we have Q HAx = Q Hb ⇒Rx = Q Hb. Since cond(A) = cond(R), the QR factorization method Rx = Q Hb has better numerical stability (i.e., a smaller condition number) than the least squares method x LS = (A HA)−1A Hb.

On the more effective methods than QR factorization for solving over-determined matrix equations, we will discuss them after introducing the singular value decomposition.

4.4 Singular Value Decomposition (SVD)

Beltrami (1835–1899) and Jordan (1838–1921) are recognized as the founders of singular value decomposition (SVD): Beltrami in 1873 published the first paper on SVD [2]. One year later, Jordan published his own independent derivation of SVD [23].

4.4.1 Singular Value Decomposition

Theorem 4.2 (SVD)
Let $$\mathbf {A}\in \mathbb {R}^{m\times n}$$ (or $$\mathbb {C}^{m\times n}$$ ), then there exist orthogonal (or unitary) matrices $$\mathbf {U} \in \mathbb {R}^{m\times m}$$ (or $$\mathbf {U}\in \mathbb {C}^{m\times m}$$ ) and $$\mathbf {V}\in \mathbb {R}^{n\times n}$$ (or $$\mathbf { V}\in \mathbb {C}^{n\times n}$$ ) such that
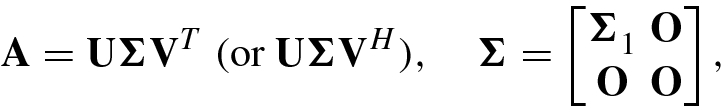
../images/492994_1_En_4_Chapter/492994_1_En_4_Equ30_HTML.png
(4.4.1)
where $$\mathbf {U}=[{\mathbf {u}}_1,\ldots ,{\mathbf {u}}_m]\in \mathbb {C}^{m\times m}, \mathbf {V}=[{\mathbf {v}}_1,\ldots ,\mathbf { v}_n]\in \mathbb {C}^{n\times n}$$ and $${\boldsymbol \Sigma }_1^{\,} = \mathbf {Diag} (\sigma _1^{\,},\ldots ,\sigma _l^{\,})$$ with diagonal entries
$$\displaystyle \begin{aligned} \sigma_1^{\,} \geq \cdots \geq \sigma_r^{\,}>\sigma_{r+1}=\ldots =\sigma_l=0,{} \end{aligned} $$
(4.4.2)

in which $$l=\min \{m,n\}$$ and r = rank of A.

This theorem was first shown by Eckart and Young [11] in 1939, but the proof by Klema and Laub [26] is simpler.

The nonzero values $$\sigma _1^{\,} ,\ldots , \sigma _r^{\,}$$ together with the zero values $$\sigma _{r+1}^{\,}=\cdots =\sigma _l^{\,} =0$$ are called the singular values of the matrix A, and u 1, …, u m and v 1, …, v n are known as the left- and right singular vectors, respectively, while $$\mathbf {U}\in \mathbb {C}^{m\times m}$$ and $$\mathbf {V}\in \mathbb {C}^{n\times n}$$ are called the left- and right singular vector matrices, respectively.

Here are several useful explanations and remarks on singular values and SVD [46].
  1. 1.
    The SVD of a matrix A can be rewritten as the vector form
    $$\displaystyle \begin{aligned} \mathbf{A}=\sum_{i=1}^r \sigma_i^{\,} {\mathbf{u}}_i^{\,} {\mathbf{v}}_i^H. {} \end{aligned} $$
    (4.4.3)

    This expression is sometimes said to be the dyadic decomposition of A [16].

     
  2. 2.
    Suppose that the n × n matrix V is unitary. Postmultiply (4.4.1) by V to get AV = U Σ, whose column vectors are given by
    $$\displaystyle \begin{aligned} \mathbf{Av}_i^{\,} =\left\{\begin{array}{ll}\sigma_i^{\,}{\mathbf{u}}_i^{\,} ,&~~i=1,2,\ldots ,r;\\ 0, &~~i=r+1,r+2,\ldots ,n.\end{array}\right.{} \end{aligned} $$
    (4.4.4)
     
  3. 3.
    Suppose that the m × m matrix U is unitary. Premultiply (4.4.1) by U H to yield U HA =  ΣV, whose column vectors are given by
    $$\displaystyle \begin{aligned} {\mathbf{u}}_i^H\mathbf{A}=\left\{\begin{array}{ll}\sigma_i^{\,} {\mathbf{v}}_i^T,&~~i=1,2,\ldots ,r;\\ 0,&~~i=r+1,r+2,\ldots ,n.\end{array} \right. \end{aligned} $$
    (4.4.5)
     
  4. 4.
    When the matrix rank $$r=\mathrm {rank}(\mathbf {A})<\min \{m,n\}$$ , because $$\sigma _{r+1}^{\,} = \cdots =\sigma _h^{\,} =0$$ with $$h=\min \{m,n\}$$ , the SVD formula (4.4.1) can be simplified to
    $$\displaystyle \begin{aligned} \mathbf{A}={\mathbf{U}}_r^{\,}{\boldsymbol \Sigma}_r^{\,}{\mathbf{V}}_r^H,{} \end{aligned} $$
    (4.4.6)

    where $${\mathbf {U}}_r^{\,} =[{\mathbf {u}}_1^{\,} ,\ldots ,{\mathbf {u}}_r^{\,} ],{\mathbf {V}}_r^{\,} =[{\mathbf {v}}_1^{\,} ,\ldots ,{\mathbf {v}}_r^{\,} ]$$ , and $${\boldsymbol \Sigma }_r^{\,} =\mathbf {Diag}(\sigma _1^{\,} ,\ldots ,\sigma _r^{\,} )$$ . Equation (4.4.6) is called the truncated singular value decomposition or the thin singular value decomposition of the matrix A. In contrast, Eq. (4.4.1) is known as the full singular value decomposition.

     
  5. 5.
    Premultiplying (4.4.4) by $${\mathbf {u}}_i^H$$ , and noting that $${\mathbf {u}}_i^H{\mathbf {u}}_i^{\,} =1$$ , it is easy to obtain
    $$\displaystyle \begin{aligned} {\mathbf{u}}_i^H\mathbf{Av}_i^{\,} =\sigma_i^{\,} ,\quad i=1,2,\ldots ,\min\{m,n\}, \end{aligned} $$
    (4.4.7)
    which can be written in matrix form as
    ../images/492994_1_En_4_Chapter/492994_1_En_4_Equ37_HTML.png
    (4.4.8)

    Equations (4.4.1) and (4.4.8) are two definitive forms of SVD.

     
  6. 6.

    From (4.4.1) it follows that AA H = U Σ 2U H. This shows that the singular value $$\sigma _i^{\,}$$ of an m × n matrix A is the positive square root of the corresponding nonnegative eigenvalue of the matrix product AA H.

     
  7. 7.
    If the matrix $${\mathbf {A}}_{m\times n}^{\,}$$ has rank r, then

    • the leftmost r columns of the m × m unitary matrix U constitute an orthonormal basis of the column space of the matrix A, i.e., $$\mathrm {Col}(\mathbf {A})\hskip -0.3mm =\hskip -0.3mm \mathrm {Span}\{{\mathbf {u}}_1^{\,} ,\ldots ,\mathbf { u}_r^{\,}\}$$ ;

    • the leftmost r columns of the n × n unitary matrix V constitute an orthonormal basis of the row space of A or the column space of A H, i.e., $$\mathrm {Row}(\mathbf {A})=\mathrm {Span}\{{\mathbf {v}}_1^{\,} ,\ldots ,\mathbf { v}_r^{\,}\}$$ ;

    • the rightmost n − r columns of V constitute an orthonormal basis of the null space of the matrix A, i.e., $$\mathrm {Null}(\mathbf {A})=\mathrm {Span}\{{\mathbf {v}}_{r+1}^{\,} ,\ldots ,{\mathbf {v}}_n^{\,}\}$$ ;

    • the rightmost m − r columns of U constitute an orthonormal basis of the null space of the matrix A H, i.e., $$\mathrm {Null}({\mathbf {A}}^H)=\mathrm {Span}\{{\mathbf {u}}_{r+1}^{\,} ,\ldots ,{\mathbf {u}}_m^{\,}\}$$ .

     

4.4.2 Properties of Singular Values

Theorem 4.3 (Eckart–Young Theorem [11])
If the singular values of $$\mathbf {A}\in \mathbb {C}^{m\times n}$$ are given by
$$\displaystyle \begin{aligned} \sigma_1^{\,} \geq \sigma_2^{\,} \geq\cdots \geq \sigma_r^{\,} \geq 0,\quad r=\mathrm{rank}(\mathbf{A}), \end{aligned}$$
then
$$\displaystyle \begin{aligned} \sigma_k^{\,} =\min_{\mathbf{E}\in\mathbb{C}^{m\times n}}\left (\|\mathbf{E}\|{}_{\mathrm{spec}}|\mathrm{rank}(\mathbf{A}+\mathbf{E})\leq k-1\right ),\quad k=1,\ldots ,r, \end{aligned} $$
(4.4.9)
and there is an error matrixE kwith $$\|{\mathbf {E}}_k\|{ }_{\mathrm {spec}}=\sigma _k^{\,}$$ such that
$$\displaystyle \begin{aligned} \mathrm{rank}(\mathbf{A}+{\mathbf{E}}_k)=k-1,\quad k=1,\ldots ,r. \end{aligned} $$
(4.4.10)

The Eckart–Young theorem shows that the singular value $$\sigma _k^{\,}$$ is equal to the minimum spectral norm of the error matrix E k such that the rank of A + E k is k − 1.

An important application of the Eckart–Young theorem is to the best rank-k approximation of the matrix A, where k < r = rank(A).

Define
$$\displaystyle \begin{aligned} {\mathbf{A}}_k=\sum_{i=1}^k\sigma_i^{\,} {\mathbf{u}}_i^{\,}{\mathbf{v}}_i^H,\quad k&lt;r; \end{aligned} $$
(4.4.11)
then A k is the solution of the optimization problem:
$$\displaystyle \begin{aligned} {\mathbf{A}}_k =\mathop{\mbox{arg min}}\limits_{\mathrm{rank}(\mathbf{X})=k}\|\mathbf{A}-\mathbf{X}\|{}_F^2,\quad k&lt;r, \end{aligned} $$
(4.4.12)
and the squared approximation error is given by
$$\displaystyle \begin{aligned} \|\mathbf{A}-{\mathbf{A}}_k\|{}_F^2=\sigma_{k+1}^2+\cdots +\sigma_r^2. \end{aligned} $$
(4.4.13)
Theorem 4.4 ([20, 21])
Let A be an m × n matrix with singular values $$\sigma _1^{\,} \geq \cdots \geq \sigma _r^{\,}$$ , where $$r=\min \{m,n\}$$ . If the p × q matrix B is a submatrix of A with singular values $$\gamma _1^{\,} \geq \cdots \geq \gamma _{\min \{p, q\}}^{\,}$$ , then
$$\displaystyle \begin{aligned} \sigma_i^{\,}\geq \gamma_i^{\,} ,\quad i=1,\ldots ,\min \{p,q\} \end{aligned} $$
(4.4.14)
and
$$\displaystyle \begin{aligned} \gamma_i^{\,} \geq \sigma_{i+(m-p)+(n-q)}^{\,} ,\quad i\leq\min \{p+q-m,p+q-n\} . \end{aligned} $$
(4.4.15)

This is the interlacing theorem for singular values.

The singular values of a matrix are closely related to its norm, determinant, and condition number.
  1. 1.
    Relationship between Singular Values and Norms:
    $$\displaystyle \begin{aligned} \|\mathbf{A}\|{}_2 &amp;=\sigma_1^{\,} =\sigma_{\max}^{\,} ,\\ \| \mathbf{A} \|{}_F^{\,}&amp;=\Bigg ( \sum_{i=1}^m\sum_{j=1}^n |a_{ij}^{\,}|{}^2 \Bigg )^{1/2}=\big\|{\mathbf{U}}^H\mathbf{AV}\big\|{}_F^{\,} =\|{\boldsymbol \Sigma} \|{}_F^{\,}=\sqrt {\sigma_1^2 +\cdots +\sigma_r^2}. \end{aligned} $$
     
  2. 2.
    Relationship between Singular Values and Determinant:
    $$\displaystyle \begin{aligned} |\det (\mathbf{A})|=|\det (\mathbf{U}{\boldsymbol \Sigma}{\mathbf{V}}^H)|=|\det {\boldsymbol \Sigma}|= \sigma_1^{\,}\cdots \sigma_n^{\,}. {} \end{aligned} $$
    (4.4.16)

    If all the $$\sigma _i^{\,}$$ are nonzero, then $$|\det (\mathbf {A})|\neq 0$$ , which shows that A is nonsingular. If there is at least one singular value $$\sigma _i^{\,}=0\, (i&gt;r)$$ , then $$\det ( \mathbf {A})=0$$ , namely A is singular. This is the reason why the $$\sigma _i^{\,}, i=1,\ldots ,\min \{m,n\}$$ are known as the singular values.

     
  3. 3.
    Relationship between Singular Values and Condition Number:
    $$\displaystyle \begin{aligned} \mathrm{cond}_2(\mathbf{A})=\sigma_1^{\,} /\sigma_p^{\,},\quad p=\min \{m,n\}. {} \end{aligned} $$
    (4.4.17)
     

4.4.3 Singular Value Thresholding

Consider the truncated SVD of a low-rank matrix $$\mathbf {W}\in \mathbb {R}^{m\times n}$$ :
$$\displaystyle \begin{aligned} \mathbf{W}=\mathbf{U}{\boldsymbol \Sigma}{\mathbf{V}}^T,\quad {\boldsymbol \Sigma}=\mathbf{Diag}(\sigma_1^{\,} ,\cdots ,\sigma_r^{\,} ){} \end{aligned} $$
(4.4.18)
where $$r=\mathrm {rank}(\mathbf {W})\ll \min \{m,n\}$$ , $$\mathbf {U}\in \mathbb {R}^{m\times r},\mathbf {V}\in \mathbb {R}^{n\times r}$$ .
Let the threshold value τ ≥ 0, then
$$\displaystyle \begin{aligned} \mathcal{D}_\tau (\mathbf{W})=\mathbf{U}\mathcal{D}_\tau ({\boldsymbol \Sigma}){\mathbf{V}}^T{} \end{aligned} $$
(4.4.19)
is called the singular value thresholding (SVT) of the matrix W, where
$$\displaystyle \begin{aligned} \mathcal{D}_\tau ({\boldsymbol \Sigma})=\mathrm{soft}({\boldsymbol \Sigma},\tau )=\mathbf{Diag}\left ((\sigma_1^{\,} -\tau )_+,\cdots ,(\sigma_r^{\,} - \tau )_+\right ) \end{aligned} $$
(4.4.20)
is known as the soft thresholding, and
$$\displaystyle \begin{aligned} (\sigma_i^{\,} -\tau )_+ =\left\{\begin{aligned} &amp;\sigma_i^{\,} -\tau ,&amp;&amp;\text{if}\, \sigma_i^{\,} &gt;\tau ;\\ &amp;0,&amp;&amp;\text{otherwise}\end{aligned}\right. \end{aligned}$$
is the soft thresholding operation.
The relationships between the SVT and the SVD are as follows.

  • If the soft threshold value τ = 0, then the SVT is reduced to the truncated SVD (4.4.18).

  • All of singular values are soft thresholded by the soft threshold value τ > 0, which just changes the magnitudes of singular values, does not change the left and right singular vector matrices U and V.

Theorem 4.5 ([6])
For each soft threshold value μ > 0 and the matrix $$\mathbf {W}\in \mathbb {R}^{m\times n}$$ , the SVT operator obeys
$$\displaystyle \begin{aligned} \mathbf{U}\mathrm{soft}({\boldsymbol \Sigma},\mu ){\mathbf{V}}^T&amp;=\mathop{\mathit{\mbox{arg min}}}\limits_{\mathbf{X}}\left (\mu\|\mathbf{X}\|{}_\ast +\frac 12\|\mathbf{X}-\mathbf{W}\|{}_F^2 \right ),{} \end{aligned} $$
(4.4.21)
$$\displaystyle \begin{aligned} \mathrm{soft}(\mathbf{W},\mu )&amp;=\mathop{\mathit{\mbox{arg min}}}\limits_{\mathbf{X}}\left (\mu\|\mathbf{X}\|{}_1+\frac 12\|\mathbf{X}-\mathbf{W} \|{}_F^2\right ),{} \end{aligned} $$
(4.4.22)
whereUΣV Tis the SVD ofW, and the soft thresholding (shrinkage) operator
$$\displaystyle \begin{aligned}{}[\mathrm{soft}(\mathbf{W},\mu )]_{ij}=\left\{\begin{aligned} &amp;w_{ij}^{\,} -\mu ,&amp;&amp;~~w_{ij}^{\,} &gt;\mu ;\\ &amp;w_{ij}^{\,} +\mu ,&amp;&amp;~~w_{ij}^{\,} &lt;-\mu ;\\ &amp;0,&amp;&amp;~~\mathrm{otherwise}.\end{aligned}\right. \end{aligned} $$
(4.4.23)

Here $$w_{ij}^{\,}\in \mathbb {R}$$ is the (i, j)th entry of $$\mathbf {W}\in \mathbb {R}^{m\times n}$$ .

4.5 Least Squares Method

In over-determined equation, the number of independent equations is larger than the number of independent unknowns, the number of independent equations appears surplus for determining the unique solution. An over-determined matrix equation Ax = b has no exact solution and thus is an inconsistent equation that may in some cases have an approximate solution. There are four commonly used methods for solutions of matrix equations: Least squares method, Tikhonov regularization method, Gauss–Seidel method, and total least squares method. From this section we will introduce these four methods in turn.

4.5.1 Least Squares Solution

Consider an over-determined matrix equation Ax = b, where b is an m × 1 data vector, A is an m × n data matrix, and m > n.

Suppose the data vector and the additive observation error or noise exist, i.e., b = b 0 + e, where b 0 and e are the errorless data vector and the additive error vector, respectively.

In order to resist the influence of the error on matrix equation solution, we use a correction vector Δb to “disturb” the data vector b for forcing Ax = b + Δb to compensate the uncertainty existing in the data vector b (noise or error). The idea for solving the matrix equation can be described by the optimization problem
$$\displaystyle \begin{aligned} \min_{\mathbf{x}}\,\big \{\|\varDelta\mathbf{b}\|{}^2 =\|\mathbf{Ax}-\mathbf{b}\|{}_2^2=(\mathbf{Ax}-\mathbf{b})^T(\mathbf{Ax}-\mathbf{b})\big \}.{} \end{aligned} $$
(4.5.1)
Such a method is known as ordinary least squares (OLS) method, simply called the least squares (LS) method.
As a matter of fact, the correction vector Δb = Ax −b is just the error vector of both sides of the matrix equation Ax = b. Hence the central idea of the LS method is to find the solution x such that the sum of the squared error $$\|\mathbf {Ax}-\mathbf { b}\|{ }_2^2$$ is minimized, namely
$$\displaystyle \begin{aligned} \hat{\mathbf{x}}_{\mathrm{LS}}^{\,} =\mathrm{arg}\min_{\mathbf{x}}\ \|\mathbf{Ax}-\mathbf{b}\|{}_2^2. \end{aligned} $$
(4.5.2)
In order to derive the analytic solution of x, expand Eq. (4.5.1) to get
$$\displaystyle \begin{aligned} \phi ={\mathbf{x}}^T {\mathbf{A}}^T\mathbf{Ax} -{\mathbf{x}}^T {\mathbf{A}}^T\mathbf{b}-{\mathbf{b}}^T \mathbf{Ax}+{\mathbf{b}}^T \mathbf{b}. \end{aligned}$$
Find the derivative of ϕ with respect to x, and let the result equal zero, then
$$\displaystyle \begin{aligned} \frac{\mathrm{d}\phi}{\mathrm{d}\mathbf{x}}=2{\mathbf{A}}^T\mathbf{Ax}-2{\mathbf{A}}^T\mathbf{b}=0. \end{aligned}$$
That is to say, the solution x must meet
$$\displaystyle \begin{aligned} {\mathbf{A}}^T \mathbf{Ax}={\mathbf{A}}^T \mathbf{b}.{} \end{aligned} $$
(4.5.3)
The above equation is identifiable or unidentifiable depending on the rank of the m × n matrix A.
  • Identifiable: When Ax = b is the over-determined equation, it has the unique solution
    $$\displaystyle \begin{aligned} {\mathbf{x}}_{\mathrm{LS}}^{\,} =({\mathbf{A}}^T\mathbf{A})^{-1}{\mathbf{A}}^T\mathbf{b}\quad \mbox{if}\ \mathrm{rank}(\mathbf{A})=n,{} \end{aligned} $$
    (4.5.4)
    or
    $$\displaystyle \begin{aligned} {\mathbf{x}}_{\mathrm{LS}}^{\,} =({\mathbf{A}}^T\mathbf{A})^{\dagger}{\mathbf{A}}^T\mathbf{b}\quad \mbox{if}\ \mathrm{rank}(\mathbf{A})&lt;n, \end{aligned} $$
    (4.5.5)
    where B † denotes the Moore–Penrose inverse matrix of B. In parameter estimation theory, the unknown parameter vector x is said to be uniquely identifiable, if it is uniquely determined.

  • Unidentifiable: For an under-determined equation Ax = b, if rank(A) = m < n, then different solutions of x give the same value of Ax. Clearly, although the data vector b can provide some information about Ax, we cannot distinguish different parameter vectors x corresponding to the same Ax. Such an unknown vector x is said to be unidentifiable.

In parameter estimation, an estimate $$\hat {{\boldsymbol \theta }}$$ of the parameter vector θ is known as an unbiased estimator, if its mathematical expectation is equal to the true unknown parameter vector, i.e., $$E\{\hat {{\boldsymbol \theta }}\}={\boldsymbol \theta }$$ . Further, an unbiased estimator is called the optimal unbiased estimator if it has the minimum variance. Similarly, for an over-determined matrix equation Aθ = b + e with noisy data vector b, if the mathematical expectation of the LS solution $$\hat {\boldsymbol \theta }_{\mathrm {LS}}^{\,}$$ is equal to the true parameter vector θ, i.e., $$E\{\hat {\boldsymbol \theta }_{\mathrm {LS}}^{\,}\}={\boldsymbol \theta }$$ , then $$\hat {{\boldsymbol \theta }}_{\mathrm {LS}}^{\,}$$ is called the optimal unbiased estimator.

Theorem 4.6 (Gauss–Markov Theorem)
Consider the set of linear equations
$$\displaystyle \begin{aligned} \mathbf{Ax}=\mathbf{b}+\mathbf{e}, \end{aligned} $$
(4.5.6)
where the m × n matrix A and the n × 1 vector x are, respectively, the constant matrix and the parameter vector; b is the m × 1 vector with random error vector $$\mathbf {e}=[e_1^{\,} ,\cdots ,e_m^{\,} ]^T$$ , and its mean vector and covariance matrix are, respectively,
$$\displaystyle \begin{aligned} E\{ \mathbf{e}\}=\mathbf{0},\qquad \mathrm{cov}(\mathbf{e})=E\{\mathbf{ee}^H\}=\sigma^2\mathbf{I}. \end{aligned}$$
Then the n × 1 parameter vector x exists the optimal unbiased solution $$\hat {\mathbf {x}}$$ , if and only if rank(A) = n. In this case, the optimal unbiased solution is given by the LS solution
$$\displaystyle \begin{aligned} \hat{\mathbf{x}}_{\mathrm{LS}}^{\,} =({\mathbf{A}}^H \mathbf{A})^{-1}{\mathbf{A}}^H \mathbf{b}, \end{aligned} $$
(4.5.7)
and its covariance
$$\displaystyle \begin{aligned} \mathrm{var}(\hat{\mathbf{x}}_{\mathrm{LS}}^{\,} )\leq \mathrm{var}(\tilde{\mathbf{x}}), \end{aligned} $$
(4.5.8)

where $$\tilde {\mathbf {x}}$$ is any other solution of the matrix equation Ax = b + e.

Proof

See e.g., [46].

In the Gauss–Markov theorem cov(e) = σ 2I implies that all components of the additive noise vector e are mutually uncorrelated, and have the same variance σ 2. Only in this case, the LS solution is unbiased and optimal.

4.5.2 Rank-Deficient Least Squares Solutions

In many science and engineering applications, it is usually necessary to use a low-rank matrix to approximate a noisy or disturbed matrix. The following theorem gives an evaluation of the quality of approximation.

Theorem 4.7 (Low-Rank Approximation)
Let $$\mathbf {A}=\sum _{i=1}^p\sigma _i^{\,}{\mathbf {u}}_i^{\,}{\mathbf {v}}_i^T$$ be the SVD of $$\mathbf {A}\in \mathbb {R}^{m\times n}$$ , where p = rank(A). If k < p and $${\mathbf {A}}_k^{\,} =\sum _{i=1}^k\sigma _i^{\,} {\mathbf {u}}_i^{\,}{\mathbf {v}}_i^T$$ is the rank-k approximation of A, then the approximation quality can be measured by the Frobenius norm
$$\displaystyle \begin{aligned} \min_{\mathrm{rank}(\mathbf{B})=k}\|\mathbf{A}- \mathbf{B}\|{}_F^{\,} =\|\mathbf{A}-{\mathbf{A}}_k^{\,}\|{}_F^{\,} =\left (\sum_{i=k+1}^q\sigma_i^2\right )^{1/2},\quad q=\min \{m,n\}. \end{aligned} $$
(4.5.9)
Proof

See, e.g., [10, 21, 30].

For an over-determined and rank-deficient system of linear equations Ax = b, let the SVD of A be given by A = U ΣV H, where $${\boldsymbol \Sigma } =\mathbf {Diag}(\sigma _1^{\,} ,\ldots ,\sigma _r^{\,} ,0,\ldots ,0)$$ . The LS solution
$$\displaystyle \begin{aligned} \hat{\mathbf{x}} ={\mathbf{A}}^{\dagger} \mathbf{b}=\mathbf{V}{\boldsymbol \Sigma}^{\dagger} {\mathbf{U}}^H\mathbf{b}, {} \end{aligned} $$
(4.5.10)
where $${\boldsymbol \Sigma }^{\dagger } =\mathbf {Diag}(1/\sigma _1^{\,} ,\ldots ,1/\sigma _r^{\,} , 0,\ldots ,0)$$ .
Equation (4.5.10) can be represented as
$$\displaystyle \begin{aligned} {\mathbf{x}}_{\mathrm{LS}}^{\,}=\sum_{i=1}^r ({\mathbf{u}}_i^H\mathbf{b} /\sigma_i^{\,} ){\mathbf{v}}_i^{\,}. \end{aligned} $$
(4.5.11)
The corresponding minimum residual is given by
$$\displaystyle \begin{aligned} r_{\mathrm{LS}}^{\,}=\| \mathbf{Ax}_{\mathrm{LS}}^{\,}-\mathbf{b} \|{}_2^{\,} =\big\| [{\mathbf{u}}_{r+1}^{\,}, \ldots , {\mathbf{u}}_m^{\,} ]^H \mathbf{b} \big\|{}_2^{\,}.{} \end{aligned} $$
(4.5.12)

Although, in theory, when i > r the true singular values $$\sigma _i^{\,} =0$$ , the computed singular values $$\hat {\sigma _i^{\,}},~i&gt;r$$ , are not usually equal to zero and sometimes even have quite a large perturbation. In these cases, an estimate of the matrix rank r is required. In signal processing and system theory, the rank estimate $$\hat r$$ is usually called the effective rank.

Effective rank can be estimated by one of the following two common methods.
  1. 1.
    Normalized Singular Value Method. Compute the normalized singular values $$\bar \sigma _i^{\,}=\hat \sigma _i^{\,}/\hat \sigma _1^{\,}$$ , and select the largest integer i satisfying the criterion $$\bar \sigma _i^{\,}\geq \epsilon $$ as an estimate of the effective rank $$\hat r$$ . Obviously, this criterion is equivalent to choosing the maximum integer i satisfying
    $$\displaystyle \begin{aligned} \hat \sigma_i^{\,} \geq \epsilon \hat \sigma_1^{\,} \end{aligned} $$
    (4.5.13)

    as $$\hat r$$ ; here 𝜖 is a very small positive number, e.g., 𝜖 = 0.1 or 𝜖 = 0.05.

     
  2. 2.
    Norm Ratio Method. Let an m × n matrix $${\mathbf {A}}_k^{\,}$$ be the rank-k approximation to the original m × n matrix A. Define the Frobenius norm ratio as
    ../images/492994_1_En_4_Chapter/492994_1_En_4_Equ66_HTML.png
    (4.5.14)
    and choose the minimum integer k satisfying
    $$\displaystyle \begin{aligned} \nu (k) \geq \alpha {} \end{aligned} $$
    (4.5.15)

    as the effective rank estimate $$\hat r$$ , where α is close to 1, e.g., α = 0.997 or 0.998.

     
After the effective rank $$\hat r$$ is determined via the above two criteria,
$$\displaystyle \begin{aligned} \hat{\mathbf{x}}_{\mathrm{LS}}^{\,}=\sum_{i=1}^{\hat r}(\hat{\mathbf{u}}_i^H \mathbf{b}/\hat\sigma_i^{\,} )\hat{\mathbf{v}}_i^{\,}{} \end{aligned} $$
(4.5.16)
can be regarded as a reasonable approximation to the LS solution $${\mathbf {x}}_{\mathrm {LS}}^{\,}$$ .

4.6 Tikhonov Regularization and Gauss–Seidel Method

The LS method is widely used for solving matrix equations and is applicable for many real-world applications in machine learning, neural networks, support vector machines, and evolutionary computation. But, due to its sensitive to the perturbation of the data matrix, the LS methods must be improved in these applications. A simple and efficient way is the well-known Tikhonov regularization.

4.6.1 Tikhonov Regularization

When m = n, and A is nonsingular, the solution of matrix equation Ax = b is given by $$\hat {\mathbf {x}} ={\mathbf {A}}^{-1}\mathbf {b}$$ ; and when m > n and A m×n is of full column rank, the solution of the matrix equation is $$\hat {\mathbf {x}}_{\mathrm {LS}}^{\,} ={\mathbf {A}}^{\dagger }\mathbf {b}=({\mathbf {A}}^H\mathbf {A})^{-1}{\mathbf {A}}^H\mathbf {b}$$ .

The problem is: the data matrix A is often rank deficient in engineering applications. In these cases, the solution $$\hat {\mathbf {x}}={\mathbf {A}}^{-1}\mathbf {b}$$ or $$\hat {\mathbf {x}}_{\mathrm {LS}}^{\,} =({\mathbf {A}}^H\mathbf {A})^{-1}{\mathbf {A}}^H \mathbf {b}$$ either diverges, or even exists, it is the bad approximation to the unknown vector x. Even if we happen to find a reasonable approximation of x, the error estimate $$\|\mathbf {x}-\hat {\mathbf {x}}\|\leq \|{\mathbf {A}}^{-1}\|\,\|\mathbf {A}\hat {\mathbf {x}}-\mathbf {b}\|$$ or $$\|\mathbf {x}-\hat {\mathbf {x}}\|\leq \|{\mathbf {A}}^{\dagger }\|\,\| \mathbf {A}\hat {\mathbf {x}}-\mathbf {b}\|$$ is very disappointing [32]. By observation, it is easily known that the problem lies in the inversion of the covariance matrix A HA of the rank-deficient data matrix A.

As an improvement of the LS cost function $$\frac 12\|\mathbf {Ax}-\mathbf {b}\|{ }_2^2$$ , Tikhonov [39] in 1963 proposed the regularized least squares cost function
$$\displaystyle \begin{aligned} J(\mathbf{x})=\frac 12\left (\|\mathbf{Ax}-\mathbf{b}\|{}_2^2+\lambda \|\mathbf{x}\|{}_2^2\right ), \end{aligned} $$
(4.6.1)
where λ ≥ 0 is called the regularization parameter.
The conjugate gradient of the cost function J(x) with respect to the argument x is given by
$$\displaystyle \begin{aligned} \frac{\partial J(\mathbf{x})}{\partial{\mathbf{x}}^H}=\frac{\partial}{\partial{\mathbf{x}}^H}\left ((\mathbf{Ax}-\mathbf{b})^H (\mathbf{Ax}-\mathbf{b})+\lambda {\mathbf{x}}^H\mathbf{x}\right )={\mathbf{A}}^H\mathbf{Ax}-{\mathbf{A}}^H\mathbf{b}+\lambda \mathbf{x}. \end{aligned}$$
Let $$\frac {\partial J(\mathbf {x})}{\partial {\mathbf {x}}^H}=\mathbf {0}$$ , then the Tikhonov regularization solution
$$\displaystyle \begin{aligned} \hat{\mathbf{x}}_{\mathrm{Tik}}^{\,} =({\mathbf{A}}^H\mathbf{A}+\lambda\mathbf{I})^{-1}{\mathbf{A}}^H\mathbf{b}. \end{aligned} $$
(4.6.2)
This method using (A HA + λI)−1 instead of the direct inversion of the covariance matrix (A HA)−1 is called the Tikhonov regularization method (or simply regularized method). In signal processing and image processing, the regularization method is sometimes known as the relaxation method.

The nature of Tikhonov regularization method is: by adding a very small disturbance λ to each diagonal entry of the covariance matrix A HA of rank-deficient matrix A, the inversion of the singular covariance matrix A HA becomes the inversion of a nonsingular matrix A HA + λI, thereby greatly improving the numerical stability of solving the rank-deficient matrix equation Ax = b.

Obviously, if the data matrix A is of full column rank, but exists the error or noise, we must adopt the opposite method to the Tikhonov regularization: adding a very small negative disturbance − λ to each diagonal entry of the covariance matrix A HA for suppressing the influence of noise. Such a method using a very small negative disturbance matrix − λI is called the anti-Tikhonov regularization method or anti-regularized method, and its solution is given by
$$\displaystyle \begin{aligned} \hat{\mathbf{x}}=({\mathbf{A}}^H\mathbf{A}-\lambda \mathbf{I})^{-1}{\mathbf{A}}^H\mathbf{b}. \end{aligned} $$
(4.6.3)
The total least square method is a typical anti-regularized method and will be discussed later.

When the regularization parameter λ varies in the definition interval [0, ∞), the family of solutions for a regularized LS problem is known as its regularization path.

Tikhonov regularization solution has the following important properties [25]:
  1. 1.

    Linearity: The Tikhonov regularization LS solution $$\hat {\mathbf {x}}_{\mathrm {Tik}}^{\,} =({\mathbf {A}}^H\mathbf {A}+\lambda \mathbf {I})^{-1}{\mathbf {A}}^H\mathbf {b}$$ is the linear function of the observed data vector b.

     
  2. 2.
    Limit characteristic when λ → 0: When the regularization parameter λ → 0, the Tikhonov regularization LS solution converges to the ordinary LS solution or the Moore–Penrose solution $$\lim _{\lambda \to 0}\hat {\mathbf {x}}_{\mathrm {Tik}}=\hat {\mathbf {x}}_{\mathrm {LS}}={\mathbf {A}}^{\dagger } \mathbf {b}=({\mathbf {A}}^H\mathbf {A})^{-1}{\mathbf {A}}^H \mathbf {b}$$ . The solution point $$\hat {\mathbf {x}}_{\mathrm {Tik}}$$ has the minimum $$\ell _2^{\,}$$ -norm among all the feasible points meeting A H(Ax −b) = 0:
    $$\displaystyle \begin{aligned} \hat{\mathbf{x}}_{\mathrm{Tik}}^{\,} =\mathop{\mbox{arg min}}\limits_{{\mathbf{A}}^T(\mathbf{b}-\mathbf{Ax})=\mathbf{0}}\| \mathbf{x}\|{}_2^{\,} . \end{aligned} $$
    (4.6.4)
     
  3. 3.

    Limit characteristic when λ →∞: When λ →∞, the optimal Tikhonov regularization LS solution converges to a zero vector, i.e., $$\lim _{\lambda \to \infty }\hat {\mathbf {x}}_{\mathrm {Tik}}^{\,} =\mathbf {0}$$ .

     
  4. 4.

    Regularization path: When the regularization parameter λ varies in [0, ∞), the optimal solution of the Tikhonov regularization LS problem is the smooth function of the regularization parameter, i.e., when λ decreases to zero, the optimal solution converges to the Moore–Penrose solution; and when λ increases, the optimal solution converges to zero vector.

     

The Tikhonov regularization can effectively prevent the divergence of the LS solution $$\hat {\mathbf {x}}{ }_{\mathrm {LS}}^{\,} =({\mathbf {A}}^T\mathbf {A})^{-1}{\mathbf {A}}^T\mathbf {b}$$ when A is rank deficient, thereby improves obviously the convergence property of the LS algorithm and the alternative LS algorithm, and is widely applied.

4.6.2 Gauss–Seidel Method

A matrix equation Ax = b can be rearranged as
../images/492994_1_En_4_Chapter/492994_1_En_4_Equw_HTML.png
Based on the above rearrangement, the Gauss–Seidel method begins with an initial approximation to the solution, x (0), and then compute an update for the first element of x:
$$\displaystyle \begin{aligned} x_1^{(1)}=\frac 1{a_{11}^{\,}}\Bigg (b_1^{\,} -\sum_{j=2}^n a_{1j}^{\,} x_j^{(0)}\Bigg ). \end{aligned} $$
(4.6.5)
Continuing in this way for the other elements of x, the Gauss–Seidel method gives
$$\displaystyle \begin{aligned} x_i^{(1)}=\frac 1{a_{ii}^{\,}}\Bigg (b_i^{\,} -\sum_{j=1}^{i-1}a_{ij}^{\,} x_j^{(1)}-\sum_{j=i+1}^n a_{ij}^{\,} x_j^{(0)}\Bigg ),\quad \text{for } i=1,\ldots ,n. \end{aligned} $$
(4.6.6)
After getting the approximation $${\mathbf {x}}^{(1)}=\big [x_1^{(1)},\ldots ,x_n^{(1)}\big ]^T$$ , we then continue this same kind of iteration for x (2), x (3), … until x converges.

The Gauss–Seidel method not only can find the solution of the matrix equation, but also are applicable for solving a nonlinear optimization problem.

Let $$X_i\subseteq \mathbb {R}^{n_i^{\,}}$$ be the feasible set of $$n_i^{\,}\times 1$$ vector $${\mathbf {x}}_i^{\,}$$ . Consider the nonlinear minimization problem
$$\displaystyle \begin{aligned} \min_{\mathbf{x}\in X}\big \{ f(\mathbf{x})=f({\mathbf{x}}_1^{\,} ,\cdots ,{\mathbf{x}}_m^{\,})\big \},{} \end{aligned} $$
(4.6.7)
where $$\mathbf {x}\in X=X_1\times \cdots \times X_m\subseteq \mathbb {R}^n$$ is the Cartesian product of a closed nonempty convex set $$X_i\subseteq \mathbb {R}^{n_i}, i=1,\cdots ,m$$ , and $$\sum _{i=1}^m n_i^{\,} =n$$ .

Equation (4.6.7) is an unconstrained optimization problem with m coupled variable vectors. An efficient approach for solving this class of the coupled optimization problems is the block nonlinear Gauss–Seidel method, called simply the GS method [3, 18].

In every iteration of the GS method, m − 1 variable vectors are fixed, one remaining variable vector is minimized. This idea constitutes the basic framework of the GS method for solving nonlinear unconstrained optimization problem (4.6.7):
  1. 1.

    Initial m − 1 variable vectors $${\mathbf {x}}_i^{\,} ,i=2,\cdots ,m$$ , and let k = 0.

     
  2. 2.
    Find the solution of separated sub-optimization problem
    $$\displaystyle \begin{aligned} {\mathbf{x}}_i^{k+1}=\mathop{\mbox{arg min}}\limits_{\mathbf{y}\in X_i} f\big ({\mathbf{x}}_1^{k+1},\cdots ,{\mathbf{x}}_{i-1}^{k+1},\mathbf{ y},{\mathbf{x}}_{i+1}^k,\cdots , {\mathbf{x}}_m^k\big ),\quad i=1,\cdots ,m. \end{aligned} $$
    (4.6.8)

    At the (k + 1)th iteration of updating $${\mathbf {x}}_i^{\,}$$ , all $${\mathbf {x}}_1^{\,} ,\cdots ,{\mathbf {x}}_{i-1}^{\,}$$ have been updated as $${\mathbf {x}}_1^{k+1},\cdots , {\mathbf {x}}_{i-1}^{k+1}$$ , so these sub-vectors and $${\mathbf {x}}_{i+1}^k,\cdots ,{\mathbf {x}}_m^k$$ to be updated are fixed as the known vectors.

     
  3. 3.

    To test whether m variable vectors are all convergent. If convergent, then output the optimization results $$({\mathbf {x}}_1^{k+1} ,\cdots ,{\mathbf {x}}_m^{k+1})$$ ; otherwise, let k ← k + 1, return to Eq. (4.6.8), and continue to iteration until the convergence criterion meets.

     

If the objective function f(x) of the optimization (4.6.7) is the LS error function (for example, $$\|\mathbf {Ax}-\mathbf {b}\|{ }_2^2)$$ , then the GS method is customarily called the alternating least squares (ALS) method.

Example 4.2
Consider the full-rank decomposition of an m × n known data matrix X = AB, where the m × r matrix A is of full column rank, and the r × n matrix B is of full row rank. Let the cost function of the matrix full-rank decomposition be
$$\displaystyle \begin{aligned} f(\mathbf{A},\mathbf{B})=\frac 12\|\mathbf{X}-\mathbf{AB}\|{}_F^2. \end{aligned} $$
(4.6.9)
Then the ALS algorithm first initializes the matrix A. At the (k + 1)th iteration, from the fixed matrix A k we update the LS solution of B as follows:
$$\displaystyle \begin{aligned} {\mathbf{B}}_{k+1}^{\,}=({\mathbf{A}}_k^T{\mathbf{A}}_k)^{-1}{\mathbf{A}}_k^T\mathbf{X}. \end{aligned} $$
(4.6.10)
Next, from the transpose of matrix decomposition X T = B TA T, we can immediately update the LS solution of A T as
$$\displaystyle \begin{aligned} {\mathbf{A}}_{k+1}^T=({\mathbf{B}}_{k+1}^{\,}{\mathbf{B}}_{k+1}^T)^{-1}{\mathbf{B}}_{k+1}^{\,}{\mathbf{X}}^T. \end{aligned} $$
(4.6.11)
The above two kinds of LS methods are performed alternately. Once the whole ALS algorithm is converged, the optimization results of matrix decomposition can be obtained.

The fact that the GS algorithm may not converge was observed by Powell in 1973 [34] who called it the “circle phenomenon” of the GS method. Recently, a lot of simulation experiences have shown [28, 31] that even converged, the iterative process of the ALS method is also very easy to fall into the “swamp”: an unusually large number of iterations leads to a very slow convergence rate. [28, 31].

A kind of simple and effective way for avoiding the circle and swamp phenomenon of the GS method is to make the Tikhonov regularization of the objective function of the optimization problem (4.6.7), namely the separated sub-optimization algorithm (4.6.8) is regularized as
$$\displaystyle \begin{aligned} {\mathbf{x}}_i^{k+1}=\mathop{\mbox{arg min}}\limits_{\mathbf{y}\in X_i}\left \{ f({\mathbf{x}}_1^{k+1},\cdots ,{\mathbf{x}}_{i-1}^{k+1},\mathbf{ y}, {\mathbf{x}}_{i+1}^k,\cdots ,{\mathbf{x}}_m^k)+\frac 12\tau_i^{\,} \|\mathbf{y}-{\mathbf{x}}_i^k\|{}_2^2\right \},{} \end{aligned} $$
(4.6.12)
where i = 1, ⋯ , m.

The above algorithm is called the proximal point versions of the GS methods [1, 3], abbreviated as PGS method.

The role of the regularization term $$\|\mathbf {y}-{\mathbf {x}}_i^k\|{ }_2^2$$ is to force the updated vector $${\mathbf {x}}_i^{k+1}= \mathbf {y}$$ close to $${\mathbf {x}}_i^k$$ , not to deviate too much, and thus avoid the violent shock of the iterative process in order to prevent the divergence of the algorithm.

The GS or PGS method is said to be well defined, if each sub-optimization problem has an optimal solution [18].

Theorem 4.8 ([18])

If the PGS method is well defined, and the sequence {x k} exists limit points, then every limit point $$\bar {\mathbf {x}}$$ of {x k} is a critical point of the optimization problem (4.6.7).

This theorem shows that the convergence performance of the PGS method is better than that of the GS method.

Many simulation experiments show [28] that under the condition achieving the same error, the iterative number of the GS method in swamp iteration is unusually large, whereas the PGS method tends to converge quickly. The PGS method is also called the regularized Gauss–Seidel method in some literature.

The ALS method and the regularized ALS method have important applications in nonnegative matrix decomposition and the tensor analysis.

4.7 Total Least Squares Method

For a matrix equation A m×nx n = b m, all the LS method, the Tikhonov regularization method, and the Gauss–Seidel method give the solution of n parameters. However, by the rank-deficiency of the matrix A we know that the unknown parameter vector x contains only r independent parameters; the other parameters are linearly dependent on the r independent parameters. In many engineering applications, we naturally want to find the r independent parameters other than the n parameters containing redundancy components. In other words, we want to estimate only the principal parameters and to eliminate minor components. This problem can be solved via the low-rank total least squares (TLS) method.

The earliest ideas about TLS can be traced back to the paper of Pearson in 1901 [33] who considered the approximate method for solving the matrix equation Ax = b when both A and b exist the errors. But, only in 1980, Golub and Van Loan [15] have first time made the overall analysis from the point of view of numerical analysis, and have formally known this method as the total least squares. In mathematical statistics, this method is called the orthogonal regression or errors-in-variables regression [14]. In system identification, the TLS method is called the characteristic vector method or the Koopmans–Levin method [42]. Now, the TLS method has been widely used in statistics, physics, economics, biology and medicine, signal processing, automatic control, system science, artificial intelligence, and many other disciplines and fields.

4.7.1 Total Least Squares Solution

Let A 0 and b 0 express unobservable error-free data matrix and error-free data vector, respectively. The actual observed data matrix and data vector are, respectively, given by
$$\displaystyle \begin{aligned} \mathbf{A}={\mathbf{A}}_0+\mathbf{E},\quad \mathbf{b}={\mathbf{b}}_0+\mathbf{e}, \end{aligned} $$
(4.7.1)
where E and e express the error data matrix and the error data vector, respectively.
The basic idea of the TLS is: not only use the correction vector Δb to perturb the data vector b, but also use the correction matrix ΔA to perturb the data matrix A, making the joint compensation for errors or noise in both A and b:
$$\displaystyle \begin{aligned} \mathbf{b}+\Delta\mathbf{b}&amp;={\mathbf{b}}_0 +\mathbf{e}+\Delta\mathbf{b}\to{\mathbf{b}}_0 ,\\ \mathbf{A}+\Delta\mathbf{A}&amp;={\mathbf{A}}_0^{\,} +\mathbf{E}+\Delta\mathbf{A}\to{\mathbf{A}}_0^{\,} , \end{aligned} $$
so that the solution of the noisy matrix equation is transformed into the solution of the error-free matrix equation:
$$\displaystyle \begin{aligned} (\mathbf{A}+\Delta\mathbf{A})\mathbf{x}=\mathbf{b}+\Delta\mathbf{b}\ \Rightarrow\ {\mathbf{A}}_0\mathbf{x}={\mathbf{b}}_0 .{} \end{aligned} $$
(4.7.2)
Naturally, we want the correction data matrix and the correction data vectors are as small as possible. Hence the TLS problem can be expressed as the constrained optimization problem
$$\displaystyle \begin{aligned} \text{TLS:}\quad \min_{\Delta\mathbf{A},\Delta\mathbf{b},\mathbf{x}}\|[\Delta\mathbf{A},\Delta\mathbf{b}]\|{}_F^2\quad \text{subject to}\quad (\mathbf{A}+\Delta\mathbf{A})\mathbf{x}=\mathbf{b}+\Delta\mathbf{b} \end{aligned} $$
(4.7.3)
or
$$\displaystyle \begin{aligned} \text{TLS:}\quad \min_{\mathbf{z}}\|\mathbf{D}\|{}_F^2\quad \text{subject to}\quad \mathbf{Dz}=-\mathbf{Bz},{} \end{aligned} $$
(4.7.4)
where D = [ ΔA,  Δb], B = [A, b], and ../images/492994_1_En_4_Chapter/492994_1_En_4_IEq123_HTML.gifis the (n + 1) × 1 vector.
Under the assumption ∥z∥2 = 1, from $$\|\mathbf {D}\|{ }_2^{\,}\leq \|\mathbf {D}\|{ }_F^{\,}$$ and $$\|\mathbf {D}\|{ }_2 =\sup _{\|\mathbf {z} \|{ }_2=1}\|\mathbf {Dz}\|{ }_2$$ , we have $$\min _{\mathbf {z}}\|\mathbf {D}\|{ }_F^2=\min _{\mathbf {z}}\|\mathbf {Dz}\|{ }_2^2$$ and thus can rewrite (4.7.4) as
$$\displaystyle \begin{aligned} \text{TLS:}\quad \min_{\mathbf{z}}\|\mathbf{Bz}\|{}_2^2\quad \text{subject to}\quad \|\mathbf{z}\|=1{} \end{aligned} $$
(4.7.5)
due to Dz = −Bz.
Case 1: Single Smallest Singular Value
The singular value $$\sigma _n^{\,}$$ of B is significantly larger than $$\sigma _{n+1}^{\,}$$ , i.e., the smallest singular value has only one. In this case, the TLS problem (4.7.5) is easily solved via the Lagrange multiplier method. To this end, define the objective function
$$\displaystyle \begin{aligned} J(\mathbf{z})=\|\mathbf{Bz}\|{}_2^2 +\lambda (1-{\mathbf{z}}^H\mathbf{z}), \end{aligned} $$
(4.7.6)
where λ is the Lagrange multiplier. Notice that $$\|\mathbf {Bz}\|{ }_2^2 ={\mathbf {z}}^H{\mathbf {B}}^H\mathbf {Bz}$$ , from $$\mbox{ {$\displaystyle \frac {\partial J(\mathbf {z})}{\partial {\mathbf {z}}^*}$}}=0$$ it follows that
$$\displaystyle \begin{aligned} {\mathbf{B}}^H\mathbf{Bz}=\lambda\mathbf{z}. \end{aligned} $$
(4.7.7)
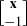This shows that we should select as the Lagrange multiplier the smallest eigenvalue $$\lambda _{\min }$$ of the matrix B HB = [A, b]H[A, b] (i.e., the squares of the smallest singular value of B), while the TLS solution vector z is the eigenvector corresponding to the smallest eigenvalue $$\lambda _{\min }$$ of [A, b]H[A, b]. In other words, the TLS solution vector ../images/492994_1_En_4_Chapter/492994_1_En_4_IEq133_HTML.gif is the solution of the Rayleigh quotient minimization problem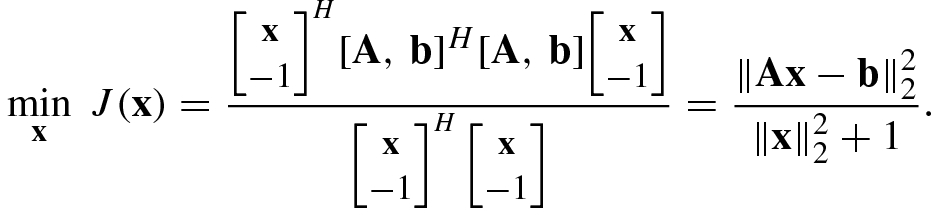
../images/492994_1_En_4_Chapter/492994_1_En_4_Equ88_HTML.png
(4.7.8)
Let the SVD of the m × (n + 1) augmented matrix B be B = U ΣV H, where the singular values are arranged in the order of $$\sigma _1^{\,}\geq \cdots \geq \sigma _{n+1}^{\,}$$ , and their corresponding right singular vectors are $${\mathbf {v}}_1^{\,} , \cdots ,{\mathbf {v}}_{n+1}^{\,}$$ . According to the above analysis, the TLS solution is $$\mathbf {z}={\mathbf {v}}_{n+1}^{\,}$$ , namely
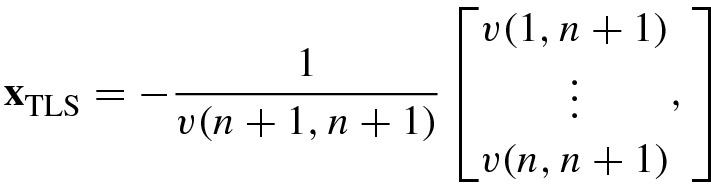
../images/492994_1_En_4_Chapter/492994_1_En_4_Equ89_HTML.png
(4.7.9)
where v(i, n + 1) is the ith entry of (n + 1)th column of V.
Remark
If the augmented data matrix is given by B = [−b, A], then the TLS solution is provided by
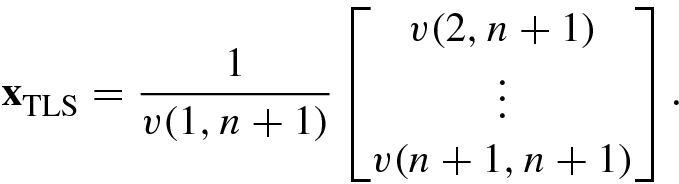
../images/492994_1_En_4_Chapter/492994_1_En_4_Equ90_HTML.png
(4.7.10)
Case 2: Multiple Smallest Singular Values
In this case, there are multiple smallest singular value of B, i.e., multiple small singular values are repeated or very close. Letting
$$\displaystyle \begin{aligned} \sigma_1^{\,} \geq \sigma_2^{\,} \geq \cdots \geq \sigma_p^{\,}&gt;\sigma_{p+1}^{\,}\approx \cdots \approx \sigma_{n+1}^{\,}, \end{aligned} $$
(4.7.11)
then the right singular vector matrix $${\mathbf {V}}_1=[{\mathbf {v}}_{p+1}^{\,} ,{\mathbf {v}}_{p+2}^{\,} ,\cdots ,{\mathbf {v}}_{n+1}^{\,}]$$ will give n − p + 1 possible TLS solutions $${\mathbf {x}}_i^{\,} =-{\mathbf {y}}_{p+i}^{\,} /\alpha _{p+i}^{\,},~i=1,\cdots ,n+1-p$$ . To find the unique TLS solution, one can make the Householder transformation Q to V 1 such that
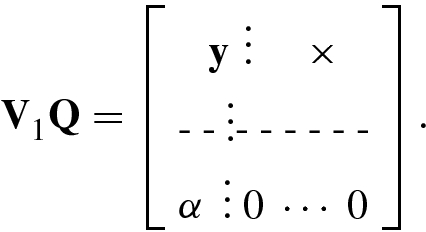
../images/492994_1_En_4_Chapter/492994_1_En_4_Equ92_HTML.png
(4.7.12)
The unique TLS solution is the minimum norm solution given by $$\hat {\mathbf {x}}_{\mathrm {TLS}}=\mathbf {y}/\alpha $$ . This algorithm was proposed by Golub and Van Loan [15], as shown in Algorithm 4.5.
Algorithm 4.5 TLS algorithm for minimum norm solution
../images/492994_1_En_4_Chapter/492994_1_En_4_Fige_HTML.png

The above minimum norm solution $${\mathbf {x}}_{\mathrm {TLS}}^{\,}=\mathbf {y}/\alpha $$ contains n parameters other than p independent principal parameters because of rank(A) = p < n.

In signal processing, system theory and artificial intelligence, the unique TLS solution with no redundant parameters is more interesting, which is the optimal LS approximate solution. To derive the optimal LS approximate solution, let the m × (n + 1) matrix $$\hat {\mathbf {B}}=\mathbf {U}{\boldsymbol \Sigma }_p {\mathbf {V}}^H$$ be an optimal approximation with rank p of the augmented matrix B, where $${\boldsymbol \Sigma }_p =\mathbf {Diag} (\sigma _1^{\,} ,\cdots ,\sigma _p^{\,} ,0,\cdots ,0)$$ . Denote the m × (p + 1) matrix $$\hat {\mathbf {B}}_j^{(p)}$$ as a submatrix among the m × (n + 1) optimal approximate matrix $$\hat {\mathbf {B}}$$ :
$$\displaystyle \begin{aligned} \hat{\mathbf{B}}_j^{(p)}:~\, \mbox{sub-matrix of the}\ j\mbox{th to the}\ (j+p)\mbox{th columns of}~\hat{\mathbf{B}}.{} \end{aligned} $$
(4.7.13)
Clearly, there are (n + 1 − p) submatrices $$\hat {\mathbf {B}}_1^{(p)},\hat {\mathbf {B}}_2^{(p)}, \cdots ,\hat {\mathbf {B}}_{n+1-p}^{(p)}$$ .
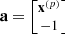As stated before, the fact that the efficient rank of B is equal to p means that p components are linearly independent in the parameter vector x. Let the (p + 1) × 1 vector ../images/492994_1_En_4_Chapter/492994_1_En_4_IEq146_HTML.gif, where x (p) is the column vector consisting of p linearly independent unknown parameters of the vector x. Then, the original TLS problem becomes the solution of the following (n + 1 − p) TLS problems:
$$\displaystyle \begin{aligned} \hat{\mathbf{B}}_j^{(p)}\mathbf{a}=0\, ,\qquad j=1,2,\cdots ,n+1-p {} \end{aligned} $$
(4.7.14)
or equivalent to the solution of one synthetic TLS problem
../images/492994_1_En_4_Chapter/492994_1_En_4_Equ95_HTML.png
(4.7.15)
where $$\hat {\mathbf {B}}(i:p+i)=\hat {\mathbf {B}}_i^{(p)}$$ is defined in (4.7.13). It is not difficult to show that
$$\displaystyle \begin{aligned} \hat{\mathbf{B}}(i:p+i)=\sum_{k=1}^p \sigma_k^{\,}{\mathbf{u}}_k^{\,}({\mathbf{v}}_k^i )^H,{} \end{aligned} $$
(4.7.16)
where $${\mathbf {v}}_k^i$$ is a windowed segment of the kth column vector of V, defined as
$$\displaystyle \begin{aligned} {\mathbf{v}}_k^i =[v(i,k),v(i+1,k),\cdots ,v(i+p,k)]^T. {} \end{aligned} $$
(4.7.17)
Here v(i, k) is the (i, k)th entry of V.
According to the least square principle, finding the LS solution of Eq. (4.7.15) is equivalent to minimize the measure (or cost) function
$$\displaystyle \begin{aligned} f(\mathbf{a})=&amp;\,[\hat {\mathbf{B}} (1:p+1)\mathbf{a}]^H \hat{\mathbf{B}}(1:p+1)\mathbf{a} +[\hat {\mathbf{B}} (2:p+2)\mathbf{a}]^H \hat{\mathbf{B}}(2:p+2)\mathbf{a}\\ &amp;\, +\cdots +[\hat{\mathbf{B}}(n+1-p:n+1)\mathbf{a}]^H\hat{\mathbf{B}}(n+1-p:n+1)\mathbf{a} \\ =&amp;\,{\mathbf{a}}^H \left [ \sum_{i=1}^{n+1-p} [\hat{\mathbf{B}}(i:p+i)]^H\hat{\mathbf{B}}(i:p+i) \right ] \mathbf{a}. \end{aligned} $$
(4.7.18)
Define the (p + 1) × (p + 1) matrix
$$\displaystyle \begin{aligned} {\mathbf{S}}^{(p)}=\sum_{i=1}^{n+1-p}[\hat{\mathbf{B}}(i:p+i)]^H \hat{\mathbf{B}}(i:p+i), {} \end{aligned} $$
(4.7.19)
then the measure function can be simply written as
$$\displaystyle \begin{aligned} f(\mathbf{a})={\mathbf{a}}^H{\mathbf{S}}^{(p)}\mathbf{a}. \end{aligned} $$
(4.7.20)
The minimal variable a of the measure function f(a) is determined by $$\frac {\partial f(\mathbf {a})}{\partial \mathbf { a}^*}=0$$ as follows:
$$\displaystyle \begin{aligned} {\mathbf{S}}^{(p)}\mathbf{a}=\alpha{\mathbf{e}}_1^{\,} \end{aligned} $$
(4.7.21)
where $${\mathbf {e}}_1^{\,} =[1,0,\cdots ,0]^T$$ , and the constant α > 0 represents the error energy. From (4.7.19) and (4.7.16) we have
$$\displaystyle \begin{aligned} {\mathbf{S}}^{(p)}=\sum_{j=1}^p \ \sum_{i=1}^{n+1-p}\sigma_j^2{\mathbf{v}}_j^i ({\mathbf{v}}_j^i )^H.{} \end{aligned} $$
(4.7.22)
Solving the matrix equation (4.7.21) is simple. Let S −(p) be the inverse matrix S (p). Then the solution vector a is only dependent of the first column of the inverse matrix S −(p). 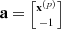It is easily known that the ith entry of $${\mathbf {x}}^{(p)}=[x_{\mathrm {TLS}}^{\,} (1),\cdots ,x_{\mathrm {TLS}}^{\,}(p)]^T$$ in the TLS solution vector ../images/492994_1_En_4_Chapter/492994_1_En_4_IEq152_HTML.gif is given by
$$\displaystyle \begin{aligned} x_{\mathrm{TLS}}^{\,}(i)=-{\mathbf{S}}^{-(p)}(i,1)/{\mathbf{S}}^{-(p)}(p+1,1),\qquad i=1,\cdots , p.{} \end{aligned} $$
(4.7.23)
This solution is known as the optimal least square approximate solution. Because the number of parameters of this solution and the efficient rank are the same, it is also called the low-rank TLS solution [5].
Notice that if the augmented matrix B = [−b, A], then
$$\displaystyle \begin{aligned} x_{\mathrm{TLS}}^{\,}(i)={\mathbf{S}}^{-(p)}(i+1,1)/{\mathbf{S}}^{-(p)}(1,1),\qquad i=1,2,\cdots , p. \end{aligned} $$
(4.7.24)
In summary, given $$\mathbf {A}\in \mathbb {C}^{m\times n},\mathbf {b}\in \mathbb {C}^n$$ , the low-rank SVD-TLS algorithm consists of the following steps [5].
  1. 1.

    Compute the SVD B = [A, b] = U ΣV H, and save V.

     
  2. 2.

    Determine the efficient rank p of B.

     
  3. 3.

    Use (4.7.22) and (4.7.17) to calculate (p + 1) × (p + 1) matrix S (p).

     
  4. 4.
    Compute the inverse S −(p) and the total least square solution
    $$\displaystyle \begin{aligned} x_{\mathrm{TLS}}^{\,}(i)=-{\mathbf{S}}^{-(p)}(i,1)/{\mathbf{S}}^{-(p)}(p+1,1),\, i=1,\cdots , p. \end{aligned}$$
     

4.7.2 Performances of TLS Solution

The TLS has two interesting explanations: one is its geometric interpretation [15], and another is its closed solution [43].

Geometric Interpretation of TLS Solution
Let $${\mathbf {a}}_i^T$$ be the ith row of the matrix A, and $$b_i^{\,}$$ be the ith entry of the vector b. Then the TLS solution $${\mathbf {x}}_{\mathrm {TLS}}^{\,}$$ is the minimal vector such that
$$\displaystyle \begin{aligned} \min_{\mathbf{x}}\frac{\|\mathbf{Ax}-\mathbf{b}\|{}_2^2}{|\mathbf{x}\|{}_2^2+1}=\sum_{i=1}^n \frac{|{\mathbf{a}}_i^T \mathbf{x}- b_i^{\,} |{}^2}{{\mathbf{x}}^T \mathbf{x}+1}, \end{aligned} $$
(4.7.25)
where $$|{\mathbf {a}}_i^T\mathbf {x}-b_i^{\,} |/({\mathbf {x}}^T\mathbf {x}+ 1)$$ is the distance from the point ../images/492994_1_En_4_Chapter/492994_1_En_4_IEq158_HTML.gif to the nearest point in the subspace $$P_x^{\,}$$ , and the subspace $$P_x^{\,}$$ is defined as
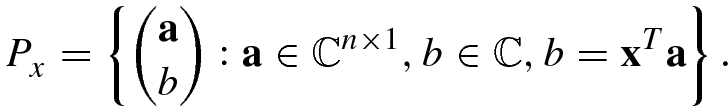
../images/492994_1_En_4_Chapter/492994_1_En_4_Equ106_HTML.png
(4.7.26)
Hence the TLS solution can be expressed by using the subspace $$P_x^{\,}$$ [15]: the square sum of the distance from the TLS solution point ../images/492994_1_En_4_Chapter/492994_1_En_4_IEq162_HTML.gifto the subspace $$P_x^{\,}$$ is minimized.
Closed Solution of TLS Problems
If the singular values of the augmented matrix B are $$\sigma _1^{\,} \geq \cdots \geq \sigma _{n+1}^{\,}$$ , then the TLS solution can be expressed as [43]
$$\displaystyle \begin{aligned} {\mathbf{x}}_{\mathrm{TLS}}^{\,}=({\mathbf{A}}^H\mathbf{A}-\sigma_{n+1}^2\mathbf{I})^{-1}{\mathbf{A}}^H\mathbf{b}. {} \end{aligned} $$
(4.7.27)
Compared with the Tikhonov regularization method, the TLS is a kind of anti-regularization method and can be interpreted as a kind of least square method with noise removal: it first removes the noise affection term $$\sigma _{n+1}^2\mathbf {I}$$ from the covariance matrix A TA, and then finds the inverse matrix of $${\mathbf {A}}^T\mathbf {A}-\sigma _{n+1}^2 \mathbf {I}$$ to get the LS solution.
Letting the noisy data matrix be $$\mathbf {A}={\mathbf {A}}_0^{\,} +\mathbf {E}$$ , then its covariance matrix $${\mathbf {A}}^H\mathbf {A}= {\mathbf {A}}_0^H {\mathbf {A}}_0^{\,} +{\mathbf {E}}^H{\mathbf {A}}_0^{\,} +{\mathbf {A}}_0^H\mathbf {E}+{\mathbf {E}}^H\mathbf {E}$$ . Obviously, when the error matrix E has zero mean, the mathematical expectation of the covariance matrix is given by
$$\displaystyle \begin{aligned} E\{{\mathbf{A}}^H\mathbf{A}\}=E\{{\mathbf{A}}_0^H{\mathbf{A}}_0^{\,}\} +E\{ {\mathbf{E}}^H\mathbf{E}\}={\mathbf{A}}_0^H{\mathbf{A}}_0^{\,} +E\{{\mathbf{E}}^H\mathbf{E}\}. \end{aligned}$$
If the column vectors of the error matrix are statistically independent, and have the same variance, i.e., E{E TE} = σ 2I, then the smallest eigenvalue $$\lambda _{n+1}^{\,} =\sigma _{n+1}^2$$ of the (n + 1) × (n + 1) covariance matrix A HA is the square of the singular value of the error matrix E. Because the square of singular value $$\sigma _{n+1}^2$$ happens to reflect the common variance σ 2 of each column vector of the error matrix, the covariance matrix $${\mathbf {A}}_0^H{\mathbf {A}}_0^{\,}$$ of the error-free data matrix can be retrieved from $${\mathbf {A}}^H\mathbf {A}-\sigma _{n+1}^2\mathbf {I}$$ , namely $${\mathbf {A}}^T\mathbf {A} -\sigma _{n+1}^2\mathbf {I}={\mathbf {A}}_0^H{\mathbf {A}}_0^{\,}$$ . In other words, the TLS method can effectively restrain the influence of the unknown error matrix.

It should be pointed out that the main difference between the TLS method and the Tikhonov regularization method for solving the matrix equation $${\mathbf {A}}_{m\times n}^{\,}{\mathbf {x}}_n^{\,} ={\mathbf {b}}_m^{\,}$$ is: the TLS solution can contain only p = rank([A, b]) principal parameters, and exclude the redundant parameters; whereas the Tikhonov regularization method can only provide all n parameters including redundant parameters.

4.7.3 Generalized Total Least Square

The ordinary LS, the Tikhonov regularization, and the TLS method can be derived and explained by a unified theoretical framework [46].

Consider the minimization problem
$$\displaystyle \begin{aligned} \min_{\Delta \mathbf{A},\Delta\mathbf{b},\mathbf{x}} \left (\|[\Delta \mathbf{A},\Delta\mathbf{b}]\|{}_F^2 +\lambda \|\mathbf{x} \|{}_2^2\right ){} \end{aligned} $$
(4.7.28)
subject to
$$\displaystyle \begin{aligned} (\mathbf{A}+\alpha \Delta \mathbf{A})\mathbf{x}=\mathbf{b}+\beta \Delta\mathbf{b}, \end{aligned}$$
where α and β are, respectively, the weighting coefficients of the perturbation ΔA of the data matrix A and the perturbation Δb of the data vector b, and λ is the Tikhonov regularization parameter. The above minimization problem is called the generalized total least squares (GTLS) problem [46].
The constraint condition (A + α ΔA)x = (b + β Δb) can be represented as
../images/492994_1_En_4_Chapter/492994_1_En_4_Equab_HTML.png
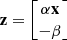If letting D = [ ΔA,  Δb] and ../images/492994_1_En_4_Chapter/492994_1_En_4_IEq175_HTML.gif, then the above equation becomes
$$\displaystyle \begin{aligned} \mathbf{Dz}=-\left [\alpha^{-1}\mathbf{A},\beta^{-1}\mathbf{b}\right ]\mathbf{z}. \end{aligned} $$
(4.7.29)
Under the assumption of z Hz = 1, then
$$\displaystyle \begin{aligned} \min \|\mathbf{D}\|{}_F^2=\min\|\mathbf{D}\mathbf{z}\|{}_2^2=\min\big\|\big [\alpha^{-1}\mathbf{A},\beta^{-1}\mathbf{b}\big ]\mathbf{z}\big\|{}_2^2, \end{aligned}$$
and thus the solution to the GTLS problem (4.7.28) can be rewritten as
$$\displaystyle \begin{aligned} \hat{\mathbf{x}}_{\mathrm{GTLS}}^{\,} =\mathrm{arg}\min_{\mathbf{z}} \left (\frac{\|[\alpha^{-1}\mathbf{A},\beta^{-1}\mathbf{b}]\mathbf{z}\|{}_2^2}{\mathbf{ z}^H\mathbf{z}} +\lambda\|\mathbf{x}\|{}_2^2\right ).{} \end{aligned} $$
(4.7.30)
Noticing that z Hz = α 2x Hx + β 2 and
../images/492994_1_En_4_Chapter/492994_1_En_4_Equad_HTML.png
the GTLS solution in (4.7.30) can be expressed as
$$\displaystyle \begin{aligned} \hat{\mathbf{x}}_{\mathrm{GTLS}}^{\,} =\mathrm{arg}\min_{\mathbf{x}}\,\left (\frac{\|\mathbf{Ax}-\mathbf{b}\|{}_2^2}{\alpha^2\|\mathbf{x}\|{}_2^2+ \beta^2}+\lambda \|\mathbf{x}\|{}_2^2\right ).{} \end{aligned} $$
(4.7.31)
The following are the comparison of the ordinary LS method, the Tikhonov regularization, and the TLS method.
  1. 1.
    Comparison of optimization problems
    • The ordinary least squares: α = 0, β = 1 and λ = 0, which gives
      $$\displaystyle \begin{aligned} \min_{\Delta \mathbf{A},\Delta\mathbf{b},\mathbf{x}} \|\Delta\mathbf{b}\|{}_2^2\quad \mbox{subject to}\quad \mathbf{A}\mathbf{ x}= \mathbf{b}+\Delta\mathbf{b}. \end{aligned} $$
      (4.7.32)
    • The Tikhonov regularization: α = 0, β = 1 and λ > 0, which gives
      $$\displaystyle \begin{aligned} \min_{\Delta \mathbf{A},\Delta\mathbf{b},\mathbf{x}} \left (\|\Delta\mathbf{b}\|{}_2^2+\lambda\|\mathbf{x}\|{}_2^2\right )\quad \mbox{subject to}\quad \mathbf{A}\mathbf{x}=\mathbf{b}+\Delta\mathbf{b}. \end{aligned} $$
      (4.7.33)
    • The total least squares: α = β = 1 and λ = 0, which yields
      $$\displaystyle \begin{aligned} \min_{\Delta \mathbf{A},\Delta\mathbf{b},\mathbf{x}} \left ( \|\Delta \mathbf{A},\Delta\mathbf{b}\|{}_2^2\right )\quad \mbox{subject to}\quad (\mathbf{A}+\Delta \mathbf{A})\mathbf{x}=\mathbf{b}+\Delta\mathbf{b}. \end{aligned} $$
      (4.7.34)
     
  2. 2.
    Comparison of solution vectors: When the weighting coefficients α, β and the Tikhonov regularization parameter λ take the suitable values, the GTLS solution (4.7.31) gives the following results:

    • $$\hat {\mathbf {x}}_{\mathrm {LS}}^{\,} =({\mathbf {A}}^H\mathbf {A})^{-1}{\mathbf {A}}^H\quad (\alpha =0,\beta =1,\lambda =0)$$ ,

    • $$\hat {\mathbf {x}}_{\mathrm {Tik}}^{\,} =({\mathbf {A}}^H\mathbf {A}+\lambda \mathbf {I})^{-1}{\mathbf {A}}^H\mathbf {b}\quad (\alpha =0,\beta =1,\lambda &gt;0)$$ ,

    • $$\hat {\mathbf {x}}_{\mathrm {TLS}}^{\,} =({\mathbf {A}}^H\mathbf {A}-\lambda \mathbf {I})^{-1}{\mathbf {A}}^H\mathbf {b}\quad (\alpha =1,\beta =1,\lambda =0)$$ .

     
  3. 3.
    Comparison of perturbation methods

    • Ordinary LS method: it uses the possible small correction term Δb = Ax −b to disturb the data vector b such that b − Δb ≈b 0.

    • Tikhonov regularization method: it adds the same perturbation term λ > 0 to every diagonal entry of the matrix A HA for avoiding the numerical instability of the LS solution (A HA)−1A Hb.

    • TLS method: by subtracting the perturbation matrix λI, the noise or disturbance in the covariance matrix of the original data matrix is restrained.

     
  4. 4.
    Comparison of application ranges

    • The LS method is applicable for the data matrix A with full column rank and the data vector b existing the iid Gaussian errors.

    • The Tikhonov regularization method is applicable for the data matrix A with deficient column rank.

    • The TLS method is applicable for the data matrix A with full column rank and both A and the data vector b existing the iid Gaussian error.

     

4.8 Solution of Under-Determined Systems

A full row rank under-determined matrix equation A m×nx n×1 = b m×1 with m < n has infinitely many solutions. In these cases, letting x = A Hy then
$$\displaystyle \begin{aligned} \mathbf{AA}^H\mathbf{y}=\mathbf{b}~\Rightarrow~ \mathbf{y}=(\mathbf{AA}^H)^{-1}\mathbf{b}~\Rightarrow~\mathbf{x}={\mathbf{A}}^H(\mathbf{AA}^H)^{-1}\mathbf{b}. \end{aligned}$$
This unique solution is known as the minimum norm solution. However, such a solution has little application in engineering. We are interested in the sparse solution x with a small number of nonzero entries.

4.8.1 ℓ 1-Norm Minimization

To seek the sparsest solution with the fewest nonzero elements, we would ask the following two questions.

  • Can it ever be unique?

  • How to find the sparsest solution?

For any positive number p > 0, the ℓ p-norm of the vector x is defined as
$$\displaystyle \begin{aligned} \|\mathbf{x}\|{}_p^{\,} =\Bigg (\sum_{i\in \mathrm{support}(\mathbf{x})}|x_i^{\,} |{}^p\Bigg )^{1/p}.{} \end{aligned} $$
(4.8.1)
Then the $$\ell _0^{\,}$$ -norm of an n × 1 vector x can be defined as
$$\displaystyle \begin{aligned} \|\mathbf{x}\|{}_0^{\,} =\lim_{p\to 0}\|\mathbf{x}\|{}_p^p =\lim_{p\to 0}\sum_{i=1}^n|x_i^{\,} |{}^p =\sum_{i=1}^n 1(x_i^{\,}\neq 0) =\#\{i|x_i^{\,} \neq 0\}, \end{aligned} $$
(4.8.2)
where $$\#\{i|x_i^{\,} \neq 0\}$$ denotes the number of all nonzero elements of x. Thus if $$\|\mathbf {x}\|{ }_0^{\,} \ll n$$ , then x is sparse.
The core problem of sparse representation is $$\ell _0^{\,}$$ -norm minimization
$$\displaystyle \begin{aligned} (P_0)\quad \min_{\mathbf{x}}\|\mathbf{x}\|{}_0^{\,} \quad \text{subject to}~ \mathbf{b}=\mathbf{Ax},{} \end{aligned} $$
(4.8.3)
where $$\mathbf {A}\in \mathbb {R}^{m\times n},\mathbf {x}\in \mathbb {R}^n,\mathbf {b}\in \mathbb {R}^m$$ .
As the observation signal is usually contaminated by noise, the equality constraint in the above optimization problem should be relaxed to the $$\ell _0^{\,}$$ -norm minimization with the inequality constraint 𝜖 ≥ 0 which allows a certain error perturbation
$$\displaystyle \begin{aligned} \min_{\mathbf{x}}\|\mathbf{x}\|{}_0^{\,}\quad \text{subject to}\quad \|\mathbf{Ax}-\mathbf{b}\|{}_2^{\,}\leq \epsilon .{} \end{aligned} $$
(4.8.4)

A key term coined and defined in [9] that is crucial for the study of uniqueness is the sparsity of the matrix A.

Definition 4.7 (Sparsity [9])

Given a matrix A, its sparsity, denoted as σ = spark(A), is defined as the smallest possible number such that there exists a subgroup of σ columns from A that are linearly dependent.

The sparsity gives a simple criterion for uniqueness of sparse solution of an under-determined system of linear equations Ax = b, as stated below.

Theorem 4.9 ([9, 17])

If a system of linear equations Ax = b has a solution x obeying ∥x∥0 < spark(A)∕2, this solution is necessarily the sparsest solution.

The index set of nonzero elements of the vector $$\mathbf {x}=[x_i^{\,} ,\cdots ,x_n^{\,} ]^T$$ is called its support, denoted by $$\mathrm {support}(\mathbf {x})=\{i|x_i^{\,}\neq 0\}$$ . The length of the support (i.e., the number of nonzero elements) is measured by $$\ell _0^{\,}$$ -norm
$$\displaystyle \begin{aligned} \|\mathbf{x}\|{}_0^{\,} =|\mathrm{support}(\mathbf{x})|.{} \end{aligned} $$
(4.8.5)
A vector $$\mathbf {x}\in \mathbb {R}^n$$ is said to be K-sparse, if $$\|\mathbf {x}\|{ }_0^{\,} \leq K$$ , where K ∈{1, ⋯ , n}.
The set of the K-sparse vectors is denoted by
$$\displaystyle \begin{aligned} \varSigma_K =\left \{\mathbf{x}\in\mathbb{R}^{n\times 1}\big |\,\|\mathbf{x}\|{}_0^{\,}\leq K\right \}. \end{aligned} $$
(4.8.6)
If $$\hat {\mathbf {x}}\in \varSigma _K$$ , then the vector $$\hat {\mathbf {x}}\in \mathbb {R}^n$$ is known as the K-sparse approximation.
Clearly, there is a close relationship between ℓ 0-norm definition formula (4.8.5) and ℓ p-norm definition formula (4.8.1): when p → 0, $$\|\mathbf {x}\|{ }_0 =\lim _{p\to 0}\|\mathbf {x}\|{ }_p^p$$ . Because ∥x∥p is the convex function if and only if p ≥ 1, the ℓ 1-norm is the objective function closest to ℓ 0-norm. Then, from the viewpoint of optimization, the ℓ 1-norm is said to be the convex relaxation of the ℓ 0-norm. Therefore, the ℓ 0-norm minimization problem (P 0) in (4.8.3) can transformed into the following convexly relaxed ℓ 1-norm minimization problem:
$$\displaystyle \begin{aligned} (P_1)\quad \min_{\mathbf{x}} \|\mathbf{x}\|{}_1 \quad \text{subject to}\quad \mathbf{b}=\mathbf{Ax}.\hskip 1.5cm \end{aligned} $$
(4.8.7)
This is a convex optimization problem, because $$\ell _1^{\,}$$ -norm $$\|\mathbf {x}\|{ }_1^{\,}$$ , as the objective function, itself is the convex function, and the equality constraint b = Ax is the affine function.
Due to observation noise, the equality constrained optimization problem (P 1) should be relaxed as the inequality constrained optimization problem below:
$$\displaystyle \begin{aligned} (P_{10})\quad \min_{\mathbf{x}}\|\mathbf{x}\|{}_1^{\,}\quad \text{subject to}\quad \|\mathbf{b}-\mathbf{Ax} \|{}_2^{\,} \leq \epsilon.\hskip 1cm{} \end{aligned} $$
(4.8.8)

The ℓ 1-norm minimization above is also called the basis pursuit (BP). This is a quadratically constrained linear programming (QCLP) problem.

If $${\mathbf {x}}_1^{\,}$$ is the solution to (P 1), and $${\mathbf {x}}_0^{\,}$$ is the solution to (P 0), then [8]
$$\displaystyle \begin{aligned} \|{\mathbf{x}}_1^{\,}\|{}_1^{\,} \leq \|{\mathbf{x}}_0^{\,}\|{}_1^{\,} , \end{aligned} $$
(4.8.9)
because $${\mathbf {x}}_0^{\,}$$ is only the feasible solution to (P 1), while $${\mathbf {x}}_1^{\,}$$ is the optimal solution to (P 1). The direct relationship between $${\mathbf {x}}_0^{\,}$$ and $${\mathbf {x}}_1^{\,}$$ is given by $$\mathbf {Ax}_1^{\,} =\mathbf {Ax}_0^{\,}$$ .
Similar to the inequality $$\ell _0^{\,}$$ -norm minimization expression (4.8.4), the inequality $$\ell _1^{\,}$$ -norm minimization expression (4.8.8) has also two variants:
  • Since x is constrained as K-sparse vector, the inequality ℓ 1-norm minimization becomes the inequality ℓ 2-norm minimization
    $$\displaystyle \begin{aligned} (P_{11})\quad \min_{\mathbf{x}}\frac 12\|\mathbf{b}-\mathbf{Ax}\|{}_2^2 \quad \text{subject to}\quad \|\mathbf{x} \|{}_1^{\,} \leq q.\hskip 0.6cm {} \end{aligned} $$
    (4.8.10)
    This is a quadratic programming (QP) problem.
  • Using the Lagrange multiplier method, the inequality constrained ℓ 1-norm minimization problem (P 11) becomes
    $$\displaystyle \begin{aligned} (P_{12})\quad \min_{\lambda ,\mathbf{x}}\frac 12\|\mathbf{b}-\mathbf{Ax}\|{}_2^2 +\lambda\|\mathbf{x}\|{}_1^{\,} .\hskip 1.5cm {} \end{aligned} $$
    (4.8.11)
    This optimization is called the basis pursuit denoising (BPDN) [7].

The optimization problems (P 10) and (P 11) are, respectively, called the error constrained ℓ 1-norm minimization and ℓ 1-penalty minimization [41]. The $$\ell _1^{\,}$$ -penalty minimization is also known as the regularized $$\ell _1^{\,}$$ linear programming or $$\ell _1^{\,}$$ -norm regularization least squares.

The Lagrange multiplier is known as the regularization parameter that controls the sparseness of the sparse solution; and the greater λ is, the more sparse the solution x is. When the regularization parameter λ is large enough, the solution x is a zero vector. With the gradual decrease of λ, the sparsity of the solution vector x gradually decreases. As λ is gradually reduced to 0, the solution vector x becomes the vector such that $$\|\mathbf {b}-\mathbf {Ax}\|{ }_2^2$$ is minimized. That is to say, λ > 0 can balance the error squares sum cost function $$\frac 12\|\mathbf {b}-\mathbf {Ax} \|{ }_2^2$$ and the ℓ 1-norm cost function $$\|\mathbf {x}\|{ }_1^{\,}$$ of the twin objectives
$$\displaystyle \begin{aligned} J(\lambda ,\mathbf{x})=\frac 12\|\mathbf{b}-\mathbf{Ax}\|{}_2^2 +\lambda \| \mathbf{x}\|{}_1^{\,} . \end{aligned} $$
(4.8.12)

4.8.2 Lasso

The solution of a system of sparse equations is closely related to regression analysis. Minimizing the least squared error may usually lead to sensitive solutions. Many regularization methods were proposed to decrease this sensitivity. Among them, Tikhonov regularization [40] and Lasso [12, 38] are two widely known and cited algorithms, as pointed out in [44].

The problem of regression analysis is one of the fundamental problems within the many fields such as statistics, supervised machine learning, optimization, and so on. In order to reduce the computational complexity of solving directly the optimization problem (P 1), consider a linear regression problem: given an observed data vector $$\mathbf {b}\in \mathbb {R}^m$$ and an observed data matrix $$\mathbf {A}\in \mathbb {R}^{m\times n}$$ , find a fitting coefficient vector $$\mathbf {x}\in \mathbb {R}^n$$ such that
$$\displaystyle \begin{aligned} \hat b_i=x_1 a_{i1}^{\,} + x_2 a_{i2}^{\,} + \cdots + x_n a_{in}^{\,} ,\quad i=1,\ldots ,m, \end{aligned} $$
(4.8.13)
or
$$\displaystyle \begin{aligned} \hat{\mathbf{b}}=\sum_{i=1}^n x_i^{\,} {\mathbf{a}}_i^{\,} =\mathbf{Ax}, \end{aligned} $$
(4.8.14)
where
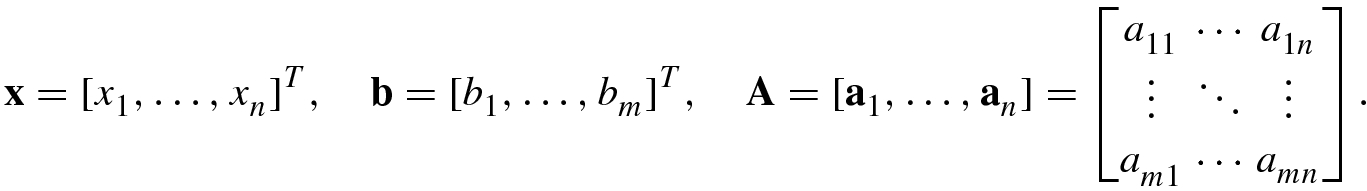
../images/492994_1_En_4_Chapter/492994_1_En_4_Equaf_HTML.png
As a preprocessing of the linear regression, it is assumed that
$$\displaystyle \begin{aligned} \sum_{i=1}^m b_i^{\,} =0,\quad \sum_{i=1}^m a_{ij}^{\,} =0,\quad \sum_{i=1}^m a_{ij}^2 =1,\quad j=1,\ldots ,n, \end{aligned} $$
(4.8.15)
and let the column vectors of the input matrix A be linearly independent. The preprocessed input matrix A is called an orthonormal input matrix, its column vector $${\mathbf {a}}_i^{\,}$$ is known as a predictor; and the vector x is simply called a coefficient vector.
Tibshirani [38] in 1996 has proposed the least absolute shrinkage and selection operator (Lasso) algorithm for solving the linear regression. The basic idea of the Lasso is: under the constraint that the $$\ell _1^{\,}$$ -norm of the prediction vector does not exceed an upper bound q, the squares sum of prediction errors is minimized, namely
$$\displaystyle \begin{aligned} \mathrm{Lasso:}\quad &amp;\min_{\mathbf{x}}\|\mathbf{b}-\mathbf{Ax}\|{}_2^2 \\ &amp;\text{subject to}\quad |\mathbf{x}\|{}_1^{\,} =\sum_{i=1}^n |x_i^{\,} |\leq q.{} \end{aligned} $$
(4.8.16)
Obviously, the Lasso model and the QP problem (4.8.10) have the exactly same form.

The bound q is a tuning parameter. When q is large enough, the constraint has no effect on x and the solution is just the usual multiple linear least squares regression of x on $$a_{i1}^{\,} , \ldots , a_{in}^{\,}$$ and $$b_i^{\,} ,i=1,\ldots ,m$$ . However, for the smaller values of q (q ≥ 0), some of the coefficients $$x_j^{\,}$$ will take zero. Choosing a suitable q will lead to a sparse coefficient vector x.

The regularized Lasso problem is given by
$$\displaystyle \begin{aligned} \text{Regularized Lasso:}\quad \min_{\mathbf{x}}\|\mathbf{b}-\mathbf{Ax}\|{}_2^2 +\lambda\|\mathbf{x}\|{}_1^{\,} .\hskip 1.2cm {} \end{aligned} $$
(4.8.17)

The Lasso problem involves both the $$\ell _1^{\,}$$ -norm constrained fitting for statistics and the data mining.

With the aid of two basic functions, the Lasso makes shrinkage and selection for linear regression.

  • Contraction function: the Lasso shrinks the range of parameters to be estimated, only a small number of selected parameters are estimated at each step.

  • Selection function: the Lasso would automatically select a very small part of variables for linear regression, yielding a spare solution.

The Lasso method achieves the better prediction accuracy by shrinkage and variable selection.

The Lasso has many generalizations, here are a few examples. In machine learning, sparse kernel regression is referred to as the generalized Lasso [36]. Multidimensional shrinkage-thresholding method is known as the group Lasso [35]. A sparse multiview feature selection method via low-rank analysis is called the MRM-Lasso (multiview rank minimization-based Lasso) [45]. Distributed Lasso solves the distributed sparse linear regression problems [29].

4.8.3 LARS

The LARS is the abbreviation of least angle regressions and is a stepwise regression method. Stepwise regression is also known as “forward stepwise regression.” Given a collection of possible predictors, X = {x 1, …, x m}, the aim of LARS is to identify the fitting vector most correlated with the response vector, i.e., the angle between the two vectors is minimized.

The LARS algorithm contains the two basic steps.
  1. 1.

    The first step selects the fitting vector having largest absolute correlation with the response vector y, say $$\mathbf { x}_{j_1}=\max _i \{|\mathrm {corr}(\mathbf {y},{\mathbf {x}}_i)|\}$$ , and performs simple linear regression of y on $${\mathbf {x}}_{j_1}$$ : $$\mathbf { y}=\beta _1{\mathbf {x}}_{j_1}+\mathbf {r}$$ , where the residual vector r denotes the residuals of the remaining variables removing $${\mathbf {x}}_{j_1}$$ from X. The residual vector r is orthogonal to $${\mathbf {x}}_{j_1}$$ . When some predictors happen to be highly correlated with x j and thus are approximately orthogonal to r, these predictors perhaps are eliminated, i.e., the residual vector r will not have information on these eliminating predictors.

     
  2. 2.

    In the second step, r is regarded as the new response. The LARS selects the fitting vector having largest absolute correlation with the new response r, say $${\mathbf {x}}_{j_2}$$ , and performs simple linear regression $$\mathbf {r}\leftarrow \mathbf {r}-\beta _2\mathbf { x}_{j_2}$$ . Repeat this selection process until no predictor has any correlation with r.

     

After k selection steps, one gets a set of predictors $${\mathbf {x}}_{j_1},\ldots ,{\mathbf {x}}_{j_k}$$ that are then used in the usual way to construct a k-parameter linear model. This selection regression is an aggressive fitting technique that can be overly greedy [12]. The stepwise regression may be said to be of under-regression due to perhaps eliminating useful predictors that happen to be correlated with current predictor.

To avoid the under-regression in forward stepwise regression, the LARS algorithm allows “stagewise regression” to be implemented using fairly large steps.

Algorithm 4.6 shows the LARS algorithm developed in [12].

Stagewise regression, called also “forward stagewise regression,” is a much more cautious version of stepwise regression, and creates a coefficient profile as follows: at each step it increments the coefficient of that variable most correlated with the current residuals by an amount ± 𝜖, with the sign determined by the sign of the correlation, as shown below [19].
  1. 1.

    Start with r = y and β 1 = β 2 = … = β p = 0.

     
  2. 2.

    Find the predictor x j most correlated with r.

     
  3. 3.

    Update β j ← β j + δ j, where $$\delta _j=\epsilon \cdot \mathrm {sign}[\mathrm {corr}(\mathbf {r},{\mathbf {x}}_j^{\,} )]$$ ;

     
  4. 4.

    Update r ←r − δ jx j, and repeat Steps 2 and 3 until no predictor has any correlation with r.

     
Brief Summary of This Chapter

  • This chapter mainly introduces singular value decomposition and several typical methods for solving the well-determined, over-determined, and under-determined matrix equations.

  • Tikhonov regularization method and ℓ 1-norm minimization have wide applications in artificial intelligence.

  • Generalized total least squares method includes the LS method, Tikhonov regularization method, and total least squares method as special examples.

Algorithm 4.6 Least angle regressions (LARS) algorithm with Lasso modification [12]LAR algorithm

../images/492994_1_En_4_Chapter/492994_1_En_4_Figf_HTML.png