© Springer Nature Singapore Pte Ltd. 2020
X.-D. ZhangA Matrix Algebra Approach to Artificial Intelligencehttps://doi.org/10.1007/978-981-15-2770-8_5

5. Eigenvalue Decomposition

Xian-Da Zhang1  
(1)
Department of Automation, Tsinghua University, Beijing, Beijing, China
 
 Deceased

This chapter is devoted to another core subject of matrix algebra: the eigenvalue decomposition (EVD) of matrices, including various generalizations of EVD such as the generalized eigenvalue decomposition, the Rayleigh quotient, and the generalized Rayleigh quotient.

5.1 Eigenvalue Problem and Characteristic Equation

The eigenvalue problem not only is a very interesting theoretical problem but also has a wide range of applications in artificial intelligence.

5.1.1 Eigenvalue Problem

If $$\mathbb {L}[\mathbf {w}]=\mathbf {w}$$ holds for any nonzero vector w, then $$\mathbb {L}$$ is called an identity transformation. More generally, if, when a linear operator acts on a vector, the output is a multiple of this vector, then the linear operator is said to have an input reproducing characteristic.

Definition 5.1 (Eigenvalue, Eigenvector)
Suppose that a nonzero vector u is the input of the linear operator $$\mathbb {L}$$ . If the output vector is the same as the input vector u up to a constant factor λ, i.e.,
$$\displaystyle \begin{aligned} \mathbb{L}[\mathbf{u}]=\lambda \mathbf{u}, \quad \mathbf{u}\neq \mathbf{0},{} \end{aligned} $$
(5.1.1)
then the vector u is known as an eigenvector of the linear operator $$\mathbb {L}$$ and the scalar λ is the corresponding eigenvalue of $$\mathbb {L}$$ .

From the above definition, it is known that if each eigenvector u is regarded as an input of a linear time-invariant system $$\mathbb {L}$$ , then the eigenvalue λ associated with eigenvector u is equivalent to the gain of the linear system $$\mathbb {L}$$ with u as the input. Only when the input of the system $$\mathbb {L}$$ is an eigenvector u, its output is the same as the input up to a constant factor. Thus an eigenvector can be viewed as description of the characteristics of the system, and hence is also called a characteristic vector. This is a physical explanation of eigenvectors in relation to linear systems.

If a linear transformation $$\mathbb {L}[\mathbf {x}]=\mathbf {Ax}$$ , then its eigenvalue problem (5.1.1) can be written as
$$\displaystyle \begin{aligned} \mathbf{Au}=\lambda \mathbf{u},\quad \mathbf{u} \neq \mathbf{0}. {} \end{aligned} $$
(5.1.2)
The scalar λ is known as an eigenvalue of the matrix A, and the vector u as an eigenvector associated with the eigenvalue λ. Equation (5.1.2) is sometimes called the eigenvalue–eigenvector equation.
As an example, we consider a linear time-invariant system h(k) with transfer function $$H(\mathrm {e}^{\mathrm {j}\omega })=\sum _{k=-\infty }^\infty h(k) \mathrm {e}^{-\mathrm {j}\omega k}$$ . When inputting a complex exponential or harmonic signal ejωn, the system output is given by
$$\displaystyle \begin{aligned}\mathbb{L}[\mathrm{e}^{\,\mathrm{j}\omega n}]=\sum_{k=-\infty}^\infty h(n-k)\mathrm{e}^{\,\mathrm{j}\omega k}=\sum_{k=-\infty}^\infty h(k)\mathrm{e}^{\,\mathrm{j}\omega (n-k)}=H(\mathrm{e}^{\,\mathrm{j}\omega})\mathrm{e}^{\,\mathrm{j}\omega n}. \end{aligned}$$
If the harmonic signal vector u(ω) = [1, ejω, …, ejω(N−1)]T is the system input, then its output is given by
../images/492994_1_En_5_Chapter/492994_1_En_5_Equb_HTML.png
That is to say, the harmonic signal vector u(ω) = [1, ejω, …, ejω(N−1)]T is an eigenvector of the linear time-invariant system, and the system transfer function H(ejω) is the eigenvalue associated with u(ω).
From Eq. (5.1.2) it is easily known that if $$\mathbf {A}\in \mathbb {C}^{n\times n}$$ is a Hermitian matrix then its eigenvalue λ must be a real number, and
$$\displaystyle \begin{aligned} \mathbf{A}=\mathbf{U}{\boldsymbol \Sigma}{\mathbf{U}}^H,{} \end{aligned} $$
(5.1.3)
where $$\mathbf {U}=[{\mathbf {u}}_1^{\,} ,\ldots ,{\mathbf {u}}_n^{\,}]^T$$ is a unitary matrix, and $${\boldsymbol \Sigma }=\mathbf {Diag}(\lambda _1^{\,} ,\ldots ,\lambda _n^{\,} )$$ . Equation (5.1.3) is called the eigenvalue decomposition (EVD) of A.

Since an eigenvalue λ and its associated eigenvector u often appear in pairs, the two-tuple (λ, u) is called an eigenpair of the matrix A. An eigenvalue may take a zero value, but an eigenvector cannot be a zero vector.

Equation (5.1.2) means that the linear transformation Au does not “change the direction” of the input vector u. Hence the linear transformation Au is a mapping “keeping the direction unchanged.” In order to determine the vector u, we can rewrite (5.1.2) as
$$\displaystyle \begin{aligned} (\mathbf{A}-\lambda \mathbf{I})\mathbf{u}=\mathbf{0}.{} \end{aligned} $$
(5.1.4)
If the above equation is assumed to hold for certain nonzero vectors u, then the only condition is that, for those vectors u, the determinant of the matrix A − λI is equal to zero:
$$\displaystyle \begin{aligned} |\mathbf{A}-\lambda \mathbf{I}|=0. {} \end{aligned} $$
(5.1.5)
Hence the eigenvalue problem solving consists of the following two steps:

  • Find all scalars λ (eigenvalues) such that the matrix |A − λI| = 0;

  • Given an eigenvalue λ, find all nonzero vectors u satisfying (A − λI)u = 0; they are the eigenvector(s) corresponding to the eigenvalue λ.

5.1.2 Characteristic Polynomial

As discussed above, the matrix (A − λI) is singular if and only if its determinant $$\det (\mathbf {A}-\lambda \mathbf {I})=0$$ , i.e.,
$$\displaystyle \begin{aligned} (\mathbf{A}-\lambda \mathbf{I})~\text{singular}\quad \Leftrightarrow\quad \det (\mathbf{A}-\lambda \mathbf{I})=0,{} \end{aligned} $$
(5.1.6)
where the matrix A − λI is called the characteristic matrix of A.
The determinant
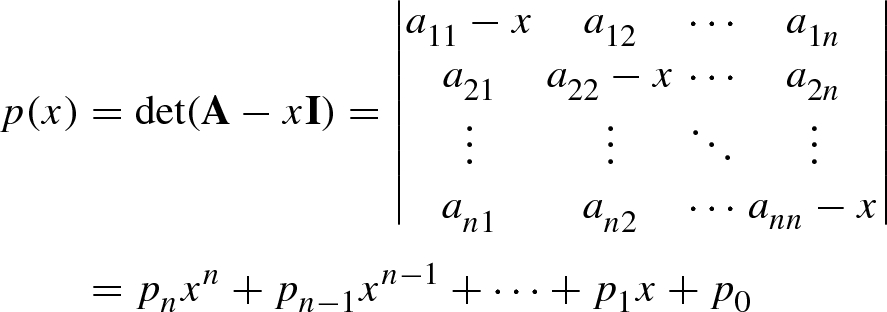
../images/492994_1_En_5_Chapter/492994_1_En_5_Equ7_HTML.png
(5.1.7)
is known as the characteristic polynomial of A, and
$$\displaystyle \begin{aligned} p(x)=\det (\mathbf{A}-x\mathbf{I})=0{} \end{aligned} $$
(5.1.8)
is said to be the characteristic equation of A.

The roots of the characteristic equation $$\det (\mathbf {A}-x\mathbf {I})=0$$ are known as the eigenvalues, characteristic values, latent values, the characteristic roots, or latent roots.

Obviously, computing the n eigenvalues $$\lambda _i^{\,}$$ of an n × n matrix A and finding the n roots of the nth-order characteristic polynomial $$p(x)=\det (\mathbf {A}-x\mathbf {I})=0$$ are two equivalent problems. An n × n matrix A generates an nth-order characteristic polynomial. Likewise, each nth-order polynomial can also be written as the characteristic polynomial of an n × n matrix.

Theorem 5.1 ([1])
Any polynomial
$$\displaystyle \begin{aligned}p(\lambda )=\lambda^n +a_1^{\,} \lambda^{n-1}+\cdots +a_{n-1}^{\,} \lambda +a_n^{\,} \end{aligned}$$
can be written as the characteristic polynomial of the n × n matrix
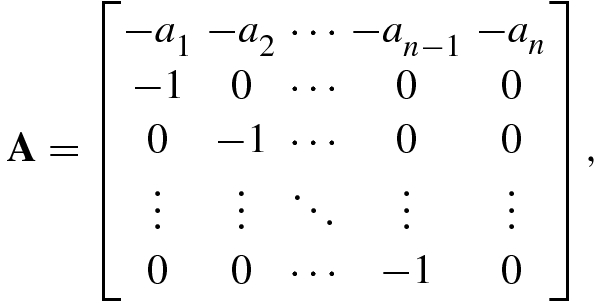
../images/492994_1_En_5_Chapter/492994_1_En_5_Equd_HTML.png

namely $$p(\lambda )=\det (\lambda \mathbf {I}-\mathbf {A})$$ .

5.2 Eigenvalues and Eigenvectors

Given an n × n matrix A, we consider the computation and properties of the eigenvalues and eigenvectors of A.

5.2.1 Eigenvalues

Even if an n × n matrix A is real, some roots of its characteristic equation may be complex, and the root multiplicity can be arbitrary or even equal to n. These roots are collectively referred to as the eigenvalues of the matrix A.

An eigenvalue λ of a matrix A is said to have algebraic multiplicity μ, if λ is a μ-multiple root of the characteristic polynomial $$\det (\mathbf {A}-x\mathbf {I})=0$$ .

If the algebraic multiplicity of an eigenvalue λ is 1, then it is called a single eigenvalue. A nonsingle eigenvalue is said to be a multiple eigenvalue.

It is well known that any nth-order polynomial p(x) can be written in the factorized form
$$\displaystyle \begin{aligned} p(x)=a(x-x_1^{\,} )(x-x_2^{\,} )\cdots (x-x_n^{\,} ). \end{aligned} $$
(5.2.1)
The n roots of the characteristic polynomial p(x), denoted $$x_1^{\,} ,x_2^{\,} ,\ldots ,x_n^{\,}$$ , are not necessarily different from each other, and also are not necessarily real for a real matrix. For example, for the Givens rotation matrix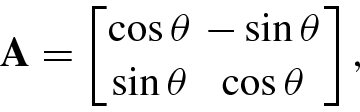
../images/492994_1_En_5_Chapter/492994_1_En_5_Eque_HTML.png
its characteristic equation is
../images/492994_1_En_5_Chapter/492994_1_En_5_Equf_HTML.png
However, if θ is not an integer multiple of π, then $$\sin ^2 \theta >0$$ . In this case, the characteristic equation cannot give a real value for λ, i.e., the two eigenvalues of the rotation matrix are complex, and the two corresponding eigenvectors are complex vectors.
The eigenvalues of an n × n matrix (not necessarily Hermitian) A have the following properties [8].
  1. 1.

    An n × n matrix A has a total of n eigenvalues, where multiple eigenvalues count according to their multiplicity.

     
  2. 2.

    If a nonsymmetric real matrix A has complex eigenvalues and/or complex eigenvectors, then they must appear in the form of a complex conjugate pair.

     
  3. 3.

    If A is a real symmetric matrix or a Hermitian matrix, then its all eigenvalues are real numbers.

     
  4. 4.
    The eigenvalues of a diagonal matrix and a triangular matrix satisfy the following:

    • if $$\mathbf {A}=\mathbf {Diag}(a_{11}^{\,} ,\ldots ,a_{nn}^{\,} )$$ , then its eigenvalues are given by $$a_{11}^{\,} , \ldots ,$$ $$a_{nn}^{\,}$$ ;

    • if A is a triangular matrix, then all its diagonal entries are eigenvalues.

     
  5. 5.
    Given an n × n matrix A:

    • if λ is an eigenvalue of A, then λ is also an eigenvalue of A T;

    • if λ is an eigenvalue of A, then λ ∗ is an eigenvalue of A H;

    • if λ is an eigenvalue of A, then λ + σ 2 is an eigenvalue of A + σ 2I;

    • if λ is an eigenvalue of A, then 1∕λ is an eigenvalue of its inverse matrix A −1.

     
  6. 6.

    All eigenvalues of an idempotent matrix A 2 = A take 0 or 1.

     
  7. 7.

    If A is an n × n real orthogonal matrix, then all its eigenvalues are located on the unit circle, i.e., |λ i(A)| = 1 for all i = 1, …, n.

     
  8. 8.
    The relationship between eigenvalues and the matrix singularity is as follows:

    • if A is singular, then it has at least one zero eigenvalue;

    • if A is nonsingular, then its all eigenvalues are nonzero.

     
  9. 9.

    The relationship between eigenvalues and trace: the sum of all eigenvalues of A is equal to its trace, namely $$\sum _{i=1}^n\lambda _i^{\,} =\mathrm {tr}(\mathbf {A})$$ .

     
  10. 10.

    A Hermitian matrix A is positive definite (semidefinite) if and only if its all eigenvalues are positive (nonnegative).

     
  11. 11.

    The relationship between eigenvalues and determinant: the product of all eigenvalues of A is equal to its determinant, namely $$\prod _{i=1}^n\lambda _i^{\,} = \det (\mathbf {A})=|\mathbf {A}|$$ .

     
  12. 12.
    The Cayley–Hamilton theorem: if $$\lambda _1^{\,} ,\lambda _2^{\,} ,\ldots ,\lambda _n^{\,}$$ are the eigenvalues of an n × n matrix A, then
    $$\displaystyle \begin{aligned} \prod_{i=1}^n (\mathbf{A}-\lambda_i^{\,} \mathbf{I})=0. \end{aligned}$$
     
  13. 13.

    If the n × n matrix B is nonsingular, then λ(B −1AB) = λ(A). If B is unitary, then λ(B HAB) = λ(A).

     
  14. 14.

    The matrix products A m×nB n×m and B n×mA m×n have the same nonzero eigenvalues.

     
  15. 15.
    If an eigenvalue of a matrix A is λ, then the corresponding eigenvalue of the matrix polynomial $$f(\mathbf {A})={\mathbf {A}}^n +c_1^{\,} {\mathbf {A}}^{n-1}+\cdots +c_{n-1}^{\,} \mathbf {A}+c_n^{\,}\mathbf {I}$$ is given by
    $$\displaystyle \begin{aligned} f(\lambda )=\lambda^n +c_1^{\,} \lambda^{n-1}+\cdots +c_{n-1}^{\,} \lambda +c_n^{\,} . \end{aligned} $$
    (5.2.2)
     
  16. 16.

    If λ is an eigenvalue of a matrix A, then eλ is an eigenvalue of the matrix exponential function eA.

     

5.2.2 Eigenvectors

If a matrix $${\mathbf {A}}_{n\times n}^{\,}$$ is a complex matrix, and λ is one of its eigenvalues, then the vector v satisfying
$$\displaystyle \begin{aligned} (\mathbf{A}-\lambda\mathbf{I})\mathbf{v} =\mathbf{0}\quad \text{or}\quad \mathbf{Av}=\lambda\mathbf{v}{} \end{aligned} $$
(5.2.3)
is called the right eigenvector of the matrix A associated with the eigenvalue λ, while the vector u satisfying
$$\displaystyle \begin{aligned} {\mathbf{u}}^H(\mathbf{A}-\lambda \mathbf{I})={\mathbf{0}}^T\quad \text{or}\quad {\mathbf{u}}^H\mathbf{A}=\lambda{\mathbf{u}}^H \end{aligned} $$
(5.2.4)
is known as the left eigenvector of A associated with the eigenvalue λ.

If a matrix A is Hermitian, then its all eigenvalues are real, and hence from Eq. (5.2.3) it is immediately known that ((A − λI)v)T = v T(A − λI) = 0 T, yielding v = u; namely, the right and left eigenvectors of any Hermitian matrix are the same.

It is useful to compare the similarities and differences between the SVD and the EVD of a matrix.

  • The SVD is available for any m × n (where m ≥ n or m < n) matrix, while the EVD is available only for square matrices.

  • For an n × n non-Hermitian matrix A, its kth singular value is defined as the spectral norm of the error matrix E k making the rank of the original matrix A decreased by 1:
    $$\displaystyle \begin{aligned} \sigma_k^{\,} =\min_{\mathbf{E}\in\mathbb{C}^{m\times n}}\left \{ \|\mathbf{E}\|{}_{\mathrm{spec}}^{\,}:\, \mathrm{rank}(\mathbf{A}+ \mathbf{E})\leq k-1 \right \},\quad k=1,\ldots ,\min\{m,n \}, \end{aligned} $$
    (5.2.5)
    while its eigenvalues are defined as the roots of the characteristic polynomial $$\det (\mathbf {A}-\lambda \mathbf {I})=0$$ . There is no inherent relationship between the singular values and the eigenvalues of the same square matrix, but each nonzero singular value of an m × n matrix A is the positive square root of some nonzero eigenvalue of the n × n Hermitian matrix A HA or the m × m Hermitian matrix AA H.

  • The left singular vector $${\mathbf {u}}_i^{\,}$$ and the right singular vector $${\mathbf {v}}_i^{\,}$$ of an m × n matrix A associated with the singular value $$\sigma _i^{\,}$$ are defined as the two vectors satisfying $${\mathbf {u}}_i^H\mathbf {Av}_i^{\,} =\sigma _i^{\,}$$ , while the left and right eigenvectors are defined by $${\mathbf {u}}^H \mathbf {A}=\lambda _i^{\,}{\mathbf {u}}^H$$ and $$\mathbf {Av}_i^{\,} =\lambda _i^{\,}{\mathbf {v}}_i^{\,}$$ , respectively. Hence, for the same n × n non-Hermitian matrix A, there is no inherent relationship between its (left and right) singular vectors and its (left and right) eigenvectors. However, the left singular vector $${\mathbf {u}}_i^{\,}$$ and right singular vector $${\mathbf {v}}_i^{\,}$$ of a matrix $$\mathbf {A}\in \mathbb {C}^{m\times n}$$ are, respectively, the eigenvectors of the m × m Hermitian matrix AA H and of the n × n matrix A HA.

From Eq. (5.1.2) it is easily seen that after multiplying an eigenvector u of a matrix A by any nonzero scalar μ, then μu is still an eigenvector of A. In general it is assumed that eigenvectors have unit norm, i.e., $$\|\mathbf {u}\|{ }_2^{\,} =1$$ .

Using eigenvectors we can introduce the condition number of any single eigenvalue.

Definition 5.2 (Condition Number of Eigenvalue [17, p. 93])
The condition number of a single eigenvalue λ of any matrix A is defined as
$$\displaystyle \begin{aligned} \mathrm{cond}(\lambda )=\frac 1{\cos \theta (\mathbf{u},\mathbf{v})}, \end{aligned} $$
(5.2.6)
where θ(u, v) represents the acute angle between the left and right eigenvectors associated with the eigenvalue λ.
Definition 5.3 (Matrix Spectrum)
The set of all eigenvalues $$\lambda \in \mathbb {C}$$ of a matrix $$\mathbf {A}\in \mathbb {C}^{n\times n}$$ is called the spectrum of the matrix A, denoted λ(A). The spectral radius of a matrix A, denoted ρ(A), is a nonnegative real number and is defined as
$$\displaystyle \begin{aligned} \rho (\mathbf{A})=\max |\lambda |:\lambda \in \lambda (\mathbf{A}). \end{aligned} $$
(5.2.7)
Definition 5.4 (Inertia)
The inertia of a symmetric matrix $$\mathbf {A} \in \mathbb {R}^{n\times n}$$ , denoted In(A), is defined as the triplet
$$\displaystyle \begin{aligned}\mathrm{In}(\mathbf{A})=(i_+ (\mathbf{A}),i_-(\mathbf{A}),i_0^{\,} (\mathbf{A})), \end{aligned}$$
where i +(A), i −(A) and $$i_0^{\,} (\mathbf {A})$$ are, respectively, the numbers of the positive, negative, and zero eigenvalues of A (each multiple eigenvalue is counted according to its multiplicity). Moreover, the quality i +(A) − i −(A) is known as the signature of A.

5.3 Generalized Eigenvalue Decomposition (GEVD)

The EVD of an n × n single matrix can be extended to the EVD of a matrix pair or pencil consisting of two matrices. The EVD of a matrix pencil is called the generalized eigenvalue decomposition (GEVD). As a matter of fact, the EVD is a special example of the GEVD.

5.3.1 Generalized Eigenvalue Decomposition

The basis of the EVD is the eigensystem expressed by the linear transformation $$\mathbb {L}[\mathbf {u}]=\lambda \mathbf {u}$$ : taking the linear transformation $$\mathbb {L}[\mathbf {u}]=\mathbf {Au}$$ , one gets the EVD Au = λu.

Now consider the generalization of the eigensystem composed of two linear systems $$\mathbb {L}_a$$ and $$\mathbb {L}_b$$ both of whose inputs are the vector u, but the output $$\mathbb {L}_a [\mathbf {u}]$$ of the first system $$\mathbb {L}_a$$ is some constant times λ the output $$\mathbb {L}_b^{\,} [\mathbf {u}]$$ of the second system $$\mathbb {L}_b^{\,}$$ . Hence the eigensystem is generalized as [11]
$$\displaystyle \begin{aligned} \mathbb{L}_a [\mathbf{u}]=\lambda\mathbb{L}_b^{\,} [\mathbf{u}]\quad (\mathbf{u}\neq \mathbf{0}); \end{aligned} $$
(5.3.1)
this is called a generalized eigensystem, denoted $$(\mathbb {L}_a ,\mathbb {L}_b )$$ . The constant λ and the nonzero vector u are known as the generalized eigenvalue and the generalized eigenvector of generalized eigensystem $$(\mathbb {L}_a ,\mathbb {L}_b )$$ , respectively.
In particular, if two linear transformations are, respectively, $$\mathbb {L}_a [\mathbf {u}]=\mathbf {Au}$$ and $$\mathbb {L}_b[\mathbf {u}]=\mathbf {Bu}$$ , then the generalized eigensystem becomes the generalized eigenvalue decomposition (GEVD):
$$\displaystyle \begin{aligned} \mathbf{Au}=\lambda\mathbf{Bu}.{} \end{aligned} $$
(5.3.2)
The two n × n matrices A and B compose a matrix pencil (or matrix pair), denoted (A, B). The constant λ and the nonzero vector u are, respectively, referred to as the generalized eigenvalue and the generalized eigenvector of the matrix pencil (A, B).

A generalized eigenvalue and its corresponding generalized eigenvector are collectively called a generalized eigenpair, denoted (λ, u). Equation (5.3.2) shows that the ordinary eigenvalue problem is a special example of the generalized eigenvalue problem when the matrix pencil is (A, I).

Although the generalized eigenvalue and the generalized eigenvector always  appear in pairs, the generalized eigenvalue can be found independently. To do this, we rewrite the generalized characteristic equation (5.3.2) as (A − λB)u = 0. In  order to ensure the existence of a nonzero solution u, the matrix A − λB cannot be nonsingular, i.e., the determinant must be equal to zero:
$$\displaystyle \begin{aligned} (\mathbf{A}-\lambda \mathbf{B})~\text{singular}\quad \Leftrightarrow\quad \det (\mathbf{A}-\lambda \mathbf{B})=0.{} \end{aligned} $$
(5.3.3)
The polynomial $$\det (\mathbf {A}-\lambda \mathbf {B})$$ is called the generalized characteristic polynomial of the matrix pencil (A, B), and $$\det (\mathbf {A}-\lambda \mathbf {B})=0$$ is known as the generalized characteristic equation of the matrix pencil (A, B). Hence, the matrix pencil (A, B) is often expressed as A − λB.

The generalized eigenvalues of the matrix pencil (A, B) are all solutions z of the generalized characteristic equation $$\det (\mathbf {A}-z\mathbf {B})=0$$ , including the generalized eigenvalues equal to zero. If the matrix B = I, then the generalized characteristic polynomial reduces to the characteristic polynomial $$\det (\mathbf {A}-\lambda \mathbf {I})=0$$ of the matrix A. In other words, the generalized characteristic polynomial is a generalization of the characteristic polynomial, whereas the characteristic polynomial is a special example of the generalized characteristic polynomial of the matrix pencil (A, B) when B = I.

The generalized eigenvalues λ(A, B) are defined as
$$\displaystyle \begin{aligned} \lambda (\mathbf{A},\mathbf{B})=\big\{ z\in \mathbb{C}\big |\det (\mathbf{A}-z \mathbf{B})=0\big\} . \end{aligned} $$
(5.3.4)
Theorem 5.2 ([9])

The pair $$\lambda \in \mathbb {C}$$ and $$\mathbf {u}\in \mathbb {C}^n$$ are, respectively, the generalized eigenvalue and the generalized eigenvector of the n × n matrix pencil (A, B) if and only if |A − λB| = 0 and u ∈Null(A − λB) with u ≠ 0.

The following are the properties of the GEVD Au = λBu [10, pp. 176–177].
  1. 1.
    If A and B are exchanged, then every generalized eigenvalue will become its reciprocal, but the generalized eigenvector is unchanged, namely
    $$\displaystyle \begin{aligned} \mathbf{Au}=\lambda\mathbf{Bu}\quad \Rightarrow \quad \mathbf{Bu}=\frac 1{\lambda}\mathbf{Au}. \end{aligned}$$
     
  2. 2.
    If B is nonsingular, then the GEVD becomes the standard EVD of B −1A:
    $$\displaystyle \begin{aligned} \mathbf{Au}=\lambda\mathbf{Bu}\quad \Rightarrow \quad ({\mathbf{B}}^{-1}\mathbf{A})\mathbf{u} =\lambda\mathbf{u}. \end{aligned}$$
     
  3. 3.

    If A and B are real positive definite matrices, then the generalized eigenvalues must be positive.

     
  4. 4.

    If A is singular then λ = 0 must be a generalized eigenvalue.

     
  5. 5.
    If both A and B are positive definite Hermitian matrices then the generalized eigenvalues must be real, and
    $$\displaystyle \begin{aligned} {\mathbf{u}}_i^H\mathbf{Au}_j^{\,} ={\mathbf{u}}_i^H\mathbf{Bu}_j^{\,} =0,\quad i\neq j. \end{aligned}$$
     
Strictly speaking, the generalized eigenvector u described above is called the right generalized eigenvector of the matrix pencil (A, B). The left generalized eigenvector corresponding to the generalized eigenvalue λ is defined as the column vector v such that
$$\displaystyle \begin{aligned} {\mathbf{v}}^H\mathbf{A} =\lambda{\mathbf{v}}^H\mathbf{B}.{} \end{aligned} $$
(5.3.5)
Let both X and Y be nonsingular matrices; then from (5.3.2) and (5.3.5) one has
$$\displaystyle \begin{aligned} \mathbf{XAu}=\lambda\mathbf{XBu},\quad \ {\mathbf{v}}^H\mathbf{AY}= \lambda {\mathbf{v}}^H\mathbf{BY}. \end{aligned} $$
(5.3.6)
This shows that premultiplying the matrix pencil (A, B) by a nonsingular matrix X does not change the right generalized eigenvector u of the matrix pencil (A, B), while postmultiplying (A, B) by any nonsingular matrix Y does not change the left generalized eigenvector v.

Algorithm 5.1 uses a contraction mapping to compute the generalized eigenpairs (λ, u) of a given n × n real symmetric matrix pencil (A, B).

Algorithm 5.1 Lanczos algorithm for GEVD [17, p. 298]
../images/492994_1_En_5_Chapter/492994_1_En_5_Figa_HTML.png

Algorithm 5.2 is a tangent algorithm for computing the GEVD of a symmetric positive definite matrix pencil.

Algorithm 5.2 Tangent algorithm for computing the GEVD [4]
../images/492994_1_En_5_Chapter/492994_1_En_5_Figb_HTML.png

When the matrix B is singular, Algorithms 5.1 and 5.2 will be unstable. The GEVD algorithm for the matrix pencil (A, B) with singular matrix B was proposed by Nour-Omid et al. [12], this is shown in Algorithm 5.3. The main idea of this algorithm is to introduce a shift factor σ such that A − σB is nonsingular.

Algorithm 5.3 GEVD algorithm for singular matrix B [12, 17]
../images/492994_1_En_5_Chapter/492994_1_En_5_Figc_HTML.png
Definition 5.5 (Equivalent Matrix Pencils)

Two matrix pencils with the same generalized eigenvalues are known as equivalent matrix pencils.

From the definition of the generalized eigenvalue $$\det (\mathbf {A}-\lambda \mathbf {B})=0$$ and the properties of a determinant it is easy to see that
$$\displaystyle \begin{aligned}\det (\mathbf{XAY}-\lambda\mathbf{XBY})=0\quad \Leftrightarrow\quad \det (\mathbf{A}-\lambda\mathbf{B})=0. \end{aligned}$$
Therefore, premultiplying and/or postmultiplying one or more nonsingular matrices, the generalized eigenvalues of the matrix pencil are unchanged. This result can be described as the following proposition.
Proposition 5.1

If X and Y are two nonsingular matrices, then the matrix pencils (XAY, XBY) and (A, B) are equivalent.

The GEVD can be equivalently written as αAu = βBu as well. In this case, the generalized eigenvalue is defined as λ = β∕α.

5.3.2 Total Least Squares Method for GEVD

As shown by Roy and Kailath [16], use of a least squares estimator can lead to some potential numerical difficulties in solving the generalized eigenvalue problem. To overcome this difficulty, a higher-dimensional ill-conditioned LS problem needs to be transformed into a lower-dimensional well-conditioned LS problem.

Without changing its nonzero generalized eigenvalues, a higher-dimensional matrix pencil can be transformed into a lower-dimensional matrix pencil by using a truncated SVD.

Consider the GEVD of the matrix pencil (A, B). Let the SVD of A be given by
../images/492994_1_En_5_Chapter/492994_1_En_5_Equ22_HTML.png
(5.3.7)
where $${\boldsymbol \Sigma }_1^{\,}$$ is composed of p principal singular values. Under the condition that the generalized eigenvalues remain unchanged, we can premultiply the matrix pencil A − γB by $${\mathbf {U}}_1^H$$ and postmultiply it by V 1 to get [18]:
$$\displaystyle \begin{aligned} {\mathbf{U}}_1^H(\mathbf{A} -\gamma \mathbf{B}){\mathbf{V}}_1 ={\boldsymbol \Sigma}_1^{\,} -\gamma {\mathbf{U}}_1^H\mathbf{B}{\mathbf{V}}_1^{\,} .{} \end{aligned} $$
(5.3.8)
Hence the original n × n matrix pencil (A, B) becomes a p × p matrix pencil $$({\boldsymbol \Sigma }_1, {\mathbf {U}}_1^H\mathbf {B}{\mathbf {V}}_1^{\,} )$$ . The GEVD of the lower-dimensional matrix pencil $$({\boldsymbol \Sigma }_1,{\mathbf {U}}_1^H\mathbf {B} {\mathbf {V}}_1^{\,} )$$ is called the total least squares (TLS) method for the GEVD of the higher-dimensional matrix pencil (A, B), which was developed in [18].

5.4 Rayleigh Quotient and Generalized Rayleigh Quotient

In physics and artificial intelligence, one often meets the maximum or minimum of the quotient of the quadratic function of a Hermitian matrix. This quotient has two forms: the Rayleigh quotient (also called the Rayleigh–Ritz ratio) of a Hermitian matrix and the generalized Rayleigh quotient (or generalized Rayleigh–Ritz ratio) of two Hermitian matrices.

5.4.1 Rayleigh Quotient

In his study of the small oscillations of a vibrational system, in order to find the appropriate generalized coordinates, Rayleigh [15] in the 1930s proposed a special form of quotient, later called the Rayleigh quotient.

Definition 5.6 (Rayleigh Quotient)
The Rayleigh quotient or Rayleigh–Ritz ratio R(x) of a Hermitian matrix $$\mathbf {A}\in \mathbb {C}^{n\times n}$$ is a scalar and is defined as
$$\displaystyle \begin{aligned} R(\mathbf{x})=R(\mathbf{x},\mathbf{A})=\frac {{\mathbf{x}}^H\mathbf{Ax}}{{\mathbf{x}}^H\mathbf{x}},{} \end{aligned} $$
(5.4.1)
where x is a vector to be selected such that the Rayleigh quotient is maximized or minimized.
The Rayleigh quotient has the following important properties [2, 13, 14].
  1. 1.

    Homogeneity: If α and β are scalars, then R(αx, βA) = βR(x, A).

     
  2. 2.

    Shift invariance: R(x, A − αI) = R(x, A) − α.

     
  3. 3.

    Orthogonality: x ⊥(A − R(x)I)x.

     
  4. 4.

    Boundedness: When the vector x lies in the range of all nonzero vectors, the Rayleigh quotient R(x) falls in a complex plane region (called the range of A). This region is closed, bounded, and convex. If A is a Hermitian matrix such that A = A H, then this region is a closed interval $$[\lambda _1^{\,} ,\lambda _n^{\,} ]$$ .

     
  5. 5.

    Minimum residual: For all vectors x ≠ 0 and all scalars μ, we have ∥(A − R(x)I)x∥≤∥(A − μI)x∥.

     
Theorem 5.3 (Rayleigh–Ritz Theorem)
Let $$\mathbf {A}\in \mathbb {C}^{n\times n}$$ be a Hermitian matrix whose eigenvalues are arranged in increasing order:
$$\displaystyle \begin{aligned} \lambda_{\mathrm{min}}^{\,}=\lambda_1^{\,} \leq \lambda_2^{\,}\leq \cdots \leq \lambda_{n-1}^{\,} \leq \lambda_n^{\,} =\lambda_{\mathrm{max}}^{\,}; \end{aligned} $$
(5.4.2)
then
$$\displaystyle \begin{aligned} \max_{\mathbf{x}\neq \mathbf{0}}\frac{{\mathbf{x}}^H \mathbf{Ax}}{{\mathbf{x}}^H\mathbf{x}}&amp;=\max_{{\mathbf{x}}^H\mathbf{x}=1}\frac {{\mathbf{x}}^H \mathbf{Ax}}{{\mathbf{x}}^H\mathbf{x}}=\lambda_{\max}^{\,} ,\quad \mathit{\text{if}}\ \mathbf{Ax}=\lambda_{\max}^{\,} \mathbf{x}, \end{aligned} $$
(5.4.3)
$$\displaystyle \begin{aligned} \min_{\mathbf{x}\neq \mathbf{0}}\frac {{\mathbf{x}}^H\mathbf{Ax}}{{\mathbf{x}}^H\mathbf{x}}&amp;=\min_{{\mathbf{x}}^H\mathbf{x}=1}\frac {{\mathbf{x}}^H \mathbf{Ax}}{{\mathbf{x}}^H\mathbf{x}}=\lambda_{\min}^{\,} ,\quad \mathit{\text{if}}\ \mathbf{Ax}=\lambda_{\min}^{\,}\mathbf{x}. \end{aligned} $$
(5.4.4)

More generally, the eigenvectors and eigenvalues of A correspond, respectively, to the critical points and the critical values of the Rayleigh quotient R(x).

This theorem has various proofs, see, e.g., [6, 7] or [3].

As a matter of fact, from the eigenvalue decomposition Ax = λx we have
$$\displaystyle \begin{aligned} \mathbf{Ax}=\lambda\mathbf{x}\quad \Leftrightarrow\quad {\mathbf{x}}^H\mathbf{Ax}=\lambda{\mathbf{x}}^H\mathbf{x}\quad \Leftrightarrow\quad \frac{{\mathbf{x}}^H\mathbf{Ax}}{{\mathbf{x}}^H\mathbf{x}}=\lambda . \end{aligned} $$
(5.4.5)
That is to say, a Hermitian matrix $$\mathbf {A}\in \mathbb {C}^{n\times n}$$ has n Rayleigh quotients that are equal to n eigenvalues of A, namely R i(x, A) = λ i(A), i = 1, …, n.

5.4.2 Generalized Rayleigh Quotient

Definition 5.7 (Generalized Rayleigh Quotient)
Let A and B be two n × n Hermitian matrices, and let B be positive definite. The generalized Rayleigh quotient or generalized Rayleigh–Ritz ratio R(x) of the matrix pencil (A, B) is a scalar, and is defined as
$$\displaystyle \begin{aligned} R(\mathbf{x})=\frac {{\mathbf{x}}^H\mathbf{Ax}}{{\mathbf{x}}^H\mathbf{Bx}},{} \end{aligned} $$
(5.4.6)
where x is a vector to be selected such that the generalized Rayleigh quotient is maximized or minimized.
In order to find the generalized Rayleigh quotient, we define a new vector $$\tilde {\mathbf {x}}={\mathbf {B}}^{1/2}\mathbf {x}$$ , where B 1∕2 denotes the square root of the positive definite matrix B. Substitute $$\mathbf {x}= {\mathbf {B}}^{-1/2} \tilde {\mathbf {x}}$$ into the definition formula of the generalized Rayleigh quotient (5.4.6); then we have
$$\displaystyle \begin{aligned} R(\tilde{\mathbf{x}})=\frac {\tilde{\mathbf{x}}^H\left ({\mathbf{B}}^{-1/2}\right )^H\mathbf{A}\left ({\mathbf{B}}^{-1/2}\right ) \tilde {\mathbf{x}}} {\tilde{\mathbf{x}}^H\tilde{\mathbf{x}}}.{} \end{aligned} $$
(5.4.7)
This implies that the generalized Rayleigh quotient of the matrix pencil (A, B) is equivalent to the Rayleigh quotient of the matrix product C = (B −1∕2)HA(B −1∕2). By the Rayleigh–Ritz theorem, it is known that, when the vector $$\tilde {\mathbf {x}}$$ is selected as the eigenvector corresponding to the minimum eigenvalue $$\lambda _{\min }$$ of C, the generalized Rayleigh quotient takes a minimum value $$\lambda _{\min }$$ , while when the vector $$\tilde {\mathbf {x}}$$ is selected as the eigenvector corresponding to the maximum eigenvalue $$\lambda _{\max }$$ of C, the generalized Rayleigh quotient takes the maximum value $$\lambda _{\max }$$ .
Consider the EVD of the matrix product $$\big ({\mathbf {B}}^{-1/2}\big )^H\mathbf {A}\big ({\mathbf {B}}^{-1/2}\big )\tilde {\mathbf {x}}=\lambda \tilde {\mathbf {x}}$$ . If $$\mathbf {B}=\sum _{i=1}^n \beta _i^{\,} {\mathbf {v}}_i^{\,} {\mathbf {v}}_i^H$$ is the EVD of the matrix B, then
$$\displaystyle \begin{aligned}\quad {\mathbf{B}}^{1/2}=\sum_{i=1}^n\sqrt{\beta_i^{\,}}{\mathbf{v}}_i^{\,} {\mathbf{v}}_i^H\quad \text{and}\quad {\mathbf{B}}^{-1/2}=\sum_{i=1}^n \frac 1{\sqrt{\beta_i^{\,}}} {\mathbf{v}}_i^{\,}{\mathbf{v}}_i^H.. \end{aligned}$$
This shows that B −1∕2 is also a Hermitian matrix, so that (B −1∕2)H = B −1∕2.

Premultiplying $$\big ({\mathbf {B}}^{-1/2}\big )^H\mathbf {A}\big ({\mathbf {B}}^{-1/2}\big )\tilde {\mathbf {x}}=\lambda \tilde {\mathbf {x}}$$ by B −1∕2 and substituting (B −1∕2)H = B −1∕2, it follows that $${\mathbf {B}}^{-1}\mathbf {AB}^{-1/2}\tilde {\mathbf {x}}=\lambda {\mathbf {B}}^{-1/2}\tilde {\mathbf { x}}$$ or B −1Ax = λx. Hence, the EVD of the matrix product (B −1∕2)HA(B −1∕2) is equivalent to the EVD of B −1A.

Because the EVD of B −1A is the GEVD of the matrix pencil (A, B), the above analysis can be summarized as follows: the conditions for the maximum and the minimum of the generalized Rayleigh quotient are:
$$\displaystyle \begin{aligned} R(\mathbf{x})&amp;=\frac{{\mathbf{x}}^H\mathbf{Ax}}{{\mathbf{x}}^H\mathbf{Bx}}=\lambda_{\max}^{\,} ,\quad \text{if we choose}~\mathbf{Ax}= \lambda_{\max}^{\,}\mathbf{Bx}, \end{aligned} $$
(5.4.8)
$$\displaystyle \begin{aligned} R(\mathbf{x})&amp;=\frac{{\mathbf{x}}^H\mathbf{Ax}}{{\mathbf{x}}^H\mathbf{Bx}}=\lambda_{\min}^{\,} ,\quad \, \text{if we choose}~\mathbf{Ax} =\lambda_{\min}^{\,}\mathbf{Bx}. \end{aligned} $$
(5.4.9)
That is to say, in order to maximize the generalized Rayleigh quotient, the vector x must be taken as the generalized eigenvector corresponding to the maximum generalized eigenvalue of the matrix pencil (A, B). In contrast, for the generalized Rayleigh quotient to be minimized, the vector x should be taken as the generalized eigenvector corresponding to the minimum generalized eigenvalue of the matrix pencil (A, B).

5.4.3 Effectiveness of Class Discrimination

Pattern recognition is widely applied in recognitions of human characteristics (such as a person’s face, fingerprint, iris) and various radar targets (such as aircraft, ships). In these applications, the extraction of signal features is crucial. For example, when a target is considered as a linear system, the target parameter is a feature of the target signal.

The divergence is a measure of the distance or dissimilarity between two signals and is often used in feature discrimination and evaluation of the effectiveness of class discrimination.

Let Q denote the common dimension of the signal-feature vectors extracted by various methods. Assume that there are c classes of signals; the Fisher class separability measure, called simply the Fisher measure, between the ith and the jth classes is used to determine the ranking of feature vectors. Consider the class discrimination of c classes of signals. Let $${\mathbf {v}}_k^{(l)}$$ denote the kth sample feature vector of the lth class of signals, where l = 1, …, c and k = 1, ⋯ , l K, with l K the number of sample feature vectors in the lth signal class. Under the assumption that the prior probabilities of the random vectors $${\mathbf {v}}^{(l)}={\mathbf {v}}_k^{(l)}$$ are the same for k = 1, …, l K (i.e., equal probabilities), the Fisher measure is defined as
$$\displaystyle \begin{aligned} m^{(i,j)}=\frac {\sum_{l=i,j}\left (\mathrm{mean}_k^{\,} ({\mathbf{v}}_k^{(l)})-\mathrm{mean}_l^{\,} (\mathrm{mean}({\mathbf{v}}_k^{(l)}))\right )^2} {\sum_{l=i,j}\mathrm{var}_k^{\,} ({\mathbf{v}}_k^{(l)})}, \end{aligned} $$
(5.4.10)
where:

  • $$\mathrm {mean}_k ({\mathbf {v}}_k^{(l)})$$ is the mean (centroid) of all signal-feature vectors of the lth class;

  • $$\mathrm {var}({\mathbf {v}}_k^{(l)})$$ is the variance of all signal-feature vectors of the lth class;

  • $$\mathrm {mean}_l (\mathrm {mean}_k ({\mathbf {v}}_k^{(l)}))$$ is the total sample centroid of all classes.

As an extension of the Fisher measure, consider the projection of all Q × 1 feature vectors onto the (c − 1)th dimension of class discrimination space.

Put $$N=N_1^{\,} +\cdots +N_c^{\,}$$ , where $$N_i^{\,}$$ represents the number of feature vectors of the ith class signal extracted in the training phase. Suppose that $${\mathbf {s}}_{i,k}^{\,} =[s_{i,k}^{\,} (1),\ldots ,s_{i,k}^{\,} (Q)]^T$$ denotes the Q × 1 feature vector obtained by the kth group of observation data of the ith signal in the training phase, while $${\mathbf {m}}_i^{\,} =[m_i^{\,} (1), \ldots ,m_i^{\,} (Q)]^T$$ is the sample mean of the ith signal-feature vector, where
$$\displaystyle \begin{aligned} m_i^{\,} (q)=\frac 1{N_i^{\,}}\sum_{k=1}^{N_i^{\,}}s_{i,k}^{\,} (q),\quad i=1,\ldots ,c,~q=1,\ldots , Q. \end{aligned}$$
Similarly, let m = [m(1), …, m(Q)]T denote the ensemble mean of all the signal-feature vectors obtained from all the observation data, where
$$\displaystyle \begin{aligned} m(q)=\frac 1c\sum_{i=1}^c m_i^{\,} (q),\quad q=1,\ldots ,Q. \end{aligned}$$
Then, we have within-class scatter matrix and between-class scatter matrix [5]:
$$\displaystyle \begin{aligned} {\mathbf{S}}_w^{\,} &amp;\stackrel{\mathrm{def}}{=}\frac 1c \sum_{i=1}^c \left ( \frac 1{N_i^{\,}}\sum_{k=1}^{N_i^{\,}} ({\mathbf{s}}_{i,k}^{\,} - {\mathbf{m}}_i^{\,} )({\mathbf{s}}_{i,k}^{\,} -{\mathbf{m}}_i^{\,} )^T\right ), \end{aligned} $$
(5.4.11)
$$\displaystyle \begin{aligned} {\mathbf{S}}_b^{\,} &amp;\stackrel{\mathrm{def}}{=}\frac 1c\sum_{i=1}^c ({\mathbf{m}}_i^{\,} -\mathbf{m})({\mathbf{m}}_i^{\,} -\mathbf{m})^T. \end{aligned} $$
(5.4.12)
Define a criterion function
$$\displaystyle \begin{aligned} J(\mathbf{U})\stackrel{\mathrm{def}}{=}\frac{\mbox{ {$\displaystyle\prod_{\mathrm{diag}}^{ }$}}{\mathbf{U}}^T {\mathbf{S}}_b^{\,}\mathbf{U}}{\mbox{ {$\displaystyle\prod_{\mathrm{diag}}^{ }$}}{\mathbf{U}}^T{\mathbf{S}}_w^{\,} \mathbf{U}},{} \end{aligned} $$
(5.4.13)
where ∏ diagA denotes the product of diagonal entries of the matrix A. As it is a measure of class discrimination ability, J should be maximized. We refer to Span(U) as the class discrimination space, if
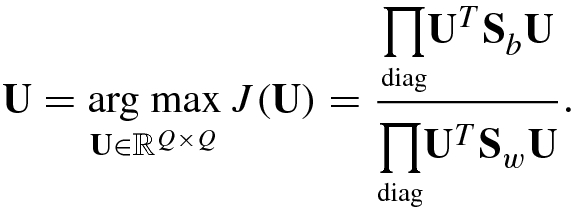
../images/492994_1_En_5_Chapter/492994_1_En_5_Equ37_HTML.png
(5.4.14)
This optimization problem can be equivalently written as
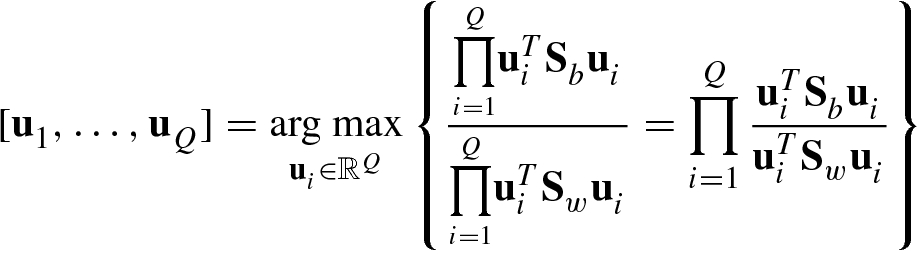
../images/492994_1_En_5_Chapter/492994_1_En_5_Equ38_HTML.png
(5.4.15)
whose solution is given by
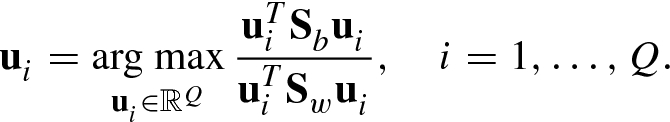
../images/492994_1_En_5_Chapter/492994_1_En_5_Equ39_HTML.png
(5.4.16)
This is just the maximization of the generalized Rayleigh quotient. The above equation has a clear physical meaning: the column vectors of the matrix U constituting the optimal class discrimination subspace which should maximize the between-class scatter and minimize the within-class scatter, namely which should maximize the generalized Rayleigh quotient.
For c classes of signals, the optimal class discrimination subspace is (c − 1)-dimensional. Therefore Eq. (5.4.16) is maximized only for c − 1 generalized Rayleigh quotients. In other words, it is necessary to solve the following generalized eigenvalue problem:
$$\displaystyle \begin{aligned} {\mathbf{S}}_b^{\,} {\mathbf{u}}_i^{\,} =\lambda_i^{\,} {\mathbf{S}}_w^{\,} {\mathbf{u}}_i^{\,} ,\quad i=1,2,\ldots ,c-1, \end{aligned} $$
(5.4.17)
for c − 1 generalized eigenvectors $${\mathbf {u}}_1^{\,} ,\ldots ,{\mathbf {u}}_{c-1}^{\,}$$ . These generalized eigenvectors constitute the Q × (c − 1) matrix
$$\displaystyle \begin{aligned} {\mathbf{U}}_{c-1}^{\,} =[{\mathbf{u}}_1^{\,} ,\ldots ,{\mathbf{u}}_{c-1}^{\,} ] \end{aligned} $$
(5.4.18)
whose columns span the optimal class discrimination subspace.
After obtaining the Q × (c − 1) matrix $${\mathbf {U}}_{c-1}^{\,}$$ , we can find its projection onto the optimal class discrimination subspace,
$$\displaystyle \begin{aligned} {\mathbf{y}}_{i,k}^{\,} ={\mathbf{U}}_{c-1}^T{\mathbf{s}}_{i,k}^{\,} ,\quad i=1,\ldots ,c,~k=1,\ldots ,N_i, \end{aligned} $$
(5.4.19)
for every signal-feature vector obtained in the training phase.

When there are only three classes of signals (c = 3), the optimal class discrimination subspace is a plane, and the projection of every feature vector onto the optimal class discrimination subspace is a point. These projections directly reflect the discrimination ability of different feature vectors in signal classification.

Brief Summary of This Chapter

This chapter focuses on the matrix algebra used widely in artificial intelligence: eigenvalue decomposition, general eigenvalue decomposition, Rayleigh quotients, generalized Rayleigh quotients, and Fisher measure.